Home A novel autonomous navigation constellation in the Earth–Moon system
Article Open Access

A novel autonomous navigation constellation in the Earth–Moon system

  • Bin Liu , Hengnian Li EMAIL logo , Xiyun Hou , Jie Yang and Zongbo Huyan
Published/Copyright: September 5, 2024
Download Article (PDF)
Open Astronomy
From the journal Open Astronomy Volume 33 Issue 1

Abstract

With more and more activities in cislunar space and deep space, a navigation system that can provide autonomous navigation service for cislunar or even deep space missions has become an urgent need. This article proposes a new type of navigation constellation which is placed on two kinds of special orbits, namely the dynamical substitutes around the triangular libration points and the distant retrograde orbits (DROs). Both types of orbits have the same characteristics of long-term stability under the full force model, so no orbit control is needed and it can operate autonomously without ground support. First, using inter-satellite range data, the autonomous orbit determination between navigation satellites on the dynamical substitutes and the DROs is investigated under the full force model. Then, taking a translunar orbit as an example, the constellation’s navigation performance based on inter-satellite range observation is evaluated. With range errors of 1, 10, and 100 m, respectively, the navigation capability of the constellation is successfully verified in the sense that the accuracy of the determined orbit reaches the level of the observation data. From the viewpoint of stable autonomous navigation, the current results are meaningful and deserve further consideration when deploying the navigation constellation in the Earth–Moon system.

Keywords: autonomous orbit determination; triangular libration points; distant retrograde orbits; navigation constellation; inter-satellite range data

1 Introduction

Compared with missions close to the Earth, the cislunar space or deep space exploration mission has the following characteristics: the probe is far away from the Earth, the communication time is long, and the measurement and control are more difficult. All of these put higher requirements on the observation means and navigation ability of the probe itself. However, for deep space probes, traditional ground observation methods, such as range measurement, are not sensitive to the position component that is perpendicular to the line-of-sight direction for the special near-line observation geometry (Guo 2007). Meanwhile, due to the remote distance, the actual angle measurement accuracy becomes too poor to be effectively utilized in the orbit determination. Furthermore, current global navigation satellite systems cannot provide effective navigation support for cislunar or deep space exploration missions (Kaplan and Hegarty 2006, Yuan et al. 2003). Besides, the increasing number of space missions also puts a heavy burden on the ground system. Therefore, it is urgent to develop a new type of satellite navigation system that not only meets the navigation requirements of cislunar or deep space exploration missions but also has strong autonomous operation capabilities.

For satellites around a central body, a well-known fact is that the rotational symmetry of the gravitational field of the central body leads to the deficient rank of the information matrix B when the satellite uses only inter-satellite range for autonomous orbit determination (Liu 2000), which leads to the inability to autonomously determine the orbit of the satellites (Tapley et al. 2004). However, in the three-body problem, due to the effects of the strong perturbation of the third body, the force environment near the libration point is non-rotationally symmetric, so it can overcome the deficient rank problem. It has been shown that the collinear libration points are unstable, and triangular libration points are stable in the linear sense (Szebehely 1967). Due to their unique position and dynamics, the collinear libration points have been widely used in space missions (Farquhar 1973, Lo and Ross 2001, Hill 2004, Sweetswer et al. 2011, Tauber et al. 2010, Hou 2008, Hou and Liu 2008, Bennett et al. 2010). In 2005, Hill and Born (2008) proposed that navigation satellites can be placed on periodic or quasiperiodic orbits near collinear libration points and can autonomously determine their own orbits using only inter-satellite range data, which is known as Liaison Navigation.

Before analyzing the navigation performance of the libration point constellation, it is necessary to study whether the constellation itself can realize the autonomous orbit determination (Hill et al. 2005a). Through theoretical analysis, Hill found that satellites placed on orbits around the libration points can perform autonomous orbit determination using only the inter-satellite range data (Hill et al. 2005b, Hill 2007). Through simulations, Parker et al. (2012) have studied the feasibility of autonomous orbit determination between the halo orbit satellite around the libration point L1 and a GEO satellite in the actual force model using the inter-satellite range data. Leonard et al. (2013) and Parker et al. (2013) studied the navigation capability of the navigation satellite located on the halo orbit around the libration point L1 in the Earth–Moon system. Du et al. (2013) studied the feasibility of using the halo orbit around L1, L2, and low moon orbit to form a satellite constellation for autonomous orbit determination using inter-satellite range data. Wang (2010) and Liu et al. (2014) studied the feasibility of autonomous orbit determination between halo orbit satellites and low lunar orbit satellites using inter-satellite range data in the absence of the ground station. Zhang (2016) and Zhang and Xu (2014) proposed a libration point navigation constellation in the circular restricted three-body model and then analyzed and verified its navigation performance. Gao et al. (2014, 2016) verified the feasibility of autonomous orbit determination using only the crosslink range measurement for a combined navigation constellation, which is formed by a global navigation constellation and a Lagrangian navigation constellation. This study has been extended to large-magnitude retrograde orbits around the Moon (Xu and Xu 2009, Liu 2016).

As mentioned in the previous paragraph, many scholars have studied the application of libration point orbits in satellite navigation. The orbits used in these studies are usually those around the collinear libration points and are generally unstable. Due to the influence of the Sun’s gravitational perturbation, the orbits near the triangular libration points of the Earth–Moon system are unstable, but the instability is generally weaker than the collinear libration points, so the orbits can be maintained through few orbit control, and navigation satellites are considered to be placed on these orbits (Hou and Liu 2010). There are a few studies about triangular libration points (Huang et al. 2022, Wang 2020). The orbits constructed in the circular restricted three-body force model are unstable in the actual force model. When the navigation satellite is placed on them, frequent orbit control is necessarily required to maintain the orbit. These operations increase the mission risk and cause the orbital accuracy of the navigation satellite to decrease. Therefore, navigation satellites placed on orbits near the triangular libration points cannot satisfactorily provide navigation services for cislunar or deep exploration missions.

Here, we propose a new type of navigation constellation that is placed on two kinds of special orbits, namely the dynamical substitutes around the triangular libration points and the distant retrograde orbits (DROs). These two orbits can be used as ideal orbits for placing navigation satellites since they have the characteristics of long-term stability under the actual force model.

The article is structured as follows. The dynamic model and coordinate system used in the article are introduced in Section 22. Then two kinds of special orbits, dynamical substitutes and DROs, are given in Section 3. The observation model is described in Section 4. The principle of orbit determination is given in Section 5. The numerical simulation of the navigation constellation is described in Section 6. Finally, some conclusions are drawn in Section 7.

2 Dynamic model and coordinate system

2.1 Dynamic model of dynamical substitutes

In the Earth-centered inertial frame, the relative geometric relationship of the Sun–Earth–Moon-Small body is shown in Figure 1 (not to scale display), where P is the small body, and m Earth, m Moon, and m Sun represent the Earth, Moon, and Sun, respectively. R, R M, and R S are the vectors from the Earth to the small body, the Moon, and the Sun. R 2 and Δ S are the vectors from the Moon to the small body and the Sun, respectively, and Δ is the vector from the Sun to the small body and satisfies R, R 2, R M ≪ R S, Δ S, Δ.

Figure 1 The geometry of the Sun–Earth–Moon–Small body.
Figure 1

The geometry of the Sun–Earth–Moon–Small body.

The equation of motion (EOM) for P is

(1) R ̈ = − μ E R R 3 − μ M R 2 R 2 3 + R M R M 3 − μ S Δ Δ 3 + R S R S 3 ,

and the EOMs for the Sun and Moon are

(2) R ̈ S = − ( μ E + μ S ) R S R S 3 − μ M Δ S Δ S 3 + R M R M 3

(3) R ̈ M = − ( μ E + μ M ) R M R M 3 + μ S Δ S Δ S 3 − R S R S 3 .

The model is used to obtain the dynamical substitutes by integrating the orbits of the Moon and the Sun with respect to the Earth under their mutual gravitation. Their initial conditions are given by the JPL ephemeris DE406, corresponding to the epoch J2000.0. We have to remark that Eqs. (1)–(3) are not actually used in this work. We list them out because the dynamical substitutes given by Hou et al. (2015a,b) are obtained by integrating these equations. In our work, only the initial point of the dynamical substitutes is used. The EOMs used for autonomous determination of the constellation itself are given in Section 2.2, and the EOMs used for determination of the user satellite are given in Section 2.3.

2.2 Dynamic model describing autonomous orbit determination of constellations

In the real Earth–Moon system, the main forces acting on the navigation satellite include the gravity of the Earth and the Moon, and the main perturbation factors include the nonspherical gravitational perturbation of the Earth and the Moon, the gravitational perturbation of third bodies such as the Sun, and major planets. Nevertheless, when the accuracy requirement is not that high, some minor perturbation factors can be ignored. For example, because the navigation satellites are far from the Earth and the Moon, the nonspherical gravitational perturbation of the Earth and the Moon in the abovementioned situation is too small, so they can be ignored.

We set M i and μ i = M i / M Earth , i = 1 ⋯ 11 , i ≠ 3 as the masses of the other major celestial bodies in the solar system except for the Earth. Only considering gravitational perturbations and neglecting the nonspherical gravity of the Earth and the Moon, as well as neglecting the solar radiation pressure and other even smaller perturbations, the EOM in the Earth-centered J2000.0 equatorial coordinate is

(4) R ̈ = − μ E R R 3 − ∑ i = 1 , i ≠ 3 11 μ i Δ i Δ i 3 + R i R i 3 ,

where R and R i are the position vectors of the small body and the third body in the Earth-centered J2000.0 equatorial coordinate, respectively, Δ i is the position vector of the small body relative to the third body, and the expression is

(5) Δ i = R − R i .

The above four EOMs (1) to (4) are all dimensionless. That is, the unit mass is the mass of the Earth, the unit distance is the radius of the Earth, and the time unit is chosen such that the gravitational constant G = 1.

2.3 Dynamic model describing autonomous navigation of constellations

The full force model described in the following is used to study the autonomous navigation of the constellations. In this section, the M i and μ i = M i / M Earth , i = 1 ⋯ 11 , i ≠ 3 have the same meaning as those mentioned in Section 2.2. The EOM of the small body in the Earth-centered J2000.0 equatorial coordinate is

(6) R ̈ = − μ E R R 3 + f third_body + f Non-spherical + f SRP ,

where f third_body, f Nonspherical, and f SRP, (solar pressure perturbation) respectively, represent the third-body perturbation in the solar system, the nonspherical gravitational perturbation of the Earth, and the perturbation of solar radiation pressure (Liu 2000).

2.4 Coordinate system

Usually, the libration point orbits are described in the synodic frame. However, in order to consider the various perturbations in the full force model more conveniently, in this article, the processes of autonomous orbit determination and navigation services to user satellites are simulated and calculated in the Earth-centered J2000.0 equatorial coordinate.

Denote r and r ̇ as the position and velocity of the probe in the J2000.0 epoch in the Earth-centered inertial frame, and express them as r 1 and r ̇ 1 in the synodic frame, then the following conversion relationships exist:

(7) r = [ C ] r 1 r ̇ = [ C ] r 1 + [ C ̇ ] r 1 + [ C ] r ̇ 1 ,

where C is converted by the following formula:

(8) [ C ] = [ e 1 , e 2 , e 3 ] ,

where the expressions for e 1, e 2, and e 3 in the formula are shown as follows, respectively:

(9) e 1 = r m ∣ r m ∣ ; e 3 = r m × r ̇ m ∣ r m × r ̇ m ∣ ; e 2 = e 3 × e 1 ,

where r m and r ̇ m represent the position vector and velocity vector of the Moon relative to the Earth.

3 Two types of special orbits

The novel navigation constellation proposed in this article is placed on two special stable orbits: dynamic substitute orbits and DROs. Their presentation is as follows.

3.1 Fundamentals of libration points

The dynamic model of a small body with negligible mass (such as a spacecraft) moving in the gravitational field of two major celestial bodies in circular orbits around each other is a circular restricted three-body problem. As shown in Figure 2, P represents a small body (such as a spacecraft), while P1 and P2 represent the two major bodies in the circular restricted three-body problem. Their masses are expressed as m 1 and m 2, respectively, and m 1 > m 2, and the parameter μ of the system can be expressed as μ = m 2/(m 1 + m 2), and O denotes the centroids of the two major celestial bodies P1 and P2.

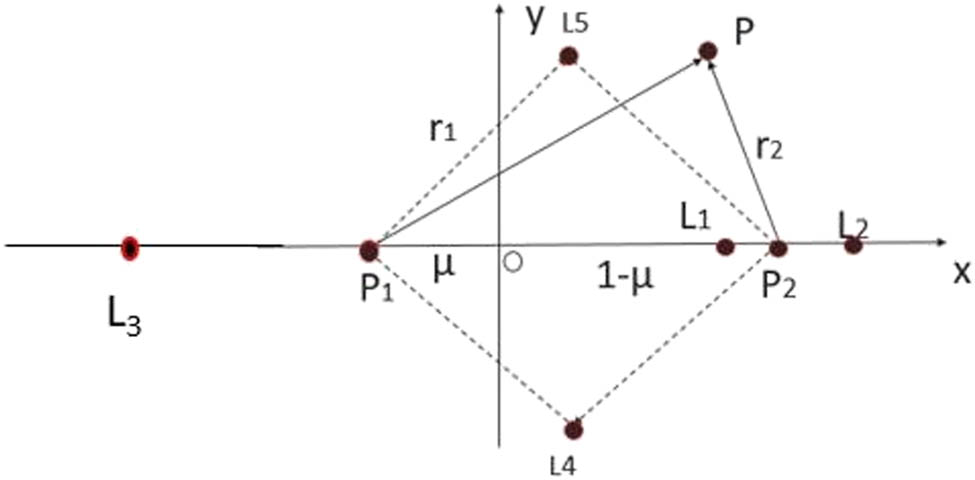
Figure 2 Five libration points in the synodic frame.
Figure 2

Five libration points in the synodic frame.

The EOM for P is

(10) X ̈ − 2 Y ̇ = ∂ Ω ∂ X , Y ̈ + 2 X = ∂ Ω ∂ Y , Z ̈ = ∂ Ω ∂ Z ,

and

(11) Ω = 1 2 ( X 2 + Y 2 ) + 1 − μ R 1 + μ R 2 + 1 2 μ ( 1 − μ ) .

The Jacobian integral C is denoted by

(12) C ( X , Y , Z , X ̇ , Y ̇ , Z ̇ ) = 2 Ω ( X , Y , Z , X ̇ , Y ̇ , Z ̇ ) − V 2 .

3.2 Dynamical substitutes around triangular libration points

The dynamical system of the probe has changed from an autonomous system in the circular restricted three-body problem to a time-varying system when the effects of the Sun and the Moon are considered. In this case, the libration points mentioned in Section 3.1 will lose the meaning of its dynamic equilibrium (Hou and Liu 2010, 2011).

In the barycentric synodic frame, ρ represents the distance between the probe and triangular libration points, and the motion equation of the probe relative to the triangular libration points can be expressed by the following formula:

(13) ρ ̈ = F 1 ( ρ , t ) + F 2 ( t ) ,

and the right part of the perturbation force (13) is divided into two parts according to whether it has a relationship with. Here, F 1(t) is the expression of the perturbation term that is related to ρ, and F 2(t) is independent of ρ. We assume that the motion of the Moon is quasiperiodic when considering the perturbation of the Sun, then F 2(t) is also quasiperiodic. In this case, the system has a frequency associated with the motion of the Moon. It has a special solution, which is a quasiperiodic orbit with the same period as the probe orbit, that is dynamical substitute (Hou et al. 2015a,b, Xin 2017).

In order to vividly illustrate the long-term stability of dynamical substitutes, under the full force model mentioned in Section 2.2, taking the epoch JD 2451695.0 as the initial epoch, the parameters of the four dynamical substitutes in the Earth-centered J2000.0 equatorial coordinate are shown in Table 1. Dynamical substitutes are simulated to calculate orbital evolution for 1,000 days, and the long-term evolution of dynamical substitutes is shown in Figure 3. L4-1 and L4-2 represent the two dynamical substitutes near the triangular libration points L4 in the Earth–Moon system, and the situation near triangular libration points L5 is shown in Figure 4.

Table 1

Initial position and speed of the four dynamical substitutes around triangular libration points in the Earth-centered J2000.0

DSs X (km) Y (km) Z (km) V X (km/s) V Y (km/s) V Z (km/s)
L4-1 135417.201136624 −411456.313724605 −168800.634246947 0.808409774 0.242289020 0.049865725
L4-2 141509.252614080 −282569.119832512 −118561.035205729 1.063457521 0.424701523 0.106325601
L5-1 −375674.318133917 −37390.071603591 6706.856240619 −0.095709233 −0.958467153 0.372003230
L5-2 −361205.715853448 214225.676784317 104978.468710688 −0.429833374 −0.746043843 0.268022339
Figure 3 Dynamical substitutes L4-1 (left) and L4-2 (right) in the Earth-centered J2000.0 equatorial coordinate.
Figure 3

Dynamical substitutes L4-1 (left) and L4-2 (right) in the Earth-centered J2000.0 equatorial coordinate.

Figure 4 Dynamical substitutes L5-1 (left) and L5-2 (right) in the Earth-centered J2000.0 equatorial coordinate.
Figure 4

Dynamical substitutes L5-1 (left) and L5-2 (right) in the Earth-centered J2000.0 equatorial coordinate.

3.3 DROs

A DRO with a moving direction in the synodic frame opposite to the primaries’ revolution direction is a special type of orbit in the circular restricted three-body problem. In the Earth–Moon system, when the amplitude of the DRO is small, the Earth’s gravitational perturbation is small because the orbit is far from the Earth, and it can be considered as a retrograde circular orbit around the Moon. However, when the amplitude becomes larger, the orbit is closer to the Earth, and the Earth’s gravitational perturbation becomes larger and larger, its orbit is “stretched” by the Earth’s perturbation, and it is no longer a circular orbit. Hénon studied the stability of retrograde small celestial bodies in the solar system by a numerical calculation method, and the results showed that the retrograde orbit is more stable than the prograde orbit. Many scholars have also studied the stability of the orbit of the DRO around the Moon and analyzed its orbit stability characteristics (Liu 2016, Xu 2008, and Hénon 1973). Under the full force model, the orbit around the Moon is more complicated. However, because the orbit is retrograde, it is still possible for the orbit to remain stable when the directional amplitude is not too large (Liu 2016).

3.4 Navigation constellation configuration

Since the four dynamic substitutes in Section 3.2 and the DROs in Section 3.3 have long-term stability, frequent orbit control is unnecessarily required to maintain the orbit, so they can be used as ideal orbits for navigation constellations. Therefore, we constructed the navigation constellation as shown in Figure 5. The navigation constellation is placed on the four stable dynamic substitutes and a DRO.

Figure 5 Navigation constellation configuration.
Figure 5

Navigation constellation configuration.

4 Observation model

In our research, through the process of autonomous orbit determination and autonomous navigation, only inter-satellite range data is used as observation data. Therefore, there are three kinds of observation data in this article: Case 1, the observation in autonomous orbit determination is the inter-satellite range data formed between the navigation satellites, with a random error in the measurement data. Case 2, the observation data during autonomous navigation is the inter-satellite range data formed between the navigation satellites and the probe, with a random error in the measurement data. Case 3, when there is an error in the orbit of the navigation satellites itself, this error is equivalent to the systematic error of the ground station, so there is a third type of observational data with a random error in the measurement data and a systematic error in the position of the navigation satellite.

4.1 Observation equation for autonomous orbit determination

The range data between the navigation satellites is shown as follows:

(14) ρ L i , j = ( x L i − x L j ) 2 + ( y L i − y L L j ) 2 + ( z L i − z L L j ) 2 + σ noise

for the navigation satellites, ρ L i , j represents the distance between the ith navigation satellite and the jth navigation satellite. ( x L i , y L i , z L i ) and ( x L j , y L j , z L j ) denote the position vector of the two navigation satellites, respectively. σ noise is the random error of the range that obeys the Gaussian random distribution.

4.2 Observation equation for autonomous navigation

The range data between the navigation satellite and the probe is shown as follows:

(15) ρ = ( x − x L ) 2 + ( y − y L ) 2 + ( z − z L ) 2 + σ noise

for the navigation satellite and the probe, ρ represents the distance between the navigation satellite and the probe. (x, y, z) denotes the position vector of the probe, and (x L , y L , z L ) denotes the position vector of the navigation satellite. The meaning of σ noise is the same as in formula (14).

4.3 Observation equation for autonomous navigation with errors in the navigation satellites

When there is an error in the orbit of the navigation satellite itself, the range data between the navigation satellite and the probe is shown as follows:

(16) r L = r L + σ noise

(17) ρ = ( x − x L ) 2 + ( y − y L ) 2 + ( z − z L ) 2 + σ noise

for the navigation satellite and the probe, σ bias represents the position error of the navigation satellite. The meaning of ρ, (x, y, z), (x L , y L , z L ), and σ noise is the same as that in formula (15).

5 Orbit determine process

5.1 Principle of orbit determination

There are many ways to determine orbit; here, we use the usual batch method of orbit determination (Liu 2000). We do not directly use x 0 in each iteration process but use x 0 / ( 1 + ε ) as the correction value of the state vector X 0. The improvement can ensure that the iteration process can still converge even when the initial state is inaccurate. ε is the root mean square error of the observational residuals, which can be used to evaluate the accuracy of the orbit determination. The calculation formula is as follows:

(18) ε = ∑ i = 1 l y i / l

5.2 The method of accuracy evaluation

By calculating the theoretical orbit value at each observation epoch t i ( i = 1 , … , l ) , and calculating the residual difference between it and the actual orbit of the orbit, the errors in the radial direction (ΔR i ), the lateral direction (ΔT), and the normal direction of the orbit surface (ΔN i ) are obtained between the two orbits. By the following formula, we can obtain the root mean square error in all directions:

(19) σ R = ∑ Δ R i 2 l , σ T = ∑ Δ T i 2 l , σ N = ∑ Δ N i 2 l ,

(20) σ = σ R 2 + σ T 2 + σ N 2 .

6 Numerical simulation

6.1 Autonomous orbit determination between the navigation satellites

The autonomous orbit determination problem of the navigation satellites is the foundation of our studies. Here, inter-satellite range data between the navigation satellites is simulated according to the measurement model mentioned in Section 4.2, taking the epoch JD 2451695.0 as the initial point, as shown in Table 1. The autonomous orbit determination of navigation satellites is studied here in the force model described in Section 2.3, and the dependence of the orbit determination accuracy on the data length is shown in Figures 6 and 7. The σ R , σ T , σ N , and σ are defined in Section 5.2.

Figure 6 The relationship between the orbit determination results of dynamical substitutes L4-1 around the triangular libration points and the length of data.
Figure 6

The relationship between the orbit determination results of dynamical substitutes L4-1 around the triangular libration points and the length of data.

Figure 7 The relationship between the orbit determination results of the DROs R1 and the length of data.
Figure 7

The relationship between the orbit determination results of the DROs R1 and the length of data.

Figures 6 and 7 show the results for the dynamical substitute L4-1 around the triangular libration point L4 and the DROs, respectively. We can see that the autonomous orbit determination of the navigation satellites using the inter-satellite range data is feasible, and the accuracy is unsatisfactory when the length of data is less than 20 days. However, it can be improved when the length of data is increased. When the data length is long enough, the same level of precision as observation data can be achieved. For a short length of data, the orbit determination accuracy in the R and the T directions of the navigation satellites is about the same but one or two magnitudes better in the N direction. This difference will disappear when the length of data is increased.

6.2 Autonomous navigation for the probe

It has been concluded in Section 6.1 that the proposed navigation constellation can achieve autonomous orbit determination using only inter-satellite range data. This section will focus on the navigation service performance of the user probe offered by this navigation constellation. With the lunar exploration mission as the background, the translunar orbit is considered. The navigation accuracy of the probe during the Earth–Moon transfer stage is of great significance to the accuracy of the subsequent capture and landing stages. Therefore, it is very meaningful to study the autonomous navigation of the Earth–Moon transfer orbit phase.

In this part, the Earth–Moon transfer orbit is the direct transfer type. The initial epoch of the example translunar orbit is JD2451695.0 and lasts 5.01309583583941 days. The initial values for the example transfer lunar orbit are shown in Table 2.

Table 2

Initial conditions of an example direct translunar orbit in the Earth’s centered J2000.0 equatorial coordinate

X (km) Y (km) Z (km) V X (km/s) V Y (km/s) V Z (km/s)
1411.940685377 −5945.764603086 −2434.007145772 10.588172443 2.636767362 0.093667291

The observation data is the inter-satellite range data between the navigation satellites and the probe. It is simulated according to the measurement model mentioned in Section 4.2. The simulation adopts the RKF7(8) integrator, and the data sampling interval is 10 min. The navigation performance of the probe with different levels of observation data accuracy is shown in the figures below.

Figures 8–10 show the navigation service performance of the proposed constellation on the translunar orbit when the inter-satellite range error is 1, 10, and 100 m, respectively. We can see that the navigation constellation can realize autonomous navigation for the lunar probe, and the navigation accuracy in the R and T directions is about the same level but one to two magnitudes better in the N direction. This difference disappears when the data length is long enough.

Figure 8 Orbit determination accuracy with a range error of 1 m.
Figure 8

Orbit determination accuracy with a range error of 1 m.

Figure 9 Orbit determination accuracy with a range error of 10 m.
Figure 9

Orbit determination accuracy with a range error of 10 m.

Figure 10 Orbit determination accuracy with a range error of 100 m.
Figure 10

Orbit determination accuracy with a range error of 100 m.

6.3 Autonomous navigation for the probe with errors in the navigation satellites

The observation data are also the inter-satellite range data between the navigation satellites and the probe, but they are simulated according to the measurement model mentioned in Section 4.3. A random distribution error of 1 m is assumed for the orbit of the navigation satellite of the navigation constellation as in formula (21), which is equivalent to the station position error of the ground station, and the range error is 1, 10, and 100 m, respectively. The navigation performance of the navigation constellation proposed in the article for the lunar probe during the transition phase is studied. The simulation calculation adopts the RKF7(8) integrator, and the data sample interval is 10 min. The navigation performance of the probe is shown as follows:

(21) σ X = σ r ⋅ cos α ⋅ cos δ , σ Y = σ r ⋅ sin α ⋅ cos δ , σ Z = σ r ⋅ sin δ .

where σ r represents the range error of the orbit of the navigation satellite of the navigation constellation, and σ X , σ Y , and σ Z denote the range error in X, Y, and Z directions of the navigation satellites, respectively, in the Earth-centered J2000.0 equatorial coordinate.

Figures 11–13, respectively, show the navigation performance of the proposed navigation constellation for the lunar probe in the transition section of the Moon when the range error is 1, 10, and 100 m. Taking Figure 11 as an example, the small graphs, respectively, show the influence of the accuracy in the R, T, and N directions and the overall navigation accuracy. Some conclusions can be drawn from the analysis:

  1. When the system error is considered in the navigation satellite, the constellation proposed in this article can still provide autonomous navigation services for the translunar user.

  2. Under the same conditions, the accuracy of the R and T directions has reached the orbit determination accuracy of within 1, 10, and 100 m, respectively. However, the orbit determination accuracy in the N direction is worse than that in the R and T directions, which is about three times the accuracy of the R and the T directions.

  3. Since the batch method is used in this section, when the arc segment is longer, the navigation accuracy is higher. The accuracy level is the same as the observation accuracy and can be reached if the time is long enough.

Figure 11 Orbit determination accuracy with a range error of 1 m.
Figure 11

Orbit determination accuracy with a range error of 1 m.

Figure 12 Orbit determination accuracy with a range error of 10 m.
Figure 12

Orbit determination accuracy with a range error of 10 m.

Figure 13 Orbit determination accuracy with a range error of 100 m.
Figure 13

Orbit determination accuracy with a range error of 100 m.

7 Conclusions

This article uses the dynamical substitutes around triangular libration points and DROs in the Earth–Moon system to form a stable autonomous navigation constellation. The ability to autonomously determine the orbits of the navigation constellation itself using only inter-satellite range data is demonstrated. Furthermore, taking the translunar orbit as an example of the user probe, under the full force model, the navigation service to the probe provided by the navigation constellation is realized by using inter-satellite range data. The simulation results show that the navigation accuracy reaches the same level as the observation accuracy. Besides, the accuracy of the N direction is worse than that of the R and the T directions, which is caused by the geometric configuration of the navigation constellation. In the future, we will further study the effects of the dynamic model on the navigation accuracy and the navigation performance of this navigation constellation.

  1. Funding information: This project is funded by the National Natural Science Foundation of China (No. 42074025) and the National Natural Science Foundation of China (U21B2050).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. BL: Conceptualization, visualisation. HL and XHL: Conceptualization, visualization, supervision. JY and ZH: Writing – review & editing. BL: Writing – original draft with contributions from all co-authors.

  3. Conflict of interest: The authors state no conflict of interest.

References

Du L, Zhang Z, Yu L, Chen SJ. 2013. SST orbit determination of Halo-LMO constellation in CRTBP. Acta Geod Cartograph Sinica. 42:184–90.Search in Google Scholar

Farquhar R. 1973. Linear control system for a satellite at the translunar libration point. Celest Mech. 7(4):458–73.10.1007/BF01227511Search in Google Scholar

Gao Y, Xu B, Zhang L. 2014. Feasibility study of autonomous orbit determination using only the crosslink range measurement for a combined navigation constellation. Chin J Aeronautics. 27(5):1199–1210.10.1016/j.cja.2014.09.005Search in Google Scholar

Gao Y, Xu B, Xiong H. 2016. A method for improving accuracy of autonomous orbit determination for navigation constellation. J Astronautics. 35(10 May).Search in Google Scholar

Guo L. 2007. Calculation of transient state parameters of spacecraft based on industrial tracking observation, PhD thesis. Shanghai Astronomical Observatory, Chinese Academy of Sciences, China.Search in Google Scholar

Hénon, M. 1973. Vertical stability of periodic orbits in the restricted problem. Celest Mech. 8:269–72.10.1007/BF01231427Search in Google Scholar

Hill KA. 2004. Autonomous Navigation in Libration Point Orbits, M.S. thesis. University of Colorado, Boulder.Search in Google Scholar

Hill KA. 2007. Autonomous navigation in libration point orbits, PhD thesis. University of Colorado, Boulder.Search in Google Scholar

Hill K, Lo MW, Born GH. 2005a. Autonomous Interplanetary Satellite Orbit Navigation (LiAISON), paper AAS 05-399, AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA; Paper AAS 05-399.Search in Google Scholar

Hill K, Lo MW, Born GH. 2005b. Linked, Autonomous Interplanetary Satellite Orbit Navigation (LiAISON) in Lunar Halo Orbits. In: AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA; Paper AAS 05-400.Search in Google Scholar

Hill K, Born GH. 2008. Autonomous orbit determination from lunar Halo orbits using crosslink range. J Space Craft Rocket. 45(3):548–53.10.2514/1.32316Search in Google Scholar

Hou XY. 2008. Dynamics and their applications of libration points, PhD thesis. Nanjing University, Nanjing, China.Search in Google Scholar

Hou XY, Liu L. 2008. The dynamics and applications of the collinear libration points in deep space exploration. J Astronautics. 29(3), 736–47.Search in Google Scholar

Hou XY, Liu L. 2010. On quasi-periodic motions around the triangular libration points of the real Earth–Moon system, Celest Mech Dynamical Astron. 108, 301–13.10.1007/s10569-010-9305-3Search in Google Scholar

Hou XY, Liu L. 2011. On quasi-periodic motions around the collinear libration points of the real Earth–Moon system, Celest Mech Dynamical Astron. 110, 71–98.10.1007/s10569-011-9340-8Search in Google Scholar

Hou XY, Scheeres DJ, Liu L. 2015a. Stable motions around triangular libration points in the real Earth–Moon system, Mon Not R Astron Soc. 454, 4172–81.10.1093/mnras/stv2216Search in Google Scholar

Hou XY, Tang JS, Liu L. 2015b. Several possible mission orbits around Earth–Moon triangular libration points. 30th International Symposium on Space Technology and Science, Kobe-Hyogo, Japan, July 4–10.Search in Google Scholar

Huang Y, Yang P, Chen Y, Li P, Zhou S, Tang C, Hu X. 2022. Cislunar space probes orbit determination using Inter-Satellite Link data. SCIENTIA SINICA Physica, Mechanica & Astronomica.,Search in Google Scholar

Kaplan ED, Hegarty CJ. 2006. Understanding GPS: Principles and applications (2nd ed.). Artech House: Norwood, MA.Search in Google Scholar

Leonard J, Parker J, Anderson R, Mcgranaghan RM, Born GH. 2013. Supporting crewed lunar exploration with Liaison navigation. Paper AAS 13-053. In: 36th Annual Guidance and Control Conference, Breckenridge, Colorado.Search in Google Scholar

Liu L. 2000. Orbit theory of spacecraft. Beijing: National Defense Industry Press; p. 86–90.Search in Google Scholar

Liu P. 2016. Orbit determination of lunar satellites based on space stations, M.S thesis. Nanjing University, Nanjing, China.Search in Google Scholar

Liu L, Liu YC. 2000. Deficient rank problem in autonomous orbit determination with Inter-satellite link measurements. J Spacecr TT&C Technol. 19(3):13–6.Search in Google Scholar

Liu P, Hou XY, Tang JS, Liu L. 2014. Application of two special orbits in the orbit determination of lunar satellites, Res Astron Astrophysics. 14, 1307–28.10.1088/1674-4527/14/10/010Search in Google Scholar

Lo M, Ross S. 2001. The Lunar L1 gateway: Portal to the stars and beyond, Pasadena. CA: Jet Propulsion Laboratory, National Aeronautics and Space Administration.10.2514/6.2001-4768Search in Google Scholar

Parker JS, Anderson RL, Born GH, Fujimoto K, Leonard JM. 2012. Navigation between geosynchronous and lunar L1 orbiters. In: Proceeding of AAS/AIAA Astrodynamics Specialist Conference, AIAA, Minneapolis, Minnesota.10.2514/6.2012-4878Search in Google Scholar

Parker JS, Leonard JM, Fujimoto K, McGranaghan RM, Born GH, Anderson RL. 2013. Navigating a crewed lunar vehicle using liaison. Paper AAS 13-053. In: 36th Annual Guidance and Control Conference, Breckenridge, Colorado.Search in Google Scholar

Sweetswer TH, Broschart SB, Angelopoilos V, Whiffen GJ, Folta DC, Chung MK, et al. 2011. Artemis mission design. Space Sci Rev. 165(1–4):27–57.10.1007/s11214-012-9869-1Search in Google Scholar

Szebehely V. 1967. Theory of orbits. New York, London, Academic Press.Search in Google Scholar

Tapley BD, Schutz BE, Born GH. 2004. Statistical orbit determination. Burlington: Elsevier Academic Press.10.1016/B978-012683630-1/50020-5Search in Google Scholar

Tauber JA, Mandolesi N, Puget JL, Banos T, Bersanelli M, Bouchet FR, et al. 2010. Planck pre-launch status: The Planck mission. Astron & Astrophys. 520:A1.10.1051/0004-6361/201015611Search in Google Scholar

Wang D. 2010. Constellation autonomous orbit determination based on lunar libration point orbit, M.S. thesis, PLA Information Engineering University, Zhengzhou, China.Search in Google Scholar

Wang WB. 2020. Autonomous navigation and timing in cislunar space enabled by DRO-LEO formation, PhD thesis. The University of Chinese Academy of Sciences, China.Search in Google Scholar

Xu M. 2008. Spacecraft orbital dynamics and control based on libration point theories, PhD thesis. Beihang University, Beijing, China.Search in Google Scholar

Xin XS. 2017. Orbital dynamics about asteroids, PhD thesis. Nanjing University, Nanjing, China.Search in Google Scholar

Xu M, Xu S. 2009. Stability analysis and transiting trajectory design for retrograde orbits around Moon. J Astronautics. 30(5):1785–91.Search in Google Scholar

Yuan JP, Luo JJ, Yue XK, Fang Q. 2003. Satellite navigation system: principle and application. Beijing: China Astronautic Publishing House. p. 40, 193 (in Chinese).Search in Google Scholar

Zhang L. 2016. Design of the Earth–Moon libration point navigation satellite constellation and navigation performance analysis, PhD thesis. Nanjing University, Nanjing, China.Search in Google Scholar

Zhang L, Xu B. 2014. A universal light house – candidate architectures of the libration point satellite navigation system, J Navigation. 67:737–52.10.1017/S0373463314000137Search in Google Scholar
Received: 2022-06-30
Revised: 2022-09-26
Accepted: 2022-09-28
Published Online: 2024-09-05

© 2024 Bin Liu et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. A generalized super-twisting algorithm-based adaptive fixed-time controller for spacecraft pose tracking
  3. Retrograde infall of the intergalactic gas onto S-galaxy and activity of galactic nuclei
  4. Application of SDN-IP hybrid network multicast architecture in Commercial Aerospace Data Center
  5. Observations of comet C/1652 Y1 recorded in Korean histories
  6. Computing N-dimensional polytrope via power series
  7. Stability of granular media impacts morphological characteristics under different impact conditions
  8. Intelligent collision avoidance strategy for all-electric propulsion GEO satellite orbit transfer control
  9. Asteroids discovered in the Baldone Observatory between 2017 and 2022: The orbits of asteroid 428694 Saule and 330836 Orius
  10. Light curve modeling of the eclipsing binary systems V0876 Lyr, V3660 Oph, and V0988 Mon
  11. Modified Jeans instability and Friedmann equation from generalized Maxwellian distribution
  12. Special Issue: New Progress in Astrodynamics Applications - Part II
  13. Multidimensional visualization analysis based on large-scale GNSS data
  14. Parallel observations process of Tianwen-1 orbit determination
  15. A novel autonomous navigation constellation in the Earth–Moon system
https://doi.org/10.1515/astro-2022-0203
Keywords for this article
autonomous orbit determination; triangular libration points; distant retrograde orbits; navigation constellation; inter-satellite range data
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. A generalized super-twisting algorithm-based adaptive fixed-time controller for spacecraft pose tracking
  3. Retrograde infall of the intergalactic gas onto S-galaxy and activity of galactic nuclei
  4. Application of SDN-IP hybrid network multicast architecture in Commercial Aerospace Data Center
  5. Observations of comet C/1652 Y1 recorded in Korean histories
  6. Computing N-dimensional polytrope via power series
  7. Stability of granular media impacts morphological characteristics under different impact conditions
  8. Intelligent collision avoidance strategy for all-electric propulsion GEO satellite orbit transfer control
  9. Asteroids discovered in the Baldone Observatory between 2017 and 2022: The orbits of asteroid 428694 Saule and 330836 Orius
  10. Light curve modeling of the eclipsing binary systems V0876 Lyr, V3660 Oph, and V0988 Mon
  11. Modified Jeans instability and Friedmann equation from generalized Maxwellian distribution
  12. Special Issue: New Progress in Astrodynamics Applications - Part II
  13. Multidimensional visualization analysis based on large-scale GNSS data
  14. Parallel observations process of Tianwen-1 orbit determination
  15. A novel autonomous navigation constellation in the Earth–Moon system
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/astro-2022-0203/html
Scroll to top button