Bound states in the continuum in resonant nanostructures: an overview of engineered materials for tailored applications

Shereena Joseph; Saurabh Pandey; Swagato Sarkar; Joby Joseph

doi:10.1515/nanoph-2021-0387

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Bound states in the continuum in resonant nanostructures: an overview of engineered materials for tailored applications

Shereena Joseph , Saurabh Pandey , Swagato Sarkar und Joby Joseph

Veröffentlicht/Copyright: 9. November 2021

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nanophotonics Band 10 Heft 17

Abstract

From theoretical model to experimental realization, the bound state in the continuum (BIC) is an emerging area of research interest in the last decade. In the initial years, well-established theoretical frameworks explained the underlying physics for optical BIC modes excited in various symmetrical configurations. Eventually, in the last couple of years, optical-BICs were exploited as a promising tool for experimental realization with advanced nanofabrication techniques for numerous breakthrough applications. Here, we present a review of the evolution of BIC modes in various symmetry and functioning mediums along with their application. More specifically, depending upon the nature of the interacting medium, the excitations of BIC modes are classified into the pure dielectric and lossy plasmonic BICs. The dielectric constituents are again classified as photonic crystal functioning in the subwavelength regime, influenced by the diffraction modes and metasurfaces for interactions far from the diffraction regime. More importantly, engineered functional materials evolved with the pure dielectric medium are explored for hybrid-quasi-BIC modes with huge-quality factors, exhibiting a promising approach to trigger the nanoscale phenomena more efficiently. Similarly, hybrid modes instigated by the photonic and plasmonic constituents can replace the high dissipative losses of metallic components, sustaining the high localization of field and high figure of merit. Further, the discussions are based on the applications of the localized BIC modes and high-quality quasi-BIC resonance traits in the nonlinear harmonic generation, refractometric sensing, imaging, lasing, nanocavities, low loss on-chip communication, and as a photodetector. The topology-controlled beam steering and, chiral sensing has also been briefly discussed.

Keywords: bound states in the continuum; functional materials; metasurfaces; photonic crystal slabs; plasmonics

1 Introduction

In recent years, a new paradigm for trapping and confining the resonant optical modes has emerged based on the bound states in the continuum (BIC) in a wave system. A BIC can be characterized as a nonradiating resonant mode in an open system which, however, cannot couple with the radiating channels propagating outside the system. At first, this phenomenon was demonstrated by Neumann and Wigner [1] in 1929 in an electronic system in the context of quantum mechanics. After that, the problem has been preserved as a mathematical curiosity with no experimental evidence to support its existence for almost five decades. Later, Stillinger [2] and Herrick [3] proposed the layered superlattice structure such as a multilayer quantum well that can exhibit discrete electronic states possessing the positive energy bound states in the potential continuum. Thus, bandgap engineering was proposed to be an effective mechanism to achieve arbitrary potential. Successively, such phenomenon has been demonstrated in other wave systems such as mechanical, electronic [4], water [5], acoustic [6, 7], and optical [8]. Other than the BICs dealing with static potential, a Fouquet BIC state in a tight-binding lattice model has also been presented. These are the Fouquet state of a time-periodic Hamiltonian with a quasi-energy embedded into the spectrum of Fouquet scattered states [9].

The optical BIC states in an optical system have been widely discussed in the last decades. The existence of optical BIC modes is classified as the symmetry-protected BIC (SP-BIC) [8] developed by the symmetry restricted out-coupling, accidental BIC or Fredrich–Wintegen (FW-BIC) [10, 11] as the outcome of the radiation suppression of all open channels, and Fabry–Perot BIC (FP-BIC) [12], [13], [14]. Nevertheless, true BIC modes are treated as a dark mode [15], whereas the quasi-BIC modes, and nearly BIC modes are the resonant modes close to the BIC states, accessible and demonstrated for applications. Fundamentally, the single optical bound modes observed in the optical system are vulnerable to perturbations. Typically, an insignificant alteration of parameters can lead to the destructions of the BIC conditions; thus, geometries supporting multiple BICs are proposed [16]. The symmetry-protected BICs are robust against slight structural imperfections that preserve the relevant symmetry. However, the alteration of opto-geometrical parameters can break this symmetry, and the BICs generally turn to a resonant mode with high-quality-factor known as quasi-BIC modes. The ever first experimental verification of the optical bound state is demonstrated by Y. Plotnik in 2011 that resulted from the interference in a two-dimensional (2D) waveguide array single-mode engrossed in a continuum of state; the observed BIC mode is an antisymmetric mode trapped in the continuum of symmetric radiated states [17]. Further, the experimental observation of SP-BIC modes is reported with reflection experiments [8] and measuring the field intensity by a photodetector embedded in the Photonic crystal (PhC) slab [18].

In the last decades, establishing the nonradiating resonant modes in different architectures is well documented, and the underlying physics leading to various applications have been explored enormously. Especially in the last couple of years, an immense number of articles are reported covering multiple applications with enhanced throughput. Interestingly, there are few literature reviews that enlighten the BIC with main focus on the general theory of the different optical system [19], dielectric structure and metasurfaces [20], [21], [22], [23], nonlinear nanophononics in metasurfaces [24], and zero-index meta-surfaces [25]. A. F. Sandreev recently proposed an effective non-Hermitian Hamiltonian to describe the FW-BIC modes in a one-dimensional (1D) system [26] along with a successful description of the BIC modes in open cavities with no symmetry [26]. This review discusses the recent trends of exploring the optical BIC modes supported by the various resonant structures and material medium along with the pioneering avenue of applications where such modes are implicitly used to improve the functions of optical systems. Especially, the last two years have witnessed an enormous number of experimental realizations based on different engineered materials and geometry, resulting in the remarkable outcome of the existing system. The structure of the review process is represented in Figure 1. In the beginning, briefly, we will discuss the optical BIC, followed by the classification of BIC modes based on the material medium and structural geometry. The discussion further extends in connection with broader existing and emerging applications and possible future prospects.

Figure 1:

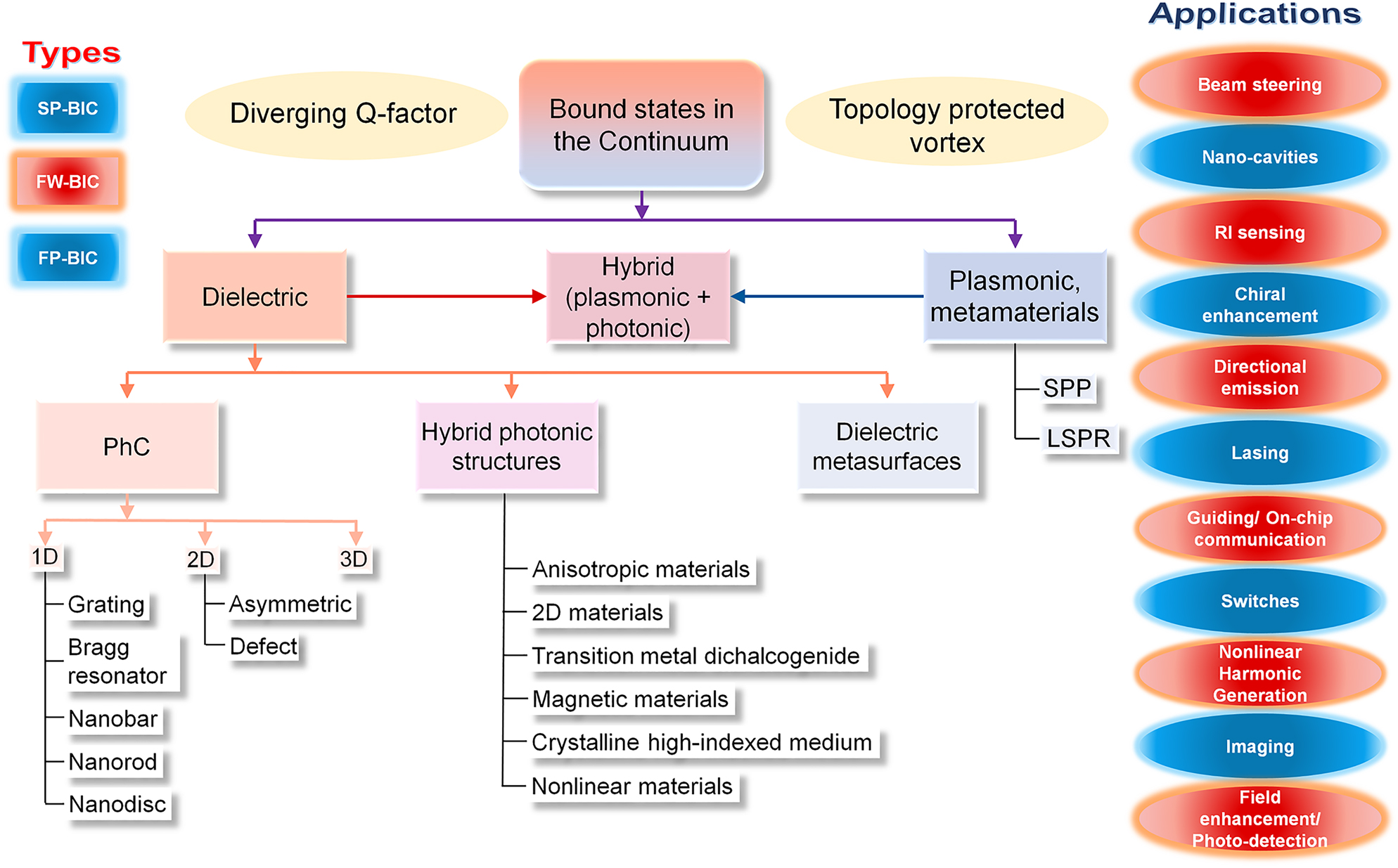
Overview of the review process.

2 Optical BIC modes

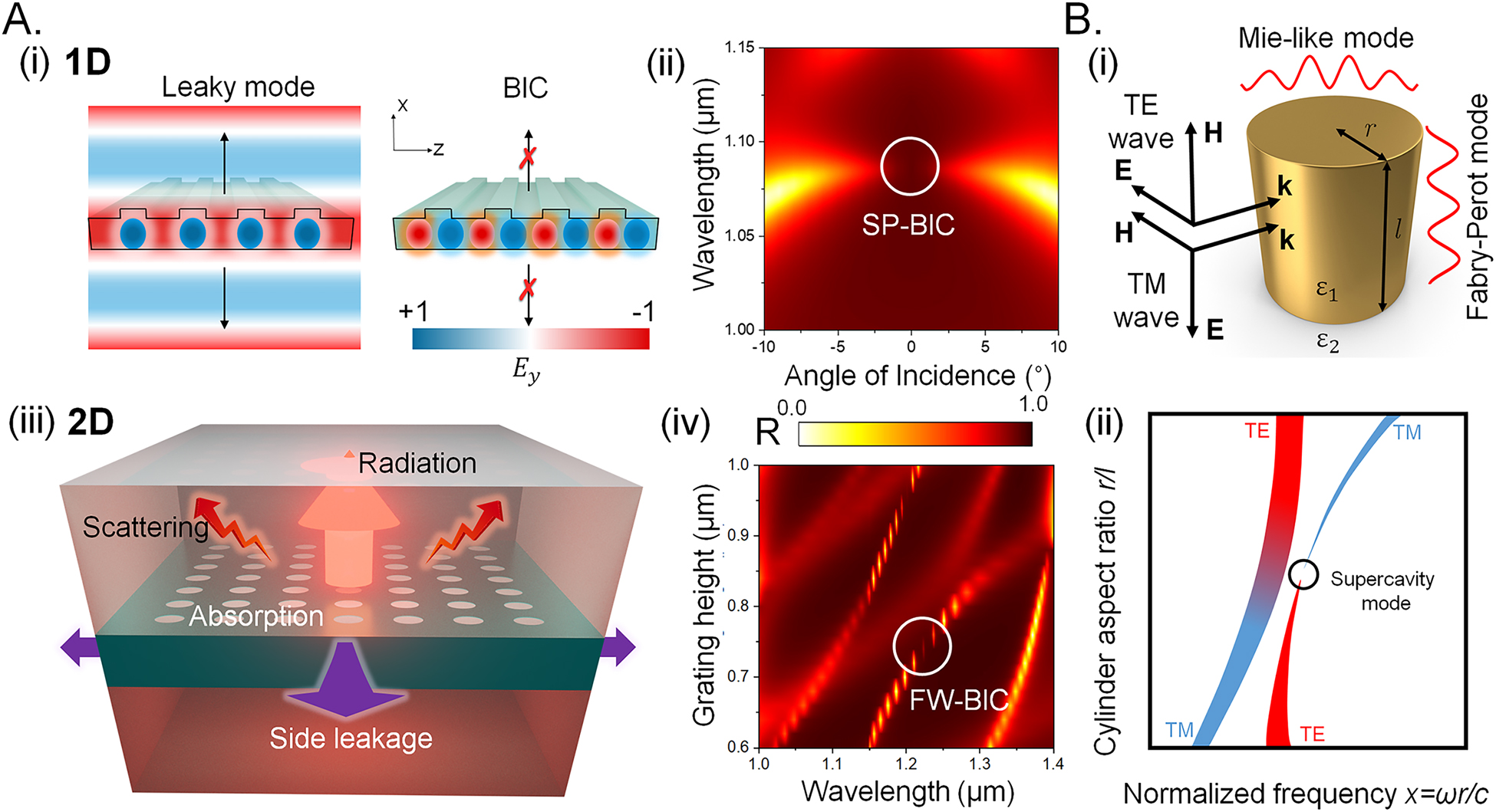
The optical BIC states in a wave system have been widely discussed in the last decade. Ideally, any optical system, with one of its dimensions extending to infinity, can support a BIC mode [8, 27]. The existence of optical BIC modes can be generally classified based on three different important mechanisms. (I) Evidently, in a wave system, the incompatibility of resonant states for coupling with radiating channels leads to the formation of the bound states, also known as the symmetry-protected BIC (SP-BIC) [8]. Typically, the antisymmetric modes persist in the in-plane symmetry structures and cannot couple to the symmetric plane waves propagating as the radiation channel [28]. The existence of the SP-BIC modes is portrayed for a 1D optical system at k = 0 in Figure 2A(i and ii). The unprotected symmetry modes are coupled with the radiation channels (leaky modes), whereas the SP-BIC modes are constrained in the symmetry plane, as shown in Figure 2A(iii).

Alternatively, the process of resonant coupling of different eigenstates that existed in any resonant optical system through an avoidable crossing at a certain set of structural parameters leads to a complete destructive interference and vanishing of one of the resonant modes [10], known as the accidental BIC. This mechanism is characterized by the Fredrich–Wintegen scenario [11], thus also being known as FW-BIC. These are the off-Γ points BIC obtained by the parametric tuning of a system [29]. The FW-BIC scenario is displayed in Figure 2A(iv), where two discrete resonant states interfere, and asymmetric Fano-resonance conditions emerge. At the FW-BIC condition, the collapse of Fano resonance occurs where the line width of the BIC mode disappears; on the contrary, the other mode becomes lossier [30]. An isolated metasurfaces system has also been demonstrated for the existence of FW-BIC modes, as shown in Figure 2B(i and ii), where the cavity-supported different leakage channels perfectly cancel out by tuning the parameters [31].
In Fabry–Perot (FP) BIC, a wave is trapped between two ideal reflectors. Each reflector acts as an independent resonant system with perfect reflection at the resonant wavelength due to the complete destructive interference between the radiation channel and the direct transmission [12], [13], [14]. This mechanism leads to enhanced interaction time through trapping of the light within the cavity for infinite time.

Figure 2:

Optical bound state in the continuum.

(A) (i) The leaky modes and bound states in the continuum (i) in a 1D-system, (ii) the SP-BIC condition (iii) leaky radiation in a 2D-system, (iv) FW-BIC through an avoided crossing. (B) (i) An isolated metasurface and associated resonance modes, (ii) its FW-BIC realization.

In reality, the origin of resonant modes and their characteristics depend on the symmetry of a system and its spatial, geometric, and material parameters. Subsequently, the evolution of BIC modes can also be classified based on underlying physics involved in the excitation of resonant modes and the permittivity of the constituent material medium. Thus, we categorize the BIC modes depending on their evolution in (i) pure dielectrics, (ii) metallic systems, and the (iii) hybrid dielectric–metallic geometries. In a pure dielectric system, the physics of origin of BIC modes received widespread attention in photonic crystal-based architectures [18, 32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59], [60], [61], [62], [63], [64], [65], [66], [67], [68], [69], [70], [71], [72], [73], [74], [75], [76], [77], [78], [79], [80], [81] with free space diffraction orders as the open channels as well as metasurfaces [82], [83], [84], [85], [86], [87], [88], [89], [90], [91], [92], [93], [94], [95], [96], [97], [98], [99], [100], [101], [102], [103], [104], [105], [106], [107], [108], [109], [110], [111], [112], [113], [114], [115], [116], [117], [118], [119], [120] which operate in the nondiffraction regime and are constituted of dielectric resonators or meta-atoms with strong electric and magnetic responses aroused by the scattering channels.

The hybrid optical systems integrated with photonic geometries and other compound mediums, such as anisotropic layered media [121], [122], [123], [124], [125], [126], 2D-layered materials [127], [128], [129], [130], [131], [132], transition metal dichalcogenide materials [133], [134], [135], [136], [137], [138], [139], [140], and the crystalline high index substrates [141], [142], [143], [144], [145], [146], [147], are associated with a fascinating and diverse optical phenomenon, characterized by independent energy dispersion relation and their interaction strength factors. The dielectric medium with nonlinear [95], [96], [97], [98], [99], [100, 108, 148], [149], [150], [151], [152], [153], [154], [155], [156], [157], [158], [159] and magnetic [110, 160] characteristics has also been presented for enhanced properties. Further, each independent material system is influenced by the dimension-dependent features yielding different dynamics of the BIC formulation. Those classifications have been addressed in the following sections.

In metallic structures, surface plasmon polariton (SPP) resonant modes are well recognized for the near field enhancement and high mode confinement [161, 162]. The resonant BIC modes, originated by the interaction of radiative channels associated with the SPPs are also well documented [163], [164], [165], [166], [167], [168], [169]. However, at visible and near-infrared (NIR) wavelength, the BIC conditions mediated by the plasmonic mode applications are limited with absorption and scattering losses. Moreover, investigations have enlightened the plasmonic metamaterials, a versatile engineered metallic medium that operates as a powerful platform for controlling the optical field through BIC modes [170], [171], [172], [173], [174], [175], [176], [177].

The hybrid photonic–plasmonic systems depict the interaction of pure photonic modes and metallic plasmonic modes [178]. Recent studies have also shown that hybrid-BIC mode formation manifested by the symmetry-protected mode as well as the avoided crossing scenario via photonic and plasmonic constituents [30, 179], [180], [181], [182]. Apparently, it has been revealed that the near hybrid-BIC and quasi-BIC modes can offer unusual light confinement with a high-quality factor [182, 183] than its pure plasmonic or photonic counterparts.

One of the unique characteristics of the optical BICs is the polarization diversity and vortex center at the BIC modes. Intrinsically it has been noticed that the BICs are topologically protected charges in the far-field polarization direction [184], [185], [186], [187], [188], [189], [190]. Another interesting mechanism is the chiral-BICs appearing in the middle of the energy bands in the optical system backed by chiral symmetry [86, 191, 192]. We will also be briefly discussing these classes of mechanisms in the upcoming sections.

The capability of trapping and confining the optical modes in the radiation continuum initiates new avenues in the investigations of physics of BIC modes and the materialization of photonic devices with exotic outcomes. The ultra-high Q-factor of the nano-optical system providing strong light–matter interactions leads to the application areas such as, nanocavities [37, 50, 68, 69], refractometric sensors [32, 63, 64, 66, 177], directional emission [89, 193], [194], [195], [196], low-threshold lasing [54, 65, 103, 133, 140, 163, 188, 197], [198], [199], [200], [201], imaging [18, 106, 202], [203], [204], [205], and so on. In particular, the ultranarrow bandwidth of the quasi-BIC states is adopted for the designing of filters [206, 207], switches [146, 208, 209] due to the large optical modulation effect, as well as for light confinement and extra-ordinary absorption, leading to photocurrent generation [18, 210], [211], [212]. More specifically, the BIC mode confinement with low loss guiding can also lead to on-chip communication applications [33, 144, 213], [214], [215], [216]. The quasi-BIC modes in the nonlinear medium have been explored for a higher harmonic generation [97, 99, 100, 138, 148], [149], [150], [151], [152], [153, 155, 159, 217, 218]. Another recognized application is the topological charge controlled beam steering [65, 200, 213, 219] and the photonic systems with higher chirality that are exploited to achieve narrow transparency in circular dichroism (CD) and molar chiral sensing [86, 101, 102, 191].

2.1 Photonic structures

2.1.1 Photonic crystals and slabs

PhCs are the much-debated optical system where different BIC modes are theoretically evolved and experimentally realized. Typically, a uniform dielectric slab retains guided modes with infinite quality-factor below the light-line. However, corrugating the surface of the slab can introduce the guided modes propagating above the light line and can easily be coupled with radiation channels propagating outside the system. Such corrugated slabs are known as the photonic crystal slabs, which have periodic modulation of the refractive index in one-, two-, or three-dimension in the wavelength scale. This periodic modulation of the index leads to the intrinsic property known as the photonic bandgap [220]. In the PhC slabs, the modes that exist above the light line are the leaky modes that can couple with the extended states and radiate; nevertheless, the bound optical modes present in the continuum cannot access the radiative channels due to the destructive interference or the symmetry restrictions [221]. A schematic representation of the scenario is shown in Figure 3A, where the dispersion curve has been used to explain the photonic BIC modes.

Figure 3:

BIC modes in PhC system.

(A) (i) Band structure of the guided resonances and BICs in the 1D-PhC, yellow shaded possess leaky channel. The blue (green) solid curve is the dispersion of guided resonances (1) and (3) are SP-BIC, while (2) and (4) are the off-Γ BIC. The gray curves indicated the guided modes below the light line, (ii) electric field distribution of the BICs. Reprinted from ref. [221]. (B) (i) 1D-grating assembled on the substrate, the BIC modes present in the grating layer and, leaky substrate modes in the substrate (ii) dispersion depicting the quasi-BIC modes coupled with the leaky modes with reasonable high Q-factor. Reprinted with permission from ref. [80] Copyright © 2017, American Chemical Society. (C) 1D-double grating (i) structure schematic, (ii) FW-BIC (iii) showing high Q-factor. Reprinted with permission from ref. [38] Copyright © 2019 WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.

Depending on the spatial arrangement of the light-holding photonic structures and its constituent dielectric medium, the BIC is always surrounded by a class of resonant modes depending on the direction wave vectors and has been distinguished as (i) the photonic transparent dielectric system including 1D-grating or PhC [18, 32], [33], [34], [35], [36], [37, 39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49, 54, 65, 76, 78], [79], [80], [81], arrays of spheres [41, 42, 44], arrays of rods [45], [46], [47], [48], nanowires [49, 55], isolated cavity resonator [37] where the wave vector is restricted in one-dimension whereas the mode confinement is in the plane of periodicity, (ii) 2D structures with periodicity and field confinement in extended in 2-dimensions including photonic crystal slabs [53, 55], [56], [57], [58], [59], [60], [61], [62], spheres, PhC defect system [167], [168], [169], [170], and asymmetric structures [222], and (iii) three-dimensional (3D) photonic crystals [74, 75, 77].

The SP-BIC modes and FW-BIC modes formed through avoided crossing have been demonstrated in numerous PhC slab structures. In a 1D-grating coupled waveguide system, the supported Bloch bound states can propagate in the waveguide layer in a direction along with the periodicity and perpendicular to the ridges. A high index deep dielectric grating placed on a glass substrate demonstrated the SP-BIC modes at high symmetry point k = 0; the geometry has also established the embedded photonic bound modes at nonsymmetry points generated by the destructive interference and suppression of radiation in the oblique interaction of incident radiation [78]. Thus, both these BIC modes can be accessed through angular variation in the form of quasi-BIC modes. Modifying the grating parameters can also break the symmetry leading to the accessibility of SP-BIC mode. For instance, introducing a narrow slit in the asymmetric point perturbed the translational symmetry of the 1D-PhC, which resulted in the emergence of transmission spectra with ultra-high quality-factor [79]. At first, Z. F. Sadrieva et al. claimed and experimentally proved that BIC modes can be converted into a resonant condition with reasonably high-quality factors through leaky losses and scattering due to surface roughness [80]. The dielectric grating placed on the silicon-on-insulator wafer excites the diffracted photonic modes (Figure 3 B(i)). The high-index Si substrate can destroy the in-plane symmetry-protected BIC modes and transform them into resonant states by the leakage radiation through the diffraction channels in the substrate as shown in Figure 3B(ii) [80]. Another investigation in a 1D-PhC with symmetric cladding layers reveals that the BICs can be originated through an avoided crossing of guided mode with the same transverse parity. The coupling of guided modes can be in-phase or anti-phase; the anti-phase modes result in a complete destructive interference condition leading to the generation of BIC modes; on the contrary, the in-phase mode interferes constructively becomes lossier [81]. S. Dai et al.; proposed a mechanism of perfect reflection in a 1D-PC slab [33]. This exhibited phenomenon is unique beyond total internal reflection and bandgap, which is developed due to the coherent interference of multiple propagating modes. The near-field analysis of these BIC modes reveals that the BICs can be characterized by the number of nodes corresponding to their constituent Bloch modes [76]. A biperiodic geometry with inversion and reflection symmetries can significantly endure the low frequency propagating BICs with only one radiation channel [34].

Another intrinsic configuration based on dual dielectric grating architectures has also resulted in the formation of BIC modes [38, 49] where the parallelly propagating Bloch modes can offer guided-mode resonances with superior spectral characteristics as compared to a single grating (Figure 3C). Moreover, by controlling the relative parameters of the gratings and the distance between them, the geometry can endure tunable BIC modes with sharp spectral features [38]. Such dual grating symmetry can also support vertically propagating FP-cavity modes and the transverse propagating guided modes. The coupling of two counter-propagating guided modes or an FP cavity mode interaction with a guided mode also endures BIC modes and quasi-BIC modes [39]. The BIC modes that existed in the guided-mode resonant (GMR) structure have also gained much interest. It is noted that such structures can also enhance the Goos–Hanchen (GH) shift with the assistance of supported quasi-BIC modes [35]. The experimentally detected reflectance peak with maximum reflectance revealed the GH shift close to four orders of wavelength.

E. N. Bulgakov et al. systematically investigated the BIC modes supported in an array of dielectric rods [45, 46, 48]. The linear array of infinite rods exhibited SP-BICs for a broad range of structural parameters; modifying the radius of the rods offers the quasi-BIC modes with enhanced Q-factor [45]. Moreover, in the high contrast dielectric rods, the supported BICs propagate along the axis of the rods with bidirectional BICs propagating both parallel to the axis of the rods and the axis of the periodicity [46]. On arranging the rods in a circular array, the architecture supports both SP-BICs and other trapped modes [48]. With a few rods, the symmetry exhibited high-Q values of the order of 10⁵ for the SP-BICs [48]. In another investigation, S. G. Kim et al. explored a set of FW-BICs supported in Si-nanowires, which can be tuned by the pitch as well as the inner and outer diameters. The nanowire configuration supported a set of Mie resonances that can interact and generate Fano resonances; the parameter tuning resulted in the formation of FW-BICs [49].

In 2D-PhC structures, the SP-BIC modes are examined in detail. Due to symmetry restrictions, the quasi-BIC modes appear as Fano resonance become localized with infinite quality factor at k = 0 [8, 53]. The investigation of optical resonant modes in a PhC slab revealed the existence of several tunable BIC for a broad range of wave vectors supported with the corresponding slab thickness [57]. A typical 2D-PhC slab can provide both rotational and translational symmetry in the transverse plane, whereas a broken flip mirror symmetry in the vertical plane. Thus, the geometry can support both transverse electric (TE) and transverse magnetic (TM) kinds of optical modes. Tuning the structural parameters can offer to couple between these different polarization states, leading to the generation of BICs [52]. The BIC modes with unprotected symmetry have also appeared at the off-Γ point at low frequencies with only one radiation channel. Remarkably, these BIC modes can exist on and below the light-line on the surface of the PhC and do not have any incompatibility with the outside radiation channels [51]. For example, suppose the PhC slab constitutes a lossless medium with both reflection and translational symmetry. In that case, the off-symmetry BIC modes propagating with a nonzero wave vector are robust against the structural perturbations if the modified structure also maintains the same symmetry [61]. Very recently, a method to achieve miniaturized BIC modes in a 2D-PhC slab is proposed [68]. It has also been observed that the available BIC can be tuned by influencing the environment of the photonic system rather than the structure parameters, opening up the new possibility of realizing the BIC modes [67]. The investigations have also pointed out that a defect introduced in a 2D-PhC system can support BICs modes, and more importantly, the symmetry mismatch between defect mode and Bloch modes in the system leads to the confinement [72]. Intrinsically, the BIC mechanism evolves in the absence of the bandgaps; thus, the scheme involves a new horizon of light confinement and interactions.

Although the BIC have been widely discussed in the 1D and 2D-photonic systems, the investigation was not extended into the 3D PhC systems until 2014 when F. Monticone et al. explored that optical BIC can also be materialized in a 3-D subwavelength structure [74]. Remarkably these are the confined optical modes in the presence of symmetry-compatible radiation channels in a 3D system. Such a 3D system can also be realized for vector waves with both the polarization [77].

2.1.2 Metasurfaces

Metasurfaces are the planar sub-wavelength period arrays in which only the zero-order specular reflection or transmission is permitted. Restricting the radiation channels only to the specular ones, the resonant mode confinement can be infinitely extended by tuning the structural parameters or by the symmetry protection [24, 88]. Dielectric geometries exhibiting Mie resonances have earned recent research interest to provide a versatile field for engineering the optical properties with exotic outcomes due to its low absorption losses and enhanced light–matter interactions in the nanoscale [83]. Thus, the dielectric metamaterials possess unconventional functionalities that can be engineered for numerous applications than their plasmonic counterparts.

The metasurfaces comprise unique architectures or meta-atoms in 2D periodic geometry that performs strong light–matter interaction through Mie scattering allowing magnetic responses ultimately arising from active dipole radiation, namely, electric dipole (ED), magnetic dipole (MD), and toroidal dipole (TD) [223]. In addition to these, the interaction of dipole resonances among themselves offers many other significant resonance phenomena and possibilities. For example, the Huygens metasurface formation can be realized by the interference of orthogonal ED and MD, which are in-phase with uniform intensity [93, 224], while the interference between them with a π/2 phase difference, resulting in the formation of Janus dipole (JD). The JD exhibits an interesting phase-dependent coupling with its adjacent one [224]. Interference of ED and TD type of resonance generates a nonradiating anapole state [225, 226]. Besides these, higher-order dipoles can also interfere with additional properties [227]. Here, we will focus on the BIC formation through the different dipole resonance and their coupling, enabling a way to boost the light–matter interaction. Indeed, a BIC manifested in metasurface has been explored for various optical process and applications such as nonlinear harmonic generation [95, 96, 98], [99], [100, 150, 217], directional light emission [89, 131, 193, 228], imaging [98, 106, 203, 204], sensing [66, 106, 109, 204] and, lasing [200, 229].

The BIC modes in metasurface have been thoroughly investigated and realized through different dipole resonances involved. BICs are realized from single dipole resonance [86, 92, 98, 105], [106], [107], [108, 115], employing the multipole decomposition approach to explain the SP-BIC and FW-BICs [116]. Far-field radiation of each isolated metasurface is contributed by the dominant mode accompanied by infinite series of multipole modes. Each multipole has its radiation channel, expressed by vector spherical harmonics through multipole expansion. In ref. [116], the authors modeled a BIC formation in terms of a multipolar decomposition model for a general case of any periodic structures. The structure consists of only those dipoles that do not radiate vertically, offering the SP-BIC condition.

The multi dipole decomposition has been studied thoroughly for quasi-BIC realization by coupling Mie resonance mode and FP cavity-like mode in a single subwavelength high dielectric nanoresonator, operating in the microwave region. It accounted for the change in the field distribution produced by the alteration in the aspect ratio of subwavelength cylindrical structure [230]. Recently, J. F. Algorri et al. proposed an SP-BIC formalism through multipole resonance at microwave regime in a metasurface structure based on split-ring resonator ultrathin slots [117]. The coupled ED and MD formulation has been theoretically investigated in a related model based on all-dielectric metasurfaces [118]. Further, they extended the investigation on Si-nanosphere metasurfaces to enhance the near field and local density of states [231].

On the other hand, the TD resonance is usually suppressed in the presence of stronger resonances due to its weak coupling with incident radiation. Moreover, it exhibits the weaker tendency of confining and enhancing the near field. Therefore, a high localized BIC state can effectively strengthen the TD because of enhanced local field density. In ref. [119], the concept of TD-BIC using Si-metasurfaces is investigated. The instigated TD quasi-BIC mode is validated for different applications for terahertz nanofilm sensing [84, 109, 120]. Similarly, TD BIC is identified in asymmetric metasurface of tetramer cluster unit, revealing its antiferromagnetic characteristics [110].

A novel approach is acquainted by combining the two valuable phenomena, Huygens surface and quasi-BIC termed “Extreme Huygens metasurface”, to reduce the radiative loss exhibited by broadband multipole resonance [85]. The spectral overlapping of two quasi-bound states with the same Q-value and different parities using zig-zag–shaped Si meta-atom is achieved. Indeed, this overlapping is mediated by multipolar modes and controllable through in-plane braking of SP-BIC. Successively, by employing a zig–zag array of elliptical silicon nanodisks, a Huygens regime is exploited via spectral overlapping of electric quasi-BIC and magnetic quasi-BIC state to accommodate the maximal transmission and highly steep spectral phase agility of 2π [115]. The considered metasurface and nonzero dipole moment introducing asymmetry has been shown in Figure 4A(i). The asymmetry factor comprehends the quasi-BIC state, enabling nonzero net induced ED and MD moment, with field profiles of opposite parties, as shown in Figure 4A(ii and iii). Manifesting the electro-optic refraction through biasing, i.e., by changing the doping level, the considered structure could tune the Huygens mode and cover a wide phase span with maintaining the excellent transmission amplitude.

Figure 4:

BIC modes in metasurfaces.

(A) (i) Schematic illustration of the electro-optically tunable metasurface, (ii) asymmetry introduces through zig–zag arrangement shows nonzero electrical and magnetic moment, (iii) transmission spectra for amplitude and phase concerning TE polarized incidence wavelength, indicates the 2π spectral phase accumulation with the maximal transmission. Reprinted with permission from ref. [115] Copyright © 2020, American Chemical Society. (B) (i) Schematic of cluster-based unit cells for symmetry breaking dimer trimer cluster through disturbing the out of plane symmetry; near field distribution of a particular BIC eigenstate in a (iii) dimer cluster, (v) trimer cluster, (ii) leaky mode in dimer, and (iv) trimer cluster unit cell. Reprinted with permission from ref. [92] copyright © 2019 American Physical Society. (C) (i) Schematic of the all-dielectric superlattice metasurface consists (i) unit cell of three silicon nanobeams at a separation of d ₂ with its adjacent unit cell, (ii) asymmetry defined by Δd = d ₁ − d ₂, (ii) transmission spectra, and (iii) quality factor variation with Δd. Reprint from ref. [91].

The quasi-BIC modes obtained by perturbing the in-plane symmetry can be tuned to operate in the desired wavelength region and to have prominent transmittance/reflectance, phase and, polarization properties. So far, the in-plane symmetry breaking has been introduced via deformation concerned with a structural parameter of the meta atom [87, 88, 109, 117, 232], inducing a relative tilt between the pair of meta-atoms [86, 100, 115], removing the meta structure from edges [89], altering the relative gap among the meta-atoms or in a unit cell [24, 91, 95], etc. Subsequently, Si nanobars unit cell-based metasurfaces are reported to extract the leaky mode by breaking the SP-BIC through relative displacement between the nanobars and unit cells, as shown in Figure 4C. The radiation through the SP-BIC state leaks through the path followed by coupling with guided resonance mode [91]. Besides the in-plane breaking of the symmetry, Anton S. Kupriianov proposed breaking the out-of-plane symmetry to access the BIC modes in dielectric metasurfaces by considering it as a dimer or trimer nanocluster [92]. The transverse asymmetry brought through altering the thickness of disk-dimer and trimer units composed of equilateral triangular unit cells is shown in Figure 4(B). The quasi-BIC through breaking out of plane symmetry has been further employed for different purposes [86, 107].

Polarization concepts governed by Brewster’s law are well familiar from the light interaction with nonmagnetic material, while in metasurfaces, this scenario is distinct, owing to its magnetic response. The underlying physics of the Brewster-like effect in metasurfaces generally can be understood in terms of the suppressed scattering at certain angles that emerge from the interference between the ED and MD resonances [93, 233, 234]. D. R. Abujetas et al. proposed the realization of Brewster quasi-BIC in all-dielectric metasurfaces [105]. They demonstrated Brewster-like phenomena for SP-BIC and quasi-BIC in high refractive index disk constituents metasurfaces with nearly unity reflection or transmission at a particular angle of incidence.

2.1.3 Hybrid photonic structures

Recent efforts are also explored various on-chip hybrid photonic functionalities that depends on the physics of BICs including, engineered dielectric media such as anisotropic photonic structures [121], [122], [123], [124], [125], [126], layered 2D materials [130, 132, 134, 138, 218], transition metal dichalcogenide, single crystals [142], [143], [144], [145], [146], [147], and magnetic medium [110, 160, 235]. In the coming sections, the physics of BIC modes evolved in various structure geometries depending on these material mediums is discussed. Moreover, PhC-slab created using nonlinear medium has also been studied for the enhanced nonlinear properties such and higher harmonic generation that we will address in the application parts.

Anisotropic photonic structures: A periodic structure constitutes the layered anisotropic birefringent medium that has been attractive for optoelectronic applications. It has been noticed that a photonic system comprised the anisotropic materials can also support optical bound states in the radiation continuum, containing the fully electric and magnetic components [121] in contrast to the bound states evolved in the dielectric photonic geometries where the trapping mechanism is treated with the scalar potential. Typically, in the isotropic photonic architectures, the bound optical states always carry the maximum energy in one linear direction, either TM or TE polarization, with insignificant energy being directed in the orthogonal direction. On the contrary, in anisotropic photonic structures, the light that propagates in any arbitrary direction concerning the optical axis constitutes ordinary and extra-ordinary waves. Therefore, there can be two radiation channels in such a photonic system compared to the isotropic photonic medium with a single one. In general, an optical bound state can be formed by suppressing the leaky mode in any optical system. In particular, the analysis of a hybrid system with anisotropic uniaxial materials placed on an optical waveguide structure reveals that BIC modes occur in a fully vectorial picture. The radiation-suppression of such anisotropic medium arises by considering the semi-leaky modes and, the BIC formation is possible both in symmetric and asymmetric structures [236]. The semi leaky wave represents the modes with its partially localized fields in the waveguide but gradually decay, and its energy propagates to the substrate through continuous bands of radiation channels [237]. These investigations explore the possibility that the anisotropy-induced BIC can be polarization separable or polarization hybrid. Remarkably, the full-vector BIC exhibits tunable angular propagation direction as well as controllable polarization hybridity. Moreover, the near BIC modes are highly directional and ultrasharp radiative states that can be applied as filters, spatial-light modulators, and sensors. Further, breaking the anisotropy leads to fundamentally different physical properties; for example, a structure with broken azimuthal anisotropy can be obtained by arranging the optical axis of the anisotropic layers aligned in the waveguide plane but are not aligned to each other. Such geometries can support only the BICs with hybrid polarization, not the polarization separable BICs. In polar symmetry breaking cases, the structure can support specific BICs for a unique and discrete sequence of wavelength and optical axis orientation [123, 124].

In a recent study, I. V. Timofeev et al. explored a hybrid isotropic–anisotropic structure consisting of alternating isotropic and anisotropic materials [122]. The geometry exhibits different band structures for different polarizations of light, and the introduction of a defect layer in the layered medium can excite a BIC in it. For an anisotropic defect layer, these BIC modes can switch to a quasi-BIC mode by tilting the principle dielectric axes of the anisotropic medium relative to the axis of the photonic crystal. Their experimental verification demonstrates that the liquid crystal defect can tune the Q-factor of the quasi-BIC mode with the applied external electric field [122]. A numerical approach has recently been established based on the full-wave analytic solution to describe the BIC modes in the anisotropic system. Subsequently, the collapsing Fano resonance phenomenon is analytically explained in the vicinity of an optical bound state in a system constructed by an anisotropic defect layer embedded into anisotropic photonic crystal [125]. In another successive work, the Brewster angle tilted BICs have been explored experimentally in the 1D PhC with the inclusion of defect anisotropic layer as shown in Figure 5A(i); where the multilayer PhC acts as a perfect mirror [238]. Remarkably, in this configuration, the Q-factor of the quasi-BIC modes is controlled by rotating the optical axis of the liquid crystal (Figure 5A(ii)) [126]. Significantly, such high tunable high-quality devices can find applications in spintronics and photonics.
2D materials: The layered 2D materials attracted renowned interests in nanophotonics as they can offer improved properties in comparison with purely passive dielectric materials [235]. Graphene is recognized as a notable 2D-layered medium for various enhanced properties due to the confined electromagnetic field developed by forming an optical-BIC [218]. The hybridization of layered materials with a dielectric medium in a waveguide configuration has shown excellent saturable absorption, controlled emission, wavelength emission, and photocurrent generation. Moreover, it has been explored that the absorption in graphene can be enhanced exceptionally by a critical coupling mechanism when the rate of radiation of guided-mode resonance approximates the internal dissipative loss rate of graphene [239, 240]. Recent efforts investigating hybrid photonic geometries integrating the 2D layer materials with a dielectric photonic medium based on the principle of BIC explored revolutionized outcomes due to remarkable absorption enhancement [129]. The selective absorption from mid-IR to visible wavelength is realized for TE and TM polarization by selecting suitable BICs [127]. In particular, the BIC mediated critical coupling has been demonstrated between monolayer graphene-asymmetric silicon nanodisk metasurfaces and, by tuning the dielectric structural parameters, the critical coupling has been achieved, resulting in an enhanced absorption [131] as shown in Figure 5B. Moreover, the absorption bandwidth can be tuned by more than one unit of magnitude by modifying asymmetric dielectric structures parameters at the critical coupling [132].
Transition metal dichalcogenide: Over the past couple of years, a monolayer of transition metal dichalcogenides such as molybdenum disulfide (MoS₂) and tungsten disulfide (WS₂), recognized as a new 2D-layered material, is gaining enormous research interest due to their exceptional optical and electric properties. The transitional metal dichalcogenide (TMD) is the direct bandgap semiconductor layered medium with a strong exciton response [241]. Z. Ye et al., have experimentally proved the existence of 2D exciton BIC modes in a WS₂ monolayer [133]. Inherently, an optical resonator constructed using the layered TMD medium supports the exciton with considerable binding energies and oscillation strengths. Hybridizing the photonic slabs with the TMD WSe₂ layer medium enhances the exciton–photon coupling, where the BIC modes supported in the PhC slab manifest a strong interaction with the exciton [134]. This scheme has demonstrated a giant 100-fold enhancement of polariton lifetime with a finite momentum [134]. Notably, the strong coupling between BICs and TMD monolayer can enhance the oscillator strength at room temperature. The key signature of the coupling strength ‘g’ mainly depends on the contributions of modal electrical field and exciton transition dipole moment in the TMD layer. One of the mechanisms identified to improve the g is to reduce the mode volume of the optical resonator [241]. An analytical study supported with numerical calculations on the WS₂ monolayer reveals that the strong coupling between q-BIC mode and excitons leads to spectral splitting. The interaction also influences the line width and quality factor of BIC modes [137]. The nonlinear polariton formation is recently demonstrated by V. Kravtsov et al. [138] with the schematic of the hybrid structure shown in Figure 3C. The photonic modes in a 1D-PhC coupled with the exciton in the MoSe₂ monolayer generate the nonlinear polariton. The interaction resulted in the Rabi splitting of >27 meV and a BIC mode with suppressed radiation in the direction normal to the surface (Figure 5C(ii)). The strong coupling is mediated by the splitting of upper and lower polariton branches (UPB and LPB) with the exciton. Indeed, the investigations based on heterostructures comprising transition-metal dichalcogenide (TMDC) layers with other photonic mediums and eventually leading to the exotic light–matter interaction strength is an emerging subject for exploiting many possible applications.
Crystalline high index substrates: Photonic structures, constructed by considering a low refractive index medium on a high refractive index medium made up of single crystals such as lithium niobate (LiNbO₃), barium borate (BBO), yttrium iron garnet (YIG), diamond, and yttrium aluminum garnet (YAG), is possessing interesting optical and electrical properties. Such photonic integrated architectures have been manipulated for photonic on-chip circuits applications, including guiding, communications, and quantum technologies. A recent theoretical framework predicted that the trapped BIC modes could be realized on such photonic architectures [142]. A low index polymer medium on the single-crystal diamond substrate can offer ultra-high-Q microring resonators for scalable quantum information processes and networks. Remarkably, in such configurations, as shown in Figure 5D, the destructive interference of leaky channels leads to the forbidden optical dissipation. Z. Yu et al. demonstrated another photonic structure by patterning the high index LiNbO₃ (LN) single crystal for propagating bound modes in the radiation continuum, which are laterally confined and modulated [143] which has been further modified for on-chip communication [144]. Owing to the higher nonlinearity of LN, the proposed configuration predicts a single photon nonlinear coupling close to 2.4 MHz, a promising tool for optical state quantum engineering. The lithium niobate (LN) waveguide has also been subjected to the BIC mode existence, and BIC mediated polarization-entangled photon pairs [147] and, efficient second-harmonic generation [145]. The interaction of two guided symmetric waves with opposite phases in a symmetric periodic waveguide based on LiTaO₃ medium provides the excitation of self-stabilizing BICs. Giving a slight change in the refractive index in the waveguide, these established BICs are electrically switchable in a broad optical range and, the design has been demonstrated a perfect switching between zero and on-state [146].
Magnetic materials: The magneto-optical (MO) relations evolved by the interaction of magnetic media and photonic modes are recent research interest. However, dielectric metasurfaces and photonic crystals exhibit an MO effect [242, 243] with a moderately low Q-factor. Significantly, the Mie resonating structure and a photonic crystal illustrate the MO effect governed by the Faraday effect and the Vought effect in the presence of the externally applied magnetic field [242]. Metasurface composed of cylindrical shaped tetramer cluster of Si possesses TD and MD resonance quasi-BIC modes that could effectively exhibit the optical antiferromagnetic nature in the high-frequency THz region [110]. In contrast, the magnetic susceptibility of all-natural material becomes very low in the THz region [243].

Investigation revealed that the BIC supporting structures could encourage a substantial improvement in intensity and polarization modulation. Taking this into account, intense terahertz MO phenomena was discovered by designing the BIC supported photonic crystal slab–graphene–slab structure for modulating its MO response through electrostatic doping or asymmetry introduced quasi-BIC formation [235]. Further, A. M. Chernyak et al. analyzed the MO effect in asymmetric bismuth substituted yttrium iron garnet (Bi: YIG)-2D nanodisks dielectric metasurfaces by symmetry protected BIC. The interactions demonstrated the intensity and polarization modulation through the Faraday effect [244]. In ref. [160], they have accounted a BIC supported photonic crystal with a magnetized cavity made of cerium substituted yttrium iron garnet (Ce: YIG) sandwiched between the two Braggs mirror, demonstrating trapped mode with TE polarized light and an extended mode with TM polarization. The BIC itself manifests the MO intensity modulation with TE polarized incident light.

$Figure 5: Hybrid photonic BICs. (A) (i) the anisotropic defect layer embedded in a layered PhC, and (ii) the BIC modes achieved by Brewster’s angle tilting. Reprinted from ref. [126]. (B) 2D graphene layer hybrid metasurface (i) absorption with parameter tuning and, (ii) maximum absorption is recorded when the critical coupling is achieved through BIC modes. Reprinted from ref. [131]. (C) (i) Picturization of hybrid MoSe2-PhC structure, (ii) angle-resolved reflectance spectra of the hybrid geometry, the splitting of upper and lower polariton branches due to strong coupling between the MoSe2 exciton and the photonic mode in the PhC slab. Reprinted from ref. [138]. (D) Schematic representation of low-refractive-index polymer on the high-refractive-index substrate (diamond), (ii) the emerged hybrid photonic BIC with minimal loss in the vicinity of the continuum of modes, (iii and iv) mode profiles. Reprinted with permission from ref. [142] Copyright © 2014 by WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.$

Figure 5:

Hybrid photonic BICs.

(A) (i) the anisotropic defect layer embedded in a layered PhC, and (ii) the BIC modes achieved by Brewster’s angle tilting. Reprinted from ref. [126]. (B) 2D graphene layer hybrid metasurface (i) absorption with parameter tuning and, (ii) maximum absorption is recorded when the critical coupling is achieved through BIC modes. Reprinted from ref. [131]. (C) (i) Picturization of hybrid MoSe₂-PhC structure, (ii) angle-resolved reflectance spectra of the hybrid geometry, the splitting of upper and lower polariton branches due to strong coupling between the MoSe₂ exciton and the photonic mode in the PhC slab. Reprinted from ref. [138]. (D) Schematic representation of low-refractive-index polymer on the high-refractive-index substrate (diamond), (ii) the emerged hybrid photonic BIC with minimal loss in the vicinity of the continuum of modes, (iii and iv) mode profiles. Reprinted with permission from ref. [142] Copyright © 2014 by WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.

2.2 Metallic plasmonic structures

The SPP excitation is known to confine optical energy in the nanometer range [162, 245]. However, the realization and tuning of plasmonic BICs are challenging since the excitation of plasmonic mode is associated with the intrinsic metallic absorption loss. However, both SP-BIC and FW-BIC conditions are theoretically investigated and experimentally realized in limited distinguished 1D and 2D architectures [164]. In a reported study, considering a metallic air–hole array structure, the excited propagating surface plasmons interact through an avoided crossing scenario resulting in the generation of a dark mode [161]. A similar FW-BIC mode formation is illustrated in the metal–insulator–metal (MIM) [170], and a 1D reflection grating [164] by the interaction of supported higher-order plasmonic modes. Intriguingly, despite the inherited loss associated with the plasmonic bound state, most plasmonic BIC structures have been demonstrated for practical applications such as lasing, switching, and filters. In particular, the SP-BIC quasi-BIC mode-mediated extraordinary transmission has been observed in an array of thin metal plates [166]. Notably, the plasmonic quasi-BIC mode assisted lasing has been exhibited in a lower lasing threshold than the typical resonant modes [165]. Moreover, the metallic nanoparticle radiation suppression instigated by both SP-BIC in normal incidence and FW-BIC in the angular interaction has also been evolved by the excited localized surface plasmon resonance (LSPR) [163, 168].

Nevertheless, these reported studies are limited in the IR-wavelength, where the metal absorption loss is significantly low. Very recently, the formation of plasmonic BIC mode in the visible wavelength range is realized in a 1D all-metallic grating [167] using the hybridized plasmonic lattice resonance by coupling the localized SPR and diffracted orders (Figure 6A). Considering around 20 more plasmonic grating samples, they could effectively prove the existence of SP-BIC modes in the localized surface plasmon (LSPRs) lattice surface plasmon (LSPPs) modes as shown in Figure 6A(i). Modifying the structure parameters, they tuned the LSPRs and LSPPs to be on resonance and the BIC is observed in an all-metallic system displayed in Figure 6A(iii and iv). Tuning the LSPR modes by keeping the same lattice pitch and simultaneously increasing the grove depth, the strong coupling of LSPR and LSPP modes are made to occur and the resultant SP-BIC modes are observed at Γ = 0. In the oblique interactions, the LSPR mode is again tuned to off-resonance condition; however, LSPP modes are still excited weakly in the period lattice. The destructive interference of all these channels outcomes the FW-BIC (Figure 6A(v)). Moreover, tuning the LSPRS by increasing the grove height witnessed a topological band inversion and a corresponding vanishing BIC mode. Such a phenomenon has not been observed in a plasmonic system before. They have discussed this band inversion by considering a ‘Zak’ phase transition [167, 246].

Figure 6:

Photonic–plasmonic hybrid BIC modes.

(A) (i) Plasmonic structure showing (i and ii) LSPP modes without strong coupling, (ii) tuning the structure parameters offer the excitation of an LSPR mode with splitted LSPP modes observation of the dark mode (BIC) at Γ = 0 in the visible range (iii and iv). Reprinted with permission from ref. [167] ©2021 American Physical Society. (B) (i) Schematic of the process of generation of bound states in the continuum (BICs) with the system supporting two modes coupled to two ports, (ii) based on the CMT concept, the numerical transmission of uncoupled modes is shown in red & green line, coupled modes in blue line with eigenvalues represented by black dots, (iii) FW-BIC obtained by for different frequency detuning and (iv) corresponding line plots [174]. (C) Photonic–plasmonic hybrid BIC (i) schematic of geometry with fabricated samples, (ii) resonance conditions, (iii) FW-BIC emerged between FP cavity mode and plasmonic mode, (iv) SP-BIC at normal incidence and corresponding line plots. Reprinted from ref. [30].

Plasmonic metamaterial engineered BIC modes ranging from microwave to infrared frequencies also attract immense attention [171, 176]. In particular, the nearby quasi-BIC modes exhibit exceptional spectral features with Q-factor and higher refractive index modulation [170, 247]. D. R. Abujetas et al. demonstrated the existence of off-Γ BIC modes in Terahertz frequency with a vanishing linewidth and enhanced lifetime employing gold-rod dimer metamaterials formed by two rods per unit cell. Intrinsically, such BIC scenarios are independent of the relative position of rods within unit cells as well as the lattice constants where no diffraction orders are present [171]. Employing lossy gold metamaterial has demonstrated the high confinement of quasi-BIC modes with high Q-factor the mid-IR wavelength. The obtained quasi-BIC modes exhibited perfect absorption in the optimal coupling condition within a relatively small mode volume [172]. The FW-BIC conditions have also been realized in metallic split-ring resonators [173], [174], [175] and dimerized chains [168]. The SP-BIC originated by the independent dual BIC in a subwavelength double split-ring resonator metamaterial structure is found to exhibit a large Q-factor in the terahertz frequency [173]. The coupled-mode theory (CMT) is established as a powerful tool for understanding the BIC formation in the metamaterial frameworks [174]. Implementing the CMT methods, X. Zhao et al. realized an FW-BIC by coupling distinct resonant modes through tuning of the geometrical parameters of the unit cell. The evolved quasi-BIC modes are found with high Q-factor within the Fano resonance line shape [174] (Figure 6B(ii)). Active control of all-dielectric BIC-based metasurfaces would enable active THz on-chip, ultrafast, low-loss components and devices such as efficient modulators, filters, and biosensors.

2.3 Plasmonic–photonic hybrid BIC

The ultra mode-confinement features of plasmonic characteristics and lossless photonic mode couplings have been proposed to eliminate the limitations owned by the individual counterparts in hybrid plasmonic–photonic structures [248]. A few numerical frameworks have been proposed to realize SP-BIC modes and FW-BIC mode in metallic grating coupled dielectric hybrid structures [179, 181], experimental realization of which is achieved very recently [30, 182]. M. Meudt et al. materialized the hybrid-BIC modes and quasi-BIC modes in a metal grating integrated with the dielectric configuration [182]. Recently we have achieved the fabrication strategies of dielectric grating coupled on thin metal layer configurations for the photonic–photonic hybrid BIC modes [248]. Considering a chalcogenide dielectric medium, a sinusoidal high contrast grating layer is designed on a 50 nm thin Au metal layer backed by the glass substrate. The grating layer is treated as a homogeneous waveguide layer in such a configuration, and each diffracted plane beam behaves like a Bloch mode (Figure 6C(ii)). The vertically propagating Bloch modes provide the resonance condition of an FP cavity-like mode while the transverse propagating waveguide modes offer the excitation of GMR. On the contrary, the evanescent waves corresponding to the diffracted beam couple with the SPP modes under the phase matching conditions lead to the propagating SPP resonant modes at the metal–dielectric interface. In Figure 6C(iii), the parametric space tuning of grating layer thickness anticipated a couple of FW-BICs by coupling higher-order FP cavity modes and SPP modes through an avoided crossing scenario. The angular space tuning of incident light explored the symmetry-protected BIC modes in the optimized parameters, as shown in Figure 6C(iv).

Apart from these studies, recent efforts also explored the hybrid plasmonic–dielectric metasurface structures for enhanced interaction of characteristic modes and BIC formation [180]. Similar interests are also shown in hybrid plasmonic-transition metal dichalcogenide metasurface structures for the enhanced plasmon–polariton resonance interaction through their BIC [136].

3 Topological charges

An important domain of interest is the topological charge conservation and polarization singularity of photonic BICs at the FW-BIC centers in the reciprocal space. The off-Γ BIC centers, unprotected by symmetry points with origination from the radiation cancellation mechanism, are intrinsically topological invariant in their polarization direction. Although the far-field radiation corresponding to a BIC is a dark mode, they are originally the vortex center with conserved and quantized topological charges in the polarization field [184] which again are defined by the number of times the polarization vectors wind around the vortex centers [184]. Figure 7A briefly explains the instigated BICs and the supported topological charges in the polarization field. Generally, if a BIC is protected topologically, it is highly robust and cannot be perturbed by a slight modification of system parameters which is unlikely to occur in the other general BICs [33]. The experimental evidence of the polarization vortices from reflection measurements by monitoring the amplitude and Q-factor of the leaky modes highlight that the BIC vortex centers are highly robust against the roughness, loss and, structural imperfections [185]. More importantly, the topological charges must follow the charge conservation rules and hence the evolution, creation, and annihilation to preserve the total charges [46].

Figure 7:

Topological charge at the BIC center.

(A) Topological charge in a 2D PhC-slab. (i) Calculated radiative quality factor Q of the TM₁ band of the 2D PhC-slab in the first Brillouin zone and five BICs are identified, (ii) the directions of the polarization vector mapping verify the vortices with topological charges of ±1 at each of the five k points, (iii) nodal lines and gray-scale colors of the polarization vector fields. Reprinted with permission from ref. [184] Copyright © 2014 American Physical Society. (B) Merging of BIC (i) schematic of the unit cell with elliptical holes, (ii) pair of BICs pair at t = 516 nm, (iii) merging BIC at with t = 512 nm, and (iv) merging BIC with t = 514 nm. Reprinted with permission from ref. [190] Copyright © 2021 American Physical Society.

The topological characteristics corroborate that the BICs can be continuously tuned in the reciprocal space with alteration of the structure parameters while keeping the symmetry of the system unchanged [19]. Therefore, tuning the multiple BICs to the same wave vector can materialize a merged BIC [188]. In PhC-slabs, the excitation of a group of guided resonance modes and the supported BIC mode couplings are discussed resulting in plane-scattering losses, strongly suppressed by the topological nature. This scenario is realized when multiple BICs carrying independent topological charges combine in the momentum space, resulting in the high-quality factor of resonance bands [188]. Thus, the proposed mechanism offers to overcome the scattering losses created by the fabrication imperfections. In the off-high symmetry points, the merging of multiple BICs is mediated by the topological charge through a combination of two FW-BICs with opposite topological charges [190] that is briefly portrayed in Figure 7B. A 2D-PhC slab with thickness t is embedded with elliptical holes where the geometry exhibits an in-plane rotation symmetry (Figure 7B). For slab thickness t = 516 nm, a pair of vortexes with charge (±1) stays away from the ΓM direction (Figure 7B(ii)). On tuning the thickness of the slab, the merging of charges is observed, as shown in Figure 7B(iii and iv). The polarization singularities associated with the BIC modes are also extended to circular [249] and elliptical polarization [190].

The BIC and the associated polarization singularities developed in periodic dielectric rods demonstrate that the BIC modes are described by the elliptical polarizer in the far-field radiation [46]. However, with a BIC in the vicinity of momentum space, the ellipse characteristics collapse, and the far-field radiation becomes nearly linearly polarized. The theoretical investigation in a 2D-PhC revealed that far-field radiation close to the BICs exhibit polarization diversity such as linear polarization, circular and elliptical polarization for various orientations, as well as polarization with topological charges showing spatial symmetry and interference among different radiation channels [250]. Recently, X. Yin et al. have realized unidirectional BIC that can radiate only in one direction even if no mirror is placed on the other side. This exotic condition is achieved in a 1D-PhC slab which is symmetric in the up–down and left–right direction, and the BIC is realized with TE-like polarization for off-normal interactions. The unidirectional emission in the upward direction is achieved in the context of topological charges where splitting and merging of two half-integer topological charges occur in the polarization axes [186]. Subsequently, it has been shown theoretically [251], as well as via experiments, the existence of higher-order topologically protected BIC modes in waveguide arrays [187]. Moreover, a method has been proposed to create various polarization singularities of far-field radiation that has effectively demonstrated off-Γ BIC with higher-order topological charges [252].

4 Applications

The rest of the discussion focused on the applications of the optical-BIC and quasi-BIC modes explored in the previous section concerning the geometries and the engineered material media.

4.1 BIC-assisted beam steering

Optical vortex intrinsically exists in the momentum space near and at the optical-BIC centers in various previously discussed systems. Thus, naturally, engineering the resonant modes and manipulating the BIC conditions results in optical vortex generation and beam steering [200]. The beam steering, i.e., steering optical energy in a controllable direction, is generally achieved using phased arrays [253]; however, these are limited with large area nonintegrated components, complexity, and poor responsiveness. The recent developments in the experimental evidence of BIC and quasi-BIC modes pave the way toward the generation and beam steering of coherent vortex beams (in any required arbitrary direction) in photonic and plasmonic structures. Such integrated structures enable generation and beam controlling of vortex beam to form an integrated, scalable source to boost major application areas such as particle trapping and manipulation, metrology, microscopy, and quantum high-capacity communication. In particular, the PhC slab with rotation symmetry has demonstrated the co-evolution of two lasing BIC with opposite topological charges to explore the particle trapping application in such symmetric structures [219]. In another PhC slab symmetric structure, the Γ-BIC optical vortex system is found to be higher-order quasi-Bessel beams [65]; hence, the photonic BIC mode assisted vortex beam offers the generation of complex beams other than the typical Gaussian beam profile.

4.2 Nanocavities

The cavity structures designed by a medium to possess enhanced light–matter interaction are quantified by the ‘figure of merit’, F = λ 3 Q V where Q is the quality factor and V is the modal volume at the resonant wavelength [254]. Typically, the nanoperiodic quasi-BIC modes possess a higher Q-factor. The unveiling of these embedded eigenmodes in a nanocavity offers the exotic confinement of the modes and an enhanced figure of merit. Such a cavity system has been designed by sandwiching a micropillar resonator between a pair of Bragg reflectors [37]. In a similar study, a numerical investigation explored that a proper BIC system can be converted into a mirrorless microcavity with ultra-high quality factor using a few unit cells [50].

A typical 2D-PhC slab is known to confine the BIC modes in the vertical direction because of the symmetry incompatibility and the destructive interference in the transverse plane. Although ideal confinement in all three dimensions is unfeasible to achieve, the miniaturization of BIC modes has been attempted in a few studies. Using a 2D-PhC slab, a unique cavity is designed to have BIC with high-quality factor and small modal volume [68]. The PhC-slab is designed to have a photonic bandgap mirror using lateral heterostructure to restrict the transverse leakage. However, the out-of-plane leaky radiation satisfying the momentum matching condition increases subsequently. Tuning the PhC unit cell parameters may lead to the eminence of multiple BICs carrying topological charges in the momentum space and can ultimately cancel out the vertical leakage radiation. The evolved mini-BIC mode is robust and demonstrates a high-quality factor of 1.09 × 10⁶ with a lower modal volume of 3.56 μm³ [68].

The coupling of mechanical BIC and optical modes are demonstrated in slab-on-substrate optomechanical crystals [69]. Micro and nanocavity-enabled optomechanical interactions provide quantum control over the associated optical and mechanical degrees of freedom. Such controlled interactions can find applications in various precision quantum networks, ground-state cooling, optical and mechanical squeezing, etc. Adopting a mechanism for tuning the optomechanical cavity through optical BIC mode can minimize the size of the system with enhanced reflection and improved mechanical quality factors. A cavity designed by employing a double PhC membrane layer, kept at a distance of lesser than one wavelength, can characterize many trapped photonic states in the continuum (Figure 8A). These trapped modes own remarkable mechanical coupling, owing to the near wavelength and relatively low decay rate which can be used for evanescent coupling toward materializing various optomechanical cavities [255]. This mechanism is beneficial over other FP cavities, as it can offer strong optical and mechanical properties to have quantum coupling interaction at the single-photon level.

Figure 8:

BIC modes for cavity design, and sensing.

(A) (i) Schematic of the double-photonic crystal slab cavity, (ii) transmittance map against frequency and slab separation for the optimized cavity period and air-hole radius for the BIC formation (ii) quality factor of the cavity eigenmodes close to the BIC. Reprinted from ref. [255]. (B) (ii) The dispersion band diagram of 2D-PhC shown in the inset, (ii) bio-detection scheme, (iii) sensitivity calculations. Reprinted from ref. [222].

4.3 Refractometric sensing

The near BIC modes excited in a passive system have been extensively implemented for refractometric sensing applications, including biosensing, gas sensing, and temperature monitoring owing to their high Q-factors. The significant fraction of trapped light in the quasi-BIC modes exhibits an evanescent tail extending into the ambiance medium, and the resonance features are strongly affected by the binding events and environmental medium changes. Moreover, the sharp spectral signature with fine linewidth offers the ultra-high figure of merit, which is considered an essential feature for minimal detection limits [256]. All-dielectric medium-based photonic crystal slabs and metamaterial structures have been investigated for quasi-BIC modes with high-quality factors and sensitivity for biosensing [32, 63, 64, 66, 82, 222]. Another remarkable investigation carried out in a dielectric asymmetric nanostructure composed of silicon bar with slightly different widths exhibited a high-quality quasi-BIC mode with an excellent figure of merit of 667 and a record bulk sensitivity of 440 nm/RIU. This system has been effectively employed to detect exosomes secretion from a single cell [222]. Moreover, the quasi-BIC modes excited in a dielectric metasurface have illustrated that ultra-high sensitivity leading to the limit of detection extends to the nM range for the sensing of protein p53 [64]. The structural profile, dispersion diagram, and sensitivity measurement are depicted in Figure 8B.

More significantly, the PhC-based architectures have also been employed for gas sensing [38] and temperature sensing [35]. Recently an active double grating-based high contrast grating exhibits cavity quasi-BIC mode that is utilized for gas sensing. In the cavity resonator geometry, an organic dye medium sandwiched between the grating layer acts as a gain medium where the SP-BIC quasi-BIC mode of the cavity is tuned to the emission wavelength of the dye molecule. Remarkably, the lasing overlapped with the quasi-BIC mode reveals good sensitivity, a high signal-to-noise ratio, and a prominent figure of merit [43]. In another prominent study, a highly sensitive temperature sensor is designed using a compound 1D-grating layer and a temperature-sensitive single crystal layer. The architecture exhibited the resonant GH shift in the reflectance spectrum with an ultra-fine resolution of the order of 10⁻⁴ °C incorporated within the temperature-sensitive medium bismuth-germanate (Bi₄Ge₃O₁₂) [35]. The compact sensor offers a high sensitivity close to 3907 µm/°C at T = 25.212 °C. Sensing in the terahertz domain is also proposed using metamaterial and meta-surfaces, as nondestructive and nonionizing evaluations characterize this domain for fast imaging and sensing [257]. In one of the reported approaches, the quasi-BIC modes evolved in terahertz frequencies are reported to detect minimal thickness [177].

4.4 Chiral enhancement

The object with nonsuperimposable mirror images is referred to as a chiral object [258]. Such chiral structures show CD toward the circularly polarized light and the absorption is quite diverse with left and right circular polarized light. Thus, the CD alters with eigenpolarization states of incoming light. In 2014, the generation of BIC was theoretically discussed in the chiral quantum system [192]. Recently, PhC-slab consisting of crossed elliptical Si is studied to manipulate the wavefront of resonant light by introducing the chiral perturbation that breaks the 2-fold rotational symmetry [191].

Plasmon-based photonic structure with chiral element shows CD enhancement; however, it is not prominent due to high metallic losses. Recent progress in dielectric metasurfaces explored that such functionalities can be realized in isolated meta medium due to their engineered electromagnetic interactions [259], [260], [261]. The coupling and cross-coupling between electric and magnetic field response of meta-structure with incidence circular polarized light offer two different refractive indexes for left and right circular polarized light together with high Q-factor. In this perspective, BIC supporting metasurfaces can be efficient in super chiral field formation and thus, offer substantial improvement in chiral field sensing and CD for inquiries of enantiomers. Discrimination between the enantiomers has been done through its interaction with the chiral field and finds emerging interest in various applications, especially in biology and pharmacy. BIC approach has also been explored to generate the super chiral field for enhanced CD signal. BIC-supported achiral nanophotonic structure of PbTe dimer with a chiral molecule placed inside the gaps on SiO₂ substrate is proposed recently, offering a 10-fold improvement in chiral optical signal compared to conventional detection schemes [102]. Advancing the BIC approach, a theoretical framework is presented to enhance the CD spectroscopy signal using FW-BIC supported TD evolved in the TiO₂ dimer-based metasurface, sitting on an optically thick gold film. The Fano resonance contributed by the leaky channel appears with altering the height of the dimer. They have concluded an enormous enhancement about 59 times of CD signal with sensitive RI-based detection of molar concentration with a prominent figure of merit, influenced by quasi-BIC generated super chiral field [101]. Moreover, chirality enabled quasi-BIC formation on a metasurface consisting of dimers of Si-bar provides a narrow peak of unit height in the CD spectrum as shown in Figure 9A, which is theoretically studied [86]. Recently it is also demonstrated through the experimental results confirming the prediction of enhanced chiral response of the BIC supported asymmetric resonant dielectric metasurface.

Figure 9:

BIC modes for chirality, directional emission, and lasing.

(A) (i) Sketch of transmission and reflection for S matrix of a rotational symmetric chiral structure where b ₊ and b ₋ are outgoing wave amplitudes with the incident wave amplitudes, a ₊ and a, considered for S-matrix formulation, (ii) a dimer of parallel bars and their lattice hosting SP-BIC resonances with two types of mirror symmetry planes and three types of rotational symmetry axes are represented and, a dimer of bars vertically offset by d and rotated by θ, breaking the SP-BIC, (iii) CD of structures with symmetry breaking parameters and losses following the scaling rule θ ² ∝ d ² ∝ κ, where κ is extinction coefficient. Reprinted with permission from ref. [86] Copyright © 2020 American Physical Society. (B) Schematic of MoS₂ nanodisk-based metasurface suspended in air, asymmetry introduces by semi-spherical of radius r _s and V shape edge cuts. Reprinted with permission from ref. [89] Copyright © 2021, American Chemical Society. (C) (i) The colloidal CdSe/CdZnS core–shell nanoplatelets arranged in titanium dioxide square symmetric of nanocylinders optically pumped, (ii) the quasi-BIC mode lasing in the visible wavelength at room temperature. Reprinted with permission from ref. [104] Copyright © 2020, American Chemical Society.

4.5 Directional emission

The quasi-BIC can play a vital role in overcoming the various loss mechanisms, e.g., dissipative optical losses [262] and fluorescence quenching problem [263] involving plasmonic and photonic resonances based directional emitters. The quasi-BIC-supported directional light emission with significant intensity can be utilized efficiently in optoelectronics, fluorescence nanoscope, and sensing applications.

In 2016, N. Rivera et al. theoretically discussed controlling the radiation directionality and dimensionality by breaking the SP-BIC via the introduction of a perturbation in one dimension keeping all other dimensions unperturbed that allows the radiation along the perturbed dimension only. The case is further studied by perturbing the potential of an ultracold atom and photonic system [193]. H. Zhou et al. developed a general temporal CMT formalism to discuss single-sided radiation due to BIC existence and absorption from the photonic crystal slab without using any mirror [213]. Further, a topologically enabled unidirectional guided resonance is demonstrated in a photonic crystal that radiates toward the front side of the slab [186]. In particular, BIC is explored as a novel approach to engineer the diffraction in silicon waveguide grating antennas (SWGA) [196]. The SWGA consists of a Si grating structure on an insulator that diffracts the guided mode into a radiation mode. Introducing periodic nanogrooves on the sidewall of the waveguide can suppress the radiation from its sidewalls and supports the FW-BIC. SWGA is commonly used to avoid interaction between guided and radiating modes to diminish the far-field beam divergence. However, due to significant diffraction from the edges of waveguide-based gating on SiO₂, the input beam travels short propagation length (up to a few hundred microns), leading to sizeable far-field divergence. Remarkably, BIC-supported SWGA exhibits an ultra-small far-field divergence ∼0.027 with a long propagation length.

Recently, N. Muhmmad et al. presented the hybrid structure consisting of transition metal dichalcogenides and waveguide layer mediating the interaction of excitons and optical modes [89]. They experimentally demonstrate the directional emission of fluorescence through the square unit cell of the MoS₂-nanodisk Mie resonator supported by the BIC, as shown in Figure 9B. The ultrathin-MoS₂ resonating structure suspended in the air possesses a BIC state, and the directional emission through the quasi-BIC mode is obtained through the semi-spherical or V cut edge. A typical PL enhancement through a PhC slab with a hexagonal unit cell of Ge nano-island is reported in ref. [194] as compared to various other established approaches to enrich the emission characteristics of CMOS compatible semiconductor materials, especially elements like Si and Ge. The PL spectra were collected experimentally, covering the 6° and 25° light cones from the designed structure. The results illustrated an enhancement of 140 times of the PL peak intensity as compared to the PL intensity of the nonprocessed film. An alternative effort has been reported to increase the photoluminescence of Si by employing the Carbon-G center assisted by the quasi-BIC in an asymmetric hole arranged as a square unit cell that can significantly enhance the PL intensity outcome about 40 times [228]. This approach has also been followed in various symmetry-breaking PL-based applications like BIC detection through imaging and vanishing of PL peak [202], elaborated in our next section while discussing imaging applications.

4.6 Lasing

The ability to trap and confine light in the radiation continuum commences the realization of robust and scalable lasing sources [188]. The plasmonic lattice modes, photonic modes in the PhC-slab and, dielectric nanoresonators-based nanocompact system have effectively demonstrated BIC-assisted lasing. Additionally, these trapped BIC modes are natural vector beam sources; hence, they provide various possible beam shapes [65, 219]. The quasi-BIC mediated laser emission is reported with an optically pumped BIC cavity in a thin layer made up of dielectric cylindrical rods. The cavities have been designed by an array of InGaAsP multiple quantum wells nanoresonator array suspended in air and exhibit unrelenting single-mode lasing for different radii and periods in room temperature [54]. Enhanced Cherenkov radiation (CR) is observed in a double grating structure mediated by the optical BIC modes. The CR through the quasi-BIC modes possesses a very narrow frequency band at a particle velocity below the common threshold [264].

Dielectric metasurfaces with minimal dissipative losses offer a more promising way to manipulate light in the nanoscale for the visible and NIR wavelength range. Intrinsically, the available optical modes associated with the metasurfaces with different morphology and configuration enable the interference effects to develop feasible opportunities to realize optical antennas ready for offering lasing with strong directionality [103, 104, 199]. Moreover, the advanced fabrication technology offers the straightforward on-chip integration of these antennas in photonic devices. A GaAs-based active metasurface designed by a 2D array of nanopillars demonstrates lasing with controlled directionality. This mechanism is purely nondiffractive, where the designed 2D array of dipoles manifest to oscillate in-phase and form a nonradiative BIC. Modifying the lattice periodicity in one direction perturbs the system, supporting a diffractive order where a unidirectional radiative channel opens up. The lasing wavelength can be explicitly tuned to any chosen wavelength [199]. Further, replacing CdSe/CdZnS NPL as a gain medium on the TiO₂ metasurface offers the tunable gain spectrum from the resonant magnetic quadrupole BIC conditions, and lasing is found to be more efficient with a lower threshold [104] (Figure 9C(i)). Subsequently, S. I. Azzam et al. have recently shown lasing from the array of TiO₂ dielectric metasurface resonator. This BIC-assisted lasing is incorporated with an organic dye, and the collective diffractive coupling of electric and magnetic coupling manages the lasing properties. The controlled emission is found to have a high directionality and a low threshold at room temperature. More importantly, their proposed all-dielectric metasurface has demonstrated both single and multi-mode lasing [103].

Plasmonic BIC are also explored for enhanced lasing featuring a miniaturized coherent laser source [201]. The lasing generation threshold in a distributed feedback-plasmonic laser is influenced by the structure parameters and the subsequent lasing modes; BIC-enabled lasing provides the generation threshold with a minimal material gain [165]. The hybrid photonic–plasmonic mode supported SP-BIC modes are effectively demonstrated for plasmonic directional lasing emission [163, 197, 265]. Moreover, engineering the band structure by modifying the index, lattice symmetry, geometry, and polarization of the pump source can tune the lasing wavelength for switchable and multimode emissions.

The hybrid photonic–exciton system and integrated plasmonic–exciton structures are proven for photon lasing [133, 140]. A robust perovskite-based micro-laser emission in the symmetry-protected BIC modes has been experimentally reported [198]. Intriguingly, pattering the perovskite film by a polymer grating can generate a symmetry-protected BIC mode. The topological symmetry and the mode interactions enhance the light trapping in the gain medium while breaking the symmetry by oblique interactions, leading to laser emission with a high Q-factor. The lasing emission is found to be single-mode with exceptional controllability and directionality with high repeatability [198].

The topologically protected lasing and vortex-mediated BIC-lasing are proposed to have dynamic and controlled emission with low energy consumption and high modulation speed [200, 219]. Such topological charge-controlled lasing emission has been proposed in a 2D-PhC slab with a square array of holes possessing four-fold rotation symmetry. The supported BIC and their topological charges are experimentally tracked with polarization-resolved k-space imaging. Manipulating the band structure by tailoring the hole diameter and periodicity of lattice effectively modifies the topological charges, resulting in lasing from any of the BICs. A hybrid metasurface combined lead bromide perovskite microlaser design has been proposed by C. Huang et al. [229]. The perovskite 2D-PhC slab is patterned with an array of circular holes. The structure-supported resonance bands corresponding to TM polarized light exhibit a topology-protected BIC. Modifying the hole radius enables the BIC-assisted lasing with an ultra-high Q-factor by embedded polarization vortex. When the lasing array is pumped with a circular beam, the symmetry-protected lasing shows a donut-shaped far-field mapping; as the incident beam is changed to ellipse, the symmetry breaking leads to the emergence of two linearly diffracted beams. Lasing from the SP-BIC modes is also realized with configured two-beam pumping, resulting in a two-lobe beam.

4.7 Guiding and on-chip communication

Reducing the leakage loss in an optical fiber is a need of the hour for fast and lossless communications. Introducing the signal modes as the BIC states can remarkably reduce the radiation loss of the existing guiding mechanism. An analytical investigation illustrates that a fiber Bragg grating (Figure 10B), even with a slight index contrast, can act as a topologically protected BIC mode where the radiation loss is drastically reduced. The destructive interference of a high Q-mode and a low-Q mode results in the destructive interference and suppression of radiation loss [215], the field distribution of BIC mode confirms the low radiation loss. A guiding mechanism is demonstrated in a photonic crystal with the associated perfect coherent reflection with the optimized structure parameters. Several propagating Bloch modes undergo the total internal reflection within the slab; the transmitted leaky modes performing coherent destructive interference lead to the perfect mirror mechanism. The corresponding propagating modes are nothing but the bound eigenmodes with a topological vortex of transmission [33]. These modes can be designed for the lossless guided mode application. The working scenario of the PhC guiding mechanism is shown in Figure 10A.

$Figure 10: BIC modes for guiding and communication. (A) Schematic illustration of perfect reflection-based guiding of BIC mode. Reprinted with permission from ref. [214] Copyright © 2020 American Physical Society. (B) (i) BIC supported by the fiber Bragg gratings and (ii) fiber BIC mode profile [215]. (C) (i) waveguide structure composed of a low-refractive-index polymer stripe patterned on high-refractive-index LiNbO3 layer, (ii) propagation loss of the TM0, TM1, TM2, and TM3 modes in the waveguide as a function of the waveguide for each mode, the BICs exist in the low-loss region as marked in the gray region. Reprinted from ref. [144].$

Figure 10:

BIC modes for guiding and communication.

(A) Schematic illustration of perfect reflection-based guiding of BIC mode. Reprinted with permission from ref. [214] Copyright © 2020 American Physical Society. (B) (i) BIC supported by the fiber Bragg gratings and (ii) fiber BIC mode profile [215]. (C) (i) waveguide structure composed of a low-refractive-index polymer stripe patterned on high-refractive-index LiNbO₃ layer, (ii) propagation loss of the TM₀, TM₁, TM₂, and TM₃ modes in the waveguide as a function of the waveguide for each mode, the BICs exist in the low-loss region as marked in the gray region. Reprinted from ref. [144].

E. Bulgakov has demonstrated that the propagation of nearly symmetry-protected BICs in the infinite array of dielectric cylinders can offer an extremely low radiation loss even above the light line as compared to the propagation of a guided mode in the cylinder below the light line without any leakage [216]. Remarkably, the Q-factor of the propagating mode increases exponentially with the number of the cylinder. A dielectric biperiodic structure immersed in an identical medium, such as elliptical holes etched into the dielectric slab, offers the propagating BIC with minimal loss from the structural imperfections. Such a structure possesses an inversion symmetry in the plane of periodicity and reflection symmetry in the vertical direction [34]. An on-chip diffraction-free guiding beyond the light cone is illustrated in a dielectric PhC slab using the concept of BIC. Here the optimized structure parameters offer the condition of canceling both the in-plane diffraction and out-of-plane scattering condition if the total internal reflection condition is not satisfied [214].

Utilizing the BIC modes supported in a hybrid photonic single crystal system in the high-dimensional communication and (de)multiplexing can significantly increase the data capacity per wavelength. Such a mechanism is established in an integrated LiNbO₃ high index substrate assembled with a low index medium platform and is proposed for on-chip communication. In particular, in the configuration, the higher-order TM-BIC modes in the TE polarized continuum can propagate in the high index waveguide with negligible propagation loss [144]. The system offers a four-channel BIC-assisted TM mode de(multiplexer) at 40 Gbps/channel (Figure 10C). The proposed system is beneficial with high thermally stable linearity in addition to the enhanced speed.

4.8 Switches

The tunable resonant quasi-BIC modes supported in the PhC slabs and reconfigurable metasurfaces via a combination of various optical processes and tuning mechanisms, including thermal, electrical, and mechanical effects, provide new opportunities for engineering advanced optical switches. In particular, to achieve significant tunability of optical processes, the background optical responses should be remarkably sensitive to the slight perturbation of the environmental factors. Therefore, extremely sensitive optical BIC and quasi-BIC states are exploited to design an effective ultrafast switching mechanism. In this section, we will be discussing the quasi-BIC mode-assisted optical switching mechanism adopted by electro-optical modulation [170], all-optical switching [23, 208], nano-electromechanical tuning [209], and thermo-optic effect [146].

The electrically tunable plasmonic modes operating in the quasi-BIC modes are demonstrated for an efficient electro-optical switching exploiting an MIM modulator. Here, high-speed response electro-optic polymer operating at the communication wavelength 1.55 μm is implemented for the tuning purpose. The design supports several plasmonic modes; the coupling of higher-order plasmonic modes eventually offers the interaction through an avoided crossing and the evolution of FW-BIC modes. More importantly, the quasi-BIC modes exhibit high modulation intensity with a refractive index variation of 8.5 × 10⁻³, resulting in the modulation voltage of 5 V [170]. Thus, their proposed design offers to operate at a bandwidth exceeding 100 GHz. Exploiting in the BIC states evolved in a double resonator structure, A. Henkel et al. recently demonstrated electro-optic switches. In the design, hybridized photonic-2D layer architecture is proposed by considering a high index electro-optic substrate LiTaO₃ integrated with a symmetric film resonator that contains a grating in its center. This photonic state of art possesses an inherent SP-BIC mode and quasi-BIC mode. More importantly, the electro-optical effect of LiTaO₃ instigates the refractive index modulation offering a switchable large bandwidth BICs between the perfect zero to an enhanced on-state [146].

Another prominent effort explored a quasi-BIC mode for all-optical tuning based on GaAs metasurfaces [208]. In practice, perturbing the in-plane symmetry of the high index metasurfaces results in quasi-BIC fano resonance mode with ultra-narrow bandwidth. Remarkably, with a minimal pump influence of 89 μJ/cm², the quasi-BIC mode can detect a spectral shift of 10 nm. Intrinsically, the observed optical modulation is attributed to the high linear absorption and the free carrier induced refractive index variation in the GaAs metasurfaces [208]. Another recent investigation explored a nano-electromechanical tuning of resonance modes that are the supported GMR and a quasi-BIC mode in the telecom wavelength. The proposed state of art consists of a grating with two pairs of doped silicon nanobars. Notably, the selected periodicity smaller than the operating wavelength ensures avoiding the unwanted diffraction effect. The modification of the structure parameter or the oblique interaction enables the coupling of both the excited modes. Subsequently, the device attains a spectral shift close to 5 nm with an absolute intensity modulation of 40% and a modulation speed of more than 10 kHz with the applied external bias of 7 V [209].

4.9 Non-linear harmonic generation

The dissipative losses in plasmon resonance-based architectures, multiple background scattering in Mie structure, and leaky resonance mode limit the nonlinear harmonic generation efficiency through optical resonances phenomena [266] in the typically established systems. Nonlinear interaction with high yield and efficiency is one of the promising application domains explored using optical BIC by exploiting the characteristics such as immense local field density with a diverging high-quality factor [108, 157], [158], [159, 267], [268], [269].

The Si-based dielectric metasurface is identified as an effective way for light manipulation in nanophotonic devices with tremendous thermal stability. K. Koshelev et al. demonstrated a third-order harmonic generation (THG) using Si meta-atoms in an asymmetric system [95]. They perceived that THG intensity is critically reliable with asymmetry parameter and is maximum at an intermediate value of its parameter as shown in Figure 11A. Later, ref. [96] extended this model for demonstrating up to the 11th harmonic generation. Z. Liu et al. demonstrated an exceptionally enhanced THG and SHG in high-Q-factor Si-metasurface through quasi-BIC phenomena merely by removing material at one corner of the square-shaped unit cell. Such resonant structure exhibited quadratic and cubic power scaling on a logarithmic scale [97]. A subsequent study demonstrated the nonlinear tuning of an optical wavefront through Si-based metasurfaces mediated by single MD quasi-BIC, which also features image switching controlled by polarization of incident light [98].

Figure 11:

BIC modes for nonlinear process.

(A) (i) Asymmetry introduction, (ii) SEM image of Si-based metasurface (iii) transmission spectra corresponding to asymmetry factor ‘α,’ (iv) numerically simulated dependence of the TH intensity on asymmetry parameter α. Reprinted with permission from ref. [95]. Copyright © 2019, American Chemical Society. (B) (i) Schematic of an elliptical cylinder of GaP based metasurface with a relative tilting of an angle θ between their major axes, arranged in the square lattice (periods, Λ = 700 nm), (ii) schematic representation of the origin of the quasi-BIC. In each particle of the dimer, the single electrical dipole is induced with x and y components; when summed up, give the origin of an out-of-plane magnetic dipole (m _z) and in-plane electric quadrupole (Q ^e _xy), and an x-oriented electric dipole (p _x). The varying the θ, the amplitude can be tuned of this p _x that can only couple with x polarized plane waves, (iii) and (iv) shows the transmission spectra and average second harmonic generation power variations with θ. Reprinted with permission from ref. [100] Copyright © 2020, American Chemical Society. (C) (i) Schematic of THG and nonlinear image tuning through quasi-BIC MD resonators, (ii) multipole decomposition for linear light scattering and TH signal with corresponding E nearfield distribution in XY plane at MD resonance, (iii) nonlinear image tuning with polarization and wavelength. Reprinted from ref. [98].

Apparently, the Si-nanodisk resonator-based structures recognized as one of the epsilon-near-zero materials that are not ideally known for exhibiting nonlinear processes nevertheless reported an efficient way to accomplish different nonlinear functions. In particular, such architecture is illustrated to boost the multifrequency generation and cascaded parametric generation at the nanoscale [99]. Moreover, the 2D-layered medium and dichalcogenide-based resonant structure supporting BIC have been utilized for nonlinear interaction. N. Bernhardt et al. theoretically reported a 2D-WS₂ monolayer hybrid structure with an asymmetric Si-square shape dielectric metasurface for the enhanced nonlinear processes [148]. They estimated a boost in SHG efficiency about 140 times than WS₂-monolayer on Si film and nearly one and a half orders of magnitude higher than reported work on dielectric resonant metasurfaces. A theoretical investigation is conducted by adopting the Fano resonance SHG generation from the near BIC supported in a hybrid structure consisting of a 1D grating structure of dielectric constant ε = 15.21 (Si_0.7Ge_0.3) and TMDC monolayer of WS_2. The study reveals that the geometry has the potential to enhance the SHG up to four orders of magnitude [149]. Subsequently, the three-layer structure consisting of monolayer dielectric spheres in a square lattice-monolayer graphene-dielectric slab has been theoretically investigated for the THG and four-wave mixing [218]. Intrinsically, the geometry has reportedly enhanced THG up to seven orders of magnitude.

The nonlinear harmonic generation has also been deliberated using isolated dielectric nanoantenna to boost nonlinear harmonic generation significantly [150, 151, 270]. The ref. [100] illustrates the efficient visible SHG using continuous source instead of typical high-power femtosecond pulses in GaP disk-based metasurfaces, as shown in Figure 11B. The square arrays of nanodimers consist of two GaP cylinders with an elliptical cross-section with a relative tilting angle θ between their major axes. The quasi-BIC region is tuned by varying the θ, which influences the SHG intensity. The nonlinear response of 2D-PhC is also studied theoretically through symmetry-protected BICs, which are supported by two identical resonators coupled with the waveguide [152]. Recently a theoretical model for understanding the second harmonic generation in quasi-BICs formed by considering the multipole model has been acquainted. It deals with the physics behind BIC-inspired nonlinear enhancement in a hybrid metal–dielectric nanoantenna [153].

Furthermore, BIC formulation is investigated theoretically on the double resonant χ ⁽²⁾ nonlinear photonic crystal [154]. Successively, the architecture is exploited to demonstrate the doubly resonant second-harmonic generation of a vortex beam using a GaN slab embedded with a hexagonal lattice of air holes [155]. This obtained quasi-BIC supported nonlinear interaction with tremendous gain efficiency features the robust engineering of nonlinear photonics and integrated optical circuits.

4.10 Imaging

The trapped mode with an infinite quality factor has been realized using various photonic crystal and metasurfaces structures in visible and IR regions. It can serve very high RI sensitivity-based imaging and a high figure of merit. On the other hand, metasurface shows superior excellency in wavefront modulation that can enable image generation either by holography method or near field interaction, carrying out the structural information of nanostructures [271], [272], [273]. L. Xu et al. experimentally demonstrated the dynamic switching of images employing the quasi-BIC modes formed due to collective MD resonance in an ultrathin silicon nonlinear metasurface as shown in Figure 11C(i and ii) [98]. The quasi-BIC MD state efficiently enhances the THG efficiency, offering ease in controlling the nonlinear emission, further utilized for nonlinear image switching. The image of the arrow shape encoded into the metasurfaces, tuned with polarization and wavelength of quasi-BIC MD state is shown in Figure 11C(iii). Such modulation in images by polarization and wavelength tuning show a promising approach for tuneable displays and hologram-based applications. Further, hybrid configurations have adopted establishing the imaging function of the phase change material Ge₂Sb₂Te₅-assisted Fano resonant metasurface governed by the quasi-BIC [203].

Plasmonic resonance-based SP-BIC mode realization has been experimentally demonstrated by recording the angle-resolved reflection spectrum with Fourier plane spectroscopy and imaging [202]. The reported work first discusses the confirmation of trapped state through Fourier plane imaging and further assures its presence with PL measurement of the luminescent dyes Rhodamine 6G mixed in a polymer matrix. The plasmonic resonances coupled with PL results in the notable near field and enhanced local density of optical states. The Fourier plane PL images correspond to three PL wavelengths at a particular wavelength (λ = 600 nm, 610 nm, and 620 nm). The break-in PL line at the hybrid-BIC condition is recorded for the yellow dotted circle at λ = 610 nm (closed proximity with perfect BIC), indicating the trapped mode by blocking the leaky channel for PL in TM polarized incident light. On the contrary, a continuous PL line appears in TE polarized incident light, confirming that no BIC state existed in TE polarization.

Alternatively, the high Q-factor of the quasi-BIC mode in the interacting medium offers a higher figure of merit in the advanced imaging process and structural information techniques like hyperspectral imaging. The hyperspectral imaging captures the visuals using a CMOS camera for different wavelengths that create a hyperspectral data cube where each CMOS pixel depicts high-resolution spectral information. Such technique, resolved to atomic-scale recognition of specimen material and structural information, has even potential to figure out the object mapping over the entire specimen region [274]. F. Yesilkoy et al. explored this imaging technique with high-Q factor through quasi-BIC realized in a square unit cell of symmetric Si-nanodisk metasurface [106]. They could effectively detect biomolecules and features of 2D materials at their relevant atomic dimension scale. Subsequently, S. Romano et al. demonstrated synergistic hyperspectral imaging that combines surface-enhanced fluorescence and spectroscopic refractometric sensing for investigating RI imaging on prostate cancer cells cultured directly on the Si₃N₄ PhCs, supported by symmetry protected-BIC [204]. In ref. [205], an experimental demonstration has been performed to revive the structural information of subwavelength structure with certain uncertainties in the sub-nanometer range using the TiO₂ grid polarizer.

4.11 Field enhancement and photodetection

The high Q factor of the BIC modes is proposed for the field enhancement in the resonant structures. The BICs formed in the array of identical dielectric lossy elements demonstrate the enhanced near field. Interestingly, arrays constituted of 10–15 silicon nanospheres can even offer an improved Q-factor of 10³–10⁴ and field enhancement in a broad wavelength range of red to NIR wavelengths [44].

Remarkably, the optical BIC offers a vast enhancement in the quality factor that makes perfect sense to enhance the performance of the photodetectors. A BIC-supported photodetector is capable of increasing its durability and efficiency by minimizing heat dissipations. In 2016, ref. [211] demonstrated quantum well-infrared photodetectors allied with the BIC in a molecular beam epitaxy grown InGaAs/InAlAs lattice-matched to InP. Their investigations reveal faster carrier extraction and narrow photocurrent spectra as an outcome.

Recent advancements in optoelectronic 2D functional material have been explored for photocurrent generation applications [275, 276]. Y. Wang et al. demonstrated a high-speed silicon nitride waveguide backed by BIC using a TMD 2D PtSe₂ on-chip photodetector [212]. Recently, the BIC approach in hot electron-based photodetector designing has been illustrated by W. Wang et al. [210] in Ag/TiO₂ metal–semiconductor. Their investigation predicts higher responsivity enhancement attributed to the BIC-mode confinement and absorption leads to the enhanced photocurrent generation in comparison to the existing hot-electron generation-based photodetector schemes [277], [278], [279].

5 Conclusions

Indeed, the bound state in continuum has been rapidly expanded into a new area of research interest in the last couple of years. Owing to the advancements in nanofabrication technologies, optical BICs have grown to their full potential via experimental realizations, thus leading into several applications as discussed in this review. We have attempted to classify the BIC generation mechanism in the different structural and material mediums in a broader perspective. Our discussion begins with the excitation of different BIC, namely the SP-BIC, FW-BIC, and FP-BIC, with a typical PhC structure and continues to the advanced metasurfaces and plasmonic constituents. Further, it extends to the integrated structures combined with functional materials like transition metal dichalcogenide, graphene, ferroelectric materials, and high index single crystal structures. Moreover, BICs got much attention in dipole resonance-based highly localized states employing its realization in single dipole resonances, coupling of ED and MD resonances, and toroidal-toroidal or toroidal magnetic dipole resonances. Intrinsically, BIC identified as the topologically protected vortex center opens up an exciting avenue of various advanced research interests.

The subwavelength feature sizes attainable via the current state of the arts in photonics, plasmonics, and metamaterials have promoted the upsurge due to its achievable extraordinary quality-factors to boost efficient nanoscale activities in contrast to other resonant leaky modes. The optics associated with the bound state in continuum feature in controlling over wavefront, light intensity, and polarization without diminished optical losses lead to numerous applications. Additionally, sensing using BIC in hybrid opto-plasmonic devices exceeds their pure counterparts (photonics/plasmonics) regarding the achievable figure of merits, as discussed in great depth in this article. Further, the possibilities of tuning engineered geometries enable the accessibility of distinct chiral-BIC modes. Subsequently, the high confinement of BIC modes encourages the designing of nanocavity for various opto-mechanic interactions. Exploiting the close vicinity of a perfect BIC state facilitates enhancement in PL intensity with a strong directionality, sustaining the lasing characteristic and super cavity modes without the requirement of layers of highly reflecting mirror units. In particular, the efficiency of nonlinear harmonic generation with low pump power mediated by the quasi-BIC modes in photonic crystals, individual dielectric subwavelength structures, metasurfaces, and hybrid photonic resonating structures have been witnessed. Moreover, the topological charge control in BIC by tailoring the opto-geometrical parameters and incident illumination sources explore the generation of vortex beam and lasing sources. This review can thus be a first-hand guide to anyone getting introduced to the BICs from a materialistic and application point of view. To our firm belief, the BIC-supported subwavelength can unfold the various nanoscale light–matter interacting phenomena with greater ease in fabrication and compactness, thus paving the way for next-generation device application in the future.

Corresponding author: Joby Joseph, Physics Department, Photonics Research Laboratory, Indian Institute of Technology Delhi, New Delhi 110016, India, E-mail: joby@physics.iitd.ac.in

Acknowledgments

The authors are thankful to the guest editors Prof. Andrey Bogdanov, Prof. Andrea Fratalocchi, and, Prof. Yuri Kivshar for their kind invitation to this special issue. S. Joseph thanks the Ministry of Electronics and Information Technology (MeitY) and Nano Research Facility (NRF) and IIT Delhi for the funding in the form of salary. S. Pandey acknowledges the Ministry of Education, Government of India, and IIT Delhi for support through fellowship. S. Sarkar acknowledges the Department of Science and Technology (DST) for providing INSPIRE fellowship and Dr. habil. Tobias König for support through a salary from his Freigeist Fellowship, Volkswagen Foundation (Germany).

Author contributions: S. Joseph and S. Pandey have written the review, S. Sarkar has constructed and arranged the figures. J. Joseph has supervised the whole work. All authors have reviewed and contributed to the final manuscript.
Research funding: None declared.
Conflict of interest statement: The authors disclose no conflict of interest.

References

[1] E. Wigner and J. von Neumann, “On some peculiar discrete eigenvalues,” Phys. Z., vol. 30, p. 467, 1929.Suche in Google Scholar

[2] F. H. Stillinger, “Potentials supporting positive-energy eigenstates and their application to semiconductor heterostructures,” Phys. B+C, vol. 85, pp. 270–276, 1976. https://doi.org/10.1016/0378-4363(76)90021-8.Suche in Google Scholar

[3] D. R. Herrick, “Construction of bound states in the continuum for epitaxial heterostructure superlattices,” Phys. B+C, vol. 85, pp. 44–50, 1976. https://doi.org/10.1016/0378-4363(76)90097-8.Suche in Google Scholar

[4] A. Albo, D. Fekete, and G. Bahir, “Electronic bound states in the continuum above (Ga,In)(As,N)/(Al,Ga)As quantum wells,” Phys. Rev. B Condens. Matter, vol. 85, pp. 1–8, 2012. https://doi.org/10.1103/physrevb.85.115307.Suche in Google Scholar

[5] C. M. Linton and P. McIver, “Embedded trapped modes in water waves and acoustics,” Wave Motion, vol. 45, pp. 16–29, 2007. https://doi.org/10.1016/j.wavemoti.2007.04.009.Suche in Google Scholar

[6] R. Parker, “Resonance effects in wake shedding from parallel plates: calculation of resonant frequencies,” J. Sound Vib., vol. 5, pp. 330–343, 1967. https://doi.org/10.1016/0022-460x(67)90113-7.Suche in Google Scholar

[7] R. Parker, “Resonance effects in wake shedding from parallel plates: some experimental observations,” J. Sound Vib., vol. 4, pp. 62–72, 1966. https://doi.org/10.1016/0022-460x(66)90154-4.Suche in Google Scholar

[8] C. W. Hsu, B. Zhen, J. Lee, et al.., “Observation of trapped light within the radiation continuum,” Nature, vol. 499, pp. 188–191, 2013. https://doi.org/10.1038/nature12289.Suche in Google Scholar PubMed

[9] S. Longhi and G. Della Valle, “Floquet bound states in the continuum,” Sci. Rep., vol. 3, pp. 1–6, 2013. https://doi.org/10.1038/srep02219.Suche in Google Scholar PubMed PubMed Central

[10] Y. Yang, C. Peng, Y. Liang, Z. Li, and S. Noda, “Analytical perspective for bound states in the continuum in photonic crystal slabs,” Phys. Rev. Lett., vol. 113, pp. 1–5, 2014. https://doi.org/10.1103/PhysRevLett.113.037401.Suche in Google Scholar PubMed

[11] H. Friedrich and D. Wintgen, “Interfering resonances and bound states in the continuum,” Phys. Rev. A, vol. 32, pp. 3231–3242, 1985. https://doi.org/10.1103/physreva.32.3231.Suche in Google Scholar PubMed

[12] S. Weimann, Y. Xu, R. Keil, et al.., “Compact surface fano states embedded in the continuum of waveguide arrays,” Phys. Rev. Lett., vol. 111, pp. 1–5, 2013. https://doi.org/10.1103/PhysRevLett.111.240403.Suche in Google Scholar PubMed

[13] S. Longhi, “Bound states in the continuum in a single-level Fano-Anderson model,” Eur. Phys. J. B, vol. 57, pp. 45–51, 2007. https://doi.org/10.1140/epjb/e2007-00143-2.Suche in Google Scholar

[14] D. C. Marinica, A. G. Borisov, and S. V. Shabanov, “Bound states in the continuum in photonics,” Phys. Rev. Lett., vol. 100, pp. 1–4, 2008. https://doi.org/10.1103/PhysRevLett.100.183902.Suche in Google Scholar PubMed

[15] E. Bulgakov and A. Sadreev, “Formation of bound states in the continuum for a quantum dot with variable width,” Phys. Rev. B Condens. Matter, vol. 83, pp. 1–9, 2011. https://doi.org/10.1103/physrevb.83.235321.Suche in Google Scholar

[16] T. Lepetit and B. Kanté, “Controlling multipolar radiation with symmetries for electromagnetic bound states in the continuum,” Phys. Rev. B Condens. Matter, vol. 90, pp. 1–4, 2014. https://doi.org/10.1103/physrevb.90.241103.Suche in Google Scholar

[17] Y. Plotnik, O. Peleg, F. Dreisow, et al.., “Experimental observation of optical bound states in the continuum,” Phys. Rev. Lett., vol. 107, pp. 28–31, 2011. https://doi.org/10.1103/PhysRevLett.107.183901.Suche in Google Scholar PubMed

[18] R. Gansch, S. Kalchmair, P. Genevet, et al.., “Measurement of bound states in the continuum by a detector embedded in a photonic crystal,” Light Sci. Appl., vol. 5, pp. 1–7, 2016. https://doi.org/10.1038/lsa.2016.147.Suche in Google Scholar PubMed PubMed Central

[19] C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljacic, “Bound states in the continuum,” Nat. Rev. Mater., vol. 1, pp. 1–44, 2016. https://doi.org/10.1038/natrevmats.2016.48.Suche in Google Scholar

[20] K. Koshelev, G. Favraud, A. Bogdanov, Y. Kivshar, and A. Fratalocchi, “Nonradiating photonics with resonant dielectric nanostructures,” Nanophotonics, vol. 8, pp. 725–745, 2019. https://doi.org/10.1515/nanoph-2019-0024.Suche in Google Scholar

[21] K. Koshelev, A. Bogdanov, and Y. Kivshar, “Engineering with bound states in the continuum,” Opt. Photon. News, vol. 31, p. 38, 2020. https://doi.org/10.1364/opn.31.1.000038.Suche in Google Scholar

[22] S. I. Azzam and A. V. Kildishev, “Photonic bound states in the continuum: from basics to applications,” Adv. Opt. Mater., vol. 9, pp. 16–24, 2021. https://doi.org/10.1002/adom.202001469.Suche in Google Scholar

[23] S. Han, L. Cong, Y. K. Srivastava, et al.., “All-dielectric active terahertz photonics driven by bound states in the continuum,” Adv. Mater., vol. 31, pp. 1–14, 2019. https://doi.org/10.1002/adma.201901921.Suche in Google Scholar PubMed

[24] K. Koshelev, A. Bogdanov, and Y. Kivshar, “Meta-optics and bound states in the continuum,” Sci. Bull., vol. 64, pp. 836–842, 2019. https://doi.org/10.1016/j.scib.2018.12.003.Suche in Google Scholar

[25] Y. Peng and S. Liao, Bound States in Continuum and Zero-Index Metamaterials: A Review, 2020. arXiv:200701361.Suche in Google Scholar

[26] A. F. Sadreev, “Interference traps waves in open system: bound states in the continuum,” Rep. Prog. Phys., vol. 84, pp. 055901–0559034, 2021.10.1088/1361-6633/abefb9Suche in Google Scholar PubMed

[27] S. D. Krasikov, A. A. Bogdanov, and I. V. Iorsh, “Nonlinear bound states in the continuum of a one-dimensional photonic crystal slab,” Phys. Rev. B, vol. 97, pp. 1–6, 2018. https://doi.org/10.1103/physrevb.97.224309.Suche in Google Scholar

[28] J. M. Foley, S. M. Young, and J. D. Phillips, “Symmetry-protected mode coupling near normal incidence for narrow-band transmission filtering in a dielectric grating,” Phys. Rev. B Condens. Matter, vol. 89, pp. 1–9, 2014. https://doi.org/10.1103/physrevb.89.165111.Suche in Google Scholar

[29] C. W. Hsu, B. Zhen, S. L. Chua, S. G. Johnson, J. D. Joannopoulos, and M. Soljačić, “Bloch surface eigenstates within the radiation continuum,” Light Sci. Appl., vol. 2, p. e84, 2013. https://doi.org/10.1038/lsa.2013.40.Suche in Google Scholar

[30] S. Joseph, S. Sarkar, S. Khan, and J. Joseph, “Exploring the optical bound state in the continuum in a dielectric grating coupled plasmonic hybrid system,” Adv. Opt. Mater., vol. 2001895, pp. 1–12, 2021. https://doi.org/10.1002/adom.202001895.Suche in Google Scholar

[31] M. V. Rybin, K. L. Koshelev, Z. F. Sadrieva, et al.., “High- Q supercavity modes in subwavelength dielectric resonators,” Phys. Rev. Lett., vol. 119, pp. 1–5, 2017. https://doi.org/10.1103/PhysRevLett.119.243901.Suche in Google Scholar PubMed

[32] S. Mesli, H. Yala, M. Hamidi, A. BelKhir, and F. I. Baida, “High performance for refractive index sensors via symmetry-protected guided mode resonance,” Opt. Express, vol. 29, p. 21199, 2021. https://doi.org/10.1364/oe.424930.Suche in Google Scholar

[33] S. Dai, L. Liu, D. Han, and J. Zi, “From topologically protected coherent perfect reflection to bound states in the continuum,” Phys. Rev. B, vol. 98, pp. 1–5, 2018. https://doi.org/10.1103/physrevb.98.081405.Suche in Google Scholar

[34] L. Yuan and Y. Y. Lu, “Conditional robustness of propagating bound states in the continuum on biperiodic structures,” Phys. Rev. A, vol. 103, 2020, Art no. 043507.10.1103/PhysRevA.103.043507Suche in Google Scholar

[35] F. Wu, J. Wu, Z. Guo, et al.., “Giant enhancement of the goos-hänchen shift assisted by quasibound states in the continuum,” Phys. Rev. Appl., vol. 12, p. 1, 2019. https://doi.org/10.1103/physrevapplied.12.014028.Suche in Google Scholar

[36] N. Enbamd, “Bound states in the continuum and Fano resonances in the Dirac cone spectrum,” J. Opt. Soc. Am. B, vol. 35, p. 1218, 2018.Suche in Google Scholar

[37] S. Kolodny and I. Iorsh, “Q/V enhancement of micropillar resonator in bound states in the continuum regime,” Opt. Lett., vol. 45, p. 181, 2020. https://doi.org/10.1364/ol.45.000181.Suche in Google Scholar

[38] H. Hemmati and R. Magnusson, “Resonant dual-grating metamembranes supporting spectrally narrow bound states in the continuum,” Adv. Opt. Mater., vol. 7, pp. 1–8, 2019. https://doi.org/10.1002/adom.201900754.Suche in Google Scholar

[39] D. A. Bykov, E. A. Bezus, and L. L. Doskolovich, “Coupled-wave formalism for bound states in the continuum in guided-mode resonant gratings,” Phys. Rev. A, vol. 99, pp. 1–9, 2019. https://doi.org/10.1103/physreva.99.063805.Suche in Google Scholar

[40] E. N. Bulgakov and D. N. Maksimov, “Avoided crossings and bound states in the continuum in low-contrast dielectric gratings,” Phys. Rev. A, vol. 98, pp. 1218–1222, 2018. https://doi.org/10.1364/josab.35.001218.Suche in Google Scholar

[41] E. N. Bulgakov and A. F. Sadreev, “Light trapping above the light cone in a one-dimensional array of dielectric spheres,” Phys. Rev. A: At., Mol., Opt. Phys., vol. 92, pp. 1–11, 2015. https://doi.org/10.1103/physreva.92.023816.Suche in Google Scholar

[42] E. N. Bulgakov and D. N. Maksimov, “Topological bound states in the continuum in arrays of dielectric spheres,” Phys. Rev. Lett., vol. 118, pp. 1–5, 2017. https://doi.org/10.1103/physrevlett.118.267401.Suche in Google Scholar PubMed

[43] H. Zhang, T. Wang, J. Sun, et al., “Quasi-BIC laser enabled by high-contrast grating resonator for gas detection,” Phys. Opt., pp. 1–10, 2021, arXiv:2105.08885.10.1515/nanoph-2021-0368Suche in Google Scholar PubMed

[44] E. N. Bulgakov and D. N. Maksimov, “Light enhancement by quasi-bound states in the continuum in dielectric arrays,” Opt. Express, vol. 25, p. 14134, 2017. https://doi.org/10.1364/oe.25.014134.Suche in Google Scholar

[45] E. N. Bulgakov and A. F. Sadreev, “Bloch bound states in the radiation continuum in a periodic array of dielectric rods,” Phys. Rev. A: At., Mol., Opt. Phys., vol. 90, pp. 1–7, 2014. https://doi.org/10.1103/physreva.90.053801.Suche in Google Scholar

[46] E. N. Bulgakov and D. N. Maksimov, “Bound states in the continuum and polarization singularities in periodic arrays of dielectric rods,” Phys. Rev. A, vol. 96, pp. 1–9, 2017. https://doi.org/10.1103/physreva.96.063833.Suche in Google Scholar

[47] L. Yuan and Y. Y. Lu, “Strong resonances on periodic arrays of cylinders and optical bistability with weak incident waves,” Phys. Rev. A, vol. 95, pp. 1–9, 2017. https://doi.org/10.1103/physreva.95.023834.Suche in Google Scholar

[48] E. N. Bulgakov and A. F. Sadreev, “Nearly bound states in the radiation continuum in a circular array of dielectric rods,” Phys. Rev. A, vol. 97, p. 33834, 2018. https://doi.org/10.1103/physreva.97.033834.Suche in Google Scholar

[49] S. Kim, K. H. Kim, and J. F. Cahoon, “Optical bound states in the continuum with nanowire geometric superlattices,” Phys. Rev. Lett., vol. 122, p. 187402, 2019. https://doi.org/10.1103/physrevlett.122.187402.Suche in Google Scholar

[50] A. Taghizadeh and I. S. Chung, “Quasi bound states in the continuum with few unit cells of photonic crystal slab,” Appl. Phys. Lett., vol. 111, pp. 0311141–0311145, 2017. https://doi.org/10.1063/1.4990753.Suche in Google Scholar

[51] Z. Hu and Y. Y. Lu, “Propagating bound states in the continuum at the surface of a photonic crystal,” J. Opt. Soc. Am. B, vol. 34, p. 1878, 2017. https://doi.org/10.1364/josab.34.001878.Suche in Google Scholar

[52] H. F. Wang, S. K. Gupta, X. Y. Zhu, M. H. Lu, X. P. Liu, and Y. F. Chen, “Bound states in the continuum in a bilayer photonic crystal with TE-TM cross coupling,” Phys. Rev. B, vol. 98, pp. 1–5, 2018. https://doi.org/10.1103/physrevb.98.214101.Suche in Google Scholar

[53] J. Lee, B. Zhen, S. L. Chua, et al.., “Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs,” Phys. Rev. Lett., vol. 109, pp. 1–5, 2012. https://doi.org/10.1103/PhysRevLett.109.067401.Suche in Google Scholar PubMed

[54] A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman, and B. Kanté, “Lasing action from photonic bound states in continuum,” Nature, vol. 541, pp. 196–199, 2017. https://doi.org/10.1038/nature20799.Suche in Google Scholar PubMed

[55] Y. Boretz, G. Ordonez, S. Tanaka, and T. Petrosky, “Optically tunable bound states in the continuum,” Phys. Rev. A: At., Mol., Opt. Phys., vol. 90, pp. 1–9, 2014. https://doi.org/10.1103/physreva.90.023853.Suche in Google Scholar

[56] S.-G. Lee, S.-H. Kim, and C.-S. Kee, “Band dynamics accompanied by bound states in the continuum at the third-order Γ point in leaky-mode photonic lattices,” Photon. Res., vol. 9, p. 1109, 2021. https://doi.org/10.1364/prj.417150.Suche in Google Scholar

[57] L. S. Li and H. Yin, “Bound states in the continuum in double layer structures,” Sci. Rep., vol. 6, pp. 1–8, 2016. https://doi.org/10.1038/srep26988.Suche in Google Scholar PubMed PubMed Central

[58] Z. Li and X. Zhang, “Enhanced optical squeezing from quasi-bound states in the continuum and Fano resonances without nonlinearity,” New J. Phys., vol. 21, p. 123050, 2019. https://doi.org/10.1088/1367-2630/ab5d9f.Suche in Google Scholar

[59] L. Li, Y. Li, Y. Zhu, and H. Yin, “Rotational symmetry of photonic bound states in the continuum,” Sci. Rep., vol. 10, pp. 1–8, 2020. https://doi.org/10.1038/s41598-020-75308-x.Suche in Google Scholar PubMed PubMed Central

[60] S. Neale and E. A. Muljarov, “Accidental and symmetry-protected bound states in the continuum in a photonic-crystal slab: a resonant-state expansion study,” Phys. Rev. B, vol. 103, p. 155112, 2021. https://doi.org/10.1103/physrevb.103.155112.Suche in Google Scholar

[61] L. Yuan and Y. Y. Lu, “Conditional robustness of propagating bound states in the continuum in structures with two-dimensional periodicity,” Phys. Rev. A, vol. 103, pp. 1–10, 2021. https://doi.org/10.1103/physreva.103.043507.Suche in Google Scholar

[62] R. Mermet-Lyaudoz, F. Dubois, N.-V. Hoang, et al.., Realization of Bound State In the Continuum induced by Vertical Symmetry Breaking in Photonic Lattice, 2019, pp. 1–6, arXiv:1905503868v1.Suche in Google Scholar

[63] D. N. Maksimov, V. S. Gerasimov, S. Romano, et al.., “Optical refractive index sensing based on high-Q bound states in the continuum in free-space coupled photonic crystal slabs,” Sensors, vol. 17, p. 38907, 2020. https://doi.org/10.1364/oe.411749.Suche in Google Scholar PubMed

[64] S. Romano, A. Lamberti, M. Masullo, et al.., “Optical biosensors based on photonic crystals supporting bound states in the continuum,” Materials, vol. 11, p. 526, 2018. https://doi.org/10.3390/ma11040526.Suche in Google Scholar PubMed PubMed Central

[65] B. Wang, W. Liu, M. Zhao, et al.., “Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum,” Nat. Photonics, vol. 14, pp. 623–628, 2020. https://doi.org/10.1038/s41566-020-0658-1.Suche in Google Scholar

[66] S. Romano, G. Zito, S. Torino, et al.., “Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum,” Photon. Res., vol. 6, p. 726, 2018. https://doi.org/10.1364/prj.6.000726.Suche in Google Scholar

[67] A. Cerjan, C. W. Hsu, and M. C. Rechtsman, “Bound states in the continuum through environmental design,” Phys. Rev. Lett., vol. 123, p. 23902, 2019. https://doi.org/10.1103/physrevlett.123.023902.Suche in Google Scholar PubMed

[68] Z. Chen, X. Yin, J. Jin, et al.., Observation of Miniaturized Bound States in the Continuum with Ultra-high Quality Factors, 2021. arXiv:210212087.10.1016/j.scib.2021.10.020Suche in Google Scholar

[69] M. Zhao and K. Fang, “Mechanical bound states in the continuum for macroscopic optomechanics,” Opt. Express, vol. 27, p. 10138, 2019. https://doi.org/10.1364/oe.27.010138.Suche in Google Scholar PubMed

[70] E. N. Bulgakov and A. F. Sadreev, “Bound states in the continuum in photonic waveguides inspired by defects,” Phys. Rev. B Condens. Matter, vol. 78, pp. 1–8, 2008. https://doi.org/10.1103/physrevb.78.075105.Suche in Google Scholar

[71] E. N. Bulgakov and A. F. Sadreev, “Bound states in photonic fabry-perot resonator with nonlinear off-channel defects,” Phys. Rev. B Condens. Matter, vol. 81, pp. 1–13, 2010. https://doi.org/10.1103/physrevb.81.115128.Suche in Google Scholar

[72] S. Vaidya, W. A. Benalcazar, A. Cerjan, and M. C. Rechtsman, “Point-defect-localized bound states in the continuum in photonic crystals and structured fibers,” Phys. Rev. Lett., vol. 127, 2021, Art no. 023605. https://doi.org/10.1103/physrevlett.127.023605.Suche in Google Scholar PubMed

[73] Y. X. Xiao, Z. Q. Zhang, and C. T. Chan, “A band of bound states in the continuum induced by disorder,” Sci. Rep., vol. 8, pp. 1–6, 2018. https://doi.org/10.1038/s41598-018-23576-z.Suche in Google Scholar PubMed PubMed Central

[74] F. Monticone and A. Alù, “Embedded photonic eigenvalues in 3D nanostructures,” Phys. Rev. Lett., vol. 112, pp. 1–5, 2014. https://doi.org/10.1103/physrevlett.112.213903.Suche in Google Scholar

[75] L. Y. Pogorelskaya, A. A. Bogdanov, K. B. Samusev, A. D. Sinelnik, and Z. F. Sadrieva, “Bound state in the continuum supported by a low refractive index contrast waveguide in a woodpile structure,” J. Phys.: Conf. Ser., vol. 1092, 2018, Art no. 012118. https://doi.org/10.1088/1742-6596/1092/1/012118.Suche in Google Scholar

[76] S. Dai, P. Hu, and D. Han, “Near-field analysis of bound states in the continuum in photonic crystal slabs,” Opt. Express, vol. 28, p. 16288, 2020. https://doi.org/10.1364/oe.390497.Suche in Google Scholar PubMed

[77] J. Li, J. Ren, and X. Zhang, “Three-dimensional vector wave bound states in a continuum,” J. Opt. Soc. Am. B, vol. 34, p. 559, 2017. https://doi.org/10.1364/josab.34.000559.Suche in Google Scholar

[78] J. W. Yoon, S. H. Song, and R. Magnusson, “Critical field enhancement of asymptotic optical bound states in the continuum,” Sci. Rep., vol. 5, pp. 1–8, 2015. https://doi.org/10.1038/srep18301.Suche in Google Scholar PubMed PubMed Central

[79] X. Cui, H. Tian, Y. Du, G. Shi, and Z. Zhou, “Normal incidence filters using symmetry-protected modes in dielectric subwavelength gratings,” Sci. Rep., vol. 6, pp. 1–6, 2016. https://doi.org/10.1038/srep36066.Suche in Google Scholar PubMed PubMed Central

[80] Z. F. Sadrieva, I. S. Sinev, K. L. Koshelev, et al.., “Transition from optical bound states in the continuum to leaky resonances: role of substrate and roughness,” ACS Photonics, vol. 4, pp. 723–727, 2017. https://doi.org/10.1021/acsphotonics.6b00860.Suche in Google Scholar

[81] S. G. Lee, C. S. Kee, and S. H. Kim, “Bound states in the continuum (BIC) accompanied by avoided crossings in leaky-mode photonic lattices,” Nanophotonics, vol. 9, pp. 4373–4380, 2020. https://doi.org/10.1515/nanoph-2020-0346.Suche in Google Scholar

[82] S. Romano, G. Zito, S. N. Lara Yépez, et al.., “Tuning the exponential sensitivity of a bound-state-in-continuum optical sensor,” Opt. Express, vol. 27, p. 18776, 2019. https://doi.org/10.1364/oe.27.018776.Suche in Google Scholar

[83] A. Arbabi, Y. Horie, M. Bagheri, and A. Faraon, “Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission,” Nat. Nanotechnol., vol. 10, pp. 937–943, 2015. https://doi.org/10.1038/nnano.2015.186.Suche in Google Scholar PubMed

[84] Y. Wang, Z. Han, Y. Du, and J. Qin, “Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface,” Nanophotonics, vol. 10, pp. 1295–1307, 2021. https://doi.org/10.1515/nanoph-2020-0582.Suche in Google Scholar

[85] M. Liu and D. Y. Choi, “Extreme Huygens’ metasurfaces based on quasi-bound states in the continuum,” Nano Lett., vol. 18, pp. 8062–8069, 2018. https://doi.org/10.1021/acs.nanolett.8b04774.Suche in Google Scholar PubMed

[86] M. V. Gorkunov, A. A. Antonov, and Y. S. Kivshar, “Metasurfaces with maximum chirality empowered by bound states in the continuum,” Phys. Rev. Lett., vol. 125, p. 93903, 2020. https://doi.org/10.1103/physrevlett.125.093903.Suche in Google Scholar

[87] X. Chen and W. Fan, “Tunable bound states in the continuum in all-dielectric terahertz metasurfaces,” Nanomaterials, vol. 10, pp. 1–11, 2020. https://doi.org/10.3390/nano10040623.Suche in Google Scholar PubMed PubMed Central

[88] K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov, and Y. Kivshar, “Asymmetric metasurfaces with high- Q resonances governed by bound states in the continuum,” Phys. Rev. Lett., vol. 121, p. 193903, 2018. https://doi.org/10.1103/physrevlett.121.193903.Suche in Google Scholar PubMed

[89] N. Muhammad, Y. Chen, C. W. Qiu, and G. P. Wang, “Optical bound states in continuum in MoS2-based metasurface for directional light emission,” Nano Lett., vol. 21, pp. 967–972, 2021. https://doi.org/10.1021/acs.nanolett.0c03818.Suche in Google Scholar PubMed

[90] M. Wang, B. Li, and W. Wang, “Symmetry-protected dual quasi-bound states in the continuum with high tunability in metasurface,” J. Opt., vol. 22, 2020, Art no. 1900383. https://doi.org/10.1088/2040-8986/abc1fb.Suche in Google Scholar

[91] T. Shi, Z.-L. Deng, Q.-A. Tu, Y. Cao, and X. Li, “Displacement-mediated bound states in the continuum in all-dielectric superlattice metasurfaces,” PhotoniX, vol. 2, pp. 7–16, 2021. https://doi.org/10.1186/s43074-021-00029-x.Suche in Google Scholar

[92] A. S. Kupriianov, Y. Xu, A. Sayanskiy, V. Dmitriev, Y. S. Kivshar, and V. R. Tuz, “Metasurface engineering through bound states in the continuum,” Phys. Rev. Appl., vol. 12, pp. 1–8, 2019. https://doi.org/10.1103/physrevapplied.12.014024.Suche in Google Scholar

[93] A. Leitis, A. Heßler, S. Wahl, et al.., “All-dielectric programmable Huygens’ metasurfaces,” Adv. Funct. Mater., vol. 30, 2020, Art no. 1910259. https://doi.org/10.1002/adfm.201910259.Suche in Google Scholar

[94] E. Melik-Gaykazyan, K. Koshelev, J. H. Choi, et al.., “From fano to quasi-BIC resonances in individual dielectric nanoantennas,” Nano Lett., vol. 21, pp. 1765–1771, 2021. https://doi.org/10.1021/acs.nanolett.0c04660.Suche in Google Scholar PubMed

[95] K. Koshelev, Y. Tang, K. Li, D. Y. Choi, G. Li, and Y. Kivshar, “Nonlinear metasurfaces governed by bound states in the continuum,” ACS Photonics, vol. 6, pp. 1639–1644, 2019. https://doi.org/10.1021/acsphotonics.9b00700.Suche in Google Scholar

[96] G. Zograf, A. Zalogina, K. Koshelev, et al.., “High-harmonic generation in dielectric metasurfaces empowered by bound states in the continuum,” in Opt InfoBase Conf Pap, 2020, Part F182.10.1364/CLEO_QELS.2020.FTh1C.5Suche in Google Scholar

[97] Z. Liu, Y. Xu, Y. Lin, et al.., “High- Q quasibound states in the continuum for nonlinear metasurfaces,” Phys. Rev. Lett., vol. 123, pp. 1–6, 2019. https://doi.org/10.1103/physrevlett.123.253901.Suche in Google Scholar PubMed

[98] L. Xu, K. Zangeneh Kamali, L. Huang, et al.., “Dynamic nonlinear image tuning through magnetic dipole quasi-BIC ultrathin resonators,” Adv. Sci., vol. 6, 2019, Art no. 1802119. https://doi.org/10.1002/advs.201802119.Suche in Google Scholar PubMed PubMed Central

[99] L. Carletti, S. S. Kruk, A. A. Bogdanov, C. De Angelis, and Y. Kivshar, “High-harmonic generation at the nanoscale boosted by bound states in the continuum,” Phys. Rev. Res., vol. 1, pp. 1–7, 2019. https://doi.org/10.1103/physrevresearch.1.023016.Suche in Google Scholar

[100] A. P. Anthur, H. Zhang, R. Paniagua-Dominguez, et al.., “Continuous wave second harmonic generation enabled by quasi-bound-states in the continuum on gallium phosphide metasurfaces,” Nano Lett., vol. 20, pp. 8745–8751, 2020. https://doi.org/10.1021/acs.nanolett.0c03601.Suche in Google Scholar PubMed

[101] Y. Chen, C. Zhao, Y. Zhang, and C. W. Qiu, “Integrated molar chiral sensing based on high- Q metasurface,” Nano Lett., vol. 20, pp. 8696–8703, 2020. https://doi.org/10.1021/acs.nanolett.0c03506.Suche in Google Scholar PubMed

[102] K. Koshelev, Y. Jahani, A. Tittl, H. Altug, and Y. Kivshar, “Enhanced circular dichroism and chiral sensing with bound states in the continuum,” in 2019 Conf Lasers Electro-Optics, CLEO 2019 - Proc, 2019, pp. 4–5.10.1364/CLEO_QELS.2019.FTh4C.6Suche in Google Scholar

[103] S. I. Azzam, K. Chaudhuri, A. Lagutchev, et al.., “Single and multi-mode directional lasing from arrays of dielectric nanoresonators,” Laser Photon. Rev., vol. 15, 2021, Art no. 2000411. https://doi.org/10.1002/lpor.202000411.Suche in Google Scholar

[104] M. Wu, S. T. Ha, S. Shendre, et al.., “Room-temperature lasing in colloidal nanoplatelets via mie-resonant bound states in the continuum,” Nano Lett., vol. 20, pp. 6005–6011, 2020. https://doi.org/10.1021/acs.nanolett.0c01975.Suche in Google Scholar PubMed

[105] D. R. Abujetas, Á. Barreda, F. Moreno, et al.., “Brewster quasi bound states in the continuum in all-dielectric metasurfaces from single magnetic-dipole resonance meta-atoms,” Sci. Rep., vol. 9, pp. 1–11, 2019. https://doi.org/10.1038/s41598-019-52223-4.Suche in Google Scholar PubMed PubMed Central

[106] F. Yesilkoy, E. R. Arvelo, Y. Jahani, et al.., “Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces,” Nat. Photonics, vol. 13, pp. 390–396, 2019. https://doi.org/10.1038/s41566-019-0394-6.Suche in Google Scholar

[107] D. R. Abujetas, Á. Barreda, F. Moreno, A. Litman, J. M. Geffrin, and J. A. Sánchez-Gil, “High-Q transparency band in all-dielectric metasurfaces induced by a quasi bound state in the continuum,” Laser Photon. Rev., vol. 15, pp. 1–8, 2021. https://doi.org/10.1002/lpor.202000263.Suche in Google Scholar

[108] D. Turkpence, G. B. Akguc, A. Bek, and M. E. Tasgin, “Engineering nonlinear response of nanomaterials using Fano resonances,” J. Opt., vol. 16, p. 105009, 2014. https://doi.org/10.1088/2040-8978/16/10/105009.Suche in Google Scholar

[109] X. Chen, W. Fan, and H. Yan, “Toroidal dipole bound states in the continuum metasurfaces for terahertz nanofilm sensing,” Opt. Express, vol. 28, p. 17102, 2020. https://doi.org/10.1364/oe.394416.Suche in Google Scholar PubMed

[110] Z. Zhang, Q. Yang, M. Gong, and Z. Long, “Toroidal dipolar bound state in the continuum and antiferromagnetic in asymmetric metasurface,” J. Phys. D Appl. Phys., vol. 53, 2020, Art no. 075106. https://doi.org/10.1088/1361-6463/ab5983.Suche in Google Scholar

[111] R. Dallapiccola, C. Dubois, A. Gopinath, F. Stellacci, and L. Dal Negro, “Near-field excitation and near-field detection of propagating surface plasmon polaritons on Au waveguide structures,” Appl. Phys. Lett., vol. 94, pp. 24–26, 2009. https://doi.org/10.1063/1.3152291.Suche in Google Scholar

[112] H. K. Gandhi, A. Laha, and S. Ghosh, “Ultrasensitive light confinement: driven by multiple bound states in the continuum,” Phys. Rev. A, vol. 102, pp. 1–6, 2020. https://doi.org/10.1103/physreva.102.033528.Suche in Google Scholar

[113] T. Liu, R. Xu, P. Yu, Z. Wang, and J. Takahara, “Multipole and multimode engineering in Mie resonance-based metastructures,” Nanophotonics, vol. 9, pp. 1115–1137, 2020. https://doi.org/10.1515/nanoph-2019-0505.Suche in Google Scholar

[114] S. G. Lee, S. H. Kim, and C. S. Kee, “Metasurfaces with bound states in the continuum enabled by eliminating first fourier harmonic component in lattice parameters,” Phys. Rev. Lett., vol. 126, p. 13601, 2021. https://doi.org/10.1103/physrevlett.126.013601.Suche in Google Scholar

[115] M. M. Salary and H. Mosallaei, “Tunable all-dielectric metasurfaces for phase-only modulation of transmitted light based on quasi-bound states in the continuum,” ACS Photonics, vol. 7, pp. 1813–1829, 2020. https://doi.org/10.1021/acsphotonics.0c00554.Suche in Google Scholar

[116] Z. Sadrieva, K. Frizyuk, M. Petrov, Y. Kivshar, and A. Bogdanov, “Multipolar origin of bound states in the continuum,” Phys. Rev. B, vol. 100, pp. 1–12, 2019. https://doi.org/10.1103/physrevb.100.115303.Suche in Google Scholar

[117] J. F. Algorri, F. Dell’Olio, P. Roldán-Varona, et al.., “Strongly resonant silicon slot metasurfaces with symmetry-protected bound states in the continuum,” Opt. Express, vol. 29, p. 10374, 2021. https://doi.org/10.1364/oe.415377.Suche in Google Scholar

[118] D. R. Abujetas, J. Olmos-Trigo, J. J. Sáenz, and J. A. Sánchez-Gil, “Coupled electric and magnetic dipole formulation for planar arrays of particles: resonances and bound states in the continuum for all-dielectric metasurfaces,” Phys. Rev. B, vol. 102, p. 125411, 2020. https://doi.org/10.1103/physrevb.102.125411.Suche in Google Scholar

[119] Y. He, G. Guo, T. Feng, Y. Xu, and A. E. Miroshnichenko, “Toroidal dipole bound states in the continuum,” Phys. Rev. B, vol. 98, pp. 1–6, 2018. https://doi.org/10.1103/physrevb.98.161112.Suche in Google Scholar

[120] B. Li, J. Yao, H. Zhu, G. Cai, and Q. H. Liu, “Asymmetric excitations of toroidal dipole resonance and the magnetic dipole quasi-bound state in the continuum in an all-dielectric metasurface,” Opt. Mater. Express, vol. 11, p. 2359, 2021.10.1364/OME.430723Suche in Google Scholar

[121] J. Gomis-Bresco, D. Artigas, and L. Torner, “Anisotropy-induced photonic bound states in the continuum,” Nat. Photonics, vol. 11, pp. 232–236, 2017. https://doi.org/10.1038/nphoton.2017.31.Suche in Google Scholar

[122] I. V. Timofeev, D. N. Maksimov, and A. F. Sadreev, “Optical defect mode with tunable Q factor in a one-dimensional anisotropic photonic crystal,” Phys. Rev. B, vol. 97, pp. 1–7, 2018. https://doi.org/10.1103/physrevb.97.024306.Suche in Google Scholar

[123] S. Mukherjee, J. Gomis-Bresco, P. Pujol-Closa, D. Artigas, and L. Torner, “Topological properties of bound states in the continuum in geometries with broken anisotropy symmetry,” Phys. Rev. A, vol. 98, pp. 1–9, 2018. https://doi.org/10.1103/physreva.98.063826.Suche in Google Scholar

[124] S. Mukherjee, J. Gomis-Bresco, P. Pujol-Closa, D. Artigas, and L. Torner, “Angular control of anisotropy-induced bound states in the continuum,” Opt. Lett., vol. 44, p. 5362, 2019. https://doi.org/10.1364/ol.44.005362.Suche in Google Scholar

[125] P. S. Pankin, D. N. Maksimov, K. P. Chen, and I. V. Timofeev, “Fano feature induced by a bound state in the continuum via resonant state expansion,” Sci. Rep., vol. 10, pp. 1–10, 2020. https://doi.org/10.1038/s41598-020-70654-2.Suche in Google Scholar PubMed PubMed Central

[126] P. S. Pankin, B. R. Wu, J. H. Yang, K. P. Chen, I. V. Timofeev, and A. F. Sadreev, “One-dimensional photonic bound states in the continuum,” Commun. Phys., vol. 3, pp. 1–8, 2020. https://doi.org/10.1038/s42005-020-0353-z.Suche in Google Scholar

[127] M. Zhang and X. Zhang, “Ultrasensitive optical absorption in graphene based on bound states in the continuum,” Sci. Rep., vol. 5, pp. 3–8, 2015. https://doi.org/10.1038/srep08266.Suche in Google Scholar PubMed PubMed Central

[128] L. H. Guessi, R. S. MacHado, Y. Marques, et al.., “Catching the bound states in the continuum of a phantom atom in graphene,” Phys. Rev. B Condens. Matter, vol. 92, pp. 1–8, 2015. https://doi.org/10.1103/physrevb.92.045409.Suche in Google Scholar

[129] J. Hu, X. Zhao, Y. Lin, et al.., “All-dielectric metasurface circular dichroism waveplate,” Sci. Rep., vol. 7, pp. 1–9, 2017. https://doi.org/10.1038/srep41893.Suche in Google Scholar PubMed PubMed Central

[130] Z. Yu, Y. Wang, B. Sun, et al.., “Hybrid 2D-material photonics with bound states in the continuum,” Adv. Opt. Mater., vol. 7, pp. 1–7, 2019. https://doi.org/10.1002/adom.201901306.Suche in Google Scholar

[131] X. Wang, J. Duan, W. Chen, C. Zhou, T. Liu, and S. Xiao, “Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance,” Phys. Rev. B, vol. 102, pp. 1–7, 2020. https://doi.org/10.1103/physrevb.102.155432.Suche in Google Scholar

[132] S. Xiao, X. Wang, J. Duan, T. Liu, and T. Yu, “Engineering light absorption at critical coupling via bound states in the continuum,” J. Opt. Soc. Am. B, vol. 38, p. 1325, 2021. https://doi.org/10.1364/josab.419191.Suche in Google Scholar

[133] Z. Ye, T. Cao, K. O’Brien, et al.., “Probing excitonic dark states in single-layer tungsten disulphide,” Nature, vol. 513, pp. 214–218, 2014. https://doi.org/10.1038/nature13734.Suche in Google Scholar PubMed

[134] K. L. Koshelev, S. K. Sychev, Z. F. Sadrieva, A. A. Bogdanov, and I. V. Iorsh, “Light-matter interaction between photonic bound states in the continuum and bright excitons in transition metal dichalcogenides,” J. Phys.: Conf. Ser., vol. 1092, pp. 012064–012069, 2018. https://doi.org/10.1088/1742-6596/1092/1/012064.Suche in Google Scholar

[135] T. Wang, Z. Li, and X. Zhang, “Improved generation of correlated photon pairs from monolayer WS 2 based on bound states in the continuum,” Photon. Res., vol. 7, p. 341, 2019. https://doi.org/10.1364/prj.7.000341.Suche in Google Scholar

[136] Q. Ren, F. Feng, X. Yao, et al.., “Multiplexing-oriented plasmon-MoS2 hybrid metasurfaces driven by nonlinear quasi bound states in the continuum,” Opt. Express, vol. 29, p. 5384, 2021. https://doi.org/10.1364/oe.414730.Suche in Google Scholar

[137] S. Cao, H. Dong, H. Dong, et al.., “Normal-incidence-excited strong coupling between excitons and symmetry-protected quasi-bound states in the continuum in silicon nitride-WS2Heterostructures at room temperature,” J. Phys. Chem. Lett., vol. 11, pp. 4631–4638, 2020. https://doi.org/10.1021/acs.jpclett.0c01080.Suche in Google Scholar PubMed

[138] V. Kravtsov, E. Khestanova, F. A. Benimetskiy, et al.., “Nonlinear polaritons in a monolayer semiconductor coupled to optical bound states in the continuum,” Light Sci. Appl., vol. 9, p. 56, 2020. https://doi.org/10.1038/s41377-020-0286-z.Suche in Google Scholar PubMed PubMed Central

[139] F. A. Benimetskiy, V. Kravtsov, E. Khestanova, et al.., “Strong coupling of excitons in 2D MoSe2/hBN heterostructure with optical bound states in the continuum,” J. Phys.: Conf. Ser., vol. 1461, pp. 8–11, 2020. https://doi.org/10.1088/1742-6596/1461/1/012012.Suche in Google Scholar

[140] S. A. I. D. R. Ahimzadeh, A. R. Odriguez, F. R. J. G. A. Idal, and J. A. G. Ó. R. Ivas, “Plasmon-exciton-polariton lasing,” Optica, vol. 4, pp. 22–27, 2017.Suche in Google Scholar

[141] E. Penzo, S. Romano, Y. Wang, et al.., “Patterning of electrically tunable light-emitting photonic structures demonstrating bound states in the continuum,” J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., vol. 35, 2017, Art no. 06G401. https://doi.org/10.1116/1.4994849.Suche in Google Scholar

[142] C. L. Zou, J. M. Cui, F. W. Sun, et al.., “Guiding light through optical bound states in the continuum for ultrahigh-Q microresonators,” Laser Photon. Rev., vol. 9, pp. 114–119, 2015. https://doi.org/10.1002/lpor.201400178.Suche in Google Scholar

[143] Z. Yu, X. Xi, J. Ma, H. K. Tsang, C.-L. Zou, and X. Sun, “Photonic integrated circuits with bound states in the continuum,” Optica, vol. 6, p. 1342, 2019. https://doi.org/10.1364/optica.6.001342.Suche in Google Scholar

[144] Z. Yu, Y. Tong, H. K. Tsang, and X. Sun, “High-dimensional communication on etchless lithium niobate platform with photonic bound states in the continuum,” Nat. Commun., vol. 11, pp. 1–9, 2020. https://doi.org/10.1038/s41467-020-15358-x.Suche in Google Scholar PubMed PubMed Central

[145] Q. Yang, Y. Liu, X. Gan, C. Fang, G. Han, and Y. Hao, “Nonlinear bound states in the continuum of etchless lithium niobate metasurfaces,” IEEE Photonics J., vol. 12, pp. 1–9, 2020. https://doi.org/10.1109/jphot.2020.3024789.Suche in Google Scholar

[146] A. Henkel, M. Meudt, A. Henkel, M. Meudt, and H. Modes, Electrically Switchable Broadband Photonic Bound States in the Continuum, 2021. arXiv:210201686.Suche in Google Scholar

[147] G. Y. Chen, Z. X. Li, Y. H. Chen, and X. D. Zhang, “Highly efficient polarization-entangled photon-pair generation in lithium niobate waveguides based on bound states in continuum,” Opt. Express, vol. 29, p. 12110, 2021. https://doi.org/10.1364/oe.420792.Suche in Google Scholar PubMed

[148] N. Bernhardt, K. Koshelev, S. J. U. White, et al.., “Quasi-BIC resonant enhancement of second-harmonic generation in WS2Monolayers,” Nano Lett., vol. 20, pp. 5309–5314, 2020. https://doi.org/10.1021/acs.nanolett.0c01603.Suche in Google Scholar PubMed

[149] T. Wang, and S. Zhang, “Large enhancement of second harmonic generation from transition-metal dichalcogenide monolayer on grating near bound states in the continuum,” Opt. Express, vol. 26, p. 322, 2018. https://doi.org/10.1364/oe.26.000322.Suche in Google Scholar PubMed

[150] L. Carletti, K. Koshelev, C. De Angelis, and Y. Kivshar, “Giant nonlinear response at the nanoscale driven by bound states in the continuum,” Phys. Rev. Lett., vol. 121, p. 33903, 2018. https://doi.org/10.1103/physrevlett.121.033903.Suche in Google Scholar

[151] K. Koshelev, S. Kruk, E. Melik-Gaykazyan, et al.., “Individual nanoantennas empowered by bound states in the continuum for nonlinear photonics,” Science, vol. 367, pp. 288–292, 2019.10.1126/science.aaz3985Suche in Google Scholar PubMed

[152] K. N. Pichugin and A. F. Sadreev, “Frequency comb generation by symmetry-protected bound state in the continuum,” J. Opt. Soc. Am. B, vol. 32, p. 1630, 2015. https://doi.org/10.1364/josab.32.001630.Suche in Google Scholar

[153] I. Volkovskaya, L. Xu, L. Huang, A. I. Smirnov, A. E. Miroshnichenko, and D. Smirnova, “Multipolar second-harmonic generation from high-Q quasi-BIC states in subwavelength resonators,” Nanophotonics, vol. 9, pp. 3953–3963, 2020. https://doi.org/10.1515/nanoph-2020-0156.Suche in Google Scholar

[154] M. Minkov, D. Gerace, and S. Fan, “Doubly resonant χ (2) nonlinear photonic crystal cavity based on a bound state in the continuum,” Optica, vol. 6, p. 1039, 2019. https://doi.org/10.1364/optica.6.001039.Suche in Google Scholar

[155] J. Wang, M. Clementi, M. Minkov, et al.., “Doubly resonant second-harmonic generation of a vortex beam from a bound state in the continuum,” Optica, vol. 7, p. 1126, 2020. https://doi.org/10.1364/optica.396408.Suche in Google Scholar

[156] S. Joseph, M. S. Khan, and A. K. Hafiz, “Compression of ultra-short pulses due to cascaded second order nonlinearities in photonic bandgap structures,” Eur. Phys. J. D, vol. 70, pp. 1–8, 2016. https://doi.org/10.1140/epjd/e2016-60442-1.Suche in Google Scholar

[157] J.-H. Yang, D. N. Maksimov, Z.-T. Huang, et al.., “Low threshold bound state in the continuum lasers in hybrid lattice resonance metasurfaces,” Laser Photonics Rev., pp. 1–18, 2020. https://doi.org/10.1002/lpor.202100118.Suche in Google Scholar

[158] L. Michaeli, S. Keren-Zur, O. Avayu, H. Suchowski, and T. Ellenbogen, “Nonlinear surface lattice resonance in plasmonic nanoparticle arrays,” Phys. Rev. Lett., vol. 118, pp. 1–6, 2017. https://doi.org/10.1103/PhysRevLett.118.243904.Suche in Google Scholar PubMed

[159] H. Linnenbank, Y. Grynko, J. Förstner, and S. Linden, “Second harmonic generation spectroscopy on hybrid plasmonic/dielectric nanoantennas,” Light Sci. Appl., vol. 5, p. e16013, 2016. https://doi.org/10.1038/lsa.2016.13.Suche in Google Scholar PubMed PubMed Central

[160] D. O. Ignatyeva, and V. I. Belotelov, “Bound states in the continuum enable modulation of light intensity in the Faraday configuration,” Opt. Lett., vol. 45, p. 6422, 2020. https://doi.org/10.1364/ol.404159.Suche in Google Scholar PubMed

[161] F. Van Beijnum, P. J. Van Veldhoven, E. J. Geluk, M. J. A. De Dood, G. W. T. Hooft, and M. P. Van Exter, “Surface plasmon lasing observed in metal hole arrays,” Phys. Rev. Lett., vol. 110, pp. 1–5, 2013. https://doi.org/10.1103/PhysRevLett.110.206802.Suche in Google Scholar PubMed

[162] S. Joseph, S. Sarkar, and J. Joseph, “Grating-coupled surface plasmon-polariton sensing at a flat metal-analyte interface in a hybrid-configuration,” ACS Appl. Mater. Interfaces, vol. 12, pp. 46519–46529, 2020. https://doi.org/10.1021/acsami.0c12525.Suche in Google Scholar PubMed

[163] T. K. Hakala, H. T. Rekola, A. I. Väkeväinen, et al.., “Lasing in dark and bright modes of a finite-sized plasmonic lattice,” Nat. Commun., vol. 8, pp. 1–7, 2017. https://doi.org/10.1038/ncomms13687.Suche in Google Scholar PubMed PubMed Central

[164] F. Monticone and A. Alù, “Bound states within the radiation continuum in diffraction gratings and the role of leaky modes,” New J. Phys., vol. 19, p. 93011, 2017. https://doi.org/10.1088/1367-2630/aa849f.Suche in Google Scholar

[165] A. Pavlov, I. Zabkov, and V. Klimov, “Lasing threshold of the bound states in the continuum in the plasmonic lattices,” Opt. Express, vol. 26, p. 28948, 2018. https://doi.org/10.1364/oe.26.028948.Suche in Google Scholar PubMed

[166] W. Zhang, C. Aaron, M. Nagai, M. D. Mittleman, and MR, “Extraordinary optical reflection resonances and bound states in the continuum from a from a Periodic Array of Thin Metal Plates,” Opt. Express, vol. 26, pp. 213–222, 2018. https://doi.org/10.1364/OE.26.013195.Suche in Google Scholar PubMed

[167] S. Sun, Y. Ding, H. Li, et al.., “Tunable plasmonic bound states in the continuum in the visible range,” Phys. Rev. B, vol. 103, pp. 1–9, 2021. https://doi.org/10.1103/physrevb.103.045416.Suche in Google Scholar

[168] Q. Song, M. Zhao, L. Liu, et al.., “Observation of bound states in the continuum in the dimerized chain,” Phys. Rev. A, vol. 100, pp. 1–7, 2019. https://doi.org/10.1103/physreva.100.023810.Suche in Google Scholar

[169] R. Kikkawa, M. Nishida, and Y. Kadoya, “Polarization-based branch selection of bound states in the continuum in dielectric waveguide modes anti-crossed by a metal grating,” New J. Phys., vol. 21, p. 113020, 2019. https://doi.org/10.1088/1367-2630/ab4f54.Suche in Google Scholar

[170] J. Zhang, Y. Kosugi, A. Otomo, Y. Nakano, and T. Tanemura, “Active metasurface modulator with electro-optic polymer using bimodal plasmonic resonance,” Opt. Express, vol. 25, p. 30304, 2017. https://doi.org/10.1364/oe.25.030304.Suche in Google Scholar

[171] D. R. Abujetas, N. van Hoof, S. ter Huurne, J. Gómez Rivas, and J. A. Sánchez-Gil, “Spectral and temporal evidence of robust photonic bound states in the continuum on terahertz metasurfaces,” Optica, vol. 6, p. 996, 2019. https://doi.org/10.1364/optica.6.000996.Suche in Google Scholar

[172] Y. Liang, K. Koshelev, F. Zhang, et al.., “Bound states in the continuum in anisotropic plasmonic metasurfaces,” Nano Lett., vol. 20, pp. 6351–6356, 2020. https://doi.org/10.1021/acs.nanolett.0c01752.Suche in Google Scholar PubMed

[173] L. Cong and R. Singh, “Symmetry-protected dual bound states in the continuum in metamaterials,” Adv. Opt. Mater., vol. 7, pp. 1–7, 2019.10.1002/adom.201900383Suche in Google Scholar

[174] X. Zhao, C. Chen, K. Kaj, et al.., “Terahertz investigation of bound states in the continuum of metallic metasurfaces,” Optica, vol. 7, p. 1548, 2020. https://doi.org/10.1364/optica.404754.Suche in Google Scholar

[175] J. Niu, Y. Zhai, Q. Han, J. Liu, and B. Yang, “Resonance-trapped bound states in the continuum in metallic THz metasurfaces,” Opt. Lett., vol. 46, p. 162, 2021. https://doi.org/10.1364/ol.410791.Suche in Google Scholar

[176] C. Kyaw, R. Yahiaoui, J. A. Burrow, et al.., “Polarization-selective modulation of supercavity resonances originating from bound states in the continuum,” Commun. Phys., vol. 3, pp. 1–8, 2020. https://doi.org/10.1364/cleo_qels.2020.fm4b.1.Suche in Google Scholar

[177] Y. K. Srivastava, R. T. Ako, M. Gupta, M. Bhaskaran, S. Sriram, and R. Singh, “Terahertz sensing of 7 nm dielectric film with bound states in the continuum metasurfaces,” Appl. Phys. Lett., vol. 115, pp. 1511051–1511055, 2019. https://doi.org/10.1063/1.5110383.Suche in Google Scholar

[178] J. Zhang, W. Bai, L. Cai, Y. Xu, G. Song, and Q. Gan, “Observation of ultra-narrow band plasmon induced transparency based on large-area hybrid plasmon-waveguide systems,” Appl. Phys. Lett., vol. 99, pp. 1–4, 2011. https://doi.org/10.1063/1.3659309.Suche in Google Scholar

[179] S. I. Azzam, V. M. Shalaev, A. Boltasseva, and A. V. Kildishev, “Formation of bound states in the continuum in hybrid plasmonic-photonic systems,” Phys. Rev. Lett., vol. 121, pp. 1–6, 2018. https://doi.org/10.1103/PhysRevLett.121.253901.Suche in Google Scholar PubMed

[180] J. Xiang, Y. Xu, J. D. Chen, and S. Lan, “Tailoring the spatial localization of bound state in the continuum in plasmonic-dielectric hybrid system,” Nanophotonics, vol. 9, pp. 133–142, 2020. https://doi.org/10.1515/nanoph-2019-0341.Suche in Google Scholar

[181] R. Kikkawa, M. Nishida, and Y. Kadoya, “Bound states in the continuum and exceptional points in dielectric waveguide equipped with a metal grating,” New J. Phys., vol. 22, 2020, Art no. 073029. https://doi.org/10.1088/1367-2630/ab97e9.Suche in Google Scholar

[182] M. Meudt, C. Bogiadzi, K. Wrobel, and P. Görrn, “Hybrid photonic–plasmonic bound states in continuum for enhanced light manipulation,” Adv. Opt. Mater., vol. 8, pp. 1–7, 2020. https://doi.org/10.1002/adom.202000898.Suche in Google Scholar

[183] L. Hsu, F. I. Baida, and A. Ndao, “Local field enhancement using a photonic-plasmonic nanostructure,” Opt. Express, vol. 29, p. 1102, 2021. https://doi.org/10.1364/oe.415956.Suche in Google Scholar

[184] B. Zhen, C. W. Hsu, L. Lu, A. D. Stone, and M. Soljačić, “Topological nature of optical bound states in the continuum,” Phys. Rev. Lett., vol. 113, pp. 1–5, 2014. https://doi.org/10.1103/PhysRevLett.113.257401.Suche in Google Scholar PubMed

[185] H. M. Doeleman, F. Monticone, W. Den Hollander, A. Alù, and A. F. Koenderink, “Experimental observation of a polarization vortex at an optical bound state in the continuum,” Nat. Photonics, vol. 12, pp. 397–401, 2018. https://doi.org/10.1038/s41566-018-0177-5.Suche in Google Scholar

[186] X. Yin, J. Jin, M. Soljačić, C. Peng, and B. Zhen, “Observation of topologically enabled unidirectional guided resonances,” Nature, vol. 580, pp. 467–471, 2020. https://doi.org/10.1038/s41586-020-2181-4.Suche in Google Scholar PubMed

[187] A. Cerjan, M. Jürgensen, W. A. Benalcazar, S. Mukherjee, and M. C. Rechtsman, “Observation of a higher-order topological bound state in the continuum,” Phys. Rev. Lett., vol. 125, p. 213901, 2020. https://doi.org/10.1103/physrevlett.125.213901.Suche in Google Scholar

[188] J. Jin, X. Yin, L. Ni, M. Soljačić, B. Zhen, and C. Peng, “Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering,” Nature, vol. 574, pp. 501–504, 2019. https://doi.org/10.1038/s41586-019-1664-7.Suche in Google Scholar PubMed

[189] D. A. Bykov, E. A. Bezus, and L. L. Doskolovich, “Bound states in the continuum and strong phase resonances in integrated gires-tournois interferometer,” Nanophotonics, vol. 9, pp. 83–92, 2020. https://doi.org/10.1515/nanoph-2019-0316.Suche in Google Scholar

[190] M. Kang, S. Zhang, M. Xiao, and H. Xu, “Merging bound states in the continuum at off-high symmetry points,” Phys. Rev. Lett., vol. 126, p. 117402, 2021. https://doi.org/10.1103/physrevlett.126.117402.Suche in Google Scholar

[191] A. Overvig, N. Yu, and A. Alù, “Chiral quasi-bound states in the continuum,” Phys. Rev. Lett., vol. 126, p. 73001, 2021. https://doi.org/10.1103/physrevlett.126.073001.Suche in Google Scholar PubMed

[192] J. Mur-Petit and R. A. Molina, “Chiral bound states in the continuum,” Phys. Rev. B Condens. Matter, vol. 90, pp. 1–9, 2014. https://doi.org/10.1103/physrevb.90.035434.Suche in Google Scholar

[193] N. Rivera, C. W. Hsu, B. Zhen, H. Buljan, J. D. Joannopoulos, and M. Soljacic, “Controlling directionality and dimensionality of radiation by perturbing separable bound states in the continuum,” Sci. Rep., vol. 6, pp. 1–7, 2016. https://doi.org/10.1038/srep33394.Suche in Google Scholar PubMed PubMed Central

[194] S. A. Dyakov, M. V. Stepikhova, A. A. Bogdanov, et al.., “Photonic bound states in the continuum in Si structures with the self-assembled Ge nanoislands,” Laser Photon. Rev., vol. 2000242, pp. 1–13, 2021.10.1002/lpor.202000242Suche in Google Scholar

[195] X. Yin, J. Jin, M. Soljačić, C. Peng, and B. Zhen, Observation of Unidirectional Bound States in the Continuum Enabled by Topological Defects, 2019, pp. 0–19.Suche in Google Scholar

[196] H. Xu and Y. Shi, “Diffraction engineering for silicon waveguide grating antenna by harnessing bound state in the continuum,” Nanophotonics, vol. 9, pp. 1439–1446, 2020. https://doi.org/10.1515/nanoph-2020-0018.Suche in Google Scholar

[197] J. Guan, L. K. Sagar, R. Li, et al.., “Engineering directionality in quantum dot shell lasing using plasmonic lattices,” Nano Lett., vol. 20, pp. 1468–1474, 2020. https://doi.org/10.1021/acs.nanolett.9b05342.Suche in Google Scholar PubMed

[198] Y. Wang, Y. Fan, X. Zhang, et al.., “Highly controllable etchless perovskite microlasers based on bound states in the continuum,” ACS Nano, vol. 15, pp. 7386–7391, 2021. https://doi.org/10.1021/acsnano.1c00673.Suche in Google Scholar PubMed

[199] S. T. Ha, Y. H. Fu, N. K. Emani, et al.., “Directional lasing in resonant semiconductor nanoantenna arrays,” Nat. Nanotechnol., vol. 13, pp. 1042–1047, 2018. https://doi.org/10.1038/s41565-018-0245-5.Suche in Google Scholar PubMed

[200] R. Contractor, B. Bahari, F. Vallini, et al.., “Integrable and steerable vortex lasers using bound states in the continuum,” in Front Opt - Proc Front Opt + Laser Sci APS/DLS., 2019.10.1364/FIO.2019.JTu3A.113Suche in Google Scholar

[201] Q. Song, J. Hu, S. Dai, et al.., “Coexistence of a new type of bound state in the continuum and a lasing threshold mode induced by PT symmetry,” Sci. Adv., vol. 6, pp. 1–10, 2020. https://doi.org/10.1126/sciadv.abc1160.Suche in Google Scholar PubMed PubMed Central

[202] I. C. Seo, S. Kim, B. H. Woo, I. S. Chung, and Y. C. Jun, “Fourier-plane investigation of plasmonic bound states in the continuum and molecular emission coupling,” Nanophotonics, vol. 9, pp. 4565–4577, 2020. https://doi.org/10.1515/nanoph-2020-0343.Suche in Google Scholar

[203] C. Zhou, X. Qu, S. Xiao, and M. Fan, “Imaging through a fano-resonant dielectric metasurface governed by quasi - bound states in the continuum,” Phys. Rev. Appl., vol. 14, p. 1, 2020. https://doi.org/10.1103/physrevapplied.14.044009.Suche in Google Scholar

[204] S. Romano, M. Mangini, E. Penzo, et al.., “Ultrasensitive surface refractive index imaging based on quasi-bound states in the continuum,” ACS Nano, vol. 14, pp. 15417–15427, 2020. https://doi.org/10.1021/acsnano.0c06050.Suche in Google Scholar PubMed

[205] T. Siefke, C. B. R. Hurtado, J. Dickmann, et al.., “Quasi-bound states in the continuum for deep subwavelength structural information retrieval for DUV nano-optical polarizers,” Opt. Express, vol. 28, p. 23122, 2020. https://doi.org/10.1364/oe.396044.Suche in Google Scholar

[206] L. L. Doskolovich, E. A. Bezus, and D. A. Bykov, “Integrated flat-top reflection filters operating near bound states in the continuum,” Photon. Res., vol. 7, p. 1314, 2019. https://doi.org/10.1364/prj.7.001314.Suche in Google Scholar

[207] E. A. Bezus, D. A. Bykov, and L. L. Doskolovich, “Bound states in the continuum and high-Q resonances supported by a dielectric ridge on a slab waveguide,” Photon. Res., vol. 6, p. 1084, 2018. https://doi.org/10.1364/prj.6.001084.Suche in Google Scholar

[208] N. Karl, P. P. Vabishchevich, S. Liu, et al., “All-optical tuning of symmetry protected quasi bound states in the continuum,” Appl. Phys. Lett., vol. 115, pp. 1411031–1411035, 2019. https://doi.org/10.1063/1.5116031.Suche in Google Scholar

[209] H. Kwon, T. Zheng, and A. Faraon, “Nano-electromechanical tuning of dual-mode resonant dielectric metasurfaces for dynamic amplitude and phase modulation,” Nano Lett., vol. 21, pp. 2817–2823, 2021. https://doi.org/10.1021/acs.nanolett.0c04888.Suche in Google Scholar PubMed PubMed Central

[210] W. Wang, L. V. Besteiro, P. Yu, et al.., “Plasmonic hot-electron photodetection with quasi-bound states in the continuum and guided resonances,” Nanophotonics, vol. 10, pp. 1911–1921, 2021. https://doi.org/10.1515/nanoph-2021-0069.Suche in Google Scholar

[211] G. M. Penello, A. P. Ravikumar, D. L. Sivco, and C. Gmachl, “Asymmetric multi-quantum well infrared photodetector with a bound state in the continuum,” Opt InfoBase Conf Pap, CLEO: 2014, OSA Technical Digest (online) ,Optical Society of America, paper FM3A.3. pp. 1–2, 2014. https://doi.org/10.1364/cleo_qels.2014.fm3a.3.Suche in Google Scholar

[212] Y. Wang, Z. Yu, Z. Zhang, et al.., “Bound-States-in-Continuum hybrid integration of 2D platinum diselenide on silicon nitride for high-speed photodetectors,” ACS Photonics, vol. 7, pp. 2643–2649, 2020. https://doi.org/10.1021/acsphotonics.0c01233.Suche in Google Scholar

[213] H. Zhou, B. Zhen, C. W. Hsu, et al.., “Perfect single-sided radiation and absorption without mirrors,” Optica, vol. 3, p. 1079, 2016. https://doi.org/10.1364/optica.3.001079.Suche in Google Scholar

[214] Y. Lin, T. Feng, S. Lan, J. Liu, and Y. Xu, “On-chip diffraction-free beam guiding beyond the light cone,” Phys. Rev. Appl., vol. 13, pp. 36–39, 2020. https://doi.org/10.1103/physrevapplied.13.064032.Suche in Google Scholar

[215] X. Gao, B. Zhen, M. Soljačić, H. Chen, and C. W. Hsu, “Bound states in the continuum in fiber Bragg gratings,” ACS Photonics, vol. 6, pp. 2996–3002, 2019. https://doi.org/10.1021/acsphotonics.9b01202.Suche in Google Scholar

[216] E. Bulgakov and A. Sadreev, “Fibers based on propagating bound states in the continuum,” Phys. Rev. B, vol. 98, pp. 1–6, 2018. https://doi.org/10.1103/physrevb.98.085301.Suche in Google Scholar

[217] L. Wang, S. Kruk, K. Koshelev, I. Kravchenko, B. Luther-Davies, and Y. Kivshar, “Nonlinear wavefront control with all-dielectric metasurfaces,” Nano Lett., vol. 18, pp. 3978–3984, 2018. https://doi.org/10.1021/acs.nanolett.8b01460.Suche in Google Scholar PubMed

[218] T. Wang and X. Zhang, “Improved third-order nonlinear effect in graphene based on bound states in the continuum,” Photon. Res., vol. 5, p. 629, 2017. https://doi.org/10.1364/prj.5.000629.Suche in Google Scholar

[219] S. Mohamed, J. Wang, H. Rekola, et al.., Topological Charge Engineering in Lasing Bound States in Continuum, 2020, arXiv:201215642v1.Suche in Google Scholar

[220] J. D. Joannopoulos, S. G. Johnson, J. N. Winn, and R. D. Meade, “Two-Dimensional Photonic Crystals,” in Photonic Crystals: Molding the Flow of Light, 2nd ed. New Jersey, Woodstock, Oxfordshire, Princeton University Press, 2008, pp. 66–92.Suche in Google Scholar

[221] X. Gao, C. W. Hsu, B. Zhen, et al.., “Formation mechanism of guided resonances and bound states in the continuum in photonic crystal slabs,” Sci. Rep., vol. 6, pp. 1–7, 2016. https://doi.org/10.1038/srep31908.Suche in Google Scholar PubMed PubMed Central

[222] A. Ndao, A. Ndao, L. Hsu, et al.., “Differentiating and quantifying exosome secretion from a single cell using quasi-bound states in the continuum,” Nanophotonics, vol. 9, pp. 1081–1086, 2020. https://doi.org/10.1515/nanoph-2020-0008.Suche in Google Scholar

[223] H. T. Chen, A. J. Taylor, and N. Yu, “A review of metasurfaces: physics and applications,” Rep. Prog. Phys., vol. 79, p. 76401, 2016. https://doi.org/10.1088/0034-4885/79/7/076401.Suche in Google Scholar PubMed

[224] M. F. Picardi, A. V. Zayats, and F. J. Rodríguez-fortuño, “Janus and Huygens dipoles: near-field directionality beyond spin-momentum locking,” Phys. Rev. Lett., vol. 120, p. 117402, 2018. https://doi.org/10.1103/physrevlett.120.117402.Suche in Google Scholar PubMed

[225] J. S. Totero Gongora, G. Favraud, and A. Fratalocchi, “Fundamental and high-order anapoles in all-dielectric metamaterials via Fano-Feshbach modes competition,” Nanotechnology, vol. 28, p. 104001, 2017. https://doi.org/10.1088/1361-6528/aa593d.Suche in Google Scholar PubMed

[226] Y. Yang and S. I. Bozhevolnyi, “Nonradiating anapole states in nanophotonics: from fundamentals to applications,” Nanotechnology, vol. 30, p. 204001, 2019. https://doi.org/10.1088/1361-6528/ab02b0.Suche in Google Scholar PubMed

[227] W. Liu and Y. S. Kivshar, “Generalized Kerker effects in nanophotonics and meta-optics [Invited],” Opt. Express, vol. 26, p. 13085, 2018. https://doi.org/10.1364/oe.26.013085.Suche in Google Scholar PubMed

[228] L. Zhu, S. Yuan, C. Zeng, and J. Xia, “Manipulating photoluminescence of Carbon G-center in silicon metasurface with optical bound states in the continuum,” Adv. Opt. Mater., vol. 8, pp. 1–5, 2020. https://doi.org/10.1002/adom.201901830.Suche in Google Scholar

[229] C. Huang, C. Zhang, S. Xiao, et al.., “Ultrafast control of vortex microlasers,” Science, vol. 367, no. 80, pp. 1018–1021, 2020. https://doi.org/10.1126/science.aba4597.Suche in Google Scholar PubMed

[230] A. A. Bogdanov, K. L. Koshelev, P. V. Kapitanova, et al.., “Bound states in the continuum and Fano resonances in the strong mode coupling regime,” Adv. Photonics, vol. 1, p. 1, 2019. https://doi.org/10.1117/1.ap.1.1.016001.Suche in Google Scholar

[231] D. R. Abujetas and J. A. Sánchez-Gil, “Near-field excitation of bound states in the continuum in all-dielectric metasurfaces through a coupled electric/magnetic dipole model,” Nanomaterials, vol. 11, p. 998, 2021. https://doi.org/10.3390/nano11040998.Suche in Google Scholar PubMed PubMed Central

[232] S. Han, P. Pitchappa, W. Wang, Y. K. Srivastava, M. V. Rybin, and R. Singh, “Extended bound states in the continuum with symmetry-broken terahertz dielectric metasurfaces,” Adv. Opt. Mater., vol. 9, pp. 1–9, 2021. https://doi.org/10.1002/adom.202002001.Suche in Google Scholar

[233] R. Paniagua-Domínguez, Y. F. Yu, A. E. Miroshnichenko, et al.., “Generalized Brewster effect in dielectric metasurfaces,” Nat. Commun., vol. 7, p. 10362, 2016.10.1038/ncomms10362Suche in Google Scholar PubMed PubMed Central

[234] W. Liu and Y. S. Kivshar, “Multipolar interference effects in nanophotonics,” Philos. Trans. R. Soc., A, vol. 375, pp. 20160317–14, 2017. https://doi.org/10.1098/rsta.2016.0317.Suche in Google Scholar PubMed PubMed Central

[235] G. Y. Chen, W. X. Zhang, and X. D. Zhang, “Strong terahertz magneto-optical phenomena based on quasi-bound states in the continuum and Fano resonances,” Opt. Express, vol. 27, p. 16449, 2019. https://doi.org/10.1364/oe.27.016449.Suche in Google Scholar PubMed

[236] A. Knoesen, T. K. Gaylord, and M. G. Moharam, “Hybrid guided modes in uniaxial dielectric planar waveguides,” J. Lightwave Technol., vol. 6, pp. 1083–1104, 1988. https://doi.org/10.1109/50.4101.Suche in Google Scholar

[237] F. Monticone and A. Alù, “Leaky-wave theory, techniques, and applications: from microwaves to visible frequencies,” Proc. IEEE, vol. 103, pp. 793–821, 2015. https://doi.org/10.1109/jproc.2015.2399419.Suche in Google Scholar

[238] S. Joseph and A. K. Hafiz, “Omnidirectional reflector using one-dimensional dispersive photonic heterostructure,” Optik, vol. 125, pp. 2734–2738, 2014. https://doi.org/10.1016/j.ijleo.2013.11.071.Suche in Google Scholar

[239] J. R. Piper and S. Fan, “Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance,” ACS Photonics, vol. 1, pp. 347–353, 2014. https://doi.org/10.1021/ph400090p.Suche in Google Scholar

[240] S. Joseph and J. Joseph, “Influence of periodic texture profile and parameters for enhanced light absorption in amorphous silicon ultra-thin solar cells,” Appl. Opt., vol. 56, p. 5013, 2017. https://doi.org/10.1364/ao.56.005013.Suche in Google Scholar

[241] J. Qin, Y. H. Chen, Z. Zhang, et al.., “Revealing strong plasmon-exciton coupling between nanogap resonators and two-dimensional semiconductors at ambient conditions,” Phys. Rev. Lett., vol. 124, p. 63902, 2020. https://doi.org/10.1103/physrevlett.124.063902.Suche in Google Scholar PubMed

[242] T. J. Yen, W. J. Padilla, N. Fang, et al.., “Terahertz magnetic response from artificial materials,” Science, vol. 303, no. 80, pp. 1494–1496, 2004. https://doi.org/10.1126/science.1094025.Suche in Google Scholar PubMed

[243] T. Wang and X. Zhang, “Magnetic response at visible and near-infrared frequencies from black phosphorus sheet arrays,” Opt. Express, vol. 23, p. 30667, 2015. https://doi.org/10.1364/oe.23.030667.Suche in Google Scholar PubMed

[244] A. M. Chernyak, M. G. Barsukova, A. S. Shorokhov, A. I. Musorin, and A. A. Fedyanin, “Bound states in the continuum in magnetophotonic metasurfaces,” JETP Lett. (Engl. Transl.), vol. 111, pp. 46–49, 2020. https://doi.org/10.1134/s0021364020010105.Suche in Google Scholar

[245] S. Sarkar, V. Gupta, T. Tsuda, et al.., “Plasmonic charge transfers in large-scale metallic and colloidal photonic crystal slabs,” Adv. Funct. Mater., vol. 31, p. 2011099, 2021.10.1002/adfm.202011099Suche in Google Scholar

[246] M. Xiao, G. Ma, Z. Yang, P. Sheng, Z. Q. Zhang, and C. T. Chan, “Geometric phase and band inversion in periodic acoustic systems,” Nat. Phys., vol. 11, pp. 240–244, 2015. https://doi.org/10.1038/nphys3228.Suche in Google Scholar

[247] T. C. W. Tan, E. Plum, and R. Singh, “Lattice-enhanced fano resonances from bound states in the continuum metasurfaces,” Adv. Opt. Mater., vol. 8, pp. 1–10, 2020. https://doi.org/10.1002/adom.201901572.Suche in Google Scholar

[248] S. Sarkar, V. Gupta, M. Kumar, et al.., “Hybridized guided-mode resonances via colloidal plasmonic self-assembled grating,” ACS Appl. Mater. Interfaces, vol. 11, pp. 13752–13760, 2019. https://doi.org/10.1021/acsami.8b20535.Suche in Google Scholar PubMed PubMed Central

[249] W. Liu, B. Wang, Y. Zhang, et al.., “Circularly polarized states spawning from bound states in the continuum,” Phys. Rev. Lett., vol. 123, p. 116104, 2019. https://doi.org/10.1103/physrevlett.123.116104.Suche in Google Scholar PubMed

[250] W. Ye, Y. Gao, and L. Jianlong, Polarization Diversity Close to the Optical Bound States in the Continuum, 2019. arXiv:190409597.Suche in Google Scholar

[251] W. A. Benalcazar and A. Cerjan, “Bound states in the continuum of higher-order topological insulators,” Phys. Rev. B, vol. 101, p. 161116, 2020. https://doi.org/10.1103/physrevb.101.161116.Suche in Google Scholar

[252] T. Yoda and M. Notomi, “Generation and annihilation of topologically protected bound states in the continuum and circularly polarized states by symmetry breaking,” Phys. Rev. Lett., vol. 125, p. 53902, 2020. https://doi.org/10.1103/physrevlett.125.053902.Suche in Google Scholar

[253] J. Sun, E. Timurdogan, A. Yaacobi, E. S. Hosseini, and M. R. Watts, “Large-scale nanophotonic phased array,” Nature, vol. 493, pp. 195–199, 2013. https://doi.org/10.1038/nature11727.Suche in Google Scholar PubMed

[254] S. Joseph and J. Joseph, “Photonic-plasmonic hybrid 2D-pillar cavity for mode confinement with subwavelength volume,” IEEE Photon. Technol. Lett., vol. 31, pp. 1433–1436, 2019. https://doi.org/10.1109/lpt.2019.2930090.Suche in Google Scholar

[255] J. M. Fitzgerald, S. K. Manjeshwar, W. Wieczorek, and P. Tassin, “Cavity optomechanics with photonic bound states in the continuum,” Phys. Rev. Res., vol. 3, p. 13131, 2021. https://doi.org/10.1103/physrevresearch.3.013131.Suche in Google Scholar

[256] P. K. Sahoo, S. Sarkar, and J. Joseph, “High sensitivity guided-mode-resonance optical sensor employing phase detection,” Sci. Rep., vol. 7, pp. 1–7, 2017. https://doi.org/10.1038/s41598-017-07843-z.Suche in Google Scholar PubMed PubMed Central

[257] T. C. W. Tan, Y. K. Srivastava, R. T. Ako, et al.., “Active control of nanodielectric-induced THz quasi-BIC in flexible metasurfaces: a platform for modulation and sensing,” Adv. Mater., vol. 33, pp. 1–11, 2021. https://doi.org/10.1002/adma.202100836.Suche in Google Scholar PubMed

[258] S. S. Oh and O. Hess, “Chiral metamaterials: enhancement and control of optical activity and circular dichroism,” Nano Convergence, vol. 2, p. 24, 2015. https://doi.org/10.1186/s40580-015-0058-2.Suche in Google Scholar PubMed PubMed Central

[259] R. Zhang, Q. Zhao, X. Wang, W. Gao, J. Li, and W. Y. Tam, “Measuring circular phase-dichroism of chiral metasurface,” Nanophotonics, vol. 8, pp. 909–920, 2019. https://doi.org/10.1515/nanoph-2019-0061.Suche in Google Scholar

[260] A. Yahyaoui and H. Rmili, “Chiral all-dielectric metasurface based on elliptic resonators with circular dichroism behavior,” Int. J. Antenn. Propag., vol. 2018, p. 7, 2018. https://doi.org/10.1155/2018/6352418.Suche in Google Scholar

[261] S. Droulias, “Chiral sensing with achiral isotropic metasurfaces,” Phys. Rev. B, vol. 102, pp. 1–15, 2020. https://doi.org/10.1103/physrevb.102.075119.Suche in Google Scholar

[262] B. Dastmalchi, P. Tassin, T. Koschny, and C. M. Soukoulis, “A new perspective on plasmonics: confinement and propagation length of surface plasmons for different materials and geometries,” Adv. Opt. Mater., vol. 4, pp. 177–184, 2016. https://doi.org/10.1002/adom.201500446.Suche in Google Scholar

[263] P. Anger, P. Bharadwaj, and L. Novotny, “Enhancement and quenching of single-molecule fluorescence,” Phys. Rev. Lett., vol. 96, pp. 3–6, 2006. https://doi.org/10.1103/PhysRevLett.96.113002.Suche in Google Scholar PubMed

[264] Y. Song, N. Jiang, L. Liu, X. Hu, and J. Zi, “Cherenkov radiation from photonic bound states in the continuum: towards compact free-electron lasers,” Phys. Rev. Appl., vol. 10, p. 1, 2018. https://doi.org/10.1103/physrevapplied.10.064026.Suche in Google Scholar

[265] J. Guan, L. K. Sagar, R. Li, et al.., “Quantum dot-plasmon lasing with controlled polarization patterns,” ACS Nano, vol. 14, pp. 3426–3433, 2020. https://doi.org/10.1021/acsnano.9b09466.Suche in Google Scholar PubMed

[266] S. Joseph, M. S. Khan, and A. K. Hafiz, “Parameters for efficient growth of second harmonic field in nonlinear photonic crystals,” Phys. Lett. Sect. A Gen. At. Solid State Phys., vol. 378, pp. 1296–1302, 2014. https://doi.org/10.1016/j.physleta.2014.02.032.Suche in Google Scholar

[267] M. Lippitz, M. A. Van Dijk, and M. Orrit, “Third-harmonic generation from single gold nanoparticles,” Nano Lett., vol. 5, pp. 799–802, 2005. https://doi.org/10.1021/nl0502571.Suche in Google Scholar PubMed

[268] S. Liu, M. B. Sinclair, S. Saravi, et al.., “Resonantly enhanced second-harmonic generation using III-V semiconductor all-dielectric metasurfaces,” Nano Lett., vol. 16, pp. 5426–5432, 2016. https://doi.org/10.1021/acs.nanolett.6b01816.Suche in Google Scholar PubMed

[269] V. Raghunathan, J. Deka, S. Menon, R. Biswas, and A. S. Lal Krishna, “Nonlinear optics in dielectric guided-mode resonant structures and resonant metasurfaces,” Micromachines, vol. 11, p. 449, 2020. https://doi.org/10.3390/mi11040449.Suche in Google Scholar PubMed PubMed Central

[270] K. Koshelev, S. Kruk, E. Melik-Gaykazyan, et al.., “Subwavelength dielectric resonators for nonlinear nanophotonics,” Science, vol. 367, no. 80, pp. 288–292, 2020. https://doi.org/10.1126/science.aaz3985.Suche in Google Scholar PubMed

[271] C. Liang, L. Deng, Q. Dai, et al.., “Single-celled multifunctional metasurfaces merging structural-color nanoprinting and holography,” Opt. Express, vol. 29, p. 10737, 2021. https://doi.org/10.1364/oe.420831.Suche in Google Scholar

[272] W. Ye, F. Zeuner, X. Li, et al.., “Spin and wavelength multiplexed nonlinear metasurface holography,” Nat. Commun., vol. 7, pp. 1–7, 2016. https://doi.org/10.1038/ncomms11930.Suche in Google Scholar PubMed PubMed Central

[273] B. J. Bohn, M. Schnell, M. A. Kats, F. Aieta, R. Hillenbrand, and F. Capasso, “Near-field imaging of phased array metasurfaces,” Nano Lett., vol. 15, pp. 3851–3858, 2015. https://doi.org/10.1021/acs.nanolett.5b00692.Suche in Google Scholar PubMed

[274] H. F. Grahn and P. Geladi, “Techniques and applications of hyperspectral image analysis,” Tech. Appl. Hyperspectral Image Anal., pp. 1–15, 2007. https://doi.org/10.1002/9780470010884.ch1.Suche in Google Scholar

[275] G. Wang, Y. Zhang, C. You, et al.., “Two dimensional materials based photodetectors,” Infrared Phys. Technol., vol. 88, pp. 149–173, 2018. https://doi.org/10.1016/j.infrared.2017.11.009.Suche in Google Scholar

[276] F. Wang, Z. Wang, L. Yin, et al.., “2D library beyond graphene and transition metal dichalcogenides: a focus on photodetection,” Chem. Soc. Rev., vol. 47, pp. 6296–6341, 2018. https://doi.org/10.1039/c8cs00255j.Suche in Google Scholar PubMed

[277] W. Li and J. Valentine, “Metamaterial perfect absorber based hot electron photodetection,” Nano Lett., vol. 14, pp. 3510–3514, 2014. https://doi.org/10.1021/nl501090w.Suche in Google Scholar PubMed

[278] X. D. Gao, G. T. Fei, S. H. Xu, et al.., “Porous Ag/TiO2-Schottky-diode based plasmonic hot-electron photodetector with high detectivity and fast response,” Nanophotonics, vol. 8, pp. 1247–1254, 2019. https://doi.org/10.1515/nanoph-2019-0094.Suche in Google Scholar

[279] W. Li, Z. J. Coppens, L. V. Besteiro, W. Wang, A. O. Govorov, and J. Valentine, “Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials,” Nat. Commun., vol. 6, pp. 1–7, 2015. https://doi.org/10.1038/ncomms9379.Suche in Google Scholar PubMed PubMed Central

Received: 2021-07-19

Accepted: 2021-09-13

Published Online: 2021-11-09

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nanoph-2021-0387

Schlagwörter für diesen Artikel

bound states in the continuum; functional materials; metasurfaces; photonic crystal slabs; plasmonics

Creative Commons

BY 4.0