Ultrahigh-Q system of a few coaxial disks

1 Introduction

The eigenfrequencies of open dielectric particle are complex because of leakage of the electromagnetic (EM) power from particle. Real parts response for positions of resonances while imaginary parts do for the resonant widths which can be measured by light scattering. The ratio − R e ( k ) 2 I m ( k ) define the Q-factor of resonances. The important feature of open cavity is that for variation of its shape resonances undergo avoided crossing of resonances (ACR) which is accompanied by strong redistribution of imaginary parts of the complex eigenfrequencies. As the result the Q-factor can be strongly enhanced [1–4] forming super-cavity modes.

The compact dielectric cavity is open to the radiation continuum whose spectrum is given by light cone ω = ck which have no cutoffs and the resonant width of the super-cavity mode cannot turn to zero and therefore cannot be true bound state in the continuum (BIC) [5, 6]. Nevertheless there are a few ways to enormously lift the Q-factor further. The one well known way is address to whispering gallery modes in the cylindrical or spherical cavities [7]. Also one can arrange enough number N of identical cavities into periodical chains from which light can leakage into only selected directions given by diffraction orders [8–10]. In practice the number of cavities in chain cannot be infinite, but the Q-factor fast grows with N [11] as Q(N) ∼ N ^α where α = 2 for symmetry protected quasi-BICs [12, 13], α = 3 for accidental BICs [12, 14] or even α ≈ 6 [15]. In practice material losses and structural losses restrict the number of cavities [13, 16], [17], [18]. Moreover this way of engineering of quasi-BICs goes away the dielectric structures (DS) from compactness when DS dimension do not exceed the wavelength. For example, in order to achieve 10⁵ for the quasi-BIC we need at least a few tens of silicon disks [13, 19, 20] or silicon cuboids [15] with eigenfrequencies within a subwavelength range. The best results for the Q-factor were reported by Taghizadeh and Chung [11] with Q = 10⁵ for 10 long silicon rods.

Recently a considerable progress in enhancement of the Q factor by a few times was achieved by Rybin et al. by engineering of super-cavity modes [1] in single dielectric disk with subsequent experimental observation [2–4]. The underlying principle of enhancement of the Q-factor is the ACR of two resonances [21] of dielectric disk under variation of the aspect ratio. Along with the ACR the hybridized resonant mode reveals multipolar conversion [22, 23] that defines it as a super-cavity mode. Afterwards, the approach of ARC was applied to a dielectric rod of rectangular cross-section [24]. The presence of the second coaxial disk substantially expands a number of ACRs due to crossing of resonances and allows elevating the Q-factor of disk’s dimer by two orders remaining in the subwavelength range [25]. In the present paper we apply the ARC to the simplest dielectric structures (DSs) composed of a few disks of different heights but equal radii. For the DS consisted of symmetrically disposed three/four silicon disks the ACRs at the subwavelength range ka ≈ 2.2 give rise to quality factors around 10⁵ and 10⁶, respectively, where a is the radius of disks.

2 A disk inside the dimer

Recently we demonstrated unprecedented values of the Q-factor in the system of two identical coaxial silicon disks (dimer) with ϵ = 12 based on engineering of the spherical Mie resonances with high orbital momentum by the two-scale optimization of the quality factor, the distance between disks and thickness of each disk [25]. For coaxial different disks we have more events of the ACR if, for example, vary the thickness of one disk relative to the thickness of the second disk. However the calculations witness that resulted enhancements of the Q-factor do not exceed the case of two identical disks. The reason is that two coaxial different disks system breaks the symmetry relative to z → −z and therefore doubles the number of radiation channels allowing the resonant modes to leak into symmetrical and anti symmetrical radiation continua [26]. For the nonsymmetrical case the outgoing waves are given by series [27]

where M _l0 are the vector spherical functions [28]. However for the symmetrical case of identical disks the summation includes only l = 1, 3, 5, … if the tangential component E _ϕ is even and l = 2, 4, 6, … if E _ϕ is odd relative to z → −z [29]. That twice diminishes the number of radiation channels.

Thereby in order to preserve symmetry and still have more events of ACRs we consider the following different subsystems. The first one is a dimer with a single disk inserted symmetrically inside the dimer as shown in the inset of Figure 1. Owing to rotational symmetry around the z-axis the azimuthal index m is preserved that allows considering each sector m independently. Moreover for m = 0 the polarizations are separated that also considerably reduces radiation losses [25]. In what follows we consider the silicon disks with the permittivity ϵ = 12 which have negligible material losses at the wavelength λ = 1.5 μm [30]. All scales are dimensionless and given in terms of the disk radius a. We consider the TE solutions of the Maxwell equations without sources in the sector m = 0 by use of software package COMSOL Multiphysics which allows to obtain numerically the complex resonant frequencies and corresponding resonant modes of a cavity of arbitrary shape embedded into the radiation continuum.

Figure 1:

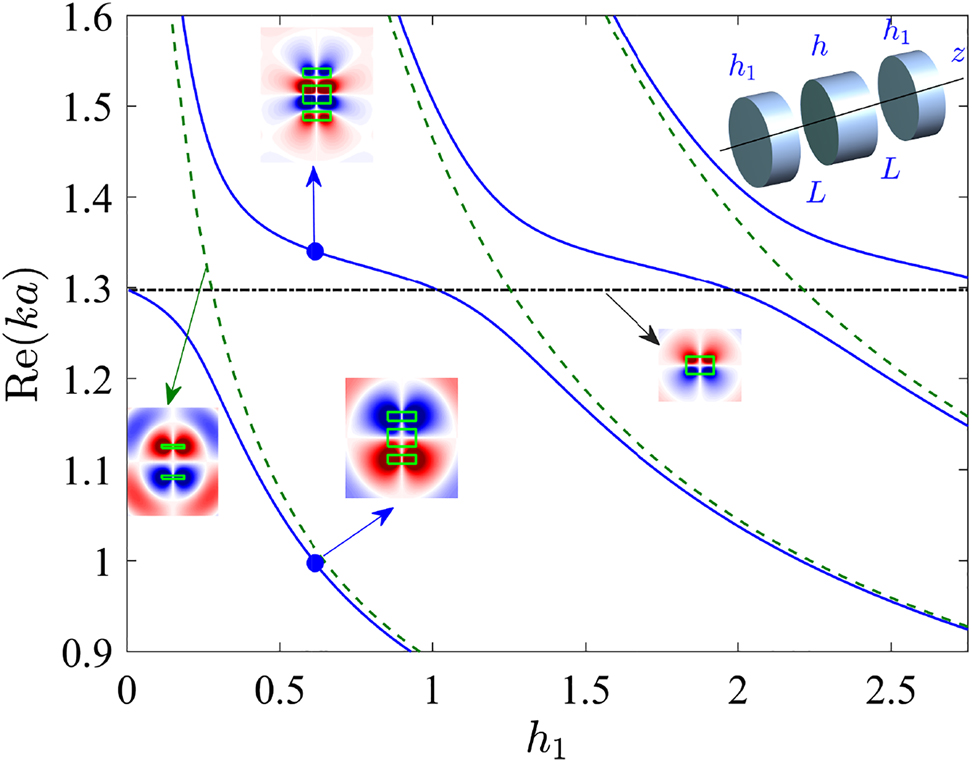
ACR of the Mie-like resonant mode with l = 2 of single disk, height h = 1.244 with the resonant modes of dimer at the distance between disks 2L + h = 2.428 for variation of height of disks h ₁. Dash and dash-dotted lines show resonant frequencies of dimer and single disk, solid line show results of ACR. The insets show resonant modes of single disk and dimer and the hybridized modes (the tangential component of electric field E _ϕ of TE modes).

Only the resonant modes of the same symmetry can undergo the ACR. In Figure 1 the ACRs of the antisymmetric resonant modes for variation of height of disks h ₁ in the dimer relative to thickness of the single disk h are presented. The Mie-like resonant mode of the single disk with prevailed multipole radiation l = 2 in Eq. (1) is shown by dash-dotted line and the resonant mode of the dimer is shown by dashed line.The resonant modes of the total system are shown by solid lines with hybridized modes shown in the insets. There are other events of the ARCs which are not shown in Figure 1 and which also give rise to enhancements of the Q-factor as shown in Figure 2. The first event of ARC shown in Figure 1 for the most thin disks in dimer results in the Q-factor Q = 890 significantly larger compared to the other events of the ARCs. That is the result of three-scale optimization over L, h, h ₁ near the frequency ka = 1.3 that makes the hybridized resonant mode with Q = 890 close to the Mie-like mode of sphere with l = 4 [25].

Figure 2:

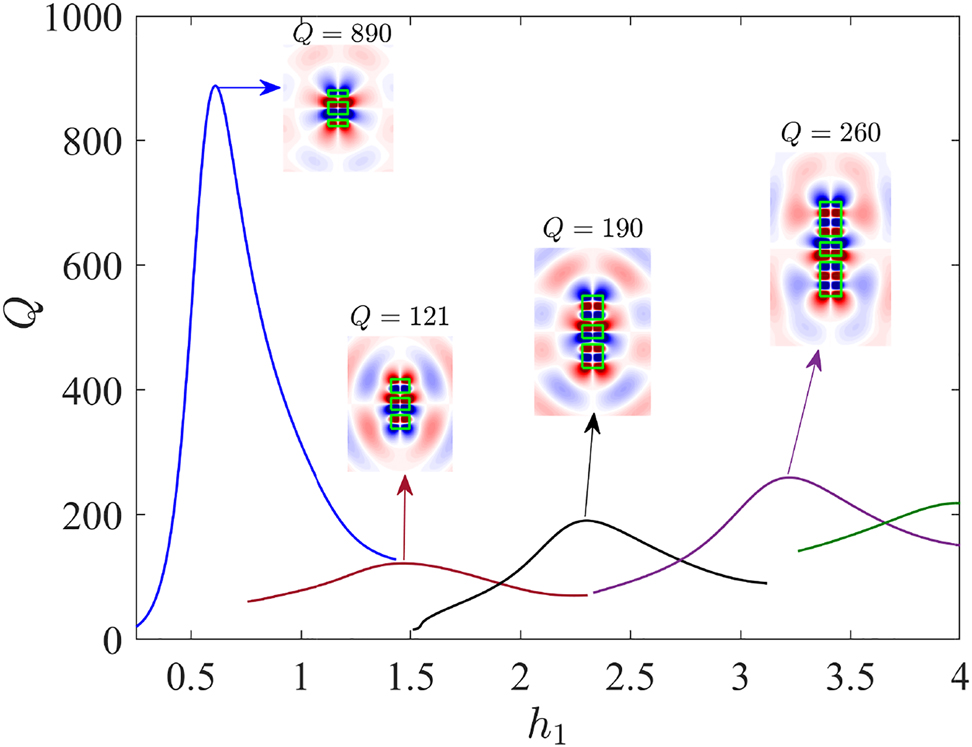
The Q-factors and corresponding resonant modes versus the thickness of disks of dimer. Other parameters are fixed: h = 1.244, L = 0.592.

Also in Figure 3 we present the Q-factors for some selected DSs assembled of one and three disks. One can see that the symmetry protected quasi-BIC [13] of three identical disks with Q = 190 considerably yields the case of three different disks with Q = 890. Moreover we show in the first inset of Figure 3 the Q-factor of a single solid disk with the same radius and height 2L + 2h ₁ + h = 3.66 equal to the total length of DS of three different disks. One can see the case of three different disks has an advantage in the Q-factor more than one order in magnitude.

Very similar ACRs occur near the frequency ka = 2.2 where Mie-like mode with l = 6 of single disk interacts with the resonant modes of the dimer. The optimization over all three dimensions h, h ₁, L in the DS gives enormous quality factors Q = 27,000 and 90,600 compared to a single disk with Q = 1430 as shown in Figure 4.For comparison we also show the case of a single solid disk with length 2L + 2h ₁ + h identical to the DS of three disks shown in the third panel. One can see three optimized disks has an enormous advantage in the Q-factor by two orders in magnitude.

Figure 3:

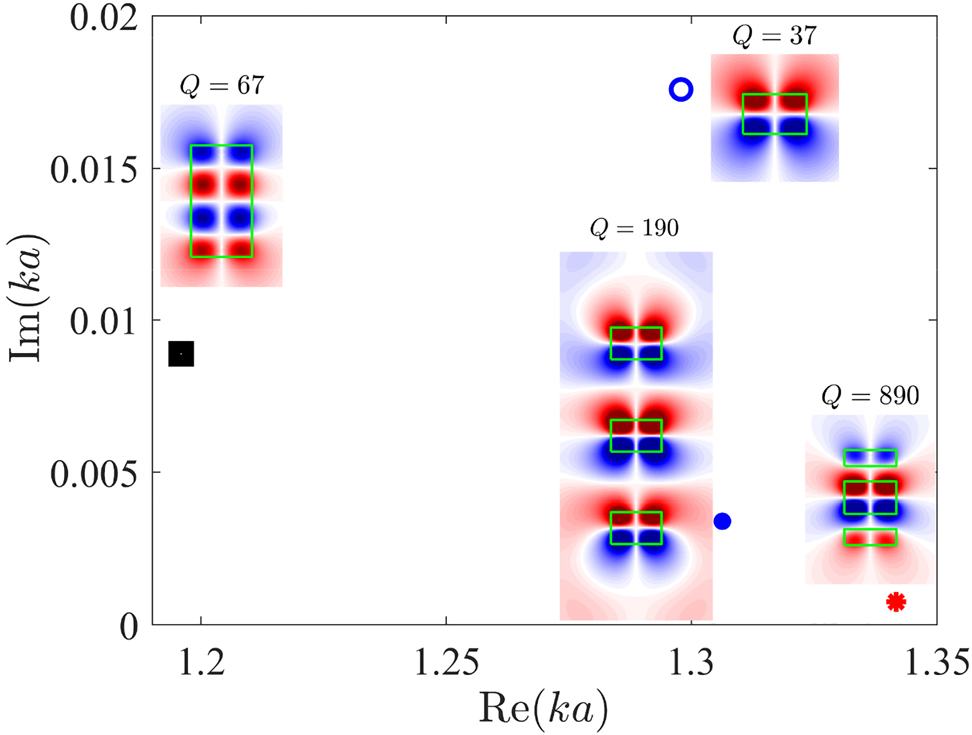
The Q-factors, resonant eigenfrequencies, and corresponding resonant modes. The first panel: a single solid disk with sizes identical to the DS shown in the fourth panel. The second panel: three identical disks with heights h = h ₁ = 1.244 separated by L = 2.38 tuned to the symmetry protected quasi-BIC. The third panel: a solitary disk with height h ₁ = 0.616. The fourth panel: the same disk as in third panel inserted symmetrically inside a dimer with h ₁ = 0.616, L = 0.592.

Figure 4:

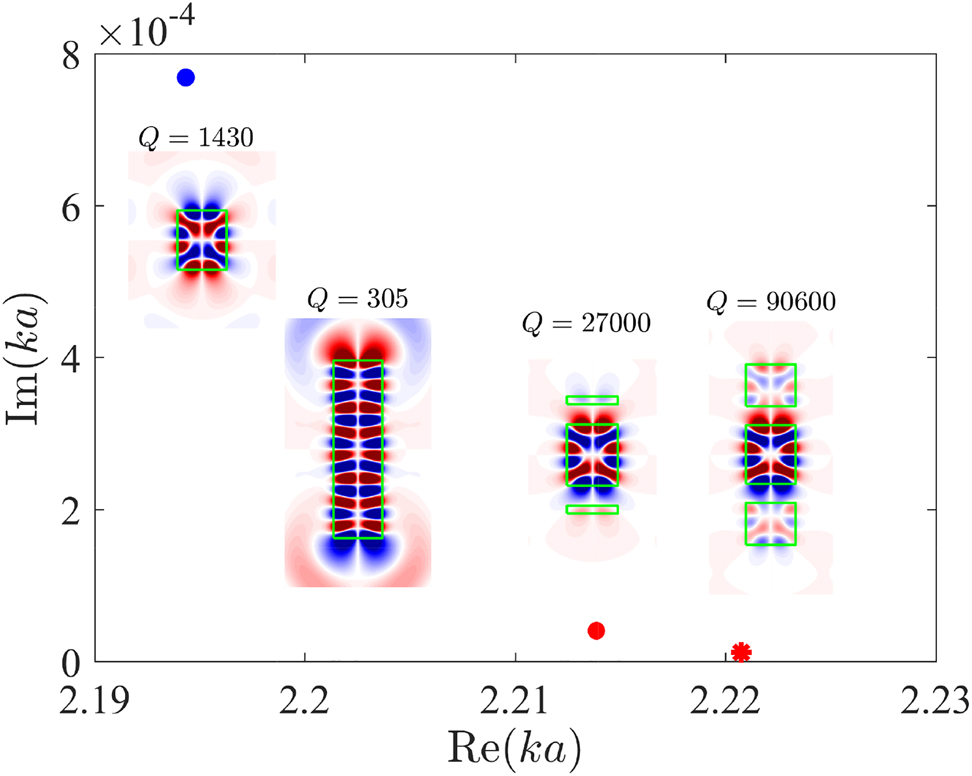
The Q-factors, resonant eigenfrequencies, and corresponding resonant modes. The first panel: A solitary disk with h = 2.41. The second panel: A single solid disk with sizes identical to those of disk’s arrangement shown in the fourth panel. The third panel: disk inserted symmetrically inside dimer of two thin disks with h ₁ = 0.303, h = 2.378, L = 0.781. The fourth panel shows the case of dimer with all scales optimized: h ₁ = 1.688, h = 2.367, L = 0.764.

Finally, we consider the ARCs of resonant modes of two different dimers with inner dimer inserted into outside dimer as shown in the inset of Figure 5 for the four-scale optimization of the Q-factor over dimensions with the result of about one million shown in the third panel in Figure 5. This results is compared to the resonant mode of the inner dimer engineered onto the Mie-like mode with orbital momentum l = 6 [25] shown in the first panel. The second panel presents the quasi-BIC in the system of two dimers with strong suppression of radial leakage. But axial leakage is remained the same as for the case of single dimer. As a result the Q factor is enhanced only twice. The two-scale optimization procedure over two distances L and D shown in the fourth panel gives the result Q = 90,600 which yields the case of full-scale optimization by one order in magnitude.

Figure 5:

The same as in Figure 4 but the resonant mode of the inner dimer is tuned to the Mie-like mode with l = 6 at h = 1.038, D = 0.734 [25]. The left bottom panel shows the SP quasi-BIC consisted of two dimers h = h ₁ = 1.038, L = 0.752, D = 1.985 (closed circle), the central and the right panels show the dimer sheltered by disks with scales respectively h = 1.03895, h ₁ = 1.01727, L = 2.2711, D = 0.6585 (square) and h = h ₁ = 1.038, L = 2.02, D = 0.661 (star).

3 Conclusion and outlook

The avoided crossing of resonances leads to hybridization of resonant modes and substantial redistribution of imaginary parts [31]. That way of enhancement turned out successful even in a single cavity shaped as disk [1] or long rod of rectangular cross-section [24]. The ACRs in two identical cavities lifts the Q-factor essentially more [21, 25, 32]. In the present paper we show that the ACRs in DS composed of different cavities gives rise to further enhancement of the Q-factor owing to increasing of events of ARCs provided that the DS is symmetric relative to z → −z. This with the procedure of multi-scale optimization in the DSs of three and four disks of equal radii but different thicknesses results in the Q-factor of order 10⁵ and 10⁶ respectively. And what is remarkable is that unprecedented values of the Q-factor refer to the compact DSs as crucially different from the extended DSs tuned to the quasi-BICs. That has a large technological advantage for sensing and lasing.

There is a useful tool to understand the nature of the extremely high quality factor for the avoided crossing through multipole expansions [33]. That tool shed light on the origin of high Q-factor in the isolated disk [2, 23] and the origin of bound states in the continuum [34, 35]. In the present case of three and four different disks we also observe that extreme Q-factor is attributed to strong redistribution of radiation that originates from compensation of dominating multipole coefficients.

Using formalism described in book [36] (Eq. (1.69)) we separate contributions from subsystems assembling the total DS in far field range. The results for complex amplitudes a _l0 of each dimer and of the total system in series Eq. (1) are presented in Figure 6.

Figure 6:

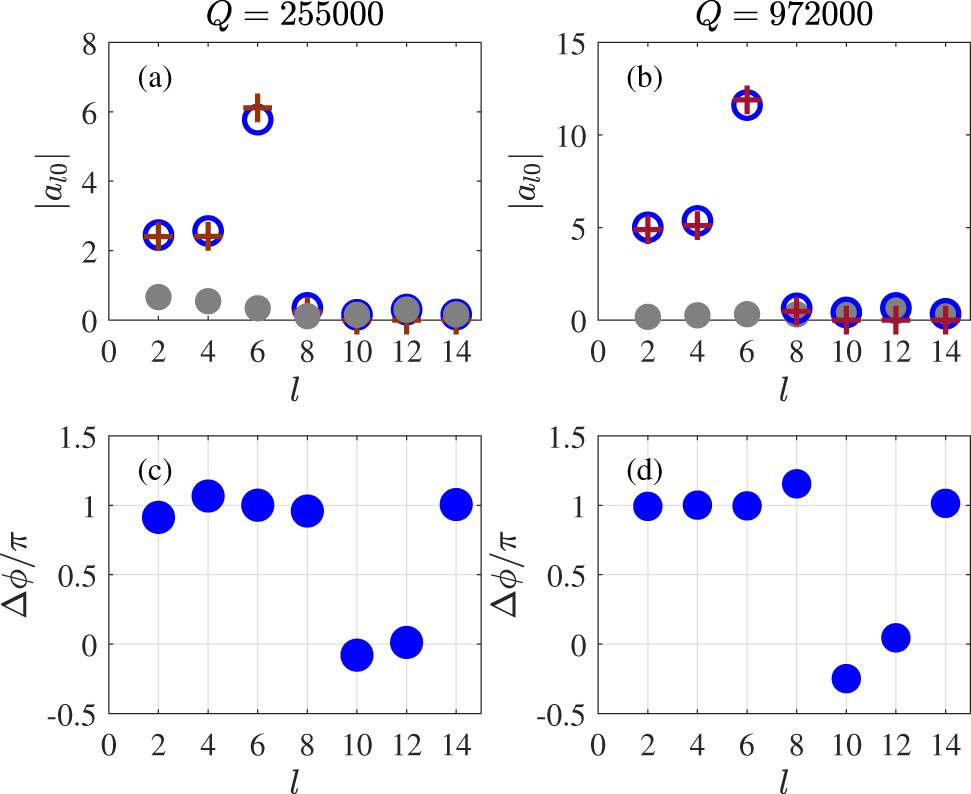
The multipole radiation amplitudes in Eq. (1) from DS of two dimers with slight difference in scales.

(a) and (b) Modules and (c) and (d) phase difference of complex amplitudes a _l0 of inner and outside dimers. In (a) and (c) subplots h = 1.04, h ₁ = 1.02, L = 2.27, D = 0.66. In (b) and (d) h = 1.03895, h ₁ = 1.01727, L = 2.2731, D = 0.6585.

In subplots (a) and (b) markers + and o are responsible for multipole amplitudes contributed from inner and outside dimers correspondingly. Dots correspond to the multipole coefficients of total DS, normalized as ∑ _l |a _0l |² = 1. In subplots (c) and (d) phase difference between amplitudes of both dimers are shown. One can observe in Figure 6 almost full destructive interference of the multipolar amplitudes at the dominant channels l = 2, 4, 6 from both dimers when modules of the coefficients are equal while phases differ by π. The destructive interference simultaneously of three amplitudes a _0l was achieved owing to the multiscale optimization procedure. Moreover comparison of the left and right panels demonstrates that extremely fine tuning of parameters of the DS when difference around 1% results in four times enhancement of the Q-factor.

It is clear that there is a large room for further enhancement of the Q-factor in DS by exploration more parameters such as radii, refractive indices or shape of the cavities.