Ultraviolet second harmonic generation from Mie-resonant lithium niobate nanospheres

1 Introduction

As a fundamental optical nonlinear effect, second harmonic generation (SHG) is a process that two identical photons convert into a double-frequency photon, which has been widely applied in signal processing, optical spectroscopy, and laser systems [1–3]. Conventional SHG devices are based on bulk materials such as nonlinear crystals of potassium dihydrogen phosphate, potassium titanyl phosphate, and beta barium borate [4–9], where high-efficiency SHG requires phase-matching conditions and long interaction length with light. With the rapid developments of nanophotonics and integrated optics, building nanoscale nonlinear optical devices becomes feasible via the greatly enhanced light matter interactions provided by photonic nanostructures [10, 11]. Specifically, photonic microresonators that strongly enhance the local electromagnetic field can greatly boost the nonlinear optical processes [12, 13]. In addition, the tight confinement of light within sizes smaller than the coherent length of light eliminates the restriction of the phase-matching condition. One of the representative photonic nanostructures is single dielectric resonators such as nanospheres, nanocubes, and nanodisks that support Mie resonances [14–17]. With strong field confinement and great wavelength tunability by the size, geometry, and material composition, Mie resonators recently enable a wide range of applications in nonlinear nanophotonics such as Raman scattering [18, 19] and harmonic generations [19–21], as well as photon-pair generations [22, 23]. For most of these works, high refractive index dielectric materials with large nonlinear susceptibility such as silicon [24], gallium arsenide [25, 26], or germanium [27, 28] are employed, benefiting from their mature fabrication techniques and low loss in the near-infrared region. However, these materials are lossy in the ultraviolet (UV) range due to strong inter-band absorption, and therefore achieving strong UV SHG enhanced by Mie-resonant nanostructures remains an open challenge. Ferroelectric metal oxide lithium niobate (LN) with a large energy bandgap of 4 eV and a wide low-loss spectral range from 0.33 to 5.5 μm [29–32] is a promising dielectric material for efficient SHG up to the UV region. Nevertheless, limited by the nanofabrication techniques, using LN single nanoparticles for nonlinear nanophotonics is not yet common. Recently, a high-efficiency SHG at 360 nm was demonstrated from Mie-resonant LN nanocubes fabricated by a solvothermal synthesis method [33]. However, bottom-up chemical synthesis is relatively complicated and the geometry of the Mie-resonators is limited to cubes. Alternatively, the femtosecond (fs) laser ablation technique has been successfully employed to fabricate Mie-resonant nanospheres with controllable size from a variety of nonlinear materials including Si, GaAs, Ge, and perovskite [34–37].

In this paper, we demonstrate a strong UV SHG from single LN nanospheres fabricated by the fs laser ablation technique. Supporting MD Mie resonance, LN nanospheres exhibit a significant field enhancement of 5.5, resulting in a high SHG conversion efficiency measured as 4.45 × 10⁻⁸. We examine the wavelength and power dependence of the SHG signals, confirming the SHG enhancement contribution from the Mie resonance. Our work shows the feasibility of fabricating nanospheres from a bulk LN wafer and extends the Mie-resonance enhanced nanoscale SHG up to the UV frequency range.

2 Device design and fabrication

The schematic of SHG from a 160 nm-radius LN nanosphere placed on SiO₂ substrate is presented in Figure 1(a). A fs laser with wavelength of 750 nm is in resonance with the MD mode and the UV SH signal is expected to be at 375 nm. The scattering spectrum of the LN nanosphere is simulated via finite-difference time-domain (FDTD) method, which reveals the multipole contributions of the Mie resonances, as shown in Figure 1(b). We further calculate the Cartesian multipoles up to the third order based on the electric field E inside the structure. By using the multipolar expansion of the polarization current density [38], the multipole terms (electric dipole ED, magnetic dipole MD, electric quadrupole EQ, and magnetic quadrupole MQ) are calculated according to the following equations:

where ω is the angular frequency. The total scattered power P _scat is calculated as the sum of each multipole contributions:

with k being the wave number and ɛ ₀ is the vacuum permittivity, and ɛ _d is the relative permittivity of LN.

Figure 1:

The design of LN nanosphere. (a) Schematic of ultraviolet SHG from an individual LN nanosphere on SiO₂ substrate. Inset: the SEM image of a fabricated nanosphere with a radius of 160 nm. (b) Simulated scattering spectra of an LN nanosphere. The calculated multipole contributions are depicted respectively with different colors (ED: electric dipole, EQ: electric quadrupole, MD: magnetic dipole, MQ: magnetic quadrupole.). (c) Electric field distribution of the Mie-resonant mode from an LN nanosphere at x–y plane, the white arrows indicate the in-plane electric field vectors.

It can be observed that the two dominant peaks around 550 and 750 nm in the scattering spectrum are mostly attributed to the MQ and MD, respectively. In addition, the summation of individual multipole components strictly follows the simulated scattering spectrum via the FDTD method, which proves the reliability of the multipole decomposition. The simulated electric field distribution of the MD and MQ modes in the x-y plane of the LN nanosphere is shown in Figure 1(c). Inside the LN nanosphere, electric field enhancements are observed in both the MD and MQ modes. In this work, we choose to generate the SHG by pumping at the MD resonance simply because the SHG of the MQ mode is out of the detection range of our spectrometer.

We employ the fs laser ablation technique to fabricate LN nanospheres with radii ranging from 50 to 200 nm. In our experiments, 800 nm laser pulse with a temporal duration of 90 fs and repetition rate of 1 kHz are delivered by an fs amplifier (Legend Elite, Coherent) and then focused on the surface of an LN wafer immersed in deionized water. We use a lens with a focusing length of 15 cm to focus the laser beam on the LN wafer with a spot diameter of ∼70.0 μm. Once the ablation process is completed, the aqueous solution containing LN nanospheres is centrifuged with a speed of 6000 rpm to separate LN nanospheres with radii of 140–200 nm from small LN nanoparticles. Subsequently, the as-prepared LN nanospheres are randomly dispersed on a SiO₂ substrate with a low refractive index for effectively localizing the electromagnetic field. The scanning electron microscope (SEM) image of a fabricated LN nanosphere with a radius of 160 nm is shown in the inset of Figure 1(a). One of the advantages of our method is that the fabricated nanospheres can be flexibly transferred to any substrates due to their aqueous environment.

3 Results

A dark field spectroscopy setup has been implemented for measuring the scattering spectra of single LN nanospheres. The white light is focused onto individual nanospheres by a 100× darkfield objective, and the scattered light is collected by the same objective and delivered to an imaging spectrometer. To verify the Mie resonances associated with the LN nanospheres, the scattering spectra of LN nanospheres with different radii are simulated, as shown in Figure 2(a). With the increase of nanosphere radius, the MD-resonance wavelength redshifts significantly, following the relation 2R ≈ λ/n, where is the refractive index of the material, is the nanosphere radius, and is the Mie-resonant wavelength. Such a trend is in very good agreement with the measured spectra, as presented in Figure 2(b). The additional peak near 650 nm in the experiment possibly originates from the contribution of ED due to the deviation of the fabricated nanosphere from the ideal geometry.

Figure 2:

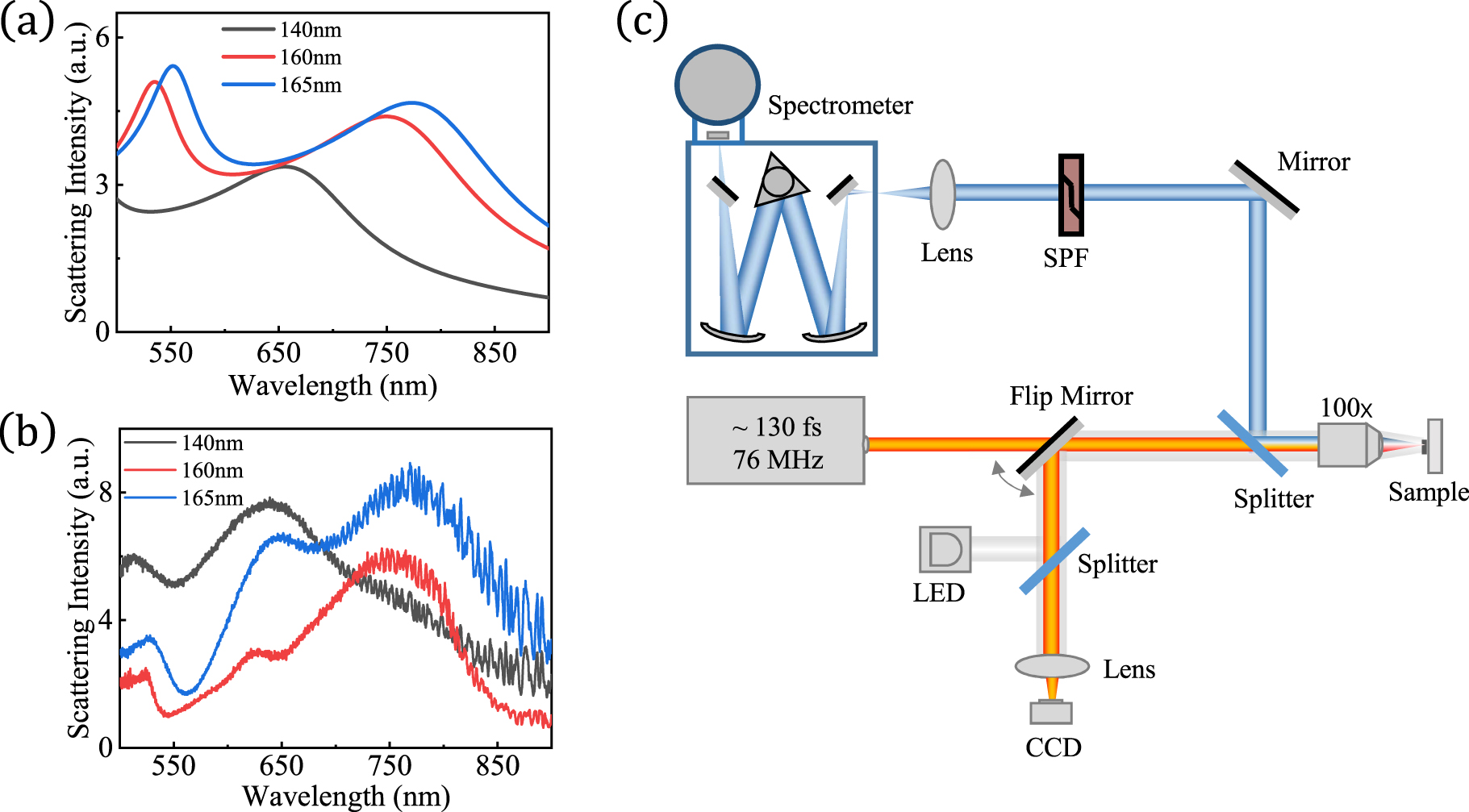
The characterization of the scattering spectra for LN nanosphere. (a) Simulated and (b) experimental scattering spectra of LN nanospheres with different radii. (c) Detection set up for collection of SHG signals from LN nanospheres. The fs incident laser beam is focused on the sample by an objective lens. The reflected incident laser is filtered by a short-pass filter (SPF) and then the backscattered SHG signal is collected by the spectrometer.

The SHG signals are characterized by using an inverted microscope (Axio Observer A1, Zeiss) equipped with a spectrometer (SR-500i-B1, Andor) and a charge-coupled device (DU970N, Andor), as schematically shown in Figure 2(c). An fs laser oscillator with a pulse duration of 130 fs and repetition rate of 76 MHz (Mira 900S, Coherent) is used as the excitation source and a 100× objective lens (ZEISS Plan-Neofluar) is employed for signals collection. The backscattered incident laser beam is filtered by a short-pass filter (SPF, Thorlabs FES0450) so that the UV SHG signal can be collected by the spectrometer for analysis.

To investigate the nonlinear optical response of the LN nanospheres, SHG is measured from a 160 nm-radius nanosphere. With a pump power of 0.4 mW, SHG signals at different wavelengths are collected when scanning the pump laser across MD resonance (Figure 3(a)). The intensity of the SHG signal reaches the maximum at the MD resonance (750 nm) and significantly reduces at other pump wavelengths, implying the resonant enhancement from the MD mode. To further confirm the critical role played by the Mie resonance, the scattering spectrum of Mie-resonant mode and wavelength-dependent SHG intensities are plotted in Figure 3(b). It can be observed that the intensities of the SHG signals follow the profile of the scattering spectrum, clearly demonstrating that the enhancement of the nonlinear interactions is provided by the MD Mie resonance.

Figure 3:

The characterization of the SHG enhancement for LN nanosphere. (a) Measured spectra of SHG when scanning the pump wavelength across MD mode under the pump power of 0.4 mW. (b) Wavelength dependence of SHG signals in (a). The scattering spectrum of the corresponding LN nanosphere is plotted for comparison.

We examine the power dependence of the UV SHG from the LN nanosphere pumped at the MD Mie resonance. The measured SHG spectra under different pump powers are displayed in Figure 4(a). The SHG intensity as a function of the pump power is plotted in Figure 4(b) in a double logarithmic scale, exhibiting an exponent value of 2.0 by fitting with P SHG = m P pump n . The strict quadratic dependence of the signal intensity on the pump power unequivocally verifies the nature of the second-order nonlinear optical process. Finally, with an incident peak irradiance of 2.0 GW/cm², the maximal measured efficiency of visible-to-UV conversion is extracted as high as 4.45 × 10⁻⁸ from the equation η = P _2ω /P _ω , which is comparable to the previous works on LN metasurfaces [39, 40]. We note that the SiO₂ substrate used in this work results in low-Q factors and weaker field enhancements for the MD Mie-resonances compared to the situation without a substrate. The SHG conversion efficiency can be further improved by engineering the substrate. E.g., replacing the SiO₂ substrate with hyperbolic metamaterials has been suggested to generate high-efficiency SHG from single LN particles [41].

Figure 4:

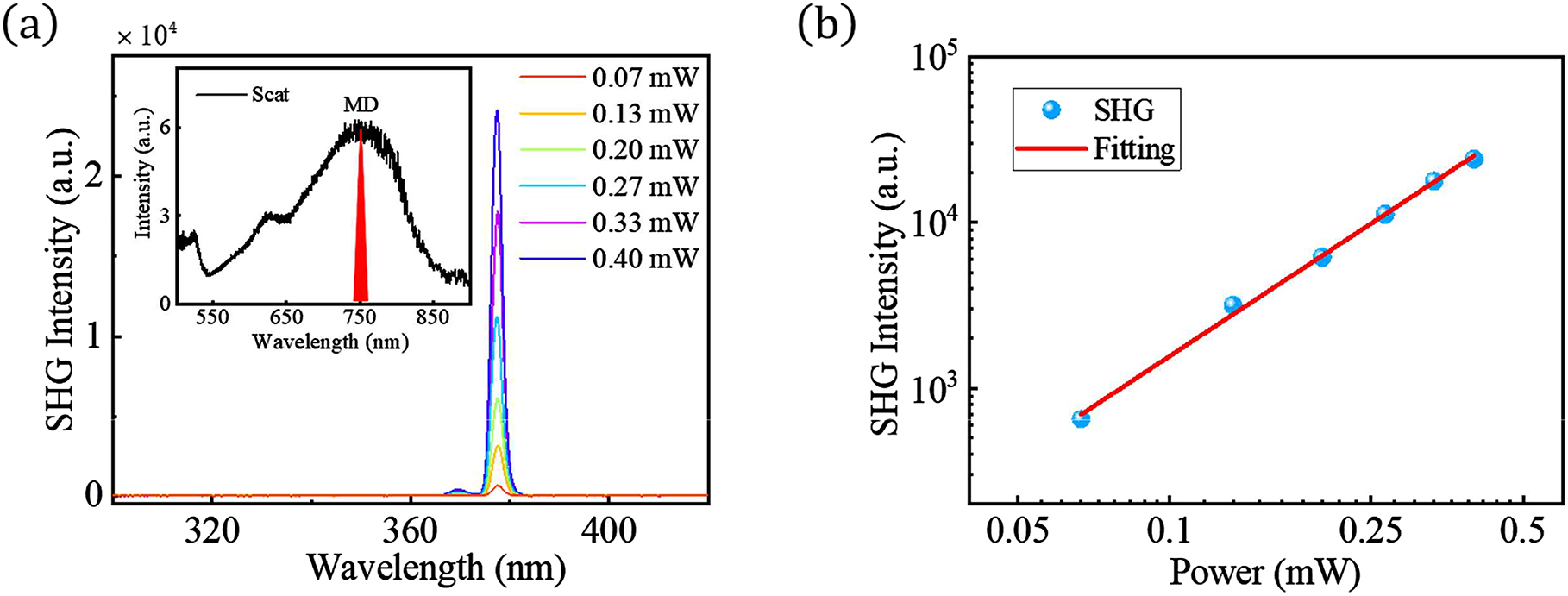
Power dependence of the SHG for LN nanosphere. (a) Measured spectra of SHG under different pump powers at MD resonance. The inset shows the spectral position of the pumping laser with respective of the MD mode. (b) Power dependence of SHG signals in (a), fitted by P SHG = m P pump n . The exponent value obtained from the fitting is 2.0.

4 Conclusion

In summary, we fabricate the LN nanosphere supporting Mie resonances in visible via the laser ablation technique. Due to the MD Mie resonance, the LN nanosphere provides a considerable field enhancement for the generation of SHG in the UV range. The SHG reaches the maximum when pumping at the MD Mie resonance, resulting in a high SHG conversion efficiency of 4.45 × 10⁻⁸. Our work provides a promising tool for enhancing nanoscale light–matter interactions in the UV regime. The Mie-resonant LN nanospheres could be further utilized to explore nonlinear nanophotonic devices such as frequency converters and quantum light sources via the nonlinear optical process, e.g., the parametric down-conversion process and four-wave mixing.