Dressed emitters as impurities

1 Introduction

Quantum emitters (“atoms”) coupled to structured and/or low-dimensional photonic environments are an important paradigm of quantum optics and nanophotonics. Important setups are photonic waveguides [1], a major focus of waveguide QED [2], [3], [4], and engineered photonic lattices implemented in various ways such as coupled cavities/resonators, photonic crystals or optical lattices [5], [6], [7], [8], [9]. Among others, a major appeal of such systems is the possibility of harnessing photon-mediated interactions between the emitters for implementing effective many-body Hamiltonians. Remarkably, for emitters energetically lying within photonic bandgaps, such effective second-order interactions can be dissipationless. These are usually explained in terms of mediating dressed bound states (BSs) [10], [11], [12], [13], [14], [15]. In one such BSs, the atom is dressed by a photon exponentially localized in its vicinity. Overlapping single-emitter dressed BSs then result in an effective interatomic potential, somewhat similarly to the formation of molecules.

A quantum emitter coupled to a homogeneous photonic reservoir has interesting analogies with the textbook impurity problem in condensed matter [16]. For instance, the reflection and transmission coefficients of a photon scattering off an atom in a waveguide are formally the same as those for an impurity described by an effective, energy-dependent, scattering potential [17, 18]. Moreover, as first suggested in Ref.  [10], the aforementioned in-gap atom-photon BSs are quite reminiscent of bound states induced by an impurity inside lattice bandgaps [16]. Recently, some of us identified a class of dressed states (dubbed “vacancy-like dressed states”) whose photonic wavefunction is just the same that would arise if the atom were replaced by a vacancy (i.e. an impurity described by a point-like potential of infinite strength) [15]. These states play a central role in topological quantum optics [19], [20], [21] and, additionally, encompass a type of dressed bound states in the continuum (BIC) that are currently investigated in waveguide QED [22], [23], [24], [25], [26], [27], [28], [29].

A natural question is to what extent the emitter-impurity analogy holds, in particular whether it can be formalized in a framework independent of the bath Hamiltonian and applied to the calculation of both bound and unbound dressed states (the latter ones rule photon scattering processes). Mostly motivated by this question, this work introduces a novel formulation of the non-perturbative resolvent-based framework for studying atom-photon dressed states [30], [31], [32]. We show that the resolvent operator (or Green function) can be expressed in a compact form structurally analogous to that arising in the standard impurity problem. This condenses the effect of atom-photon coupling in a single rank-one projector, thus allowing for a unified treatment of several kinds of dressed states (either bound and unbound). The framework is then extended to the case that more than one emitter is present and used to derive a general expression of dissipationless effective Hamiltonians (mentioned above), which explicitly connects the interatomic potential to overlapping single-atom dressed states independently of the specific photonic bath.

2 Model and Hamiltonian

We consider a two-level quantum emitter (“atom”) coupled under the usual rotating-wave approximation to an unspecified photonic bath which is effectively modelled as a discrete set of N coupled cavities (see sketch in Figure 1). The Hamiltonian reads (we set ℏ = 1 throughout the paper)

with H ₀ = H _e + H _B (unperturbed Hamiltonian), where

with σ − = σ + † = g e and b _x the annihilation operators of the cavities fulfilling usual bosonic commutation rules ( g and e are the atom’s ground and excited states, respectively, and ω ₀ their energy separation). Here, x = 0 (in the following sometimes referred to as the “position” of the atom) labels the cavity directly coupled to the atom. Finally, ω _x is the bare frequency of cavity x, while J x ′ x = J x x ′ * denote the cavity–cavity hopping rates.

Figure 1:

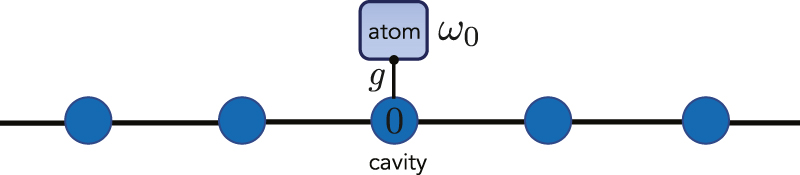
Schematic sketch of the considered model: a two-level quantum emitter (atom) coupled with strength g to a photonic bath B (field) modelled as a set of coupled cavities. The coupling is local in that the atom is directly coupled to only one cavity (labelled with 0). Here, B is represented as a simple one-dimensional lattice (although our framework applies to a generic bath).

In all the remainder, we will be concerned solely with the single-excitation subspace spanned by { e v a c , { g x } } with v a c the field’s vacuum state and x = b x † v a c single-photon states. We conveniently introduce a light notation such that e v a c → e , g x → x , that is e ( x ) is the state with one excitation on the atom (xth cavity). Accordingly, in the single-excitation sector the Hamiltonian terms (2)–(4) take the effective forms

The essential problem we are interested in is working out all the stationary states of the total Hamiltonian, i.e.  all single-photon dressed states.

Before concluding this section, we mention that the model defined by Eqs. (5)–(7) is a special case of the so called Friedrichs–Lee model investigated in the Mathematical Physics literature (see e.g. Refs. [33, 34]). In particular, the local coupling we assume [cf. Eq. (7)] constraints the shape of the function that measures the coupling strength between the emitter and each normal mode of H _B .

3 Resolvent

The resolvent method [16] is a powerful non-perturbative approach to compute eigenstates and eigenvalues of a Hamiltonian H, which is routinely used in many fields including quantum optics (see e.g. Refs. [30], [31], [32, 35]). A few basics of the approach are briefly recalled next.

The resolvent operator or Green function is defined as

where z = ω + iω′ (with ω, ω′ real) runs over the entire complex plane. Here, { n } are the bound eigenstates of H with corresponding discrete energies {ω _n }, while { k } is the continuum of all unbound eigenstates with energy ω(k) [index k is in general a multi-dimensional variable and D ( k ) the associated density of states^[1]]. Energies and eigenstates of H can be inferred from the non-analyticity points of G(z) on the real axis. Specifically, the stationary bound states (BSs) { n } are the residues of G(z) around real poles z = ω _n . Instead, unbound eigenstates { k } are associated with branch cuts of G(z) on the real axis, each cut generally corresponding to an energy band of H [at each point z = ω(k) on a branch cut, G(E(k) + iω′) jumps at ω′ = 0].

Usually, the Hamiltonian is the sum of an unperturbed Hamiltonian H ₀ and a perturbation V, H = H ₀ + V. In this case, if { φ k } are the unbound eigenstates of H ₀ each with energy ω _k and provided that the perturbation is compact [36], the unbound eigenstates of H have the same spectrum and are worked out from these through the Lippmann–Schwinger equation as

where we introduced the compact notation h ( ω + ) = lim δ → 0 + h ( ω + i δ ) . These thus fulfil H Φ k = ω k Φ k .

For our model in Eq. (1), the bare atomic and field resolvents (in the thermodynamic limit N ≫ 1) are respectively given by

Here, we assumed that G _B (z) has no poles, i.e. H _B has no bound eigenstates (as it is typically the case when H _B describes a photonic lattice or waveguide). Accordingly, the only eigenstates of H _B are the continuum of single-photon states { k } , associated with the field normal modes, such that H B k = ω k k with ω _k the corresponding normal frequency.

In order to simplify the notation, in the remainder we will follow a frequent convention (see e.g. Ref.  [37]) and formally write G _B (z) as a discrete sum

with the understanding that the thermodynamic limit N ≫ 1 must be eventually carried out.

3.1 Resolvent in the impurity problem: review

A longstanding topic in condensed matter and beyond is studying the effect of introducing an impurity into a lattice (although what follows does not require B to be a lattice). The impurity is usually modelled as a contact potential of the form [16].

(13) V imp = ϵ 0 0 ,

where ϵ is the potential strength and x = 0 the impurity position. When contextualized to our coupled-cavity lattice [cf. Eq. (3)], the impurity corresponds to an effective detuning of cavity x = 0 [see Figure 2], which changes the field Hamiltonian as H _B → H _B + V _imp. Correspondingly, the field’s resolvent G _B (z) [cf. Eq. (12)] turns into G ( z ) = ( z − H B − V imp ) − 1 . This can be worked out as [16]

(14) G ( z ) = G B ( z ) + 1 f ( z ) ψ ( z ) ψ ( z )

with

(15) ψ ( z ) = G B ( z ) 0 ,

(16) f ( z ) = 1 ϵ − ⟨ 0 | G B ( z ) | 0 ⟩ .

Eq. (14) states that the entire effect of the impurity is condensed in the rank-one projector featuring the z-dependent (unnormalized) state ψ ( z ) .

Figure 2:

Impurity problem. A local static potential is added to the photonic bath, which is equivalent to a detuning ϵ changing the frequency of cavity 0 as ω _x=0 → ω _x=0 + ϵ.

4 Dressed states

In line with the previous section, we will first quickly review the scheme for calculating bound and unbound eigenstates in the standard impurity problem and next consider dressed states in our atom-field system.

5 More than one emitter

It is natural to ask how the one-emitter framework developed so far generalizes when another emitter is present. We thus consider next two atoms, labelled 1 and 2, each coupled to the photonic bath at site x _i (for i = 1, 2) with strength g, see sketch in Figure 3. Accordingly, Eq. (5) is now replaced by H e = ω 0 ∑ i = 1 2 e i e i (with ω ₀ the frequency of each atom), while Eq. (7) now turns into V = g x 1 e 1 + g x 2 e 2 + H . c . (we consider equal couplings for the sake of simplicity).

Figure 3:

Schematics of two atoms, 1 and 2, coupled to a photonic bath (in this case sketched as a simple lattice). Each emitter has frequency ω ₀ and is coupled to the cavity x _i with strength g.

The total resolvent in this case can be arranged as (see Supp. Mater.)

where we defined the z-dependent states Ψ i ( z ) and the z-dependent matrix F(z) as [their z-dependence is implicit in Eq. (32)]

with ⟨x _j |Ψ _i ⟩ = ⟨Ψ _j |x _i ⟩ = ⟨x _j |G _B (z)|x _i ⟩. Notice that, for z ∉ R , generally F 12 ≠ F 21 * , and that Ψ i ( z ) and F _ii (z) coincide with Eqs. (18) and (19), respectively, when 0 is replaced by x i .

This exact expression already points towards an effective interaction mediated by one-emitter dressed states. Indeed, the resolvent G(z) reduces to G ₁(z) + G ₂(z) (isolated emitters) when F(z) is diagonal, i.e. F ₁₂ = F ₂₁ = 0: this can only occur when Ψ i ( z ) has a node on x _j≠i [cf. Eq. (34)]. This shows that the crosstalk between the emitters is mediated by Ψ i ( z ) (via its photonic component ψ i ( z ) ).

Each BS energy ω _BS fulfils the pole equation det F(ω _BS) = 0, whose solutions are implicitly given by

where the function ω ̃ 0 ( z ) and δ(z) (here calculated at z = ω BS ± ) are defined as

with A ( z ) = g 2 2 F 22 − F 11 [the dependence on z of F _ij and A is implicit in Eq. (37)].

The residues of G(z), Ψ BS ± Ψ BS ± , on the two poles ω BS ± can be calculated directly although their expression is too lengthy to be reported here (see Supp. Mater.). The states Ψ BS ± are especially relevant when the emitters are far-detuned from all unbound photonic modes. Under weak-coupling condition, this guarantees that ω BS ± will also be far-detuned from the unbound photonic modes and close to ω ₀. Correspondingly, the emitters bare states e i will have vanishing overlap with the unbound dressed states and lie (up to second order in g) in the eigenspace spanned by Ψ BS ± . Thus, the atomic dynamics is described by the effective Hamiltonian H eff ≃ ∑ i = ± ω BS i Ψ BS i Ψ BS i . In this regime, we can derive the approximate explicit expressions for ω BS ± and Ψ BS ± , which provides the following effective Hamiltonian (see Supp. Mater.)

with

where

Here, all z-dependent quantities such as Ψ i , F _ij , ω BS ( i ) , A and δ [cf. Eqs. (33)–(37)] are calculated at z = ω ₀. In particular, Ψ i and ω BS ( i ) are the (unnormalized) dressed BS of atom i and the corresponding energy in the absence of the other emitter, respectively.

Eq. (38) expresses the effective Hamiltonian explicitly in terms of overlapping one-atom dressed BSs. A similar task was carried out in Ref. [12] yet for the specific model of a simple homogeneous photonic lattice.

Notably, terms H _s and H _a are interpreted as follows. When the two atoms are located in equivalent positions then ⟨Ψ₁|Ψ₁⟩ = ⟨Ψ₂|Ψ₂⟩ and thus H _a = 0. Otherwise, in general ⟨Ψ₁|Ψ₁⟩ ≠ ⟨Ψ₂|Ψ₂⟩ so that both H _s and H _a contribute to H _eff. Thus the term H _a describes the effect of inequivalent emitters’ positions. A noteworthy example is a translationally-invariant bath featuring a unit cell with more than one site. In this case it is known that changing from equivalent to inequivalent positions (or vice versa) can dramatically affect the effective coupling strength (which may even vanish) [15, 19].

We conclude by noting that for equivalent positions we get the particularly compact form

where Ψ ̃ i = ⟨ Ψ i | Ψ i ⟩ − 1 / 2 Ψ i is a normalized dressed BS (due to the hypothesis of equivalent positions, ⟨Ψ₁|Ψ₁⟩ = ⟨Ψ₂|Ψ₂⟩).

The above arguments can be generalised (see Supp. Mater.) to the case of M emitters. Indeed, Eqs. (32)–(34) are naturally generalized, yielding in the weak coupling regime the effective Hamiltonian

with x _i the location of the ith atom and where Ψ ̃ i and ω BS ( i ) are defined exactly as in the M = 2 case.

6 Conclusions

To sum up, we considered a general model of quantum emitter coupled to an unspecified photonic bath under the rotating wave approximation. Inspired by analogies between an atom and a standard impurity, we have shown that the resolvent operator used in the non-perturbative description of atom-photon interactions can be re-arranged in a compact form so as to make it structurally analogous to that occurring in the textbook impurity problem. This complements the usual picture according to which the atom acquires a self-energy, showing that the field sees the atom as a fictitious impurity with an associated self-potential. As a hallmark, the presence of the atom in the resolvent is fully captured by a rank-one projector term appearing in the resolvent. This in turn features a dressed-state function Ψ ( z ) (defined on the complex plane) which in a sense encompasses already the stationary states (especially BSs). An extension of the framework to the case of more than one emitter was carried out, which allows for a natural derivation of dispersive Hamiltonians explicitly in terms of overlapping one-atom dressed states.

This work settles the atom-photon resolvent formalism in a form arguably easier to handle. This can be beneficial for instance in view of generalizations to the topical paradigm of giant atoms [40], i.e. emitters non-locally coupled to the bath and as such more complicated to describe [21, 41, 42]. Moreover, the connection with the familiar impurity problem makes the atom-photon resolvent apparatus physically more intuitive. We took advantage from the last circumstance in order to highlight some general properties having an impurity-problem counterpart (e.g. the coexistence of dressed BICs with unperturbed photonic states).