Abstract
In this study, fly ash cenospheres were added to semisolid AZ91D Mg alloy to prepare fly ash cenosphere/AZ91D (FAC/AZ91D) composites by means of compo-casting. The high-temperature damping capacity of FAC/AZ91D composites was investigated as compared with AZ91D Mg alloy. The results show that the damping capacities of FAC/AZ91D composites and AZ91D Mg alloy strongly depend on the measuring temperature. The FAC/AZ91D composites show better damping capacity than AZ91D Mg alloy. The 10 wt.% FAC/AZ91D composites exhibit the best damping capacity from room temperature to 125°C, whereas the 2 wt.% FAC/AZ91D composites show the highest damping capacity at 125°C–320°C. The damping mechanism was analyzed by microstructure observation at elevated temperatures. The damping-temperature curves exhibit a damping peak at approximately 150°C, and the activation energy of the damping peak was calculated according to the Arrhenius equation. Furthermore, the peak temperature increases with increasing frequencies. The damping peak is related to the thermal activation relaxation process, and its mechanism is the dislocation-induced damping.
1 Introduction
Fly ash cenosphere (FAC)/magnesium alloy composites are a new trial for developing composite materials and a new application direction of FAC. FAC, with low price and rich sources, will open broad prospects for FAC/magnesium alloy composites. Magnesium matrix materials have become promising materials because of their combination properties of low density, high specific strength and specific stiffness, and good castability, and they have received wide attention in the material field in recent years. At the same time, magnesium has the highest damping capacity among light alloys. These advantages make magnesium alloys have a wide range of applications in the automotive, aerospace, and electronics industries [1], [2], [3]. It has been a fundamental issue to develop new magnesium matrix materials with a good mechanical property and a high damping capacity in recent years [4]. However, the use of Mg alloys is limited because of their inferior heat resistance and mechanical strength compared with other structural materials [1]. In the abstract, the damping capacity of a material is an ability to convert mechanical vibration energy into other energy. At present, the high damping materials are mainly polymers and not suitable for the use of structural materials owing to low mechanical properties at high temperatures [5], [6]. The magnesium metal matrix composites have also been proven to be one of the best selections for high damping materials [3].
FACs composed of silica and alumina are generated during the combustion of the pulverized coal in coal-fired power plants. As the industrial by-products, if FACs are not put to efficient use, they will be a recognized environmental pollutants [7]. FACs have a wide range of applications in multiple industries owing to their low densities (0.2–0.8 g cm−3), low thermal conductivities (approximately 0.065 Wm−1 K−1), and high stability at high temperatures [8], [9], [10]. Recently, Huang et al. [11] added the FAC into AZ91D Mg alloy to prepare in situ Mg2Si/AZ91D composites by compo-casting and found that the tensile strength of the composites is higher than that of AZ91D Mg alloy. The FAC/AZ91D composites contain Mg2Si phase, which can ensure its high mechanical properties, and have more interfaces because of the addition of FAC particles compared with Mg2Si/AZ91D composites, resulting in higher damping capacity at high temperatures. It was reported that cenosphere aluminum matrix composites have been fabricated through pressure infiltration, which showed better damping properties [12]. However, there is less study on the damping capacity of magnesium matrix composite with cenospheres as the reinforcement. Different kinds of reinforcements have been used to enhance the damping capacities of Mg matrix composites in recent years, such as Mg2Si [13], TiC [14], AlN [15], and graphite [16], but the cost of these reinforcements is relatively high, and these reports mainly focused on the damping capacity of Mg matrix composites at room temperature. However, the temperature has important effects on the microstructure and damping capacity of Mg alloys. Zheng et al. [17] found that the as-ECAPed magnesium alloy exhibited better damping capacity than pure magnesium at high temperatures. Liao et al. [18] studied the high-temperature damping properties of Mg-9Al-Si alloy and found that there was a damping peak at 420 K. The significance of the damping peak is equivalent to a mechanical vibration energy absorption line, and this line will provide basic data on the design and application of damping materials. Furthermore, the mechanism of new spectrum can offer theoretical guidance to develop new damping materials [19].
In this paper, the FAC/AZ91D composites were prepared by compo-casting. The effects of FAC on the microstructure and damping capacity of the composites at high temperatures were investigated. By analyzing the microstructure of the composites at elevated temperatures, the damping mechanisms of AZ91D Mg alloy influenced by FAC were revealed.
2 Materials and methods
2.1 Materials
AZ91D Mg alloy ingots and FAC particles were selected as the raw materials for preparing FAC/AZ91D composites. The chemical composition of AZ91D Mg alloy ingots (wt.%) is given as follows: Al, 9.07; Zn, 0.62; Mn, 0.21; Si, 0.034; Cu, 0.003; Fe, 0.0022; Ni, 0.00033; and Mg, balance. The contents of various phases in FAC particles (wt.%) are given as follows: SiO2, 62.79; Al2O3, 24.24; Fe2O3, 3.86; CaO, 1.78; MgO, 1.28; K2O, 2.29; Na2O, 1.30; SO3, 0.21; and others, balance.
2.2 Sample preparation
Before the experiment, the FAC particles whose median particle size is 145.7 μm were washed with 5 wt.% NaOH solution to remove the impurities adsorbed on the surface of FAC. The experimental setup for preparing the FAC/AZ91D composites is shown in Figure 1. The technology for preparing the composites comprises the following steps: first, AZ91D Mg alloy ingot was melted at 720°C at an electrical resistance furnace under a (3 vol.% SF6+CO2) protection gas. Then the melt was moved into another little furnace under the protection gas and stirred at 590°C as semisolid fluid. Simultaneously, 2, 6, and 10 wt.% FAC particles were added to the melt, respectively, and the slurry was stirred at a rotation speed of 675 rpm for 3 min with a stirring paddle to ensure the uniform distribution of FAC particles. After that, the slurry was rapidly reheated to 720°C and stirred for 1 min, and then the slurry was poured into a graphite mold preheated to 120°C. To study the evolution of the microstructure of the composites at elevated temperatures, 6 wt.% FAC/AZ91D composites were cut into the size of ϕ28 mm×20 mm, heated to 100°C, 150°C, and 200°C, respectively, and held for 30 min, then taken out for water quenching (approximately 20°C) rapidly to preserve the microstructure characteristics at elevated temperatures.

The experimental setup for preparing the FAC/AZ91D composites.
2.3 Measurements and instruments
The damping capacity was measured by a dynamic mechanical analysis meter (DMA-Q800) in the double cantilever beam mode. The specimens for damping test were cut into the size of 60×6×1 mm with electric spark cutting. The test conditions were as follows: the strain amplitude (ε) was 1×10−5; the vibration frequencies (f) were 0.5, 1, and 5 Hz, respectively; the temperature (T) range was from room temperature to 320°C; and the heating rate (dT/dt) was 5°C/min. The damping capacity was evaluated as loss tangent (tan ϕ).
The microstructure was observed with an optical microscopy (OM, Nikon Epiphot-300), and the etching solution was 5 wt.% oxalic acid solution. The crystalline phases were determined by X-ray diffraction (D/MAX-2000 PC) with Cu Kα radiation.
3 Results
3.1 Microstructures at elevated temperatures
Figure 2 shows the microstructures of AZ91D Mg alloy and FAC/AZ91D composites at room temperature. It can be found that the discontinuous second phase (Figure 2A) was distributed along the grain boundaries in AZ91D Mg alloy. After FACs were added, the interfacial reaction occurred between FAC and AZ91D Mg alloy, and the reaction products increased with the increase in FAC content (Figure 2B–D). It can also be found that the grain sizes of the matrix in FAC/AZ91D composites are finer than that of AZ91D Mg alloy, indicating that the addition of FAC particles has an obvious effect on the grain refinement, which accords with the report in the literature [20]. The discrete second phase became continuous and fine after the addition of FAC. Figure 3 shows the XRD patterns of AZ91D Mg alloy and 6 wt.% FAC/AZ91D composites. It can be found that the phases in the matrix are mainly α-Mg and β (Mg17Al12), and the reaction between FAC and AZ91D Mg alloy matrix forms two new phases of Mg2Si and MgO. According to Figure 2, there are fewer reaction products (Mg2Si) when the content of FAC is 2 wt.%. When the content of FAC is up to 6 wt.%, some sharp polygonal Mg2Si particles distribute in the matrix or near the wall of FAC. When the content of FAC is 10 wt.%, massive cloddy Mg2Si particles are attached on the wall of FAC. The more the content of FAC, the more intense the reaction between AZ91D Mg alloy and FAC. Some Mg2Si particles dispersed along the grain boundaries can hinder the boundary motion and limit the growth of the matrix grain. Hence, the reaction between the wall of the FAC and the molten Mg matrix can lead to the refinement of microstructure of the composites. It can also be found that some tiny pores exist at the walls of FAC in FAC/AZ91D composites.

Microstructures of AZ91D Mg alloy and FAC/AZ91D composites with different FAC contents at room temperature. (A) AZ91D Mg alloy matrix, (B) 2 wt.% FAC/AZ91D composites, (C) 6 wt.% FAC/AZ91D composites, and (D) 10 wt.% FAC/AZ91D composites.

XRD patterns of (A) AZ91D Mg alloy and (B) 6 wt.% FAC/AZ91D composites.
The microstructures of 6 wt.% FAC/AZ91D composites after being heat treated at 100°C, 150°C, and 200°C, respectively, are shown in Figure 4. It can be found that a certain amount of the β phase is dissolved in the matrix after heat treatment and becomes smaller (compared with Figure 2C). The β phase is the smallest and more continuous after heat treatment at 200°C, which means that the β phase is gradually dissolved in the matrix as the temperature increases, and then the β phase shows a continuous reticular structure. It can also be found that the element diffusion capacity of Si is enhanced with increasing temperature. Some Mg2Si particles are distributed in the vicinity of FAC as a small granular at first and then move to the matrix and grow at elevated temperatures, and a partial agglomeration situation appears at 200°C.

Microstructures of 6 wt.% FAC/AZ91D composites after heat treatment at different temperatures: (A) 100°C, (B) 150°C, and (C) 200°C.
3.2 High-temperature damping capacity
Figure 5 shows the temperature dependence of the damping capacities of AZ91D Mg alloy and FAC/AZ91D composites at ε=1×10−5 and f=1 Hz. It can be noted that the damping capacities of both the composites and the AZ91D Mg alloy enhance with the increase in temperature, and the damping capacities of the composites are higher than that of AZ91D Mg alloy under different temperatures. As reinforcements, FACs significantly enhance the damping capacity of AZ91D Mg alloy, but FACs themselves are very low intrinsic damping materials, and the high damping capacity of FAC/AZ91D composites is derived from the interaction between FAC and AZ91D Mg alloy matrix. The damping capacities of the matrix and the composites improve slowly at temperatures lower than approximately 125°C, and 10 wt.% FAC/AZ91D composites show the highest damping capacity. The damping capacities of the matrix and composites increase quickly at temperatures higher than 125°C, and 2 wt.% FAC/AZ91D composites possess the highest damping capacity. When the temperature approaches 225°C, the damping capacity shows a sharp increasing trend. However, the damping capacity of AZ91D Mg alloy is always the lowest compared with the composites.

High-temperature damping capacities of FAC/AZ91D composites and AZ91D Mg alloy.
Figure 6 shows the high-temperature damping capacity of 6 wt.% FAC/AZ91D composites under different frequencies. It shows that the damping capacities of AZ91D Mg alloy and the composites are almost frequency independent at low temperatures; however, they become much sensitive to frequency at elevated temperatures. The damping capacity of the composites increases with deceasing frequency, which shows a typical anelastic relaxation characteristic. After subtracting a background damping consisting of a superposition of an exponential term and fitting damping peaks according to the Gaussian function, bare damping peaks of 6 wt.% FAC/AZ91D composites at three testing frequencies can be obtained, as shown in Figure 7. The background damping
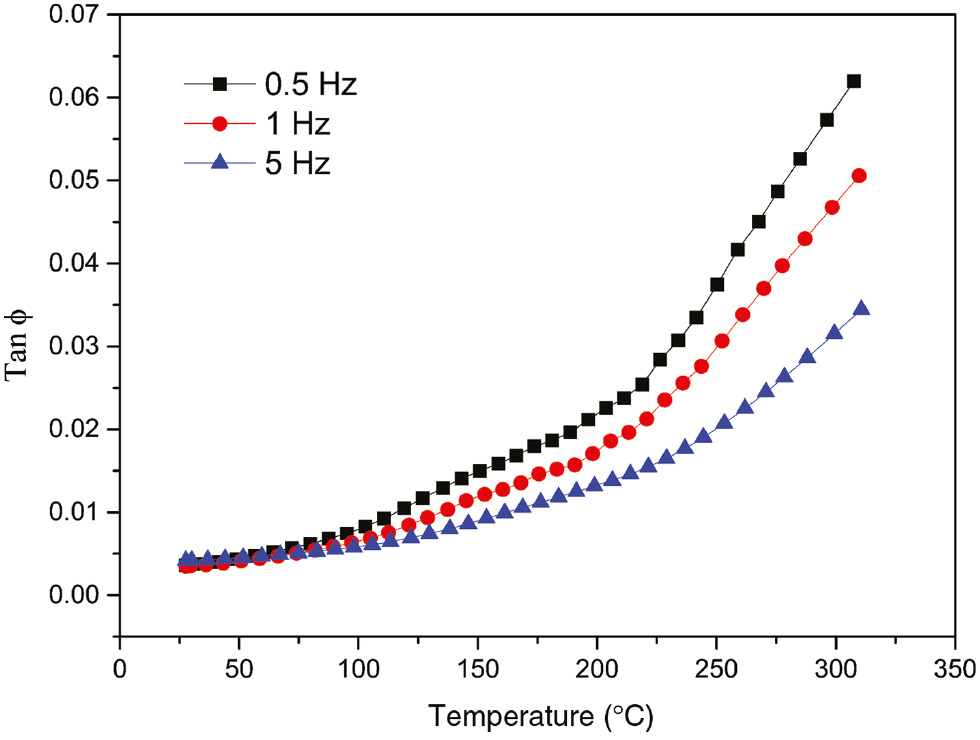
Temperature dependence of damping capacity under different frequencies of 6 wt.% FAC/AZ91D composites.

Damping peak of fitting for 6 wt.% FAC/AZ91D composites.
where A is a material constant, k is the Boltzmann constant, T is the absolute temperature, and B and C are the empirical parameters determined by the intercept and slope of a plot of ln
where τ0 and k are the exponent factor and the constant and H is the activation energy. At the peak position, ωτ=1 is met. Thus, the activation energy (H) can be calculated by the slope of ln (2πf)−1000/Tp, where Tp is the peak temperature. In light of the data in Figure 7, the Arrhenius plot of 6 wt.% FAC/AZ91D composites can be obtained and is shown in Figure 8. The data (Tp, H) of the matrix and the composites obtained by the same process are listed in Table 1.

Arrhenius relation between the circle frequency and the peak temperature of 6wt.% FAC/AZ91D composites.
Variation of the peak temperature and heat activation energy H in AZ91D Mg alloy and FAC/AZ91D composites.
| Samples | The temperature of damping peak Tp/°C | Activation energy H/eV | ||
|---|---|---|---|---|
| 0.5 Hz | 1 Hz | 5 Hz | ||
| AZ91D | 137.91 | 151.00 | 183.23 | 1.90 |
| 2 wt.% FAC/AZ91D | 140.14 | 152.75 | 183.93 | 198 |
| 6 wt.% FAC/AZ91D | 139.43 | 153.80 | 184.28 | 1.94 |
| 10 wt.% FAC/AZ91D | 144.34 | 155.90 | 179.38 | 2.49 |
4 Discussion
4.1 The influence of FAC on damping capacity
As demonstrated in Figure 5, the damping capacities of the composites are better than that of AZ91D Mg alloy because of the addition of FAC. The addition of FAC can modify the microstructures of the AZ91D Mg alloy matrix, including the grain size, the thermal mismatch inducing dislocations, and the interfaces between FAC and matrix.
The thermal mismatch due to the different coefficients of thermal expansion between AZ91D Mg alloy and FAC results in the residual strain, which can cause high dislocation density in the matrix alloy. The dislocation density in FAC/AZ91D composites is higher than that of AZ91D Mg alloy, which can lead to higher dislocation damping. Thus, the dislocation damping is one reason for the higher damping capacity of the composites when compared with AZ91D Mg alloy at the testing temperature range. In polycrystalline materials, the grain boundaries tend to exhibit anelastic characteristic, which can play an important role in improving the damping capacity. Grain boundary damping is very sensitive to temperature, and the viscous flow at grain boundaries converts the strain energy into other energy [23]; thus, the damping capacities substantially increase at high temperatures. The refinement of grains will lead to massive grain boundaries. Thus, the material with fine grains shows high damping capacity at high temperatures. According to Figure 2, the addition of FAC has an obvious influence on the grain refinement of AZ91D Mg alloy matrix. The grain size of FAC/AZ91D composites is finer than that of AZ91D Mg alloy, and they have higher grain boundary damping. Thus, the grain boundary damping is another reason for the high damping capacity of the composites as compared with AZ91D Mg alloy at the testing temperature range. The interfaces between FAC and AZ91D Mg alloy matrix are easy to slip at high temperatures; thus, interfaces have important influence on the damping properties of the composites. The interface damping is mainly affected by the bonding strength, interfacial reaction products, and porosities at the interface. After FACs were added into AZ91D Mg alloy, the elements of the FAC wall diffused to the matrix and formed the reaction products Mg2Si and MgO, and then some tiny holes appeared in the walls of FACs. In addition, the differences between the crystal structure of FAC and AZ91D Mg alloy are large; thus, the interface between FAC and matrix may be incoherent, so the interface bonding is weak. In the case of a weak bonding interface, Lederman [24] has derived an upper bound of the damping component (η) owing to the initiation of the interfacial slip at the interface:
where C is the correction factor, μ is the coefficient of friction between the particulate and the matrix, k is the coefficient of the radial stress concentration at the interface, and VP is the volume fraction of the particulates. According to Equation (3), interface damping is proportional to the volume fraction of FAC particulates. The existence of the interface damping is one reason for the better damping capacity of the composites at high temperatures. Therefore, the damping capacity of FAC/AZ91D composites is superior to that of AZ91D Mg alloy.
The difference in the damping capacity between AZ91D Mg alloy and composites can be explained by a dislocation damping mechanism at temperatures lower than approximately 125°C. According to the Granato–Lücke theory [25], [26], the damping mechanism of alloys is determined by the dislocation movement. The dislocation loops bow out between weak pinning points, which contribute to strain-independent damping (δ0). The value of the strain-independent damping (δ0) can be expressed as
when the breakaway stress is reached, the dislocation loops break away from the weak pinning points but are still pinning by strong points, which causes strain-dependent damping (δH). δH can be expressed as
where ρ and Ld are the dislocation density and the average distance between weak pinning points, FB is the binding force between dislocations and weak pinning points, LN is the average distance between strong pinning points, E is the elastic modulus, b is the magnitude of Burger vector, K is a constant, and η is the size ratio of the solvent atoms to solute atoms. The more the content of FAC, the more the products (Mg2Si), which can reduce the LN and enlarge the dislocation density ρ. At temperatures lower than approximately 125°C, the δ0 component may play a leading role due to a low strain amplitude (ε=1×10−5); thus, 10 wt.% FAC/AZ91D composites possess the highest damping capacity because of their highest dislocation density ρ. At temperatures higher than 125°C, the grain boundary damping and the interface damping become more important. The existence of Mg2Si phase around grain boundary can hinder the slide of the grain boundary, making the slide difficult, which will reduce the grain boundary damping. In addition, a lot of Mg2Si phase gather in the wall of FAC in 10 wt.% FAC/AZ91D composites according to Figure 2, which could make the interface slip between FAC and matrix become difficult. Thus, 2 wt.% FAC/AZ91D composites show the highest damping capacity at temperatures higher than 125°C because of fewer Mg2Si particles. The damping capacities of both composites and AZ91D Mg alloy show a sharp increasing trend due to the grain boundary damping after the temperature approaches 225°C.
4.2 Analysis of damping peak
As mentioned at Table 1, a damping peak around 150°C is found in the damping-temperature curves of AZ91D Mg alloy and FAC/AZ91D composites. Actually, the damping peak around 150°C in the damping-temperature curves of Mg alloy and its composites has been investigated in previous reports. Gu et al. [27] found the damping peak around 150°C in pure Mg and (SiC+Al2O3·SiO2)/Mg composites, and the values of the calculated activation energy of the damping peaks were 1.22 and 1.44 eV, respectively. The damping peak is believed to be attributed to the dislocation movement. Deng et al. [28] also found the damping peak around 150°C in SiCp/AZ91 and AZ91 Mg alloy in the solution state, and the values of the calculated activation energy were 1.76 and 1.30 eV, respectively. In Gr/AZ91 Mg alloy composites prepared by Wu et al. [29], the calculated H value of damping peak around 150°C was 1.28 eV. The peaks at approximately 150°C were also found in TiC/AZ91D magnesium alloy composites heat treated with T4 and T6 by Zhang et al. [30] and the values of the calculated activation energy of these composites were 2.18 eV for foundry composites, 1.52 eV for T4-treated composites, and 1.96 eV for T6-treated composites. The literature has shown that the grain boundary diffusion energy was 0.85–1.09 eV and the self-diffusion activation energy was 1.39 eV [28]. In this study, the calculated H values of AZ91D Mg alloy, 2 wt.%, 6 wt.%, and 10 wt.% FAC/AZ91D composites are 1.90, 1.98, 1.94, and 2.49 eV, respectively. The result shows that the addition of FAC can increase the activation energy of the composites, which are much larger than the grain boundary diffusion energy and the self-diffusion energy of the pure magnesium. Combined with previous studies, the damping peaks at approximately 150°C of AZ91D Mg alloy and its composites should be associated with the motion of dislocation. With the increase in temperature, the β phase gradually dissolves into the matrix, and the Mg2Si phase slowly moves into the matrix and grows up in light of Figure 4. According to the G-L mechanism, the dislocation is pinned by the weak pinning such as solute atom and the strong pinning such as reinforcement particulates (Mg2Si) and precipitation (β phase). The β phase dissolved in the matrix can result in the decrease in the average distance between the weak pinning points (Ld), and the decrease in the β phase, agglomeration, and growth of Mg2Si phase can increase the average distance between the strong pinning points (LN). Thus, the damping capacity can increase continuously at low temperatures. When temperature reaches a certain value (approximately 150°C), the dislocation would move quickly and then break away in the avalanche-like mode from the weak pinning points. It would only be pinned by the strong pinning points, and then the dislocation damping would not increase; consequently, the damping peak is generated. After that, the damping can increase again owing to the contribution of the grain boundary damping and interface damping.
5 Conclusions
FAC/AZ91D composites were prepared successfully by compo-casting method. The FAC particulates were added to the Mg alloy matrix and had a relatively uniform distribution. The reaction between FAC and Mg alloy matrix formed two new phases of Mg2Si and MgO.
The temperature has an obvious effect on the damping capacity of FAC/AZ91D composites. The damping capacity of FAC/AZ91D composites is higher than that of AZ91D Mg alloy because of dislocation damping, grain boundary damping, and interface damping. At temperatures lower than approximately 125°C, 10 wt.% FAC/AZ91D composite shows the highest damping capacity owing to the dislocation damping. At temperatures higher than approximately 125°C, 2 wt.% FAC/AZ91D composite has the highest damping capacity because of grain boundary damping and interface damping.
A damping peak is found in all the damping-temperature curves of AZ91D Mg alloy and FAC/AZ91D composites. The damping peak shifts to higher temperature with the increase in frequency. The calculated H values of AZ91D Mg alloy, 2 wt.%, 6 wt.%, and 10 wt.% FAC/AZ91D composites are 1.90, 1.98, 1.94, and 2.49 eV, respectively. The damping peak at approximately 150°C is attributed to the avalanche effect of the dislocation anchor.
Acknowledgments
This work was supported by the Key Grant Project of Chinese Ministry of Education (grant no. 313056) and the Open Fund (grant no. OGE201402-01) of Key Laboratory of Oil and Gas Equipment, Ministry of Education.
References
[1] Mordike BL, Ebert T. Mater. Sci. Eng. A. 2001, 302, 37–45.10.1016/S0921-5093(00)01351-4Suche in Google Scholar
[2] Polmear IJ. Mater. Sci. Technol. 1994, 10, 1–16.10.1179/mst.1994.10.1.1Suche in Google Scholar
[3] Ritchie IG, Pan ZL, Sprungmann KW, Schmidt HK, Dutton R. Can. Metall. Q. 1987, 26, 239–250.10.1179/cmq.1987.26.3.239Suche in Google Scholar
[4] Ma N, Peng Q, Pan J, Li H, Xiao WL. J. Alloys Compd. 2014, 592, 24–34.10.1016/j.jallcom.2013.12.249Suche in Google Scholar
[5] Chen Z, Pal K, Byeon JU, Han SM, Jin KK. J. Appl. Polym. Sci. 2011, 119, 2737–2741.10.1002/app.31697Suche in Google Scholar
[6] Huang WB, Liu C, Huang J. Mater. Rev. 2012, 26, 89–91.10.1096/fasebj.26.1_supplement.855.7Suche in Google Scholar
[7] Blissett RS, Rowson NA. Fuel 2012, 97, 1–23.10.1016/j.fuel.2012.03.024Suche in Google Scholar
[8] Shao Y, Jia D, Zhou Y, Liu B. J. Am. Ceram. Soc. 2010, 124, 97–101.10.1016/j.matchemphys.2010.05.073Suche in Google Scholar
[9] Tao H, Yao J, Zhang L, Xu N. Mater. Lett. 2009, 63, 203–205.10.1016/j.matlet.2008.09.034Suche in Google Scholar
[10] Wu H, Sun P. Constr. Build. Mater. 2007, 21, 211–217.10.1016/j.conbuildmat.2005.06.052Suche in Google Scholar
[11] Huang ZQ, Yu SR, Liu J, Zhu XY. Mater. Des. 2011, 32, 4714–4719.10.1016/j.matdes.2011.06.043Suche in Google Scholar
[12] Wang ZX, Wen W, Ma NH, Wang HW. Hot Work. Technol. 2009, 38, 128–130.Suche in Google Scholar
[13] Jun JH. Mater. Trans. 2012, 53, 2064–2066.10.2320/matertrans.M2012255Suche in Google Scholar
[14] Cao W, Zhang C, Fan T, Zhang D. Mater. Sci. Eng. A. 2008, 496, 242–246.10.1016/j.msea.2008.06.032Suche in Google Scholar
[15] Zhang CF, Fan T, Cao W, Zhang D. Mater. Sci. Eng. A. 2009, 508, 190–194.10.1016/j.msea.2009.01.060Suche in Google Scholar
[16] Wu YW, Wu K, Deng KK, Nie KB, Wang XJ, Zheng MY, Hu XS. Mater. Des. 2010, 31, 4862–4865.10.1016/j.matdes.2010.05.033Suche in Google Scholar
[17] Zheng M, Fan G, Tong L, Hu X, Wu K. T. Nonferr. Metal. Soc. 2008, 18, 33–38.10.1016/S1003-6326(08)60007-2Suche in Google Scholar
[18] Liao LH, Zhang XQ, Wang HW, Li XF, Ma NH. J. Alloys Compd. 2007, 429, 163–166.10.1016/j.jallcom.2006.04.020Suche in Google Scholar
[19] Fang QF, Zhu ZG, Ge TS. Physics 2000, 9, 541–545.10.1016/S0261-3069(00)00024-8Suche in Google Scholar
[20] Rohatgi PK, Daoud A, Schultz BF, Puri T. Composites Part A 2009, 40, 883–896.10.1016/j.compositesa.2009.04.014Suche in Google Scholar
[21] Liu SW, Hu XF, Jiang HC, Li XY, Rong LJ. Acta. Metall. Sin. 2011, 24, 335–342.Suche in Google Scholar
[22] Schoeck G, Bisogni E, Shyne J. Acta Metall. 1964, 12, 1466–1468.10.1016/0001-6160(64)90141-5Suche in Google Scholar
[23] Tam KF, Tjong SC. Mater. Sci. Technol. 2004, 20, 1055–1058.10.1179/026708304225019939Suche in Google Scholar
[24] Lederman WA. PhD dissertation. University of Wisconsin: Milwaukee, WI, 1991, p.17.Suche in Google Scholar
[25] Granato A, Lucke K. J. Appl. Phys. 1956, 27, 583–593.10.1063/1.1722436Suche in Google Scholar
[26] Granato A, Lucke K. J. Appl. Phys. 1956, 27, 789–805.10.1063/1.1722485Suche in Google Scholar
[27] Gu J, Zhang X, Gu M. J. Alloys Compd. 2004, 385, 104–108.10.1016/j.jallcom.2004.04.106Suche in Google Scholar
[28] Deng KK, Li JC, Nie KB, Wang XJ, Fan JF. Mater. Sci. Eng. A. 2015, 624, 62–70.10.1016/j.msea.2014.11.069Suche in Google Scholar
[29] Wu YW, Wu K, Deng KK, Nie KB, Wang XJ, Hu XS, Zheng MY. J. Alloys Compd. 2010, 506, 688–692.10.1016/j.jallcom.2010.07.043Suche in Google Scholar
[30] Zhang XQ, Liao LH, Ma NH, Wang HW. Mater. Lett. 2006, 60, 600–604.10.1016/j.matlet.2005.09.038Suche in Google Scholar
©2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Review
- A model on the curved shapes of unsymmetric laminates including tool-part interaction
- Original articles
- Enhanced catalytic performance of β-FeOOH by coupling with single-walled carbon nanotubes in a visible-light-Fenton-like process
- Investigation of the microstructure and properties of W75-Cu/W55-Cu brazed joint with Cu-Mn-Co filler metal
- In situ polymerization approach to poly(arylene ether nitrile)-functionalized multiwalled carbon nanotube composite films: thermal, mechanical, dielectric, and electrical properties
- Fabrication and characterization properties of polypropylene/polycarbonate/clay nanocomposites prepared with twin-screw extruder
- Torsional vibration of functionally graded carbon nanotube reinforced conical shells
- A comparative study performance of cationic organic montmorillonite prepared by different methods
- Design and analysis with different substrate materials of a new metamaterial for satellite applications
- An investigation on dry sliding wear behaviour of pressure infiltrated AA1050-XMg/B4C composites
- Investigation of mechanical performances of composite bolted joints with local reinforcements
- Effect of alkali treatment on the flexural properties of a Luffa cylindrica-reinforced epoxy composite
- Thermal expansion, electrical conductivity and hardness of Mn3Zn0.5Sn0.5N/Al composites
- Effect of modified layered double hydroxide on the flammability and mechanical properties of polypropylene
- A unified formulation for free vibration of functionally graded plates
- Friction-stir welding of aluminum alloy with an iron-based metal as reinforcing material
- Hybridization effect of coir fiber on physico-mechanical properties of polyethylene-banana/coir fiber hybrid composites
- Micromechanical properties of unidirectional composites filled with single and clustered shaped fibers
- Structure and microwave absorbing properties of carbon-filled ultra-high molecular weight polyethylene
- Investigation and optimization of the electro-discharge machining parameters of 2024 aluminum alloy and Al/7.5% Al2O3 particulate-reinforced metal matrix composite
- Structural behavior of load-bearing sandwich wall panels with GFRP skin and a foam-web core
- Synthesis, thermal and magnetic behavior of iron oxide-polymer nanocomposites
- High-temperature damping capacity of fly ash cenosphere/AZ91D Mg alloy composites
- Investigation of penetration into woven fabric specimens impregnated with shear thickening fluid
Artikel in diesem Heft
- Frontmatter
- Review
- A model on the curved shapes of unsymmetric laminates including tool-part interaction
- Original articles
- Enhanced catalytic performance of β-FeOOH by coupling with single-walled carbon nanotubes in a visible-light-Fenton-like process
- Investigation of the microstructure and properties of W75-Cu/W55-Cu brazed joint with Cu-Mn-Co filler metal
- In situ polymerization approach to poly(arylene ether nitrile)-functionalized multiwalled carbon nanotube composite films: thermal, mechanical, dielectric, and electrical properties
- Fabrication and characterization properties of polypropylene/polycarbonate/clay nanocomposites prepared with twin-screw extruder
- Torsional vibration of functionally graded carbon nanotube reinforced conical shells
- A comparative study performance of cationic organic montmorillonite prepared by different methods
- Design and analysis with different substrate materials of a new metamaterial for satellite applications
- An investigation on dry sliding wear behaviour of pressure infiltrated AA1050-XMg/B4C composites
- Investigation of mechanical performances of composite bolted joints with local reinforcements
- Effect of alkali treatment on the flexural properties of a Luffa cylindrica-reinforced epoxy composite
- Thermal expansion, electrical conductivity and hardness of Mn3Zn0.5Sn0.5N/Al composites
- Effect of modified layered double hydroxide on the flammability and mechanical properties of polypropylene
- A unified formulation for free vibration of functionally graded plates
- Friction-stir welding of aluminum alloy with an iron-based metal as reinforcing material
- Hybridization effect of coir fiber on physico-mechanical properties of polyethylene-banana/coir fiber hybrid composites
- Micromechanical properties of unidirectional composites filled with single and clustered shaped fibers
- Structure and microwave absorbing properties of carbon-filled ultra-high molecular weight polyethylene
- Investigation and optimization of the electro-discharge machining parameters of 2024 aluminum alloy and Al/7.5% Al2O3 particulate-reinforced metal matrix composite
- Structural behavior of load-bearing sandwich wall panels with GFRP skin and a foam-web core
- Synthesis, thermal and magnetic behavior of iron oxide-polymer nanocomposites
- High-temperature damping capacity of fly ash cenosphere/AZ91D Mg alloy composites
- Investigation of penetration into woven fabric specimens impregnated with shear thickening fluid

