A large-scale single-mode array laser based on a topological edge mode

2.1 Theoretical model

We discuss a large-scale topological array laser composed of a number of site resonators. Figure 1(a) shows a schematic implementation of such a laser based on Fabry–Pérot cavities, which can in principle be substituted by any other laser resonators. Each cavity supports a well-defined single lateral mode and optically couples to neighboring cavities. Well-designed couplings between the cavities allow for the appearance of a topological lateral mode distributed over the nearly all of the cavity array, as we will describe shortly later. Electrodes are patterned on specific site cavities to selectively supply gain, which promotes lasing from the designed topological mode. We target a system including a few hundred resonators. If each resonator delivers ∼100 mW output, the topological laser could be operated as a 10W-class laser.

Figure 1:

Investigated topological edge-mode array laser.

(a) Schematic of the investigated topological laser structure. (b) Tight-binding model of the laser structure. An edge mode deterministically emerges at the interface of the two topologically distinct photonic lattices. N and L correspond to the total number of dimers and the number specifying the topological phase boundary, respectively. Note that there exists a single auxiliary site at the end of the topological chain. κ ₁ (single line) and κ ₂ (double lines) indicate weak and strong coupling strengths between neighboring sites, respectively. γ _gain expresses gain supplied on A-site. The application of this tight binding model to the system described in (a) would be valid as long as the longitudinal cavity modes behave independently or when assuming arrays of cavities supporting only single longitudinal mode such as λ/4-shifted distributed feedback resonators.

For theoretical analysis, we map this array laser to a simple tight binding model. We consider an array of single-mode resonators that resembles the Su–Schriffer–Heeger (SSH) model [56]. In the SSH model, the resonator chain is dimerized and its unit cell contains two resonators called A- and B-sites. When the coupling strengths for both the inter- and intra-unit cell hopping are the same, the model exhibits gapless energy bands in momentum space. Meanwhile, when the two coupling strengths are unequal, a gap appears between the two bands. For an SSH chain with a larger inter-cell coupling than the intra-cell coupling, its band topology becomes topologically non-trivial and topological localized modes emerge at the edges of the bulk chain according to the bulk-edge correspondence. More quantitatively, the topological properties of the energy bands can be characterized using Zak phases, which are defined by the integral of the Berry connection over the first Brillouin zone [57]. For a topological band, its Zak phase takes a nonzero value and becomes π when inversion symmetry is preserved in the system.

To obtain the desired laser cavity mode, we interface two SSH chains at the center of the system, as schematically illustrated in Figure1(b). The two chains are topologically trivial and non-trivial, respectively. In this case, a single topological interface mode appears deterministically around the interface [28, 58], with which we design a single mode laser. Since the other end of the topological SSH chain could support another edge state, we terminate the chain with an auxiliary site resonator strongly coupled to the bulk chain, by which we can suppress the emergence of the unwanted extra edge state. Note that this configuration is similar to the design reported in Reference [26]. However, they studied a tightly localized edge mode at the interface in a small lattice, in stark contrast with the current work investigating a broadly distributed interface mode in a large-scale lattice. It is also interesting to note that the topological cavity structure illustrated in Figure 1(a) is reminiscent to that of distributed feedback lasers. Indeed, the laser mode in a lambda/4-shifted distributed feedback laser can be interpreted as a special case of a topological interface mode. Nevertheless, the discrete topological lattice model preserving chiral symmetry discussed in this paper will lead to a unique field distribution capable of robust single mode lasing, making a stark contrast with conventional distributed feedback lasers, as we will demonstrate later.

The system under consideration is described by the following Hamiltonian,

where ω _A,m and ω _B,m are the resonant frequencies of site A and B in a dimer m, respectively, while γ _A,m and γ _B,m denote gain and loss. Site-to-site coupling strengths are described by κ _1,m and κ _2,m . We suppose κ _1,m < κ _2,m , such that the topological SSH chain always remains topological. The total number of the dimers and the number specifying the topological phase boundary are set as N = 100 and L = 50, respectively. Thus, the number of sites in the trivial array becomes n _tri = 2L = 100, while that in the topological array does n _topo = 2(N − L) + 1 = 101. The latter number includes the single auxiliary site at the end of the topological chain. We neglect the presence of unwanted longitudinal modes in each resonator to simplify the analysis. This model is valid as long as the longitudinal modes behave independently or when assuming arrays of single longitudinal mode cavities such as λ/4-shifted distributed feedback resonators. Note that, in this section, we consider an ideal case where we henceforth set (κ _1,m , κ _2,m , γ _A,m , γ _B,m ) = (κ ₁, κ ₂, γ _A , γ _B ) and ω _A,m = ω _B,m = ω for any dimer m, unless otherwise indicated.

2.2 Eigenmodes in the absence of gain and loss

To understand the basic properties of the investigated system formulated in Eq. (1), we first analyze it in the absence of gain and loss. We set the coupling parameters to (κ _1,m , κ _2,m ) = (1.0, 1.04), which serves as a basic parameter set for the subsequent discussion. We diagonalize the Hamiltonian and analyze the energy spectrum and the spatial profiles of the eigenmodes of the system. Figure 2(a) shows computed eigenenergies ɛ plotted in the complex energy plane. In the real energy spectrum, Re(ɛ), one can see an energy gap of approximately 2|κ ₁ − κ ₂|, in which an in-gap mode exists as expected from the topological design discussed above. The topological mode is fixed to the zero energy and the entire energy spectrum is symmetric with respect to the zero energy according to chiral symmetry existing in the system. Note that the chiral symmetry is preserved when Hamiltonian H satisfies Γ^† HΓ = −H with an operator Γ² = 1, where Γ is Hermitian and unitary. In general, a lattice with chiral symmetry will be bipartite and has two sublattices such that no direct transition occurs between the same sublattice sites. We inspect the spatial profile of the zero energy topological mode and plot this in Figure 2(b). The mode profile distributes over the entire lattice with amplitudes only on A-sites [25, 26]. The spatial profile is well described by an approximated analytical expression given as a m = ( − κ 1 / κ 2 ) | m − L | × a L , b m = 0 for any m, where a _m (b _m ) is the field amplitude at mth A-site (B-site). The extent of the spatial profile depends on the ratio of coupling constants. The current ratio of κ ₂/κ ₁ = 1.04 is sufficiently small so that the edge mode profile is distributed over the entire 201 sites. Figure 2(c) shows a spatial profile of one of the two band-edge bulk modes. In contrast to the topological edge mode, the amplitudes are essentially equally distributed over both A- and B-site. The difference of the mode profile suggests that lasing from the topological edge mode can be selectively promoted by supplying gain only to A-sites.

Figure 2:

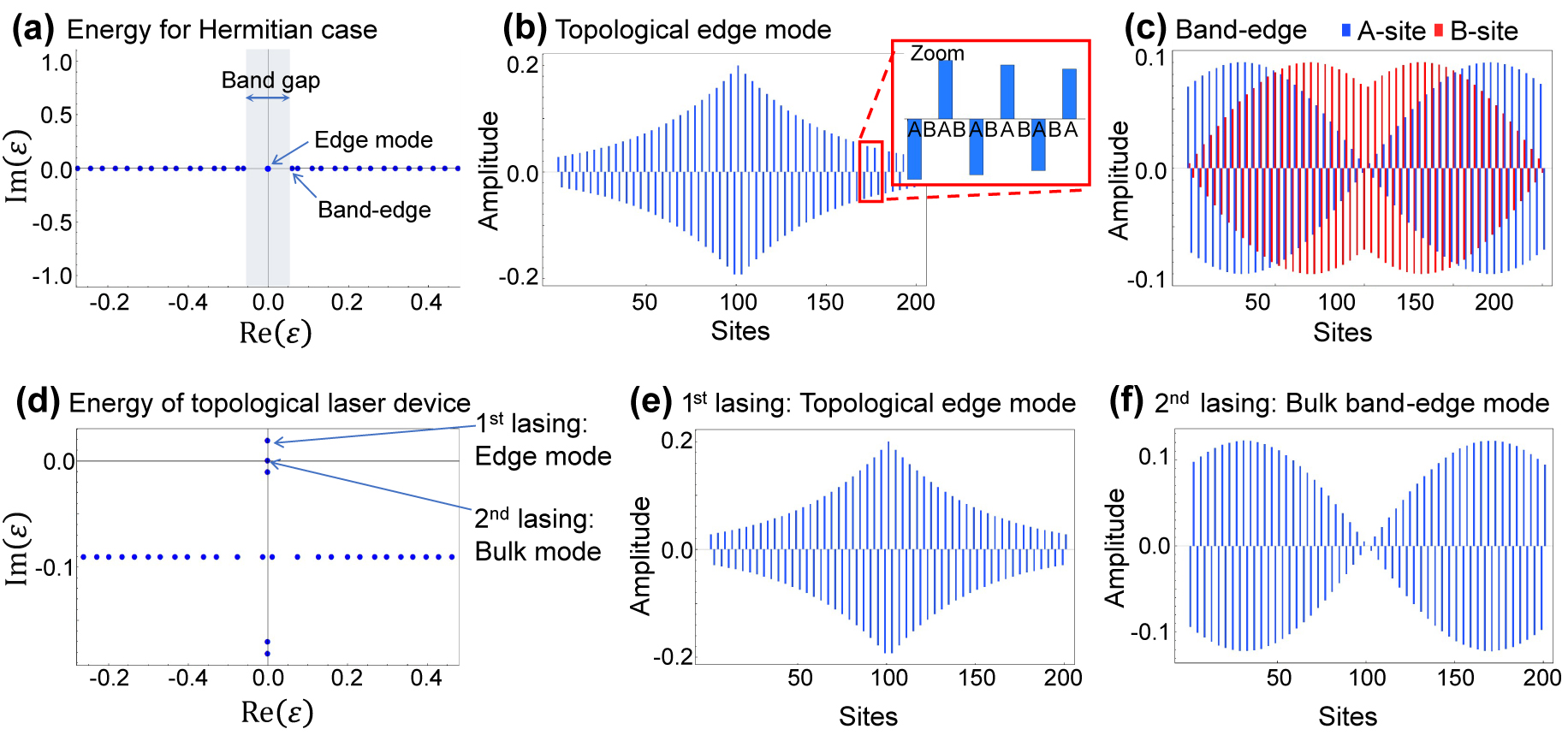
Eigenstates of the edge mode and band-edge bulk mode.

(a) The eigenenergies ɛ in the complex energy plane for the Hermitian case, zoomed around origin. (b) Spatial profile of the topological edge mode. The inset shows that the edge mode has non-zero amplitudes only on A-sites. (c) Spatial profile of the band-edge bulk mode for comparison. For (a)–(c), the parameters used are κ ₂/κ ₁ = 1.04, γ _loss = γ _gain = 0, n _tri = 100 and n _topo = 101. (d) The eigenenergies ɛ in the complex energy plane for the topological laser system with gain and loss, zoomed around origin. (e) Spatial profile of the first lasing mode, i.e., topological edge mode. (f) Spatial profile of the second lasing mode stemming from an amplified bulk mode, exhibiting non-zero amplitudes only on A-sites. For (d)–(f), the parameters used are κ ₁ = 1.0, κ ₂ = 1.04, γ _loss = 0.2, and γ _gain = 0.219. The system size is n _tri = 100 and n _topo = 101. In ((b), (c), (e) and (f)), blue and red bars indicate the amplitudes on A-site and B-site, respectively.

2.3 Eigenmodes under the presence of gain and loss

Next, we investigate the properties of the system when introducing gain and loss to assess the capability of single mode lasing. To account for modal loss normally existing in photonic devices, we assume that all site resonators experience an uniform loss at a rate γ _loss. Then, we supply gain on the A-sites at a rate of γ _gain. Thus, we introduce γ _A = γ _gain − γ _loss and γ _B = −γ _loss as imaginary onsite potentials across all the sites. Figure 2(d) shows representative eigenenergies in the complex energy plane with γ _loss = 0.2 and γ _gain = 0.218. Most eigenstates show negative Im(ɛ) and are expected to behave as lossy states. In contrast, the topological edge state solely acquires an explicit positive Im(ɛ), indicating that the state becomes the first lasing mode in the system. This result confirms that our design can promote single mode lasing from the designed topological edge state broadly distributed in the lattice. Meanwhile, in the plot, there is a bulk state with nearly zero real and imaginary energies, which, with additional gain, could be positive in the imaginary part and hence a second lasing state. The presence of such a bulk mode capable of lasing leads to the unwanted competition of lasing modes in the system. To stabilize the single mode lasing from the topological edge state, it is vital to design a system that suppresses lasing from the bulk modes.

The reason why the topological edge and bulk states under concern preferentially acquire non-negative Im(ɛ) can be understood from their mode profiles presented in Figure 2(e) and (f). Both of their mode profiles have dominant amplitudes on A-sites, where gain is selectively supplied. We identified that the bulk mode with spatial profile only on the A-sites arises from a phase transition similar to that occurring in parity-time (PT) symmetric systems [59–61]. Note that, while the gain and loss are totally balanced in PT symmetric systems, we consider a system with varied gain and fixed loss. Subjected to a large supplied gain, some bulk modes experience a phase transition and choose to split in its imaginary energies (while in turn degenerate in real energies), which accompanies a drastic change of the field profiles. To gain more insight into the phase transition, we consider an infinite bulk SSH chain without any interface. In this case, the Hamiltonian represented in momentum space takes the form

where a is the lattice constant and k is a wave number. For band edge modes supported at the Brillouin zone edge, the eigenvalues are given by ε ( ω ) = i ( γ A + γ B ) ± − ( γ A − γ B ) 2 + 4 ( κ 1 − κ 2 ) 2 / 2 . The eigenvalues split in either real or imaginary part depending on the sign in the square root. One of the modes split in imaginary energy corresponding to the second lasing bulk mode in our case, as we will discuss later. Since we define γ _A = γ _gain − γ _loss and γ _B = −γ _loss, the critical gain that induces the imaginary energy splitting in the bulk mode is given by

Across γ gain c r i t i c a l , one observes a phase transition in the bulk eigenstates. As has been anticipated from the Hamiltonian and the expression of eigenvalues above, the phase transition in the bulk system resembles that in PT symmetric systems. When γ gain < γ gain critical , the band-edge modes are in a phase analogous to the PT symmetric phase and exhibit mode profiles homogeneously-distributed for both sites. In contrast, when γ gain > γ gain critical , the band-edge modes are in a phase analogous to the broken-PT phase and therefore exhibit mode profiles that dominantly populate in either A- or B-site. The spatial profile of the bulk mode in Figure 2(f) shows the one in the broken phase. We note that γ gain critical becomes larger when considering a bulk system with a finite size. For our system with 201 arrays, γ gain critical is computed to be ∼ 0.12 , instead of the analytical value γ gain critical = 0.08 for the infinite system with |κ ₁ − κ ₂| = 0.04.

2.4 Threshold gain difference

A way to assess the capability of single mode lasing is to measure the threshold gain difference among the lasing modes. In this work, the threshold gain for a mode is defined as the supplied gain at which the mode reaches Im(ɛ) = 0. We will consider the threshold gain difference Δα between the first lasing topological mode and the second lasing bulk trivial mode. The former is defined to lase at γ _gain = γ t h 1 s t and the latter at γ t h 2 n d , thus Δ α = γ t h 2 n d − γ t h 1 s t . It is known that single mode lasing becomes more stable as Δα increases. The analysis based on Δα employs only the eigenmode analysis and thus is very simple, but nevertheless can effectively evaluate the single mode lasing stability.

Figure 3(a) shows the calculated Im(ɛ) as a function of γ _gain for a system with γ _loss = 0.2. A loss value of γ _loss = 0.2 is consistent with conventional Fabry Perot semiconductor lasers as we will discuss in Section 4. In the plot, it is clearly seen that the topological mode (colored in red) acquires gain much faster than the bulk modes (blue) and exhibits positive Im(ɛ) at the lowest γ _gain among all the modes. The threshold gain for the edge mode γ t h 1 s t equals to γ _loss, since the edge mode distributes only on A-sites where gain is selectively supplied. With increasing γ _gain, a bulk mode also reaches Im(ɛ) = 0 at γ t h 2 n d = 0.219 . Thus, Δα is equal to 0.019 in this particular example. If all bulk modes maintained an equal mode distribution on the A- and B-sites, Δα is expected to be |γ _loss| = 0.2, since they simply need additional gain to compensate the loss also in B-site. However, as already discussed above, some bulk modes undergo a phase transition that largely modifies their mode profiles. As such, the branched bulk modes acquire gain much faster than the rest of the bulk modes. This is the reason why Δα reduces in the case in Figure 3(a). Meanwhile, the largest Δα can be obtained when the bulk mode reaches its lasing threshold γ th 2 nd at γ gain critical , that is γ th 2 nd = γ gain critical , which is more preferable for stable single mode lasing from the topological mode. This situation is realized in Figure 3(b), where γ _loss is set to 0.06. The overall behaviors of the Im(ɛ) curves are exactly the same as those in Figure 3(a), except for the difference in the imaginary energy offset. This indicates that γ _loss is a critical factor for controlling Δα. We note that γ _loss = 0.06 may be too small to properly account for conventional loss in semiconductor lasers, which we will discuss in Section 4.

Figure 3:

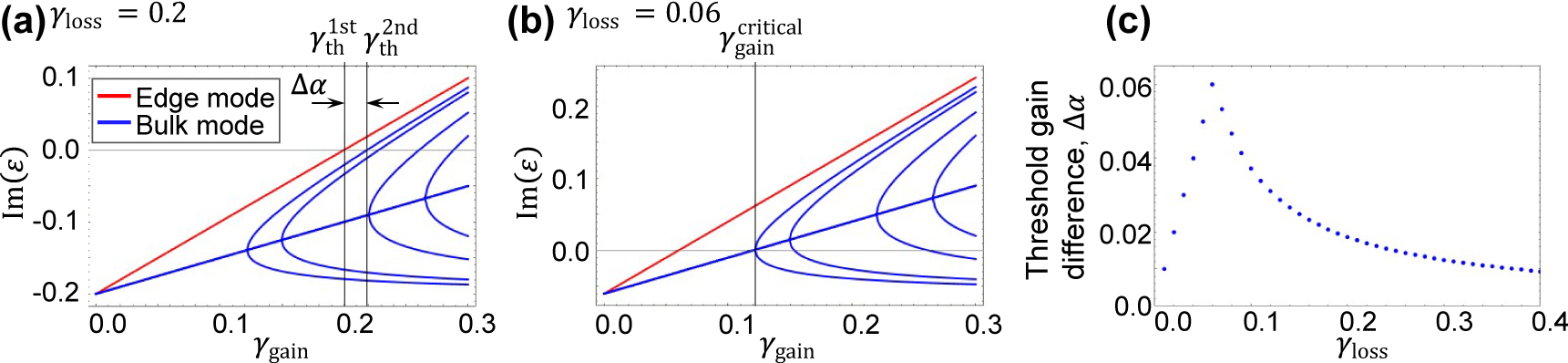
Threshold gain of the lasing modes.

(a) and (b) Imaginary parts of eigenenergies of the system plotted as a function of supplied gain on A-site γ _gain for γ _loss = 0.2 and 0.06, respectively. The red and blue lines indicate the energy of the edge mode and bulk modes. (c) Loss dependence of the threshold gain difference Δα. The parameters used are κ ₁ = 1.0 and κ ₂ = 1.04, with a finite system consisting of n _tri = 100 trivial and n _topo = 101 topological cavities.

In Figure 3(c), we evaluate Δα as a function of γ _loss for the system defined in Figure 1(b) with κ ₁ = 1.0 and κ ₂ = 1.04. The plot of Δα shows a peak at γ _loss = 0.06 where γ th 2 nd = γ gain critical holds, as discussed in Figure 3(b). For the region of γ _loss < 0.06, there is a linear increase of Δα with increasing γ _loss. In this situation, γ th 2 nd is lower than γ gain critical and the second lasing starts before the bulk modes get branched. For the region of γ _loss > 0.06, there is a monotonic decrease of Δα with increasing γ _loss. In this situation, the second bulk-mode lasing occurs from a branched mode and thus γ t h 2 n d becomes closer to γ t h 1 s t .

We here summarize the points to be considered for increasing Δα in our system. (i) The maximum possible Δα is obtained when γ th 2 nd = γ gain critical . (ii) A large γ gain critical is preferable for enhancing Δα. (iii) γ gain critical can be increase by increasing |κ ₁ − κ ₂|, while |κ ₁/κ ₂| should be close to one for maintaining a large field extent of the topological mode. Thus, one should take large κ ₁ and κ ₂ with |κ ₁/κ ₂| ∼ 1. (iv) There is an optimal γ _loss in the system with respect to γ gain critical for maximizing Δα. For semiconductor array lasers based on conventional lossy resonators, the above discussion suggests that it is important to employ low-loss resonators with high resonator-resonator couplings. We will revisit more practical considerations for achieving a single-mode large-area topological laser in Section 4.

3.1 Inhomogeneous coupling strengths

First, we investigate the effects of inhomogeneity in the coupling strengths on the laser array systems discussed so far, i.e. those constructed with κ ₁ = 1.0 and κ ₂ = 1.04 for 201 sites. We prepare coupling strengths randomly distributed among all sites by generating different sets of Gaussian random variables with means κ ₁ = 1.0 (for intra-dimer coupling) and κ ₂ = 1.04 (inter-dimer) and a common standard deviation of randomness r _κ . For each set of parameters with the randomness, we solve the Hamiltonian in Eq. (1) by diagonalization. In order to study r _κ dependence of the laser system, we generate 100 different sets of parameters for each r _κ , and average the outcomes. The error bar represents the half of the standard deviation σ/2, throughout this section. We note that the disorder discussed here can be interpreted as random distances between the site resonators, hence it only breaks parity symmetry, while preserving chiral symmetry.

Figure 4(a) shows the computed threshold gain differences Δα’s for a system subject to γ _loss = 0.06. This is the case for realizing the largest Δα for the disorder-free case. As the randomness or r _κ increases, a decreased Δα is observed. However, Δα remains ∼70% of the maximum even when r _κ = 0.1, where the strength of randomness as the standard deviation exceeds the bandgap of the infinite Hermitian system, 2|κ ₁ − κ ₂| = 0.08. This result indicates the robustness of the single mode lasing from the resonator array device. In the current case, the threshold gain for the first lasing mode, γ th 1 st , remains unchanged even when introducing the disorders. This is a consequence of the preserved chiral symmetry, which leads to a zero-energy mode with its mode amplitude only on A-sites, thus always reaching the threshold gain exactly when compensating the loss in A-sites. Therefore, the observed decrease of Δα arises solely from the decrease of the threshold gain for the second lasing mode γ th 2 nd . As discussed in the previous sections, γ th 2 nd diminishes for a lower γ gain critical , which scales with 2|κ ₁ − κ ₂| for the unperturbed case. We consider that the introduction of randomness masks the difference between the couplings by κ ₁ and κ ₂ and hence effectively reduces |κ ₁ − κ ₂|. Accordingly, we found a gradual reduction of the width of average bandgap in the system with increasing r _κ . To further verify the above discussion, we computed the spatial profile of the first and second lasing mode for the case with r _κ = 0.1, as plotted in the insets in Figure 4(a). We plot typical mode profile providing the average Δα among the 100 trials. The mode profiles resemble those computed for r _κ = 0. This observation confirms that the first lasing mode originates from the topological interface mode and the second one originates from the bulk edge mode as observed in the unperturbed case. Figure 4(b) shows a computed Im(ɛ) as a function of γ _gain for the parameter set used in the insets in Figure 4(a). As anticipated above, one can see the reduction of γ gain critical to 0.10 and hence of Δα by 70% in comparison to the disorder-free case in Figure 3(b). Overall, it was found that the topological mode robustly behaves even under the presence of the disorder for coupling strengths with r _κ > 2|κ ₁ − κ ₂|. In Section 4, we will quantitatively discuss r _κ by referring a required accuracy in the actual device fabrication for an example case. It is interesting to note that the interface of the two topologically distinct chains may effectively remain even with such a large r _κ , as indicated in the spatial profile of the zero-energy mode plotted in the insets in Figure 4(a). The mode has a peak near the center of the system, where the interface is originally located. Another important note is that a very similar tendency was observed for the case that only replaces γ _loss from 0.06 to 0.2. Even in this case, we observed a reduction of the average Δα by 70% when r _κ = 0.1. This result implies that loss does not essentially alter the behavior of the system subject to inhomogeneous coupling strengths.

Figure 4:

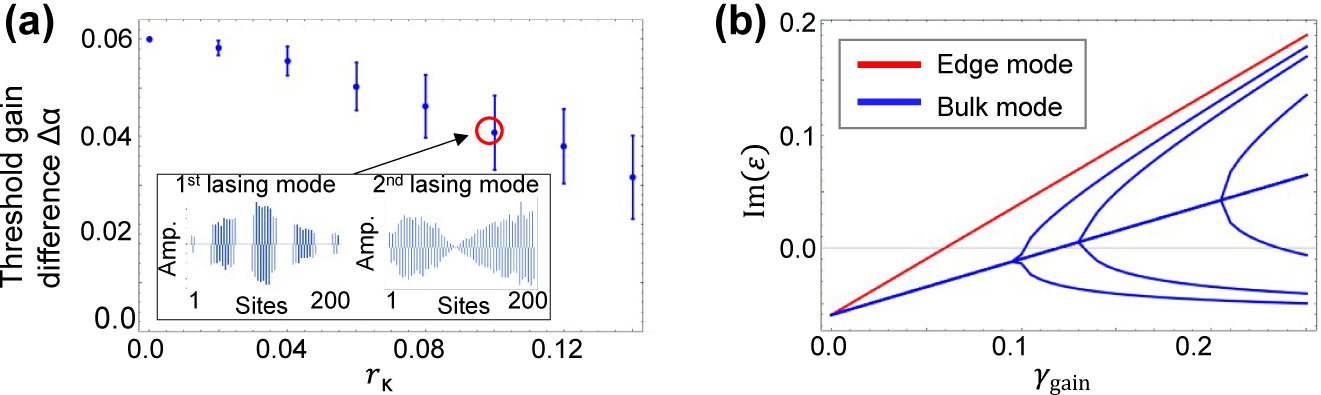
Robustness against inhomogeneous coupling strengths.

(a) Threshold gain difference between the first and second lasing modes as a function of coupling disorder r _κ in a finite system consisting of n _tri = 100 trivial and n _topo = 101 topological cavities. The insets show representative mode profiles of the edge mode and bulk mode. Blue bars indicate the amplitudes on A-site. (b) Imaginary parts of eigenenergies of the system plotted as a function of supplied gain on A-site γ _gain. The red and blue lines indicate the energy of the edge mode and bulk modes, respectively. The parameters used are κ ₁ = 1.0, κ ₂ = 1.04 and γ _loss = 0.06. In (b), the randomness is r _κ = 0.1.

3.2 Inhomogeneous site resonator frequencies

Next, we perform calculations for the cases with fluctuations in the resonance frequencies of the site resonators. We treat inhomogeneity in the resonator detunings Δ after subtracting a common frequency offset ω from the Hamiltonian in Eq. (1). For the perfectly regular case, Δ equals to zero for any mth resonator. We prepare 100 sets of random Δ’s distributed by Gaussian random variables with means Δ = 0 and the standard deviation r _Δ. We introduce each set of generated random detunings in Eq. (1) and solve it by diagonalization for the system with κ ₁ = 1.0 and κ ₂ = 1.04. The ways of averaging the data for each r _Δ and of its plot are the same as in the previous section.

Figure 5(a) shows the average γ t h 1 s t with varying r _Δ for a system with γ _loss = 0.06. Unlike the case with the coupling disorders, the average γ t h 1 s t slightly increases with r _Δ. In the system with non-zero r _Δ, chiral symmetry is broken and thus the topological mode acquires a field amplitude also in lossy B-sites, resulting in the increase of γ th 1 st . This behavior can be confirmed in the mode profile in the inset in Figure 5(a) calculated for a representative example when r _Δ = 0.1. The mode profile consists mainly of the original topological interface mode, but slightly contains B-site amplitudes, which is consistent with the modest increase of γ th 1 st . Figure 5(b) shows average Δα calculated for the system with γ _loss = 0.06. A monotonic decrease of Δα is found, which is much larger amount than the increase in γ t h 1 st . Thus, the drop of Δα is expected to stem from a decrease of γ th 2 nd . Figure 5(c) shows the computed Im(ɛ) for the system discussed in the inset in Figure 5(a). As anticipated, an earlier growth of Im(ɛ) for a bulk mode is seen when increasing γ _gain, making the Δα smaller. In the plot, it is seen that the phase transition in the bulk modes is blurred and a diagonal bundle of the bulk modes are formed. These are the consequences of the symmetry breaking by the fluctuating Δ. While sharp branches of the bulk modes are not observed in Figure 5(c), the overall behaviors of branched curves in Im(ɛ) are similar with those in Figure 3(b), in particular for large γ _gain roughly over 0.15. This comparison suggests that the fluctuation in Δ mainly influences how the Im(ɛ) curves branch out from the bulk mode bundle. Figure 5(d) shows Δα computed for the system with γ _loss = 0.2. In contrast to the case with lower loss, the computed Δαs are less sensitive with large γ _loss. This is because introducing the fluctuating Δ does not alter the overall behaviors of Im(ɛ) curves in particular for large γ _gain, at which Δα is measured for the case of γ _loss = 0.2. In other words, for large γ _gain, the relationship between the Im(ɛ) curves of the topological mode and the competing bulk mode does not change largely, neither does Δα.

Figure 5:

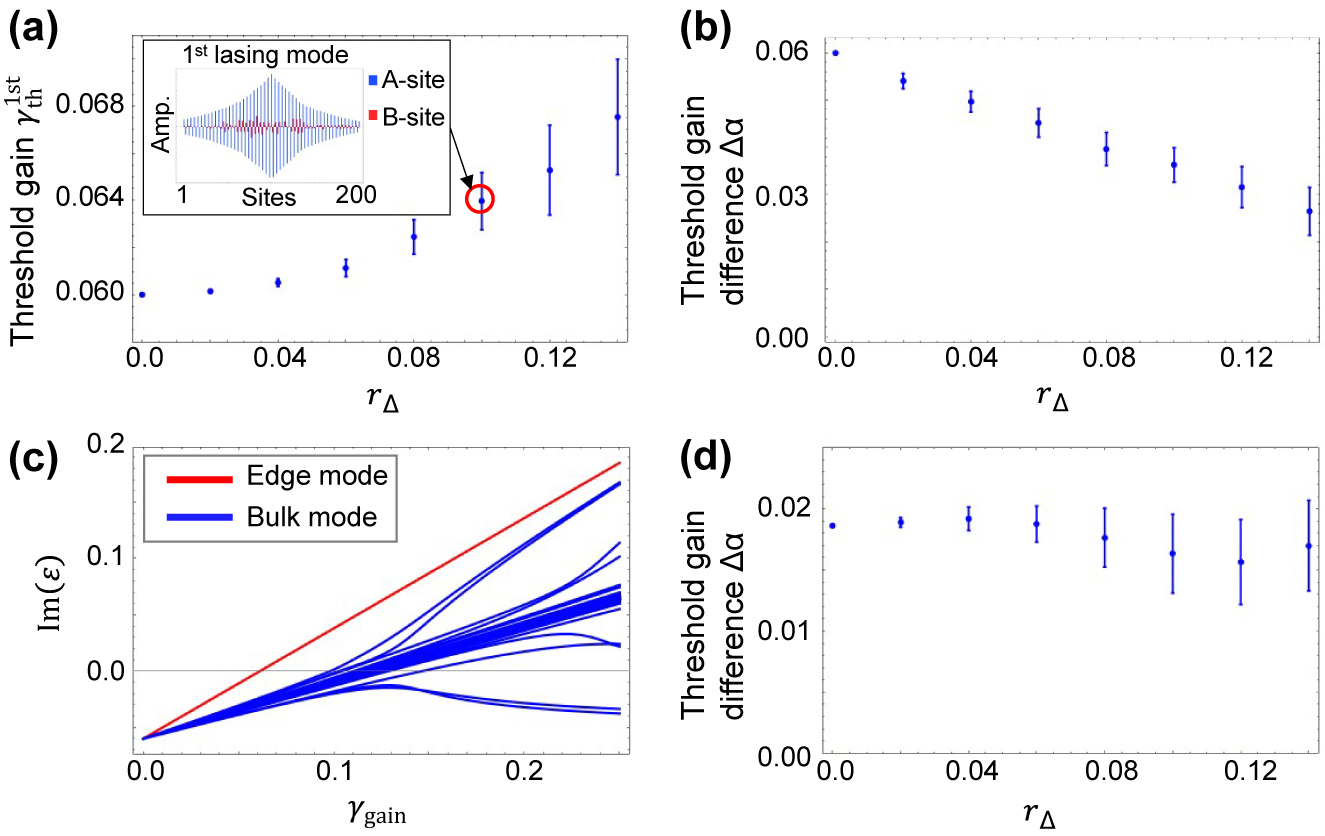
Robustness against inhomogeneous site resonator frequencies.

(a) Threshold gain of the first lasing mode as a function of strength of inhomogeneity in detuning r _Δ in a finite system consisting of n _tri = 100 trivial and n _topo = 101 topological cavities. The inset shows a representative sample of the edge mode profile for r _Δ = 0.1 where blue and red bars indicate the amplitudes on A-site and B-site, respectively. (b) Threshold gain difference Δα. (c) Imaginary parts of eigenenergies versus supplied gain on A-site γ _gain. The red and blue lines indicate the energy of the edge mode and bulk modes, respectively. (d) Threshold gain difference Δα for the system with higher resonator loss of γ _loss = 0.20. The coupling constant is κ ₂/κ ₁ = 1.04 and the loss is γ _loss = 0.06 in (a)–(c) and γ _loss = 0.20 in (d).

3.3 Next-nearest-neighbor cavity coupling

The discussion in Section 2 reveals that larger coupling strengths between the site resonators are advantageous for achieving a large Δα and thus for stable single mode lasing from a broadly-distributed topological edge mode. Cavity array designs for increasing the coupling strengths between the NN cavities may inevitably induce non-negligible next-nearest-neighbor (NNN) couplings, which will break chiral symmetry and thus could modify the performance of the laser device. In this section, we analyze the influence of NNN couplings on the investigated array laser.

Figure 6(a) explains the model we consider in this section. We define the ratio of the NNN couplings to NN couplings by a factor g: g = κ N N N / κ 1 N N , where κ ^NN and κ ^NNN denote the coupling strength between NN and NNN cavities, respectively. We add a term of the NNN couplings to the Hamiltonian in Eq. (1) with κ ₁ = 1.0 and κ ₂ = 1.04 and solve it by diagonalization. Figure 6(b) shows computed Δα as a function of g. The plot contains two curves calculated for the system with γ _loss = 0.06 and 0.2, respectively. Interestingly, both two curves do not show significant changes in Δα even when increasing the strength of NNN coupling as far as g < 0.5. For both cases, the change in Δα is only 20% at maximum. These behaviors can be understood by the combination of the computed mode profile and Im(ɛ), as plotted in Figure 6(b) and (c) for the case with γ _loss = 0.06. We find that the introduction of the NNN coupling do not largely modify the mode profile and the Im(ɛ) curves compared to those computed with only NN coupling. We note that, under the presence of the NNN couplings, the topological edge mode includes B-site amplitudes in its mode profile as shown in the inset in Figure 6(b) and the bulk modes resolve their degeneracy and form a bundle in Im(ɛ) curves as in Figure 6(c). These are the results of the absence of chiral symmetry in the system. We also note that g > 0.5 may be unlikely to occur for laser arrays based on evanescent mode coupling. Since evanescence fields exponentially decay in space, NN coupling is tend to be much larger than NNN coupling for most laser cavities. These insights obtained in this section are encouraging for increasing Δα by strengthening NN coupling with virtually ignoring the increase of NNN coupling.

Figure 6:

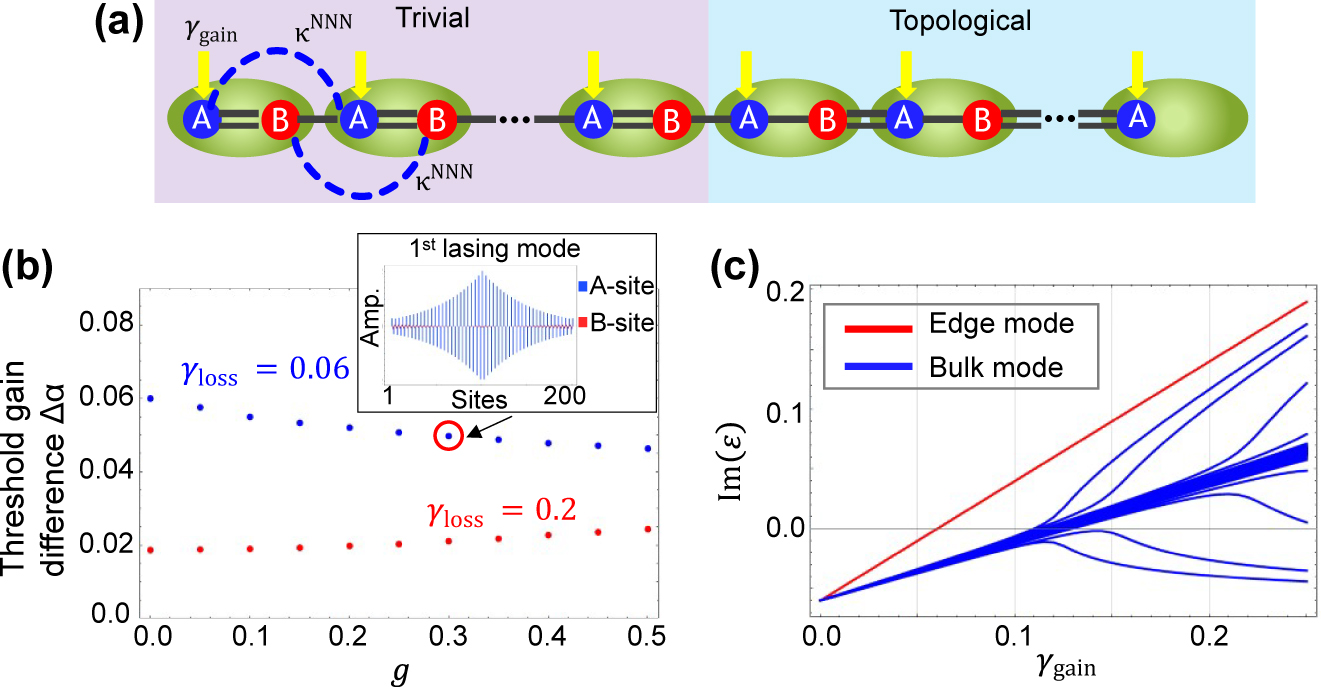
Robustness against next-nearest-neighbor cavity couplings.

(a) Extended tight-binding model for the topological laser, including the NNN couplings. NN couplings and NNN couplings are given as κ 1 N N , κ 2 N N and κ ^NNN, respectively. All sites are subject to loss at a rate of γ _loss, while gain γ _gain is additionally supplied only to the A-sites. (b) Threshold gain difference Δα as a function of ratio g of NNN couplings to NN couplings in a finite system consisting of n _tri = 100 trivial and n _topo = 101 topological cavities. Blue and red dots are for the loss γ _loss = 0.06 and 0.2, respectively. The inset in (b) provides a representative sample of the edge mode profile for g = 0.3 where blue and red bars indicate the amplitudes on A-site and B-site, respectively. (c) Imaginary parts of eigenenergies versus supplied gain on A-site γ _gain. The red and blue lines indicate the energy of the edge mode and bulk modes, respectively. The parameters used are κ ₁ = 1.0, κ ₂ = 1.04 and the loss is set to γ _loss = 0.06 in (c).