Engineering gallium phosphide nanostructures for efficient nonlinear photonics and enhanced spectroscopies

1 Introduction

Dielectric optical nanoantennas and metasurfaces have the ability to locally enhance incident electromagnetic fields with low absorption, tailor light dispersion, and efficiently generate nonlinear light. In the last decade, they have shown great promise for a wide range of applications, including wavefront manipulation [1, 2], ultrafast all-optical switching [3, 4], entangled photon pairs generation [5], bio-sensing [6], photocatalysis [7, 8], and metrology [9], among others. This has served as motivation to extensively explore geometrical resonances of varying character, where in particular, Mie magnetic modes [10], anapole excitations [11, 12], and engineered Fano resonances [13], have shown very high light confinement and large nonlinear conversion efficiencies.

In recent years, a different resonant condition originating from the concept of bound states in the continuum (BICs) has demonstrated extremely high quality factors [14], allowing record-breaking electric field amplifications and nonlinear efficiencies in nanostructured dielectric platforms. BICs are perfectly confined states with an infinite lifetime, with eigen-energies embedded in a radiation continuum from which they are fully decoupled [15]. By definition, they cannot be externally excited, unless they are perturbatively coupled to the continuum, turning a BIC with an infinite Q-factor into an observable high-Q quasi-BIC (QBIC). This can be achieved, for instance, by weakly breaking certain geometrical symmetries in a structure supporting a symmetry-protected BIC. Demonstrated examples in periodic metasurfaces include the use of disk meta-atoms with carved noncentered apertures [16], tilted elliptical cylinder elements [17], pairs of rods of slightly different sizes [18], and blocks with missing corners [14]. Because of their particular nature, BICs are only supported by periodic arrays and not by individual resonators. QBICs, however, can be excited in single nanostructures, yielding Q-factors of order 10² [19], although they usually need of structured light beams and specially engineered substrates for their efficient excitation. In comparison, QBICs with Q-factors up to >10⁴ can be attained in periodic metasurfaces on a simple glass substrate under linearly polarized light [14].

High-index dielectric materials like silicon, germanium, gallium arsenide (GaAs), aluminum gallium arsenide (AlGaAs), and gallium phosphide (GaP), have been widely studied for linear and nonlinear optical processes at the nanoscale in the visible and near-infrared spectrum. Enhanced fluorescence and Raman spectroscopies [20], [21], [22], as well as lasing [23], [24], [25], second [26], [27], [28], third [13, 29], and high harmonic generation [30], and also wave-mixing phenomena [31], have been reported using Mie modes, Fano resonances, anapole states, and QBIC resonances. However, although a vast number of Mie modes and anapole states have been analyzed, a systematic comparison of their nonlinear response using the same nanostructure design is still lacking. Moreover, while low-Q resonators have been studied for wave-mixing effects by combining (a few) different Mie modes using dual pump excitation [32, 33], the analog system supporting several QBICs has not yet been nonlinearly characterized.

Among the various high-index materials available with mature fabrication technologies, GaP is the only one with negligible absorption in the majority of the visible and the near-infrared spectrum. This dielectric also possesses high second- and third-order susceptibilities [34, 35], making it attractive for both enhanced spectroscopies [36], were most studies are performed in the visible range, and nonlinear optics [28, 37]. In this work, we numerically study linear and nonlinear second- and third-order phenomena in GaP individual resonators and metasurfaces in the 400–1200 nm wavelength range. We investigate single nanodisks supporting (low-Q) Mie modes and anapole states, as well as periodic arrays of dimers of elliptical cylinders excited at multiple (high-Q) QBIC resonances (see schematics of the studied systems in Figure 1). We explore second-harmonic generation (SHG) and degenerate four-wave mixing (DFWM), showing nonlinear conversion efficiencies surpassing previous theoretical and experimental reports on both low-Q and high-Q categories. We further demonstrate that the nonlinear light can be radiated mostly in the forward or backward directions, depending on the excited resonance and in-plane crystal orientation of the dielectric. Finally, we design a novel dielectric nanocavity for enhanced spectroscopies by slotting the meta-atoms of the examined metasurface. We study the radiative enhancement of dipolar emitters inserted in the slots and show extremely high radiative decay enhancements with no losses.

Figure 1:

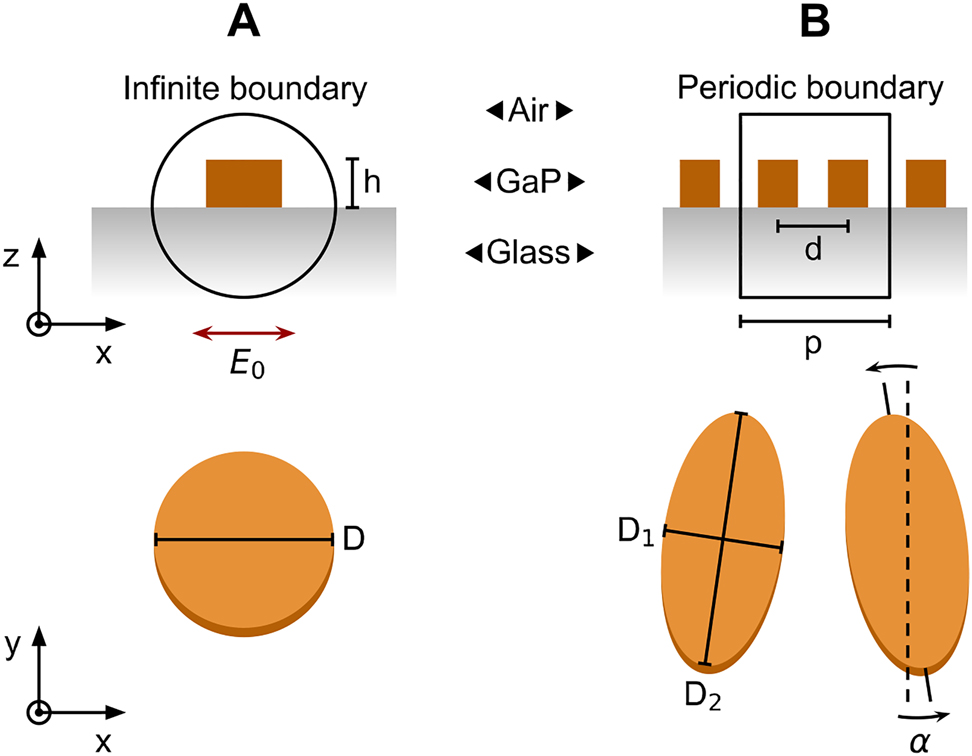
Schematic of the studied GaP platforms.

(A) Different views of the individual disk resonator including all relevant geometrical parameters. For the linear and nonlinear studies, the nanostructures were excited by linearly polarized light along the x-axis. Perfectly matched layers were used to simulate a semi-infinite glass substrate and air surrounding. (B) Same as A but for the metasurface. The bottom of B shows the unit cell of the periodic array. To describe an infinite lattice, periodic boundary conditions were defined in the lateral edges of the square unit cell.

2 Linear analysis

(100)-GaP nanodisks on a glass substrate were characterized in terms of their linear scattering efficiency and average electric field intensity inside the dielectric (⟨|E/E ₀|²⟩) when illuminated by linearly polarized light, as shown in Figure 2. The simulations were carried out using the RF module of the commercial software COMSOL Multiphysics (see Section 6 for more details on the numerical calculations). The height of the nanodisks was kept fixed at 200 nm and the diameters were varied in the 200–800 nm range. Several resonances with high field confinement can be recognized in Figure 2A, which can be categorized as radiating or (quasi) non-radiating. The first kind presents a maximum scattering efficiency, while the second features a minimum. Registered radiating Mie modes in the 800–1200 nm wavelength range, which is the region chosen to pump the nonlinear processes, are the magnetic dipole (MD) and electric quadrupole (EQ) modes. For simplicity, only the leading contributions are considered to define each resonance (the full multipolar decomposition for selected disk diameters can be found in the Supplementary material, Figure S2). The blue end of the spectrum in Figure 2, corresponding to the second harmonic (SH) emission region, is dominated by higher-order multipoles. The absorption edge, starting at about 450 nm, can be clearly distinguished.

Figure 2:

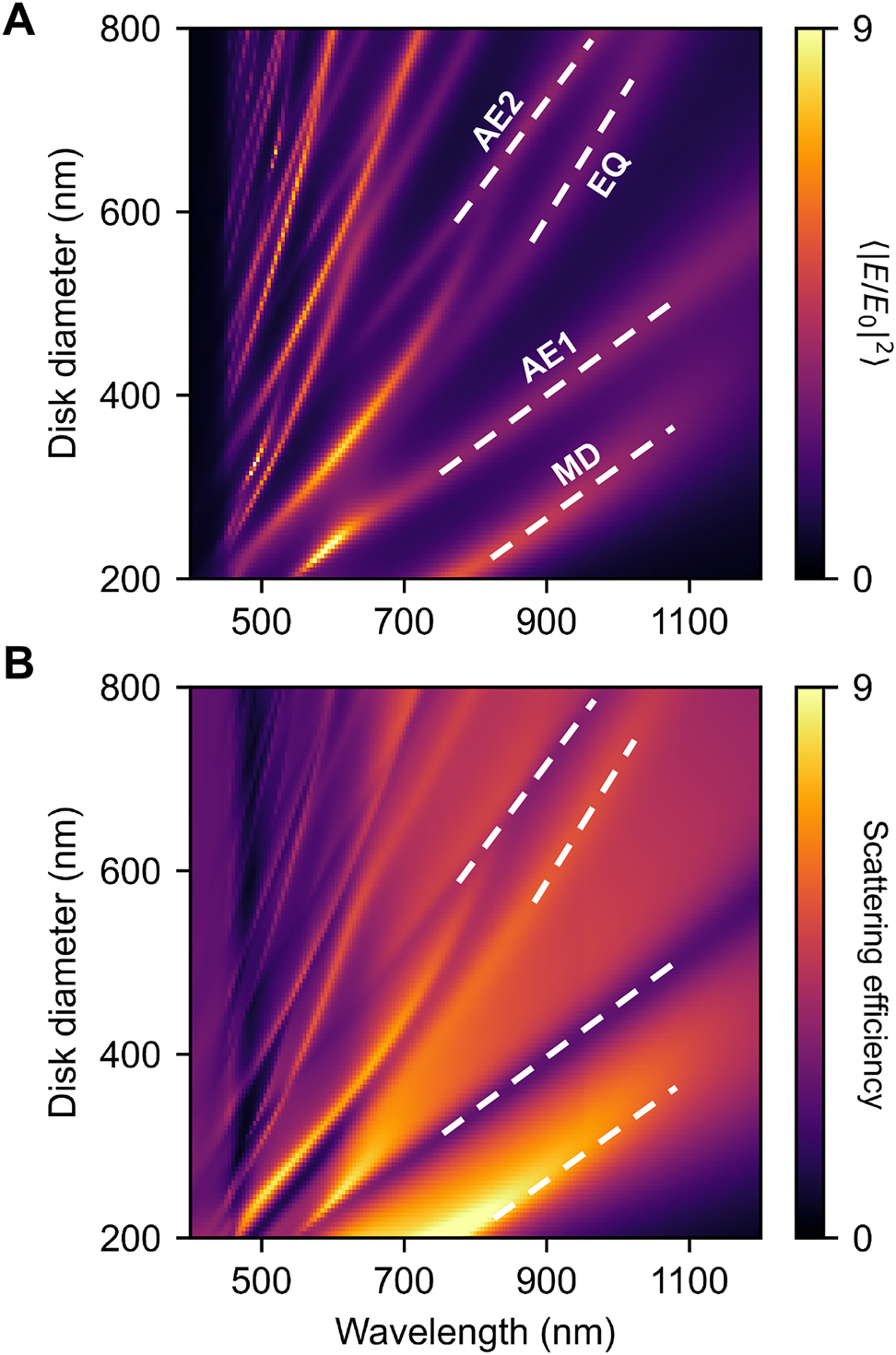
Linear analysis of GaP nanodisks.

(A) Average enhancement of the electric field intensity inside the dielectric as a function of incident wavelength and disk diameter. Identified resonances in the pump region of the nonlinear processes are highlighted in white. MD, magnetic dipole; EQ, electric quadrupole; AE1, first-order anapole excitation; AE2, second-order anapole excitation. (B) Corresponding scattering efficiency spectrum.

Nonradiating anapole excitations (AEs) of first and second order, denoted as AE1 and AE2, correspondingly, can also be identified in Figure 2 (see the associated electric field distributions in Figure S1 of the Supplementary material). The fundamental anapole (AE1) arises from a combination of Cartesian electric and toroidal dipole modes that cancel each other’s far-field radiation [11], while the higher-order anapole (AE2) can be described as a hybridization between AE1 and a Fabry–Perot resonance [38, 39].

The linear optical results characterizing the studied GaP periodic metasurfaces are exhibited in Figure 3, by exciting with linearly polarized light along the x-axis. The unit cell is composed by a pair of elliptical cylinders tilted by an angle α in opposite directions, as illustrated in Figure 1B. When the elliptical disks are parallel to each other (α = 0°), the metasurface supports a BIC with in-plane electric quadrupole and out-of-plane magnetic dipole components, as has been previously reported [17]. When the asymmetry parameter, α, is increased, a nonzero electric dipole can be induced in the horizontal direction, enabling a weak coupling with the radiation continuum that converts the ‘invisible’ BIC into an accessible QBIC. The smaller the value of α, the higher the quality factor of the resonance and the larger the electromagnetic field confinement. We choose a fixed angle of α = 5°, as it has been suggested as the current experimental limit for this kind of metasurface, below which no QBIC condition could be detected [28].

Figure 3:

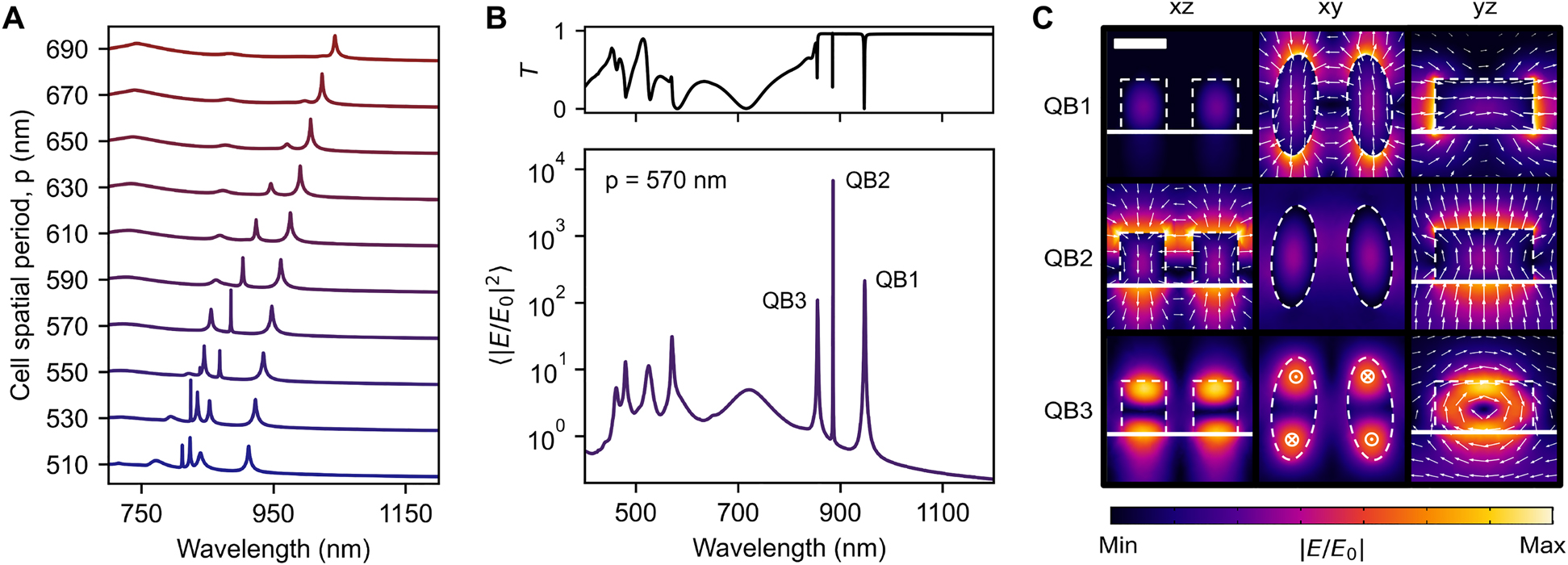
Linear characterization of GaP metasurfaces.

(A) Spectrum of the average enhancement of the electric field intensity inside the dielectric for different cell spatial periods, p. (B) The bottom graph shows the result for p = 570 nm as taken from A, with an extended wavelength range to the blue. The top graph displays the corresponding transmission spectrum. (C) Electric field distributions for different cuts of the unit cell at the three high-Q resonances highlighted in B. Scale bar, 200 nm.

In Figure 3A we analyze the average electric field intensity inside the dielectric when varying the period p of the array. The height of the metasurface is set at 200 nm, the minor and major axes of the elliptical basis are D ₁ = 170 nm and D ₂ = 380 nm, respectively, and the center-to-center distance between the elements in the unit cell is d = 280 nm. For p = 690 nm (top curve in Figure 3A), a high-Q resonance with ⟨|⟨E/E ₀|²⟩ ∼ 10² is registered, whose multipolar decomposition matches the previously reported QBIC for this metasurface design (see Figure S3 in the Supplementary material). In the Supplementary material (Figure S4) we further show that the spectral linewidth of this state increases when enlarging the D ₂/D ₁ geometrical aspect ratio, from 0.5 nm (D ₂/D ₁ = 1.6) to 2.3 nm (D ₂/D ₁ = 5.2), without significantly compromising its field confinement ability, which could serve for a more efficient coupling of the resonance to ultrashort laser pulses. Pulsed lasers have a relatively wide spectrum, with roughly 2–20 nm bandwidth for 1–0.1 ps pulse width at 900 nm wavelength. When decreasing the magnitude of p in Figure 3A, the described peak blueshifts, while other high-Q maxima are seen to emerge in the spectrum. This coexistence of resonances with large field confinement in the same system is of particular interest for investigating enhanced wave-mixing nonlinear processes, such as DFWM.

For a representative analysis of the metasurface we select a spatial period p = 570 nm from Figure 3A, which features three maxima denoted as QB1, QB2, and QB3, from longer to lower wavelength, as can be appreciated in more detail in Figure 3B. Their quality factors are about 8 × 10², 4 × 10⁴, and 8 × 10², in that order, and their corresponding ⟨|E/E ₀|²⟩ values expand from 10² to almost 10⁴, representing an enhancement of up to three orders of magnitude compared to the single disks (Figure 2A). The spectral range of the plot in Figure 3B has been extended to include the SH emission wavelength region, at which multiple high-order Mie modes are present. The top part of the figure displays the transmission spectrum of the metasurface, showing three sharp minima at the QB1, QB2, and QB3 wavelengths. Figure 3C exhibits three different views of the electric field distribution in the vicinity of the elliptical resonators for each of the high-Q states indicated in Figure 3B. Note that QB1 is the only one of the three resonances that has already been reported for the analyzed geometry. In fact, our metasurface does not support QB2 and QB3 when lowering the height below 180 nm, as shown in Figure S4 of the Supplementary material. A QB2-like field distribution has been observed, however, in arrays of coupled circular [40] or D-shaped cylinders [41]. In our system, this QBIC condition disappears when all elliptical disks in the lattice are equidistant to each other (refer to Figure S4 in the Supplementary material). The introduced asymmetry behind QB2 is the 10 nm difference between the center-to-center distance of meta-atoms within a single unit cell (280 nm) and that across neighboring unit cells (290 nm). Its multipolar decomposition, included in Figure S3 of the Supplementary material, reveals the presence of in-plane magnetic dipole and out-of-plane electric quadrupole contributions, with a minor toroidal magnetic dipole component. The weakest of the three high-Q resonances, QB3, which has been detected in metasurfaces composed by parallel rectangular rods of slightly different sizes [18], arises from the interaction between induced in-plane magnetic dipoles with nearly opposite directions in each element of the unit cell. It is important to remark that we have ignored in our analysis the influence of the nonradiative quality factor (which covers sample imperfections), as it has been shown to be one order of magnitude larger than the Q-factor of our narrowest resonance (QB2), in precision-fabricated dielectric metasurfaces [14]. We have then made the usual approximation, 1/Q = 1/Q_r + 1/Q_nr ≈ 1/Q_r, where Q_r (Q_nr) is the radiative (nonradiative) quality factor.

3 Nonlinear study

The nonlinear characterization of the GaP nanostructures was performed by first computing the second- and third-order nonlinear polarizations generated by the linearly excited modes in the resonators, and then calculating the induced nonlinear fields at the different emission wavelengths (see Section 6 for specifics). The conversion efficiencies of the SHG and DFWM processes, evaluated in the perturbative regime, were determined as η SHG = P SH / P p 2 and η DFWM = P i / ( P p 2 × P s ) , respectively, where P _p and P _s are the pump and signal incident powers at ω _p and ω _s , and P _SH and P _i are the corresponding nonlinear radiated SH and idler powers at 2ω _p and ω _i  = 2ω _p  − ω _s . In the case of the metasurface, these quantities were computed as per unit cell to enable direct comparison with the individual nanoantennas.

In Figure 4A, the SHG efficiency of the nanodisks is shown as a function of both diameter and pump wavelength. Interestingly, exciting at the MD mode (λ = 900 nm, D = 280 nm) demonstrates a much stronger nonlinear response compared to the EQ, AE1, and AE2 resonances, even though they all present similar field confinement in the near-infrared pumping range (see Figure 2A). To explain this behavior, it is important to analyze the nonlinear interaction between the modes sustained at the fundamental frequency (ω _p ) with those supported at the SH frequency (2ω _p ), as mediated by the second-order susceptibility tensor, χ ⁽²⁾. In essence, for the SH emission to be maximized, the induced nonlinear polarization, proportional to χ ( 2 ) : E ( ω p ) E ( ω p )  , and the linear field defining the mode at the emission frequency, E ( 2 ω p ) , need to be maximum and overlap in space with the same vectorial nature [42]. To weigh this effect, we compute the nonlinear integral Γ SHG = | ∫ Ω χ ( 2 ) : E ( ω p ) E ( ω p ) E ∗ ( 2 ω p )   d Ω | , evaluated inside the volume Ω of the nanoantenna. In Figure 4B, we plot the factor Γ SHG for the same range of parameters as in Figure 4A, revealing a very good agreement. For reference, in Figure S5 of the Supplementary material we include the spatial distribution of the nonlinear polarization when pumping at the MD and AE1 resonances, together with the corresponding linear fields at 2ω _p , where the differences in the nonlinear mode-matching can be examined. Notably, the attained maximum conversion efficiency of η SHG ∼ 3 × 10 − 3   W − 1 in Figure 4A is a factor of four larger than that predicted for a AlGaAs nanodisk suspended in air excited at the MD mode [43]. This difference is even more striking when noting that we have included a substrate in our modeling, which is generally expected to diminish the nonlinear response of the nanostructure because of the reduced index contrast with the surrounding.

Figure 4:

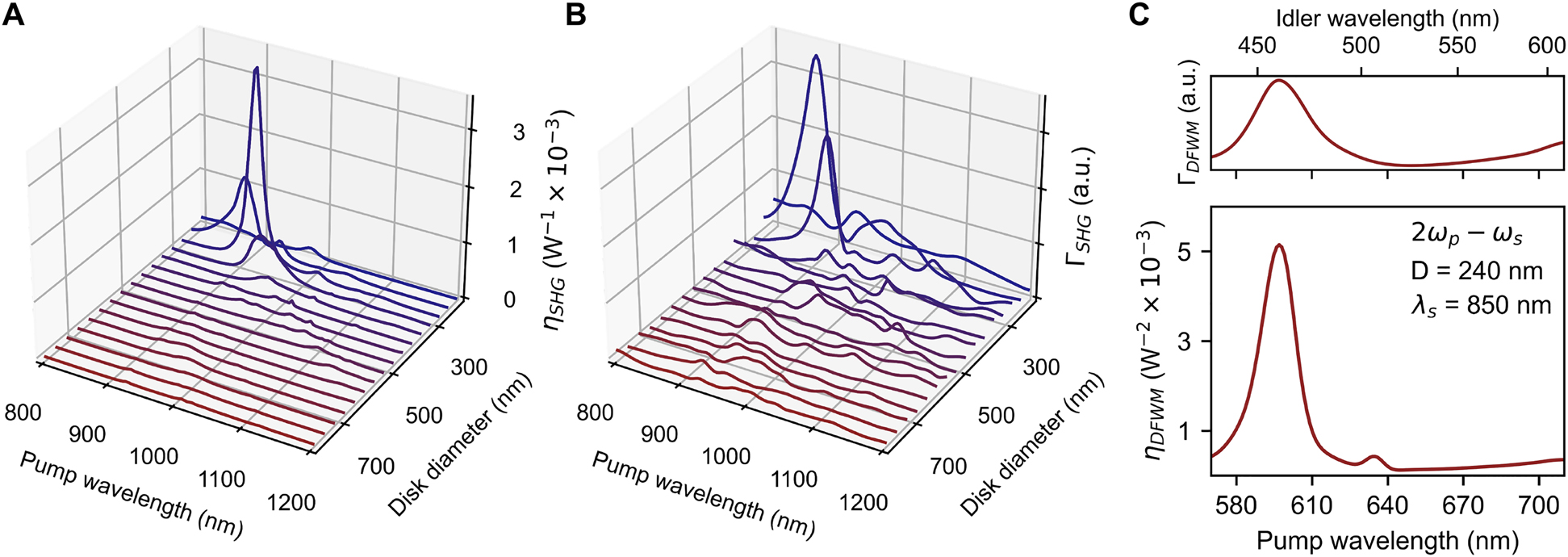
SHG and DFWM in individual nanoantennas.

(A) SHG conversion efficiency of nanodisks of different diameters pumped at varying wavelength. (B) Nonlinear factor Γ SHG computed in the same range of disk sizes and excitation wavelengths as in A. (C) DFWM conversion efficiency (bottom) and third-order coupling factor Γ DFWM (top) as a function of pump wavelength, with signal wavelength at 850 nm (MD), for a nanodisk with D = 240 nm. The top axis displays the output idler wavelength.

The study of the DFWM nonlinear process was performed using linearly polarized pump and signal incident beams at selected wavelengths. The third-order nonlinear factor measuring the strength of the idler output at ω _i  = 2ω _p  − ω _s was computed as Γ DFWM = | ∫ Ω χ ( 3 ) : E ( ω p ) E ( ω p ) E ∗ ( ω s ) E ∗ ( ω i )   d Ω | , where χ ( 3 ) is the third-order susceptibility tensor. Figure 4C exhibits the obtained η DFWM efficiencies and Γ DFWM values for a representative disk diameter of D = 240 nm, when the signal is fixed at the MD mode (λ = 850 nm) and the pump wavelength is varied. As for SHG, we find that Γ DFWM is a good description of η DFWM . Figure 4C shows that the highest conversion efficiency is registered when the pump is tuned at λ = 600 nm, corresponding to the AE1 resonance hybridized with the magnetic quadrupole (MQ) mode (see Figure 2 and Figure S1, S2 in the Supplementary material). This condition, yielding η DFWM = 5.2 × 10 − 3   W − 2 , surpasses several other mixings tested (refer to Figure S6 in the Supplementary material), and represents an enhancement of more than three orders of magnitude compared to the estimated response for a Si nanodisk pumped at the MQ mode with signal at the MD [44].

We move now to the analysis of the nonlinear results achieved for the GaP metasurface characterized linearly in Figure 3B and C. The central graph of Figure 5A presents the dependence of the simulated SHG efficiency on the pump wavelength, while the curve of the nonlinear factor Γ SHG is displayed on top (note that the logarithmic scales magnify the relatively small differences between η SHG and Γ SHG ). We find that the three maxima of η SHG follow the same relative order in amplitude as their fundamental field intensities in Figure 3B. We observe that pumping the QB2 resonance produces the highest nonlinear response, with a value of η SHG ∼ 2   W − 1 , which is more than one (two) orders of magnitude larger than that for QB1 (QB3), and about three orders of magnitude higher than the maximum efficiency registered for the nanoantennas. Experimentally, the reported SHG efficiency at the QB1 resonance for a similar GaP metasurface is 0.04 W⁻¹ at continuous-wave excitation [28], which is comparable to our corresponding numerical prediction of 0.05 W⁻¹ for that state. In such report, however, the geometrical parameters of the metasurface were not engineered to support the QB2 and QB3 QBICs as in this work.

Figure 5:

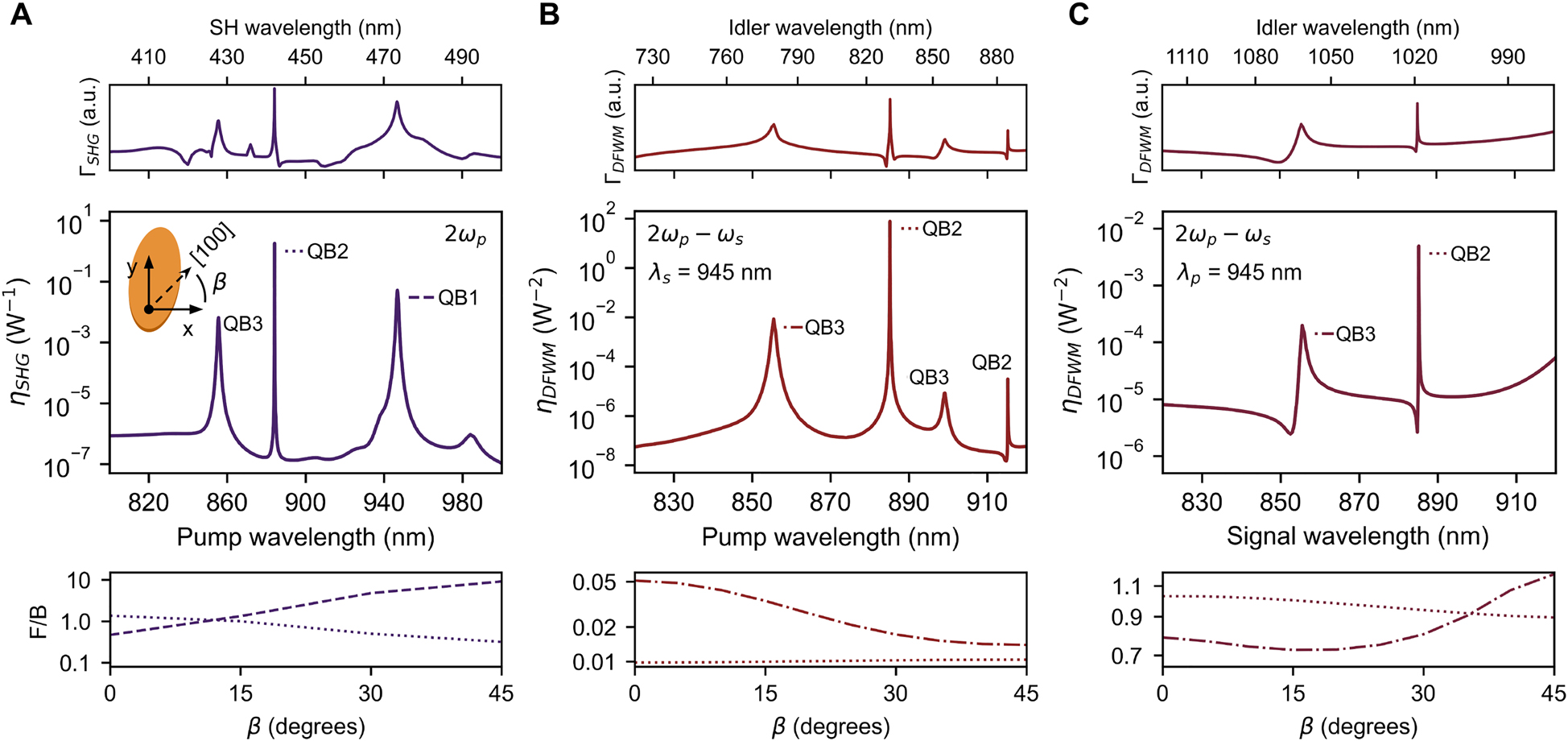
Nonlinear results of the metasurface.

(A) SHG efficiency (central graph) of the metasurface described in Figure 3B and C for pump wavelengths in the 800–1000 nm range. The main excited resonances in the nonlinear process are indicated next to the associated peaks. The plot in the top shows the corresponding spectrum of Γ SHG in logarithmic scale. The bottom graph presents the forward-to-backward ratio (F/B) of the SH emission power for the two most prominent peaks in η SHG as a function of the in-plane crystal orientation angle β (see illustration in the middle graph). (B, C) Same as in A but for DFWM. In B (C) the signal (pump) is set at QB1 and the pump (signal) wavelength is varied.

To explore other possibilities for SHG control in this periodic array, we studied the effect of modifying the in-plane orientation of the underlying (100)-GaP crystal lattice. We remark that this is not equivalent to simply changing the polarization direction of the pump beam, as it needs to be kept along the x-axis to efficiently excite all QBIC resonances. Experimentally, this can be achieved instead by rotating the electron-beam lithography pattern to be written over the GaP crystal sample. Given that the χ ⁽²⁾ tensor moves together with the crystal frame, we expect that the directionality of the nonlinear emission can be controlled in this manner. The bottom graph of Figure 5A shows the calculated forward-to-backward ratio (F/B) of the SH radiated power as a function of the angle β between the [100] direction (crystal frame) and the x-axis (simulation frame) for the two most efficient resonances (see schematic in the central graph of Figure 5A). The associated nonlinear emission patterns can be found in Figure S9 of the Supplementary Material. We find that increasing β from 0° to 45° enlarges the SHG F/B ratio from 0.5 to 9 for QB1, while for QB2 it decreases from 1.3 to 0.3. The metasurface can then be tuned to radiate mostly in the forward or backward directions at both ends of β, depending on the pumped resonance. Our simulations also indicate that the associated SHG efficiencies are nearly constant (within a factor of ∼2) throughout the whole β range (see corresponding plots in Figure S7 of the Supplementary material). In contrast, the emission directionality of the studied nanoantennas is found to be rather insensitive to β, as the SH power is always radiated preferentially in the backward direction (refer to Figure S8 in the Supplementary material for the numerical results). Moreover, the value of η SHG for the most efficient nanodisk in Figure 4A drops substantially when changing β (which in this case is equivalent to rotating the input polarization, given the circular symmetry of the structure) as the mode-matching condition is lost.

In Figure 5B and C we present the DFWM simulations for the GaP metasurface when setting the signal or pump wavelength at the QB1 resonance (λ = 945 nm), respectively, while varying the wavelength of the other parameter. Four peaks can be identified in the central graph of Figure 5B, where the two maxima on the left (right) occur when the pump (idler) wavelength coincides with the QB3 or QB2 resonances, as denoted in the figure. We observe that the idler output is significantly larger when the enhancement occurs via the excitation (peaks on the left) rather than the emission (peaks on the right), as is also evident in the Γ DFWM top graph. This is largely because the nonlinear effect is quadratic on E ( ω p ) , while it is only linear on E ( ω i ) . The highest obtained conversion efficiency is η DFWM ∼ 60   W − 2 , which is more than four orders of magnitude larger than the case of the single nanodisk in Figure 4C.

In the middle plot of Figure 5C, when tuning the signal instead of the pump wavelength, only two DFWM emission maxima are seen, as no resonances are supported at the idler wavelengths in this condition (the same behavior can be seen for Γ DFWM at the top). Contrasting with the central panel in Figure 5B reveals that the nonlinear emission is only highest when the pump (signal) is tuned at the QB2 (QB3) resonance, and not the other way around. The reason is that the field intensity enhancement is larger for QB2 compared to QB3, as seen in Figure 3B, and the amplification of the nonlinear process is stronger through the pump (quadratic) than through the signal (linear). Also, as deduced from Figure 3B, the field intensity at the emission wavelength is about one order of magnitude higher in the range evaluated in Figure 5B, compared to that in Figure 5C. In the bottom graphs of Figure 5B and C, the F/B ratios of the idler radiation powers are shown for varying β (only the two main maxima of η DFWM are considered in Figure 5B). While the nonlinear light is emitted principally in the backward direction for all β when pumping at QB1 (Figure 5B), it is more equilibrated between both directions when the pump is set at QB2 or QB3 (Figure 5C).

4 Enhanced spectroscopies

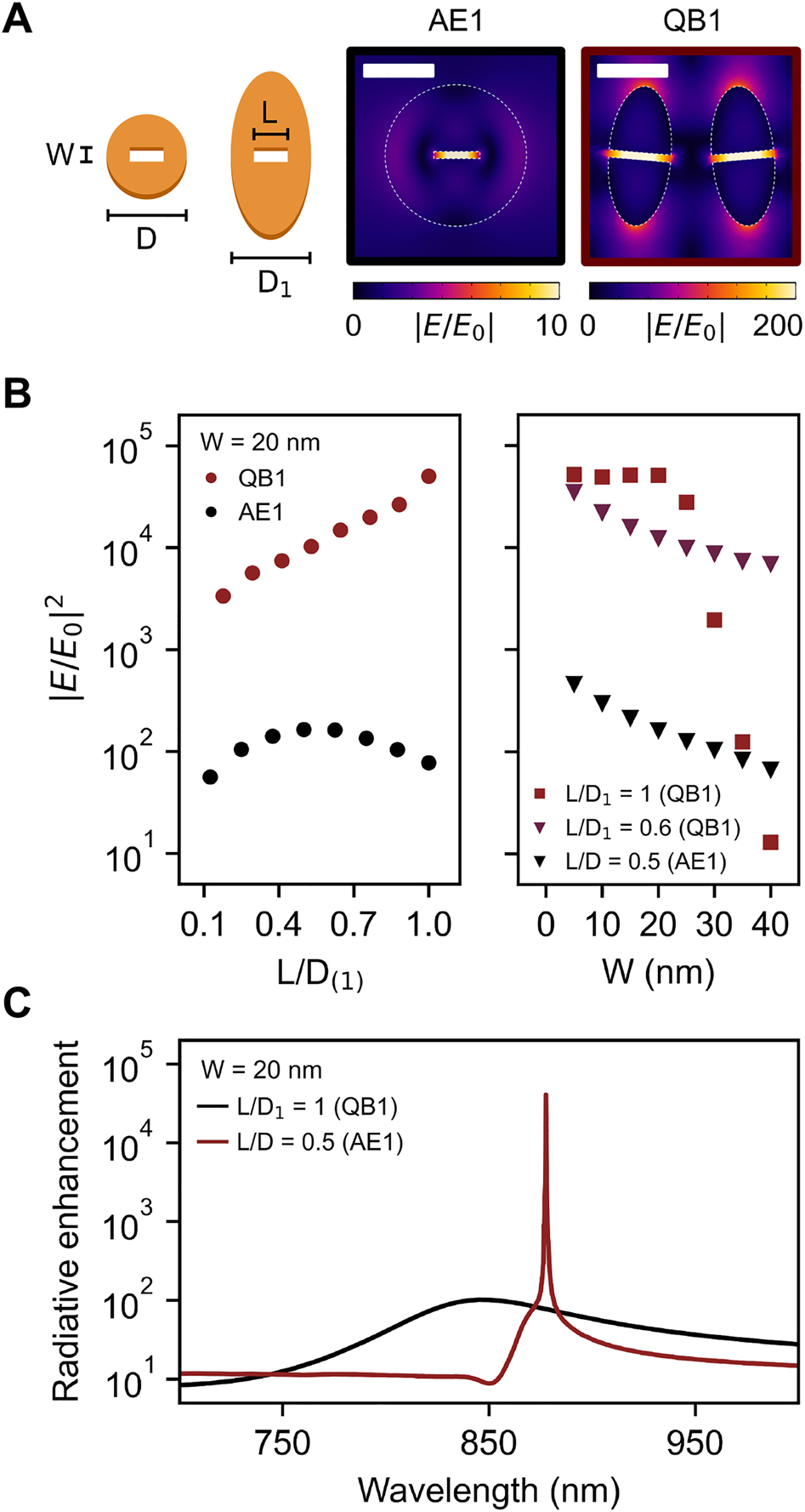
The in-plane distribution and straight orientation of the electric field inside the dielectric at the QB1 resonance (see Figure 3C) inspired us to design an open nanocavity for enhanced spectroscopies, following the theoretical work by Yang et al. [45] on single Si nanodisks. They showed that carving a slot in the nanoantenna, elongated in the direction perpendicular to the electric field confined by an anapole state, could greatly amplify the fields inside the aperture, due to the high permittivity contrast between air and Si, and the required continuity of the electric displacement field at the air/Si interface. We investigated this strategy in our metasurface – using the case of the individual disk as reference – by opening a slot at the center of the elliptical cylinder meta-atoms along the minor axis, as illustrated on the left side of Figure 6A. In Figure 6B (left panel), we evaluate the field intensity enhancement at the middle of an aperture of width W = 20 nm, comparing the GaP metasurface at QB1 and the GaP nanodisk at AE1, as a function of the slot length (L) normalized by the width of the resonator (i.e., D for the nanodisk and D ₁ for the metasurface). We find that the high-Q resonance outperforms the anapole state by more than two orders of magnitude. In Figure 6A we include the electric field patterns for the two resonances in their condition of highest confinement, revealing a uniform distribution of the fields inside the apertures, with a factor of 20 larger field amplitude for the QBIC. Notably, in contrast to the case of the nanoantenna, the most favorable result in the metasurface is observed when cutting the meta-atoms from end to end, allowing field intensity enhancements in the gap as high as 6 × 10⁴ (maximum value in Figure 6B). We highlight that this can be a convenient configuration in experiments, where accessing the confined field regions to deposit the quantum emitters to be analyzed can become very challenging.

Figure 6:

Slotted metasurface for enhanced spectroscopies.

(A) On the left side, illustrations of the slot in the nanodisk and elliptical cylinder meta-atom are shown, including the relevant geometrical details. The right side displays the electric field distribution for the slotted nanodisk at AE1 and the slotted metasurface at QB1, considering L = 170 nm and W = 20 nm in both cases. Scale bars, 200 nm. (B) The left panel shows the electric field intensity enhancement at the center of the aperture for varying slot length for the AE1 and QB1 resonances. The horizontal axis is normalized by the relevant width of the resonator (D for the nanodisk and D ₁ for the elliptical cylinder meta-atom). The right panel displays the results obtained at fixed slot lengths when changing the width. (C) Radiative enhancement spectrum of an electric point dipole placed at the center of the aperture for the best slotted nanodisk and metasurface at W = 20 nm.

In the right panel of Figure 6B we assess the effect of varying the slot width at fixed lengths. We discover that the fully opened slot in the metasurface (L/D ₁ = 1) provides approximately constant field amplification for W values up to 20 nm, before it starts to decrease monotonically, crossing the AE1 curve at W ∼ 35 nm. This is an important aspect for applications, as fabrication imperfections yielding a different slot width within the plateau range (W ≤ 20 nm) would have no impact on the performance of the optical cavity. When lowering L/D ₁ to 0.6, we find that the field intensity inside the aperture slightly reduces for W ≤ 20 nm, but it can be sustained much more efficiently when further increasing W.

Experimentally, the QB1 state has been recently investigated for enhanced spectroscopies and sensing using the edges of the elliptical cylinders as sources of enhanced excitation fields [46, 47]. Here, we see that the field intensity inside the slot can be one order of magnitude larger than at the edges. We also note that the mode volume of our nanocavity can be easily controlled by choosing the desired lateral dimensions of the aperture. To further characterize our system, we place an electric point dipole at the center of a slot with W = 20 nm and L/D ₁ = 1, and calculate the radiative decay enhancement. The attained result is presented in Figure 6C, showing an amplification of more than four orders of magnitude with respect to the dipole placed in vacuum, and more than two orders of magnitude compared to the case of the slot in the individual nanoantenna.

5 Conclusions

In summary, we have studied second- and third-order nonlinear frequency conversion effects in a GaP metasurface supporting three QBICs of different nature, contrasting the results with the case of the GaP nanodisk nanoantenna at various resonant conditions. We find that the QBIC with in-plane magnetic dipole and out-of-plane electric quadrupole components (QB2) produces the highest SHG efficiency in the metasurface, as well as the largest DFWM efficiency when mixed with the QB1 state (out-of-plane magnetic dipole and in-plane electric quadrupole contributions). This represents an enhancement of several orders of magnitude compared to the case of the single nanodisk excited at the MD mode, which showed the greatest nonlinear response among all studied Mie and anapole resonances. By either rotating the orientation of the GaP crystal lattice in the high-Q metasurface, or exciting the adequate QBIC, we observe that the forward-to-backward SH emission power ratio can be controlled to achieve mostly forward or backward nonlinear radiation. Moreover, by slotting the elliptical cylinder meta-atoms we find that the incident electric field can be highly amplified and uniformly distributed inside the aperture, with an enhancement of nearly three orders of magnitude in intensity compared to the slotted nanodisk counterpart excited at the AE1 state. The engineered optical nanocavity provides extremely high radiative enhancements for a dipolar emitter placed inside the slot, positioning this metasurface as a very promising design for applications in enhanced spectroscopies and sensing.

6 Methods

The linear and nonlinear numerical calculations were performed using the RF module of the COMSOL Multiphysics software. For the individual nanoantennas, the simulation domain consisted of a sphere with perfectly matched layer (PML) boundary conditions, containing the GaP nanodisk on glass surrounded by air medium. For the metasurface, the pair of GaP elliptical cylinders composing the unit cell was placed in square prism geometry with periodic boundary conditions in the four lateral faces and a PML in the top and bottom faces, considering the same surrounding media as for the single nanodisk.

The linear optical studies were carried out by solving the problem for the scattered field, using the analytical expressions of the reflection and transmission Fresnel coefficients at the air/glass interface to define the background field. The obtained field distributions were then employed to calculate the average electric field intensity enhancement in the GaP domain, 1 Ω ∫ Ω | E / E 0 | 2   d Ω , the scattering efficiency of the nanodisk, 1 π r 2 I 0 ∫ S ⋅ n   d A , and the transmittance of the metasurface, where the parameters in the equations have their usual meaning. The complex permittivity of GaP used for the simulations was taken from the literature [48]. For the glass (air) medium a constant value of ε = 2.25 (ε = 1) was utilized.

The nonlinear calculations were performed under the undepleted pump approximation. A two-step simulation was carried out for the SHG process. First, the linearly excited fields within the nanostructures were computed to define a second-order polarization in the material, which was then used as a source at the SH frequency to obtain the nonlinear fields. Similarly, in the case of DFWM, two incident waves were utilized to determine the third-order polarization in the dielectric and then compute the nonlinear idler output.

The second- and third-order susceptibility tensors of GaP, needed to calculate the nonlinear polarizations, were taken from the literature. GaP has a zinc-blend crystal structure with a second-order tensor of the form χ i j k ( 2 ) ≠ 0    if  i ≠ j ≠ k , where all six nonzero components have the same value [49]. We used experimental χ ⁽²⁾ values [34, 35] to define a susceptibility ranging from ∼3.6 × 10⁻¹⁰ to 1.0 × 10⁻¹⁰ m/V in the 800–1200 nm wavelength range. The third-order tensor of GaP has 21 nonzero components with four independent elements [49]. To a first approximation, all four elements were set to ∼4.3 × 10⁻¹⁹ m²/V², as derived from the experimentally reported magnitude of the nonlinear index n ₂ [35, 50]. With these considerations, the resulting nonlinear polarizations for SHG and DFWM are, respectively:

where, in all cases, i ≠ j ≠ k and E 1,2 = E ( ω 1,2 ) .

The SHG (DFWM) conversion efficiency was computed as the ratio between the nonlinear Poynting vector integrated over the relevant surface and the square (cube) of the total incident power impinging the geometric cross-section of the nanoantenna or the surface area of a unit cell. For the nanoantennas, the Poynting vector was integrated over a sphere surrounding the scatterer, while for the metasurface, the integration was performed over the top and bottom limits of the simulation domain.

The radiative enhancement of the electric point dipole located in the middle of the slotted resonators was calculated as the ratio between the total radiated power with and without the dielectric nanostructure. Nonradiative contributions were neglected given the ultra-low GaP absorption in the analyzed wavelength range.

The multipole decompositions in spherical and cartesian coordinates of the scattering spectra of the nanoantennas and metasurfaces (suspended in air), as shown in Figure S2 and Figure S3 in the Supplementary material, were calculated using the equations found in references [51, 52].

The near-to-far field transformation, included in Figure S8 and Figure S9 in the Supplementary material, was computed with a method based on reciprocity arguments using the open source software package RETOP [53]. The code requires as an input the near-field solution inside a closed box. For the nanoantennas, the box completely surrounded the scatterer, while for the metasurface, the box contained an artificial 15 × 15 array created using the solution of a single unit cell.