Assessment of the beam configuration effects on designed beam–column connection structures using FE methodology based on experimental benchmarking
-
Cakram Yudhifa Ganda Satriawan
, Teguh Muttaqie
Abstract
Purpose
This article aims to investigate the structural behavior of beam–column joints subjected to axial force. The geometry used is the addition of a number of beam connections to the column, and the differences in the numbers of beams used are 1, 2, 4, and 4, denoted as V1, V2, V3, and V4, respectively.
Design/methodology/approach
In this work, the analysis was performed using the numerical finite element method with ABAQUS software. A benchmarking analysis was also conducted to validate the numerical results.
Findings
Several numerical simulations showed that of the variations tested, the V2 model demonstrated the highest force value among the four test models, at 130.883 kN. The displacement caused by the force was 227.32 mm, which was the lowest value among the four test models. On the other hand, the V3 model received the smallest force value among the four test models, at 24.576 kN, with a displacement of 227.49 mm. The displacement value was greater than that for the V2 model, further indicating that the V2 model was the stiffest of the four models tested.
Originality/value
This study shows that the influence of beam–column joint geometry is not limited to double-extended end-plate bolted connections.
1 Introduction
Steel materials are widely used in construction design, such as in buildings, bridges, and other infrastructures [1,2,3,4,5,6,7]. One of the reasons why steel materials are widely used is the ease and effectiveness with which they can be used in the field [8]. Steel structures consist of three main components, namely, beams, columns, and connections between the two [9]. Experiments investigating the classification of connections were reported in the study of Bjorhovde et al. [10], where connections were categorized as (i) flexible connections (pinned), (ii) rigid connections (fixed), or (iii) semi-rigid joints. These three types of connections were studied in order to determine the behavior of beam-to-column connections, including with respect to their strength, stiffness, and ductility.
Research on end-plate-bolted connections has been widely performed using analytical, experimental, and numerical approaches to predict torque–rotation behavior. Various types of connections have been studied [11,12,13,14,15], and with respect to a number of different parameters, including the end-plate thickness and extended end-plates, the type of stiffener, diameter and number of bolts, the bolt pretension force, the yield strength of the steel material, and beam and column dimensions, among others. Experimental tests of extended end-plate joints as a function of the parameters of end-plate thickness, column stiffener, and the pre-tensioning force on the bolts were carried out to study the behavior of the joint under cyclic loads on major-axis connections [16]. It was concluded that the use of a properly designed end-plate can provide good ductility as a moment-resisting component in earthquake-resistant frame designs. Subsequently, experimental tests of beam-to-column joints were carried out using various web angles, seat angles, and the use of stiffeners with the aim of predicting the behavior of minor axis joints on the basis of force–displacement and moment–rotation [17]. The thickness of the column web and the location of the stiffeners in the column affect the strength and stiffness of the connection. Research on connections employing different thicknesses and bolt diameters demonstrated that variations in these parameters influence the response of the structure [18]. In another study, the production of connections using different column stiffeners and end-plate stiffeners demonstrated an effect on the acceptable moment magnitude [19]. In addition to performing experimental testing, the computer-based finite element method (FEM) can be used. FEM has been demonstrated to be able to perform a good simulation for the prediction of the response of connection structures on the basis of validating previously obtained experimental results [20]. The FEM approach can be used as an alternative method for analyzing the behavior of connection structures.
This research was conducted to analyze the response of a connection structure using FEM in ABAQUS software. Specifically, variations in the beam configuration on the major axis and minor axis were investigated to determine their effect on the response of the connection structure in terms of the force–displacement, moment–rotation, and structure–response contours. Many variations have been discussed in the literature mentioned in the previous paragraphs, including with respect to the type of connection, the plate thickness, the bolt diameter, the use of stiffeners, and the configuration of the connection installation. The FEM approach is able to save time and testing costs for the analysis of connection structures.
2 Literature review
2.1 Standard for design
The component method, available in EN 1993-1-8 [21], is widely applied to predict the performance of structural steel joints. In this method, many types of connections can be modeled as an assemblage of basic components. The initial rotational stiffness and moment resistance are calculated using Eqs. (1) and (2). However, the calculation of the rotational capacity for the end-plate joints is not explicitly given:
where the stiffness ratio μ is taken as 1 for the initial rotational stiffness, ki is the stiffness coefficient for the base connection member i, z is the lever arm, and Ftr, Rd is the effective design tension resistance of the bolt r, h r is the row distance of the bolt r from the center of compression, which is assumed to lie in the middle of the thickness direction of the compression flange of the beam.
Based on the design procedure for bolted extended end-plate joints in ANSI/AISC 358-16 [22], the unstiffened and stiffened joints were covered with four rows of bolts. The moment resistance can be calculated using the bolt diameter d b,req, the thickness of the end – plate t p,req, and the thickness of the column flange t cf, determined using Eqs. (3)–(5), respectively. Note that no calculation equations for the initial rotational stiffness and rotational capacity are provided:
where M f is the moment of the face at the column, F nt is the nominal tensile strength of the bolt, h 0 is the distance from the centerline of the compression flange to the tension – side outer bolt row, h 1 is the distance from the centerline of the compression flange to the tension – side inner bolt row, F yp and F yc are the minimum yield strength of the end – plate material and the column flange material, Y p and F yc are the yield line mechanism parameters of the end-plate and column flange, respectively, and Φ n = 0.90 and Φ d = 1.00.
The moment resistance of the connection, as per code GB 51022-2015 [23], can be determined using Eq. (6), which shows the shear strength of the column web panel. The rotational stiffness of the joint is the sum of the shear rotational strength of the column web panel and the flexural strength of the joint, which can be calculated using Eqs. (7)–(9). However, no design provisions for joint rotation capacity are currently available. It is worth noting that the Chinese code, which is based on EN 1993-1-8 [21], considers the shear rotation stiffness of the panel zone for beam-to-interior column joints under symmetrical loads to be negligible:
where f v is the shear strength of the web panel column; d b, d c, and t c are the height,width,and thickness of the web panel column,respectively; R is the rotational stiffness of the joints; R 1 and R 2 are the rotational stiffness of the web panel column and joint rotational stiffness, G and E 0 are the shear modulus and elastic modulus of the material, le is the moment of inertia of the end – plate; and e f is the distance between the center of the outer tension side of the bolt row and the outer edge of the stiffener rib. The formula for calculating the splice rotational capacity is not provided in the above design code, although some design code recommendations are presented to ensure adequate splice rotational capacity.
2.2 Moment–rotation and force–displacement relations
The moment–rotation M–ϕ describes the amount of rotation that occurs in a structural element when it is subjected to a bending moment. Moment M occurs in the beam–column connection because the acting force F does not pass through the center of gravity of the connection, also referred to as an eccentric connection. Force–displacement F–∆ describes the amount of displacement that occurs in a structural element due to the acting force. The general equation for the moment is shown in the following equation:
where M is the moment (N m), F is the force (N), and d is the arm length (m). Several factors affect the amount of material deflection:
The length/sectional area, A, of the material, such as a beam, affects the amount of deflection. Beams that undergo the same force values but have different lengths will produce varying deflections.
The working force value, F. Beams with the same cross-sectional area or length that are subjected to different values of force will produce different values of deflection.
Young’s modulus, E, is a measure of the strength of a material. It tends to be more difficult for beams that have high values of Young’s modulus to experience deflection and deformation.
In addition, the geometry of the beam also affects the value of the moment of inertia of the cross section, I. The value of E and the moment of inertia are referred to as flexural rigidity or bending stiffness; the greater the bending stiffness value, the more difficult it is for the beam to experience deflection.
The moment of inertia for the square is shown in Eq. (11), where I is the moment of inertia of the section, b is the thickness, and h is the height.
Deflection is a change in the shape of the beam in the y direction due to loading acting on the beam, which can be called the deflection or displacement of the beam. Deflection is measured from the initial neutral surface to the neutral position after deformation occurs. The assumed configuration with neutral surface deformation is known as the elastic curve of the beam. Figure 1a shows the beam in its initial position before deformation occurs, and Figure 1b shows a beam in a deformed configuration, assuming the effect of loading action.
![Figure 1
Beam deformation: (a) beam before deformation and (b) beam in deformed configuration [24].](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_001.jpg)
Beam deformation: (a) beam before deformation and (b) beam in deformed configuration [24].
The displacement distance y is defined as the deflection of the beam. Many methods can be used to determine beam deflection, such as the multiple integration method, the moment area method, the conjugate beam method, and the energy method. The multiple integration method is a method used to derive deflection equations for theoretical analysis. With this method, the deflection formula is obtained by deriving the deflection equation according to the type of support used. Eq. (12) shows the beam deflection differential equation:
Figure 2 shows the deflection in the beam. The one-time integral for obtaining the rotation is shown as follows:

Deflection in the beam.
The two-fold integral for obtaining the deflection is shown as follows:
where v is the vertical distance (deflection of the beam), θ is the rotation, M is the bending moment, E is the modulus of elasticity, and I is the moment of inertia. C 1 and C 2 are integral result constants whose values will be searched on the basis of the boundary conditions. A boundary condition is a known v or a known θ, usually a position. In the placement of pins and rollers, the limit condition v = 0, because the placement of pins and rollers is able to withstand vertical displacement but is not able to withstand rotation, whereas in fixing bearings, v = 0 and θ = 0, because fixed bearings are designed to be able to withstand displacement and rotation [24].
The junction rotation ϕ is defined as the relative rotation between the upper and lower centerlines of the beam flange at the end of the beam and is derived from the shear rotation ϕ s and the slit rotation ϕ ep [25]. The slot rotation consists of the bending deformation of the end-plate, the column flange, and the bolt extension, as shown in Figure 3, and can be determined using the following equations:
where ∆ is the difference in the displacement of the panel zone on the center line of the upper and lower beam flange at the end of the beam, δ is the gap between the end – plate and column flange on the center line of the beam tension flange, and h t is the distance between the upper and lower center lines of the beam flange, resulting in a moment–rotation M–ϕ curve.
![Figure 3
Definition of the joint rotation [25].](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_003.jpg)
Definition of the joint rotation [25].
2.3 Stress–strain
Material characteristics such as stress and strain also have an impact on deflection. Stress, which is the ratio between the tensile force F on the metal and its cross-sectional area A, can be defined as force per unit area [19]. The stress value can be formulated as shown in Eq. (18), thus illustrating its influence on deflection:
where σ is the stress
where ɛ is the strain value, L is the initial length (m), and ∆L is the length increment value (m).
2.4 Failure mode
Failure mode describes the way or mode in which something (e.g., a connection structure) might fail. The failure of bolts and bolted joints can occur in the structure, and good design planning aims to minimize failure. Several failure factors can occur in cases of the shear failure of the bolt, which occurs when a shear force is generated in the bolt due to the applied load exceeding the shear strength capacity of the bolt. Figure 4 shows bolt failure due to the shear force occurring on the plate exceeding the shear strength of the bolt. For two plates connected by bolts, failure may occur in only one plane, which is called a single-shear failure. If there are three connecting plates, bolt failure may occur in only two planes, which is therefore referred to as double-shear failure, as shown in Figure 5. Failure due to shear can also cause damage to the bolt threads.

Single-shear failure.

Double-shear failure.
Shear failure can also occur in the bolt bearings due to the fact that the plate strength is lower than the bolt joint shear strength, as shown in Figure 6. If the tip spacing is smaller than the recommended tip spacing, a tear in the plate may be caused, dislodging the bolt from the remaining area.

Shear failure of the plate.
Bolt stress failure can occur when the bolt is subjected to an applied tensile force greater than the tensile strength of the bolt. The tensile capacity of bolts is dependent on the tensile strength of the bolts and the minimum cross-sectional area of the bolt threads. This can result in the occurrence of cracking or fracture in the bolt, as shown in Figure 7. Stress failure can also occur in the plate in cases where the strength of the plate is lower than the strength of the bolt, as shown in Figure 8.

Bolt tension failure.

Plate tension failure.
Bolt bearing failure occurs in cases where the bolt strength is lower than the plate strength. This can cause the bolt to undergo deformation, as shown in Figure 9. In addition, the failure of the bearing on the plate can occur due to the strength of the bolt being higher than the strength of the plate holding the load. This can cause the plate to undergo deformation, as shown in Figure 10. When a high-quality bolt is tightened, the area immediately under the head of the bolt or the face of the supporting nut will be subjected to a high degree of bearing stress. If the maximum stress limit of the bearing material is exceeded, deformation of the bearing may occur. Fatigue failure occurs due to loads occurring repeatedly over a relatively long time. This can result in damage to the bolt threads, cracks, and fractures in the bolt.

Bearing failure of the bolt.

Bearing failure of the plate.
2.5 State of the art
This research was conducted using the method and some of the calculations described in the foregoing literature review. In this study, we also aim to further develop the existing body of research. Flush end-plate and extended end-plate moment retaining joints have been tested to determine the effect of bolt diameter, plate thickness, or the use of end-plate stiffeners on cyclic loading behavior or monotonic loads [27,28]. Further testing of double-extended end-plate connections was carried out focusing on the characterization of the web panel component [29,30]. The FEM method has been used to analyze the mechanical behavior of double-extended end-plate joints when varying the end-plate thickness, bolt diameter, and use of column stiffeners [18,19]. Moment-resisting joints have also been evaluated with different cross-sectional beam shapes and column profiles [31]. Connections have been studied with respect to the response of the structure in the beam arm laying configuration [20,32,33].
Research on the behavior of beam–column joints has been carried out using various methods. Table 1 lists research on each of the criteria affecting the behavior of the connection structure. Research addressing several criteria at once, such as modeling joints on the major and minor axes, is still rarely carried out. Therefore, this research was conducted to predict the behavior of structures on the basis of the modeling of stainless-steel beam–column joints with major- and minor-axis connections.
Previous works on beam and column joint
| No. | Reference | Title | Calculation method | Conclusion |
|---|---|---|---|---|
| 1 | Shi et al. [27] | Behavior of end-plate moment connections under earthquake loading | Experimental method | Connections with double extended end-plates can provide the strength, joint rotational stiffness, ductility, and energy dissipation capacity required to withstand seismic moments |
| 2 | Shi et al. [28] | Numerical simulation of steel pre-tensioned bolted end-plate connections of different types and details | FEM with ANSYS | Bolt tension, the moment at connection, and the principle of connection stress can affect the distribution of pressure and friction between the end-plate and column flange |
| 3 | Augusto et al. [29] | Characterization of web panel components in double-extended bolted end-plate steel joints | Experimental method and FEM with ABAQUS | Double-end-plate steel connections are a solution in moment-resistant frame structures because they have good ductility, load-bearing ability, and energy dissipation capacity |
| 4 | Augusto et al. [30] | Cyclic behavior characterization of web panel components in bolted end-plate steel joints | Experimental method and FEM with ABAQUS | The effect of web panel components with bolted end-plate steel joints on cyclic treatment can be seen in comparison with the addition and without stiffener. Web panel components without stiffeners experience large deformations due to increased load. Meanwhile, components with stiffeners are able to absorb compression that is distributed to the stiffeners |
| 5 | Boudia et al. [19] | Modeling of bolted end-plate beam-to-column joints with various stiffeners | FEM with ANSYS | Bolt diameter affects the failure mode of the joint but has no significant consequence on initial stiffness and resistance. This can be anticipated with a plate thickness that matches the bolt diameter. The addition of a stiffener can significantly increase the initial stiffness and ultimate strength |
| 6 | Gao et al. [33] | Structural behavior and design of stainless steel end-plate beam-to-exterior column minor-axis joints | FEM with ABAQUS | Monotonic and cyclic loading on austenitic stainless steel on the minor-axis end-plate is influenced by the column axial force, bolt tension, column web thickness, column flange width and thickness, bolt diameter, and bolt hole tip spacing |
| 7 | Maggi et al. [18] | Parametric analysis of steelbolted end-plate connections using FEM | FEM with ANSYS | The results obtained are in the form of failure modes for each model. The T-stub analogy has limitations in the form of yield lines at the end-plate both in calculating the prying action and predicting the strength and stiffness values of the joints |
| 8 | Costa et al. [32] | Experimental behavior of 3D end-plate beam-to-column bolted steel joints | Experimental method | The results obtained for the slenderness of the column body tested indicate that the minor-axis joints only have a relevant relationship that affects the stiffness of the major-axis connections. In addition, the two minor axle joints have a reciprocal interaction that can increase the stiffness and strength |
| 9 | Gao et al. [20] | Structural behavior of stainless steel double extended end-plate beam-to-column joints under monotonic loading | Experimental method and FEM with ABAQUS | Stainless steel joints show good ductility. The plastic resistance and ultimate resistance of beam-to-column joints are close to those of the beam-to-column joints on the exterior. Meanwhile, the initial rotational stiffness values of the beam connection to the interior column are much higher than those of the latter joints |
| 10 | Wang et al. [31] | Moment–rotation relationship of hollow-section beam-to-column steel joints with extended end-plates | Experimental method and FEM with ABAQUS | The FE model can predict the bending behavior of steel beam-to-column joints in terms of initial stiffness and moment capacity. End-plate thickness and column wall thickness are the two most important factors with a significant influence on structural response |
3 Benchmarking particulars
3.1 Experimental study
3.1.1 Specimen configuration
The experimental study presented in the study of Gao et al. [20] employed stainless steel beam-to-column double-extended end-plate connections under monotonic loading. The geometries of the beams and columns were as follows: I 300 × 180 × 6 × 10 profiles with a length of 1,800 mm for columns, and I 250 × 150 × 6 × 10 with a length of 1,280 mm for beams. More details are presented in Figure 11.
![Figure 11
Geometric details of the joint specimens (all dimensions in mm) [20]. (a) Beam-to-exterior column joints. (b) Details of end plates.](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_011.jpg)
Geometric details of the joint specimens (all dimensions in mm) [20]. (a) Beam-to-exterior column joints. (b) Details of end plates.
The slenderness of the web panel, the end-plate thickness, and the bolt diameter were set in accordance with EN 1993-1-8 [21]. The column web slenderness ratio (d c/t w) was calculated as shown in Eq. (20), while the thickness t of the column flange and the end – plate were calculated as shown in Eq. (21), where d c is the clear depth of the column web panel in shear, f ub is the ultimate tensile strength of the bolt, and f y is the yield strength of the plate:
Using the bolt pretension force determined using Eq. (22), the designed value of axial force F c applied to the column, taken to be 20% of the yield resistance of the column, is shown in Table 2, where f ub and A s are the ultimate tensile strength and tensile stress area of the bolts, respectively, and a partial factor of safety yM7 = 1.1.
Details of the joint specimen configuration
| Material grade | Bolt grade | Bolt pretension force F pre (kN) | Column axial force F c (kN) | End-plate rib stiffener | Joint type |
|---|---|---|---|---|---|
| EN 1.4301 | A4-80 | 124 | 290 | Yes | Beam-to-exterior column joint |
3.1.2 Tensile test on plates and bolts
Among the material properties of the EN 1.4301 plate and A4-80 bolts, the mechanical properties were taken from the results of the tensile coupon test [34]. The results of the tensile coupon test, in the form of stress–strain curve values, are presented in Table 3. E 0 is the initial Young’s modulus; σ 0.01, σ 0.2, σ 1.0, and σ 3.0 are proving stress 0.01, 0.2, 1.0, and 3.0, respectively, where σ 0.2 is generally taken as the nominal yield strength of stainless steel, σ y is the yield strength, σ u is the ultimate tensile stress, ε 0.2(εy) is the strain at yield strength, ε u is the strain at ultimate tensile stress, and ε u corresponds to elongation at fracture. The ratio of ultimate tensile stress to yield strength σ u/σ y(σ 0.2) is also provided for all tested materials.
Measured material properties of stainless steel plates and stainless steel bolts
| Material | t or d (mm) | E 0 (MPa) | σ 0.01 (MPa) | σ 0.2 (σ y) (MPa) | ε 0.2 (ε y) (%) | σ 1.0 (MPa) | σ 3.0 (MPa) | σ u (MPa) | ε u (%) | ε f (%) | σ u/σ 0.2 (σ u/σ y) | ε u/ε 0.2 (ε u/ε y) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EN 1.4301 for column | 5.81 | — | 185.65 | 287.59 | 0.378 | 322.68 | 368.11 | 751.66 | 56.3 | 66.8 | 2.61 | 148.89 |
| 9.94 | 179,400 | 177.06 | 275.94 | 0.352 | 319.05 | 368.01 | 757.41 | 53.6 | 65.5 | 2.74 | 151.96 | |
| EN 1.4301 for beam | 5.78 | 183,700 | 175.87 | 282.88 | 0.355 | 315.17 | 357.71 | 755.15 | 60.5 | 72.9 | 2.67 | 170.29 |
| 9.78 | 204,200 | 204.80 | 296.31 | 0.346 | 328.53 | 372.10 | 707.33 | 62.6 | 71.0 | 2.39 | 181.14 | |
| Grade A4-80 bolt | 10.00 | 177,900 | 406.05 | 574.12 | 0.526 | 663.45 | 736.02 | 746.89 | 14.0 | 36.8 | 1.30 | 26.54 |
3.1.3 Experimental setup
A 600 kN hydraulic actuator controlled by a hydraulic servo system was used to subject the joints to load. Two hinges were employed at both ends of the column to achieve the boundary conditions. The hydraulic cylinder was applied to the column to load the axial force acting on the column as shown in Table 2, which remained constant throughout the experiment. The actuators and cylinders were equipped with calibrated load cells and displacement transducers to accurately record the force applied and the corresponding displacement values. To prevent torsional and lateral deformation at the end of the beam, lateral support was installed. Figure 12 shows a schematic diagram of the beam–column connection experimental setup. The specimens were loaded using displacement control at a constant loading rate of 0.5 mm/min until plastic resistance was reached, at which point the loading rate was increased to 1.2 mm/min. The loading process continued until bolt failure or component breakage was observed.
![Figure 12
Test setup for beam-to-exterior column joint specimen [20].](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_012.jpg)
Test setup for beam-to-exterior column joint specimen [20].
3.1.4 Experimental results
The F–∆ curve is shown in Figure 13. From the F–∆ curve data, the ultimate resistance F u, and the ultimate deformation from the loading point ∆ u were determined, as shown in Table 4. Connection components that affect end – plate connection deformation include the column web under shear,the column flange under bending,the end – plate under bending,and bolts under tension [35]. The column web deformation under compression and tension is negligible due to the presence of transverse stiffeners [35,36]. The M–ϕ curve is shown in Figure 14,where the moment M was determined by multiplying the force by the length of the lever arm (1.1 m),and the total joint rotation ϕ is the sum of the shear rotation ϕ s and the gap rotation ϕ ep. It should be noted that the reported M–ϕ curve is truncated before reaching the maximum rotational capacity of the tested joint due to insufficient recording of the two diagonal LVDTs in the panel zone. The ultimate moment M u was obtained by multiplying the ultimate resistance F u by the distance between the column face and the loading point (1.1 m). The experimental values obtained are listed in Table 4.
![Figure 13
The F–∆ curve of the tested joint specimen [20].](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_013.jpg)
The F–∆ curve of the tested joint specimen [20].
![Figure 14
The M–ϕ curve of the tested joint specimen [20].](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_014.jpg)
The M–ϕ curve of the tested joint specimen [20].
Experimental results of the tested joint specimen
| Specimen | F Rd (kN) | F u (kN) | K (kN/mm) | ∆ u (–) | S j,ini (kN m/rad) | M Rd (kN m) | M u (kN m) |
|---|---|---|---|---|---|---|---|
| EN 1.4301 | 85.43 | 123.58 | 5.14 | 378.84 | 10974.24 | 93.97 | 135.94 |
With respect to the failure mode on the test specimen (beam-to-exterior column with stiffener), significant bending deformation of the end-plate and column flange can be observed, as well as shear deformation in the panel zone. In addition, there was also damage to the bolts, rib stiffener, and beam flange, which experienced buckling and limited cracking on the fillet welds.
3.2 Numerical configuration
3.2.1 Mesh convergence study
Using the ABAQUS device, a finite element analysis was conducted to simulate the behavior of extended end-plate beam–column joints. The column had an I-profile geometry of 300 mm × 180 mm × 6 mm × 10 mm and the beam had an I-profile geometry of 250 mm × 150 mm × 6 mm × 10 mm. The lengths of the column and the beam were 1,800 and 1,100 mm, respectively. Solid elements with a C3D8R-type mesh were used for all parts. Mesh sizes of 6, 8, 10, 12, and 4 mm (the latter only for the bolt elements, as shown in Figure 15) were used for all components. The results of varying the mesh size with respect to stress and displacement values are presented in Figure 16 and Table 5. Additionally, the contour results of the connection structure with respect to stress, strain, and displacement are shown in Figure 17. The use of partitions on the components aims to maintain accuracy while reducing computation time, making the simulation more efficient. Without the use of partitions, the computation time will be longer, which can cause errors in the simulation. This method is applied to each layer of the plate beam, column, and bolt.

Mesh size configuration for the benchmarking model.

Results of mesh size variation: (a) stress and (b) displacement.
Results of the mesh convergence study
| Mesh size (mm) | Stress (Pa) | Strain (mm/mm) | Displacement (mm) |
|---|---|---|---|
| 6 | 746.9 | 0.3016 | 388.3 |
| 8 | 746.9 | 0.3648 | 388.4 |
| 10 | 746.9 | 0.4407 | 388.1 |
| 12 | 746.9 | 0.5121 | 388.2 |
| Average | 746.9 | 0.4048 | 388.25 |

Results of contour variation: (a) stress; (b) strain; and (c) displacement.
3.2.2 Benchmarking results
When performing numerical simulations, the experiment performed in the study of Gao et al. [20] was used as a reference. This experiment involved monotonic loading on stainless steel connection structures. The F–∆ load–displacement curves and failure modes obtained from the numerical simulations were compared with the experimental results. The numerically predicted F–∆ curves closely matched the experimentally obtained ones,as shown in Figures 18 and 19. However, the numerical curves were slightly higher than the experimental test results.The experimental and numerical failure modes for the joints tested demonstrated the ability of the modes to accurately represent the failure modes, as shown in Figure 20. The numerically predicted values of the final resistance F u, FE of the tested joints are reported in Table 6, along with the numerical differences from the corresponding experimental values. The difference value of F u, EXP/F u, FE was 0.00014%. The full M–ϕ curve obtained by means of FE modeling is plotted in Figure 19, and the numerically predicted moment M u, FE versus the rotation of the tested joint is summarized in Table 6. A comparison of the predicted FEA results with the test values is also shown in Table 6. The difference in the value of M u, EXP/M u, FE was calculated to be 0.00014%. Thus, the validity of the test was further verified through the application of the developed FEA model, which could be used in future parametric studies. The simulation results are shown in Table 6.
![Figure 18
Comparison of the results obtained using FE (current study) and the experimental results [20]: F–∆ curves.](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_018.jpg)
Comparison of the results obtained using FE (current study) and the experimental results [20]: F–∆ curves.
![Figure 19
Comparison of the results obtained using FE (current study) and the experimental results [20]: M–ϕ curves.](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_019.jpg)
Comparison of the results obtained using FE (current study) and the experimental results [20]: M–ϕ curves.
![Figure 20
Comparison of the experimental results with the benchmarking results for failure mode. (a) Experimental results [20]. (b) Benchmarking results.](/document/doi/10.1515/jmbm-2022-0284/asset/graphic/j_jmbm-2022-0284_fig_020.jpg)
Comparison of the experimental results with the benchmarking results for failure mode. (a) Experimental results [20]. (b) Benchmarking results.
Comparison of experimental results with benchmarking results
| Specimen | F u, EXP (kN) | F u, FE (kN) | F u, EXP/F u, FE (%) | M u, EXP (kN m) | M u, FE (kN m) | M u, EXP/M u, FE (%) |
|---|---|---|---|---|---|---|
| EN. 1.4301 | 123.58 | 121.86 | 0.00014 | 135.94 | 134.04 | 0.00014 |
4 FE configuration and settings
4.1 Methodology
This study was conducted in several stages, starting with a literature study on related research studies. In the early stages, the design of the beam–column connection was performed using the ABAQUS software package by replicating a design used in previous experiments. The simulation results were then validated on the basis of the experimental results. After obtaining appropriate results, the geometric configuration of the beam–column joints was changed, using a beam-to-column configuration with different numbers of beams (1, 2, 4, and 4). Data were collected for each variation in the form of force–displacement, moment–rotation, and structural response contours occurring at the beam–column joints. The steps followed in this work are shown in Figure 21.

Flowchart for this research methodology.
4.2 Geometrical model and parametric study
In this study, the beam-to-column connection was used with an I-column profile of 300 mm × 180 mm × 6 mm × 10 mm and an ×-beam profile of 250 mm × 150 mm × 6 mm × 10 mm, where the lengths of the column and beam were 1,800 mm and 1,100 mm, respectively. Four variations of beam configuration were used in the column, denoted by V1, V2, V3, and V4. To determine the structural behavior capacity of each of the different models when subjected to the same treatment, a parametric study design matrix was created for each variation in the simulation, as shown in Table 7. Each of the blocks in the matrix is denoted using the notation B1, B2, B3, and B4.
Details of the configuration of different variations in the numerical simulation
| Model | Material grade | Bolt grade | Number of beams used | Location of the beam axis | Column stiffeners |
|---|---|---|---|---|---|
| V1 | EN 1.4301 | A4-80 | 1 | 1 at the major axis (B1) | Yes |
| V2 | EN 1.4301 | A4-80 | 2 | 2 at the major axis (B1, B2) | Yes |
| V3 | EN 1.4301 | A4-80 | 3 | 2 at the major axis (B1, B2) and 1 at minor axis (B3) | No |
| V4 | EN 1.4301 | A4-80 | 4 | 2 at the major axis (B1, B2) and 2 at minor axis (B3, B4) | No |
The beam–column connection design, as shown in Figure 22, includes the installation of a pair of rib stiffeners on the beam wings and end-plates, each with a thickness of 6 mm. The bolt diameter used in the connection is 20 mm. It is important to note that the model of each variation possesses the same dimensions for each of its geometric components. The joints in the design can be classified as interior or exterior joints on the basis of their position relative to the axis. Joints with two sides on the same axis are called interior joints, while joints with one side on the axis are called exterior joints.

Geometric model of the parametric study (all dimensions in mm). (a) Configuration for V1 model. (b) Configuration for V2 model. (c) Configuration for V3 model. (d) Configuration for V4 model.
4.3 Material definition
Stainless steel EN 1.4301 is used as the material for the beam–column connection, while stainless steel A4-80 is used for the bolt components, in accordance with a previous study. The strength of the material used is shown in Table 8, which presents the test results [34].
Material properties
| Material component | Young’s modulus (MPa) | Poisson’s ratio | Yield stress (MPa) | Plastic strain (%) |
|---|---|---|---|---|
| EN 1.4301 for Beam web | 183,700 | 0.3 | 282.88 | 0 |
| 755.15 | 0.605 | |||
| EN 1.4301 for Beam flange | 204,200 | 0.3 | 296.31 | 0 |
| 707.33 | 0.626 | |||
| EN 1.4301 for Column web and rib stiffeners | 179,400 | 0.3 | 287.59 | 0 |
| 751.66 | 0.563 | |||
| EN 1.4301 for column flange, end-plate, column plate | 179,400 | 0.3 | 275.94 | 0 |
| 757.41 | 0.536 | |||
| A4-80 for bolt | 177,900 | 0.3 | 574.12 | 0 |
| 746.89 | 0.14 |
4.4 Boundary conditions
The ABAQUS software package was used to perform the simulations using the block–column connection model. The stress–strain curve obtained from the results of a previous study [34] was converted into a true stress versus logarithmic plastic strain relationship, and then input into ABAQUS. Solid elements were used for each part of the model, with a C3D8R-type mesh and a mesh size of 10 mm for all parts, except for the bolts, for which a mesh size of 4 mm was used, as shown in Figure 23. All degrees of freedom at each end of the column were retained, except for rotation about the major or minor axis of the column section, depending on the beam configuration being used. Additionally, the longitudinal translations at the lower end of the column were released in order to incorporate the axial loads specified in Table 2. To apply the necessary constraints, reference points RP1 and RP2 were used, enabling the kinematic coupling of the top and bottom end sections of the column. The reference points RP3, RP4, RP5, and RP6 were used to control the degrees of freedom of the beam ends, as the load application takes the form of the specified vertical displacement, as shown in Figure 24. The bolt pretension force was determined using the BOLT LOAD command using the values presented in Table 2. Four pairs of contacts were subjected to different loads in the simulation, namely, between the end-plate and the column flange, the bolt head and the column flange, the bolt nut and the end-plate, and the bolt stem and the bolt hole. A contact pair was defined as being finite-sliding, and a surface-to-surface model with friction using the penalty method was employed to describe the tangential behavior of all contact surfaces, while a default hard contact was used for normal behavior to simulate bearing. In ABAQUS, Step Static and General were used. The friction coefficient used for the end-plate contact pair with the column flange, the bolt head with the column flange, and the bolt nut with the end-plate were 0.2, as reported in the study of Bu et al. [37], while the tangential behavior of the bolt rod contact pair with the bolt hole was assumed to be frictionless.

Meshing for the FE model specimen. (a) Model V1, (b) Model V2, (c) Model V3, and (d) Model V4.

Boundary conditions for the FE model specimen. (a) Model V1, (b) Model V2, (c) Model V3, and (d) Model V4.
5 Numerical results
In this section, the simulation results for the beam–column connection structure are described, including with respect to force–displacement, moment–rotation, and failure modes. Each end of the beam was subjected to monotonic loading via the same treatment. The force–displacement graph presented in Figure 25 shows that the ultimate force values for the two major connection models, V1 and V2, were different. Specifically, the ultimate force value of model V2 was higher than that of model V1, but the ultimate displacement value of model V2 was smaller than that of model V1. On the basis of V1, it can be found that the shear deformation in the column interior panel zone in connection V2 is limited under symmetric loading, which is also true in the case of connection V4. The average ultimate force values that can be accepted by the four connection models are 108,893 kN for model V1, 130,793 kN for model V2, 54,680 kN for model V3, and 105,761 kN for model V4. The V2 model can handle the force with the highest average value, corresponding to 130,793 kN, whereas the V3 model, which is the minor connection (B3), can handle the force with the lowest value among the four models tested, namely 24,575 kN. Table 9 displays the simulation results for the force–displacement relation, with the magnitude of the force on the vertical axis and displacement on the horizontal axis in Figure 25.

Force–displacement curve of the different models. (a) V1 model, (b) V2 model, (c) V3 model, and (d) V4 model.
Finite element results
| Model | F u (kN) | ∆ u (mm) | M u (kN m) | ϕ (rad) | |
|---|---|---|---|---|---|
| V1 | B1 | 108.893 | 228.321 | 119.782 | 0.206 |
| V2 | B1 | 130.704 | 227.316 | 143.774 | 0.205 |
| B2 | 130.883 | 227.316 | 143.971 | 0.205 | |
| V3 | B1 | 69.655 | 227.494 | 76.620 | 0.204 |
| B2 | 69.811 | 227.488 | 76.792 | 0.204 | |
| B3 | 24.575 | 227.492 | 27.053 | 0.206 | |
| V4 | B1 | 93.481 | 228.151 | 102.830 | 0.205 |
| B2 | 92.776 | 228.164 | 102.053 | 0.204 | |
| B3 | 121.073 | 228.159 | 133.180 | 0.206 | |
| B4 | 115.713 | 228.155 | 127.284 | 0.205 |
The seismic design specifications provide explicit limits for rotational capacities. For high-ductility-class structures, EN 1998-1 [38] specifies a rotational capacity of less than 0.035 rad, while for medium-ductility-class structures, a rotational capacity of 0.025 rad is specified. Meanwhile, ANSI/AISC 360-16 [39] considers a rotational capacity of 0.03 rad to be sufficient for beam–column connections. As can be observed in Figure 26, rotations greater than 0.1 rad were recorded for austenitic stainless steel connections using A4-80 bolts, indicating significant ductility, as reported in Table 3. The simulation results for the moment–rotation relationship are presented in Table 9. In Figure 26, the vertical axis shows the moment magnitude, while the horizontal axis corresponds to rotation.

Moment–rotation curve of the different models. (a) V1 model, (b) V2 model, (c) V3 model, and (d) V4 model.
The V1 model can be subjected to an ultimate moment of 119.782 kN m and a rotation of 0.206 rad. Model V2 can be subjected to ultimate moments of 143.774 and 143.971 kN m for beam configurations B1 and B2, respectively, with the same rotation value for both configurations, namely 0.205 rad. The acceptable rotation values for the V1 and V2 models were not too different from the rotation values for the V3 and V4 models. This is related to the use of column stiffeners in the V1 and V2 models. In the V3 model, the influence of the B3 beam configuration on the minor axis and the absence of column stiffeners cause the loading to be asymmetrical, such that the V3 model is able to be subjected to the ultimate moment with the smallest value, of 60.155 kN m, with a deflection value of 0.204 rad. In model V4, connections B1 and B2 can be subjected to ultimate moment values of 102.830 and 102.053 kN m, respectively, with rotational values of 0.205 and 0.204 rad, respectively. Meanwhile, the connections B3 and B4 in the V4 model are able to be subjected to a higher ultimate moment value than connections B1 and B2 in the V4 model because the configuration of the beam located on the major axis of the column can be subjected to 133,180 and 127,284 kN m, respectively, with rotational values of 0.206 and 0.205 rad. Due to the configuration of beams B1 and B2 on the minor axis of column model V4 under symmetrical loading, this connection can be subjected to a higher ultimate moment value than the minor-axis connection in model V3, connection B3. On the basis of these results, numerical prediction values are obtained from the ultimate force values F u, FE, and the final displacement ∆ u of the joints tested. The ultimate moment value M u, FE, and the final rotation value ϕ (rad), determined according to the endpoint, are shown in Table 9.
On the basis of the von Mises failure mode contours obtained for the four test models, the numerical failure modes for the four joints tested are described in Figures 27– 30. The highest stress is on the bolts; in particular, the bolts in the first row undergo collapse after an ever-increasing tensile force, and slightly lower bolt forces can be observed in the second row. The variation in the bolt forces in the third row is relatively small during the loading process, which is related to the fact that this row of bolts is close to the center of compression of the joint. As expected, the force on the bottom bolt row decreases with increasing applied load because the bottom bolt row is located in a compression zone where the contact effect between the end-plate and column flange reduces the bolt pretension forces.

von Mises stress progressive contour of model V1: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

von Mises stress progressive contour of model V2: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

von Mises stress progressive contour of model V3: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

von Mises stress progressive contour of model V4: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.
On the basis of these figures, failure occurring due to bending deformation on the end-plate and column flange, buckling on the rib stiffeners, buckling on the beam flanges, significant shear deformation on the panel zone, and damage to the bolts can be observed. The highest stress concentration in the V1 model is on the bolts. The von Mises stress contour for the V1 model is shown in Figure 27. The V2 model experiences bending deformation failure on the end-plate and column flange, buckling on the rib stiffeners, buckling on the beam flanges, and damage to the bolts, as shown in Figure 28.
In the V3 and V4 models, bending deformation failures on the end-plate and column flange, buckling on the rib stiffeners, buckling on the beam flanges, and damage to the bolts occurred. Column web models V3 and V4 underwent tension and compression deformation due to the absence of stiffeners in the column; of the two models V3 and V4, this failure can be seen to have been greater in model V3 because the geometry of model V4 causes the column deformation to occur under symmetrical loading, as shown in Figures 29 and 30.
Figures 31–34 present and compare the distributions of plastic strain PEEQ at each of the various connection models when simulating monotonic loads. Then, the results for the occurring strain are compared. Based on the PEEQ plastic contour, it can be observed that there are parts of the joint structure that are not subjected to heavy strain. This situation is indicated by the blue and green contours of the connection structure, indicating that the element is not subjected to any significant strain, or can be described as exhibiting minimum deformation. The PEEQ plastic strain values at the joints of the V1, V2, V3, and V4 models reached 0.209, 0.280, 0.310, and 0.572, respectively.

Strain progressive contour of model V1: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.
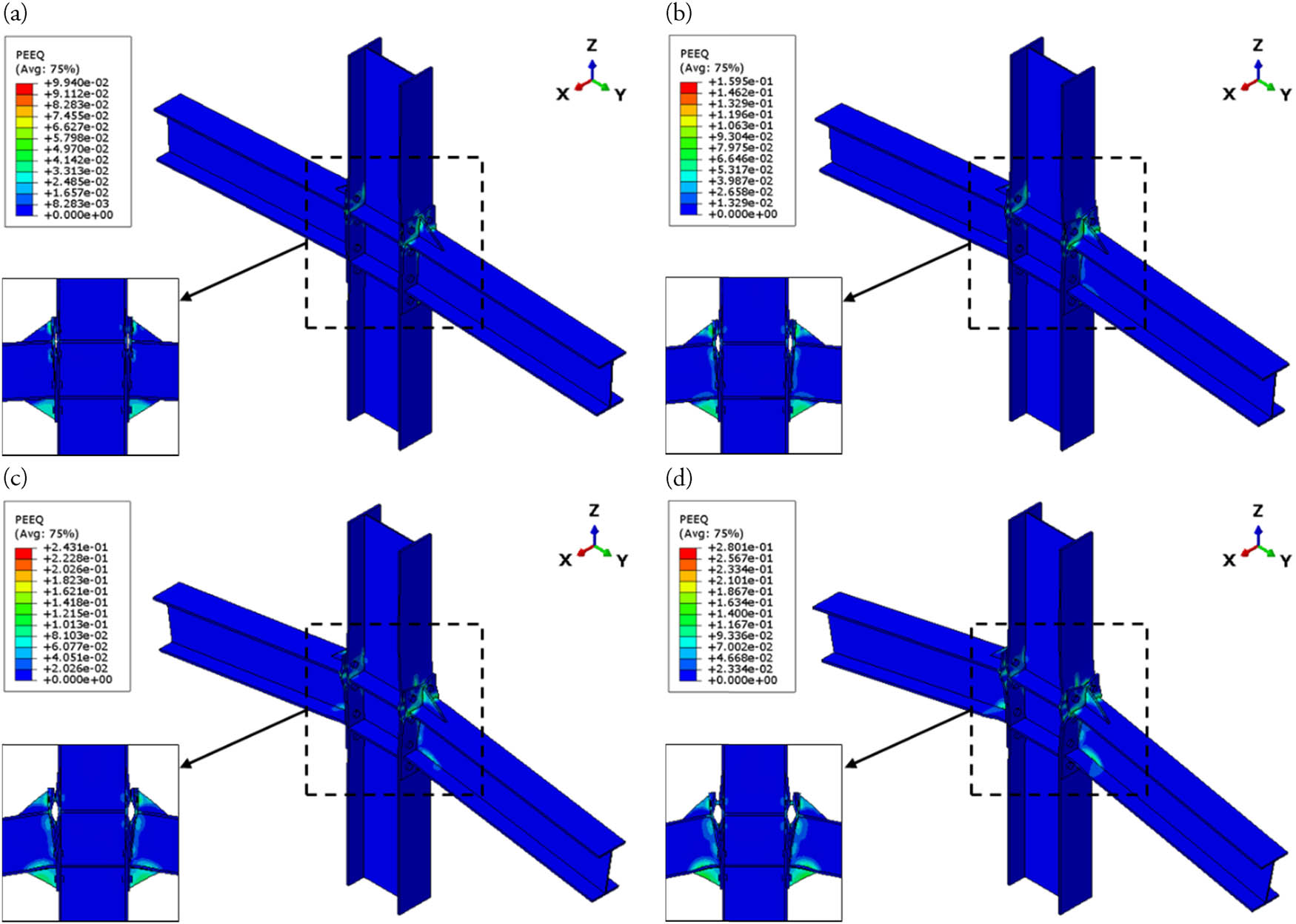
Strain progressive contour of model V2: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

Strain progressive contour of model V3: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

Strain progressive contour of model V4: (a) t = 0.15 s; (b) t = 0.3 s; (c) t = 0.45 s; and (d) t = 0.6 s.
Model V1 experienced the lowest plastic strain value of the four models tested, namely 0.209. Plastic strain has been significant in the columns, end-plates, bolts, and rib stiffeners. The highest value of the plastic strain for the V1 model was located in the rib stiffeners, as shown in Figure 31. The highest value of the plastic strain for the V2 model was in the first-row bolts, with a value of 0.280. The spread of the plastic strain on the V2 model column is relatively small, such that the deformation of the V2 model column shape is not too visible when compared to the V1 model. The plastic strain contour of the V2 model is shown in Figure 32.
It can be seen from Figure 33 that the distribution of the plastic strain occurs mostly in the column body. This is because the V3 model does not use column stiffeners. The highest value of the plastic strain in the V3 model was 0.310.
The V4 model experienced the highest degree of plastic strain of the four test models, with a value of 0.572, located on the bolt on the minor axis. The four rows of bolts on the minor axis are used to facilitate two minor-axis connections, namely the joints of the B3 beam and the B4 beam. In addition, the rib stiffeners at the minor-axis joints also experienced a relatively high degree of plastic strain, as shown in red in Figure 34.
The displacement magnitude values on the four test models V1, V2, V3, and V4 reached 231.4, 231.2, 241.5, and 235.9 mm, respectively. Figures 35–38 show the distribution of the displacement magnitude of the model tested via simulation under monotonic loading. The V3 model was the model with the highest displacement magnitude value among the four test models, while the V4 model was the model with the lowest displacement magnitude value.

Displacement progressive contour of model V1: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

Displacement progressive contour of model V2: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.

Displacement progressive contour of model V3: (a) t = 0.15 s, (b) t = 0.30 s, (c) t = 0.45 s, and (d) t = 0.6 s.

Displacement progressive contour of model V4: (a) t = 0.15 s, (b) t = 0.3 s, (c) t = 0.45 s, and (d) t = 0.6 s.
6 Conclusions
By employing different loading configurations for each geometry, the FEA study was carried out via the modeling of beam–column joints, and FE testing was performed under monotonic loading. The research results obtained were then used to evaluate the response behavior of the structure on the basis of the tested beam–column connection models. Based on this research, it can be concluded that the behavior of the tested beam–column connection models could be evaluated using the results obtained.
Tests were performed under variations in the number of beams, namely one beam (major axis) with column stiffeners, two beams (major axis) with column stiffeners, three beams (two beams on the major axis and one beam on the minor axis) without column stiffeners, and four beams (two beams on the major axis and two beams on the minor axis) without column stiffeners.
Numerical predictions of the F–∆ curve, the FE M–ϕ curve, and the failure mode were obtained in this workresearch using the FEA method. The FE modeling was validated against results obtained via experimental testing. The difference between the results obtained via the two methods, F u, EXP/F u, FE, was 0.00014% on the basis of the F–∆ curve data obtained.Subsequent analysis of the M–ϕ curve showed that the difference in the results M u, EXP/M u, FE was also 0.00014%. The failure mode contour results were then evaluated. The deformation of the resulting structural response in the FE model did not show a difference that was too great or significant with respect to the response contour obtained from the experimental test results. These three points verify the validity of the FE model, and the performance characteristics predicted by FEM were in accordance with the experimentally obtained values. This shows that ABAQUS software can be used to simulate the modeling of beam–column joints with high accuracy.
Modeling variations in the geometry of the number of beams and the use of stiffeners in the columns affected the responses of the connection structures. Among the variants tested, the V2 model, specifically at the B2 connection, can be subjected to the highest ultimate force value of the four test models, namely 130,883 kN, where the displacement caused by the force was 227.32 mm; this displacement value was the lowest value observed among the four test models. Meanwhile, the V3 model, specifically at the B3 connection, can be subjected to the smallest force among the four test models, namely 24,576 kN, with a displacement of 227.49 mm; this displacement value is greater than that obtained for the V2 model. This indicates that the V2 model is the stiffest of the four models tested.
The modeling of beam–column connection structures was successfully performed in several configurations in this work. However, in its implementation, it is still necessary to consider other production factors such as material weight, cost, and other parameters that affect the design of beam–column connection structures. The study of the influence of beam–column joint geometry is not limited to double-extended end-plate bolted connections. There are many other joint geometry models that may represent future research opportunities for the creation of beam–column connection structures with improved performance. Finally, the structural modeling of double-extended end-plate beam–column bolted connections using ABAQUS software package can be considered for component planning in various sectors, including in applications related to building structures, bridges, and traffic infrastructure, among others.
Nomenclature
- A s
-
tensile stress area of the bolts
- b
-
thickness of the section
- b pz
-
width of the panel zone
- d
-
arm length
- d b
-
height of the web panel column
- d b,req
-
bolt diameter
- d c
-
width of the web panel column
- d c
-
clear depth of the column web panel in shear
- E
-
elastic modulus
- e f
-
distance between the center of the outer tension side of the bolt row and the outer edge of the rib stiffener
- F
-
force
- FE
-
finite element
- FEA
-
finite element analysis
- FEM
-
finite element method
- F nt
-
nominal tensile strength of the bolt
- F pre
-
bolt pretension force
- F Rd
-
plastic resistance
- Ftr, Rd
-
effective design tension resistance of the bolt row r
- F u
-
ultimate resistance/ultimate force
- f ub
-
ultimate tensile strength of the bolt
- f v
-
shear strength of the web panel column
- f y
-
yield strength of steel
- F yc
-
minimum yield strength of the column flange material
- F yp
-
minimum yield strength of the end-plate material
- G
-
shear modulus of the material
- h 0
-
distance from the centerline of the compression flange to the tension-side outer bolt row
- h 1
-
distance from the centerline of the compression flange to the tension-side inner bolt row
- h
-
height of the section
- h pz
-
height of the panel zone
- h r
-
row distance of the bolt row r to the center of compression
- h t
-
distance between the upper and lower centerlines of the beam flange
- I
-
moment of inertia of the section
- I e
-
moment of inertia of the end-plate
- K
-
initial stiffness
- k i
-
stiffness coefficient for the base connection member i
- L
-
length of the cross section
- M
-
moment
- M f
-
Moment of the face at the column
- M j,R d
-
moment resistance
- M p
-
plastic moment of the element
- M Rd
-
plastic moment joint
- M u
-
ultimate moment joint
- M y
-
elastic moment of the element
- R
-
rotational stiffness of the joint
- R 1
-
rotational stiffness of the web column panel
- R 2
-
rotational stiffness of the connection
- S j,ini
-
initial rotational stiffness
- S x
-
elastic cross-sectional modulus
- t c
-
thickness of the web panel column
- t cf
-
thickness of the column flange
- t p,req
-
thickness of the end-plate used
- v
-
deflection
- Y c
-
yield line mechanism parameters of the column flange
- Y p
-
yield line mechanism parameters of the end-plate
- z
-
lever arm
- Z x
-
plastic section modulus
- γ M7
-
partial factor of safety
- δ
-
gap between the end-plate and column flange on the centerline of the flange tension of the beam
- δ N1, δ N2
-
horizontal deformation values between the end-plates and column flanges
- δ P1, δ P2
-
deformation values along the diagonal line of the web panel
- δ S1, δ S2
-
horizontal deformation values between the end-plates and column flanges
- Δ
-
difference in the displacement of the panel zone on the centerline of the upper and lower beam flanges at the end of the beam
- ΔL
-
increase in the length of the cross section
- ∆ u
-
ultimate deformation of the point loading
- ε
-
strain
- μ
-
stiffness ratio
- σ
-
stress
- ϕ/θ
-
rotation
- ϕ b
-
overall rotation at the ends of the beam
- ϕ cb
-
elastic beam rotation
- ϕ ep
-
gap rotation
- ϕ s
-
shear rotation
-
Funding information: The authors state no funding involved.
-
Conflict of interest: The authors declare that they have no conflict of interest.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Data availability statement: The authors confirm that the data supporting the findings of this study are available within the article.
References
[1] Pratama AA, Prabowo AR, Muttaqie T, Muhayat N, Ridwan R, Cao B, et al. Hollow tube structures subjected to compressive loading: implementation of the pitting corrosion effect in nonlinear FE analysis. J Braz Soc Mech Sci. 2023;45(3):143. 10.1007/s40430-023-04067-3.Suche in Google Scholar
[2] Tuswan T, Rezaldy A, Mursid O, Yudo H, Prabowo AR. Application of sandwich plate system (SPS) on 155 m barge: framing system configuration, weight saving, and dynamic characteristic assessment. Nase More. 2023;70(1):58–76. 10.17818/NM/2023/1.6.Suche in Google Scholar
[3] Do QT, Muttaqie T, Nhut PT, Vu MT, Khoa ND, Prabowo AR. Residual ultimate strength assessment of submarine pressure hull under dynamic ship collision. Ocean Eng. 2022;266:112951. 10.1016/j.oceaneng.2022.112951.Suche in Google Scholar
[4] Prabowo AR, Ridwan R, Tuswan T, Imaduddin F. Forecasting the effects of failure criteria in assessing ship structural damage modes. Civ Eng J. 2022;8(10):2053–68. 10.28991/CEJ-2022-08-10-03.Suche in Google Scholar
[5] Prabowo AR, Ridwan R, Muttaqie T. On the resistance to buckling loads of idealized hull structures: FE analysis on designed-stiffened plates. Designs. 2022;6(3):46. 10.3390/designs6030046.Suche in Google Scholar
[6] Mubarok MAH, Prabowo AR, Muttaqie T, Muhayat N. Dynamic structural assessment of blast wall designs on military-based vehicle using explicit finite element approach. Math Probl Eng. 2022;2022:5883404. 10.1155/2022/5883404.Suche in Google Scholar
[7] Alwan FHA, Prabowo AR, Muttaqie T, Muhayat N, Ridwan R, Laksono FB. Assessment of ballistic impact damage on aluminum and magnesium alloys against high velocity bullets by dynamic FE simulations. J Mech Behav Mater. 2022;31(1):595–616. 10.1515/jmbm-2022-0064.Suche in Google Scholar
[8] Sulistiyo MB, Hayu GA, Hidayah E. Analysis of structural steel frame beam column bolt connection with IWF profile using finite element auxiliary program. Rekayasa Sipil. 2019;13:199–206. 10.21776/ub.rekayasasipil.2019.013.03.7 (in Indonesian).Suche in Google Scholar
[9] Yang CM, Kim YM. Cyclic behavior of bolted and welded beam-to-column joints. Int J Mech Sci. 2007;49:635–49. 10.1016/j.ijmecsci.2006.09.022.Suche in Google Scholar
[10] Bjorhovde R, Colson A, Brozzetti J, Member A. Classification system for beam-to-column connections. J Struct Eng. 1990;116:3059–76.10.1061/(ASCE)0733-9445(1990)116:11(3059)Suche in Google Scholar
[11] Dong Q, Liu X, Qi H, Zhou Y. Vibro-acoustic prediction and evaluation of permanent magnet synchronous motors. Proc Inst Mech Eng Part D J Automob Eng. 2020;234:2783–93. 10.1177/0954407020919659.Suche in Google Scholar
[12] Radha A, Arunkumar C, Umamaheswari N. Investigations on prying forces in flexible connections of steel beams. Int J Struct Integr. 2019;10:415–24. 10.1108/IJSI-01-2019-0003.Suche in Google Scholar
[13] Zhu SP, Liu Q, Peng W, Zhang XC. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int J Mech Sci. 2018;142–143:502–17. 10.1016/j.ijmecsci.2018.04.050.Suche in Google Scholar
[14] Kan F, Liu X, Xin X, Xu J, Huang H, Wang Y. Analysis and evaluation of the leakage failure for clutch sleeve and shell. Eng Fail Anal. 2018;88:1–12. 10.1016/j.engfailanal.2018.02.008.Suche in Google Scholar
[15] Katkhuda H, Shatarat N, Hyari K. Damage detection in steel structures with semi-rigid connections using unscented Kalman filter. Int J Struct Integr. 2017;8:222–39. 10.1108/IJSI-04-2016-0014.Suche in Google Scholar
[16] Ghobarah A, Osman A, Korol RM. Behaviour of extended end-plate connections under cyclic loading. Eng Struct. 1990;12:15–27. 10.1016/0141-0296(90)90034-P.Suche in Google Scholar
[17] De Lima LRO, De Andrade SAL, Vellasco PCG, da S, Da Silva LS. Experimental and mechanical model for predicting the behaviour of minor axis beam-to-column semi-rigid joints. Int J Mech Sci. 2002;44:1047–65. 10.1016/S0020-7403(02)00013-9.Suche in Google Scholar
[18] Maggi YI, Gonçalves RM, Leon RT, Ribeiro LFL. Parametric analysis of steel bolted end plate connections using finite element modeling. J Constr Steel Res. 2005;61:689–708. 10.1016/j.jcsr.2004.12.001.Suche in Google Scholar
[19] Boudia SBM, Boumechra N, Bouchair A, Missoum A. Modeling of bolted endplate beam-to-column joints with various stiffeners. J Constr Steel Res. 2020;167:105953. 10.1016/j.jcsr.2020.105963.Suche in Google Scholar
[20] Gao JD, Yuan HX, Du XX, Hu XB, Theofanous M. Structural behaviour of stainless steel double extended end-plate beam-to-column joints under monotonic loading. Thin-Walled Struct. 2020;151:106743. 10.1016/j.tws.2020.106743.Suche in Google Scholar
[21] EN 1993-1-8. Eurocode 3. Design of steel structures – part 1.8: design of joints. Vol. 1. European Standard (CEN); 2005.Suche in Google Scholar
[22] ANSI/AISC 358-16 & ANSI/AISC 358s1-18. Prequalified connections for special and intermediate steel moment frames for seismic applications with supplement no. 1. Vol. 2016. American Institute of Steel Construction; 2016.Suche in Google Scholar
[23] GB 51022-2015. Technical code for steel structure of light-weight building with gabled frames. 2015.Suche in Google Scholar
[24] Pala’biran OA, Windah RS, Pandaleke R. Calculation of cantilever taper beam deflection using SAP2000. J Sipil Statik. 2019;7:1039–48. (in Indonesian)Suche in Google Scholar
[25] Shi Y, Shi G, Wang Y. Experimental and theoretical analysis of the moment-rotation behaviour of stiffened extended end-plate connections. J Constr Steel Res. 2007;63:1279–93. 10.1016/j.jcsr.2006.11.008.Suche in Google Scholar
[26] Sulaeman B. Modulus of elasticity for various types of materials. PENA Tek J Ilm Ilmu-Ilmu Tek. 2018;3:127–38. 10.51557/pt_jiit.v3i2.176. (in Indonesian)Suche in Google Scholar
[27] Shi G, Shi Y, Wang Y. Behaviour of end-plate moment connections under earthquake loading. Eng Struct. 2007;29:703–16. 10.1016/j.engstruct.2006.06.016.Suche in Google Scholar
[28] Shi G, Shi Y, Wang Y, Bradford MA. Numerical simulation of steel pretensioned bolted end-plate connections of different types and details. Eng Struct. 2008;30:2677–86. 10.1016/j.engstruct.2008.02.013.Suche in Google Scholar
[29] Augusto H, Silva LSDa, Rebelo C, Castro JM. Characterization of web panel components in double-extended bolted end-plate steel joints. J Constr Steel Res. 2015;116:271–93. 10.1016/j.jcsr.2015.08.022.Suche in Google Scholar
[30] Augusto H, Silva LS, da Rebelo C, Castro JM. Cyclic behaviour characterization of web panel components in bolted end-plate steel joints. J Constr Steel Res. 2017;133:310–33. 10.1016/j.jcsr.2017.01.021.Suche in Google Scholar
[31] Wang J, Zhu H, Uy B, Patel V, Aslani F, Li D. Moment-rotation relationship of hollow-section beam-to-column steel joints with extended end-plates. Steel Compos Struct. 2018;29:717–34. 10.12989/scs.2018.29.6.717.Suche in Google Scholar
[32] Costa R, Valdez J, Oliveira S, Silva LS, da Bayo E. Experimental behaviour of 3D end-plate beam-to-column bolted steel joints. Eng Struct. 2019;188:277–89. 10.1016/j.engstruct.2019.03.017.Suche in Google Scholar
[33] Gao JD, Yuan HX, Qian H, Chen XW. Structural behaviour and design of stainless steel end-plate beam-to-exterior column minor-axis joints. Thin-Walled Struct. 2022;181:110119. 10.1016/j.tws.2022.110119.Suche in Google Scholar
[34] GB/T 228.1-2010. Metallic materials – tensile testing – part 1: method of test at room temperature; 2011.Suche in Google Scholar
[35] Beg D, Zupančič E, Vayas I. On the rotation capacity of moment connections. J Constr Steel Res. 2004;60:601–20. 10.1016/S0143-974X(03)00132-9.Suche in Google Scholar
[36] Shi G, Fan H, Bai Y, Yuan F, Shi YJ, Wang YQ. Improved measure of beam-to-column joint rotation in steel frames. J Constr Steel Res. 2012;70:298–307. 10.1016/j.jcsr.2011.07.012.Suche in Google Scholar
[37] Bu Y, Wang Y, Zhao Y. Study of stainless steel bolted extended end-plate joints under seismic loading. Thin-Walled Struct. 2019;144:106255. 10.1016/j.tws.2019.106255.Suche in Google Scholar
[38] EN 1998-1. Eurocode 8. Design of structures for earthquake resistance – part 1; General rules: seismic actions and rules for buildings, European Standard (CEN). Brussels, Belgium; 2004.Suche in Google Scholar
[39] ANSI/AISC 360-16. Specification for structural steel buildings, American Institute of Steel Construction (AISC). Chicago, USA; 2016.Suche in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Research Articles
- The mechanical properties of lightweight (volcanic pumice) concrete containing fibers with exposure to high temperatures
- Experimental investigation on the influence of partially stabilised nano-ZrO2 on the properties of prepared clay-based refractory mortar
- Investigation of cycloaliphatic amine-cured bisphenol-A epoxy resin under quenching treatment and the effect on its carbon fiber composite lamination strength
- Influence on compressive and tensile strength properties of fiber-reinforced concrete using polypropylene, jute, and coir fiber
- Estimation of uniaxial compressive and indirect tensile strengths of intact rock from Schmidt hammer rebound number
- Effect of calcined diatomaceous earth, polypropylene fiber, and glass fiber on the mechanical properties of ultra-high-performance fiber-reinforced concrete
- Analysis of the tensile and bending strengths of the joints of “Gigantochloa apus” bamboo composite laminated boards with epoxy resin matrix
- Performance analysis of subgrade in asphaltic rail track design and Indonesia’s existing ballasted track
- Utilization of hybrid fibers in different types of concrete and their activity
- Validated three-dimensional finite element modeling for static behavior of RC tapered columns
- Mechanical properties and durability of ultra-high-performance concrete with calcined diatomaceous earth as cement replacement
- Characterization of rutting resistance of warm-modified asphalt mixtures tested in a dynamic shear rheometer
- Microstructural characteristics and mechanical properties of rotary friction-welded dissimilar AISI 431 steel/AISI 1018 steel joints
- Wear performance analysis of B4C and graphene particles reinforced Al–Cu alloy based composites using Taguchi method
- Connective and magnetic effects in a curved wavy channel with nanoparticles under different waveforms
- Development of AHP-embedded Deng’s hybrid MCDM model in micro-EDM using carbon-coated electrode
- Characterization of wear and fatigue behavior of aluminum piston alloy using alumina nanoparticles
- Evaluation of mechanical properties of fiber-reinforced syntactic foam thermoset composites: A robust artificial intelligence modeling approach for improved accuracy with little datasets
- Assessment of the beam configuration effects on designed beam–column connection structures using FE methodology based on experimental benchmarking
- Influence of graphene coating in electrical discharge machining with an aluminum electrode
- A novel fiberglass-reinforced polyurethane elastomer as the core sandwich material of the ship–plate system
- Seismic monitoring of strength in stabilized foundations by P-wave reflection and downhole geophysical logging for drill borehole core
- Blood flow analysis in narrow channel with activation energy and nonlinear thermal radiation
- Investigation of machining characterization of solar material on WEDM process through response surface methodology
- High-temperature oxidation and hot corrosion behavior of the Inconel 738LC coating with and without Al2O3-CNTs
- Influence of flexoelectric effect on the bending rigidity of a Timoshenko graphene-reinforced nanorod
- An analysis of longitudinal residual stresses in EN AW-5083 alloy strips as a function of cold-rolling process parameters
- Assessment of the OTEC cold water pipe design under bending loading: A benchmarking and parametric study using finite element approach
- A theoretical study of mechanical source in a hygrothermoelastic medium with an overlying non-viscous fluid
- An atomistic study on the strain rate and temperature dependences of the plastic deformation Cu–Au core–shell nanowires: On the role of dislocations
- Effect of lightweight expanded clay aggregate as partial replacement of coarse aggregate on the mechanical properties of fire-exposed concrete
- Utilization of nanoparticles and waste materials in cement mortars
- Investigation of the ability of steel plate shear walls against designed cyclic loadings: Benchmarking and parametric study
- Effect of truck and train loading on permanent deformation and fatigue cracking behavior of asphalt concrete in flexible pavement highway and asphaltic overlayment track
- The impact of zirconia nanoparticles on the mechanical characteristics of 7075 aluminum alloy
- Investigation of the performance of integrated intelligent models to predict the roughness of Ti6Al4V end-milled surface with uncoated cutting tool
- Low-temperature relaxation of various samarium phosphate glasses
- Disposal of demolished waste as partial fine aggregate replacement in roller-compacted concrete
- Review Articles
- Assessment of eggshell-based material as a green-composite filler: Project milestones and future potential as an engineering material
- Effect of post-processing treatments on mechanical performance of cold spray coating – an overview
- Internal curing of ultra-high-performance concrete: A comprehensive overview
- Special Issue: Sustainability and Development in Civil Engineering - Part II
- Behavior of circular skirted footing on gypseous soil subjected to water infiltration
- Numerical analysis of slopes treated by nano-materials
- Soil–water characteristic curve of unsaturated collapsible soils
- A new sand raining technique to reconstitute large sand specimens
- Groundwater flow modeling and hydraulic assessment of Al-Ruhbah region, Iraq
- Proposing an inflatable rubber dam on the Tidal Shatt Al-Arab River, Southern Iraq
- Sustainable high-strength lightweight concrete with pumice stone and sugar molasses
- Transient response and performance of prestressed concrete deep T-beams with large web openings under impact loading
- Shear transfer strength estimation of concrete elements using generalized artificial neural network models
- Simulation and assessment of water supply network for specified districts at Najaf Governorate
- Comparison between cement and chemically improved sandy soil by column models using low-pressure injection laboratory setup
- Alteration of physicochemical properties of tap water passing through different intensities of magnetic field
- Numerical analysis of reinforced concrete beams subjected to impact loads
- The peristaltic flow for Carreau fluid through an elastic channel
- Efficiency of CFRP torsional strengthening technique for L-shaped spandrel reinforced concrete beams
- Numerical modeling of connected piled raft foundation under seismic loading in layered soils
- Predicting the performance of retaining structure under seismic loads by PLAXIS software
- Effect of surcharge load location on the behavior of cantilever retaining wall
- Shear strength behavior of organic soils treated with fly ash and fly ash-based geopolymer
- Dynamic response of a two-story steel structure subjected to earthquake excitation by using deterministic and nondeterministic approaches
- Nonlinear-finite-element analysis of reactive powder concrete columns subjected to eccentric compressive load
- An experimental study of the effect of lateral static load on cyclic response of pile group in sandy soil
Artikel in diesem Heft
- Research Articles
- The mechanical properties of lightweight (volcanic pumice) concrete containing fibers with exposure to high temperatures
- Experimental investigation on the influence of partially stabilised nano-ZrO2 on the properties of prepared clay-based refractory mortar
- Investigation of cycloaliphatic amine-cured bisphenol-A epoxy resin under quenching treatment and the effect on its carbon fiber composite lamination strength
- Influence on compressive and tensile strength properties of fiber-reinforced concrete using polypropylene, jute, and coir fiber
- Estimation of uniaxial compressive and indirect tensile strengths of intact rock from Schmidt hammer rebound number
- Effect of calcined diatomaceous earth, polypropylene fiber, and glass fiber on the mechanical properties of ultra-high-performance fiber-reinforced concrete
- Analysis of the tensile and bending strengths of the joints of “Gigantochloa apus” bamboo composite laminated boards with epoxy resin matrix
- Performance analysis of subgrade in asphaltic rail track design and Indonesia’s existing ballasted track
- Utilization of hybrid fibers in different types of concrete and their activity
- Validated three-dimensional finite element modeling for static behavior of RC tapered columns
- Mechanical properties and durability of ultra-high-performance concrete with calcined diatomaceous earth as cement replacement
- Characterization of rutting resistance of warm-modified asphalt mixtures tested in a dynamic shear rheometer
- Microstructural characteristics and mechanical properties of rotary friction-welded dissimilar AISI 431 steel/AISI 1018 steel joints
- Wear performance analysis of B4C and graphene particles reinforced Al–Cu alloy based composites using Taguchi method
- Connective and magnetic effects in a curved wavy channel with nanoparticles under different waveforms
- Development of AHP-embedded Deng’s hybrid MCDM model in micro-EDM using carbon-coated electrode
- Characterization of wear and fatigue behavior of aluminum piston alloy using alumina nanoparticles
- Evaluation of mechanical properties of fiber-reinforced syntactic foam thermoset composites: A robust artificial intelligence modeling approach for improved accuracy with little datasets
- Assessment of the beam configuration effects on designed beam–column connection structures using FE methodology based on experimental benchmarking
- Influence of graphene coating in electrical discharge machining with an aluminum electrode
- A novel fiberglass-reinforced polyurethane elastomer as the core sandwich material of the ship–plate system
- Seismic monitoring of strength in stabilized foundations by P-wave reflection and downhole geophysical logging for drill borehole core
- Blood flow analysis in narrow channel with activation energy and nonlinear thermal radiation
- Investigation of machining characterization of solar material on WEDM process through response surface methodology
- High-temperature oxidation and hot corrosion behavior of the Inconel 738LC coating with and without Al2O3-CNTs
- Influence of flexoelectric effect on the bending rigidity of a Timoshenko graphene-reinforced nanorod
- An analysis of longitudinal residual stresses in EN AW-5083 alloy strips as a function of cold-rolling process parameters
- Assessment of the OTEC cold water pipe design under bending loading: A benchmarking and parametric study using finite element approach
- A theoretical study of mechanical source in a hygrothermoelastic medium with an overlying non-viscous fluid
- An atomistic study on the strain rate and temperature dependences of the plastic deformation Cu–Au core–shell nanowires: On the role of dislocations
- Effect of lightweight expanded clay aggregate as partial replacement of coarse aggregate on the mechanical properties of fire-exposed concrete
- Utilization of nanoparticles and waste materials in cement mortars
- Investigation of the ability of steel plate shear walls against designed cyclic loadings: Benchmarking and parametric study
- Effect of truck and train loading on permanent deformation and fatigue cracking behavior of asphalt concrete in flexible pavement highway and asphaltic overlayment track
- The impact of zirconia nanoparticles on the mechanical characteristics of 7075 aluminum alloy
- Investigation of the performance of integrated intelligent models to predict the roughness of Ti6Al4V end-milled surface with uncoated cutting tool
- Low-temperature relaxation of various samarium phosphate glasses
- Disposal of demolished waste as partial fine aggregate replacement in roller-compacted concrete
- Review Articles
- Assessment of eggshell-based material as a green-composite filler: Project milestones and future potential as an engineering material
- Effect of post-processing treatments on mechanical performance of cold spray coating – an overview
- Internal curing of ultra-high-performance concrete: A comprehensive overview
- Special Issue: Sustainability and Development in Civil Engineering - Part II
- Behavior of circular skirted footing on gypseous soil subjected to water infiltration
- Numerical analysis of slopes treated by nano-materials
- Soil–water characteristic curve of unsaturated collapsible soils
- A new sand raining technique to reconstitute large sand specimens
- Groundwater flow modeling and hydraulic assessment of Al-Ruhbah region, Iraq
- Proposing an inflatable rubber dam on the Tidal Shatt Al-Arab River, Southern Iraq
- Sustainable high-strength lightweight concrete with pumice stone and sugar molasses
- Transient response and performance of prestressed concrete deep T-beams with large web openings under impact loading
- Shear transfer strength estimation of concrete elements using generalized artificial neural network models
- Simulation and assessment of water supply network for specified districts at Najaf Governorate
- Comparison between cement and chemically improved sandy soil by column models using low-pressure injection laboratory setup
- Alteration of physicochemical properties of tap water passing through different intensities of magnetic field
- Numerical analysis of reinforced concrete beams subjected to impact loads
- The peristaltic flow for Carreau fluid through an elastic channel
- Efficiency of CFRP torsional strengthening technique for L-shaped spandrel reinforced concrete beams
- Numerical modeling of connected piled raft foundation under seismic loading in layered soils
- Predicting the performance of retaining structure under seismic loads by PLAXIS software
- Effect of surcharge load location on the behavior of cantilever retaining wall
- Shear strength behavior of organic soils treated with fly ash and fly ash-based geopolymer
- Dynamic response of a two-story steel structure subjected to earthquake excitation by using deterministic and nondeterministic approaches
- Nonlinear-finite-element analysis of reactive powder concrete columns subjected to eccentric compressive load
- An experimental study of the effect of lateral static load on cyclic response of pile group in sandy soil

