Home Effect of solid solution rare earth (La, Ce, Y) on the mechanical properties of α-Fe
Article Open Access

Effect of solid solution rare earth (La, Ce, Y) on the mechanical properties of α-Fe

  • Chunying Bai , Guojun Bai , Xiangjun Liu EMAIL logo and Ting Wang
Published/Copyright: June 27, 2025
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
High Temperature Materials and Processes
From the journal High Temperature Materials and Processes Volume 44 Issue 1

Abstract

In view of the fact that the current experimental method is not very satisfactory to study the solid solution behavior of rare earth elements (RE) in steel, it is an effective and economical method to replace the experimental research with the simulation calculation method. In this article, the Fe-RE (La, Ce, Y) systems were constructed based on the density functional theory, and mechanical properties of doping systems were calculated. The calculation results of the solvation energy show that La, Ce, and Y can form stable solid solutions in α-Fe, and Ce has the highest solid solubility in α-Fe, followed by Y and La. The results of elastic moduli show that the doping of RE (La, Ce, Y) reduces the incompressibility, shear strain resistance, stiffness, and Vickers hardness of the doping system, while increasing the toughness and machinability. The strength properties of the doping systems are Fe–Ce > Fe–La > Fe–Y, and the toughness and machinability are opposite. In Fe–RE (La, Ce, Y) doping systems, RE (La, Ce, Y) reduce the metal bond strength of the Fe system, which is the fundamental reason for the decrease of the strength properties of the doping system. In addition, in doping system, Fe atoms gain electrons and RE (La, Ce, Y) atoms lose electrons. And the increase of electron cloud density in the doping system can be used to explain the improvement of toughness and machinability of the system.

Keywords: first-principles calculation; rare earth; mechanical properties; geometric structure; electronic properties

1 Introduction

RE plays a beneficial role in enhancing the overall performance of steel. In recent years, La, Ce, and Y have been widely adopted as microalloying additions in ferrous alloys due to their high cost performance. For example, Wang et al. [1] reported that the incorporation of 0.0015 wt% Ce into Q690E steel increased its transverse and longitudinal strength-ductility balance values from 12.853 and 14.820 GPa·% to 15.373 and 15.737 GPa·%, respectively. Oleksak et al. [2] observed that Ce addition to pipeline steel induced slight grain refinement and modest strength gains while markedly improving transverse impact toughness. The results of Liu et al. [3] showed that the addition of Ce and La to 4Cr5MoSiV1 steel significantly refined the coarse eutectic microstructure and eutectic carbides, thereby increasing its yield strength. Zang et al. [4] also obtained a similar conclusion: after adding 0.02 wt% Y to 20Cr13 martensitic stainless steel, its tensile strength and elongation were improved. The aforementioned studies have shown that the addition of rare earth can effectively improve the mechanical properties of steel materials, but they are all descriptions of experimental phenomena (or data), and the mechanism of RE to improve the mechanical properties of steel is not systematically discussed.

Current research has predominantly focused on the effects of RE on the microstructures [5,6] and inclusions in steel [7,8], while there are comparatively few studies on the solid solution behavior of RE in steel. Since the radius of RE atom is much larger than that of Fe atom, and its electronegativity is relatively small, the solid solubility of RE in the Fe matrix is extremely low [9,10]. Ji [11] confirmed that RE can exist in iron and iron alloys in solid solution form from the atomic scale by studying the internal consumption peaks of Fe-P-La, Fe-P-La-N, Fe-C-La systems. Lin et al. [12] investigated the solid solubility of La and Ce in 16Mn steel, and the results showed that the maximum solid solubility of Ce in 16Mn steel was 0.011 wt% at room temperature, the solid solution laws of La and Ce in steel are similar, and the solid solution amount of Ce is slightly higher than that of La. Yue et al. [13] added 0.0065–0.0160 wt% RE to weathering steel with O and S content less than 0.002 and 0.004 wt%, and the solid solubility of REs was 0.0014–0.0020 wt%. The aforementioned studies show that the content of RE in steel is generally low when it is applied with microalloying element, and its solid solution content is lower. Existing micro-area characterization techniques struggle to precisely detect such low levels of solid solution RE, and experimental results have thus far fallen short of expectations. With advances in computer science and computational materials science, simulation methods have become increasingly powerful. Our previous work [14,15] showed that when RE atoms solubilize into the steel matrix, they interact with other elements in steel by transferring electrons, thus affecting the properties of steel. In addition, steel materials are sensitive to the types of RE [16], and the effects of adding different types of RE on the mechanical properties of steel are different.

To address these issues and consider the high abundance of La, Ce, and Y resources in Baotou, Inner Mongolia, in this work, the effects of solid solution behavior of RE (La, Ce, Y) on the mechanical properties of steel were investigated from a computational simulation perspective. The solid solution ability of RE (La, Ce, Y) in α-Fe and the effect of RE (La, Ce, Y) doping on the mechanical properties of α-Fe were calculated by first-principles calculation. In addition, the influence mechanism of RE (La, Ce, Y) on the mechanical properties of the doping systems was analyzed from the microscopic perspectives of geometric structure and electronic structure. Furthermore, the results of this study aim to deepen the microscopic understanding of mechanisms of RE microalloying, thereby facilitating the broader application of different kinds of RE in steel.

2 Computational methods and models

In this study, the Vienna ab-initio Simulation Package (VASP) was employed to calculate the solvation energy, elastic modulus, and electronic structure of pure Fe, Fe–Ce, Fe–La, and Fe–Y systems. The electron interactions were described using the Perdew–Burke–Ernzerhof functional within the generalized gradient approximation [17]. The interaction between electrons and ions was treated using the projector augmented wave (PAW) method, with a cutoff energy of 450 eV. The Brillouin zone was sampled using a 5 × 5 × 5 Monkhorst–Pack (MP) k-point mesh [18]. The energy convergence criterion was set to 1.0 × 10⁻⁵ eV·atom−1, and the force acting on each atom was constrained to ≤0.02 eV·Å−1. Spin polarization was considered in all calculations, the initial magnetic moment of Fe atoms was set to 3 μ B, while that of RE (La, Ce, Y) atoms was set to 0 μ B.

The body-centered cubic α-Fe structure was selected as the base model, with a space group of Im-3m and a lattice constant of a = b = c = 2.866 Å [19]. A 4 × 4 × 4 supercell of α-Fe containing 128 Fe atoms was constructed. Structural optimization of the Fe supercell, a = b = c = 2.831 Å, B = 159.04 GPa (B represents bulk modulus), and M(Fe) = 2.24 μ B (M represents the magnetic moment). Table 1 lists the parameters of α-Fe in the equilibrium state, as well as the calculated and experimental values. It can be seen from Table 1 that the error between the calculated value of this work and the experimental value is about 3%, which is within the acceptable range, indicating that the selection of calculation parameters is reasonable and the subsequent calculation results are reliable. The RE (La, Ce, Y) was doped into the Fe supercell, and the crystal structures of the doping systems are illustrated in Figure 1.

Table 1

Parameters of α-Fe in equilibrium state

Methods Lattice constant a (Å) Bulk modulus B (GPa) Magnetic moment M (μ B) Cohesion energy E coh (eV)
Present work 2.831 159.04 2.24 5.06
Other works [20,21] 2.84 196 2.20 5.04
2.84 174 2.17
Experimental [22] 2.87 168 2.22
Figure 1 Crystal structure models of Fe–RE (La, Ce, Y) systems: (a) Fe–Ce, (b) Fe–La, and (c) Fe–Y.
Figure 1

Crystal structure models of Fe–RE (La, Ce, Y) systems: (a) Fe–Ce, (b) Fe–La, and (c) Fe–Y.

3 Results and discussion

3.1 Solvation energy

To characterize the solubility of RE (La, Ce, Y) in Fe supercell, the solvation energy (Eₛₒₗ) of the doping systems was calculated, as shown in Eq. (1) [23,24]:

(1) E sol = E tot − n − 1 n E ( Fe ) − E ( RE ) ,

where Eₜₒₜ denotes the total energy of the Fe–RE (La, Ce, Y) system, (eV); E(Fe) and E(RE) denote the energy of an isolated Fe atom and an isolated RE (La, Ce, Y) atom, respectively, (eV); and n is the number of Fe atoms in the Fe-RE (La, Ce, Y) system.

A negative solvation energy indicates that the dopant element can solubilize spontaneously in matrix [25], and the lower the value, the easier it is to solubilize into the matrix. The calculation results of the solvation energies of Fe–RE (La, Ce, Y) systems are shown in Figure 2. As shown in Figure 2, the solvation energies of Fe–Ce, Fe–La, and Fe–Y systems are all negative, indicating that Ce, La, and Y can spontaneously solubilize in Fe system. Among them, the Fe–Ce system exhibits the lowest Eₛₒₗ value of −0.029 eV, followed by the Fe–Y system with −0.018 eV, and the Fe–La system has the highest value of −0.015 eV. This suggests that Ce atoms have the highest solubility in Fe. The higher solubility of Ce is mainly attributed to its weakly shielded outer electrons (4f¹ 5d¹ 6s²), which result in a higher effective charge and stronger attraction to surrounding Fe atoms [15,26].

Figure 2 Solvation energies of Fe–RE (La, Ce, Y) systems.
Figure 2

Solvation energies of Fe–RE (La, Ce, Y) systems.

3.2 Mechanical properties

3.2.1 Elastic constants

The crystal structures of α-Fe and Fe–Ce, Fe–La, and Fe–Y systems remain cubic after structural optimization, with three independent elastic constants: C11, C12, and C44. According to the Born–Huang criterion [27], a system can exist stably only if its independent elastic constants satisfy the conditions in Eq. (2):

(2) C 11 > 0 , C 44 > 0 , C 11 > C 12 , C 11 + 2 C 12 > 0 .

The calculated elastic constants of α-Fe and Fe–RE doping systems are presented in Figure 3. Substituting the values into the criterion, it is evident that C11, C12, and C44 of all three doping systems satisfy Eq. (2), indicating that these three doping systems can stably exist.

Figure 3 Elastic constants C11, C12, and C44 of Fe and Fe–RE (La, Ce, Y) doping systems.
Figure 3

Elastic constants C11, C12, and C44 of Fe and Fe–RE (La, Ce, Y) doping systems.

As shown in Figure 3, the doping of Ce, La, and Y reduces the elastic constants of Fe, and the ability to reduce is Ce < La < Y. In a cubic crystal system, C11 is equal to C33, representing the incompressibility of the material along the Z-axis and X-axis [28]. The doping of Ce, La, and Y decreases the C11 value of Fe from 260.07 to 253.03, 250.03, and 244.54 GPa, respectively. Therefore, the addition of Ce, La, and Y reduces the incompressibility of Fe along the Z-axis and X-axis. C44 reflects the shear rigidity of Fe on the (100) plane [29]. The values of C44 decreased with the doping of Ce, La, and Y, and decreased from 98.87 to 94.31, 92.31, and 89.98 GPa, respectively. Thus, the addition of Ce, La, and Y reduces the shear rigidity of Fe on the (100) plane.

3.2.2 Elastic modulus and Vickers hardness

The elastic moduli, including bulk modulus (B), shear modulus (G), and Young’s modulus (E), are essential parameters for describing the mechanical properties of materials. The elastic moduli can be calculated using the Voigt–Reuss–Hill approximation [30,31], based on the elastic constants. The calculation formulas are given in Eqs. (3)–(8):

(3) B H = 1 2 ( B V + B R ) ,

(4) B V = B R = 1 3 ( C 11 + 2 C 12 ) ,

(5) G H = 1 2 ( G V + G R ) ,

(6) G V = 1 5 ( C 11 − C 12 + 3 C 44 ) ,

(7) G R = 5 ( C 11 − C 12 ) C 44 4 C 44 + 3 ( C 11 − C 12 ) ,

(8) E = 9 BG 3 B + G ,

where B H, B V, and B R represent the Hill, Voigt, and Reuss approximations of the bulk modulus, respectively, and G H, G V, and G R represent the corresponding shear modulus approximations.

Candan et al. [32] derived an empirical formula for predicting Vickers hardness, as shown in Eq. (9):

(9) H V = 2 ( k 2 G ) 0.585 − 3 , ( k = G / B ) .

The calculated elastic moduli and Vickers hardness values are presented in Figure 4. As shown in Figure 4, doping with Ce, La, and Y reduces the elastic moduli and Vickers hardness of Fe system. This indicates that adding Ce, La, and Y decreases the incompressibility, shear resistance, stiffness, and Vickers hardness of Fe system. Moreover, it can be clearly observed that the B, E, G, and HV values of Fe, Fe–Ce, Fe–La, and Fe–Y systems gradually decrease. Specifically, Ce doping reduces the B, E, G, and HV values of Fe by 3.19, 5.41, 5.75, and 4.41%, respectively. La doping reduces these values by 4.10, 7.11, 7.56, and 7.44%, respectively. When doping Y, they reduce by 6.10, 9.40, 9.89, and 9.96%, respectively. It can be seen from the aforementioned analysis that doping Y has a great influence on reducing the strength of Fe, while the effect of Ce is relatively small.

Figure 4 Elastic moduli and Vickers hardness of Fe and Fe–RE (La, Ce, Y) systems.
Figure 4

Elastic moduli and Vickers hardness of Fe and Fe–RE (La, Ce, Y) systems.

3.2.3 Toughness and machinability

The toughness of a material can be characterized by Poisson’s ratio (σ) and Pugh’s ratio (B/G). When σ > 0.26 and B/G > 1.75, the material is considered ductile; otherwise, it is brittle. Moreover, the larger the values of σ and B/G, the higher the toughness of the material [33]. The calculation formula for σ is given by Eq. (10):

(10) σ = 3 B − 2 G 2 ( 3 B + G ) .

For metallic materials, machinability is an essential parameter in mechanical processing. Based on elastic constants, Sun et al. [34] proposed a machinability index (μ M), the higher μ M value, the better the processing performance. μ M can be calculated by Eq. (11):

(11) μ M = B C 44 .

Figure 5 presents the σ, B/G, and μ M values for Fe and Fe–RE (La, Ce, Y) systems. The σ value of Fe is 0.294 (>0.26), and the B/G value is 2.09 (>1.75), indicating a ductile behavior. After doping La, Ce, and Y, σ increases to 0.298 for Fe–Ce, 0.300 for Fe–La, and 0.301 for Fe–Y, and B/G rises to 2.15, 2.17, and 2.19, respectively. The results show that the Fe–Y system exhibits the highest toughness, followed by the Fe–La system and Fe–Ce system. In addition, doping Ce increases the μ M value from 1.78 to 1.81, doping La raises it to 1.83, and doping Y doping enhances it to 1.84, indicating that the La, Ce, and Y system effectively improves the machinability of Fe.

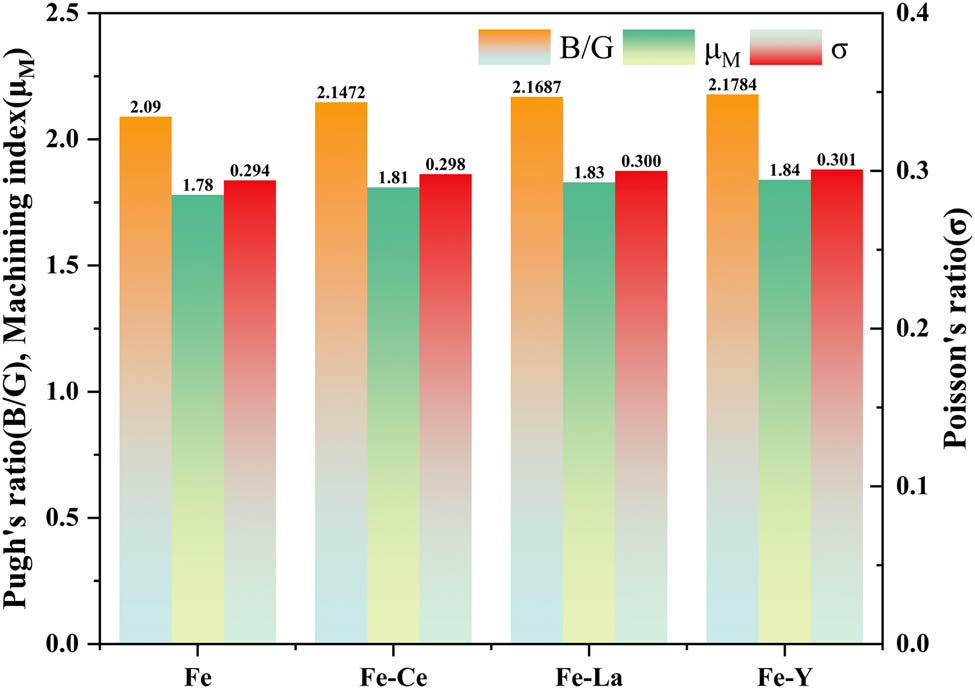
Figure 5 Pugh’s ratio (B/G), Poisson’s ratio (σ), and machinability index (μ M) for Fe and Fe–RE (La, Ce, Y) systems.
Figure 5

Pugh’s ratio (B/G), Poisson’s ratio (σ), and machinability index (μ M) for Fe and Fe–RE (La, Ce, Y) systems.

3.3 Electronic properties

3.3.1 Geometric structure

Figure 6 is the schematic diagram of the (001) plane for Fe and Fe–RE (La, Ce, Y) systems. As shown in Figure 6(a), the Fe–Fe bond length is 2.452 Å. After doping La, Ce, and Y, the surrounding Fe atoms are “pushed apart.” The Fe–Ce bond length increases to 2.547 Å (as shown in Figure 6(b)), which is smaller than the sum of the atomic radii of Fe and Ce (1.17 + 1.65 = 2.82 Å). The Fe–La and Fe–Y bond lengths increase to 2.600 and 2.602 Å, respectively, which are smaller than the sum of the atomic radii of Fe and La (1.17 + 1.69 = 2.86 Å) and Fe and Y (1.17 + 1.62 = 2.79 Å). From the perspective of lattice distortion, the smaller the degree of lattice distortion, the stronger the stability of the doping system [35]. After doping La, Ce, and Y, the lattice distortions are 0.406, 0.014, and 0.192%, respectively, suggesting that the stability of the doping systems follows the order Fe–Ce > Fe–Y > Fe–La, which is consistent with the calculation results of the solvation energy. In addition, from Figure 6, it can be observed that the bond lengths of Fe, Fe–Ce, Fe–La, and Fe–Y gradually increase (Fe–Fe < Fe–Ce < Fe–La < Fe–Y). Since shorter bond lengths correspond to stronger bond energies, it can be concluded that the Fe–Fe bond energy is the strongest, followed by Fe–Ce, Fe–La, and Fe–Y. The gradual decrease in metallic bond strength can explain the decreasing trend of the strength properties (such as incompressibility, stiffness, and Vickers hardness) of the system.

Figure 6 Structure schematic diagram of (001) plane of systems: (a) Fe, (b) Fe–Ce, (c) Fe–La, and (d) Fe–Y.
Figure 6

Structure schematic diagram of (001) plane of systems: (a) Fe, (b) Fe–Ce, (c) Fe–La, and (d) Fe–Y.

3.3.2 Density of states

The total density of states (TDOS) and partial density of states (PDOS) represent the interaction between atoms in the doping system. The TDOS and PDOS of Fe–RE (La, Ce, Y) systems are shown in Figure 7, where the dashed line represents the Fermi level (energy = 0). As shown in Figure 7, the PDOS near the Fermi level for all three doping systems is nonzero, indicating the presence of metallic bonds in the doping systems. From Figure 7(a), it can be clearly observed that the Fe–Ce system has two small bonding peaks in the energy range of −33.7 to −33.4 eV and −17.2 to −16.7 eV, contributed by Ce s and Ce p orbitals, respectively. Between −8.6 and +6.0 eV, the peaks are mainly a hybridization of Fe d, Ce d, and Ce f orbitals. From Figure 7(b), the Fe–La system has two small bonding peaks in the energy range of −41.1 to −40.4 eV and −21.5 to −20.8 eV, contributed by La s and La p orbitals, respectively. Between −8.5 and +6.0 eV, the peaks are mainly a hybridization of Fe d and La d orbitals. From Figure 7(c), the Fe–Y system has two small bonding peaks in the energy range of −31.3 to −30.6 eV and −15.7 to −15.2 eV, contributed by Y s and Y p orbitals, respectively. Between −8.5 and +6.0 eV, the peaks are mainly a hybridization of Fe d and Y d orbitals.

Figure 7 DOS diagram of Fe–RE (La, Ce, Y) systems: (a) Fe–Ce, (b) Fe–La, and (c) Fe–Y.
Figure 7

DOS diagram of Fe–RE (La, Ce, Y) systems: (a) Fe–Ce, (b) Fe–La, and (c) Fe–Y.

3.3.3 Differential charge density

The bonding characteristics and charge transfer between atoms in the doping systems can be analyzed using the differential charge density [36]. In the differential charge density diagram, red represents the charge accumulation, while blue represents the charge dissipation. The charge density diagram of Fe and the differential charge density diagrams of Fe–RE (La, Ce, Y) systems are shown in Figure 8, with the charge density range set from −0.02 to 0.02 e·Å−3.

Figure 8 Differential charge density of Fe and Fe–RE (La, Ce, Y) systems: (a) Fe, (b) Fe–Ce, (c) Fe–La, and (d) Fe–Y.
Figure 8

Differential charge density of Fe and Fe–RE (La, Ce, Y) systems: (a) Fe, (b) Fe–Ce, (c) Fe–La, and (d) Fe–Y.

From Figure 8(a), it can be clearly observed that the charge density distribution between Fe atoms in Fe system is relatively uniform, indicating that Fe atoms in the Fe system are connected by metallic bonds. As shown in Figure 8(b)–(d), in Fe–RE (La, Ce, Y) systems, a large amount of electron cloud is distributed between the Fe atoms and RE (La, Ce, Y) atoms. The charge density around the RE (La, Ce, Y) atoms appears blue, indicating electron loss, while the charge density around the Fe atoms appears red, indicating electron gain. This means that there is a charge transfer between RE (La, Ce, Y) atoms and Fe atoms. In addition, the electron cloud density between Fe–RE (La, Ce, Y) atoms is greater than that of Fe–Fe atoms, which is the main reason for the increased toughness and machinability of the doping systems. Moreover, from Figure 8(b) to (d), it can be clearly observed that the order of electron cloud density between Fe and RE is Fe–Y > Fe–La > Fe–Ce, which can be used to explain the reason why the toughness and machinability of the doping systems decrease in that order (Fe–Y > Fe–La > Fe–Ce).

3.3.4 Bader charge

The interaction between solute and solvent atoms in the doping system can be characterized by the charge transfer between atoms [37]. Bader charge can quantify the charge transfer between atoms. Bader charge values of the atoms in Fe–RE (La, Ce, Y) systems are listed in Table 2.

Table 2

Bader charge of RE (La, Ce, Y) atom, coordinated Fe atom in Fe–RE (La, Ce, Y) systems

Systems Ce La Y Fe Total
Fe–Ce 0.331 −0.036 1.387
Fe–La 0.455 −0.037 1.421
Fe–Y 1.084 −0.048 2.209

When Bader charge is positive, the atom loses electrons; conversely, when Bader charge is negative, the atom gains electrons. As shown in Table 2, Bader charge of Fe atoms in the doping systems is negative, indicating that Fe atoms gain electrons. However, Bader charges of Ce, La, and Y atoms are positive, the values of 0.331, 0.455, and 1.084, respectively, which indicates that Ce, La, and Y atoms lose electrons. Therefore, it can be inferred that there is an obvious interaction between Fe and RE (La, Ce, Y) atoms. In addition, the total charge transfer follows the order Fe–Y > Fe–La > Fe–Ce, which is consistent with the calculation results of the differential charge density.

4 Conclusions

  1. The calculation results of the solvation energy indicate that RE (La, Ce, Y) atoms can spontaneously solubilize into Fe, and the solid solution of Ce atoms in Fe is the easiest, followed by Y, and La is relatively difficult.

  2. After doping with RE (La, Ce, Y), the bulk modulus, shear modulus, Young’s modulus, and Vickers hardness of Fe system are reduced to varying degrees, while the Poisson’s ratio and machinability index are improved, i.e., the doping of RE (La, Ce, Y) reduces the strength of Fe system, but increases its toughness.

  3. The doping of RE (La, Ce, Y) reduces the metal bond strength of Fe system, which is the fundamental reason for the decrease of the incompressibility, shear strain resistance, stiffness, and Vickers hardness of the doping system. The strength properties of the doping systems are in the order of Fe–Ce > Fe–La > Fe–Y.

  4. In Fe–RE (La, Ce, Y) doping system, Fe atoms gain electrons and RE (La, Ce, Y) atoms lose electrons. The increase of electron cloud density in the doping system can be used to explain the improvement of toughness and machinability of the system. The toughness and machinability of the doping systems are in the order of Fe–Y > Fe–La > Fe–Ce.

Acknowledgments

The authors sincerely acknowledge the support of the College of Mining, Chemistry and Chemical Engineering at Hulunbuir University and School of Rare Earth Industry at Inner Mongolia University of Science and Technology for providing experimental equipment for this study.

  1. Funding information: This study received funding support from National Natural Science Foundation of China (No. 52204364), Scientific Research Special Project for First-Class Disciplines of Education Department of Inner Mongolia Autonomous Region (No. YLXKZX-NKD-011), Basic Scientific Research Business Expenses of Colleges and Universities of Inner Mongolia Autonomous Region (No. 2023QNJS011), and Keju Plan of Inner Mongolia University of Science and Technology (No. KJJH2023945).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results, and approved the final version of the manuscript. Chunying Bai, Guojun Bai, and Xiangjun Liu conceived and designed the experiments; Xiangjun Liu and Ting Wang analyzed the data; Chunying Bai wrote the original draft; Xiangjun Liu provided the guidance for writing. All authors participated in discussing the results, drafting the manuscript, and providing feedback during the review process.

  3. Conflict of interest: The authors state no conflict of interest.

  4. Data availability statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

[1] Wang, H., Y. P. Bao, M. Zhao, M. Wang, X. M. Yuan, and S. Gao. Effect of Ce on the cleanliness, microstructure and mechanical properties of high strength low alloy steel Q690E in industrial production process. International Journal of Minerals, Metallurgy, and Materials, Vol. 26, 2019, pp. 1371–1384.10.1007/s12613-019-1871-0Search in Google Scholar

[2] Oleksak, R. P., M. Detrois, P. D. Jablonski, K. A. Rozman, and Ö. N. Doğan. Influence of rare earth Ce additions on microstructure and mechanical properties of experimental pipeline steels. Steel Research International, Vol. 95, No. 3, 2024, id. 202300652.10.1002/srin.202300652Search in Google Scholar

[3] Liu, H., P. Fu, H. Liu, C. Sun, J. Gao, and D. Li. Carbides evolution and tensile property of 4Cr5MoSiV1 die steel with rare earth addition. Metals, Vol. 7, No. 10, 2017, id. 436.10.3390/met7100436Search in Google Scholar

[4] Zang, Q. Y., Y. F. Jin, T. Zhang, and Y. T. Yang. Effect of yttrium addition on microstructure, mechanical and corrosion properties of 20Cr13 martensitic stainless steel. Journal of Iron and Steel Research International, Vol. 27, 2020, pp. 4451–4460.10.1007/s42243-020-00377-1Search in Google Scholar

[5] Wang, J. F., L. Z. Wang, C. Y. Chen, X. Wang, and F. Zhao. Effect of rare earth on primary carbides in H13 die steel and their addition method: a review. Journal of Iron and Steel Research International, Vol. 31, 2024, pp. 531–551.10.1007/s42243-023-01149-3Search in Google Scholar

[6] Bao, D., G. Cheng, Y. Huang, T. Qiao, and W. Dai. Refinement of solidification structure of H13 steel by rare earth sulfide. Steel Research Internation, Vol. 93, 2022, id. 2100304.10.1002/srin.202100304Search in Google Scholar

[7] Yan, Z. R., W. Zheng, H. R. Zhang, G. Zhao, G. Q. Li, and J. Liu. Aggregation behavior of Ce-Mg-Mn-O-S composite inclusions in silicon-killed bearing steel and their evolution during heat treatment. Journal of Rare Earths, Vol. 43, No. 3, 2025, pp. 628–640.10.1016/j.jre.2024.07.016Search in Google Scholar

[8] Han, Y. L., L. Hao, J. Q. Wang, and W. Ke. Effect of rare earth addition on corrosion sensitivity of GCr15 bearing steel in marine environment. Materials Letters, Vol. 333, 2023, id. 133693.10.1016/j.matlet.2022.133693Search in Google Scholar

[9] Zhang, W. and C. Li. The Fe-La (iron-lanthanum) system. Journal of Phase Equilibria, Vol. 18, No. 3, 1997, pp. 301–304.10.1007/BF02647859Search in Google Scholar

[10] Dong, H., X. T. Lian, C. D. Hu, H. C. Lu, W. Peng, H. S. Zhao, and D. X. Xu. High performance steels: the scenario of theory and technology. Acta Metallurgica Sinica, Vol. 56, No. 4, 2020, pp. 558–582. (in Chinese).Search in Google Scholar

[11] Ji, J. Addition of the rare earth element to steels - An important approach to developing steels in the 21st century. Chinese Rare Earths, Vol. 22, No. 4, 2001, pp. 7–24. (in Chinese).Search in Google Scholar

[12] Lin, Q., W. Ye, and S. L. Li. Rare earth dissolved in solid solution of steel and its effect on micro structure. Journal of the Chinese Society of Rare Earths, Vol. 7, No. 2, 1989, pp. 54–58. (in Chinese).Search in Google Scholar

[13] Yue, L. J., L. M. Wang, and J. S. Han. Effects of rare earth on inclusions and corrosion resistance of 10PCuRE weathering steel. Journal of Rare Earths, Vol. 28, No. 6, 2010, pp. 952–956.10.1016/S1002-0721(09)60219-2Search in Google Scholar

[14] Liu, X. J., J. C. Yang, F. Zhang, and C. Q. Yang. Effect of solute Ce on mechanical properties and electronic structure of γ-Fe: Insights from a first-principles study. ISIJ International, Vol. 61, No. 10, 2021, pp. 2636–2643.Search in Google Scholar

[15] Liu, X. J., J. C. Yang, H. P. Ren, X. B. Jia, M. Y. Zhang, and C. Q. Yang. Effect of solute Ce, Mn, and Si on mechanical properties of silicon steel: insights from DFT calculations. Journal of Iron and Steel Research International, Vol. 31, No. 3, 2024, pp. 700–709.10.1007/s42243-023-01080-7Search in Google Scholar

[16] Yu, X. Mechanical properties and ductility improvement mechanisms of rare earth microalloyed high silicon electrical steel, University of Science and Technology, Beijing, 2020. (in Chinese).Search in Google Scholar

[17] Khalid, S., Y. Ma, X. Sun, G. Zhou, H. Wu, G. Lu, Z. Yang, J. Khan, R. Khenata, and A. Bouhemadou. Electronic and optical properties of Ti4GeX3 (X = S, Se and Te) compounds for optoelectronics applications: insights from DFT-computations. Journal of Materials Research and Technology, Vol. 9, No. 1, 2020, pp. 413–420.10.1016/j.jmrt.2019.10.070Search in Google Scholar

[18] Blöchl, P. E., O. Jepsen, and O. K. Andersen. Improved tetrahedron method for Brillouin-zone integrations. Physical Review B, Vol. 49, No. 23, 1994, pp. 16223–16233.10.1103/PhysRevB.49.16223Search in Google Scholar PubMed

[19] Britvin, S. N., A. N. Bogdanova, M. M. Boldyreva, and G. Y. Aksenova. Rudashevskyite, the Fe-dominant analogue of sphalerite, a new mineral: Description and crystal structure. American Mineralogist, Vol. 93, No. 5–6, 2008, pp. 902–909.10.2138/am.2008.2582Search in Google Scholar

[20] Liu, Y., Y. C. Huang, Z. B. Xiao, C. G. Yang, and X. W. Reng. First principles calculations of formation energies and elastic constants of inclusions α-Al2O3, MgO and AlN in aluminum alloy. International Journal of Modern Physics B, Vol. 30, No. 16, 2016, id. 1650085.10.1142/S0217979216500855Search in Google Scholar

[21] Sandberg, N., K. O.E. Henriksson, and J. Wallenius. Carbon impurity dissolution and migration in bcc Fe-Cr: first-principles calculations. Physical Review B: Condensed Matter, Vol. 78, No. 9, 2008, pp. 1884–1898.10.1103/PhysRevB.78.094110Search in Google Scholar

[22] Kittel, C. Introduction to solid state physics, Wiley, Hoboken, 1996.Search in Google Scholar

[23] Boulechfar, R., A. T. Khodja, Y. Khenioui, H. Meradji, S. Drablia, Z. Chouahda, S. Ghemid, S. H. Naqib, R. Khenata, and X. T. Wang. First-principle study of the structural, mechanical, electronic and thermodynamic properties of intermetallic compounds: Pd3M (M = Sc,Y). International Journal of Modern Physics, Vol. 33, 2019, id. 1950321.10.1142/S0217979219503211Search in Google Scholar

[24] Liu, X. J., J. C. Yang, F. Zhang, and C. Q. Yang. Effect of solute Ce on mechanical properties and electronic structure of γ-Fe: Insights from a first-principles study. ISIJ International, Vol. 61, No. 10, 2021, pp. 2636–2643.10.2355/isijinternational.ISIJINT-2021-139Search in Google Scholar

[25] Yang, Y., X. Z. Dai, X. R. Yang, S. H. Zhang, and D. Y. Li. First-principles analysis on the role of rare-earth doping in affecting nitrogen adsorption and diffusion at Fe surface towards clarified catalytic diffusion mechanism in nitriding. Acta Materialia, Vol. 196, 2020, pp. 347–354.10.1016/j.actamat.2020.06.020Search in Google Scholar

[26] Liu, X. J., C. Q. Yang, H. P. Ren, J. C. Yang, and Z. L. Jin. Mechanism study of effect of solute rare earth Ce on mechanical properties of α-Fe. Journal of Functional Materials, Vol. 53, No. 08, 2022, pp. 8024–8030. (in Chinese).Search in Google Scholar

[27] Feng, J., B. Xiao, R. Zhou, W. Pan, and D. R. Clarke. Anisotropic elastic and thermal properties of the double perovskite slab-rock salt layer Ln2SrAl2O7 (Ln = La, Nd, Sm, Eu, Gd or Dy) natural superlattice structure. Acta Materialia, Vol. 60, No. 8, 2012, pp. 3380–3392.10.1016/j.actamat.2012.03.004Search in Google Scholar

[28] Huang, B., Y. H. Duan, Y. Sun, M. J. Peng, and S. Chen. Electronic structures, mechanical and thermodynamic properties of cubic alkaline-earth hexaborides from first principles calculations. Journal of Alloys and Compounds, Vol. 635, 2015, pp. 213–224.10.1016/j.jallcom.2015.02.128Search in Google Scholar

[29] Zhou, W., L. J. Liu, B. L. Li, P. Wu, and Q. G. Song. Structural, elastic and electronic properties of inter metallics in the Pt-Sn system: A density functional investigation. Computational Materials Science, Vol. 46, No. 4, 2009, pp. 921–931.10.1016/j.commatsci.2009.04.044Search in Google Scholar

[30] Pugh, S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Vol. 45, 1954, pp. 823–843.10.1080/14786440808520496Search in Google Scholar

[31] Zhang, J., H. Z. Liu, S. K. Zhang, Q. Ren, and L. F. Zhang. Application of first-principles calculation method in study of inclusions in steel. China Metallurgy, Vol. 33, No. 08, 2023, pp. 6–16. (in Chinese).Search in Google Scholar

[32] Candan, A., S. Akbudak, Ş. Uğur, and G. Uğur. Theoretical research on structural, electronic, mechanical, lattice dynamical and thermodynamic properties of layered ternary nitrides Ti2AN (A =  Si, Ge and Sn). Journal of Alloys and Compounds, Vol. 771, 2019, pp. 664–673.10.1016/j.jallcom.2018.08.286Search in Google Scholar

[33] Ju, L. Y., S. P. Gu, and M. Tan. First principles calculation of non-metallic inclusions properties in steel. China Metallurgy, Vol. 34, No. 02, 2024, pp. 69–82. (in Chinese).Search in Google Scholar

[34] Sun, Z. M., D. Music, R. Ahuja, and J. M. Schneider. Theoretical investigation of the bonding and elastic properties of nanolayered ternary nitrides. Physical Review B, Vol. 71, No. 19, 2005, id. 193402.10.1103/PhysRevB.71.193402Search in Google Scholar

[35] Zheng, Y. B., F. Wang, T. T. Ai, and C. Li. Structural, elastic and electronic properties of B2-type modified by ternary additions FeAl-based intermetallics: First-principles study. Journal Alloys Compounds, Vol. 710, No. 5, 2017, pp. 581–588.10.1016/j.jallcom.2017.03.308Search in Google Scholar

[36] Yang, G. M., Z. C. Liang, and H. H. Huang. First-principles calculations of graphene adsorption of Li clusters. Acta Physica Sinica, Vol. 66, No. 05, 2017, pp. 298–306. (in Chinese).Search in Google Scholar

[37] G. Lim, K. B. Lee, and H. C. Ham. Effect of N-containing functional groups on CO2 adsorption of carbonaceous materials: A density functional theory approach. Journal of Physical Chemistry C, 120, 15, 2016, pp. 8087–8095.10.1021/acs.jpcc.5b12090Search in Google Scholar
Received: 2025-03-20
Revised: 2025-05-11
Accepted: 2025-05-12
Published Online: 2025-06-27

© 2025 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Endpoint carbon content and temperature prediction model in BOF steelmaking based on posterior probability and intra-cluster feature weight online dynamic feature selection
  3. Thermal conductivity of lunar regolith simulant using a thermal microscope
  4. Multiobjective optimization of EDM machining parameters of TIB2 ceramic materials using regression and gray relational analysis
  5. Research on the magnesium reduction process by integrated calcination in vacuum
  6. Microstructure stability and softening resistance of a novel Cr-Mo-V hot work die steel
  7. Effect of bonding temperature on tensile behaviors and toughening mechanism of W/(Ti/Ta/Ti) multilayer composites
  8. Exploring the selective enrichment of vanadium–titanium magnetite concentrate through metallization reduction roasting under the action of additives
  9. Effect of solid solution rare earth (La, Ce, Y) on the mechanical properties of α-Fe
  10. Impact of variable thermal conductivity on couple-stress Casson fluid flow through a microchannel with catalytic cubic reactions
  11. Effects of hydrothermal carbonization process parameters on phase composition and the microstructure of corn stalk hydrochars
  12. Wide temperature range protection performance of Zr–Ta–B–Si–C ceramic coating under cyclic oxidation and ablation environments
  13. Influence of laser power on mechanical and microstructural behavior of Nd: YAG laser welding of Incoloy alloy 800
  14. Aspects of thermal radiation for the second law analysis of magnetized Darcy–Forchheimer movement of Maxwell nanomaterials with Arrhenius energy effects
  15. Use of artificial neural network for optimization of irreversibility analysis in radiative Cross nanofluid flow past an inclined surface with convective boundary conditions
  16. The interface structure and mechanical properties of Ti/Al dissimilar metals friction stir lap welding
  17. Significance of micropores for the removal of hydrogen sulfide from oxygen-free gas streams by activated carbon
  18. Experimental and mechanistic studies of gradient pore polymer electrolyte fuel cells
  19. Microstructure and high-temperature oxidation behaviour of AISI 304L stainless steel welds produced by gas tungsten arc welding using the Ar–N2–H2 shielding gas
  20. Mathematical investigation of Fe3O4–Cu/blood hybrid nanofluid flow in stenotic arteries with magnetic and thermal interactions: Duality and stability analysis
  21. Topical Issue on Conference on Materials, Manufacturing Processes and Devices - Part II
  22. Effects of heat treatment on microstructure and properties of CrVNiAlCu high-entropy alloy
  23. Enhanced bioactivity and degradation behavior of zinc via micro-arc anodization for biomedical applications
  24. Study on the parameters optimization and the microstructure of spot welding joints of 304 stainless steel
  25. Research on rotating magnetic field–assisted HRFSW 6061-T6 thin plate
  26. Special Issue on A Deep Dive into Machining and Welding Advancements - Part II
  27. Microwave hybrid process-based fabrication of super duplex stainless steel joints using nickel and stainless steel filler materials
  28. Special Issue on Polymer and Composite Materials and Graphene and Novel Nanomaterials - Part II
  29. Low-temperature corrosion performance of laser cladded WB-Co coatings in acidic environment
  30. Special Issue for the conference AMEM2025
  31. Effect of thermal effect on lattice transformation and physical properties of white marble
https://doi.org/10.1515/htmp-2025-0081
Keywords for this article
first-principles calculation; rare earth; mechanical properties; geometric structure; electronic properties
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Endpoint carbon content and temperature prediction model in BOF steelmaking based on posterior probability and intra-cluster feature weight online dynamic feature selection
  3. Thermal conductivity of lunar regolith simulant using a thermal microscope
  4. Multiobjective optimization of EDM machining parameters of TIB2 ceramic materials using regression and gray relational analysis
  5. Research on the magnesium reduction process by integrated calcination in vacuum
  6. Microstructure stability and softening resistance of a novel Cr-Mo-V hot work die steel
  7. Effect of bonding temperature on tensile behaviors and toughening mechanism of W/(Ti/Ta/Ti) multilayer composites
  8. Exploring the selective enrichment of vanadium–titanium magnetite concentrate through metallization reduction roasting under the action of additives
  9. Effect of solid solution rare earth (La, Ce, Y) on the mechanical properties of α-Fe
  10. Impact of variable thermal conductivity on couple-stress Casson fluid flow through a microchannel with catalytic cubic reactions
  11. Effects of hydrothermal carbonization process parameters on phase composition and the microstructure of corn stalk hydrochars
  12. Wide temperature range protection performance of Zr–Ta–B–Si–C ceramic coating under cyclic oxidation and ablation environments
  13. Influence of laser power on mechanical and microstructural behavior of Nd: YAG laser welding of Incoloy alloy 800
  14. Aspects of thermal radiation for the second law analysis of magnetized Darcy–Forchheimer movement of Maxwell nanomaterials with Arrhenius energy effects
  15. Use of artificial neural network for optimization of irreversibility analysis in radiative Cross nanofluid flow past an inclined surface with convective boundary conditions
  16. The interface structure and mechanical properties of Ti/Al dissimilar metals friction stir lap welding
  17. Significance of micropores for the removal of hydrogen sulfide from oxygen-free gas streams by activated carbon
  18. Experimental and mechanistic studies of gradient pore polymer electrolyte fuel cells
  19. Microstructure and high-temperature oxidation behaviour of AISI 304L stainless steel welds produced by gas tungsten arc welding using the Ar–N2–H2 shielding gas
  20. Mathematical investigation of Fe3O4–Cu/blood hybrid nanofluid flow in stenotic arteries with magnetic and thermal interactions: Duality and stability analysis
  21. Topical Issue on Conference on Materials, Manufacturing Processes and Devices - Part II
  22. Effects of heat treatment on microstructure and properties of CrVNiAlCu high-entropy alloy
  23. Enhanced bioactivity and degradation behavior of zinc via micro-arc anodization for biomedical applications
  24. Study on the parameters optimization and the microstructure of spot welding joints of 304 stainless steel
  25. Research on rotating magnetic field–assisted HRFSW 6061-T6 thin plate
  26. Special Issue on A Deep Dive into Machining and Welding Advancements - Part II
  27. Microwave hybrid process-based fabrication of super duplex stainless steel joints using nickel and stainless steel filler materials
  28. Special Issue on Polymer and Composite Materials and Graphene and Novel Nanomaterials - Part II
  29. Low-temperature corrosion performance of laser cladded WB-Co coatings in acidic environment
  30. Special Issue for the conference AMEM2025
  31. Effect of thermal effect on lattice transformation and physical properties of white marble
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 22.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/htmp-2025-0081/html
Scroll to top button