Abstract: This paper studies uniqueness of equilibrium in symmetric  Bayesian games. It shows that if signals are highly but not perfectly dependent, then players play their risk-dominant actions for all but a vanishing set of signal realizations. In contrast to the literature on global games, noise is not assumed to be additive. Dependence is modeled using the theory of copulas.
Bayesian games. It shows that if signals are highly but not perfectly dependent, then players play their risk-dominant actions for all but a vanishing set of signal realizations. In contrast to the literature on global games, noise is not assumed to be additive. Dependence is modeled using the theory of copulas.
Appendix
Proof of Theorem 1
The game satisfies the assumptions of Van Zandt and Vives (2007). It follows that there are least and greatest equilibria and these are monotone. Since the game is symmetric these must be symmetric. For if, say 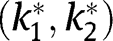 is the least equilibrium in cutoff strategies, then
is the least equilibrium in cutoff strategies, then  must also be the least equilibrium by symmetry. Hence,
must also be the least equilibrium by symmetry. Hence,  . To prove the result it is therefore sufficient to show that any symmetric equilibrium in cutoff strategies has the desired properties.
. To prove the result it is therefore sufficient to show that any symmetric equilibrium in cutoff strategies has the desired properties.
The interim payoff to player i at cutoff k from choosing action 1 rather than 0 is
![[30]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq30.png)
On the other hand, since 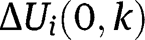 and
and 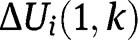 are strictly increasing and continuous, so uniformly continuous on
are strictly increasing and continuous, so uniformly continuous on  , for any
, for any 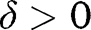 , one can find
, one can find 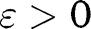 so that
so that
![[31]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq31.png)
From Assumption 4, an equilibrium cutoff k must belong to the compact interval 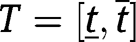 in the interior of
in the interior of  . Applying 2, proved below,
. Applying 2, proved below, 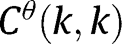 is uniformly close to
is uniformly close to 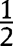 for all
for all 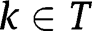 for large enough
for large enough 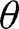 , so applying this to [31], one obtains that for all
, so applying this to [31], one obtains that for all 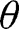 greater than some
greater than some  for
for 
![[32]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq32.png)
Hence, for 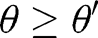 any symmetric equilibrium cutoff must belong to
any symmetric equilibrium cutoff must belong to 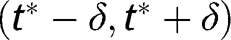 , which proves the result.
, which proves the result.
Proof of Lemma 2
The proof follows the lines indicated in the text. By letting u be its mid-point, any open interval in the interior of 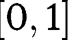 can be written as
can be written as  . It will be shown that for any such interval
. It will be shown that for any such interval
![[33]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq33.png)
Since 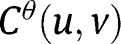 converges to
converges to 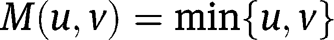 , the associated measures converge in distribution, so the measure under
, the associated measures converge in distribution, so the measure under  of any set whose boundary has measure zero under M converges to that under M (see Billingsley (1995, Theorem 29.1)). In particular, the areas of the rectangles
of any set whose boundary has measure zero under M converges to that under M (see Billingsley (1995, Theorem 29.1)). In particular, the areas of the rectangles 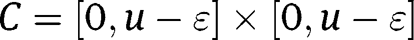 and
and 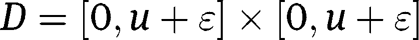 converge to their areas under M, since M is concentrated on the diagonal and is atomless. On the other hand,
converge to their areas under M, since M is concentrated on the diagonal and is atomless. On the other hand, 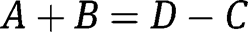 , so as argued in the text,
, so as argued in the text,  converges to
converges to 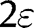 , which, together with symmetry, establishes [33].
, which, together with symmetry, establishes [33].
Suppose now that 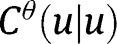 does not converge pointwise to
does not converge pointwise to 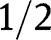 for some u in the interior of
for some u in the interior of 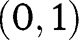 . If, say,
. If, say, 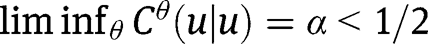 , then one can find a subsequence
, then one can find a subsequence 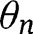 , with
, with 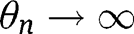 with
with 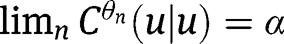 . In particular, given
. In particular, given 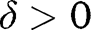 with
with 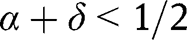 ,
, 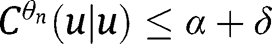 for all n greater than some N. Since
for all n greater than some N. Since 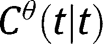 is increasing
is increasing 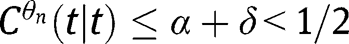 for all
for all  if
if  . This, however, contradicts [33]: consider an interval
. This, however, contradicts [33]: consider an interval 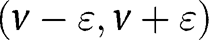 ,
, 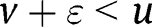 – from what has been shown on the left hand-side of [33] is bounded above by
– from what has been shown on the left hand-side of [33] is bounded above by 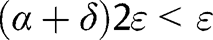 for all
for all  . Similarly, if
. Similarly, if 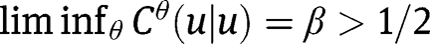 , then
, then 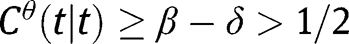 for all
for all  for all sufficiently large
for all sufficiently large 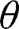 , which leads to a contradiction of [33]. It follows that
, which leads to a contradiction of [33]. It follows that 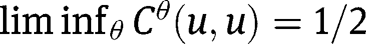 . A similar argument shows that
. A similar argument shows that 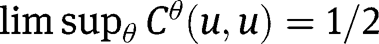 , so
, so 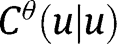 indeed converges to
indeed converges to 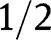 .
.
To prove uniform convergence, let 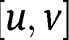 be a closed interval in the interior of
be a closed interval in the interior of  . Since
. Since  converges to
converges to 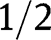 at u, given
at u, given 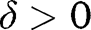 one can find
one can find 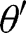 such that
such that  for all
for all 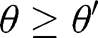 . Similarly, given
. Similarly, given 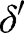 , one can find
, one can find 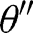 such that
such that  for all
for all  . Let
. Let 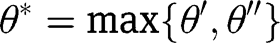 . Since
. Since 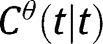 is increasing,
is increasing, 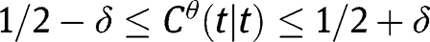 for all
for all  if
if  . This implies the stated uniform convergence.21
. This implies the stated uniform convergence.21
Proof of Theorem 2
The proof is almost identical to that of Theorem 1 with 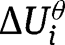 replacing
replacing 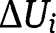 . Since
. Since  converges uniformly to
converges uniformly to 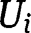 , given
, given 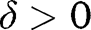 , one can find
, one can find  such that [31] holds for
such that [31] holds for 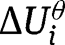 for all large enough
for all large enough 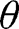 . Similarly, since Assumption 4 holds for
. Similarly, since Assumption 4 holds for 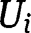 , one can find a compact interval T in the interior of
, one can find a compact interval T in the interior of 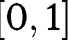 such that for all large enough
such that for all large enough 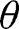 , equilibrium cutoffs must belong to T. The remainder of the proof is as before with
, equilibrium cutoffs must belong to T. The remainder of the proof is as before with 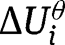 replacing
replacing 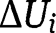 .
.
Proof of Theorem 3
By Assumption 13, interim payoffs can be uniformly approximated by [30], replacing  by
by 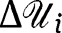 . The proof then proceeds as in the proof of Theorem 1 replacing
. The proof then proceeds as in the proof of Theorem 1 replacing 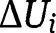 by
by 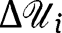 .
.
Proof of Lemma 4
![[34]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq34.png)
Now
![[35]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq35.png)
as 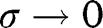 since
since  for any x,
for any x, 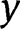 , and
, and  as F is a joint distribution function.22 In the case
as F is a joint distribution function.22 In the case 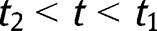 (or mutatis mutandis with inequalities reversed) note that
(or mutatis mutandis with inequalities reversed) note that 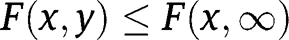 and
and  as
as 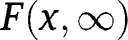 is the marginal distribution of the first component.
is the marginal distribution of the first component.
So, by the dominated convergence theorem
![[36]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq36.png)
The last equality holds since G is increasing.
Now
![[37]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq37.png)
So, by a similar argument as above
![[38]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq38.png)
Now, G is strictly increasing on its support, as g is strictly positive, and so it follows that  is continuous. Hence, it follows from van der Vaart (1998, 305, Lemma 21.2) that
is continuous. Hence, it follows from van der Vaart (1998, 305, Lemma 21.2) that
![[39]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq39.png)
where 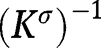 is defined as in [5]. Since from [4]
is defined as in [5]. Since from [4]
![[40]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq40.png)
![[41]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq41.png)
as was to be shown.
Proof of Lemma 5
Parts (a) and (b) were proven in the text. For part (c), note from the discussion in Sections 4 and 5 that part (iii) of Assumption 5 is equivalent to the assertion that the distribution of 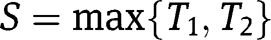 dominates that of
dominates that of 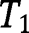 and
and 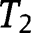 in the likelihood ratio order.
in the likelihood ratio order.
Now
![[42]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq42.png)
under [25].
The density function of 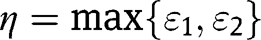 is
is
![[43]](/document/doi/10.1515/bejte-2012-0012/asset/graphic/bejte-2012-0012_eq43.png)
where h and H are the density and distribution functions of the 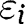 (assumed identically distributed).
(assumed identically distributed). 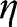 clearly dominates each
clearly dominates each 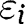 in the likelihood ratio order.
in the likelihood ratio order.
According to Theorem 2.1(d) of Keilson and Sumita (1982), if 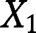 and
and 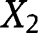 are two random variables such that
are two random variables such that 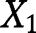 dominates
dominates 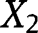 in the likelihood ratio order and
in the likelihood ratio order and 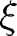 has a log-concave density function and is independent of
has a log-concave density function and is independent of 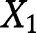 and
and 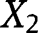 , then
, then 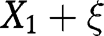 dominates
dominates 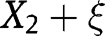 in the likelihood ratio order. Taking
in the likelihood ratio order. Taking 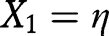 and
and 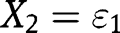 ,
, 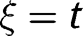 proves the result since
proves the result since 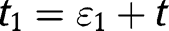 and from [42],
and from [42], 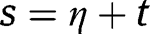 .
.
References
Athey, S.2001. “Single Crossing Properties and the Existence of Pure Strategy Equilibria in Games of Incomplete Information.”Econometrica69:861–89.10.1111/1468-0262.00223Search in Google Scholar
Billingsley, P.1995. Probability and Measure. New York: John Wiley and Sons, 3rd edition.Search in Google Scholar
Carlsson, H., and E.van Damme. 1993. “Global Games and Equilibrium Selection.”Econometrica61:989–1018.10.2307/2951491Search in Google Scholar
Doob, J.1994. Measure Theory. New York: Springer.10.1007/978-1-4612-0877-8Search in Google Scholar
Frankel, D., S.Morris, and A.Pauzner. 2003: “Equilibrium Selection in Global Games with Strategic Complementarities.”Journal of Economic Theory108:1–44.10.1016/S0022-0531(02)00018-2Search in Google Scholar
Joe, H.1997. Multivariate Models and Dependence Concepts. London: Chapman and Hall.10.1201/9780367803896Search in Google Scholar
Keilson, J., and U.Sumita. 1982. “Uniform Stochastic Ordering and Related Inequalities.”The Canadian Journal of Statistics10:181–98.10.2307/3556181Search in Google Scholar
Krishna, V.2002. Auction Theory. San Diego: Academic Press.Search in Google Scholar
Mathevet, L.2010. “A Contraction Principle for Finite Global Games.”Economic Theory42:539–63.10.1007/s00199-008-0411-3Search in Google Scholar
Mathevet, L.2012. “Beliefs and Rationalizablity in Games with Complementarities.”Technical Report, University of Texas at Austin.Search in Google Scholar
Milgrom, P., and J.Roberts. 1990. “Rationalizabilty, Learning and Equilibrium in Games with Strategic Complementarities.”Econometrica58:1255–77.10.2307/2938316Search in Google Scholar
Milgrom, P., and R.Weber. 1982. “A Theory of Auctions and Competitive Bidding.”Econometrica50:1089–122.10.2307/1911865Search in Google Scholar
Morris, S., and H.Shin. 2003. “Global Games: Theory and Applications.” In Advances in Economics and Econometrics: Theory and Applications, Proceedingsof the Eighth World Congress of the Econometric Society, edited by M.Dewatripont, L.Hansen, and S.Turnovsky, 56–114. Cambridge: Cambridge University Press.10.1017/CBO9780511610240.004Search in Google Scholar
Morris, S., and H.Shin. 2006. “Heterogeneity and Uniqueness in Interaction games.” In The Economy as a Complex Evolving System, III, edited by L.Blume and S.Durlauf, 207–42. Oxford: Oxford University Press.10.1093/acprof:oso/9780195162592.003.0009Search in Google Scholar
Müller, A., and M.Scarsini. 2005. “Archimedean copulae and Positive Dependence.”Journal of Multivariate Analysis93:434–45.10.1016/j.jmva.2004.04.003Search in Google Scholar
Müller, A., and D.Stoyan. 2002. Comparison Methods for Stochastic Models and Risks. Chichester: John Wiley.Search in Google Scholar
Nelsen, R.2006. An Introduction to Copulas. New York: Springer, 2nd edition.Search in Google Scholar
Nelsen, R., J.Quesada-Molina, J.Rodríguez-Lallena, and M.Úbeda-Flores. 2008. “On the Construction of Copulas and Quasi-Copulas with Given Diagonal Sections.”Insurance: Mathematics and Economics42:473–8.10.1016/j.insmatheco.2006.11.011Search in Google Scholar
Patton, A.2009. “Copula Models for Financial Time Series.” In Handbook of Financial Times Series, edited by T.Andersen, R.Davis, J.-P.Kreiss, and T.Mikosch. 767–86. Berlin: Springer.10.1007/978-3-540-71297-8_34Search in Google Scholar
van der Vaart, A.1998. Asymptotic Statistics. Cambridge: Cambridge University Press.10.1017/CBO9780511802256Search in Google Scholar
Van Zandt, T., and X.Vives. 2007. “Monotone Equilibria in Bayesian Games of Strategic Complementarities.”Journal of Economic Theory134:339–60.10.1016/j.jet.2006.02.009Search in Google Scholar
- 1
The body of their paper considers common values but, as they note, their arguments extend to the case of private values, as in this example.
- 2
This is shown formally in Section 7.2.
- 3
One can of course always write
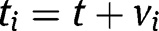 , where
, where  , but in general the
, but in general the 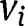 will not be independent of t nor will
will not be independent of t nor will 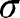 enter multiplying
enter multiplying 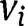 .
. - 4
See Nelsen (2006, Section 2.3) for a proof.
- 5
see for example Billingsley (1995, Exercise 14.3).
- 6
See for example Joe (1997, Exercise 2.10, 54).
- 7
See for example, Müller and Stoyan (2002, Theorem 3.8.2). Note, however, that this equivalence does not hold in more than two dimensions and that the definition of the concordance order needs to be adapted in higher dimensions – see Müller and Stoyan (2002, Chapter 3). This definition of the supermodular ordering is analogous to that of first-order stochastic dominance, which imposes the condition that u be increasing rather than supermodular.
- 8
See for example Joe (1997, 140–42) for these facts. Note that he refers to the Clayton copula as the Kimeldorf–Sampson copula.
- 9
See for example Morris and Shin (2003).
- 10
See Müller and Scarsini (2005, Theorem 2.8(d)) and note that they define an Archimedean copula to have form the
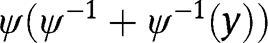 .
. - 11
Indeed, as Nelsen et al. (2008, 480) note it holds for all but one copula (4.2.18) in the table of 22 Archimedean copulas on pp. 116–118 of Nelsen (2006).
- 12
See, for example, Müller and Stoyan (2002, 12, Theorem 1.4.4) for a proof that the likelihood ratio order is stronger than first-order stochastic dominance.
- 13
In the language of functional analysis, without it, the argument shows that
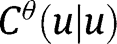 converges weakly to the constant function
converges weakly to the constant function 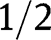 , that is
, that is 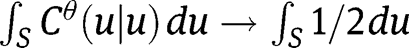 for every interval, and by an approximation argument any set S, in the interior of
for every interval, and by an approximation argument any set S, in the interior of 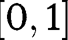 . In general, weak convergence does not imply pointwise convergence.
. In general, weak convergence does not imply pointwise convergence. - 14
Convexity is not however invariant to monotone transformations of the dependent variables, so
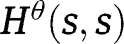 need not be convex in s even if
need not be convex in s even if 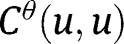 is convex in u.
is convex in u. - 15
See for example Billingsley (1995, Exercise 14.8).
- 16
See for example Appendix D of Krishna (2002).
- 17
This is true even if the signals are transformed to have uniform marginals.
- 18
See Milgrom and Weber (1982, Theorem 3).
- 19
Note that since
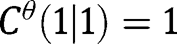 and, if the joint distribution has a density,
and, if the joint distribution has a density, 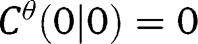 ,
, 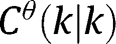 cannot be decreasing everywhere but it is enough that it be outside the dominance regions, since equilibrium cutoffs must lie outside them.
cannot be decreasing everywhere but it is enough that it be outside the dominance regions, since equilibrium cutoffs must lie outside them. - 20
It is easy to see that the argument in the proof of 2 would also go through if
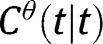 were decreasing, although in this case, equilibrium is unique for finite
were decreasing, although in this case, equilibrium is unique for finite 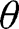 by the argument above. As noted in Section 5, the assumption of monotonicity of
by the argument above. As noted in Section 5, the assumption of monotonicity of 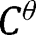 may not be necessary.
may not be necessary. - 21
The result also follows from the standard result that if a sequence of monotonic functions converges uniformly to a monotonic function F at each point of continuity of F, then convergence is uniform on each compact interval of continuity of F (see for example Doob (1994, 166) but the direct proof is easy, so is given.
- 22
See for example Billingsley (1995, 260).
©2013 by Walter de Gruyter Berlin / Boston
Articles in the same Issue
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
Articles in the same Issue
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations


