Higher-Order Rogue Waves for a Fifth-Order Dispersive Nonlinear Schrödinger Equation in an Optical Fibre

1 Introduction

Rogue waves, also known as the freak waves or monster waves, have been used to describe the isolated and large waves with higher amplitudes than the average wave crests around in the ocean and have also been seen in the Bose–Einstein condensates, plasmas, and optical fibres [1–6]. A model for the rogue waves in optical fibre communication is the ‘self-focusing’ nonlinear Schrödinger (NLS) equation [7, 8],

(1)iψx + 12ψtt + ψ|ψ|2 = 0, (1)

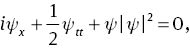
where i²=−1, x is the propagation variable, t is the transverse variable (“time” in a moving frame) and ψ=ψ(x, t) is the complex envelope of the modulated wave, whose absolution value describes the intensity of the wave [6–8]. However, (1) is an approximation to the different physical systems [6, 7, 9]. For the better approximations, higher-order effects should be considered via the inclusion of additional terms [6, 9–12]. If the self-steeping, self-frequency-shift, supercontinuum-generation, pulse-deforming phenomena and the fourth-order dispersion are considered in an optical fibre, the cubic and quartic terms need to be incorporated in (1) [6, 9, 11–16]. Furthermore, when the ultrashort optical pulses, up to the attosecond duration, propagate in a high-intensity optical field, the quintic terms are required to be taken into account [9, 13–15, 17].

Motivated by the reasons mentioned, in this article, we will consider a fifth-order dispersive NLS equation [9],

(2)iψx + 12ψtt + ψ|ψ|2 − f0ψ − if1ψt − iαH[ψ(x, t)]+γP[ψ(x, t)] − iδQ[ψ(x, t)] = 0, (2)

with

(3)H[ψ(x, t)] = ψttt + 6|ψ|2ψt,P[ψ(x, t)] = ψtttt + 8|ψ|2ψtt      + 6ψ|ψ|4 + 4ψ|ψt|2 + 6ψt2ψ* + 2ψ2ψtt*,Q[ψ(x, t)] = ψttttt + 10|ψ|2ψttt      + 10(ψ|ψt|2)t + 20ψ*ψtψtt + 30|ψ|4ψt, (3)

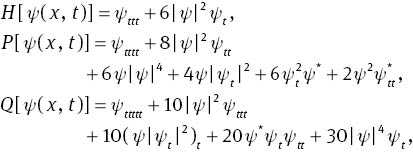
which describes the propagation of ultrashort optical pulses, up to attosecond duration, in an optical fibre, where H is the third-order Hirota operator, P is the fourth-order Lakshmanan–Porsezian–Daniel (LPD) operator, Q is the quintic operator, f₀ represents the phase parameter in the fibre, f₁ represents the group velocity of the modulated wave, α, γ, and δ are all the real coefficients of the cubic, quartic, and quintic terms, respectively [9, 13]. Especially, α is related to the supercontinuum-generation and pulse-deforming phenomena, γ is related to the fourth-order dispersion, and δ is related to the fifth-order dispersion, which should be considered when we investigate the ultrashort optical pulses [6, 9, 11–16]. For (2), Lax pair, Darboux transformation (DT) and multi-solition solutions have been obtained [9]. Special cases of (2) have been seen

1. when f₀=0, f₁=0, α=0, γ=0, and δ=0, (2) is degenerated into (1), the rogue wave solutions for (1) have been derived via the modified DT and generalised DT [8, 18]. Multi-soliton solutions and structures for (1) have been presented [19, 20];

2. when f₀=0, f₁=0, γ=0, and δ=0, (2) reduces to the Hirota equation for the third-order dispersion, self-steepening, and time-delay correction to the cubic nonlinearity in ocean waves [21, 22]. Painlevé analysis and higher-order rogue wave solutions for the Hirota equation based on the parameterized DT have been derived [23, 24]. Multi-soliton solutions for the Hirota equation have been obtained via the direct method [21]. Multi-solitons, breathers, and the first-order rogue waves for the Hirota equation have been derived via the DT and the limiting processes [25];

3. when f₀=0, f₁=0, α=0, and δ=0, (2) is simplified as the LPD equation for the ultrashort optical-pulse propagation in a long-distance, high-speed optical fibre transmission system [6, 9, 26, 27], and nonlinear spin excitations in the one-dimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole–dipole interaction [27, 28]. The first- and second-order rouge wave solutions for the LPD equation have been obtained via the modified DT [29]. The n^th-order rogue wave solutions for the LPD equation in the determinant form have been presented [6].

Moreover, some effects of the higher-order terms on the first-order rogue waves have been investigated [30–34]. Rational W-shaped solitons on a continuous-wave background for the Sasa–Satsuma equation have been obtained, and the stability properties of solutions have been investigated via the DT [30], with the relevant issues in [31, 32]. Solutions on the non-zero background for the Sasa–Satsuma equation have been derived, such as the breathers and rogue wave solutions, and the condition to form the rogue wave has been obtained via the limiting processes [33]. Properties of the rational solutions for the integrable Kundu–Eckhaus equation have been discussed [34].

However, to our knowledge, for (2), neither the generalised DT and rogue wave solutions nor structures and interaction of rogue waves have been discussed, which is the aim of our article. In Section 2, based on the Lax pair and DT in [9], generalised DT are constructed via the Taylor expansion and limiting processes. In Section 3, rogue wave solutions for (2) are derived. In Section 4, higher-order rogue wave structures and interaction are studied. In Section 5, our conclusions are given.

2 Generalised DT for Equation (2)

In this section, we present the generalised DT for (2). With the 2×2 Ablowitz–Kaup–Newell–Segur (AKNS) scheme, the Lax pair associated with (2) has been given as [9]

(4)Φt = UΦ,Φx = VΦ, (4)

where Φ=(ϕ₁, ϕ₂)^T is a vector function, ϕ₁ and ϕ₂ are both the functions of x and t, the superscript T signifies the vector transpose, and the 2×2 matrices U and V have the forms

(5a)U = i(λψ*ψ−λ), (5a)

(5b)V = ∑j = 05λjVj, (5b)

with

Vj = i(AjBj*Bj−Aj),A5 = 16δ,B5 = 0,A4 = −8γ,B4 = 16δψ,A3 = −4α − 8δ|ψ|2,B3 = −8γψ + 8iδψt,A2 = 1 + 4γ|ψ|2 + 4iδ(ψt*ψ − ψtψ*),B2 = −4αψ − 8δ|ψ|2ψ − 4iγψt − 4δψtt,A1 = f1 + 2α|ψ|2 + 6δ|ψ|4 − 2iγ(ψt*ψ − ψtψ*) + 2δ(ψtt*ψ − |ψt|2 + ψttψ*),B1 = ψ + 4γ|ψ|2ψ − 2iαψt − 12iδ|ψ|2ψt + 2γψtt − 2iδψttt,A0 = 12f0 − 12|ψ|2 − 3γ|ψ|4 − iα(ψt*ψ − ψtψ*) − γ(ψtt*ψ − |ψt|2 + ψttψ*) − iδ(ψttt*ψ − ψtt*ψt + ψttψt* − ψtttψ*) − 6iδ(ψt*ψ − ψtψ*)|ψ|2,B0 = f1ψ + 2α|ψ|2ψ + 6δ|ψ|4ψ + i12ψt + 6iγ|ψ|2ψt + αψtt + 2δψtt*ψ2 + 4δ|ψt|2ψ + 6δ(ψt)2ψ* + 8δψtt|ψ|2 + iγψttt + δψtttt,

where λ is a complex parameter independent of x and t and the compatibility condition U_x−V_t + [U, V] =0 returns to (2).

By virtue of Lax pair (4), the DT matrix T[1] can be derived as [9]

(6)T[1] = [λ00λ] − [ϕ1[1]−ϕ2*[1]ϕ2[1]ϕ1*[1]][λ100λ1*][ϕ1[1]−ϕ2*[1]ϕ2[1]ϕ1*[1]]−1, (6)

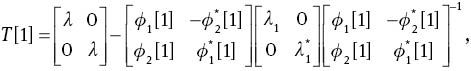
where the eigenfunction (ϕ₁[1], ϕ₂[1])^T is a solution for Lax pair (4) at λ=λ₁, ϕ₁[1], and ϕ₂[1] are the functions of x and t and λ is a complex parameter independent of x and t, the superscript ‘−1’ is the inverse matrix. The sign [k] (k=1, 2, 3, …) indicates that the matrice/function is engendered from the k^th order DT.

With DT matrix (6), the generalised DT can be derived [8]. We assume that

(7)Γ˜ = Γ(λ1 + ε) (7)

where Γ˜ is a solution for Lax pair (4) at λ=λ₁ + ε and ψ = ψ˜[0], where ψ˜ is a solution for (2) whereas ε is the parameter independent of x and t. Expanding Γ˜ at λ=λ₁,

(8)Γ˜ = Γ[0] + Γ[1]ε + Γ[2]ε2 + …, (8)

where Γ[k] = limε → 01k!∂k∂λkΓ˜(λ)|λ = λ1 (k=0, 1, 2, …), Γ[0] is a solution for Lax pair (4) at ψ = ψ˜[0] and λ=λ₁. Furthermore, the first-order generalised DT matrix T[1] can be derived as

(9)T[1] = [λ00λ] − [φ1[1]−φ2*[1]φ2[1]φ1*[1]][λ100λ1*][φ1[1]−φ2*[1]φ2[1]φ1*[1]]−1 , (9)

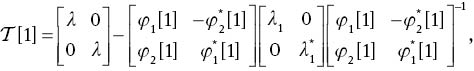
where the eigenfunction (φ₁[1], φ₂[1])^T=Γ[0], while φ₁[1] and φ₂[1] are both the functions of x and t. Therefore, the first-order solutions ψ˜[1] can be obtained as

(10)ψ˜[1] = ψ˜[0] + 2(λ1* − λ1)φ2[1]φ1*[1]|φ1[1]|2 + |φ2[1]|2. (10)

Through the limiting process on first order of the DT, we derive

(11)limϵ → 0(T[1]|λ = λ1 + ϵ)Γ˜ϵ = limϵ → 0(ϵ + T[1]|λ = λ1)[Γ[0] + Γ[1]ϵ + o(ϵ)]ε=Γ[0] + T[1]|λ = λ1Γ[1] . (11)

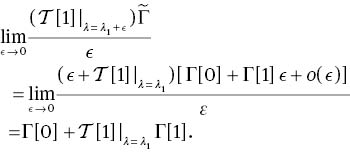
Thus, we obtain a new eigenfunction (φ₁[2], φ₂[2])^T, which is a solution for Lax pair (4) at ψ = ψ˜[1] and λ=λ₁, whereas φ₁[2] and φ₂[2] are the functions of x and t. The eigenfunction (φ₁[2], φ₂[2])^T can be used for iterating to obtain the second-order generalised DT matrix and the solutions for (2) at λ=λ₁. Thus, we can derive the second-order generalised DT matrix T [2] as

(12)T[2] = [λ00λ] − [φ1[2]−φ2*[2]φ2[2]φ1*[2]][λ100λ1*][φ1[2]−φ2*[2]φ2[2]φ1*[2]]−1 . (12)

Then, the second-order solutions ψ˜[2] can be obtained as

(13)ψ˜[2] = ψ˜[1] + 2(λ1* − λ1)φ2[2]φ1*[2]|φ1[2]|2 + |φ2[2]|2. (13)

Similarly, the limiting process on the second order of the DT can be derived as

(14)limϵ → 0(T1[1]|λ = λ1 + ϵ)(T[2]|λ = λ1 + ϵ)Γ˜ϵ2=Γ[0]+(T[1]|λ = λ1 + T[2]|λ = λ1)Γ[1] +T[2]|λ = λ1T[1]|λ = λ1Γ[2].   (14)

Then, we get the eigenfunction (φ₁[3], φ₂[3])^T, which is a solution for Lax pair (4) at ψ = ψ˜[2] and λ=λ₁, whereas φ₁[3] and φ₂[3] are the functions of x and t. Meanwhile, we can derive the third-order solutions for (2) as

(15)ψ˜[3] = ψ˜[2] + 2(λ1* − λ1)φ2[3]φ1*[3]|φ1[3]|2 + |φ2[3]|2 . (15)

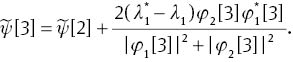
By the same token, the fourth-, even n^th-order generalised DT for the (2) could be obtained.

3 Rogue Wave Solutions for Equation (2)

In this section, we seek rouge wave solutions for (2). Once the seed solution, ψ˜[0], is chosen as a periodic plane wave solution, rogue wave solutions can be obtained [6, 8], ψ˜[0] for (2) could be chosen as

(16)ψ˜[0] = ei(1+6γ−f0)x. (16)

Furthermore, we get the eigenfunction Γ˜ for Lax pair (4) at λ=ih as

(17)Γ˜(h) = ((c1eA + c2e−A)e−i(1 + 6γ − f0)x/2i(c3eA + c4e−A)ei(1 + 6γ − f0)x/2), (17)

with

(18)A = μ[t + ωx + S(ε)] , μ = −1 − λ2,c3 = c1(iλ + μ), c4 = c2(iλ − μ),ω = 2α + 6δ + λ + 4γλ − 4αλ2 − 8δλ2 − 8γλ3 + 16δλ4 + f1, (18)

where c₁ and c₂ are both the complex constants, S(ϵ) = ∑k = 0n − 1(τk + iTk)ϵ2k is a separating function which consists of 2n real parameters, τ₀, T₀, ..., τ_n−1, T_n−1, N indicates the number of times for the n^th order generalised DT.

For simplification, we set

(19)c1 = h − h2 − 1h2 − 1,c2 = −h + h2 − 1h2 − 1. (19)

Then, we take h=1 + ϵ² and expand Γ˜(ϵ) at λ=i

(20)Γ˜ = Γ[0] + Γ[1]ϵ2 + Γ[2]ϵ4 + …, (20)

where ϵ is a parameter independent of x and t. We exhibit the expression of Γ[0] as

(21)Γ[0] = (e−12 ix(1 + 6γ − f0)(−1 + 2ix + 2t + 12xα + 24ixγ + 60xδ + 2xf1 + 2τ0 + 2iT0)−ie12 ix(1 + 6γ − f0)(1 + 2ix + 2t + 12xα + 24ixγ + 60xδ + 2xf1 + 2τ0 + 2iT0)). (21)

By virtue of (10), we can obtain the first-order rogue wave solutions, ψ˜[1], as

(22)ψ˜[1]= − 4eix(1 + 6γ − f0)(−54 − 2ix + 2t + 12xα − 24ixγ + 60xδ + 2xf1 + 2τ0 − 2iT0)× (1 + 2ix + 2t + 12xα + 24ixγ + 60xδ + 2xf1 + 2τ0 + 2iT0)/{[(−1 − 2ix + 2t + 12xα − 24ixγ + 60xδ + 2xf1 + 2τ0 − 2iT0)× (−1 + 2ix + 2t + 12xα + 24ixγ + 60xδ + 2xf1 + 2τ0 + 2iT0)]+ [(1−2ix + 2t + 12xα − 24ixγ + 60xδ + 2xf1 + 2τ0 − 2iT0)× (1 + 2ix + 2t + 12xα + 24ixγ + 60xδ + 2xf1 + 2τ0 + 2iT0)]}. (22)

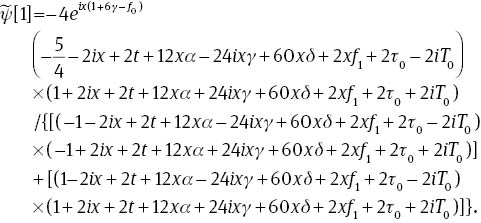
The first-order rogue wave solutions are W-shaped in the spatial-temporal pattern, which are similar to the solutions for the Sasa–Satsuma equation [25, 30–34]. It’s noted that, taking S(ϵ)=0, we can calculate that the maximum value of the amplitude, |ψ˜[1]|, is equal to 3 at (x=0, t=0). The maximum values and positions remain the same about the first-order rogue wave, no matter how the parameters in (2) are chosen, which is different from the situations in Refs. [25, 30–34]. In this article, we can derive the higher-order rogue wave solutions via the generalised DT to investigate the effects of the higher-order terms, which have not been discussed in Refs. [25, 30–34].

We can derive the first-order generalised DT matrix, T[1], with (9). Then, we get the eigenfunction, (φ₁[2], φ₂[2])^T, with (11). Finally, we obtain the second-order solutions, ψ˜[2], with (13). By the same token, we can obtain the third-order rogue wave solutions, ψ˜[3], for (2) with (12), (14), and (15).

The second-order rogue waves solutions, ψ˜[2], for (2) are given in Supplementary Material. Explicit expressions for the third-order rogue waves is complicated due to its written length. Therefore, the third-order rogue waves solutions, ψ˜[3], for (2) are given in Supplementary Material with f₀=0, f₁=0, α=0, γ=0, τ₀=0, T₀=0, τ₁=0, τ₂=0.

4 Higher-Order Rogue Wave Structures and Interaction for Equation (2)

We investigate the properties and interaction of the second- and third-order rogue waves by means of illustrations.

Figure 1 shows that the group velocity, f₁, affects the velocity of the rogue wave with f₁=−1, 0, and 1, respectively. With f₁ increasing, the rogue wave moves counterclockwise in the spatial-temporal pattern, as shown in Figure 1.

Figure 1:

The second-order rogue waves via the solutions, ψ˜[2], in Supplementary Material with parameters: f₀=0, α=0, γ=0, τ₀=0, T₀=0, τ₁=0, T₁=0, δ=0, (a) f₁=−1; (b) f₁=0; (c) f₁=1.

Figure 2 illustrates the second-order rogue waves when the coefficient of third-order term, α=−0.5, 0, and 0.5. With α increasing, the rogue wave moves counterclockwise in the spatial-temporal pattern around the point (x=0, t=0), which is similar to the effects caused by f₁. With the effects inducing by the cubic terms, the time of appearance for the rogue wave elongates, while the distance does a little. In Figure 3, we can observe that the variation of the coefficient of the fourth-order term, γ, does not change the shape of the rogue wave in the spatial-temporal pattern. However, with the increase of the absolute value of γ, elongation firstly and compression on the direction of the spatiality, x, occurs in Figure 3, which means that the distance of the appearance of the rogue wave is elongating firstly, next, with γ continued growth, the distance is shrinking, while the time elongates along with the maximum value of the rogue wave invariant.

Figure 2:

The same as Figure 1 except that f₁=0 (a) α=−0.5; (b) α=0; (c) α=0.5.

Figure 3:

The same as Figure 1 except that f₁=0 (a) γ=0; (b) γ=−0.1; (c) γ=−0.3.

Next, discussion focuses on the coefficient of the quintic terms, δ. Figure 4 shows that the second-order rogue waves with δ=0, −0.03, and −0.06, respectively. In Figure 4a, the symmetric rogue wave for the NLS equation is shown. Positions of the rogue wave troughs and crests localise on the x=0 axis. In Figure 4b and c, the rogue waves become asymmetric and turn counterclockwise in the spatial-temporal pattern, if a larger δ is taken, because δ changes the velocity of the rouge wave. If α=δ, the effect on the second-order rogue waves caused by δ is larger than that caused by α, as shown in Figures 2 and 4. However, the distance of the appearance for the second-order rogue wave elongates, which is different from that for the first-order rogue wave. The reason might be the interaction among a few rogue waves to form a second-order rogue wave. Meanwhile, positions of rogue-wave troughs and crests remain the same, which induces the asymmetric structure.

Figure 4:

The second-order rogue waves via the solutions, ψ˜[2], in Supplementary Material with parameters: f₀=0, f₁=0, α=0, γ=0, τ₀=0, T₀=0, τ₁=0, T₁=0, (a) δ=0; (b) δ=−0.03; (c) δ=−0.06.

Table 1 presents that the maximum values and positions of the second-order rogue waves remain the same, 5 at (x=0, t=0). If f₀, f₁, γ, α, and δ have different values, the minimum values of the rogue waves remain the same, 0. Asymmetric structure occurs, because the quintic terms have the effects on the rogue waves to change the velocity of the rogue wave; meanwhile, the positions and values of the wave troughs and crests remain the same. Conversely, the same-order rogue waves have the same maximum and minimum values of the rogue waves with the separating function, S(ϵ)=0.

Next, we discuss the interaction among the rogue waves by virtue of the separating function, S(ϵ). In Figure 5, the second-order rogue wave is separated into three single first-order rogue waves. In Figure 5a, the second-order rogue wave for the NLS equation shows a single higher hump and double lower symmetric humps. If the quintic terms have an impact on the rogue waves, the symmetric structure turns to the asymmetric one. The second-order rogue wave turns counterclockwise if a larger δ is taken and the distance and time of appearance for the second-order rogue wave elongate, which fits the law mentioned in Figure 4. Then, the right one of the double humps in Figure 5b and c becomes higher than the left one, caused by the quintic terms. Meanwhile, the single hump has a little position shift. Therefore, the amplitude of a single hump and the right one of the double become equal.

Figure 5:

The same as Figure 4 except that T₁=10.

To be specific, we find that the maximum values of the single hump and the right one of the double become equal, caused by the quintic terms, as shown in Table 2. If δ becomes larger enough, the left hump of the double becomes the lower single one, and the other ones become double higher symmetric. No matter how the three humps move, they come out to be a “Triangular Cascades” pattern as mentioned in [35]. Therefore, the second-order rogue wave is composed of the three single first-order rogue waves via the interaction. By virtue of the separating function S(ϵ), the second-order rogue wave shows a “Triangular Cascades” state in the spatial-temporal pattern.

In Figure 6, the second-order rogue wave is separated into three first-order rogue waves with S(ϵ)=20. We can find that the second-order rogue wave in Figure 6a is similar to the image in Figure 5a except for the spatial-temporal reversal. The other characteristics are similar to what we find in Figure 5.

Figure 6:

The same as Figure 4 except that τ₁=20.

Furthermore, we investigate the effects on the third-order rogue wave caused by the quintic terms and interaction among the rogue waves to form the third-order rogue wave by virtue of S(ϵ). Figure 7 shows the third-order rogue wave for (2) with δ=0, −0.03, and −0.06. In Figure 7a with f₀=0, f₁=0, α=0, γ=0, and δ=0, the third-order rogue wave for (1) shows a symmetric structure about the x=0 axis. With the effects caused by the quintic terms increasing, the third-order rogue wave has a certain degree turn in the spatial-temporal pattern. The distance and time of appearance of the rogue wave elongate, with δ increasing. Moreover, when the rogue wave damps in the spatial-temporal pattern, the small wave crest occurs at the point away from the core (x=0, t=0). Therefore, we might conclude that the higher-order rogue wave is formed by some first-order rogue waves via the interaction, and the quintic terms would affect the interaction to form a small wave crest away from the core.

Figure 7:

The third-order rogue waves via the solutions, ψ˜[3], in Supplementary Material with parameters: f₀=0, f₁=0, α=0, γ=0, τ₀=0, T₀=0, τ₁=0, T₁=0, τ₂=0, T₂=0, (a) δ=0; (b) δ=−0.03; (c) δ=−0.06.

Meanwhile, the symmetric structure becomes asymmetric about the x=0 axis. However, if we turn the semi-plane, x> 0, 180 degrees about the point (x=0, t=0), we find that the semi-plane, x> 0, coincides with the semi-plane, x< 0. If a larger δ is taken, the distortion of symmetric structure of the third-order rogue wave becomes larger. With S(ϵ)=0, the maximum value of the third-order rogue wave is equal to 7.

Comparing the results with those we have gotten previously, we note that the maximum value of the n^th-order rogue wave is equal to (2n + 1). Meanwhile, the third-order rogue wave has six minimum-value points whose values are equal to zero. We also note that the number of the minimum values of the n^th-order rogue wave is equal to (2n). Those results fit in those from (1) in [18], which means that the quintic terms have no impact on those characteristics for (2), such as the maximum/minimum values of the n^th-order rogue wave aforementioned.

Figure 8 illustrates that the third-order rogue wave is separated into six single first-order rogue waves with δ=0, −0.03, −0.06. We find that the six first-order rogue waves show a so-called “Triangular Cascades” pattern, as mentioned in [35], with S(ϵ)=200iϵ⁴. With the effects on the rogue wave caused by the quintic terms increasing, the third-order rogue wave turns a certain degree in the spatial-temporal pattern. Duration of time for the third-order rogue wave elongates, whereas the increase in distance duration is not obvious, because the third-order rogue wave is split into six first-order rogue waves, and the interaction among them attenuates, i.e., the effects induced by the quintic terms on the rouge wave are weakened. In Figure 8a, the third-order rogue wave for (1) is symmetrical about the t=0 axis. With the value of δ increasing, the symmetric structure disappears caused by the quintic terms as shown in Figure 8.

Figure 8:

The same as Figure 7 except that T₁=200.

Comparing Figure 8a with c, we observe that the distortion of each single rogue wave becomes larger, which has a kind of compression effect. The compression effect shows the width of the single rogue wave on the x direction with δ=−0.06 is longer than that with δ=0. However, the relative positions of the six single rogue waves remain unchanged which is a kind of a slanting “Triangular Cascades” pattern induced by the quintic terms. Observing Figures 5 and 8, we may find that the n^th-order rogue wave consists of [n(n + 1)2] first-order rogue waves via the interaction, which fits the results in [6].

With S(ϵ)=9000iϵ⁴, we find that the third-order rogue wave shows a so-called “Pentagrams” pattern [35], as shown in Figure 9. The six single rogue waves are compressed in the x=−t direction and prolonged in the x=t direction induced by the quintic terms. If we analyse the rogue waves for (2) at the viewpoint of the optical fibre, the rogue waves become longer in the time and distance duration with the effects caused by the quintic terms which might influence the information transmission in the optical fibre due to higher-order nonlinear effect. Moreover, the symmetric structure is also changed as shown in Figure 9, which is called a slanting “Pentagrams” pattern. If we take S(ϵ)=(τ₁ + T₁i)ϵ², the rogue wave would show a “Triangular Cascades” pattern as shown in Figure 8. Moreover, if we take S(ϵ)=(τ₂ + T₂i)ϵ⁴, the rogue wave would show a “Pentagrams” pattern as shown in Figure 9.

Figure 9:

The same as Figure 7 except that T₂=9000.

5 Conclusions

We have investigated a fifth-order dispersive NLS equation, i.e., (2), which describes the propagation of the pulses, up to the attosecond duration, in an optical fibre. Generalised DTs (11) and (14) have been constructed. First-order rogue wave solutions (22), the second-order rogue wave solutions and the third-order rogue wave solutions presented in Supplementary Material have been obtained. Other results in this article are summarised as follows:

1. Effects caused by the phase parameter, f₀, group velocity of the pulse, f₁, coefficient of cubic terms, α , quartic terms, γ, and quintic terms, δ, on the second-order rogue wave for (2), have been studied. Group velocity of the pulse, f₁, coefficient of cubic terms, α, and coefficient of quintic terms, δ, elongate the time of appearance of the rogue wave, with the distance invariant, as shown in Figures 1, 2, and 4. Coefficient of quartic terms, γ, makes the distance of the appearance of the rogue wave elongating firstly, next, with γ continued growth, the distance shrinking, while the time elongates, as shown in Figure 3.

2. Characteristics of the higher-order rogue waves for (2) have been summarised with the separating function S(ϵ)=0, as shown in Table 3, which are similar to the results for (1) in Yang et al. and Akhmediev et al. [6, 18].

3. Effects caused by the quintic terms after δ in (2), on the second- and third-order rogue waves, and interaction among the first-order rogue waves have been illustrated, compared with those for (1). The higher-order rogue waves can be recognized to consist of some first-order rogue waves via each interaction, as shown in Figures 5, 6, 8, and 9. Time and distance of the appearance of the rogue waves both elongate, caused by those quintic terms, as shown in Figures 4 and 7. Increase of such a distance is different from the results obtained from the first-order rogue waves. Coefficient of the quintic terms, δ, affects not only the first-order rogue waves but also the interaction among them, so that the distance of appearance for a higher-order rogue wave elongates.

4. Spatial-temporal pattern of the higher-order rogue wave for (2) has been discussed via S(ϵ), compared with that for (1). With different S(ϵ), different spatial-temporal patterns for the rogue waves have been observed, such as the “Triangular Cascades” and “Pentagrams” patterns, as shown in Figures 5, 6, 8, and 9. Also, influence on a spatial-temporal pattern caused by δ has been investigated: With the effects of δ increasing, the time of the appearance of the rogue waves elongates, while the distance increases a little.