Zusammenfassung
Die Deflektometrie analysiert Messproben durch indirekte Beobachtung einer bekannten Referenzszene als Reflexion in der Oberfläche. Sie benötigt jedoch Zusatzwissen, z.B. über mindestens einen Oberflächenpunkt, um sehr präzise Oberflächengradienten zu messen. Lichtfeldkameras als optische 3D-Messgeräte erlauben es bei teilspiegelnden Oberflächen, die Entfernung sowohl zur Oberfläche als auch zur Referenzszene zu messen. In diesem Beitrag wird ein Ansatz präsentiert, bei dem diese doppelte Tiefenschätzung effektiv mit der Deflektometrie kombiniert wird. Durch Formulieren der Oberflächenrekonstruktion als Variationsproblem wird die Tiefenschätzung mit den deflektometrischen Gradienten fusioniert. Experimente bestätigen die Methode und zeigen, dass hohe Rekonstruktionsgenauigkeiten erreicht werden.
Abstract
Deflectometry analyses surfaces by indirect observation of a known reference scene via the reflection in the surface itself. But, it requires additional knowledge, e.g. about one surface point, in order to measure surface gradients very precisely. Light field cameras as optical 3D measuring devices allow to measure the distance to the surface as well as to the reference scene when observing partially reflecting surfaces. In this paper an approach is presented that effectively combines this dualdepth estimation with deflectometry. By formulating the surface reconstruction as a variation problem, the depth is fused with the deflectometric gradients. Experiments validate the method and show that high accuracy in the reconstruction is achieved.
1 Einleitung
Die Sichtprüfung spiegelnder Oberflächen gehört in der Messtechnik immer noch zu den größeren Herausforderungen. Für die Analyse solcher Oberflächen haben sich die deflektometrischen Messverfahren durchgesetzt. Sie ermöglichen es, hochpräzise Neigungsinformationen der Messprobe zu erhalten, indem sie die durch die spiegelnde Oberfläche verzerrten Bilder einer Referenzszene auswerten. Da die spiegelnde Oberfläche für den Beobachter quasi unsichtbar ist, kann die absolute Höhe mit einer herkömmlichen Kamera ohne Zusatzwissen nicht rekonstruiert werden und stattdessen erhält man eine unendliche Anzahl möglicher Oberflächen [2]. Diese Mehrdeutigkeit kann jedoch durch spezielle Messaufbauten aufgelöst werden. Mehrfachmessungen und Verschieben eines Referenzmonitors, präzise konfokale Vermessung eines einzelnen Oberflächenpunktes, telezentrische Optiken oder auch Stereo-Kamera-Ansätze können das Problem weitgehend beheben [7], benötigen jedoch aufwändige und teure Hardware, einen großen Bauraum oder zusätzlich eine sehr zuverlässige Kalibrierung.
In diesem Beitrag wird eine Lichtfeldkamera als Aufnahmegerät benutzt, da sie durch ihre sehr kompakte Bauweise leicht in einen Standard-Deflektometrieaufbau integriert werden kann. Gleichzeitig kann sie als 3D-Kamera genutzt werden, um eine effiziente Tiefenschätzung zu ermöglichen. Dabei erlauben es die speziellen Eigenschaften der Lichtfeldkamera, bei der Vermessung von teilspiegelnden Oberflächen sowohl Tiefenmerkmale auf der direkten Oberfläche zu finden als auch die Tiefe der reflektierten Szene zu bestimmen. Diese unabhängigen Messungen können als zusätzliche Informationsquelle regularisierend für die Deflektometrie genutzt werden. Da deflektometrische Messungen hochpräzise Neigungsinformationen in Form von Oberflächennormalen liefern, wird in diesem Beitrag die Oberflächenrekonstruktion als Energie-Optimierung formuliert. Minimieren des Funktionals durch einen Variationsansatz und mittels des Primal-Dual-Formalismus fusioniert die Tiefenmessungen mit den Oberflächennormalen und erhöht die Genauigkeit der 3D-Rekonstruktion.
2 Lichtfeld-Tiefenschätzung
In der geometrischen Optik kann die Strahldichte einer Szene durch das 4D-Lichtfeld L(u, v, x, y) mit zwei örtlichen Dimensionen x, y und zwei angulären Dimensionen u, v beschrieben werden. Lichtfeldkameras besitzen einen ähnlichen Aufbau wie Standard-Kameras mit dem entscheidenden Unterschied, dass vor dem Sensor ein Array von Mikrolinsen platziert ist [3]. Mit dieser Bauweise wird es möglich, das Lichtfeld der beobachteten Szene aufzunehmen. Hierbei sind x, y vergleichbar zu den Pixelkoordinaten der Standard-Kamera und u, v entsprechen dem Durchstoßpunkt des Lichtstrahls durch die Hauptlinse. Jede u, v -Koordinate repräsentiert daher eine virtuelle Subkamera, welche nur einen Teil der Hauptlinse beobachtet, weshalb eine Lichtfeldkamera auch als Multi-Kamera-Array interpretiert werden kann, siehe Abb. 1a. Die im Vergleich zur Standard-Kamera zusätzliche Information erlaubt es, nach der Aufnahme die Perspektive auf die Szene zu ändern, wodurch Tiefeninformation extrahiert werden kann, oder den Fokus im Nachhinein neu zu setzen.
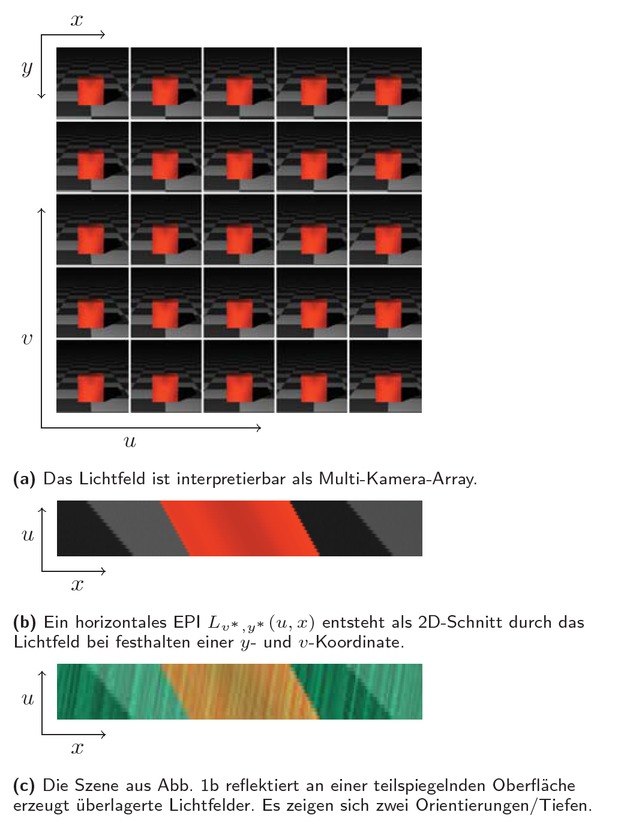
Im Lichtfeld einer Szene ist Tiefeninformation enthalten.
Die Tiefe der Szene, bzw. die Entfernung eines beobachteten Objektpunktes, lässt sich im Lichtfeld über die Analyse der Epipolarebenen (engl.: epipolar plane image, EPI) bestimmen. Diese EPIs sind 2D-Schnitte durch das Lichtfeld, bei denen jeweils eine anguläre und eine örtliche Koordinate festgehalten werden. Abb. 1b zeigt ein Beispiel. Es sind Linien unterschiedlicher Steigungen zu erkennen, wobei die Orientierung der Linien die Tiefe des Objektpunktes repräsentiert [11]. Die Tiefenschätzung reduziert sich daher zu einer einfachen lokalen Orientierungsschätzung in den EPIs. Im Gegensatz zu einem Stereo-Kamera-Aufbau muss dabei kein Feature Matching durchgeführt werden. Bekannte Ansätze zur Lichtfeld-Tiefenschätzung nutzen zur Orientierungsschätzung bspw. den Strukturtensor, Hough-Transformation, oder auch neuronale Faltungsnetze [9, 11].
Untersucht man Lichtfelder, die teilspiegelnde oder transparente Objekte zeigen, so tritt ein besonderer Effekt auf. Das resultierende Lichtfeld lässt sich als Addition zweier Teillichtfelder L = Ldiffus + Lreflektiert interpretieren [14]. Für klassische Stereo-Kamera-Systeme ist diese Addition meist störend und resultiert in fehlerhaften Tiefenschätzungen. Für Lichtfelder jedoch zeigt eine Analyse der EPIs nun auch eine Überlagerung der Orientierungen, siehe Abb. 1c. Eine gleichzeitige Schätzung beider Orientierungen liefert damit sowohl eine Tiefenschätzung des teilspiegelnden Objekts als auch der reflektierten Szene. Methoden zum Schätzen der Tiefen nutzen z.B. Strukturtensoren höherer Ordnung oder optischen Fluss [12, 14].
3 Deflektometrie
Während die Lichtfeld-Tiefenschätzung für strukturierte Oberflächen gute Ergebnisse liefern kann, versagt sie an unstrukturierten Szenen, da sich jetzt keine Information mehr aus den EPIs extrahieren lässt. Noch aufwändiger wird die direkte Tiefenschätzung spiegelnd reflektierender Objekte, denn jetzt sieht die Kamera nicht die Oberfläche selbst, sondern das verzerrte Spiegelbild der Umgebung. Die spiegelnde Oberfläche ist quasi unsichtbar. Um die Struktur von Spiegeln vermessen zu können, bieten sich Verfahren mit aktiver Beleuchtung wie die Deflektometrie an. Sie erlaubt es, hochpräzise Neigungsinformationen der Oberfläche zu erhalten, welche zur 3D-Rekonstruktion oder Fehlererkennung genutzt werden können.
In der Deflektometrie wird die Oberfläche eines spiegelnden Objekts rekonstruiert, indem eine Kamera einen aktiven Mustergenerator (z.B. einen Monitor) indirekt als Reflexion in der Messprobe beobachtet. Das Messprinzip ist in Abb. 2 dargestellt. Folgt man der Ausbreitung des Lichts von der Kamera zurück zur Quelle, dann trifft hierbei ein Kamerasichtstrahl

Messprinzip der Deflektometrie. Für jeden Punkt s′ kann eine hypothetische Normale n′ berechnet werden.
Die Zuordnung von Kamerasichtstrahlen ŝ zu Monitorpunkten m kann dabei mithilfe einer zeitlichen Codierung der Monitorpixel gefunden werden. Hier bieten sich Phasenschieber-Mustersequenzen an, da sie eine subpixelgenaue Codierung in der Monitorebene erlauben, sie sogar bei Defokussierung gute Ergebnisse liefern und sie das Messrauschen durch Verlängerung der Mustersequenz kontrolliert auf die gewünschte Größe reduzieren können [6, 15]. Eine geometrische Kalibrierung der Kamera und des Kamera-Monitor-Systems [3, 13] erlaubt es anschließend, den Vektor m zu bestimmen, womit die Normale der Spiegeloberfläche berechnet werden kann:
Um die Mehrdeutigkeit der deflektometrischen Messung aufzulösen, wird regularisierendes Zusatzwissen benötigt. Es reicht prinzipiell aus, nur einen Punkt der Oberfläche zu messen und ausgehend von diesem Punkt die Oberfläche aus dem Normalenfeld zu rekonstruieren [2]. Liegen jedoch mehr Messwerte vor, kann dies helfen, den Einfluss einer unsicheren und verrauschten Messung eines einzelnen Oberflächenpunktes zu reduzieren.
Die Tiefenschätzung der Lichtfeldkamera erlaubt es, Kandidaten für mögliche Oberflächenpunkte zu finden, und sie macht es damit möglich, die Mehrdeutigkeit der deflektometrischen Normalenschätzung aufzulösen. Hier ergeben sich zwei Situationen. Zunächst, wenn die Oberfläche der Messprobe diffuse Bereiche hat, kann eine Standard-Lichtfeldkamera-Tiefenschätzung benutzt werden, um direkt die Entfernung zwischen Kamera und Oberfläche für jedes Pixel bzw. für jeden Sichtstrahl zu messen. Die Menge der Tiefenwerte ddirekt schätzt dabei ║s║ und kann anschließend direkt genutzt werden, um die deflektometrische Normalenschätzung zu regularisieren. Wenn die Messprobe jedoch voll spiegelnd ist, kann die Lichtfeldkamera nicht direkt die Entfernung zur Oberfläche bestimmen. Für ebene Spiegel wird sie stattdessen die Entfernung ║s║+║r║ der reflektierten Referenzszene als Tiefe dref schätzen. Dennoch kann mithilfe des Wissens über den deflektometrischen Messaufbau und mit der Registrierung von Kamerasichtstrahlen zu Monitorpixeln aus der indirekten Lichtfeld-Tiefenmessung die direkte Entfernung zur Oberfläche berechnet werden. Mit den Messungen m = s + r und dref ≙=║s║ + ║r║ folgt:
Durch Gleichsetzen von (1) und (2) und mit
Durch die im Abschnitt 2 beschriebenen besonderen Eigenschaften der Lichtfeldkamera wird es hierbei möglich, im Gegensatz zu einem Stereokamera-Aufbau selbst bei teilspiegelnden Oberflächen sowohl die Entfernung zur Oberfläche als auch die Entfernung der Reflexion gleichzeitig sehr robust zu schätzen. Zusätzlich stehen neben der reinen Lichtfeld-Tiefenschätzung auch noch andere Möglichkeiten zur Verfügung, um auf Oberflächenpunkte zu schließen. Es kann z.B. die Lichtfeldkamera als Kamera-Array interpretiert werden, womit ein Multi-Stereo-Deflektometrie-Ansatz realisiert werden kann, bei dem die Tiefe dmulti erhalten wird [10]. Somit stehen für eine deflektometrische Messung drei unabhängige Messungen der Spiegeloberfläche zur Verfügung, welche gemeinsam zur Regularisierung der deflektometrischen Normalenschätzung genutzt werden können.
4 Rekonstruktion der Oberfläche
Prinzipiell können die Tiefenmessungen aus Abschnitt 3 direkt genutzt werden, um die Oberfläche beispielsweise durch eine Mittelwertbildung zu rekonstruieren. Da jedoch Multi-Stereo-Messsysteme wie die Lichtfeldkamera in ihrer Messgüte durch die effektive Stereo-Basisweite begrenzt sind, erreicht man mit dieser Tiefenschätzung nicht die gewünschte Genauigkeit. Dem gegenüber misst die Deflektometrie Neigungen bzw. Oberflächennormalen in einer um Größenordnungen höheren Präzision, benötigt aber Oberflächenpunkte zur Regularisierung [2]. Es ist daher sinnvoll, sich nicht nur auf die Tiefenschätzung zu verlassen. Stattdessen können die dichten deflektometrischen Messungen der Oberflächennormalen mit den verschiedenen Tiefenschätzungen, die möglicherweise auch nur spärlich vorliegen, fusioniert werden. Das Problem lässt sich durch eine Energie-Minimierung modellieren:
Die gesuchte Oberfläche soll minimalen Abstand zu den Regularisierungspunkten di besitzen und gleichzeitig soll der Unterschied von berechneten zu deflektometrisch gemessenen Normalen nmess minimiert werden. Dies löst die Mehrdeutigkeit der Deflektometrie auf und resultiert in einem robusteren Gesamtergebnis für die 3D-Rekonstruktion.
Da die Tiefen- und Neigungsinformationen pixelweise auf einem diskreten Gitter angeordnet sind, macht es Sinn, das Problem als diskrete Gradientenintegration zu formulieren und die gemessenen Oberflächenpunkte auf eine Tiefenkarte z(x, y) zu projizieren. Aufgrund der in der Lichtfeldkamera auftretenden perspektivischen Projektion muss hierzu eine Variablensubstitution durchgeführt werden, damit der Oberflächengradient aus den gemessenen Oberflächennormalen bestimmt werden kann [8]:
wobei nmess = (n1, n2, n3)T, f die Fokuslänge der Kamera bezeichnet und wir den Akzent ˇ für den Rest des Abschnitts vernachlässigen. Da (4) ein schlecht gestelltes Problem ist, würde eine Minimierung kein sinnvolles Fusionsergebnis liefern. Es müssen zusätzliche regularisierende Annahmen zur Oberfläche getroffen werden. In vielen Bereichen der Bildverarbeitung wird die Totale Variation als beliebte Regularisierungmethode genutzt, da sie Unstetigkeiten in den Daten abbilden kann und gleichzeitig verrauschte Messungen glättet [5]. Sie hat jedoch den Nachteil, dass schräge Ebenen eine ungewollte, treppenförmige Struktur ausbilden können. Im Gegensatz dazu vermeidet die Totale Generalisierte Variation (TGV) diesen Effekt, indem sie Lösungen höherer Ordnung zulässt [4]. Der TGV-Term minimiert den Abstand zwischen dem Oberflächengradienten und einem Gradienten g. Zusätzlich kann g durch einen Datenterm in die Nähe des deflektometrisch gemessenen Gradienten gn gedrängt werden [1]. Gleichzeitig wird eine Abweichung der Oberfläche von den gemessenen Tiefen zi bestraft. Das diskrete Optimierungsproblem ergibt sich zu:
mit
Mithilfe der zu ∇, 𝓔 adjungierten Divergenzoperatoren div∇, divE kann das Problem durch iterativen Gradientenabstieg in den Primal-Variablen z, g und Gradientenaufstieg in den Dual-Variablen p, q gelöst werden [4, 5]:
| Primal-Dual-Optimierung: |
|---|
| Initialisierung: |
| |
| 1: fork = 1, 2, 3, . . . , kmaxdo |
| 2: Gradientenaufstieg in den Dual-Variablen |
| 3: |
| 4: |
| 5: Aktualisiere gemessenen Gradienten mit Glg. (6) |
| 6: |
| 7: Gradientenabstieg in den Primal-Variablen |
| 8: |
| 9: |
| 10: Extrapolation |
| 11: |
| 12: |
| 13: end for |
Die Proximal-Operatoren lassen sich durch Lösen des separaten Problems
Da die deflektometrisch gemessenen Normalen von der Entfernung zur Oberfläche abhängen, wird in jeder Iteration das gemessene Gradientenfeld gn aktualisiert. Nachdem ein Minimum für Glg. (7) gefunden wurde, kann die wahre Oberfläche durch Rücksubstitution aus Glg. (5) zu z = exp(z̃) bestimmt werden.
5 Ergebnisse
Die vorgestellte Methode wurde anhand von realen Experimenten mit zwei Referenzszenen verifiziert. Zur Aufnahme der Bilder wurde die Lytro Illum Lichtfeldkamera verwendet und als Mustergenerator diente ein handelsüblicher LCD-Monitor (BenQ GW2765HT, Auflösung 2560×1440, Pixelgröße 0,233mm). Die Registrierung von Kamera- zu Monitorpixeln erfolgte mittels Multi-Frequenz-Phasenschubmustersequenzen [2].
Die erste Testszene besteht aus einer Festplattendisk, die teilspiegelnde Oberflächenbereiche in Form von Farbmarkierungen und Rauheiten zeigt. Da die Disk eine sehr hohe Planarität aufweist, wird die Güte der Rekonstruktion durch Vergleich mit einer idealen Ebene bewertet.
Abbildung 3 zeigt die Vermessung der Disk und das Ergebnis der 3D-Rekonstruktion. Hier sieht man den Rekonstruktionsfehler der Oberflächenrekonstruktion mittels direkter Tiefenschätzung, den Fehler bei Schätzung der reflektierten Entfernung, den Fehler mit Multi-Stereo-Deflektometrie [10] und das Ergebnis der hier beschriebenen Fusion. Die reine Lichtfeld-Tiefenschätzung der diffusen Oberfläche liegt nur spärlich in Bereichen großer Rauheit oder in der Nähe der Farbmarkierungen vor. Alle anderen Bereich werden von der Tiefenschätzung als ungültig bewertet, was durch wi = 0 in der Fusion berücksichtigt wird. Die indirekte Schätzung über die Reflexion und die Schätzung mittels Multi-Stereo-Deflektometrie sind wesentlich dichter und weniger verrauscht. Obwohl alle Schätzungen Rekonstruktionsfehler im unteren Millimeterbereich aufweisen, kann durch Fusion der Tiefen- und Normalenschätzung der Fehler deutlich reduziert werden. Ein Fehler von RMSE = 822,7 μm wird erreicht.

Rekonstruktionsfehler der Festplattendisk im Vergleich zu einer idealen Ebene. (b-d) und (e-f) jeweils mit eigener Skala.
Die zweite Testszene zeigt einen Planspiegel mit sehr hoher Planarität (λ/20) und soll demonstrieren, dass die vorgestellte Methode auch für voll spiegelnde Oberflächen gute Resultate liefert. Die Reproduktionsgenauigkeit wird wieder durch Vergleich mit einer idealen Ebene bewertet.
Abbildung 4 zeigt die Vermessung der Szene und das Ergebnis der 3D-Rekonstruktion. Auf dem Planspiegel können keine diffusen Tiefenwerte gefunden werden, was mit wi = 0 in der Fusion berücksichtigt wird. Die indirekten Tiefenwerte und die Multi-Stereo Schätzung können jedoch beide gute Ergebnisse liefern. Da die indirekte Tiefenschätzung die Referenzszene trianguliert und die Multi-Stereo-Deflektometrie die Oberfläche, liegen zwei Messwerte mit unterschiedlicher Unsicherheit vor, wobei beide zur Verbesserung der Rekonstruktion beitragen können. Wird die Oberfläche nur anhand jeweils einer Tiefenschätzung rekonstruiert, ergeben sich größere Fehler als bei Fusion beider Tiefen, wobei die Abweichungen des mit der vorgestellten Methode rekonstruierten Planspiegels von der idealen Ebene sich im Bereich ±250μm bewegen. Es ergibt sich ein Fehler von RMSE = 167,10μm.

Planspiegel: Auswertung der Rekonstruktion.
Um zu zeigen, dass die Fusion zwischen Oberflächenpunkten und Oberflächengradienten einen sehr großen Einfluss auf die Rekonstruktionsgenauigkeit hat, zeigen Abbildung 3e und 4a jeweils den Rekonstruktionsfehler, der sich bei Anwendung eines einfachen gewichteten Mittelwertes auf die verschiedenen Tiefenschätzung ergeben würde. Es wird sichtbar, dass das Ergebnis durch die vorgeschlagene Methode deutlich verbessert werden kann.
Bei genauerer Beobachtung der Rekonstruktion des Planspiegels fällt eine Überhöhung in der Mitte auf. Diese ist nicht auf eine Verformung des Spiegels zurückzuführen, sondern wird durch den Messaufbau beeinflusst. Da in unserem Messaufbau der Referenzmonitor über dem Objekt hängt, wird er leicht verbogen, was eine Verzerrung der Ergebnisse zur Folge hat. Ein genaues Modellieren des Referenzmonitors könnte die Rekonstruktionsgenauigkeit daher noch weiter erhöhen.
6 Zusammenfassung
In diesem Beitrag wurde demonstriert, wie eine Lichtfeldkamera in einen Deflektometrie-Aufbau zur Messung (teil)spiegelnder Oberflächen integriert werden kann. Die speziellen Eigenschaften der Lichtfeldkamera ermöglichen, es die Entfernung (bzw. die Tiefe) zur teilspiegelnden Oberfläche zu schätzen und simultan die Distanz zur reflektierten Referenzszene zu bestimmen. Dies ermöglicht es, unabhängige Schätzungen der 3D-Struktur derselben Oberfläche zu erhalten. Weiter wurden in diesem Beitrag die verschiedenen Tiefenschätzungen der Lichtfeldkamera zur Regularisierung der deflektometrischen Messung genutzt und mithilfe eines Variationsansatzes fusioniert. Durch Modellieren mittels Totaler Generalisierter Variation ließ sich die Oberfläche durch einen Primal-Dual-Algorithmus rekonstruieren. Messungen an realen Oberflächen zeigten letztendlich, dass trotz Tiefeninformation verschiedener Güte die Methode gute Ergebnisse liefert und sowohl diffus spiegelnde als auch voll spiegelnde Oberflächen rekonstruiert werden können.
Literatur
[1] D. Antensteiner, S. Štolc und T. Pock. A review of depth and normal fusion algorithms. Sensors (Basel, Switzerland), 18(2), 2018. ISSN 1424-8220. 10.3390/s18020431.10.3390/s18020431Search in Google Scholar PubMed PubMed Central
[2] J. Balzer und S. Werling. Principles of shape from specular reflection. Measurement, 43(10):1305–1317, 2010. ISSN 02632241. 10.1016/j.measurement.2010.07.013.10.1016/j.measurement.2010.07.013Search in Google Scholar
[3] Y. Bok, H.-G. Jeon und I. S. Kweon. Geometric calibration of micro-lens-based light field cameras using line features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39(2):287–300, 2017. ISSN 0162-8828. 10.1109/TPA-MI.2016.2541145.10.1007/978-3-319-10599-4_4Search in Google Scholar
[4] K. Bredies, K. Kunisch und T. Pock. Total generalized variation. SIAM Journal on Imaging Sciences, 3(3):492–526, 2010. ISSN 1936-4954. 10.1137/090769521.10.1137/090769521Search in Google Scholar
[5] A. Chambolle und T. Pock. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision, 40(1):120–145, 2011. ISSN 1573-7683. 10.1007/s10851-010-0251-1.10.1007/s10851-010-0251-1Search in Google Scholar
[6] M. Fischer, M. Petz und R. Tutsch. Vorhersage des Phasenrauschens in optischen Messsystemen mit strukturierter Beleuchtung. tm - Technisches Messen, 79(10):451–458, 2012. ISSN 0171-8096. 10.1524/teme.2012.0256.10.5162/sensoren2012/3.4.2Search in Google Scholar
[7] L. Huang, M. Idir, C. Zuo und A. Asundi. Review of phase measuring deflectometry. Optics and Lasers in Engineering, 107:247–257, 2018. ISSN 01438166.10.1016/j.optlaseng.2018.03.026Search in Google Scholar
[8] Y. Quéau, J.-D. Durou und J.-F. Aujol. Normal integration: A survey, 2017.10.1007/s10851-017-0773-xSearch in Google Scholar
[9] C. Shin, H.-G. Jeon, Y. Yoon, I. So Kweon und S. Joo Kim. Epinet: A fully-convolutional neural network using epipolar geometry for depth from light field images. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.10.1109/CVPR.2018.00499Search in Google Scholar
[10] D. Uhlig und M. Heizmann. Multi-Stereo-Deflektometrie mit einer Lichtfeldkamera / Multi-stereo deflectometry with a light-field camera. tm - Technisches Messen, 85(s1):s59–s65, 2018. ISSN 0171-8096. 10.1515/teme-2018-0042.10.1515/teme-2018-0042Search in Google Scholar
[11] A. Vianello, G. Manfredi, M. Diebold und B. Jähne. 3d reconstruction by a combined structure tensor and hough transform light field approach. tm - Technisches Messen, 84 (7-8), 2017. ISSN 0171-8096. 10.1515/teme-2017-0010.10.1515/teme-2017-0010Search in Google Scholar
[12] S. Wanner und B. Goldluecke. Reconstructing reflective and transparent surfaces from epipolar plane images. In Pattern Recognition, S. 1–10, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg. ISBN 978-3-642-40602-7.10.1007/978-3-642-40602-7_1Search in Google Scholar
[13] Y.-L. Xiao, S. Li, Q. Zhang, J. Zhong, X. Su und Z. You. Optical fringe-reflection deflectometry with bundle adjustment.Optics and Lasers in Engineering, 105:132–140, 2018. ISSN 01438166. 10.1016/j.optlaseng.2018.01.013.10.1016/j.optlaseng.2018.01.013Search in Google Scholar
[14] J. Yang, H. Li, Y. Dai und R. T. Tan. Robust optical flow estimation of double-layer images under transparency or reflection. In 29th IEEE Conference on Computer Vision and Pattern Recognition, S. 1410–1419, Piscataway, NJ, 2016. IEEE. ISBN 978-1-4673-8851-1. 10.1109/CVPR.2016.157.Search in Google Scholar
[15] C. Zuo, S. Feng, L. Huang, T. Tao, W. Yin und Q. Chen. Phase shifting algorithms for fringe projection profilometry: A review. Optics and Lasers in Engineering, 109:23–59, 2018. ISSN 01438166. 10.1016/j.optlaseng.2018.04.019.10.1016/j.optlaseng.2018.04.019Search in Google Scholar
© 2020 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Editorial
- XXXIV. Messtechnisches Symposium
- Beiträge
- Detektion der Auflagestege von Flachbett-Laserschneidmaschinen mittels Nahinfrarot-Beleuchtung
- Lichtfeld-Tiefenschätzung für die Vermessung teilspiegelnder Oberflächen
- Ganzheitliche Kalibrierung von Gewinden auf Basis eines dreidimensionalen Ansatzes
- Analyse von 3D-CT-Aufnahmen von Spänen zur Extrahierung der Segmentspanbildungsfrequenz
- Resolution enhancement through nearfield-assistance in interference microscopy
- Fertigung polymerer optischer Phasenplatten zur Erzeugung von Ringmoden mittels direkter Laserlithografie
- Direct-imaging DOEs for high-NA multi-spot confocal microscopy
- Methoden zur Minimierung des Rauscheinflusses durch Hitzeflimmern bei einem heterodynen Laser-Doppler-Vibrometer
- Inverse piezoelectric material parameter characterization using a single disc-shaped specimen
- Klassifikation von Grübchenschäden an Zahnrädern mittels Vibrationsmessungen
- Incorporation of phase information for improved time-dependent instrument recognition
- Akustische Zeitumkehrfokussierung in Wasser mittels FPGA-basierter Plattform
- De-Embedding-Ansatz zur Messung nichtidealer Kapazitäten mit kommerziellen Kapazitätssensoren
- Low-cost Indirect Measurement Methods for Self-x Integrated Sensory Electronics for Industry 4.0
- Reconfigurable Wide Input Range, Fully-Differential Indirect Current-Feedback Instrumentation Amplifier with Digital Offset Calibration for Self-X Measurement Systems
- A Compact Four Transistor CMOS-Design of a Floating Memristor for Adaptive Spiking Neural Networks and Corresponding Self-X Sensor Electronics to Industry 4.0
- Monte-Carlo-Methode zur Verringerung von Messfehlern bei der Materialparameterbestimmung mit Hohlraumresonatoren
- Bestimmung des Anregungsspektrums für kontaktlose breitbandige Messungen der Übertragungsfunktion mit Plasmaanregung und Laser-Doppler-Vibrometrie
- Self-sufficient vibration sensor for high voltage lines
- Flexibler organischer elektrochemischer Transistor als Biosensor für Organ-on-a-Chip
- Erkennung und Kompensation von Vergiftung durch Siloxane auf Halbleitergassensoren im temperaturzyklischen Betrieb
Articles in the same Issue
- Frontmatter
- Editorial
- XXXIV. Messtechnisches Symposium
- Beiträge
- Detektion der Auflagestege von Flachbett-Laserschneidmaschinen mittels Nahinfrarot-Beleuchtung
- Lichtfeld-Tiefenschätzung für die Vermessung teilspiegelnder Oberflächen
- Ganzheitliche Kalibrierung von Gewinden auf Basis eines dreidimensionalen Ansatzes
- Analyse von 3D-CT-Aufnahmen von Spänen zur Extrahierung der Segmentspanbildungsfrequenz
- Resolution enhancement through nearfield-assistance in interference microscopy
- Fertigung polymerer optischer Phasenplatten zur Erzeugung von Ringmoden mittels direkter Laserlithografie
- Direct-imaging DOEs for high-NA multi-spot confocal microscopy
- Methoden zur Minimierung des Rauscheinflusses durch Hitzeflimmern bei einem heterodynen Laser-Doppler-Vibrometer
- Inverse piezoelectric material parameter characterization using a single disc-shaped specimen
- Klassifikation von Grübchenschäden an Zahnrädern mittels Vibrationsmessungen
- Incorporation of phase information for improved time-dependent instrument recognition
- Akustische Zeitumkehrfokussierung in Wasser mittels FPGA-basierter Plattform
- De-Embedding-Ansatz zur Messung nichtidealer Kapazitäten mit kommerziellen Kapazitätssensoren
- Low-cost Indirect Measurement Methods for Self-x Integrated Sensory Electronics for Industry 4.0
- Reconfigurable Wide Input Range, Fully-Differential Indirect Current-Feedback Instrumentation Amplifier with Digital Offset Calibration for Self-X Measurement Systems
- A Compact Four Transistor CMOS-Design of a Floating Memristor for Adaptive Spiking Neural Networks and Corresponding Self-X Sensor Electronics to Industry 4.0
- Monte-Carlo-Methode zur Verringerung von Messfehlern bei der Materialparameterbestimmung mit Hohlraumresonatoren
- Bestimmung des Anregungsspektrums für kontaktlose breitbandige Messungen der Übertragungsfunktion mit Plasmaanregung und Laser-Doppler-Vibrometrie
- Self-sufficient vibration sensor for high voltage lines
- Flexibler organischer elektrochemischer Transistor als Biosensor für Organ-on-a-Chip
- Erkennung und Kompensation von Vergiftung durch Siloxane auf Halbleitergassensoren im temperaturzyklischen Betrieb

