Abstract
The increasingly simulation-driven design process of ultrasonic transducers requires several reliable parameters for the description of the material behaviour. Exact results can only be achieved when a single specimen is used in the identification process, which typically is prone to the problem of low sensitivities to certain material parameters and thus high uncertainties. Therefore, a custom electrode topology for increased sensitivity is proposed for a piezoceramic disc. The thereupon conducted measurements of the electric impedance can be used as a starting point for an inverse approach where an equivalent simulation model is used to identify fitting material parameters. An optimisation strategy based on a preliminary sensitivity analysis is presented that leads to a good agreement between measurement and simulation. Furthermore, the proposed measurement procedure is able to evaluate the quality of the simulation model. Hence, different frequency-dependent damping models are presented and evaluated.
Zusammenfassung
Das immer mehr durch Simulationen geprägte Design von Schallwandlern benötigt verlässliche Daten zur Beschreibung des Materialverhaltens. Gute Ergebnisse können dabei nur erzielt werden, wenn für die Identifikation der Materialparameter nur ein einzelner Probekörper genutzt wird. Hierbei tritt jedoch normalerweise das Problem zu geringer Sensitivitäten bezüglich ausgewählter Materialparameter und damit großer Unsicherheiten auf. Daher wird eine angepasste Elektrodentopologie für scheibenförmige Piezokeramiken entworfen, um diese Sensitivitäten zu erhöhen. Die daran durchgeführten Messungen der elektrischen Impedanz werden für einen inversen Ansatz genutzt, bei dem ein äquivalentes Simulationsmodell eingesetzt wird, um passende Materialparameter zu identifizieren. Eine Optimierungsstrategie basierend auf einer vorherigen Sensitivitätsanalyse ermöglicht es, eine gute Übereinstimmung zwischen Messung und Simulation zu erreichen. Darüber hinaus kann mit Hilfe des beschriebenen Messsystems die Qualität des Simulationsmodells beurteilt werden. Dazu werden hier unterschiedliche Dämpfungsmodelle vorgestellt und evaluiert.
1 Introduction
The characterization of piezoelectric material is an ongoing and relevant topic in the current state of research. The increasing use of simulation tools in the design process of transducers even raises the need for fitting material descriptions since this significantly influences the simulation results. A standardized procedure [1] uses four differently shaped specimens with distinct resonances and several measurements that are combined to form a single set of material parameters. This procedure is prone to inconsistencies because of the different processing and poling conditions when fabricating the different geometries. Moreover, estimates are always an average of several specimens which leads to greater deviations that are oftenquantified by values up to 20% by manufacturers. Thus, a single specimen should be used for the characterization. Unfortunately, the simple geometries typically used in applications are not suitable for such an identification since they do not provide a sufficient sensitivity to all material parameters. This is especially true when only frequency-dependent electrical impedance measurements are used. These measurements are easy to obtain, unlike mechanical measurement using laser Doppler vibrometry. Since an application-related geometry is preferred and should be used for the characterization process, only the specimen’s electrode topology can be adjusted to increase the sensitivity of the measurement procedure. This more complex system leads to a non-uniform distribution of electric and mechanical field quantities and encourages mode-coupling. On the one hand, this yields the desired increase in sensitivity. On the other hand, this also leads to a much more complex model for describing the set-up. The simple geometries in the standardized procedure can be calculated using analytic approximations, whereas the custom electrode topology can only be solved numerically using e.g. the Finite Element (FE) Method. Therefore, an inverse procedure is used for fitting measured impedances with the FE-model by an optimization algorithm. Furthermore, the material modelling itself is not obvious. Especially the modelling of damping mechanisms is still a much discussed topic. The suggested inverse measurement approach can be used here to determine which damping model is able to simulate the measured impedances. This approach is especially suited since the measurements are conducted over a large frequency range so that the frequency-dependency of damping can be considered.
2 Inverse measurement procedure
The standardized procedure includes only straightforward calculations to determine the material parameters from the measured resonance frequencies. In the case of the custom electrode topology (described in the following section) the problem can no longer be solved analytically. Since the relation between the measured impedances and the material parameters is not directly given, an inverse measurement approach (see figure 1) is used. Therefore, besides the actual measurement system, a parametrized simulation model is used to replicate the outcome of the real measurement. This is done by finding a material parameter set for the simulation, which results in the best fit of the simulated and measured impedances in the sense of a given objective function. The value of the objective function is to be minimized using an optimization algorithm that typically finds a local minimum starting at an initial value p0.
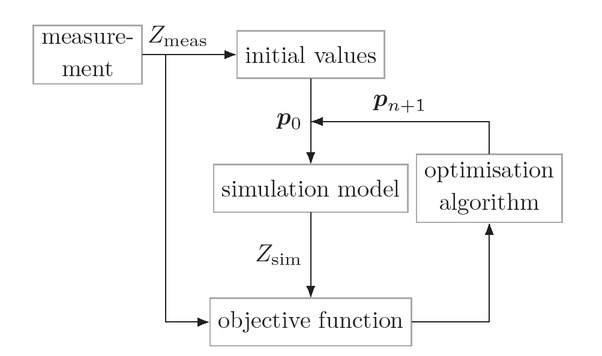
Schematic diagram of an inverse measurement approach.
3 Piezoelectric equations
Describing the behaviour of piezoelectric materials can mathematically be achieved by coupling electrical and mechanical quantities:
where T /S denote the mechanical stress/strain, E /D are the electrical field strength/electrical displacement and cE, ε and e are the matrices of material parameters, namely the mechanical stiffness, the permittivity and the piezoelectric coupling. Using Voigt notation [10] and applying symmetry conditions given by a transversely isotropic piezoceramic material, only 10 independent material parameters remain to be determined:
The partial differential equations determining the piezoelectric behaviour are given by [6, 8]:
with the mechanical displacement u, the electric potential φ, the charge q and the density ρ, the latter being assumed to be given. B is the operator of spatial derivatives in Voigt notation.
4 Simulation model
A simulation model is developed to calculate the frequency- dependent impedance from a given geometry and a set of material parameters. This can be done by a Finite Element approximation [6] (e.g. implemented in the simulation tool CFS++). For the harmonic case the Fourier transform of the piezoelectric differential equations are calculated and solved for a given set of discrete frequencies. Implementing the electrodes as Dirichlet boundary conditions for the potential, the potential and mechanical displacement represent the simulation’s result. The electrical impedance Z(f) then can be calculated by
where the charge can be calculated via an integral over the electrode’s area Aelec:
with
5 Damping model
In the model above, no damping is present. In order to implement a realistic model, damping should be taken into consideration. Typically, in simulation tools, a Rayleigh damping model is implemented, which can be written as a frequency-dependent complex mechanical stiffness [7]:
with the mass-proportional Rayleigh damping parameter αM and the stiffness-proportional Rayleigh damping parameter αK. As alternatives the constant damping model
with the single constant damping parameter α0 or the physically motivated and causal Zener model [11]
with the relaxation time τ and modulus ratio d are taken into consideration. To extend these one-dimensional models to the three-dimensional problem, an eigenvalue decomposition of the stiffness matrix is used [2]:
with the eigenvector matrix P and the diagonal matrix of the eigenvalues λm:
where λ∗ denotes the complex conjugate. Now, for each eigenvalue a damping model with distinct damping parameters is applied, i.e. each eigenvalue λ1, λ2, λ3 is multiplied with a different characteristic damping term. The damping parameters for λ3 and
6 Increasing sensitivity
A disc-shaped ceramic with full-surface electrodes is the most used geometry for single element transducers. Unfortunately, the impedance measured with this set-up does not yield a sufficient sensitivity with respect to all material parameters. In order to increase this sensitivity, a custom electrode topology is aimed for. Nevertheless, in order to reduce the computation time per simulation the geometry should be kept axisymmetric which allows the problem to be reduced to a two dimensional one. Therefore, a triple-ring set-up is chosen (see figure 2). The radii r = [r1, r2, r3, r4] are optimized to get the best overall sensitivity ϒ:
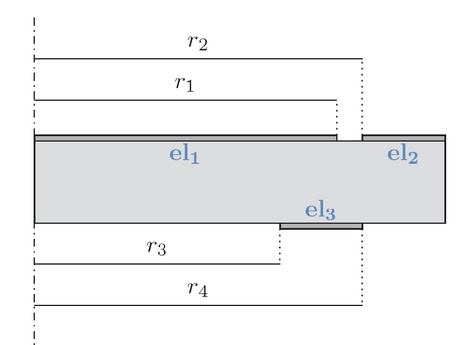
Triple-ring electrode set-up.
with the discrete frequency samples fj , a scaling parameter ωi and each material parameter pi ∈ pmat. The optimization procedure is described in detail by Jurgelucks (e.g. [5]). For a piezoceramic of type PIC255 (PI Ceramic GmbH, Lederhose, Germany) with a outer radius of 5mm and a thickness of 1mm the electrode’s radii result in ropt = [3.68, 4, 4, 5]mm.
7 Impedance measurement
Due to the three electrodes, three different frequency- dependent impedance measurements can be performed by shorting two electrodes and measuring the impedance between these two and the remaining electrode:
Z1: el2 and el3 to el1
Z2: el1 and el3 to el2
Z3: el1 and el2 to el3
The impedances are measured using a Keysight E4991A Impedance Analyzer (Keysight Inc., Santa Rosa, CA, USA) in a frequency range up to 3.0 MHz.
8 Initial value estimation
To solve the inverse problem the three measured impedances are tobe replicated by a simulated equivalent with appropriate material parameters. For this optimization, an initial guess for the parameters is needed. Since the triple-ring electrode set-up does not yield clear resonance frequencies, a disc with fully-covered base faces is utilized. Here, radial and thickness resonance frequency are well-separated and can uniquely be found. An exemplary impedance is shown in figure 3 with the thickness resonance at 2MHz and the radial resonances at lower frequencies. Using the IEEE standard [1] at least several material parameters can be determined. Since the initial values are only supposed to be rough estimates, the missing parameters are taken from the known ones by only scaling them by a factor [9]. In order to get even closer to the measured impedance, an optimization with a fixed gradient only regarding the resonance frequencies is applied [3]. A resonance frequency is assigned to each parameter with the highest sensitivity. Then, the optimization is carried out matching this frequency only by adapting each parameter at a time. This leads to good results in a short computation time that can be seen in figure 4. Nevertheless, since the sensitivity with respect to several material parameters is is not sufficient, the following optimization using the custom electrode set-up is necessary for the determination of reliable parameters.
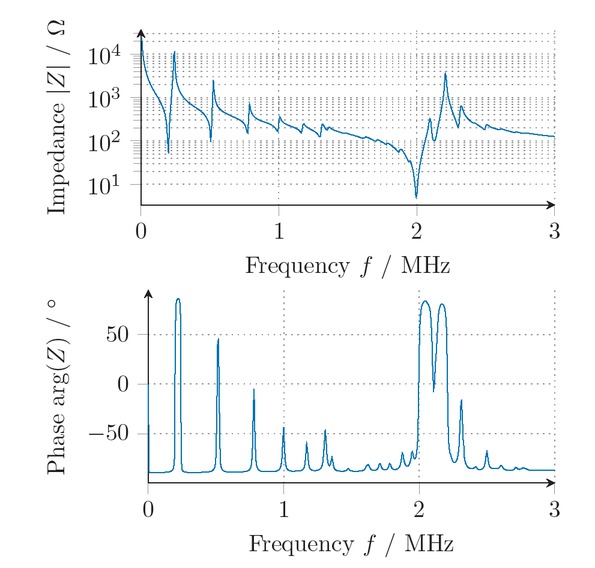
Complex impedance of a piezoceramic disc with base faces fully covered with electrodes.
Absolute impedance value of a piezoceramic disc with base faces fully covered with electrodes.  measurement,
measurement,  initial estimate,
initial estimate,  first optimization.
first optimization.
9 Optimization strategy
Applying the determined initial values, the optimization on the triple-ring set-up uses the whole frequency range of the measured impedances. As the objective function the deviation of the absolute value of the logarithmically scaled impedance is used:
Since the optimization problem is quite complex due to cross sensitivities between the different material parameters, a preliminary sensitivity analysis is used to determine an optimization strategy [4]. Different parameters incorporate different sensitivities on different frequency ranges. These sensitivities, normalized to ϒmax which is the highest sensitivity for a given parameter over the whole frequency range, are depicted in figure 5 where high sensitivities are illustrated by darker colours.

Normalized sensitivities for different frequency ranges (FR) (from table 1).
Frequency ranges (FR)
| FR | name | frequency range in MHz |
|---|---|---|
| 0 | 1. radial resonance | 0.125–0.38 |
| 1 | 2. radial resonance | 0.3875–0.6625 |
| 2 | 3. radial resonance | 0.66875–0.875 |
| 3 | 3. radial–1. thickness resonance | 0.88125–1.63125 |
| 4 | 1. thickness resonance | 1.6375–2.1875 |
| 5 | 1. thickness anti-resonance | 2.19375–3.125 |
| 6 | 1.–2. thickness resonance | 3.13125–5.475 |
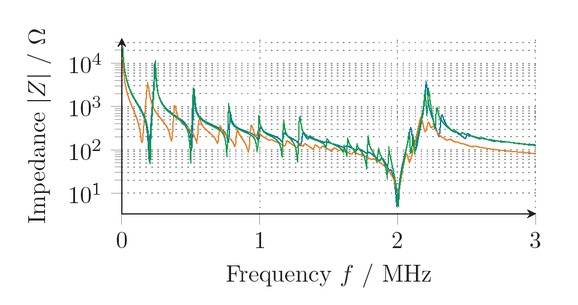
Thus, it is useful to optimize certain parameters in frequency ranges in which sensitivities are high for only this single parameter. If that is not possible it must be ensured that the other parameters have been optimized before- hand. The order of parameters in figure 5 thus depicts the optimization order and the black dots assign the frequency ranges, respectively. The optimization strategy followed to solve the inverse problem is to optimize only one parameter at a time before optimising all parameters in all frequency ranges afterwards. In order to evaluate the efficiency of this strategy, the simulated impedances are used instead of the measured ones since in this case the true material parameters are known. The described strategy allows to reobtain the full set of material parameters with negligible deviations for several exemplary materials. For measured impedances on PIC255, a good fit between measured and simulated impedances is archived for frequencies up to 2 MHz (see figure 6).
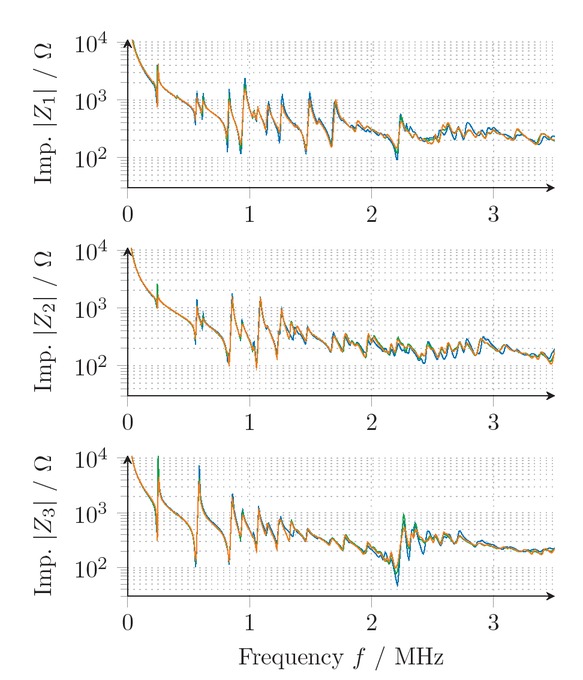
Optimized  and measured
and measured  impedances of PIC255.
impedances of PIC255.
10 Evaluating damping models
The results achieved show that the Rayleigh damping model does not allow to reach a good fit for the whole frequency range. Therefore, the constant and a Zener model (see section 5) is extended to three dimensions leading to further three or six parameters, respectively. The optimization strategy is used as before whereas the damping parameters are included at the end. Both alternative damping strategies yield similar results, but the constant model fits slightly better and needs significantly less parameters for the material description and is thus preferable. The estimated material parameters are given by the values in table 2.
Estimated material parameters
| c11 | 113GPa | e15 | 12.2Cm−2 |
| c12 | 87GPa | e31 | −5.9Cm−2 |
| c13 | 85GPa | e33 | 16.2Cm−2 |
| c33 | 125GPa | 0.02 | |
| c44 | 21GPa | 0.054 | |
| ε11 | 7.8nFm−1 | 0.004 | |
| ε3 | 7.87 nFm−1 |
11 Conclusions
It has been shown in advance that a triple-ring electrode set-up provides sufficient sensitivity for a material parameter characterization using a single disc-shaped piezoceramic specimen. This set-up is used for the determination of all material parameters. With a sensitivity analysis, distinct frequency ranges are identified that are best suitable for the optimization of single parameters. This is used to state a custom optimization strategy. The results show that using this strategy it is possible to reobtain simulated material data and to rebuild impedances measured on real piezoceramic discs. Furthermore, different damping models are compared and evaluated. Their extensions based on the eigenvalues of the stiffness matrix are able to represent the transversely isotropic material. It can be concluded that a constant damping term that only adds three more parameters leads to a good fit of measured and simulated impedances over a large frequency range.
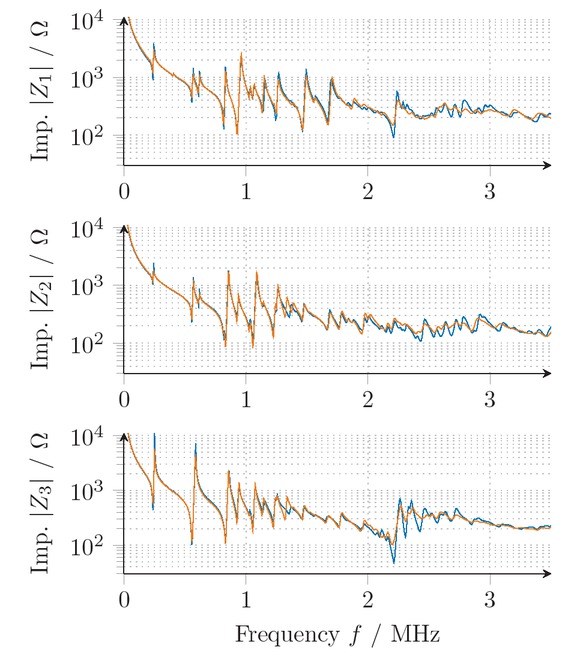
Measured  and optimized impedances using Zener
and optimized impedances using Zener  and constant
and constant  damping model of PIC255.
damping model of PIC255.
Acknowledgment
The authors would like to thank the German Research Foundation (DFG) for financial support of the research project 321120716.
References
[1] IEEE Standard on Piezoelectricity, 1987.Suche in Google Scholar
[2] F. Bause, J. Rautenberg, N. Feldmann, M. Webersen, L. Claes, H. Gravenkamp und B. Henning. Ultrasonic transmission measurements in the characterization of viscoelasticity utilizing polymeric waveguides. Measurement Science and Technology, 27(10):105601, 2016. 10.1088/09570233/27/10/105601.10.1088/0957-0233/27/10/105601Suche in Google Scholar
[3] N. Feldmann und B. Henning. Efficient optimisation of initial values for characterising piezoelectric material parameters. In Deutsche Gesellschaft für Akustik e.V., Fortschritte der Akustik, S. 1275–1278, 2018.Suche in Google Scholar
[4] N. Feldmann, B. Jurgelucks, L. Claes und B. Henning. A sensitivity-based optimisation procedure for the characterisation of piezoelectric discs. In 2019 International Congress on Ultrasonics, Proceedings of Meetings on Acoustics. ASA, 2019. 10.1121/2.0001070.10.1121/2.0001070Suche in Google Scholar
[5] B. Jurgelucks. Increased sensitivity in parameter identification problems for piezoelectrics doctoral thesis, Paderborn University, Paderborn, 2019.Suche in Google Scholar
[6] M. Kaltenbacher. Numerical Simulation of Mechatronic Sensors and Actuators Springer-Verlag, 2 Auflage, 2007. ISBN 354071359X.Suche in Google Scholar
[7] T. Lahmer. Forward and Inverse Problems in Piezoelectricity doctoral thesis, Universität Erlangen-Nürnberg, Erlangen-Nürnberg, 2008.Suche in Google Scholar
[8] S. J. Rupitsch. Piezoelectric Sensors and Actuators: Fundamentals and Applications Topics in Mining, Metallurgy and Materials Engineering. Springer Berlin Heidelberg, 2019. 10.1007/978-3-662-57534-5.10.1007/978-3-662-57534-5Suche in Google Scholar
[9] C. Unverzagt. Sensitivitätssteigerung durch Elektrodenmodifikation für die Materialparameterbestimmung von Piezokeramiken doctoral thesis, Paderborn University, Paderborn, 2018.Suche in Google Scholar
[10] W. Voigt. Lehrbuch der Kristallphysik B.G. Teubner, 1910.Suche in Google Scholar
[11] C. Zener. Elasticity and Anelasticity of Metals University of Chicago Press, 1948.Suche in Google Scholar
© 2020 Walter de Gruyter GmbH, Berlin/Boston
Artikel in diesem Heft
- Frontmatter
- Editorial
- XXXIV. Messtechnisches Symposium
- Beiträge
- Detektion der Auflagestege von Flachbett-Laserschneidmaschinen mittels Nahinfrarot-Beleuchtung
- Lichtfeld-Tiefenschätzung für die Vermessung teilspiegelnder Oberflächen
- Ganzheitliche Kalibrierung von Gewinden auf Basis eines dreidimensionalen Ansatzes
- Analyse von 3D-CT-Aufnahmen von Spänen zur Extrahierung der Segmentspanbildungsfrequenz
- Resolution enhancement through nearfield-assistance in interference microscopy
- Fertigung polymerer optischer Phasenplatten zur Erzeugung von Ringmoden mittels direkter Laserlithografie
- Direct-imaging DOEs for high-NA multi-spot confocal microscopy
- Methoden zur Minimierung des Rauscheinflusses durch Hitzeflimmern bei einem heterodynen Laser-Doppler-Vibrometer
- Inverse piezoelectric material parameter characterization using a single disc-shaped specimen
- Klassifikation von Grübchenschäden an Zahnrädern mittels Vibrationsmessungen
- Incorporation of phase information for improved time-dependent instrument recognition
- Akustische Zeitumkehrfokussierung in Wasser mittels FPGA-basierter Plattform
- De-Embedding-Ansatz zur Messung nichtidealer Kapazitäten mit kommerziellen Kapazitätssensoren
- Low-cost Indirect Measurement Methods for Self-x Integrated Sensory Electronics for Industry 4.0
- Reconfigurable Wide Input Range, Fully-Differential Indirect Current-Feedback Instrumentation Amplifier with Digital Offset Calibration for Self-X Measurement Systems
- A Compact Four Transistor CMOS-Design of a Floating Memristor for Adaptive Spiking Neural Networks and Corresponding Self-X Sensor Electronics to Industry 4.0
- Monte-Carlo-Methode zur Verringerung von Messfehlern bei der Materialparameterbestimmung mit Hohlraumresonatoren
- Bestimmung des Anregungsspektrums für kontaktlose breitbandige Messungen der Übertragungsfunktion mit Plasmaanregung und Laser-Doppler-Vibrometrie
- Self-sufficient vibration sensor for high voltage lines
- Flexibler organischer elektrochemischer Transistor als Biosensor für Organ-on-a-Chip
- Erkennung und Kompensation von Vergiftung durch Siloxane auf Halbleitergassensoren im temperaturzyklischen Betrieb
Artikel in diesem Heft
- Frontmatter
- Editorial
- XXXIV. Messtechnisches Symposium
- Beiträge
- Detektion der Auflagestege von Flachbett-Laserschneidmaschinen mittels Nahinfrarot-Beleuchtung
- Lichtfeld-Tiefenschätzung für die Vermessung teilspiegelnder Oberflächen
- Ganzheitliche Kalibrierung von Gewinden auf Basis eines dreidimensionalen Ansatzes
- Analyse von 3D-CT-Aufnahmen von Spänen zur Extrahierung der Segmentspanbildungsfrequenz
- Resolution enhancement through nearfield-assistance in interference microscopy
- Fertigung polymerer optischer Phasenplatten zur Erzeugung von Ringmoden mittels direkter Laserlithografie
- Direct-imaging DOEs for high-NA multi-spot confocal microscopy
- Methoden zur Minimierung des Rauscheinflusses durch Hitzeflimmern bei einem heterodynen Laser-Doppler-Vibrometer
- Inverse piezoelectric material parameter characterization using a single disc-shaped specimen
- Klassifikation von Grübchenschäden an Zahnrädern mittels Vibrationsmessungen
- Incorporation of phase information for improved time-dependent instrument recognition
- Akustische Zeitumkehrfokussierung in Wasser mittels FPGA-basierter Plattform
- De-Embedding-Ansatz zur Messung nichtidealer Kapazitäten mit kommerziellen Kapazitätssensoren
- Low-cost Indirect Measurement Methods for Self-x Integrated Sensory Electronics for Industry 4.0
- Reconfigurable Wide Input Range, Fully-Differential Indirect Current-Feedback Instrumentation Amplifier with Digital Offset Calibration for Self-X Measurement Systems
- A Compact Four Transistor CMOS-Design of a Floating Memristor for Adaptive Spiking Neural Networks and Corresponding Self-X Sensor Electronics to Industry 4.0
- Monte-Carlo-Methode zur Verringerung von Messfehlern bei der Materialparameterbestimmung mit Hohlraumresonatoren
- Bestimmung des Anregungsspektrums für kontaktlose breitbandige Messungen der Übertragungsfunktion mit Plasmaanregung und Laser-Doppler-Vibrometrie
- Self-sufficient vibration sensor for high voltage lines
- Flexibler organischer elektrochemischer Transistor als Biosensor für Organ-on-a-Chip
- Erkennung und Kompensation von Vergiftung durch Siloxane auf Halbleitergassensoren im temperaturzyklischen Betrieb

