Home Calculation method of elastic modulus for carbon fiber-reinforced plastics considering inhomogeneous interphase
Article Open Access

Calculation method of elastic modulus for carbon fiber-reinforced plastics considering inhomogeneous interphase

  • Pengfei Bu , Huiqi Ren , Wenjun Ruan and Kai Dong EMAIL logo
Published/Copyright: December 2, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Science and Engineering of Composite Materials
From the journal Science and Engineering of Composite Materials Volume 29 Issue 1

Abstract

The characteristic of interphase has a significant influence on the macroscopic performance of carbon fiber-reinforced plastics (CFRP). To investigate the effect of interphase on composite elastic modulus, a representative volume element (RVE) of unidirectional CFRP with inhomogeneous interphase was established. Based on the bridging model, a theoretical calculation method of composite elastic modulus was given. The elastic modulus of T300/BSL914C composites was obtained by the theoretical method. Results are in good agreement with the finite element method and experimental data. Four types of interphase models were given including inhomogeneous transversely isotropic, inhomogeneous isotropic, homogeneous transversely isotropic, and homogeneous isotropic. The results demonstrate that interphase type has an influence on the prediction of CFRP composites’ elastic modulus. With the increase of thickness, the prediction error of elastic modulus caused by interphase type increases rapidly. Furthermore, the relationship between composite elastic modulus and interphase thickness and stiffness is analyzed. With the increase in thickness, the changes in shear modulus G 12 and Poisson’s ratio ν23 are more evident than in other elastic properties, and with the enhancement of interphase stiffness, the increase of G 12 is the most significant.

Keywords: composites; interphases; microstructures; bridging model; micro-mechanics

1 Introduction

Carbon fiber-reinforced plastics (CFRP) are widely used in aerospace, weapons, and other fields because of their excellent mechanical property and design ability [1,2,3]. However, it is challenging to predict the mechanical properties due to the complicated micro-structures and insufficient knowledge of the interface between fiber and matrix. Several micromechanical theoretical models have been developed to predict the elastic property of composites, including the Mori-Tanaka model [4,5,6], self-consistent model [7], and bridging model [8,9,10]. Based on Eshelby’s equivalent inclusion theory and ideal interface assumption, several homogenization methods are presented to evaluate the mechanical properties of the fiber-reinforced composite [11]. The relationship between microstructure characteristics and macro properties is established by the two-phase models, which brings great convenience to the design of composites.

However, scholars found that there is an interphase region with a thickness of tens to hundreds of nanometers between fiber and matrix through experiments [12,13,14], and its mechanical properties are different from those of the fiber and matrix and change in a gradient from matrix to the fiber [15,16]. To analyze the effect of interphase characteristics on the properties of composites, three-phase micromechanical models containing interphase have been established [17,18,19,20,21,22,23]. Wang et al. [2] established a three-phase representative volume element (RVE) model with interphase by pre-inserted cohesive layer between fiber and matrix and analyzed the effect of interphase modulus, thickness, and Poisson’s ratio on the mechanical properties of CFRP. Bohayra Mortazavi [24] assumed that the interphase thickness is related to the fillers radius, and there are perfect bonding contacts between fiber, matrix, and interphase. Kari et al. [25] used square and hexagon three-phase RVE models, respectively, to evaluate the effect of interphase stiffness and volume fraction on the overall properties of unidirectional CFRP and spherical inclusion composites with random distribution.

Interphase plays an important role in the stress–strain transfer between fiber and matrix. It is of great significance for predicting the properties of composites to the accurate description of interphase mechanical properties [26,27,28]. However, the interphase is a non-uniform region with a complex structure and thin thickness [29], and the mechanical properties are variable from the fiber surface to the matrix surface [30,31]. It is difficult to obtain the complete mechanical properties of interphase, including thickness, stiffness, and strength. To study the effect of interphase on composite properties, the mechanical properties of interphase need to be assumed and simplified to a certain extent [2,21]. Sun et al. [1] simplified the interphase as an isotropic material, adopted the exponential gradient model to describe the variation of interphase properties and took the average value of the model as the mechanical properties of interphase, and established a three-phase RVE model. Compared with the traditional two-phase model, the modified RVE model adding the interphase region has a higher accuracy of simulation results. Lim et al. [15] assumed that the interphase properties were constant and gradient functions, respectively, and analyzed the effect of mass fractions of fiber on the equivalent elastic modulus E c of composites by Mori Tanaka and the finite element (FE) model. The results showed that interphase parameters must be considered carefully when predicting E c using the FE model. Wang et al. [32] regarded the interphase as a non-uniform isotropic region and assigned its properties as exponential variation and established an RVE model with interphase. The interphase thickness was divided into 10 layers of pixels along the radius directions to consider the non-uniform mechanical properties of the interphase. And Wang studied the macroscopic mechanical behavior of unidirectional CFRP by using a fast Fourier transform simulation. Compared to the RVE model with a zero-thickness interface, the stress–strain results of the three-phase RVE model are in good agreement with the experiment data.

Most of the studies, which deal with the three-phase RVE model of composites, are restricted to the isotropic interphase model, and the assumption of isotropic interphase is different from the actual mechanical properties of interphase to a certain extent, which affects the prediction accuracy of macro mechanical properties of composites and limits the application scope of this kind of model. To accurately describe the interphase characteristics and investigate the influence of interphase on the elastic modulus of CFRP, an RVE model with inhomogeneous interphase was established. Using the discretization method, the interphase was divided into several transverse isotropic layers along the radial direction to consider the non-uniform interphase mechanical properties. Based on the bridging model and the concept of equivalent fiber, a calculation method of composite equivalent mechanical properties was proposed. The effects of the interphase characteristics (material type, thickness, stiffness, etc.) on the composite elastic modulus were discussed. This study provides a theoretical calculation method for the macro elastic modulus of CFRP, which considers the influence of interphase mechanical properties in more detail. Compared with the FE method, this method could rapidly predict the elastic properties of CFRP composites with different kinds of interphase. And it could be useful to guide the design of the RVE model with interphase and provide guidance for the optimization design of CFRP composites

2 Micromechanics theoretical model

2.1 RVE model with the inhomogeneous interphase

The distribution of fibers in the matrix is approximately periodic, and the relationship between the micro characteristics and the macro mechanical properties of composites can be obtained by selecting an appropriate RVE model [33,34]. Because there is a transition region between fiber and matrix, a non-uniform interphase region was added between fiber and matrix. Assuming that fibers are regularly arranged in CFRP composites [21], a square RVE model was established (Figure 1). The model consists of three phases, namely fiber, interphase, and matrix, respectively.

(1) l = π ( R f ) 2 V f ,

where l is the length of RVE, R f is the fiber radius, t is the thickness of interphase, t = R i − R f , and V f is the volume fraction of fiber.

Figure 1 Three-phase RVE model of composites with interphase.
Figure 1

Three-phase RVE model of composites with interphase.

In the three-phase RVE model, the fiber and matrix are assumed to be transverse isotropic and isotropic, respectively. It has been demonstrated that the mechanical properties of the interphase region decrease as it transitioned from the fiber to the matrix [15,16]. In this article, it is assumed that interphase region properties exhibit a gradient as shown in Figure 2, and its variation obeys the power function [22,31], as shown in equation (2). The elastic properties of component constituents are listed in Table 1, where E is the elastic modulus, G is the shear modulus, ν is Poisson’s ratio, the superscripts f, m, and i represent the fiber, matrix, and interphase, respectively. The subscript 1 represents the fiber axis direction; 2 and 3 donate the transverse direction.

(2) F ( r ) = a × r b ,

where F represents the composite elastic property; a and b are constants; r is the distance from the position to the fiber axis.

Figure 2 Gradient distribution of interphase mechanical property.
Figure 2

Gradient distribution of interphase mechanical property.

Table 1

Elastic properties of composite constituents

Material Elastic modulus Shear modulus Poisson’s ratio
Fiber E 11 f E 22 f G 12 f ν 12 f ν 23 f
Interphase E 11 i ( r ) E 22 i ( r ) G 12 i ( r ) ν 12 i ( r ) ν 23 i ( r )
Matrix E m G m ν m

It is assumed that there are perfect bonding conditions between fiber, interphase, and matrix. The elastic properties change continuously at the inner ( r = R f ) and outer ( r = R i ) boundaries of the interphase [1]. The elastic properties of the interphase at the boundaries are listed in Table 2.

Table 2

Elastic properties of interphase at the boundaries

E 11 i ( r ) E 22 i ( r ) G 12 i ( r ) ν 12 i ( r ) ν 23 i ( r )
r = R f E 11 f E 22 f G 12 f ν 12 f ν 23 f
r = R i E m E m G m ν m ν m

2.2 The bridging model

Based on the traditional two-phase composite theory, the stress and strain tensors of homogenized composites meet equations (3) and (4) in the initial stage of loading [35,36].

(3) σ = V f σ f + V m σ m ,

(4) ε = V f ε f + V m ε m ,

where σ and ε are the average stress and strain tensors of composites respectively, and V is the volume fraction. The superscript, f and m denote fiber and matrix, respectively.

Considering the internal stress tensors at the interface between fiber and matrix are equal, there is a bridging matrix a making the stress tensors of the fiber and matrix satisfy equation (5). And the constitutive equation of fiber, matrix, and composites could be expressed as the equation (6).

(5) σ m = a σ f ,

(6) ε = S σ ε f = S f σ f ε m = S m σ m .

Substituting equations (5) and (6) into equations (3) and (4), the flexibility tensor S of composites is derived by

(7) S = ( V f I + V m a ) − 1 ( S f V f + S m V m a ) .

The relationship between three-dimensional stress tensor σ and strain tensor ε and flexibility tensor S could be expressed as

(8) ε 11 ε 22 ε 33 ε 23 ε 12 ε 13 = 1 E 11 − ν 12 E 11 − ν 12 E 11 0 0 0 − ν 12 E 11 1 E 22 − ν 23 E 22 0 0 0 − ν 12 E 11 − ν 23 E 22 1 E 22 0 0 0 0 0 0 1 G 23 0 0 0 0 0 0 1 G 12 0 0 0 0 0 0 1 G 12 σ 11 σ 22 σ 33 σ 23 σ 12 σ 13 .

Based on the Mori-Tanaka model, considering the consistency of the bridging matrix, Huang [36] modified the calculation method of the bridging matrix and proposed the bridging model. By adding bridging parameters α and β , the explicit expression of the bridging matrix is given. The modified bridging model greatly simplifies the expression and improves the calculation accuracy. The bridging matrix a of the bridging model could be expressed as

a = a 11 a 12 a 13 0 0 0 0 a 22 0 0 0 0 0 0 a 33 0 0 0 0 0 0 a 44 0 0 0 0 0 0 a 55 0 0 0 0 0 0 a 66 .

When the matrix is transversely isotropic material, the parameters of the bridging matrix could be expressed as [37]

(9) a 11 = E 11 m / E 11 f a 22 = a 33 = a 44 = β + ( 1 − β ) E 22 m / E 22 f a 55 = a 66 = α + ( 1 − α ) G 12 m / G 12 f a 12 = a 13 = E 11 f ν 12 m − E 12 m ν 12 f E 11 f − E 11 m ( a 22 − a 11 ) α = β = 0.3 .

Substituting the bridging matrix a into equation (7), the equivalent elastic modulus of composites is derived based on equation (8) [36]. The explicit expression of composite elastic modulus could be expressed as

(10) E 1 1 = V f E 11 f + V m E 11 m ,

(11) ν 12 = V f ν 12 f + V m ν 12 m ,

(12) E 2 2 = ( V f + V m a 11 ) ( V f + V m a 22 ) ( V f + V m a 11 ) ( V f S 22 f + a 22 V m S 22 m ) + V f V m ( S 21 m − S 21 f ) a 12 ,

(13) G 12 = G 12 f G 12 m ( V f + V m a 66 ) V f G 12 m + V m G 12 f a 66 ,

(14) G 23 = G 23 f G 23 m ( V f + V m a 22 ) V f G 23 m + V m G 23 f a 22 .

2.3 The calculation method of elastic modulus of CFRP

Considering the inhomogeneity of interphase mechanical properties, the interphase was discretized into a multi-layer concentric cylinder structure along the radial direction, and every sub interphase layer is assumed to be a uniform transversely isotropic material [8], as shown in Figure 3. The mechanical properties of sub-interphase layer are obtained based on the equation (15). Where the subscript j represents the sub-interphase layer j.

(15) F = F ( R f ) + F ( R 1 i ) 2 , j = 1 , F = F ( R j − 1 i ) + F ( R j i ) 2 , 1 < j < n , F = F ( R j − 1 i ) + F ( R i ) 2 , j = n .

Figure 3 RVE model after discretization of interphase.
Figure 3

RVE model after discretization of interphase.

In this model, the inhomogeneous interphase is divided into n layers of uniform interphase firstly, and the thickness of every layer is t/n. Then, a two-phase RVE model could be composed of the fiber and the first sub-interphase layer, and its elastic modulus could be obtained by the bridging model. And then, as an equivalent fiber, it forms a new two-phase RVE model with the next sub-interphase layer. Finally, the elastic modulus of composites with inhomogeneous interphase could be obtained by cycling calculation, as shown in Figure 4. The theoretical calculation framework is shown in Figure 5. And the equivalent flexibility tensor S k of the material in cycle k could be expressed as equation (16). Substituting equation (7) into equations (10)–(14), the elastic modulus of composites in the kth cycle can be obtained.

(16) S k = ( V k f I + ( 1 − V k f ) a k ) − 1 ( S k f V k f + S k m ( 1 − V k f ) a k ) .

Where

(17) V 1 f = ( R f ) 2 ( R 1 i ) 2 S 1 f = S f S 1 m = S 1 i a 1 = a ( ( S 1 f ) − 1 , ( S 1 m ) − 1 ) k = 1 ,

(18) V k f = ( R k − 1 i ) 2 ( R k i ) 2 S k f = S k − 1 S k m = S k i a k = a ( ( S k f ) − 1 , ( S k m ) − 1 ) 1 < k < n + 1 ,

(19) V n + 1 f = π ( R f + t ) 2 l 2 S n + 1 f = S n S n + 1 m = S m a n + 1 = a ( ( S n + 1 f ) − 1 , ( S n + 1 m ) − 1 ) k = n + 1 .

Figure 4 The modal of equivalent fiber.
Figure 4

The modal of equivalent fiber.

Figure 5 Theoretical calculation framework of elastic modulus of composites with inhomogeneous interphase.
Figure 5

Theoretical calculation framework of elastic modulus of composites with inhomogeneous interphase.

3 FE modeling

Through FE simulation, the mechanical properties of composites can be obtained [38,39]. In this section, the finite element method (FEM) and theoretical calculation method were used to simulate the elastic properties of unidirectional T300 carbon fiber-reinforced BSL914C polymer (T300/BSL914C) composites, and the comparative analyses of results against experimental data were presented. The elastic properties of T300 fiber and BSL914C epoxy resin are listed in Table 3.

Table 3

Elastic properties of the constituent phases of T300/BSL914C composites

Material E z (GPa) E y (GPa) G xz (GPa) ν zy ν xy
T300 230 15 15 0.2 0.07
BSL914C 4.0 1.48 0.35

3.1 The FE model of RVE

The FE model of RVE with inhomogeneous interphase was established, as shown in Figure 6. The geometric dimensions of the model are l x × l y × l z = 8 × 8 × 10 μm. The diameter of the T300 fiber is 7 μm. The fiber volume fraction V f is 0.6. The interphase thickness is 0.1 μm, which is divided into five layers on average. The interphase elastic properties of sub-layers are listed in Table 4. Where Z of the coordinate axis represents the axial direction of the fiber, X and Y represent the transverse direction.

Figure 6 FE Model of RVE with inhomogeneous interphase.
Figure 6

FE Model of RVE with inhomogeneous interphase.

Table 4

Elastic properties of sub-interphase layers

Interphase layer E z (GPa) E y (GPa) G xz (GPa) ν zy ν xy
Layer 1 165.7 13.2 12.2 0.21 0.08
Layer 2 73.1 10.1 7.6 0.24 0.12
Layer 3 32.4 7.8 4.8 0.27 0.16
Layer 4 14.4 6.0 3.0 0.30 0.22
Layer 5 6.5 4.6 1.9 0.33 0.30

3.2 Periodic boundary conditions (PBC) of RVE

The unidirectional CFRP composite is formed by the periodic arrangement of RVE. The stress and strain fields meet the continuity and periodicity [40,41]. The PBC were applied to the RVE model to simulate the composite macroscopic deformations of axial tensile, transverse tensile, and XZ in-plane shear [13,15,22]. The boundary conditions of tensile and shear deformation were set as equations (20)–(22), where Z (x, y, l z ) is the displacement of points on the plane (x, y, l z ) in the Z direction, and ε z is the strain of the model in the Z direction.

The PBC of uniaxial tensile deformation on the RVE model:

(20) X ( l x , y , z ) − X ( 0 , y , z ) = l x ε x X ( x , l y , z ) − X ( x , 0 , z ) = 0 X ( x , y , l z ) − X ( x , y , 0 ) = 0 ,

(21) Y ( l x , y , z ) − Y ( 0 , y , z ) = 0 Y ( x , l y , z ) − Y ( x , 0 , z ) = l y ε y Y ( x , y , l z ) − Y ( x , y , 0 ) = 0 ,

(22) Z ( l x , y , z ) − Z ( 0 , y , z ) = 0 Z ( x , l y , z ) − Z ( x , 0 , z ) = 0 Z ( x , y , l z ) − Z ( x , y , 0 ) = l z ε z .

The PBC of shear deformation on the RVE model:

(23) X ( l x , y , z ) − X ( 0 , y , z ) = l x ε x X ( x , y , l z ) − X ( x , y , 0 ) = l x γ x z Y ( x , l y , z ) − Y ( x , 0 , z ) = l y ε y Z ( x , y , l z ) − Z ( x , y , 0 ) = l z ε z .

3.3 Result analysis

The PBC was imposed on the corresponding surface in the form of node coupling pairs and constraint equations. Under the action of the PBC, the parallel planes of the RVE model have the same stress and deformation fields, and the stress contour plots of the RVE are shown in Figure 7.

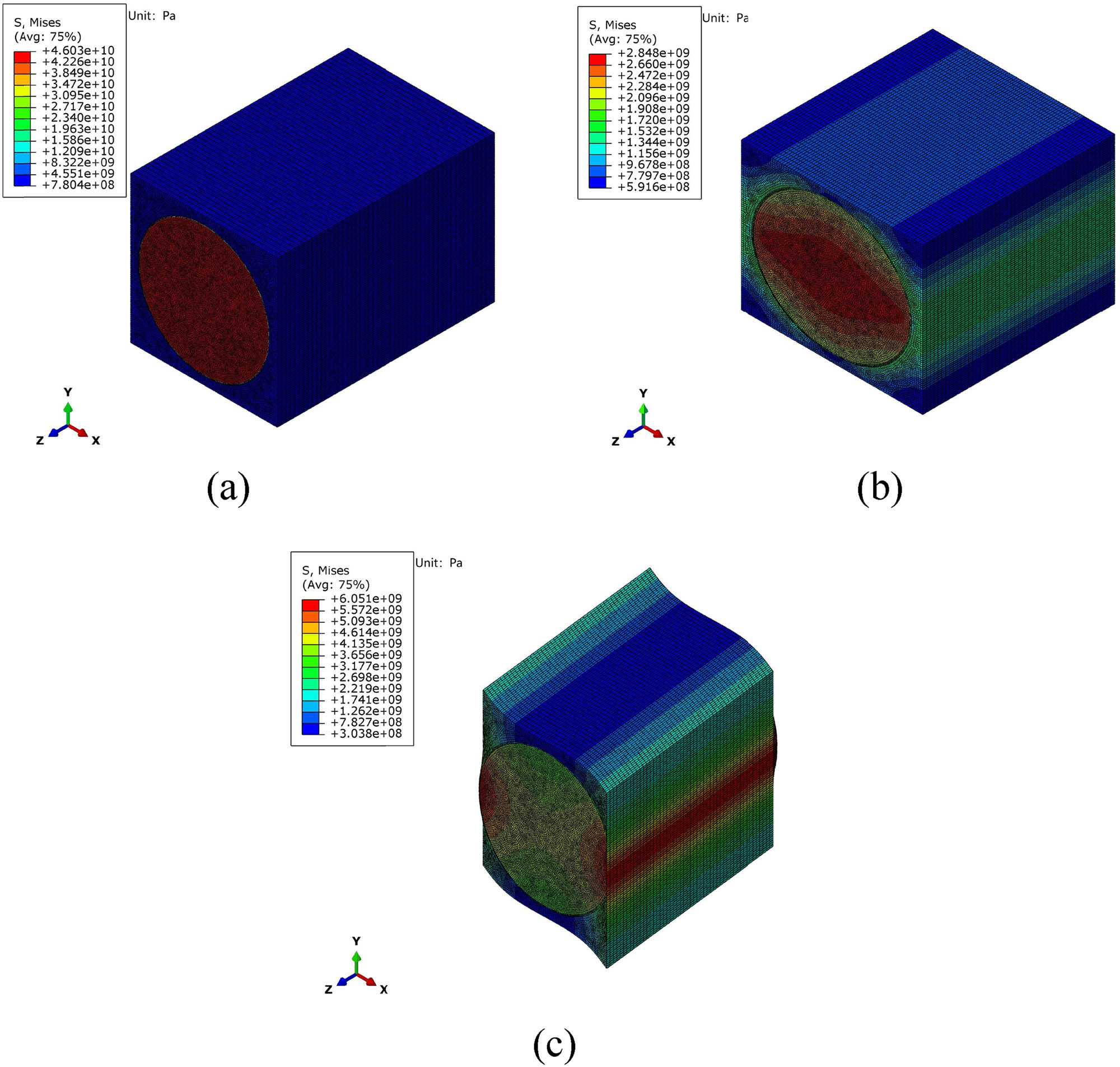
Figure 7 Von Mises stress contour plot of RVE modal: (a) tensile deformation in the Z direction, (b) tensile deformation in the X direction, and (c) the shear deformation of the plane ZX.
Figure 7

Von Mises stress contour plot of RVE modal: (a) tensile deformation in the Z direction, (b) tensile deformation in the X direction, and (c) the shear deformation of the plane ZX.

Loaded the axial strain ε z on the RVE model, the sum of reaction forces F z (x, y, 0) in the Z direction of the plane (x, y, 0) and the average displacements Y (x, 0, z) and Y (x, l y , z) were obtained by FE simulation. The equivalent elastic modulus E z and Poisson’s ratio ν zy of the RVE model could be calculated based on the equations (24) and (25).

(24) E z = F z ( x , y , 0 ) l x l y ε z ,

(25) ν z y = ∣ Y ( x , l y , z ) − Y ( x , 0 , z ) ∣ l y ε z .

The transverse strain ε y and shear strain γ xz were loaded on the RVE, respectively. The equivalent elastic modulus E y , Poisson’s ratio ν xy and shear modulus G xz could be obtained from equations (26)–(28).

(26) E y = F y ( x , 0 , z ) l x l z ε y ,

(27) ν x y = ∣ X ( l x , y , z ) − X ( 0 , y , z ) ∣ l x ε y ,

(28) G x z = τ x z γ x z .

Figure 8 shows the result of element convergence verification and the elastic modulus E 2 becomes stable when the number of elements reached 0.74 million. The FEM and theoretical calculation results are compared with the results given in reference [22] and experimental data of T300/BSL914C composites [42]. The results are shown in Table 5. The calculation results of the bridging model for E z , E y , G xz , ν zy , and ν xy are close to the experimental data; the errors are 2.4, 11.3, 1.8, 8.2, and 26.3% respectively, as shown in Figure 9. In general, the predicted results of the elastic properties calculation method of CFRP composites with inhomogeneous interphase based on the bridging model are in good agreement with the experimental data.

Figure 8 The element convergence verification in accordance with the elastic modulus E 2. The blue bar shows the results for different numbers of elements, and the red line shows the trend of results.
Figure 8

The element convergence verification in accordance with the elastic modulus E 2. The blue bar shows the results for different numbers of elements, and the red line shows the trend of results.

Table 5

Comparison of T300/BSL914C composite equivalent properties

E z (GPa) E y (GPa) G xz (GPa) ν zy ν xy
FEM 142 9.6 4.8 0.25 0.26
Bridging model 141 9.8 5.6 0.26 0.30
Reference 145 8.5 5.9 0.23 0.10
Experiment 138 11 5.5 0.28 0.40
Figure 9 Comparison of errors in the prediction results of composite elastic properties by different calculation methods compared with the experiment data.
Figure 9

Comparison of errors in the prediction results of composite elastic properties by different calculation methods compared with the experiment data.

4 Effect of interphase characteristics on composite elastic properties

Interphase controls the transfer of stress and strain between fiber and matrix and affects the macro mechanical properties of composites [25,43,44]. In this section, the effects of interphase type and stiffness on the calculation results of elastic modulus of T300/BSL914C composites and the trend of composite equivalent elastic properties with interphase thickness were analyzed.

4.1 Effect of interphase type on composite elastic properties

Based on the theoretical model in Section 2, four types of interphase models were established, including inhomogeneous transverse isotropy (ITI), inhomogeneous isotropy (II), homogeneous transverse isotropy (HTI), and homogeneous isotropy (HI). The composite elastic properties calculation methods with different interphase types were used to predict the elastic properties of T300/BSL914C, and the effect of interphase thickness on the prediction results was analyzed. The elastic properties and their determination methods of interphase are shown in Table 6.

Table 6

Elastic properties and their determination methods of different interphase types

Interphase type Mechanical parameters F The law of interphase properties
ITI E 11 i , E 22 i , G 12 i , ν 12 i , ν 23 i F ( r ) = a × r b
II E 22 i , ν 23 i F ( r ) = a × r b
HTI E 11 i , E 22 i , G 12 i , ν 12 i , ν 23 i F = ( F f + F m ) / 2
HI E 22 i , ν 23 i F = ( F f + F m ) / 2

Compared with the experimental data, the prediction errors of elastic property of RVE models with different interphase types are shown in Figure 10. For axial elastic modulus E 1 and shear modulus G 12, the model of interphase type II has the highest prediction accuracy, which error is less than 1%, and the error of interphase type HTI is the largest, which is 4%. For the transverse elastic modulus E 2, the errors of interphase ITI and HI are 10.6 and 10.7% respectively, which are less than those of interphase types II and HTI (11.3%). For Poisson’s ratio ν 12, the prediction accuracy of transversely isotropic interphase type is higher than that of isotropic. For the Poisson’s ratio ν 23, the errors of the four interphase types are about 26%.

Figure 10 Errors of T300/BSL914C elastic property with four interphase types compared with the experiment data.
Figure 10

Errors of T300/BSL914C elastic property with four interphase types compared with the experiment data.

The effect of interphase thickness on composite elastic properties with different interphase types was analyzed, as shown in Figures 11 and 12. When the thickness increases from 0.1 to 0.5 μm, the calculation results of different interphase types are significantly different. The increase of E 1 of isotropic interphase is less than 1% and that of transverse isotropic interphase is more than 5%. The elastic modulus E 2 has the same increase for different interphase types. Poisson’s ratio ν 12 of transversely isotropic interphase decreased by 4.3% and that of isotropic interphase decreased by 8.1 and 9.9%, respectively. Poisson’s ratio ν 23 of the interphase type HTI decreases by 26%, which is higher than that of the interphase type II by 19%. The ν 23 of interphase types ITI and HI have the same decrease, which is 24%. The increase in shear modulus G 12 of the interphase type HTI by 32% is significantly higher than that of the II by 16%. The increases of G 12 of ITI and HI interphase types are the same, which are 21%.

Figure 11 Effect of interphase thickness on the composite elastic property with different interphase types: (a) elastic modulus E 1, (b) elastic modulus E 2, (c) Poisson’s ratio ν 12, (d) Poisson’s ratio ν 23 and (e) shear modulus G 12.
Figure 11

Effect of interphase thickness on the composite elastic property with different interphase types: (a) elastic modulus E 1, (b) elastic modulus E 2, (c) Poisson’s ratio ν 12, (d) Poisson’s ratio ν 23 and (e) shear modulus G 12.

Figure 12 The variation of composite elastic property with different interphase types when the interphase thickness increases from 0.1 to 0.5 μm.
Figure 12

The variation of composite elastic property with different interphase types when the interphase thickness increases from 0.1 to 0.5 μm.

The calculation results of mechanical property of four interphase types RVE models show that when the interphase thickness is 0.1 μm, the calculation error caused by the interphase type is less than 3%, and it increases rapidly with the increase of interphase thickness, and the maximum error increases from 2.7 to 16.2% as shown in Figure 13. Based on the method of Linear Interpolation, the conclusions can be obtained, when the ratio of interphase thickness to the fiber radius t R f is less than 0.04, which error is less than 5%, the influence of interphase type on the calculation results of elastic property of CFRP composites can be ignored, and when the ratio is more than 0.09, which error is more than 10%, it is necessary to accurately consider the properties of composite interphase in order to improve the accuracy of prediction results.

Figure 13 Effect of interphase thickness on the composite elastic property parameter calculation errors: (a) the effect of interphase type on composite elastic properties with the interphase thickness of 0.1 μm, and (b) the effect of interphase type on composite elastic properties with the interphase thickness of 0.5 μm.
Figure 13

Effect of interphase thickness on the composite elastic property parameter calculation errors: (a) the effect of interphase type on composite elastic properties with the interphase thickness of 0.1 μm, and (b) the effect of interphase type on composite elastic properties with the interphase thickness of 0.5 μm.

The results of four interphase models show that the elastic properties of CFRP composites are linearly related to the interphase thickness. With the thickness increasing, the equivalent moduli E 1, E 2, and G 12 of the composites increase. Poison’s ratios ν 12 and ν 23 decrease. And the variation range of G 12 and ν 23 are significantly higher than other elastic property parameters.

4.2 Effect of mechanical properties of interphase on the CFRP elastic properties

In this section, the effect of interphase stiffness on the CFRP composite elastic properties was analyzed by changing the gradient of mechanical properties in the interphase region. It is assumed that the interphase is an inhomogeneous transversely isotropic material, and its properties change in cubic function, quadratic function, and linear function, respectively, as shown in Figure 14.

Figure 14 Gradients of elastic modulus of interphase material with different functions.
Figure 14

Gradients of elastic modulus of interphase material with different functions.

The results show that with the increase of interphase thickness, the elastic properties of CFRP with different interphase properties gradients have different change rates (Figure 15). With the increase in interphase thickness, the modulus E 1, E 2, and G 12 of the linear function increase faster than that of the cubic function. Poisson’s ratios ν 12 and ν 23 of the cubic function decrease faster than those of the linear function.

Figure 15 Effect of interphase thickness on composite properties with different interphase mechanical property gradients: (a) elastic modulus E 1, (b) elastic modulus E 2, (c) Poisson’s ratio ν 12, (d) Poisson’s ratio ν 23, and (e) shear modulus G 12.
Figure 15

Effect of interphase thickness on composite properties with different interphase mechanical property gradients: (a) elastic modulus E 1, (b) elastic modulus E 2, (c) Poisson’s ratio ν 12, (d) Poisson’s ratio ν 23, and (e) shear modulus G 12.

The mechanical properties of composites with different property gradient interphases are compared when the thickness of the interphase is 0.5 μm, as shown in Figure 15. It can be included that when the interphase properties increase, the macroscopic mechanical properties of the composites are enhanced in varying degrees. E 1 and E 2 increased by 6.9 and 6.4% respectively, and the increase in Poison’s ratio is less than 5%. The increase of G 12 is significantly higher than that of other elastic properties, which is 13.4% (Figure 16).

Figure 16 Effect of the increase of interphase properties on composite mechanical properties when the interphase thickness is 0.5 μm.
Figure 16

Effect of the increase of interphase properties on composite mechanical properties when the interphase thickness is 0.5 μm.

5 Conclusion

In this article, the RVE model of CFRP with inhomogeneous interphase was constructed, and the theoretical calculation method of composite elastic modulus considering the inhomogeneity of interphase was established. The calculation results of this method are agreed with the FEM results and experimental data, indicating that the method is effective for predicting the elastic modulus of CFRP.

The calculation results of theoretical models with four different interphase types show that the interphase type has an important influence on the elastic property of CFRP composites and the prediction error of elastic property caused by interphase type increases rapidly with the increase in interphase thickness. When the ratio of interphase thickness to the fiber radius is less than 0.04, the influence of interphase type on elastic property of CFRP composites can be ignored. When the ratio rise to 0.09, which the prediction error is more than 10%, it is necessary to accurately consider the properties of composite interphase in order to improve the accuracy of prediction results.

The interphase thickness and stiffness have an important effect on the composite elastic properties G 12 and ν 23. The results show that with the increase of interphase thickness, the variation range of G 12 and ν 23 is significantly higher than that of other properties. The elastic modulus of the composites is enhanced in varying degrees with the interphase properties increased, and the increase of G 12 is the most significant compared with other modulus.

  1. Funding information: The authors state no funding involved.

  2. Conflict of interest: The authors state no conflict of interest.

  3. Data availability statement: The raw/processed data required to reproduce these findings cannot be shared at this time as the data also form part of an ongoing study.

Reference

[1] Sun Q, Meng Z, Zhou G, Zhou G, Lin S, Kang H, et al. Multi-scale computational analysis of unidirectional carbon fiber reinforced polymer composites under various loading conditions. Compos Struct. 2018;196(7):30–43.10.1016/j.compstruct.2018.05.025Search in Google Scholar

[2] Wang X, Zhang J, Wang Z, Zhou S, Sun X. Effects of interphase properties in unidirectional fiber reinforced composite materials. Mater Des. 2011;32(6):3486–92.10.1016/j.matdes.2011.01.029Search in Google Scholar

[3] Grisol de Melo, dos Santos S, Christina J, Klein TB, Polte J, Uhlmann E, et al. Evaluation of carbon fiber reinforced polymer – CFRP – machining by applying industrial robots. Sci Eng Compos Mater. 2021;28:285–98.10.1515/secm-2021-0026Search in Google Scholar

[4] Vorel J, Sejnoha M. Evaluation of homogenized thermal conductivities of imperfect carbon-carbon textile composites using the mori-tanaka method. Struct Eng Mech. 2009;33(4):429–46.10.12989/sem.2009.33.4.429Search in Google Scholar

[5] Yun G, Zhu F, Lim H, Choi H. A damage plasticity constitutive model for wavy CNT nanocomposites by incremental Mori-Tanaka approach. Compos Struct. 2021;258:113178.10.1016/j.compstruct.2020.113178Search in Google Scholar

[6] Fedotov AF. Mori-Tanaka experimental-analytical model for predicting engineering elastic moduli of composite materials. Compos Part B-Eng. 2022;232:109635.10.1016/j.compositesb.2022.109635Search in Google Scholar

[7] Zhang B, Yu X, Gu B. A generalized self-consistent model for interfacial debonding behavior of fiber reinforced rubber matrix sealing composites. J Shanghai Jiaotong Univ (Sci). 2017;22(3):343–8.10.1007/s12204-017-1841-5Search in Google Scholar

[8] Yin D, Li B, Xiao H. Prediction of three-dimensional elastic behavior of filament-wound composites based on the bridging model. Def Technol. 2021;17(2):609–16.10.1016/j.dt.2020.04.006Search in Google Scholar

[9] Peng X, Yong H, Zhou Y. Damage analysis of superconducting composite wire with bridging model. Acta Mech Solida Sin. 2018;31(1):19–31.10.1007/s10338-018-0012-zSearch in Google Scholar

[10] Tan Q, Liu L, Liu Y, Leng J. Thermal mechanical constitutive model of fiber reinforced shape memory polymer composite: Based on bridging model. Compos Part A-Appl S. 2014;64:132–8.10.1016/j.compositesa.2014.05.003Search in Google Scholar

[11] Tornabene F, Bacciocchi M, Fantuzzi N, Reddy JN. Multiscale approach for three‐phase CNT/polymer/fiber laminated nanocomposite structures. Polym Composite. 2019;40(S1):E102–E126.10.1002/pc.24520Search in Google Scholar

[12] Lee S, Wang S, Pharr GM, Xu H. Evaluation of interphase properties in a cellulose fiber-reinforced polypropylene composite by nanoindentation and finite element analysis. Compos Part A. 2007;38(6):1517–24.10.1016/j.compositesa.2007.01.007Search in Google Scholar

[13] Guessasma S, Bassir D, Hedjazi LL. Influence of interphase properties on the effective behaviour of a starch-hemp composite. Mater Des. 2015;65(1):1053–63.10.1016/j.matdes.2014.10.031Search in Google Scholar

[14] Würkner M, Berger H, Gabbert U. Numerical investigations of effective properties of fiber reinforced composites with parallelogram arrangements and imperfect interface. Compos Struct. 2014;116(9):388–94.10.1016/j.compstruct.2014.05.012Search in Google Scholar

[15] Lim JY, Kim H, Park M. Effect of interphase parameters on elastic modulus prediction for cellulose nanocrystal fiber reinforced polymer composite. Sci Eng Compos Mater. 2020;27(1):226–35.10.1515/secm-2020-0024Search in Google Scholar

[16] Kostopoulos V, Vellios L, Paipetis SA. Thermal expansivities of fibrous composites with anisotropic constituents and varying interphase properties. Sci Eng Compos Mater. 1993;2(3):195–210.10.1515/SECM.1993.2.3.195Search in Google Scholar

[17] Riaño L, Chailan J, Joliff Y. Evolution of effective mechanical and interphase properties during natural ageing of glass-fibre/epoxy composites using micromechanical approach. Compos Struct. 2021;258:113399.10.1016/j.compstruct.2020.113399Search in Google Scholar

[18] Chang C, Zhang Y, Wang H. Micromechanical modeling of unidirectional composites with random fiber and interphase thickness distributions. Arch Appl Mech. 2019;89(12):2563–75.10.1007/s00419-019-01595-0Search in Google Scholar

[19] Ahmadi M, Ansari R, Hassanzadeh-Aghdam MK. Finite element analysis of thermal conductivities of unidirectional multiphase composites. Compos Interfaces. 2019;26(12):1035–55.10.1080/09276440.2019.1578588Search in Google Scholar

[20] Johnston JP, Koo B, Subramanian N, Chattopadhyay A. Modeling the molecular structure of the carbon fiber/polymer interphase for multiscale analysis of composites. Compos Part B-Eng. 2017;111(2):27–36.10.1016/j.compositesb.2016.12.008Search in Google Scholar

[21] Pathan MV, Tagarielli VL, Patsias S. Effect of fibre shape and interphase on the anisotropic viscoelastic response of fibre composites. Compos Struct. 2017;162(2):156–63.10.1016/j.compstruct.2016.11.046Search in Google Scholar

[22] Yang Z. Study on prediction of mechanical performance for unidirectional composite considering interphase [PhD dissertation]. Harbin: Harbin Institute of Technology; 2010 (in Chinese).Search in Google Scholar

[23] Fang G, Sun J, Gao X, Song Y. Micromechanical finite element analysis of effect of multilayer interphase on crack propagation in SiC/SiC composites. Model Simul Mater Sc. 2021;29(5):055010.10.1088/1361-651X/abf846Search in Google Scholar

[24] Mortazavi B, Bardon J, Ahzi S. Interphase effect on the elastic and thermal conductivity response of polymer nanocomposite materials: 3D finite element study. Comp Mater Sci. 2013;69(3):100–6.10.1016/j.commatsci.2012.11.035Search in Google Scholar

[25] Kari S, Berger H, Gabbert U, Guinovart-Diaz R, Bravo-Castillero J, Rodriguez-Ramos R. Evaluation of influence of interphase material parameters on effective material properties of three phase composites. Compos Sci Technol. 2008;68(3):684–91.10.1016/j.compscitech.2007.09.009Search in Google Scholar

[26] Matzenmiller A, Gerlach S. Parameter identification of elastic interphase properties in fiber composites. Compos Part B-Eng. 2005;37(2):117–26.10.1016/j.compositesb.2005.08.003Search in Google Scholar

[27] Kaewkuk S, Sutapun W, Jarukumjorn K. Effects of interfacial modification and fiber content on physical properties of sisal fiber/polypropylene composites. Compos Part B-Eng. 2013;45(1):544–9.10.1016/j.compositesb.2012.07.036Search in Google Scholar

[28] Li S, Zhang C, Fu J, Zhou Y, Sun J, He Y, et al. Interfacial modification of carbon fiber by carbon nanotube gas-phase dispersion. Compos Sci Technol. 2020;195(7):108196.10.1016/j.compscitech.2020.108196Search in Google Scholar

[29] Wang K, Okuno K, Banu M, Epureanu B. Vibration-based identification of interphase properties in long fiber reinforced composites. Compos Struct. 2017;174(8):244–51.10.1016/j.compstruct.2017.04.018Search in Google Scholar

[30] Lin J, Lin Z, Chen J, Luo C. Manufacturing technique and interfacial modification of polypropylene/short glass fiber composites. Adv Mat Res. 2014;910(3):250–3.10.4028/www.scientific.net/AMR.910.250Search in Google Scholar

[31] Sburlati R, Cianci R. Shear modulus prediction of a particulate composite reinforced with hollow spheres surrounded by a graded interphase. Compos Struct. 2020;250(10):112528.10.1016/j.compstruct.2020.112528Search in Google Scholar

[32] Wang B, Fang G, Liu S, Liang J. Effect of heterogeneous interphase on the mechanical properties of unidirectional fiber composites studied by FFT-based method. Compos Struct. 2019;220(1):642–51.10.1016/j.compstruct.2019.04.049Search in Google Scholar

[33] Nkb A, Bz A, Ntca B, Am C, Ms B, Gmp A. Micro-mechanical analysis on random RVE size and shape in multiscale finite element modelling of unidirectional FRP composites. Compos Struct. 2022;282:115081.10.1016/j.compstruct.2021.115081Search in Google Scholar

[34] Qi Z, Liu Y, Chen W. An approach to predict the mechanical properties of CFRP based on cross-scale simulation. Compos Struct. 2019;210:339–47.10.1016/j.compstruct.2018.11.056Search in Google Scholar

[35] Benveniste Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech Mater. 1987;6(2):147–57.10.1016/0167-6636(87)90005-6Search in Google Scholar

[36] Huang Z. Simulation of the mechanical properties of fibrous composites by the bridging micromechanics model. Compos Part A. 2001;32(2):143–72.10.1016/S1359-835X(00)00142-1Search in Google Scholar

[37] Zhang C, Wang Y, Huang Z. Effective elastic properties of transversely isotropic matrix based composites. Appl Math Mech. 2018;39(7):750–65 (in Chinese).Search in Google Scholar

[38] González C, LLorca J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling. Compos Sci Technol. 2007;67(13):2795–806.10.1016/j.compscitech.2007.02.001Search in Google Scholar

[39] Arteiro A, Catalanotti G, Melro AR, Linde P, Camanho PP. Micro-mechanical analysis of the effect of ply thickness on the transverse compressive strength of polymer composites. Compos Part A-Appl S. 2015;79:127–37.10.1016/j.compositesa.2015.09.015Search in Google Scholar

[40] Tian W, Chao X, Fu MW, Qi L, Ju L. New numerical algorithm for the periodic boundary condition for predicting the coefficients of thermal expansion of composites. Mech Mater. 2021;154:103737.10.1016/j.mechmat.2020.103737Search in Google Scholar

[41] Garoz D, Gilabert FA, Sevenois RDB, Spronk SWF, Van Paepegem W. Consistent application of periodic boundary conditions in implicit and explicit finite element simulations of damage in composites. Compos Part B-Eng. 2019;168:254–66.10.1016/j.compositesb.2018.12.023Search in Google Scholar

[42] Soden PD, Hinton MJ, Kaddour AS. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates. Compos Sci Technol. 1998;58(7):1011–22.10.1016/B978-008044475-8/50003-2Search in Google Scholar

[43] Lei Y, Luo L, Kang Z, Zhang J, Zhang B. Modified Halpin–Tsai equation for predicting interfacial effect in water diffusion process. Sci Eng Compos Mater. 2021;28:180–9.10.1515/secm-2021-0017Search in Google Scholar

[44] Vaughan TJ, McCarthy CT. Micromechanical modelling of the transverse damage behaviour in fibre reinforced composites. Compos Sci Technol. 2011;71(3):388–96.10.1016/j.compscitech.2010.12.006Search in Google Scholar
Received: 2022-07-11
Revised: 2022-10-16
Accepted: 2022-11-05
Published Online: 2022-12-02

© 2022 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Experimental investigations of a novel pressure microfoam preparation device for dust removal
  3. Influence of hydrothermal aging on the mechanical performance of foam core sandwich panels subjected to low-velocity impact
  4. Experimental study on surface wrapping strengthening of EPS particles and its concrete performance
  5. Modification of mechanical properties of Shanghai clayey soil with expanded polystyrene
  6. A new EPS beads strengthening technology and its influences on axial compressive properties of concrete
  7. A novel superabsorbent material based on soybean straw: Synthesis and characterization
  8. Use of line laser scanning thermography for the defect detection and evaluation of composite material
  9. Research on back analysis of meso-parameters of hydraulic cemented sand and gravel based on Box-Behnken design response surface
  10. Hot deformation behavior and microstructure of a 0.5 wt% graphene nanoplatelet reinforced aluminum composite
  11. Analysis of electromagnetic characteristics of the proposed composite four-rail electromagnetic launcher
  12. Preparation and characterization of a graphene hybridizing polyurethane damping composite
  13. Effects of layup parameters and interference value on the performance of CFRP–metal interference fit joints
  14. Vibration and noise reduction of pipelines using shape memory alloy
  15. Finite element analysis of behavior and ultimate strength of composite column
  16. Dynamic response of functionally graded plate under harmonic load with variable gradient parameters
  17. Deformation behavior of rubber composite based on FEA and experimental verification
  18. Effects of Z-pin on moisture absorption property and damage mode under flexural load for carbon fiber composite
  19. Design and testing of a smart rubber stave for marine water-lubricated bearings
  20. Study of carbon nano-modifier of fly ash in cement concrete mixtures of civil engineering
  21. Analysis of multiple impact tests’ damage to three-dimensional four-directional braided composites
  22. Theoretical analysis of aluminum honeycomb sandwich panel supported by reinforced concrete wall under low-speed impact load
  23. Effects of local fiber discontinuity on the fatigue strength parameter at the fiber inclusion corner in fiber-reinforced composites
  24. Experimental investigation on compressive properties of three-dimensional five-directional braided composites in hygrothermal environment
  25. Failure process of steel–polypropylene hybrid fiber-reinforced concrete based on numerical simulations
  26. A simple method for measuring the monofilament diameter of continuous filament yarn with high bending stiffness via synthetic laser imaging
  27. Span length effect on flexural properties of composite laminate reinforced with a plain weave carbon fiber fabric in a polymer matrix
  28. Mechanical properties improving and microstructure characterization of inorganic artificial stone binder
  29. Effect of thermal treatment process on the structure of C/SiO2 composite aerogels
  30. Mechanical and corrosion resistance analysis of laser cladding layer
  31. Wear and corrosion mechanisms of Ni–WC coatings modified with different Y2O3 by laser cladding on AISI 4145H steel
  32. Damage and failure analysis of composite stiffened panels under low-velocity impact and compression after impact with damp-heat aging
  33. In-situ CT characterization of 2D woven SiCf/SiC composite loading under compression
  34. Effect of the manufacturing process on the equivalency qualification of glass fiber reinforced polymer
  35. Study of concrete properties based on crushed stone sand mixture and fiber of fly ash of thermal power plants
  36. Establishment of wear mechanism distribution diagram of ZTAp-reinforced iron matrix composites
  37. Calculation method of elastic modulus for carbon fiber-reinforced plastics considering inhomogeneous interphase
  38. An experimental study on the failure and enhancement mechanism of bolt-strengthening GFRP T-joint subjected to tensile loading
  39. The viability of cell that encapsulated in calcium alginate hydrogel beads
  40. Discussion of ceramic bar reinforced TWIP steel composite structure
  41. A theoretical framework underlying an accelerated testing method and its application to composites under constant strain rates and fatigue loading
  42. Theoretical analysis of interfacial design and thermal conductivity in graphite flakes/Al composites with various interfacial coatings
  43. Multiscale heat conduction and fractal oxidation behaviors of needle-punched carbon/carbon composites
  44. Numerical simulation of composite grid sandwich structure under low-velocity impact
  45. Wear properties of Al/TiO2 composites fabricated via combined compo-casting and APB process
  46. Review Articles
  47. Application of melanin as biological functional material in composite film field
  48. Review on research progress of cemented sand and gravel dam
  49. Communication
  50. Fabrications and microstructure analysis of cobalt-based coatings by an easy-coating and sintering process
  51. Letter to the Editor
  52. Investigation on mechanical and conductive behaviors of nano-graphite-based concrete
https://doi.org/10.1515/secm-2022-0171
Keywords for this article
composites; interphases; microstructures; bridging model; micro-mechanics
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Experimental investigations of a novel pressure microfoam preparation device for dust removal
  3. Influence of hydrothermal aging on the mechanical performance of foam core sandwich panels subjected to low-velocity impact
  4. Experimental study on surface wrapping strengthening of EPS particles and its concrete performance
  5. Modification of mechanical properties of Shanghai clayey soil with expanded polystyrene
  6. A new EPS beads strengthening technology and its influences on axial compressive properties of concrete
  7. A novel superabsorbent material based on soybean straw: Synthesis and characterization
  8. Use of line laser scanning thermography for the defect detection and evaluation of composite material
  9. Research on back analysis of meso-parameters of hydraulic cemented sand and gravel based on Box-Behnken design response surface
  10. Hot deformation behavior and microstructure of a 0.5 wt% graphene nanoplatelet reinforced aluminum composite
  11. Analysis of electromagnetic characteristics of the proposed composite four-rail electromagnetic launcher
  12. Preparation and characterization of a graphene hybridizing polyurethane damping composite
  13. Effects of layup parameters and interference value on the performance of CFRP–metal interference fit joints
  14. Vibration and noise reduction of pipelines using shape memory alloy
  15. Finite element analysis of behavior and ultimate strength of composite column
  16. Dynamic response of functionally graded plate under harmonic load with variable gradient parameters
  17. Deformation behavior of rubber composite based on FEA and experimental verification
  18. Effects of Z-pin on moisture absorption property and damage mode under flexural load for carbon fiber composite
  19. Design and testing of a smart rubber stave for marine water-lubricated bearings
  20. Study of carbon nano-modifier of fly ash in cement concrete mixtures of civil engineering
  21. Analysis of multiple impact tests’ damage to three-dimensional four-directional braided composites
  22. Theoretical analysis of aluminum honeycomb sandwich panel supported by reinforced concrete wall under low-speed impact load
  23. Effects of local fiber discontinuity on the fatigue strength parameter at the fiber inclusion corner in fiber-reinforced composites
  24. Experimental investigation on compressive properties of three-dimensional five-directional braided composites in hygrothermal environment
  25. Failure process of steel–polypropylene hybrid fiber-reinforced concrete based on numerical simulations
  26. A simple method for measuring the monofilament diameter of continuous filament yarn with high bending stiffness via synthetic laser imaging
  27. Span length effect on flexural properties of composite laminate reinforced with a plain weave carbon fiber fabric in a polymer matrix
  28. Mechanical properties improving and microstructure characterization of inorganic artificial stone binder
  29. Effect of thermal treatment process on the structure of C/SiO2 composite aerogels
  30. Mechanical and corrosion resistance analysis of laser cladding layer
  31. Wear and corrosion mechanisms of Ni–WC coatings modified with different Y2O3 by laser cladding on AISI 4145H steel
  32. Damage and failure analysis of composite stiffened panels under low-velocity impact and compression after impact with damp-heat aging
  33. In-situ CT characterization of 2D woven SiCf/SiC composite loading under compression
  34. Effect of the manufacturing process on the equivalency qualification of glass fiber reinforced polymer
  35. Study of concrete properties based on crushed stone sand mixture and fiber of fly ash of thermal power plants
  36. Establishment of wear mechanism distribution diagram of ZTAp-reinforced iron matrix composites
  37. Calculation method of elastic modulus for carbon fiber-reinforced plastics considering inhomogeneous interphase
  38. An experimental study on the failure and enhancement mechanism of bolt-strengthening GFRP T-joint subjected to tensile loading
  39. The viability of cell that encapsulated in calcium alginate hydrogel beads
  40. Discussion of ceramic bar reinforced TWIP steel composite structure
  41. A theoretical framework underlying an accelerated testing method and its application to composites under constant strain rates and fatigue loading
  42. Theoretical analysis of interfacial design and thermal conductivity in graphite flakes/Al composites with various interfacial coatings
  43. Multiscale heat conduction and fractal oxidation behaviors of needle-punched carbon/carbon composites
  44. Numerical simulation of composite grid sandwich structure under low-velocity impact
  45. Wear properties of Al/TiO2 composites fabricated via combined compo-casting and APB process
  46. Review Articles
  47. Application of melanin as biological functional material in composite film field
  48. Review on research progress of cemented sand and gravel dam
  49. Communication
  50. Fabrications and microstructure analysis of cobalt-based coatings by an easy-coating and sintering process
  51. Letter to the Editor
  52. Investigation on mechanical and conductive behaviors of nano-graphite-based concrete
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 30.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/secm-2022-0171/html?lang=en&srsltid=AfmBOopRmISPho3EbeQhqgX27saMKZXpkbWBKGHliNCmgbk1cAsEEonb
Scroll to top button