Abstract
Sandwich panels made of fibre-reinforced plastic (FRP) skins and a honeycomb core can be effectively damped through the choice of the skin and especially of the core materials. Because the core is often highly damped, a lateral deflection that causes more shearing of the core than bending of the skin increases sandwich damping. Aside from the skin and the core material properties, the shearing/bending ratio depends on a number of other, often interacting, factors, including the sandwich planar as well as transverse dimensions, the particular modal pattern in which the panel vibrates and its relationship to the type of skin layup, as well as the panel end conditions. In the present work, using a simple, first-order shear deformation theory, damping results have been produced for simple modes of vibration of a sandwich panel comprising composite skins and a damped honeycomb core, demonstrating the mechanisms by which the above factors affect the FRP skin/honeycomb core sandwich damping.
1 Introduction
Composite sandwich panels comprising fibre-reinforced plastic (FRP) skins and a damped honeycomb core have a higher stiffness/weight ratio than metals and are substantially more damped, both of which properties are highly desirable in aerospace structures. Interest in the vibration damping properties of these materials has been growing with their increasing use. Depending on the response characteristics of the materials used for the skins and the core, there have been two main approaches in analysing vibration damping of sandwich structures. Some works on sandwich damping have used a rate-dependent, viscoelastic damping model [1], [2], [3], [4], while others [5], [6], [7] have used a simpler, rate-independent structural damping model. Aerospace-grade sandwich often comprises FRP composite skins made from carbon (CFRP) or glass fibres embedded in a thermosetting epoxy resin matrix and a thermosetting resin-based honeycomb core. As such, both the skin and the core can be considered to be rigid enough to render the viscoelastic effect negligible. A viscoelastic analysis, however, lends itself more to situations where highly viscoelastic materials are purposely added to the structure as a constrained or free layer to increase damping.
In a sandwich with a damped core, the latter is expected to provide most of the damping. However, if the skins are also made from a damped, orthotropic material such as FRP composites, they also can have considerable influence on the overall sandwich damping, depending on a number of factors including the nature of the FRP layup [6], [7], [8], [9].
Early work on the damping properties of FRP composites include that by Adams and Bacon [10], who proposed a damping model based on separable damping energies due to the three in-plane stress components. Several subsequent works using the same model have shown the validity of this model [11], [12], [13]. Yim and Gillespie [12] used the laminated beam theory together with a damping model used by Ni and Adams [11] to predict the damping properties of laminated FRP cantilever beams in which the transverse shear effects had also been included. Koo and Lee [14] investigated the dynamic properties of symmetric FRP laminates of varying thickness, showing that the damping properties of laminates were significantly influenced by their thickness. Maheri [13] considered the influence of the layup and boundary conditions on the modal damping of FRP panels.
Working on the damping of sandwich beams, Adams and Maheri [15] introduced a test methodology for obtaining the shear modulus and damping of honeycomb materials. In a later work [6], they used essentially the Adams-Bacon model to compute the individual contributions to the overall damping in a sandwich beam by the skins and the core, attributing all the in-plane stresses to the FRP skins and the out-of-plane stresses to the honeycomb core. They reported a reasonably good correlation between the experimental and theoretical results.
Thamburaj and Sun [3] studied the effect of material properties on the dampening of sound and vibration in a sandwich beam. They found that sandwich beams made with anisotropic materials were more damped than those made with isotropic materials.
The use of ecologically friendly, recyclable, biodegradable materials for the fibre-reinforced skins as well the core of structural sandwich is deservedly gaining attention. Works have been carried out on measuring the modal properties of these materials [16], [17], [18]. Sargianis et al. [16] reported considerable improvement in the vibrational properties of sandwich structures made from natural fibres and resins at the expense of a relatively small loss in the bending stiffness.
Maheri et al. [5] used a first-order shear deformation theory together with the Rayleigh-Ritz method to analyse the dynamic behaviour of FRP sandwich panels. They tested the sandwich constituent parts (skin and core) individually to obtain their dynamic moduli and damping data. They used these data in their theory in order to predict the dynamic response of a sandwich panel. They showed that a good correlation between the theoretical and experimental results existed only when the panels were tested in-vacuo. They concluded that air damping can constitute a major part of the overall damping in a sandwich panel.
In the present work, using the method of Rayleigh-Ritz as outlined in Ref. [5], the specific damping capacity (SDC) for composite sandwich panels has been calculated. These panels, which are mid-plane symmetric, comprise two outer FRP composite skins and an inner honeycomb core. A highly damped honeycomb material such as the polymer-based Nomex has been considered as the sandwich core.
Several factors affect the sandwich damping. To investigate how each given factor will influence the damping, all other factors should be kept constant. Sandwich-relative dimensions are one of these factors, particularly when the sandwich skin and core have highly different levels of material damping. For that reason, the variation of damping in rectangular sandwich panels as a function of the planar aspect ratio has been considered. The aspect ratio has been varied from unity (a square panel) to 2.
The nature of the modal patterns developed and the bending/shearing ratio will also depend on the panel boundary conditions. These also will therefore influence modal damping. In the present work, sandwich panels with all-free, cantilevered, and all-clamped edges have been considered.
Damping in sandwich materials having FRP skins is also a factor of the skin layup arrangement. The modal stiffness, and thus the modal damping, will depend not only on the stacking sequence of individual skin layers having a particular fibre orientation, but also on the relative orientation of the nodal lines with respect to the lay of the fibres in individual layers [13]. In simple situations, such as when a panel having all-zero or cross-ply skins is vibrating in lower modes such as the 1-1 or the 0-2 modes, it is relatively easy to realise how the skin layup arrangement is affecting the modal damping. For that reason, and also because the lower modes are more significant in design considerations, particular attention has been paid to lower mode shapes of panels with simple skin layups.
2 Theory
The SDC is used as a measure of structural damping. This is defined as the ratio of the energy dissipated to the maximum strain energy attained, per cycle of vibration:
For a sandwich configuration, the total strain and damping energies of the sandwich are assumed to be the sum of separable strain and damping energies of the skins and of the core in each case, such that one may write
in which the suffixes S and C refer to the skins and the core, respectively.
The contributions of the skin strain energy US and the core strain energy UC to the overall sandwich strain energy U in modal deformation will depend on a number of factors, including the modal pattern, boundary conditions, sandwich dimensions, as well as skin and core materials. When there exists orthogonality of material properties in the skin and/or core, this introduces an additional factor governing the relative skin/core modal stiffness and, hence, the relative contribution of each to the overall strain energy.
A proportion of the strain energies of the skin and of the core, namely ∆US and ∆UC, respectively, is dissipated in each case in one cycle of vibration. The energy dissipation, or the damping energy, is essentially a function of the modal strain energies US and UC, and the inherent capacity of the skin and the core materials to dissipate energy.
In the theory used for the present work, the sandwich plate has been discretised into a number of sandwich beam elements whose boundary conditions satisfy the plate boundary conditions, and whose modal deformation can be readily found in closed form. The Rayleigh-Ritz energy minimisation of these beam elements is then used to arrive at the modal properties of the sandwich plate, including the strain energies attributable to the skins and to the core. A detailed account of the theory can be found in Ref. [5]. In that work, a good correlation was shown to exist between the theoretical predictions and experimental results, as typically is shown in Table 1.
In vacuo modal data of an all-free, [−60, 0, 60] CFRP/Al honeycomb sandwich panel, cited from Ref. [5].
| Mode shape |  |  |  |  |
|---|---|---|---|---|
| Frequency (Hz) | ||||
| Experiment | 757 | 1202 | 1471 | 1755 |
| Rayleigh-Ritz method | 796 | 1221 | 1469 | 1817 |
| SDC (%) | ||||
| Experiment | 1.11 | 1.51 | 1.06 | 1.21 |
| Rayleigh-Ritz method | 1.39 | 0.84 | 0.84 | 0.94 |
It should be pointed out, however, that those results were obtained for plates with all-free boundary conditions where a closer correlation between the theoretical and experimental results is expected. This is because compared to an all-free plate, a plate with one or more clamped edges experiences extraneous damping at the clamped edge.
3 Results and discussion
Unless otherwise indicated in the figures, all the sandwich panels considered are made from the same CFRP skins and Nomex honeycomb core materials. Two skin layups have been considered, namely the all-zero and the planar-isotropic (or quasi-isotropic) [−60, 0, 60]. The faint, parallel lines in the graph key indicate the direction of the fibres for the all-zero FRP skins, while the crisscrossing lines indicate that the FRP skin is planar-isotropic. The bold lines in the key are the nodal lines.
The elastic and damping properties of the skins and the core are given in Tables 2–5 . It is noted that these data are actual test results that have been obtained in previous works for the CFRP skin [5] and the honeycomb core [15]. It is noted that Table 2 shows the in-plane elastic and damping properties of the CFRP material obtained from tests on the 0° and 90° beams. The Young’s modulus E, the shear modulus G, the Poisson’s ratio ν, and the SDC ψ are all given in the 12 plane for the FRP skins (Figure 1), with the fibres aligned in the 1-direction, and in the x, y, z orthogonal axes for the sandwich panel, with the honeycomb node aligned in the x-direction.
All-zero CFRP skin elastic and damping data [5].
| E1 (GPa) | E2 (GPa) | G12 (GPa) | ψ1 (%) | ψ2 (%) | ψ12 (%) | ν12 | ρ (kg/m3) |
|---|---|---|---|---|---|---|---|
| 271.0 | 6.02 | 5.46 | 0.45 | 7.30 | 8.16 | 0.34 | 1563.3 |
Nomex honeycomb core elastic and damping data [15].
| Gxz (MPa) | Gyz (MPa) | ψxz (%) | ψyz (%) | ρ (kg/m3) |
|---|---|---|---|---|
| 40.0 | 29.5 | 11.2 | 10.5 | 40.43 |
Aluminium skin elastic and damping data [5].
| E (GPa) | G (GPa) | ψ1 (%) | ψ2 (%) | ψ12 (%) | ν | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 68.7 | 25.4 | 0.1 | 0.1 | 0.1 | 0.34 | 2687.1 |
Aluminium honeycomb core elastic and damping data [5].
| Gxz (MPa) | Gyz (MPa) | ψxz (%) | ψyz (%) | ρ (kg/m3) |
|---|---|---|---|---|
| 140 | 75.4 | 0.74 | 1.02 | 39.5 |

Sandwich panel and material orientations.
In Figures 2–10, the variation of modal damping with respect to the planar aspect ratio in the first four modes of sandwich panels with different conditions has been shown. The overall panel thickness [h=0.02491(m)], the thickness of the core [hc=0.024315(m)], and the panel width [b=0.4(m)] have all been kept constant, while the aspect ratio a/b has been varied from 1.0 to 2.0. The sequence of the circled letters a, b, c, and d in these figures correspond to an increasing modal frequency for the square plate (a=b), although this sequence might change with the change in the modal stiffness as the aspect ratio is varied.

Damping of an all-free, all-zero CFRP/Nomex honeycomb sandwich panel versus aspect ratio in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
![Figure 3: Damping of an all-free, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.](/document/doi/10.1515/secm-2015-0444/asset/graphic/j_secm-2015-0444_fig_003.jpg)
Damping of an all-free, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
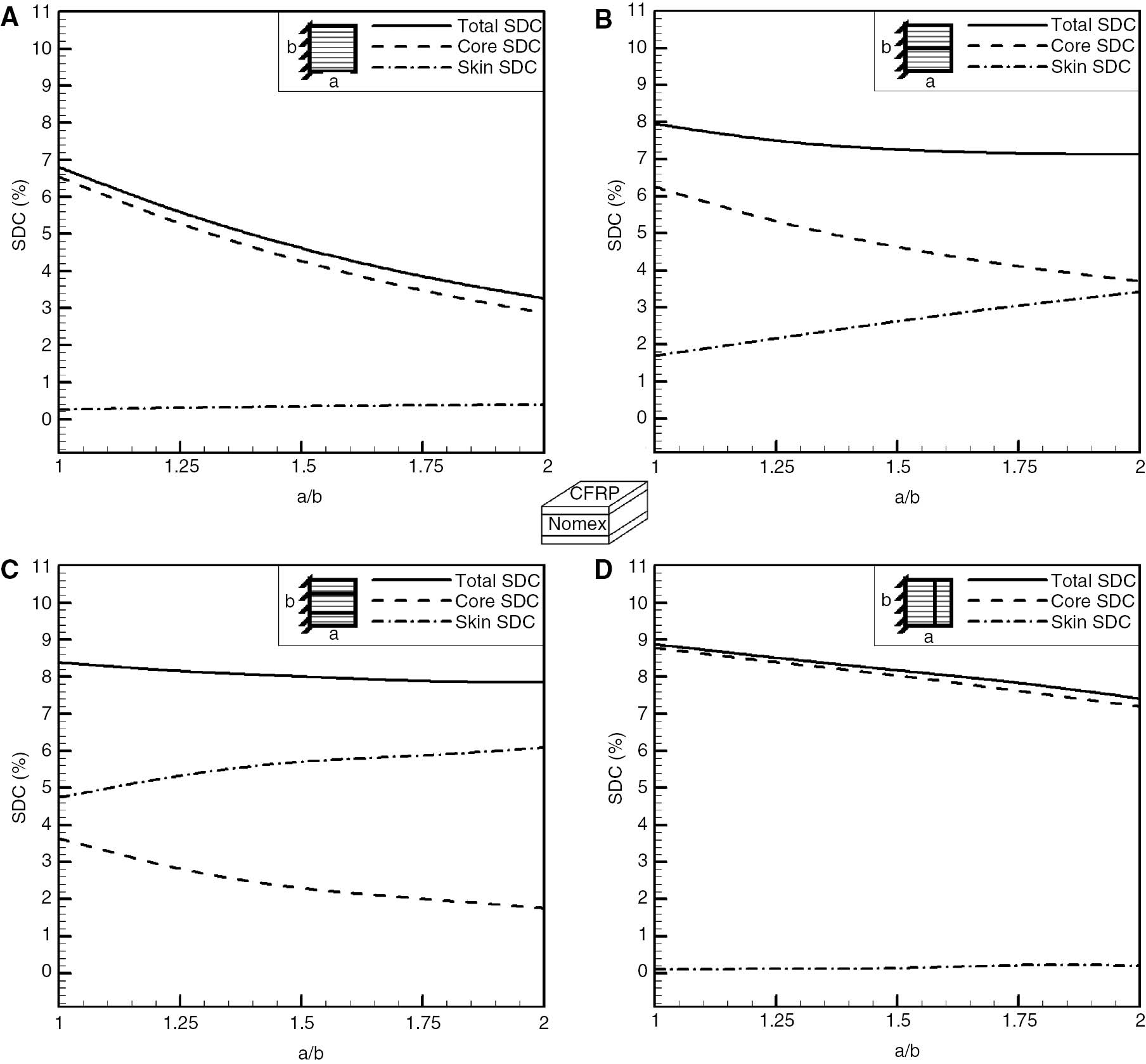
Damping of a cantilevered, all-zero CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
![Figure 5: Damping of a cantilevered, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.](/document/doi/10.1515/secm-2015-0444/asset/graphic/j_secm-2015-0444_fig_005.jpg)
Damping of a cantilevered, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.

Damping of an all-clamped, all-zero CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
![Figure 7: Damping of an all-clamped, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.](/document/doi/10.1515/secm-2015-0444/asset/graphic/j_secm-2015-0444_fig_007.jpg)
Damping of an all-clamped, [−60, 0, 60] CFRP/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.

Damping of an all-free, all-zero CFRP/Al honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
![Figure 9: Damping of an all-free, [−60, 0, 60] CFRP/Al honeycomb sandwich panel versus aspect ratio in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.](/document/doi/10.1515/secm-2015-0444/asset/graphic/j_secm-2015-0444_fig_009.jpg)
Damping of an all-free, [−60, 0, 60] CFRP/Al honeycomb sandwich panel versus aspect ratio in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
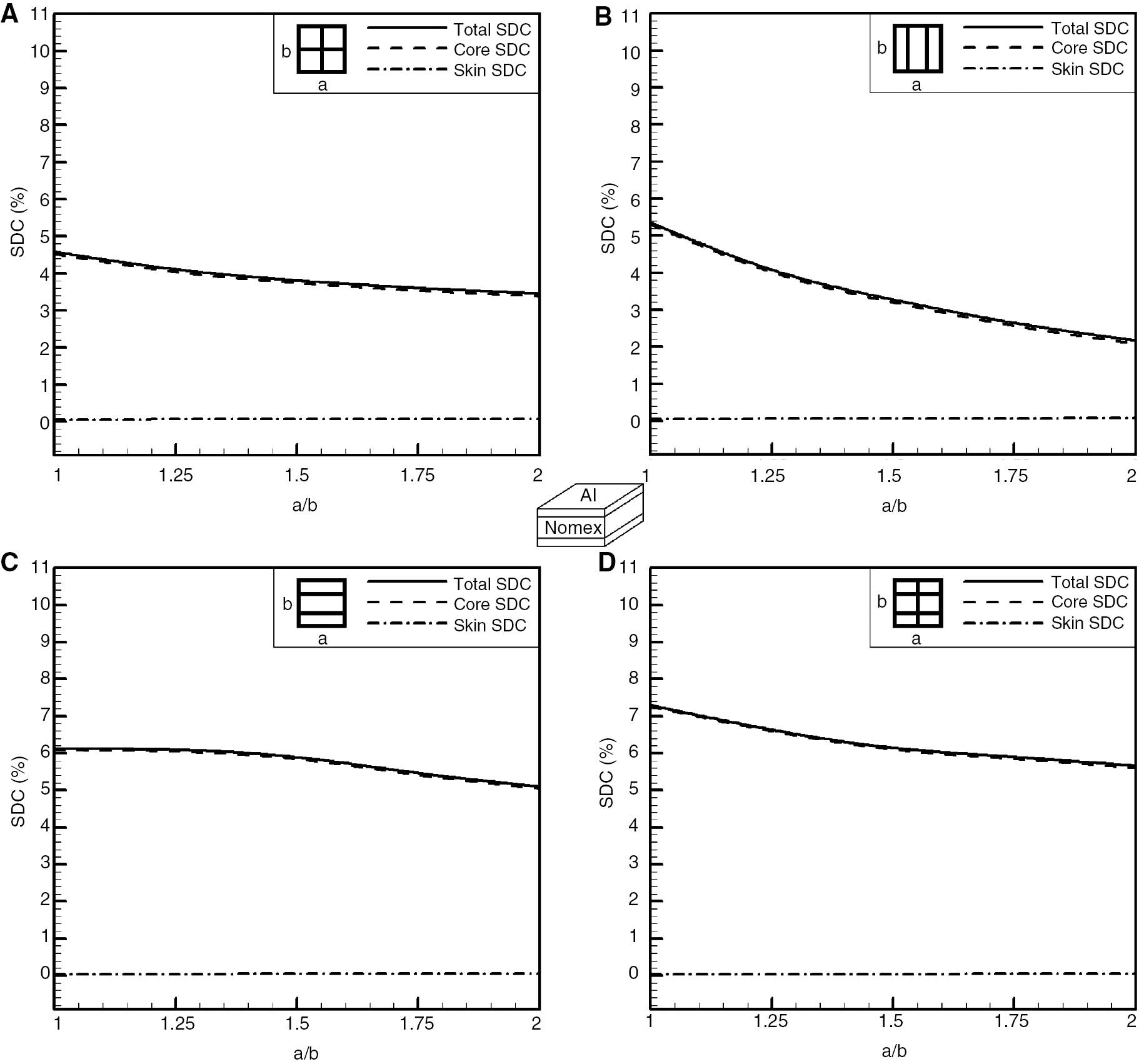
Damping of an all-free, Al/Nomex honeycomb sandwich panel versus aspect ratio, in various modes. (A) First mode, (B) second mode, (C) third mode, (D) fourth mode.
In Figure 2, the damping results of an all-free sandwich panel, having all-zero CFRP skins and a Nomex honeycomb core, are shown. The deformation in the 0-2 mode (Figure 2B) is essentially of a cylindrical nature, in that the deformation of the skin does not involve the fibres and, consequently, the variation in the length a has no significant effect on the skin bending stiffness. As a result, no change in damping is observed with respect to the ratio a/b. Furthermore, as the skin deformation is confined to the shearing of the resin matrix, the skin damping predominates. Considering the beam-like, 2-0 mode in Figure 2D, this mode occurs at a higher frequency than the 0-2 mode, and it is expected to occur only under favourable conditions. Nevertheless, it would be instructive to compare the results of the 0-2 and the 2-0 modes, as they show the underlying process involved in the damping of FRP-skin sandwich panels. In contrast to the results of the 0-2 mode where sandwich damping is invariant of the aspect ratio, the 2-0 results show a marked decrease in damping as the aspect ratio a/b is increased. The decrease in damping is a reflection of the fact that there exists a relatively large difference between the modal stiffness and the damping properties of the skin and the core. In this latter case (Figure 2D), the nodal lines are perpendicular to the lay of the fibres. With increasing length of the side a, the deflection in the panel is governed increasingly by bending of the skins than shearing of the core. Because the bending stiffness of the skin along the fibres is some order of magnitude more than the shearing stiffness of the core, while at the same time the skin is less damped than the core, this results in a decrease in the overall SDC as the deformation moves from a predominately shearing one to a predominately bending one [cf. Eq. (2)].
From Figure 2, it is also noted that in those modes in which there exists a nodal line parallel to the lay of the fibres, skin damping predominates, as such nodal lines cause shearing of the skin.
Comparing the results in Figures 2 and 8, the above arguments are seen to hold as the core damping is removed by replacing Nomex with aluminium honeycomb.
In Figure 3, the damping results of an all-free sandwich panel, having quasi-isotropic [−60, 0, 60] skins and a Nomex honeycomb core, are shown. Considering the 2-0 mode of the quasi-isotropic skin in Figure 3B, the variation of the SDC with the aspect ratio is seen to follow the same trend as that of the all-zero panel (Figure 2B). The reason for this is the same as before; that is, an increase in the side a will lead to an increase in the ratio of bending/shearing, as a consequence of which the overall SDC will drop. Comparing the like modes in Figures 2 and 3, it is noted that the all-zero sandwich generally experiences more damping than the planar isotropic one, and that any reduction in the SDC with aspect ratio is more subtle in the former panel. These variations are caused by the fact that the all-zero panel is generally stiffer than the quasi-isotropic panel in the direction of side a.
From Figure 3, it is noted that in an all-free sandwich with a damped core, when the skin stiffness becomes invariant of direction, there is negligible skin contribution to the overall damping, and that the core damping always predominates. It is of interest to note that in such a panel, when the core damping is removed (Figure 9), the sandwich experiences little structural damping in any mode. Indeed, the results in Figure 9 correlate well with the earlier results published in table 6 of Ref. [5], where a similar panel had been tested in-vacuo.
In Figure 4, the damping results of a cantilevered sandwich panel, having all-zero CFRP skins and a Nomex honeycomb core, are shown. The damping behaviour in mode 1-0 (Figure 4A) is similar to that shown by mode 2-0 of the all-free panel (Figure 2D), in that with an increasing aspect ratio a/b, the ratio bending/shearing deformation in the sandwich increases, resulting in a reduction of the core shear damping and, therefore, of the overall sandwich damping. Indeed, the same trend is observed also in the 2-0 mode in Figure 4D, although compared to the mode 1-0, here the addition of a nodal line across the fibres helps shear damping of the core, resulting in a more gradual decrease of the overall damping with the aspect ratio.
The increasing significance of the skin contribution to the overall damping due to the nodal lines being parallel to the lay of the fibres was observed in the all-free, all-zero panel in Figure 2. The same mechanism is evident from the cantilever results in Figure 4. Furthermore, comparing Figure 4B and C, it is noted that this contribution could increase with an increase in the number of the said nodal lines to a point where the skin damping predominates.
In Figure 5, the damping results of a cantilevered sandwich panel, having quasi-isotropic [−60, 0, 60] CFRP skins and a Nomex honeycomb core, are shown. The damping results in this figure are essentially a repetition of those produced when the panel was all-free (Figure 3). Not only is there a reduction in the overall damping with respect to the aspect ratio, albeit at different rates, but also as in the previous case, the uniform in-plane stiffness of the panel restricts the shear damping of the skin under different modal deformations, resulting in the predominance of the core damping in all of the modes.
In Figure 6, the damping results of an all-clamped sandwich panel, having all-zero CFRP skins and a Nomex honeycomb core, are shown. Comparing the results in Figures 2, 4, and 6, it is evident that the sandwich panel experiences more damping with the increasing number of the clamped sides. Furthermore, because core damping always predominates in the all-clamped panel (Figure 6), this results in only a modest reduction of the overall damping with the aspect ratio in all modes, although the skin damping becomes increasingly more significant.
In Figure 7, the damping results of an all-clamped sandwich panel, having quasi-isotropic [−60, 0, 60] CFRP skins and a Nomex honeycomb core, are shown. The results in this figure show that, generally, in an all-clamped sandwich panel with a damped core, and with a skin whose stiffness is invariant of direction, the sandwich damping in all modes approaches that of the core, it is sustained reasonably well with the aspect ratio, and it is almost entirely due to the core.
In Figure 8, the damping results of an all-free sandwich panel, having all-zero CFRP skins and an aluminium honeycomb core, are shown. The panel here is the same as the one whose results are shown in Figure 2, except that the Nomex honeycomb in the core has been replaced by an aluminium honeycomb. In effect, these results are seen to replicate the results in Figure 2 when the core damping is removed.
In Figure 9, the damping results of an all-free sandwich panel, having quasi-isotropic [−60, 0, 60] CFRP skins and an aluminium honeycomb core, are shown. Similarly, the panel here is the same as the one whose results are shown in Figure 3, except that the Nomex honeycomb in the core has been replaced by an aluminium honeycomb. Accordingly, these results are seen to reflect the removal of the core contribution to the overall damping in the results of Figure 3. Comparing the results in Figures 8 and 9, it is of interest to note that little modal damping can be expected from a sandwich panel that has an undamped core but has a damped skin, if the skin is isotropic.
In Figure 10, the damping results of an all-free sandwich panel, having aluminium skins and a Nomex honeycomb core, are shown. One interesting result emerges from comparing the 2-0 modes in Figures 10B and 2D. No skin contribution to the overall damping is experienced in either cases; however, the stiffer FRP skin in the former case has resulted in enhanced core shear damping and, therefore, in an increased overall sandwich damping.
4 Conclusions
Modal damping in an FRP/honeycomb sandwich panel is a function of the relative bending/shearing stiffness of the sandwich and the damping properties of the skins and the core. The particular mode of vibration, the sandwich dimensions, and its end conditions, as well as the particular layup of the FRP skin, all influence the bending/shearing stiffness.
It was shown that in a sandwich panel with a highly directional FRP skin such as the all-zero layup, a major part of the sandwich damping could be due to the skin, and that there is a large variation in the skin contribution to the overall damping in different modes. It was further shown that, generally, when the relative orientation of the nodal lines is such that it induces a high bending stiffness in the FRP skin, the damping becomes a function of the plate size; the longer the stiffer side of the plate is, the less will be the modal damping. By the same token, the less the flexure of the skin involves straining of the fibres, the less will be the variation of damping with the plate aspect ratio.
Damping in a sandwich with a damped core is generally increased with the increasing number of the clamped sides, as this induces the shear damping of the core.
When the skin stiffness of a sandwich panel, whether free or clamped, is invariant of direction, nodal patterns have no significant effect on the skin contribution to the overall damping, and the sandwich damping emanates from the shear damping of the core. This means that relatively little modal damping can be expected from a sandwich panel that has a damped skin, if the skin is isotropic and the core is not damped.
Finally, a more uniform orientation of the skin stiffness helps maximise shear damping of the core, thereby avoiding sharp fluctuation of sandwich damping between different modes.
References
[1] Meunier M, Shenoi RA. Compos. Struct. 2001, 54, 243–254.10.1016/S0263-8223(01)00094-0Search in Google Scholar
[2] Sainsbury MG, Zhang QJ. Comput. Struct. 1999, 71, 239–256.10.1016/S0045-7949(98)00242-9Search in Google Scholar
[3] Thamburaj P, Sun JQ. J. Vibrat. Acoust. 2001, 123, 205–212.10.1115/1.1343083Search in Google Scholar
[4] Jung WY, Aref AJ. Mech. Mater. 2003, 35, 831–844.10.1016/S0167-6636(02)00210-7Search in Google Scholar
[5] Maheri MR, Adams RD, Hugon J. J. Mater. Sci. 2008, 43, 6604–6618.10.1007/s10853-008-2694-ySearch in Google Scholar
[6] Maheri MR, Adams RD. Compos. Sci. Technol. 1994, 52, 333–347.10.1016/0266-3538(94)90168-6Search in Google Scholar
[7] Yaman M, Onal T. J. Sandw. Struct. Mater. 2016, 18, 397–414.10.1177/1099636215582216Search in Google Scholar
[8] Nagasankar P, Balasivanandha Prabu S, Velmurugan R. Mech. Mater. 2015, 91, 252–261.10.1016/j.mechmat.2015.08.002Search in Google Scholar
[9] Hazrati Nayeri A. Mater. Des. 2013, 46, 842–848.10.1016/j.matdes.2012.11.008Search in Google Scholar
[10] Adams RD, Bacon DGC. J. Compos. Mater. 1973, 7, 53–67.10.1177/002199837300700104Search in Google Scholar
[11] Ni RG, Adams RD. Composites 1984, 15, 193–199.10.1016/0010-4361(84)90274-XSearch in Google Scholar
[12] Yim JH, Gillespie JW. Compos. Struct. 2000, 50, 217–225.10.1016/S0263-8223(00)00087-8Search in Google Scholar
[13] Maheri MR. J. Compos. Mater. 2010, 45, 1411–1422.10.1177/0021998310382314Search in Google Scholar
[14] Koo KN, Lee I. J. Sound Vibrat. 1995, 184, 553–566.10.1006/jsvi.1993.0333Search in Google Scholar
[15] Adams RD, Maheri MR. Compos. Sci. Technol. 1993, 47, 15–23.10.1016/0266-3538(93)90091-TSearch in Google Scholar
[16] Sargianis JJ, Kim HI, Andres E, Suhr J. Compos. Struct. 2013, 96, 538–544.10.1016/j.compstruct.2012.09.006Search in Google Scholar
[17] Petrone G, D’Alessandro V, Franco F, Mace B, De Rosa S. Compos. Struct. 2014, 113, 362–368.10.1016/j.compstruct.2014.03.026Search in Google Scholar
[18] Petrone G, D’Alessandro V, Franco F, De Rosa S. J. Vibrat. Control 2015, 21, 3328–3338.10.1177/1077546314522507Search in Google Scholar
©2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- Review
- Research review of diversified reinforcement on aluminum metal matrix composites: fabrication processes and mechanical characterization
- Original articles
- On the mechanisms of modal damping in FRP/honeycomb sandwich panels
- Innovative experimental and finite element assessments of the performance of CFRP-retrofitted RC beams under fatigue loading
- Mixed-mode I/III fracture toughness of polymer matrix composites toughened with waste particles
- A novel analytical curved beam model for predicting elastic properties of 3D eight-harness satin weave composites
- Microwave absorption and mechanical properties of double-layer cement-based composites containing different replacement levels of fly ash
- Electrical and rheological properties of carbon black and carbon fiber filled low-density polyethylene/ethylene vinyl acetate composites
- Effect of neutron irradiation on neat epoxy resin stability in shielding applications
- Study on the relation between microstructural change and compressive creep stress of a PBX substitute material
- Chemical synthesis and densification of a novel Ag/Cr2O3-AgCrO2 nanocomposite powder
- Reinforcing polypropylene with calcium carbonate of different morphologies and polymorphs
- Fabrication, mechanical, thermal, and electrical characterization of epoxy/silica composites for high-voltage insulation
- Synergy of cashew nut shell filler on tribological behaviors of natural-fiber-reinforced epoxy composite
- Fabrication and Failure Prediction of Carbon-alum solid composite electrolyte based humidity sensor using ANN
- Investigation of three-body wear of dental materials under different chewing cycles
- Structural and physico-mechanical characterization of closed-cell aluminum foams with different zinc additions
- Mechanical performance of polyester pin-reinforced foam filled honeycomb sandwich panels
- Effect of chemical treatment on thermal properties of hair fiber-based reinforcement of HF/HDPE composites
- Indium doping in sol-gel synthesis of In-Sm co-doped xIn-0.05%Sm-TiO2 composite photocatalyst
- Effect of the meso-structure on the strain concentration of carbon-carbon composites with drilling hole
Articles in the same Issue
- Frontmatter
- Review
- Research review of diversified reinforcement on aluminum metal matrix composites: fabrication processes and mechanical characterization
- Original articles
- On the mechanisms of modal damping in FRP/honeycomb sandwich panels
- Innovative experimental and finite element assessments of the performance of CFRP-retrofitted RC beams under fatigue loading
- Mixed-mode I/III fracture toughness of polymer matrix composites toughened with waste particles
- A novel analytical curved beam model for predicting elastic properties of 3D eight-harness satin weave composites
- Microwave absorption and mechanical properties of double-layer cement-based composites containing different replacement levels of fly ash
- Electrical and rheological properties of carbon black and carbon fiber filled low-density polyethylene/ethylene vinyl acetate composites
- Effect of neutron irradiation on neat epoxy resin stability in shielding applications
- Study on the relation between microstructural change and compressive creep stress of a PBX substitute material
- Chemical synthesis and densification of a novel Ag/Cr2O3-AgCrO2 nanocomposite powder
- Reinforcing polypropylene with calcium carbonate of different morphologies and polymorphs
- Fabrication, mechanical, thermal, and electrical characterization of epoxy/silica composites for high-voltage insulation
- Synergy of cashew nut shell filler on tribological behaviors of natural-fiber-reinforced epoxy composite
- Fabrication and Failure Prediction of Carbon-alum solid composite electrolyte based humidity sensor using ANN
- Investigation of three-body wear of dental materials under different chewing cycles
- Structural and physico-mechanical characterization of closed-cell aluminum foams with different zinc additions
- Mechanical performance of polyester pin-reinforced foam filled honeycomb sandwich panels
- Effect of chemical treatment on thermal properties of hair fiber-based reinforcement of HF/HDPE composites
- Indium doping in sol-gel synthesis of In-Sm co-doped xIn-0.05%Sm-TiO2 composite photocatalyst
- Effect of the meso-structure on the strain concentration of carbon-carbon composites with drilling hole

