Magnetic characterization of magnetoactive elastomers containing magnetic hard particles using first-order reversal curve analysis

2.1 Sample preparation

The MAE samples considered in this paper are based on a polydimethylsiloxane (PDMS) matrix. Usually a two-component composition with an organometallic crosslinking agent (Pt catalysts) is used. Tuning of the matrix stiffness is achieved by different mixing ratios of the individual polymer components and by dilution of the composition with a silicone oil. Details on a manufacturing processes are given elsewhere [5]. In addition particle-matrix-systems with an inelastic epoxy resin matrix are used as reference samples.

Magnetically hard NdFeB-alloy microparticles or combinations of hard magnetic NdFeB-alloy microparticles with soft magnetic carbonyl iron microparticles are used as filling components. The NdFeB-alloy particles have either a spherical (MQP-S-11 from Magnequench) or a flake-like shape (MQA-38-14 from Magnequench), with a size distribution of the spherical particles between 5 and 50 µm and a length distribution of the flake-like particles between 10 and 100 µm [11]. Before adding to the noncrosslinked matrix, the NdFeB particles are modified with a mixture of volatile alcohol and silicone oil to improve adhesion to the polymer chains [5]. The mean diameter of the precoated by the manufacturer spherical carbonyl iron particles (BASF, grade CC)) is ∼5 µm.

The particles are added before the crosslinking reaction and distributed homogeneously during polymerization using mechanical stirring. The total particle content as well as the ratio of hard magnetic to soft magnetic components is varied for different samples as given in [8], [11].

2.2 FORC method

Magnetic characterization of MAEs was performed using vibrating sample magnetometers (VSM) of 7407 series from Lake Shore. All measurements have been conducted at room temperature. The magnetization behavior of the MAEs containing hard magnetic components used in this work was characterized using the FORC method.

The FORC method divides the measuring process (see Figure 1) into the following steps: (1) possibly training of the MAE sample by multiple repetition of the full magnetization cycle, (2) magnetization of the sample in a maximum positive field, (3) reduction of the magnetic field until the reverse field H _r is reached, (4) measurement of a FORC curve, (5) n-fold repetition of the steps (2) – (4) with regular intervals between H _r to H _r  = −H_max. Set of the reversal magnetization curves obtained in this way is exemplary demonstrated in Figure 1. The resulting set of functions M (H _a , H _r ) provides the magnetization of the examined MAE at any point depending on the respective reverse field H _r and the respectively applied magnetic field H _a . The FORC distribution is defined by the mixed derivation of the functional group according to H _r and H _a

and the FORC diagrams are in turn the result of a coordinate transformation by 45°,

so that the horizontal axis now corresponds to the coercive field H _c and the vertical axis to the interaction field H _u . The FORCinel analysis software with a smoothing factor of 10 was used for the data treatment and calculations of FORC diagrams. In the measurements according to [8], 699 FORC curves were recorded based on the original algorithm of the MicroMag^TM software of the Princeton Measurements Corporation. Further measurements include 250–350 curves based on an algorithm provided by the Lake Shore Software. The measuring time per point was between 1 and 2 s in all experiments.

Figure 1:

Function set of the reversal curves of an MAE with hard magnetic NdFeB particles and hard elastic matrix represented as magnetization M over the applied magnetic field H (H _a ). A reversal or FORC curve starts at H _r and runs to H_max (or H_Sat). The saturation magnetization M _S is reached when more than 95% of the magnetic particles are magnetized. H _c (coercive field) indicates the particles own magnetic field which remains after external magnetization.

2.3 Microstructure analysis

Computed X-ray microtomography (μCT) is a nondestructive method for analyzing the internal microstructure of MAEs [12]. Paired with modern algorithms of digital image processing, the high resolution μCT makes it possible to differentiate individual particles and to track their movements under the influence of magnetic fields as demonstrated in Figure 2 [13], [14], [15]. The microstructural analysis performed using μCT is attended to assists in the interpretation of FORC diagrams.

Figure 2:

On the left side the µCT scan of a sample MAE with flake-like NdFeB-alloy particles before magnetization is shown. The particles are evenly distributed. The right side, in contrast, shows the scan of the same sample after it was magnetized at 2 T. Now the particles have shifted within the soft elastic matrix and chain-like structures have formed [14], [15].

3.1 Training effects

The so-called training effect of magnetoactive elastomers with magnetically hard, flake-shaped NdFeB alloy particles has been investigated in [11]. During the magnetization of the samples it was observed that the first magnetization curve of a virgin sample differs significantly from the following curves. By stepwise magnetization of the sample with µCT scans in between, it was possible to follow the particle movements and the alignment of their main axes relative to the magnetic field direction, as it is show in Figure 3. From the angular distribution of the particles, which was evaluated from the µTC scans at the different magnetization stages, it was possible to conclude that the particle-matrix coupling in the first magnetization loop is strong and only a part of the particles rotate. Only after further magnetization loops and the saturation of the sample the particles were able to rotate reversibly and align themselves along the magnetic field. As a consequence of the µCT scans with the corresponding angular distributions and the simulation model introduced in, a first, indirect impression of the irreversible matrix deformation behavior was obtained.

Figure 3:

Combined µCT scans of a MAE with flake-shaped NdFeB-alloy particles, with and without an applied magnetic field, showing the movements and rotations of the particles by single particle tracking [15], [16].

In [17], [18] the phenomena of training of MAE with hard magnetic spherical NdFeB-alloy particles were also analyzed experimentally and theoretically. According to this, complex magnetization processes of the individual grains take place in the multigrain particles, which interact with each other. The training effect is based on the fact that the magnetic moments within the individual grains change their orientation along the anisotropy axis during the magnetization loops and switch moments in some of the grains. The more often the magnetization loop is passed through, the more stable the system becomes since grains turn by the same angle under the influence of the magnetic field, and the same groups of grains begin to switch their magnetic moment. The magnetization of microparticles thus depends on the strength of the applied magnetic field as well as on the number of grains and does not correspond to the saturation magnetization of NdFeB-alloy powder, which is about 7.3 T [17], [18].

Figures 4–6 demonstrate influence of the training effect on the FORC distribution obtained for the MAE with hard magnetic spherical NdFeB-alloy particles. The sample has a soft elastic PDMS matrix (E ∼50 kPa) and filled with 10 vol% of particles having a size of 5–20 µm. In Figure 4 the FORC distribution of a sample which was not premagnetized before the FORC measurement is presented, while Figure 5 shows the results from a sample which was initially magnetized (from H = 0 to H_max) and then passed through a magnetization loop. In contrast in Figure 6 a sample passing through six magnetization loops was used for FORC measurement. From the FORC diagrams it can be seen that the peak of the coercivity field in the untrained sample is relatively large due to the still strong particle–matrix interactions. As the magnetization state of the system becomes increasingly stable, analogous to [17], the magnetization becomes larger and the peak of the coercivity field narrower. The particles can rotate reversibly in the meanwhile stable particle–matrix-system and show comparable movement patterns when a magnetic field is applied again (e.g., during further FORC measurements).

Figure 4:

FORC diagram of an untrained sample of MAE with 10 vol% NdFeB particles (<20 µm) in soft elastic matrix (E ∼50 kPa).

Figure 5:

FORC diagram of MAE with 10 vol% NdFeB particles (<20 µm) in soft elastic matrix (E ∼50 kPa), sample was premagnetized one time.

Figure 6:

FORC diagram of MAE with 10 vol% NdFeB particles (<20 µm) in soft elastic matrix (E ∼50 kPa), sample was premagnetized six times.

3.2 Matrix influence

The elasticity of the polymer matrix has a significant influence on the magnetization behavior of magnetoactive elastomers [19]. The more soft the matrix is, the more the particles can move within it under the influence of the applied magnetic field. Various particle–matrix MAEs containing magnetic hard particles were considered using FORC analysis. Corresponding results are shown in Figures 7 and 8.

Figure 7:

FORC diagrams of MAE with mixed magnetic filler components at a total particle content of 28 vol% and a mixing ratio of NdFeB particles to iron particles of 55:45. The elasticity of the polymer matrix increases from left to right: 50 kPa (left), 120 kPa (middle) and 440 kPa (right) [8].

Figure 8:

FORC diagrams of MAE with exclusively hard magnetic filling components at a particle content of 5 vol%. The samples are trained before passing FORC measurement.

Figure 7 shows that the central peak moves to the right along the coercive field axis with increasing modulus of elasticity. This drastic shift can be explained by the increasing restriction of particle movement. The stiffer the matrix, the less the particles can move and rotate. After all, in completely inelastic matrices, only inner-particle domain processes can take place in response to an external magnetic field. The interaction between the different particles type is also restricted with increasing matrix stiffness. The narrow ridge along the interaction axis represents the coupling between reversible magnetization of the soft magnetic iron particles and the irreversible magnetization state of the entire system. The diagonal feature in the FORC diagrams, however, indicates magnetostatic coupling and the movement of the iron particles in the matrix as discussed in [8].

FORC measurement performed on specimens solely based on magnetic hard powder confirmed the significant influence of matrix elasticity on the movement behavior of the particles under the influence of magnetic fields (Figure 8). The stiffer the matrix system is, the less the particles can rotate and move. Inner-particle domain processes increase, the magnetization of the system decreases. In the hard epoxy matrix the particles are firmly anchored which means that the particles can no more rotate, and the magnetization of the system is based entirely on the inner-particle processes of the multidomain particles, whose individual regions align themselves along the magnetic field lines or, according to [17], switch over at sufficiently high fields. In addition, a weak diagonal ridge is visible in the FORC diagrams obtained for the samples without magnetic soft powder. According to [20], this could be due to soft magnetic fractions in the magnetically hard NdFeB particles, but this has not been proven, so the origin of this FORC feature is still to be investigated.

3.3 Particles influence

3.3.1 Particle ration

The influence of the ratio of the mixed magnetic filling components on the magnetization behavior of the MAE was investigated in [8] to evaluate whether there are interactions between the different particle types that have a possible influence on the material properties. For this purpose, MAEs with a constant total particle content of 28 vol% were used, but the ratio of magnetically hard NdFeB-alloy particles to magnetically soft carbonyl iron particles was varied. Figure 9 shows that as the iron particle content increases, the intensity of the irreversible features decreases while the reversible portions increase. The asymmetric degree along the H _u axis results from the coupling of the reversible magnetization behavior of the iron particles and the irreversible magnetization state of the whole system. In contrast, the areas of irreversible magnetization that occur at interaction fields of H _u  < −50 kA/m are caused by the magnetostatic coupling and the movement of the particles within the matrix. In the case of higher contents of magnetically soft carbonyl iron particles, there are furthermore effects with positively and negatively applied fields. In the negative range, these are probably caused by a magnetization reverse of iron particles in the immediate vicinity of positively magnetized NdFeB-alloy particles. The magnetization of these soft magnetic particles can only be reversed at this point by a negative field that compensates the positive remanent field of the nearby NdFeB-alloy particles. The effect in the positive region probably comes from the movement and restructuring of the iron particles in the matrix.

Figure 9:

FORC diagrams of MAE with mixed magnetic filling components at a total particle content of 28 vol%, a constant matrix stiffness and a varied mixing ratio of NdFeB-alloy particles to iron particles. For example, the FORC diagram at the top on the left side has a ratio of 100% NdFeB particles to 0% Fe particles. The ratios of the other three diagrams are obtained in analogy (76:24, 57:43, 36:64) [8].

3.3.2 Particle size

According to the manufacturer’s specifications the diameter of the spherical NdFeB-alloy particles used by Magnequench is between 5 and 100 µm. To analyze the influence of particle size on the magnetic behavior of a composite, the particles were fractionated into different size ranges by the dry sieve method. Therefore the HAVER EML 200 Premium Remote Test Sieve Shaker with different nominal sizes of test sieves was used to fractionize the particles. FORC diagrams obtained for two samples with soft-elastic PDMS matrix (E ∼50 kPa) but different particle size classes are compared in Figure 10. The larger particles show a much higher magnetization, which may be explained by the correspondingly higher number of domains within the multigrain particles. Furthermore, the feature corresponding to the coercive field is larger in the FORC diagram obtained for the sample with the smaller particles. This can be explained by a more tightly structured particlepolymer network, which, in analogy to Figure 8, is accompanied by an increase in the coercive field. In relation to the larger NdFeB alloy particles, the smaller particle fraction has higher total surface area, which potentially allows more rubbers between coated particles and polymer chains as discussed in [21]. However, the exact reasons for the different behavior is not clear and still need to be investigated.

Figure 10:

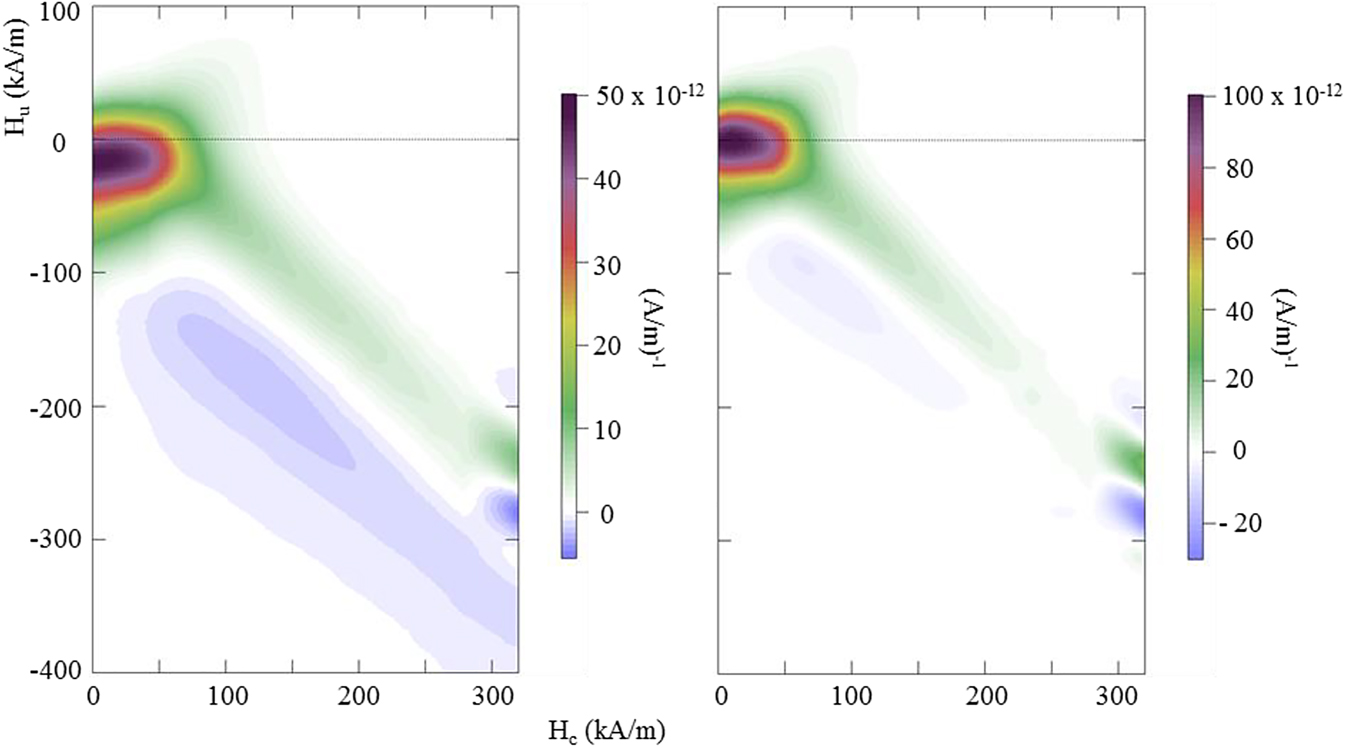
FORC diagrams of MAE with 10 vol% hard magnetic NdFeB particles in a polymer matrix with an elasticity of E ∼50 kPa and varying particle size distribution: 20–39 µm (left) and 63–79 µm (right). Both samples were trained in advance.