Home Exact solutions of the Biswas-Milovic equation, the ZK(m,n,k) equation and the K(m,n) equation using the generalized Kudryashov method
Article Open Access

Exact solutions of the Biswas-Milovic equation, the ZK(m,n,k) equation and the K(m,n) equation using the generalized Kudryashov method

  • EL Sayed M.E. Zayed EMAIL logo and Abdul-Ghani Al-Nowehy
Published/Copyright: April 28, 2016
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 14 Issue 1

Abstract

In this article, we apply the generalized Kudryashov method for finding exact solutions of three nonlinear partial differential equations (PDEs), namely: the Biswas-Milovic equation with dual-power law nonlinearity; the Zakharov--Kuznetsov equation (ZK(m,n,k)); and the K(m,n) equation with the generalized evolution term. As a result, many analytical exact solutions are obtained including symmetrical Fibonacci function solutions, and hyperbolic function solutions. Physical explanations for certain solutions of the three nonlinear PDEs are obtained.

Key words: Nonlinear PDEs; Generalized Kudryashov method; Exact solutions; Symmetrical hyperbolic Fibonacci function; The Biswas-Milovic equation; The Zakharov–Kuznetsov equation; The K(m,n) equation
MSC 2010: 02.30 Jr; 02.30.Ik; 05.45.Yv

1 Introduction

The research area of nonlinear partial differential equations (PDEs) has been very active for the past few decades. There are many types of nonlinear PDEs that appear in various areas of the physical and mathematical sciences. Much effort has been expended on constructing exact solutions to these nonlinear PDEs, motivated by their important role in the study of nonlinear physical phenomena. Nonlinear phenomena appears in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics, and geo-chemistry. In recent years, a number of powerful and efficient methods for finding analytic solutions to nonlinear equations have drawn a lot of interest by a diverse group of scientists. These include, for example: Hirota’s bilinear transformation method [1, 2]; the tanh-function method [3, 4]; the (G′/G)-expansion method [5–10]; the Exp-function method [11–14]; the multiple exp-function method [15–17]; the symmetry method [18, 19]; the modified simple equation method [20–22]; the improved (G′/G)-expansion method [23]; a multiple extended trial equation method [24]; the Jacobi elliptic function expansion method [25, 26]; the Bäcklund transform method [27, 28]; the generalized Riccati equation method [29]; the modified extended Fan sub equation method [30]; the auxiliary equation method [31, 32]; the first integral method [33, 34]; the modified Kudryashov method [35–42], and the soliton ansatz method [43–70].

The objective of this paper is to apply the generalized Kudryashov method [42] to find the exact solutions of the Biswas-Milovic equation with dual-power law nonlinearity [71, 72], the ZK(m,n,k) [73, 74], and the K(m,n) equation with the generalized evolution term [75].

This paper is organized as follows: in Sec. 2, the description of the generalized Kudryashov method is given. In Sec. 3, we use this method to solve the three aforementioned nonlinear PDEs. In Sec. 4, physical explanations of certain results are presented, and conclusions are discussed in Sec. 5.

2. Description of the generalized Kudryashov method

Starting with a nonlinear PDE in the following form:

(2.1)F(u,ut,ux,utt,uxt,uxx,...)=0,

where u = u(x, t) is an unknown function, F is a polynomial in u = u (x, t) and its partial derivatives, in which the highest order derivatives and nonlinear terms are involved.

The main steps of the generalized Kudryashov method are described as follows:

Step 1. First, we use the wave transformation:

(2.2)u(x,t)=U(ζ),  ζ=kx±λt,

where k and λ are arbitrary constants with k, λ ≠ 0, in order to reduce equation (2.1) into a nonlinear ordinary differential equation (ODE) with respect to the variable ζ of the form

(2.3)H(U,U′,U′′,U′′′,...)=0,

where H is a polynomial in U(ζ) and its total derivatives U′, U″, U‴, ... such that U′=dUdζ, U′′=d2Udζ2 and so on.

Step 2. We assume that the formal solution of the ODE (2.3) can be written in the following rational form:

(2.4)U(ζ)=∑i=0naiQi(ζ)∑j=0mbjQj(ζ)=AQ(ζ)BQ(ζ),

where Q=11±aζ,A[Q(ζ)]=∑i=0naiQi(ζ) and B[Q(ζ)]=∑j=0mbjQj(ζ).. The function Q is the solution of the equation

(2.5)Q′=Q(Q−1)ln(a),  0<a≠1.

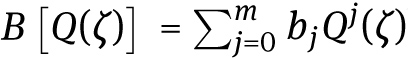
Taking into consideration (2.4), we obtain

(2.6)U′(ζ)=Q(Q−1)[A′B−AB′B2]ln(a),
(2.7)U′′(ζ)=QQ−1(2Q−1)A′B−AB′B2ln2(a)+Q2Q−12B(A′′B−AB′′)−2A′B′B+2A(B′)2B3ln2(a),
(2.8)U′′′(ζ)=Q3Q−13ln3(a)×(A′′′B−AB′′′−3A′′B′−3A′B′′)B+6B′(A′B′+AB′′)B3−6A(B′)3B4+3Q2(Q−1)2(2Q−1)×(A′′B−AB′′−2A′B′)B+2A(B′)2B3In3(a)+Q(Q−1)(6Q2−6Q+1)A′B−AB′B2In3(a),

and that similar solutions apply for higher order differentiation terms.

Step 3. Under the terms of the given method, we suppose that the solution of Eq. (2.3) can be written in the following form:

(2.9)U(ζ)=a0+a1Q+a2Q2++anQnb0+b1Q+b2Q2++bmQm.

To calculate the values m and n in (2.9), i.e. the pole order for the general solution of Eq. (2.3), we progress as per the classical Kudryashov method by balancing the highest order nonlinear terms and the highest order derivatives of U() in Eq. (2.3). This allows us to derive a formula for m and n and determine their values.

Step 4. We substitute (2.4) into Eq. (2.3) to get a polynomial R (Q) of Q and equate all the coefficients of Qi, (i = 0, 1, 2, ...) to zero, to yield a system of algebraic equations for ai (i = 0, 1, ..., n) and bj (j = 0, 1, ..., m).

Step 5. We solve the algebraic equations obtained in Step 4 using Mathematica or Maple, to get k , and the coefficients of ai (i = 0, 1, ..., n) and bj (j = 0, 1, ..., m). In this way, we attain the exact solutions to Eq. (2.3).

The obtained solutions depended on the symmetrical hyperbolic Fibonacci functions given in [76]. The symmetrical Fibonacci sine, cosine, tangent, and cotangent functions are, respectively, defined as:

(2.10)sFs(x)=ax−a−x5,cFs(x)=ax+a−x5,tanFs(x)=ax−a−xax+a−x,cotFs(x)=ax+a−xax−a−x,
(2.11)sFs(x)=25sh(x.In(a)),cFs(x)=25ch(x. In(a)),tanFs(x)=tanh(x. In(a)),cotFs(x)=coth(x. In(a)).

3. Applications

In this section we construct the exact solutions in terms of the symmetrical hyperbolic Fibonacci functions of the following three nonlinear PDEs using the generalized Kudryashov method described in Sec. 2:

3.1 Example 1. The Biswas-Milovic equation with dual-power law nonlinearity

In this subsection, we study the Biswas-Milovic equation with dual-power law nonlinearity [71, 72]

(3.1.1)i(qm)t+a(qm)xx+b(|q|2n+k|q|4n)qm=0,

where a, b and k are constants, while m, n are positive integers.

If m = 1, then Eq. (3.1.1) becomes the nonlinear Schrödinger equation (NLSE) with dual-power law nonlinearity. In Eq. (3.1.1), the first term is the temporal evolution, while a is the coefficient of group-velocity dispersion (GVD), while b and k are the coefficients of the nonlinear terms. Let us now solve Eq. (3.1.1) using the method of Sec. 2. To this end, we use the wave transformation

(3.1.2)q(x,t)=U(ζ)exp(iθ),  θ=λx−wt,  ζ=μ(x−νt),

where λ, w, μ and v are constants.

Substituting (3.1.2) into (3.1.1), we obtain the nonlinear ODE:

(3.1.3)aμ2(Um)′′+iμ(−ν+2amλ)(Um)′+m(w−amλ2)Um+bU2n+m+bkU4n+m=0.

From Eq. (3.1.3) , we deduce that

(3.1.4)ν=2amλ,

and

(3.1.5)aμ2(Um)′′+m(w−amλ2)Um+bU2n+m+bkU4n+m=0.

Balancing (Um)″ and U4n + m in (3.1.5), then the following relation is attained:

(3.1.6)mN+2=(4n+m)N⇒N=12n.

Then we take into consideration the transformation

(3.1.7)U(ζ)=[v(ζ)]12n.

Substituting (3.1.7) into equation (3.1.5) we have the new equation

(3.1.8)2amnμ2vv′′+amμ2(m−2n)v′2+4mn2(w−amλ2)v2+4bn2v3+4bkn2v4=0.

Balancing the vv″ and v4 in (3.1.8), then the following relation is obtained:

(3.1.9)(N−M)+(N−M)+2=4(N−M)⇒N=M+1.

If we choose M = 1 and N = 2, then the formal solution of Eq. (3.1.8) has the form:

(3.1.10)v(ζ)=a0+a1Q+a2Q2b0+b1Q,

and consequently

(3.1.11)v′(ζ)=Q(Q−1)(b0+b1Q)2[(a1+2a2Q)(b0+b1Q)−b1(a0+a1Q+a2Q2)]ln(a),
(3.1.12)v′′(ζ)=Q(Q−1)(2Q−1)(b0+b1Q)2[(a1+2a2Q)(b0+b1Q)−b1(a0+a1Q+a2Q2)]ln2(a)+Q2(Q−1)2ln2(a)(b0+b1Q)3×[2a2(b0+b1Q)2−2b1(a1+2a2Q)(b0+b1Q)+2b12(a0+a1Q+a2Q2)].

Substituting (3.1.10), (3.1.11) and (3.1.12) into (3.1.8), collecting the coefficients of each power of Qi, (i = 0, 1, ..., 8) and setting each of the coefficients to zero, we obtain the following system of algebraic equations:

Q8:am2a22b12μ2ln2(a)+2amna22b12μ2ln2(a)  +4bkn2a24=0,
Q7:−2amna22b12μ2ln2(a)+16bkn2a1a23 +4am2a22b0b1μ2ln2(a)+4amna22b0b1μ2ln2(a) +4amna2b12a1μ2ln2(a)−2am2a22b12μ2ln2(a) +4bn2a23b1=0,
Q6:12bn2a1a22b1+4amna22b02μ2ln2(a) −2amna22b0b1μ2ln2(a)+2am2a1b0a2b1μ2ln2(a) −4n2m2aλ2a22b12−2am2a2b12a0μ2ln2(a) −8am2a22b0b1μ2ln2(a)+24bkn2a12a22 +8amna1b0b1a2μ2ln2(a)+4bn2a23b0 −6amna2b12a1μ2ln2(a)+4am2a22b02μ2ln2(a) +am2a22b12μ2ln2(a)+16bkn2a0a23+4n2mwa22b12 +8amna2b12a0μ2ln2(a)=0,
Q5:12bn2a12a2b1+48bkn2a0a1a22 +16amna2b0b1a0μ2ln2(a)+8n2mwa22b0b1 +12bn2a0a22b1+4am2a22b0b1μ2ln2(a) −8amna1b0b1a2μ2ln2(a)−2amna22b0b1μ2ln2(a) +12bn2a1a22b0−4am2a1b0a2b1μ2ln2(a) −16amna2b12a0μln2(a)+4am2a1b02a2μ2ln2(a) −4am2a2b0b1a0μ2ln2(a)+8amna2b02a1μ2ln2(a)  +16bkn2a13a2+8n2mwa1a2b12 +2amna2b12a1μ2ln2(a)+4am2a2b12a0μ2ln2(a) −8n2m2aλ2a22b0b1−8n2m2aλ2a1a2b12 −4amna22b02μ2ln2(a)−8am2a22b02μ2ln2(a)=0,
Q4:−8n2m2aλ2a0a2b12−2am2a2b12a0+16n2mwa1a2b0b1+2am2a1b0a2b1μ2ln2(a)+4bkn2a14+8amna2b12a0μ2ln2(a)−4n2m2aλ2a12b12−4n2m2aλ2a22b02+8n2mwa0a2b12+24bn2a0a1a2b1+48bkn2a0a12a2+am2a12b02μ2ln2(a)+4bn2a13b1+2amna12b02μ2ln2(a)+8am2a2b0b1a0μ2ln2(a)−2amnb12a02μ2ln2(a)+4n2mwa12b12+4n2mwa22b02+12bn2a0a22b0−16n2m2aλ2a1a2b0b1+12bn2a12a2b0+4am2a22b02μ2ln2(a)−8am2a1b02a2μ2ln2(a)−28amna2b0b1a0μ2ln2(a)−10amna2b02a1μ2ln2(a)+24bkn2a02a22+am2b12a02μ2ln2(a)+2amna12b0b1μ2ln2(a)+12amna2b02a0μ2ln2(a)−2amnb12a0a1μ2ln2(a)−2am2a1b0b1a0μ2ln2(a)=0,
Q3:−2am2a12b02μ2ln2(a)−2amna12b02μ2ln2(a)+2amnb12a02μ2ln2(a)−16n2m2aλ2a0a2b0b1+8n2mwa0a1b12+8n2mwa12b0b1+8n2mwa1a2b02+24bn2a0a1a2b0+48bkn2a0a1a2+4bn2a13b0+12bn2a02a2b1+12amna2b0b1a0μ2ln2(a)+12bn2a0a12b1+16bkn2a0a13+4amna1b02a0μ2ln2(a)−4amnb1a02b0μ2ln2(a)+4am2a1b02a2μ2ln2(a)+2amna2b02a1μ2ln2(a)−2am2b12a02μ2ln2(a)−8n2m2aλ2a0a1b12−8n2m2aλ2a12b0b1−8n2m2aλ2a1a2b02+16n2mwa0a2b0b1−2amna12b0b1μ2ln2(a)−20amna2b02a0μ2ln2(a)−4am2a2b0b1a0μ2ln2(a)+2amnb12a0a1μ2ln2(a)+4am2a1b0b1a1μ2ln2(a)=0,
Q2:12bn2a02a2b0−4n2m2aλ2a12b02+am2b12a02μ2ln2(a)−8n2m2aλ2a0a2b02−4n2m2aλ2a02b12+am2a12b02μ2ln2(a)+12bn2a02a1b1+6amnb1a02b0μ2ln2(a)+4n2mwa12b02+16bkn2a03a2+8amna2b02a0μ2ln2(a)+12bn2a0a12b0+24bkn2a02a12+4n2mwa02b12−16n2m2aλ2a0a1b0b1+8n2mwa0a2b02−2am2a1b0b1a0μ2ln2(a)+16n2mwa0a1b0b1−6amna1b02a0μ2ln2(a)=0,
Q1:−8n2m2aλ2a0a1b02−2amnb1a02b0μ2ln2(a)−8n2m2aλ2a02b0b1+8n2mwa0a1b02+4bn2a03b1+16bkn2a03a1+12bn2a02a1b0+2amna1b02a0μ2ln2(a)+8n2mwa02b0b1=0,
(3.1.13)Q0:−4n2m2aλ2a02b02+4bkn2a04+4bn2a03b0+4n2mwa02b02=0.

Solving the system of algebraic equations (3.1.13) by Maple or Mathematica, we obtain the following sets:

Set 1:

(3.1.14)μ=1ln(a)−bn2(2n+m)amk(n+m)2,w=amλ2+b(2n+m)4k(n+m)2,a0=0,a1=−b0(2n+m)2k(n+m),a2=−b1(2n+m)2k(n+m),b0=b0,b1=b1,λ=λ,m=m,n=n,k=k,a=a,b=b.

Substituting (3.1.14) into (3.1.10), we get the following solution:

(3.1.15)v(ζ)=−(2n+m)2k(n+m)1(1±aζ).

From (3.1.7) and (3.1.15) we have

(3.1.16)U(ζ)=[−(2n+m)2k(n+m)1(1±aζ)]12n.

With the help of (2.10) and (2.11) the exact solution of Eq. (3.1.1) has the form:

(3.1.17)q(x,t)={−(2n+m)4k(n+m)×[1−tanFs(12ln(a)−bn2(2n+m)amk(n+m)2(x−2amλt))]}12n×exp(iθ),
(3.1.18)​=​{​−(2n+m)4k(n+m)[1−tanh(12−bn2(2n+m)amk(n+m)2(x−2amλt))]​}12n×exp(iθ),

or

(3.1.19)q(x,t)={−(2n+m)4k(n+m)×[1−cotFs(12ln(a)−bn2(2n+m)amk(n+m)2(x−2amλt))]}12n×exp(iθ),
(3.1.20)={−(2n+m)4k(n+m)×[1−coth(12−bn2(2n+m)amk(n+m)2(x−2amλt))]}12n×exp(iθ),

where θ=λx−(amλ2+b(2n+m)4k(n+m)2)t, provided that ab > 0 and k < 0.

set 2:

(3.1.21)μ=1ln(a)−bn2(2n+m)amk(n+m)2,w=amλ2+b(2n+m)4k(n+m)2,a0=0,a1=−b1(2n+m)2k(n+m),a2=b1(2n+m)2k(n+m),b0=0,b1=b1,  λ=λ,m=m,n=n,k=k,a=a,b=b.

Substituting (3.1.21) into (3.1.10), we get the following solution:

(3.1.22)v(ζ)=−(2n+m)2k(n+m)aζ(aζ±1).

From (3.1.7) and (3.1.122) we have

(3.1.23)U(ζ)=[−(2n+m)2k(n+m)aζ(aζ±1)]12n.

With the help of (2.10) and (2.11) the exact solution of Eq. (3.1.1) has the form:

(3.1.24)q(x,t)=[−(2n+m)4k(n+m)(1+tanhη)]12nexp(iθ),

or

(3.1.25)q(x,t)=[−(2n+m)4k(n+m)(1+cothη)]12nexp(iθ),

where η=12−bn2(2n+m)amk(n+m)2(x−2amλt), θ=λx−(amλ2+b(2n+m)4k(n+m)2)t provided that ab > 0 and k < 0.

set 3:

(3.1.26)μ=1ln(a)−bn2(2n+m)amk(n+m)2,w=amλ2+b(2n+m)4k(n+m)2,a1=−(b0+b1)(2n+m)2k(n+m),a0=0,a2=0,b0=b0,b1=b1,  λ=λ,m=m,n=n,k=k,a=a,b=b.

Consequently,we have the exact solutions of Eq. (3.1.1) in the form:

(3.1.27)q(x,t)=[−(b0+b1)(2n+m)[1−tanhη]2k(n+m)[2b0+b1(1−tanhη)]]12nexp(iθ),

or

(3.1.28)q(x,t)=[−(b0+b1)(2n+m)[1−cothη]2k(n+m)[2b0+b1(1−cothη)]]12nexp(iθ),

where η=12−bn2(2n+m)amk(n+m)2(x−2amλt), θ=λx−(amλ2+b(2n+m)4k(n+m)2)t, provided that ab > 0 and k < 0.

On comparing our result (3.1.24), with the result (18) obtained in [71], we conclude that the two results are equivalent with λ = −κ, while our results (3.1.18), (3.1.20), (3.1.25), (3.1.27) and (3.1.28) are new, and not discussed elsewhere.

3.2 Example 2. The Zakharov–Kuznetsov equation (ZK(m,n,k))

In this subsection, we apply the given method to solve the ZK(m,n,k) [73, 74]

(3.2.1)ut+λ0(um)x+λ1(un)xxx+λ2(uk)xyy=0,

where u = u (x, y, t) is a readily differentiable function, λ0, λ1 and λ2 are arbitrary constants while m, n and k are positive integers. The function governs the behaviour of weakly nonlinear ion acoustic waves in a plasma comprising cold ions and hot isothermal electrons in the presence of a uniform magnetic field [77]. Recently, Ma et al. [73] used the auxiliary equation method to find the solutions of the ZK(2,1,1) equation with λ0=12,λ1=13,λ2=23.

This work is concerned with two cases of Eq. (3.2.1):

3.2.1 Case 1: ZK(2,1,1)

In this case Eq. (3.2.1) becomes the form:

(3.2.2)ut+λ0(u2)x+λ1uxxx+λ2uxyy=0.

To seek travelling wave solutions, we use the wave transformation

(3.2.3)u(x,y,t)=U(ζ),  ζ=x+βy+γt,

where β and γ are arbitrary constants with β, γ ≠ 0, to reduce equation (3.2.2) to the ODE:

(3.2.4)γU′+λ0(U2)′+λ1U′′′+λ2β2U′′′=0.

Integrating Eq. (3.2.4) with respect to ζ, with zero constant of integration, we get

(3.2.5)γU+λ!0U2+(λ1+λ2β2)U′′=0.

Balancing the U˶ and U2 in (3.2.5), then we have N = M + 2. If we choose M = 1 and N = 3, then the formal solution of Eq. (3.2.5) has the form:

(3.2.6)U(ζ)=a0+a1Q+a2Q2+a3Q3b0+b1Q,

and consequently,

(3.2.7)U′(ζ)=Q(Q−1)(b0+b1Q)2[(a1+2a2Q+3a3Q2)(b0+b1Q)−b1(a0+a1Q+a2Q2+a3Q3)]ln(a),
(3.2.8)U′′(ζ)=Q(Q−1)(2Q−1)(b0+b1Q)2[(a1+2a2Q+3a3Q2)(b0+b1Q)−b1(a0+a1Q+a2Q2+a3Q3)]ln2(a)+Q2(Q−1)2(b0+b1Q)3[(b0+b1Q)2(2a2+6a3Q)−2b1(a1+2a2Q+3a3Q2)(b0+b1Q)+2b12(a0+a1Q+a2Q2+a3Q3)]ln2(a).

Substituting (3.2.6) and (3.2.8) into (3.2.5), and equating all the coefficients of Qi, (i = 0, 1, ..., 7) to zero, we get a system of algebraic equations, which can be solved using the Maple, to get the following sets:

Set 1:

(3.2.9)a0=0,a1=6b0(λ1+λ2β2)ln2(a)λ0,a2=−6(b0−b1)(λ1+λ2β2)ln2(a)λ0,a3=−6b1(λ1+λ2β2)ln2(a)λ0,b0=b0,b1=−2b0,γ=−(λ1+λ2β2)ln2(a),β=β,λ0=λ0,λ1=λ1,λ2=λ2. 

Substituting (3.2.9) into (3.1.10), we get the following solution of Eq. (3.2.6):

(3.2.10)U(ζ)=±6(λ1+λ2β2)ln2(a)λ0aζ(aζ±1)2.

With the help of (2.10) and (2.11) the exact solution of Eq. (3.2.2) in the form:

(3.2.11)u(x,y,t)=3(λ1+λ2β2)ln2(a)2λ0sech2 η,
(3.2.12)u(x,y,t)=−3(λ1+λ2β2)ln2(a)2λ0csch2 η,

where η=12[x+βy−(λ1+λ2β2)ln2(a).t] in(a).

set 2:

(3.2.13)a0=−b0(λ1+λ2β2)ln2(a)λ0,a1=(6b0−b1)(λ1+λ2β2)ln2(a)λ0,a2=−6(λ1+λ2β2)(b0−b1)ln2(a)λ0,a3=−6b1(λ1+λ2β2)ln2(a)λ0,γ=(λ1+λ2β2)ln2(a),b0=b0,b1=b1,β=β,λ0=λ0,λ1=λ1,λ2=λ2.

Consequently, we have the exact solutions of Eq. (3.2.2) in the form:

(3.2.14)u(x,y,t)=(λ1+λ2β2)ln2(a)2λ0[1−3tanh2η],
(3.2.15)u(x,y,t)=(λ1+λ2β2)ln2(a)2λ0[1−3coth2η],

where η=12[x+βy−(λ1+λ2β2)ln2(a).t] in(a).

If we choose λ0=12, λ1=13, λ2=23, a =e in our results (3.2.11),(3.2.12),(3.2.14) and (3.2.15) we have the well-known results u1, u2 of (10) and u1, u2 of (13) obtained in [73].

3.2.2 Case 2: ZK(m,1,1), m ⩾ 3

In this case Eq. (3.2.1) becomes the form:

(3.2.16)ut+λ0(um)x+λ1uxxx+λ2uxyy=0.

Using the same wave transformation (3.2.3), to reduce equation (3.2.16) to the ODE:

(3.2.17)γU′+λ!0(Um)′+λ1U‴+λ2β2U‴=0.   

Integrating Eq. (3.2.17) with respect to ζ, with zero constant of integration, we get

(3.2.18)γU+λ!0Um+(λ1+λ2β2)U′′=0.

By balancing U″ with Um we have N=2m−1, m ≥ 3. Then we use the transformation

(3.2.19)U(ζ)=[v(ζ)]2m−1.  

Substituting (3.2.19) into equation (3.2.18) we have the new equation

(3.2.20)(m−1)2(γv2+λ0v4)+(λ1+λ2β2)×6−2m(v′)2+2(m−1)vv′′=0. 

Balancing the vv″ and v4 in (3.2.21), then we have N = M + 1. If we choose M = 1 and N = 2, then Eq. (3.2.20) has the same formal solution (3.1.10).

Substituting (3.1.10),(3.1.11) and (3.1.12) into (3.2.20), and equating all the coefficients of Qi,(i = 0, 1, ..., 8) to zero, we get a system of algebraic equations, which can be solved using the aid of Maple or Mathematica, to get the following result:

(3.2.21)a0=0,a1=±2b0ln(a)(m−1)−2(λ1+λ2β2)(m+1)λ0,a2=∓2b0ln(a)(m−1)−2(λ1+λ2β2)(m+1)λ0,    b0=b0,b1=−2b0,γ=−4(λ1+λ2β2)ln2(a)(m−1)2,β=β,λ0=λ0,λ1=λ1,λ2=λ2.  

provided that (λ1+λ2β2)λ0<0.

Substituting (3.2.21) into (3.1.10), we get the following solution of Eq. (3.2.20):

(3.2.22)v(ζ)=±2ln(a)(m−1)−2(λ1+λ2β2)(m+1)λ0aζ(a2ζ−1).  

From (3.2.22) and (3.2.19) we have

(3.2.23)U(ζ)​=​[±2ln(a)(m−1)−2(λ1+λ2β2)(m+1)λ0aζ(a2ζ−1)]2m−1.  

With the help of (2.10) and (2.11) the exact solution of Eq. (3.2.16) in the form:

(3.2.24)u(x,y,t)​=​[±ln(a)(m−1)−2(λ1+λ2β2)(m+1)λ0cschη]2m−1​​​,    

where η=(x+βy−4(λ1+λ2β2)ln2(a)(m−1)2t)ln(a).

3.3 Example 3. The K(m,n) equation

The K(m,n) equation with the generalized evolution term [75, 78, 79] is given by

(3.3.1)(ql)t+aqmqx+b(qn)xxx=0,    

where, the first term is the generalized evolution term, the second term represents the nonlinearity, and the third term is the dispersion. Also, a , b ∈ R and are constants, while l, m and n ∈ Z+.

Eq. (3.3.1) is the generalized form of the KdV equation, where, in particular, the case l = m = n = 1 leads to the KdV equation. Eq. (3.3.1) appeared for the first time in [78] for l = 1. Thus, Eq. (3.3.1) reduces to the K(m,n) equation for l = 1. Therefore, for l = 1, K(1,1) is the KdV equation while K(2,1) is the mKdV equation. Eq. (3.3.1) has been discussed in [75] using the (G′/G)-expansion method and its exact solutions have been found.

In order to solve Eq. (3.3.1) using the method of section 2, we introduce the wave transformation

(3.3.2)q(x,t)=U(ζ),  ζ=μ(x−ct),    

where µ and c are constants, to reduce Eq. (3.3.1) to the ODE:

(3.3.3)−μc(Ul)′+μaUmU′+μ3bUn′′′=0. 

Integrating Eq. (3.3.3) with respect to ζ, with zero constant of integration, we have

(3.3.4)−μcUl+μam+1Um+1+μ3bUn′′=0. 

Let l = n, balancing (Un)′ and Um+1 in (3.3.4) yields N=2m+1−n, where m + 1 ≠ n. In order to obtain the closed form solutions, we use the transformation

(3.3.5)U(ζ)=[v(ζ)]1m+1−n,

to reduce Eq. (3.3.4) into the ODE

(3.3.6)−cm+1−n2v2+am+1−n2m+1v3+bnμ22n−m−1v′2+bnμ2m+1−n2vv′′=0.

Balancing the vv″ and v3 in (3.3.6), then we have N = M + 2. If we choose M = 1 and N = 3, then Eq. (3.3.6) has the same formal solution (3.2.6).

Substituting (3.2.6),(3.2.7) and (3.2.8) into (3.3.6), and equating all the coefficients of Qi,(i = 0, 1, ..., 10) to zero, we get a system of algebraic equations, which can be solved using the aid of Maple or Mathematica, to get the following result:

(3.3.7)a0=0,a1=2cb0(m+1)(m+1+n)na,a2=−2c(b0−b1)(m+1)(m+1+n)na,  a3=−2cb1(m+1)(m+1+n)na,μ=±cb(m+1−n)nln(a),b0=b0,b1=b1,c=c,

provided that bc>0.

Substituting (3.3.7) into (3.2.6), we get the following solution of Eq. (3.3.6):

(3.3.8)v(ζ)=±2c(m+1)(m+1+n)naaζ(aζ±1).  

From (3.2.8) and (3.2.5) we have

(3.3.9)U(ζ)=[±2c(m+1)(m+1+n)naaζ(aζ±1)]1m+1−n.  

With the help of (2.10) and (2.11) the exact solution of Eq. (3.3.1) in the form:

(3.3.10)u(x,y,t)=[c(m+1)(m+1+n)2nasech2η]1m+1−n,  

or

(3.3.11)u(x,y,t)=[−c(m+1)(m+1+n)2nacsch2η]1m+1−n,  

where η=±cb(m+1−n)2n(x−ct)

4 Physical explanations for some of our solutions

In this section, we will illustrate the application of the results established above. Exact solutions of the results describe different nonlinear waves. The established exact solutions with symmetrical hyperbolic Fibonacci functions are special kinds of solitary waves.

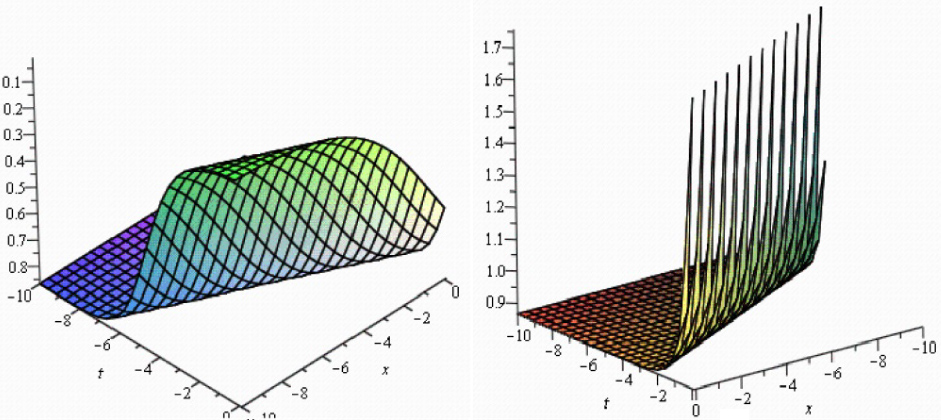
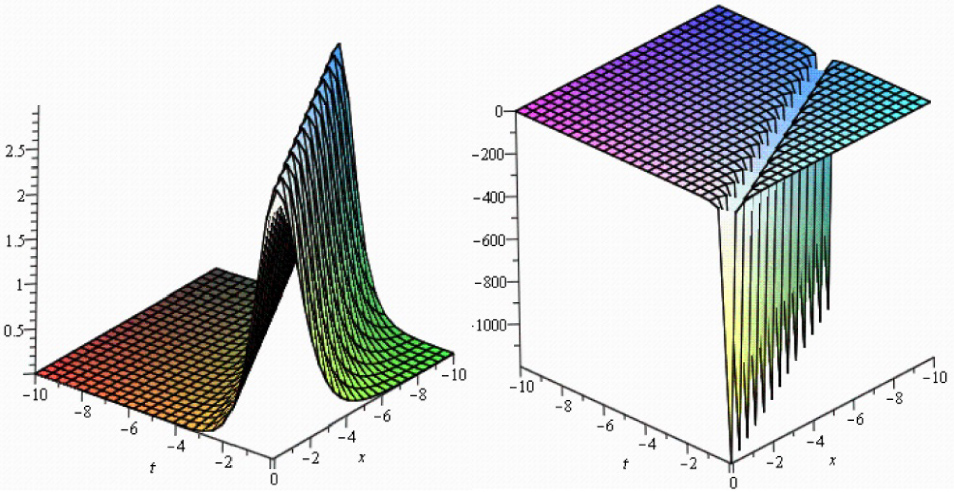
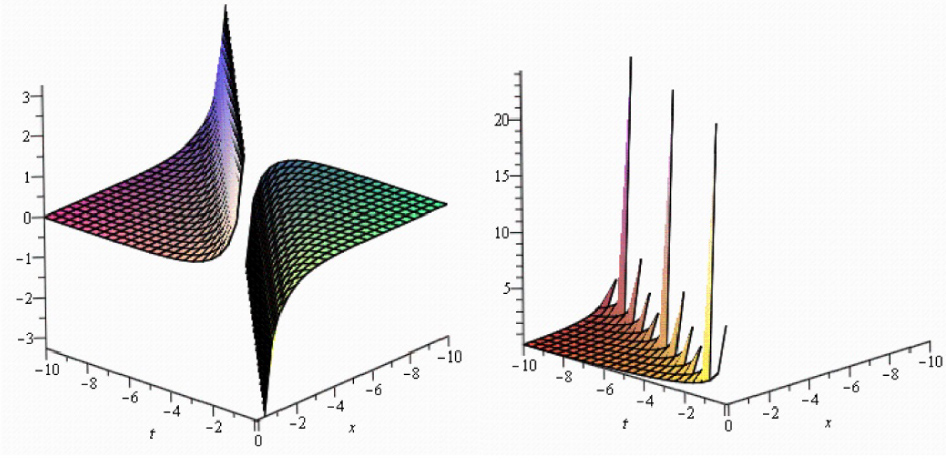
We now examine Figures (1–4) which illustrate a selection of the results obtained above. Specific parameter values are selected, for example: in some of the solutions (3.1.24) and (3.1.25) of the Biswas-Milovic equation with dual-power law nonlinearity with −10 < x, t < 10, solutions (3.2.11) and (3.2.12) of the ZK(2,1,1) with −10 < x, t < 10, solution (3.2.24) of the ZK(m,1,1) with −10 < x, t < 10, solutions (3.3.10) and (3.3.11) of the K(m,n) equation with the generalized evolution with −10 < x, t < 10.

Figure 1 Symmetrical Fibonacci hyperbolic function solutions of the Biswas-Milovic equation with dual-power law nonlinearity when a = b = λ = n = m = 1, K = −1.
Figure 1

Symmetrical Fibonacci hyperbolic function solutions of the Biswas-Milovic equation with dual-power law nonlinearity when a = b = λ = n = m = 1, K = −1.

Figure 2 Symmetrical Fibonacci hyperbolic function solutions of the ZK(2,1,1) when λ0 = λ1 = λ2 = β = 1, a = e, y = 0.
Figure 2

Symmetrical Fibonacci hyperbolic function solutions of the ZK(2,1,1) when λ0 = λ1 = λ2 = β = 1, a = e, y = 0.

Figure 3 Symmetrical Fibonacci hyperbolic function solutions of the ZK(m,1,1) when λ0 = −1, λ1 = λ2 = 1, β = 0, a = e.
Figure 3

Symmetrical Fibonacci hyperbolic function solutions of the ZK(m,1,1) when λ0 = −1, λ1 = λ2 = 1, β = 0, a = e.

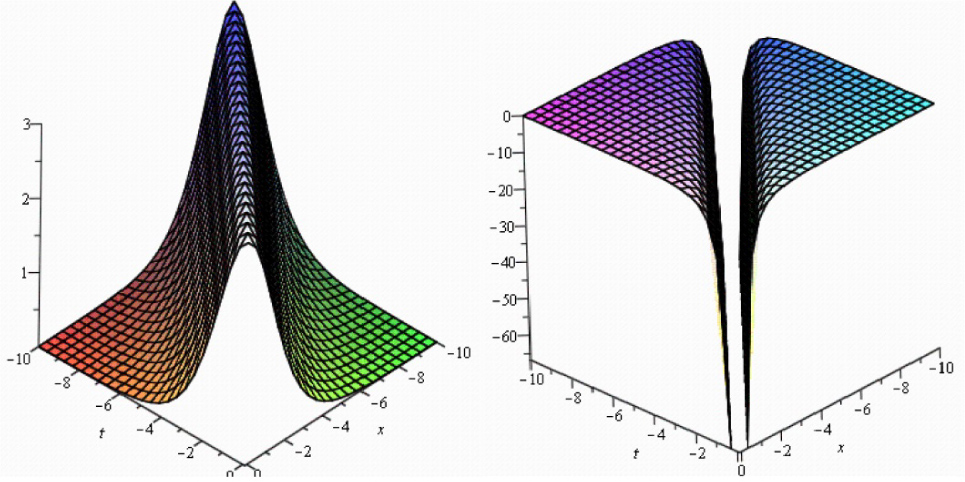
Figure 4 Symmetrical Fibonacci hyperbolic function solutions of K(m,n) equation with the generalized evolution when a = b = c = m = n = 1.
Figure 4

Symmetrical Fibonacci hyperbolic function solutions of K(m,n) equation with the generalized evolution when a = b = c = m = n = 1.

5 Conclusions

In this paper we have shown that the symmetrical hyperbolic Fibonacci function solutions can be obtained for the general Expa- function by using generalized Kudryashov method. We have successfully extended the generalized Kudryashov method to solve three nonlinear partial differential equations. In terms of practical applications, we have obtained many new symmetrical hyperbolic Fibonacci function solutions for the Biswas-Milovic equation with dual-power law nonlinearity, the ZK(m,n,k) and the K(m,n) equation with the generalized evolution term. This demonstrates that the generalized Kudryashov method is powerful, effective and convenient for solving nonlinear PDEs. The physical explanation for certain solutions of such equations have been presented. The generalized Kudryashov method provides a powerful mathematical tool to obtain more general exact analytical solutions of many nonlinear PDEs in mathematical physics.

Acknowledgement

The authors wish to thank the referees for their comments on this paper.

References

[1] R. Hirota, Exact envelope soliton solutions of a nonlinear wave equation,, J. Math. Phys. 14, 805 (1973)10.1063/1.1666399Search in Google Scholar

[2] R. Hirota, J. Satsuma, Soliton solutions of a coupled KDV equation, Phys. Lett. A 85, 404 (1981)10.1016/0375-9601(81)90423-0Search in Google Scholar

[3] M.A. Abdou, The extended tanh-method and its applications for solving nonlinear physical models, Appl. Math. Comput. 190, 988 (2007)10.1016/j.amc.2007.01.070Search in Google Scholar

[4] E.G. Fan, Extended tanh-method and its applications to nonlinear equations, Phys. Lett. A 277, 212 (2000)10.1016/S0375-9601(00)00725-8Search in Google Scholar

[5] M.A. Akbar, N.H.M. Ali, E.M.E. Zayed, A generalized and improved (G″/G)-expanshon method for nonlinear evolution equations, Math. Probl. Eng. 22, 459879 (2012)10.1155/2012/459879Search in Google Scholar

[6] E.M.E. Zayed, S. Al-Joudi, Applications of an extended (G″/G)-expansion method to find exact solutions of nonlinear PDEs in mathematical physics, Math. Probl. Eng. 2010, 768573 (2010)10.1155/2010/768573Search in Google Scholar

[7] E.M.E. Zayed, New traveling wave solutions for higher dimensional nonlinear evolution equations using a generalized (G″/G)-expansion method, J. Phys. A: Math. Theor. 42, 195202 (2009)10.1088/1751-8113/42/19/195202Search in Google Scholar

[8] E.M.E. Zayed, Khaled A. Gepreel, Gepreel, Some applications of the (G″/G)-expansion method to non-linear partial differential equations, Appl. Math. Comput. 212, 1 (2009)10.1016/j.amc.2009.02.009Search in Google Scholar

[9] E.M.E. Zayed, The (G″/G)-expansion method combined with the Riccati equation for finding exactsolutions of nonlinear PDEs, J. Appl. Math. Inform. 29, 351 (2011)Search in Google Scholar

[10] E.M.E. Zayed, Traveling wave solutions for higher dimensional nonlinear evolution equations using the (G″/G)-expansion, J. Appl. Math. Inform. 28, 383 (2010)Search in Google Scholar

[11] M.A. Akbar, N.H.M. Ali, Exp-function method for duffing equation and new solutions of (2+1) dimensional dispersive long wave equations, Prog. Appl. Math. 1, 30 (2011)Search in Google Scholar

[12] J.H. He, X.H. Wu, Exp-function method for nonlinear wave equations, Chaos Soliton Fractals 30, 700 (2006)10.1016/j.chaos.2006.03.020Search in Google Scholar

[13] H. Naher, A.F. Abdullah, M.A. Akbar, New traveling wave solutions of the higher dimensional nonlinear partial differential equation by the Exp-function method, J. Appl. Math. 2012, 575387 (2012)10.1155/2012/575387Search in Google Scholar

[14] A.H. Bhrawy et al., New solutions for (1+1)-dimensional and (2+1)-dimensional Kaup- Kupershmidt equations, Results Math. 63, 675 (2013)10.1007/s00025-011-0225-7Search in Google Scholar

[15] W.X. Ma, T. Huang, Y. Zhang, A multiple exp-function method for nonlinear differential equations and its application, Phys. Script. 82, 065003 (2010)10.1088/0031-8949/82/06/065003Search in Google Scholar

[16] W.X. Ma, Z. Zhu, Solving the (3+1)-dimensional generalized KP and BKP by the multiple exp-function algorithm, Appl. Math. Comput. 218, 11871 (2012)10.1016/j.amc.2012.05.049Search in Google Scholar

[17] E.M.E. Zayed, Abdul-Ghani Al-Nowehy, The multiple exp-function method and the linear superposition principle for solving the (2+1)-Dimensional Calogero-Bogoyavlenskii-Schiff equation, Z. Naturforsch. 70a, 775 (2015)10.1515/zna-2015-0151Search in Google Scholar

[18] G.M. Moatimid, Rehab M. El-Shiekh, Abdul-Ghani A.A.H. Al-Nowehy, Exact solutions for Calogero-Bogoyavlenskii-Schiff equation using symmetry method, Appl. Math. Comput. 220, 455 (2013)10.1016/j.amc.2013.06.034Search in Google Scholar

[19] M.H.M. Moussa, Rehab M. El Shikh, Similarity reduction and similarity solutions of Zabolotskay-Khoklov equation with dissipative term via symmetry method, Physica A 371, 325 (2006)10.1016/j.physa.2006.04.044Search in Google Scholar

[20] A.J.M. Jawad, M.D. Petkovic, A. Biswas, Modified simple equation method for nonlinear evolution equations, Appl. Math. Comput. 217, 869 (2010)10.1016/j.amc.2010.06.030Search in Google Scholar

[21] E.M.E. Zayed, A note on the modified simple equation method applied to Sharma-Tasso-Olver equation, Appl. Math. Comput. 218, 3962 (2011)10.1016/j.amc.2011.09.025Search in Google Scholar

[22] E.M.E. Zayed, S.A.H. Ibrahim, Exact solutions of nonlinear evolution equations in mathematical physics using the modified simple equation method, Chinese Phys. Lett. 29, 060201 (2012)10.1088/0256-307X/29/6/060201Search in Google Scholar

[23] E.M.E. Zayed, Yasser A. Amer, Reham M.A. Shohib, Exact traveling wave solutions for nonlinear fractional partial differential equations using the improved (G″/G)-expansion method, Int. J. Eng. Appl. Scie. 7, 18 (2014)Search in Google Scholar

[24] Y. Pandir, Y. Gurefe, E. Misirli, A multiple extended trial equation method for the fractional Sharma-Tasso-Olver equation, Int. Conference Nume. Analy. Appl. Math. 1558, 1927 (2013)10.1063/1.4825910Search in Google Scholar

[25] Z. Yan, Abundant families of Jacobi elliptic function solutions of the (G″/G)-dimensional integrable Davey-Stewartson-type equation via a new method, Chaos, Solitons and Fractals 18, 299 (2003)10.1016/S0960-0779(02)00653-7Search in Google Scholar

[26] A.H. Bhrawy, M.A. Abdelkawy, A. Biswas, Cnoidal and snoidal wave solutions to coupled nonlinear wave equations by the extended Jacobi's elliptic function method, Commun. Nonlinear Sci. Nume. Simul. 18, 915 (2013)10.1016/j.cnsns.2012.08.034Search in Google Scholar

[27] M.R. Miura, Backlund Transformation (Springer, Berlin, Germany, 1978)Search in Google Scholar

[28] C. Rogers, W.F. Shadwick, Büacklund Transformations and Their Applications (Math. Sci. Eng., Academic Press, New York, NY, USA, 1982)Search in Google Scholar

[29] Z. Yan, H. Zhang, New explicit solitary wave solutions and periodic wave solutions for Whitham-Broer-Kaup equation in shallow water, Phys. Lett. A 285, 355 (2001)10.1016/S0375-9601(01)00376-0Search in Google Scholar

[30] E. Yomba, The modified extended Fan sub-equation method and its application to the (2+1)- dimensional Broer-Kaup-Kupershmidt equation, Chaos, Solitons and Fractals 27,187 (2006)10.1016/j.chaos.2005.03.021Search in Google Scholar

[31] Sirendaoreji, A new auxiliary equation and exact traveling wave solutions of nonlinear equations, Phys. Lett. A 356, 124 (2006)10.1016/j.physleta.2006.03.034Search in Google Scholar

[32] Sirendaoreji, Exact travelling wave solutions for four forms of nonlinear Klein-Gordon equations, Phys. Lett. A 363, 440 (2006)10.1016/j.physleta.2006.11.049Search in Google Scholar

[33] R.M. El-Shiekh, Abdul-Ghani Al-Nowehy, Abdul-Ghani Al-Nowehy, Integral methods to solve the variable coefficient NLSE, Z. Naturforsch. 68a, 255 (2013)10.5560/ZNA.2012-0108Search in Google Scholar

[34] G.M. Moatimid, Rehab M. El-Shiekh, Abdul-Ghani A.A.H. Al-Nowehy, New exact solutions for the variable coeficient two-dimensional Burger equation without restrictions on the variable coeficient, Nonlinear Sci. Lett. A 4, 1 (2013)10.5923/j.ajcam.20120201.03Search in Google Scholar

[35] M.M. Kabir, Modified Kudryashov method for generalized forms of the nonlinear heat conduction equation, Int. J. Phys. Sci. 6, 6061 (2011)Search in Google Scholar

[36] N.A. Kudryashov, One method for finding exact solutions of nonlinear differential equations, Comm. Nonl. Sci. Simul. 6, 6061 (2012)10.1016/j.cnsns.2011.10.016Search in Google Scholar

[37] J. Lee, R. Sakthivel, Exact travelling wave solutions for some important nonlinear physical models, Pramana-J. Phys. 80, 757 (2013)10.1007/s12043-013-0520-9Search in Google Scholar

[38] Y. Pandir, Symmetric Fibonacci function solutions of some nonlinear partial differantial equations, Appli. Math. Inf. Sci. 8, 2237 (2014)10.12785/amis/080518Search in Google Scholar

[39] P.N. Ryabov, D.I. Sinelshchikov, M. B. Kochanov, Application of the Kudryashov method for finding exact solutions of the high order nonlinear evolution equations, Appl. Math. Comput. 218, 3965 (2011)10.1016/j.amc.2011.09.027Search in Google Scholar

[40] Y.A. Tandogan, Y. Pandir, Y. Gurefe, Solutions of the nonlinear differential equations by use of modified Kudryashov method, Turkish J. Math. Computer Sci. 20130021 (2013)Search in Google Scholar

[41] G.M. Moatimid, Rehab M. El-Shiekh, Abdul-Ghani A.A.H. Al-Nowehy, Modified Kudryashov method for finding exact solutions of the (2+1)-dimensional modified Korteweg-de Vries equation and nonlinear Drinfeld-Sokolov system, American J. Comput. Appl. Math. 1,1 (2011)10.5923/j.ajcam.20110102.20Search in Google Scholar

[42] E.M.E. Zayed, G.M. Moatimid, Abdul-Ghani Al-Nowehy, The generalized Kudryashov method and its applications for solving nonlinear PDEs in mathematical physics, Scientific J. Math. Res. 5, 19 (2015)Search in Google Scholar

[43] A.H. Bhrawy et al., Solitons and other solutions to quantum Zakharov-Kuznetsov equation in quantum magneto-plasmas, Indian J. Phys. 87, 455 (2013)10.1007/s12648-013-0248-xSearch in Google Scholar

[44] A.H. Bhrawy, M.A. Abdelkawy, A. Biswas, Topological solitons and cnoidal waves to a few nonlinear wave equations in theoretical physics, Indian J. Phys. 87, 1125 (2013)10.1007/s12648-013-0338-9Search in Google Scholar

[45] A.H. Bhrawy et al., Solitons and other solutions to Kadomtsev-Petviashvili equation of B-type, Rom. J. Phys. 58, 729 (2013)Search in Google Scholar

[46] G. Ebadi et al., Solitons and other solutions to the (3+1)-dimensional extended Kadomtsev-Petviashvili equation with power law nonlinearity, Rom. Rep. Phys. 65, 27 (2013)Search in Google Scholar

[47] A.H. Bhrawy, M.A. Abdelkawy, A. Biswas, Optical solitons in (1 + 1) and (2 + 1) dimensions, Optik 125, 1537 (2014)10.1016/j.ijleo.2013.08.036Search in Google Scholar

[48] A. Biswas et al., Thirring optical solitons with Kerr law nonlinearity, Optik 125, 4946 (2014)10.1016/j.ijleo.2014.04.026Search in Google Scholar

[49] A.H. Bhrawy et al., Optical solitons in birefringent fibers with spatio-temporal dispersion, Optik 125, 4935 (2014)10.1016/j.ijleo.2014.04.025Search in Google Scholar

[50] A.H. Bhrawy et al., Optical soliton perturbation with spatio-temporal dispersion in parabolic and dual-power law media by semi-inverse variational principle, Optik 125, 4945 (2014)10.1016/j.ijleo.2014.04.024Search in Google Scholar

[51] A.H. Bhrawy et al., Bright and dark solitons in a cascaded system, Optik 125, 6162 (2014)10.1016/j.ijleo.2014.06.118Search in Google Scholar

[52] A.A. Alshaery et al., Bright and singular solitons in quadratic nonlinear media, J. Electromagnetic Waves Appl. 28, 275 (2014)10.1080/09205071.2013.861752Search in Google Scholar

[53] A.H. Bhrawy et al., Optical solitons with polynomial and triple-power law nonlinearities and spatio-temporal dispersion, Proc. Rom. Acad. Ser. A 15, 235 (2014)Search in Google Scholar

[54] M. Savescu et al., Optical solitons in birefringent fibers with four-wave mixing for Kerr law nonlinearity, Rom. J. Phys. 59, 582 (2014)Search in Google Scholar

[55] M. Savescu et al., Optical solitons in nonlinear directional couplers with spatio-temporal dispersion, J. Modern Optics 61, 442 (2014)10.1080/09500340.2014.894149Search in Google Scholar

[56] A.H. Bhrawy et al., Dispersive optical solitons with Schrödinger-Hirota equation, J. Nonlinear Optical Phys. Materials 23, 1450014 (2014)10.1142/S0218863514500143Search in Google Scholar

[57] M. Savescu et al., Optical solitons with quadratic nonlinearity and spatio-temporal dispersion, J. Optoelectronics and Advanced Materials 16, 619 (2014)Search in Google Scholar

[58] J.V. Guzman et al., Optical soliton perturbation in magneto-optic waveguides with spatio-temporal dispersion, J. Optoelectronics and Advanced Materials 16, 1063 (2014)Search in Google Scholar

[59] Q. Zhou et al., Solitons in optical metamaterials with parabolic law nonlinearity and spatio-temporal dispersion, J. Optoelectronics and Advanced Materials 16, 1221 (2014)Search in Google Scholar

[60] Q. Zhou et al., Bright-Dark combo optical solitons with non-local nonlinearity in parabolic law medium, Optoelectronics and Advanced Materials-Rapid Commun. 8, 837 (2014)Search in Google Scholar

[61] A. Biswas et al., Optical soliton perturbation with extended tanh function method, Optoelectronics and Advanced Materials-Rapid Commun. 8, 1029 (2014)Search in Google Scholar

[62] M. Savescu et al., Optical solitons in magneto-optic waveguides with spatio-temporal dispersion, Frequenz 68, 445 (2014)10.1515/freq-2013-0164Search in Google Scholar

[63] Q. Zhou et al., Bright, dark and singular optical solitons in a cascaded system, Laser Phys. 25, 025402 (2015)10.1088/1054-660X/25/2/025402Search in Google Scholar

[64] J.V. Guzman et al., Thirring optical solitons, with spatio-temporal dispersion Proc. Rom. Acad. Ser. A 16, 41 (2015)Search in Google Scholar

[65] Q. Zhou et al., Optical solitons with nonlinear dispersion in parabolic law medium, Proc. Rom. Acad. Ser. A 16, 152 (2015)Search in Google Scholar

[66] J.V. Guzman et al., Optical solitons in cascaded system with spatio-temporal dispersion, J. Optoelectronics and Advanced Materials 17, 74 (2015)Search in Google Scholar

[67] J.V. Guzman et al., Optical solitons in cascaded system with spatio-temporal dispersion by ansatz approach, J. Optoelectronics and Advanced Materials 17, 165 (2015)Search in Google Scholar

[68] M. Mirzazadeh et al., Optical solitons in DWDM system with spatio-temporal dispersion, J. Nonlinear Optical Phys. Materials 24, 1550006 (2015)10.1142/S021886351550006XSearch in Google Scholar

[69] Y. Xu et al., Bright solitons in optical metamaterials by traveling wave hypothesis, Optoelectronics and Advanced Materials-Rapid Commun. 9, 384 (2015)Search in Google Scholar

[70] M. Savescu et al., Optical solitons in DWDM system with four-wave mixing, Optoelectronics and Advanced Materials-Rapid Commun. 9, 14 (2015)Search in Google Scholar

[71] M. Mirzazadeh, M. Eslami, A.H. Arnous, Dark optical solitons of Biswas-Milovic equation with dual-power law nonlinearity, Eur. Phys. J. Plus 130, 4 (2015)10.1140/epjp/i2015-15004-xSearch in Google Scholar

[72] H. Trikia, A. Biswas, Dark solitons for a generalized nonlinear Schrödinger equation with parabolic law and dual-power law nonlinearities, Math. Meth. Appl. Sci. 34, 958 (2011)10.1002/mma.1414Search in Google Scholar

[73] H.C. Ma , Y.D. Yu, D.J Ge, The auxiliary equation method for solving the Zakharov Kuznetsov (ZK) equation, Comput. Math. Appl. 58, 2523 (2009)10.1016/j.camwa.2009.03.036Search in Google Scholar

[74] H.C. Ma , Y.D. Yu, D.J Ge, New exact travelling wave solutions for Zakharov-Kuznetsov equation, Commun. Theor. Phys. 51, 609 (2009)10.1088/0253-6102/51/4/07Search in Google Scholar

[75] G. Ebadi, A. Biswas, The (G″/G) method and topological soliton solution of the K(m,n) equation, Comm. Nonlinear Sci. Numer. Simul. 16, 2377 (2011)10.1016/j.cnsns.2010.09.009Search in Google Scholar

[76] A. Stakhov, B. Rozin, On a new class of hyperbolic functions, Chaos Solitons Fractals 23, 379 (2005)10.1016/j.chaos.2004.04.022Search in Google Scholar

[77] S. Monro, E.J. Parkes, he derivation of a modified Zakharov-Kuznetsov equation and the stat, J. Plasma Phys. 62, 305 (1999)10.1017/S0022377899007874Search in Google Scholar

[78] P. Rosenau, J.M. Hyman, Compactons: solitons with finite wavelength, Phys. Rev. Lett. 70, 564 (1993)10.1103/PhysRevLett.70.564Search in Google Scholar PubMed

[79] M.S. Bruzon, M.L. Gandarias, Classical potential symmetries of the K(m,n) equation with generalized evolution term, WSEAS Trans. Math. 9, 275 (2010)Search in Google Scholar

Received: 2015-10-3
Accepted: 2016-2-12
Published Online: 2016-4-28
Published in Print: 2016-1-1

© 2016 EL Sayed M. E. Zaye and Abdul-Ghani Al-Nowehy, published by De Gruyter Open

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 3.0 License.

Articles in the same Issue

  1. Regular articles
  2. Speeding of α Decay in Strong Laser Fields
  3. Regular articles
  4. Multi-soliton rational solutions for some nonlinear evolution equations
  5. Regular articles
  6. Thin film flow of an Oldroyd 6-constant fluid over a moving belt: an analytic approximate solution
  7. Regular articles
  8. Bilinearization and new multi-soliton solutions of mKdV hierarchy with time-dependent coefficients
  9. Regular articles
  10. Duality relation among the Hamiltonian structures of a parametric coupled Korteweg-de Vries system
  11. Regular articles
  12. Modeling the potential energy field caused by mass density distribution with Eton approach
  13. Regular articles
  14. Climate Solutions based on advanced scientific discoveries of Allatra physics
  15. Regular articles
  16. Investigation of TLD-700 energy response to low energy x-ray encountered in diagnostic radiology
  17. Regular articles
  18. Synthesis of Pt nanowires with the participation of physical vapour deposition
  19. Regular articles
  20. Quantum discord and entanglement in grover search algorithm
  21. Regular articles
  22. On order statistics from nonidentical discrete random variables
  23. Regular articles
  24. Charmed hadron photoproduction at COMPASS
  25. Regular articles
  26. Perturbation solutions for a micropolar fluid flow in a semi-infinite expanding or contracting pipe with large injection or suction through porous wall
  27. Regular articles
  28. Flap motion of helicopter rotors with novel, dynamic stall model
  29. Regular articles
  30. Impact of severe cracked germanium (111) substrate on aluminum indium gallium phosphate light-emitting-diode’s electro-optical performance
  31. Regular articles
  32. Slow-fast effect and generation mechanism of brusselator based on coordinate transformation
  33. Regular articles
  34. Space-time spectral collocation algorithm for solving time-fractional Tricomi-type equations
  35. Regular articles
  36. Recent Progress in Search for Dark Sector Signatures
  37. Regular articles
  38. Recent progress in organic spintronics
  39. Regular articles
  40. On the Construction of a Surface Family with Common Geodesic in Galilean Space G3
  41. Regular articles
  42. Self-healing phenomena of graphene: potential and applications
  43. Regular articles
  44. Viscous flow and heat transfer over an unsteady stretching surface
  45. Regular articles
  46. Spacetime Exterior to a Star: Against Asymptotic Flatness
  47. Regular articles
  48. Continuum dynamics and the electromagnetic field in the scalar ether theory of gravitation
  49. Regular articles
  50. Corrosion and mechanical properties of AM50 magnesium alloy after modified by different amounts of rare earth element Gadolinium
  51. Regular articles
  52. Genocchi Wavelet-like Operational Matrix and its Application for Solving Non-linear Fractional Differential Equations
  53. Regular articles
  54. Energy and Wave function Analysis on Harmonic Oscillator Under Simultaneous Non-Hermitian Transformations of Co-ordinate and Momentum: Iso-spectral case
  55. Regular articles
  56. Unification of all hyperbolic tangent function methods
  57. Regular articles
  58. Analytical solution for the correlator with Gribov propagators
  59. Regular articles
  60. A New Algorithm for the Approximation of the Schrödinger Equation
  61. Regular articles
  62. Analytical solutions for the fractional diffusion-advection equation describing super-diffusion
  63. Regular articles
  64. On the fractional differential equations with not instantaneous impulses
  65. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  66. Exact solutions of the Biswas-Milovic equation, the ZK(m,n,k) equation and the K(m,n) equation using the generalized Kudryashov method
  67. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  68. Numerical solution of two dimensional time fractional-order biological population model
  69. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  70. Rotational surfaces in isotropic spaces satisfying weingarten conditions
  71. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  72. Anti-synchronization of fractional order chaotic and hyperchaotic systems with fully unknown parameters using modified adaptive control
  73. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  74. Approximate solutions to the nonlinear Klein-Gordon equation in de Sitter spacetime
  75. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  76. Stability and Analytic Solutions of an Optimal Control Problem on the Schrödinger Lie Group
  77. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  78. Logical entropy of quantum dynamical systems
  79. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  80. An efficient algorithm for solving fractional differential equations with boundary conditions
  81. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  82. A numerical method for solving systems of higher order linear functional differential equations
  83. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  84. Nonlinear self adjointness, conservation laws and exact solutions of ill-posed Boussinesq equation
  85. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  86. On combined optical solitons of the one-dimensional Schrödinger’s equation with time dependent coefficients
  87. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  88. On soliton solutions of the Wu-Zhang system
  89. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  90. Comparison between the (G’/G) - expansion method and the modified extended tanh method
  91. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  92. On the union of graded prime ideals
  93. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  94. Oscillation criteria for nonlinear fractional differential equation with damping term
  95. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  96. A new method for computing the reliability of consecutive k-out-of-n:F systems
  97. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  98. A time-delay equation: well-posedness to optimal control
  99. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  100. Numerical solutions of multi-order fractional differential equations by Boubaker polynomials
  101. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  102. Laplace homotopy perturbation method for Burgers equation with space- and time-fractional order
  103. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  104. The calculation of the optical gap energy of ZnXO (X = Bi, Sn and Fe)
  105. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  106. Analysis of time-fractional hunter-saxton equation: a model of neumatic liquid crystal
  107. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  108. A certain sequence of functions involving the Aleph function
  109. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  110. On negacyclic codes over the ring ℤp + uℤp + . . . + uk + 1 ℤp
  111. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  112. Solitary and compacton solutions of fractional KdV-like equations
  113. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  114. Regarding on the exact solutions for the nonlinear fractional differential equations
  115. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  116. Non-local Integrals and Derivatives on Fractal Sets with Applications
  117. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  118. On the solutions of electrohydrodynamic flow with fractional differential equations by reproducing kernel method
  119. Special issue on Information Technology and Computational Physics
  120. On uninorms and nullnorms on direct product of bounded lattices
  121. Special issue on Information Technology and Computational Physics
  122. Phase-space description of the coherent state dynamics in a small one-dimensional system
  123. Special issue on Information Technology and Computational Physics
  124. Automated Program Design – an Example Solving a Weather Forecasting Problem
  125. Special issue on Information Technology and Computational Physics
  126. Stress - Strain Response of the Human Spine Intervertebral Disc As an Anisotropic Body. Mathematical Modeling and Computation
  127. Special issue on Information Technology and Computational Physics
  128. Numerical solution to the Complex 2D Helmholtz Equation based on Finite Volume Method with Impedance Boundary Conditions
  129. Special issue on Information Technology and Computational Physics
  130. Application of Genetic Algorithm and Particle Swarm Optimization techniques for improved image steganography systems
  131. Special issue on Information Technology and Computational Physics
  132. Intelligent Chatter Bot for Regulation Search
  133. Special issue on Information Technology and Computational Physics
  134. Modeling and optimization of Quality of Service routing in Mobile Ad hoc Networks
  135. Special issue on Information Technology and Computational Physics
  136. Resource management for server virtualization under the limitations of recovery time objective
  137. Special issue on Information Technology and Computational Physics
  138. MODY – calculation of ordered structures by symmetry-adapted functions
  139. Special issue on Information Technology and Computational Physics
  140. Survey of Object-Based Data Reduction Techniques in Observational Astronomy
  141. Special issue on Information Technology and Computational Physics
  142. Optimization of the prediction of second refined wavelet coefficients in electron structure calculations
  143. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  144. Droplet spreading and permeating on the hybrid-wettability porous substrates: a lattice Boltzmann method study
  145. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  146. POD-Galerkin Model for Incompressible Single-Phase Flow in Porous Media
  147. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  148. Effect of the Pore Size Distribution on the Displacement Efficiency of Multiphase Flow in Porous Media
  149. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  150. Numerical heat transfer analysis of transcritical hydrocarbon fuel flow in a tube partially filled with porous media
  151. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  152. Experimental Investigation on Oil Enhancement Mechanism of Hot Water Injection in tight reservoirs
  153. Special Issue on Research Frontier on Molecular Reaction Dynamics
  154. Role of intramolecular hydrogen bonding in the excited-state intramolecular double proton transfer (ESIDPT) of calix[4]arene: A TDDFT study
  155. Special Issue on Research Frontier on Molecular Reaction Dynamics
  156. Hydrogen-bonding study of photoexcited 4-nitro-1,8-naphthalimide in hydrogen-donating solvents
  157. Special Issue on Research Frontier on Molecular Reaction Dynamics
  158. The Interaction between Graphene and Oxygen Atom
  159. Special Issue on Research Frontier on Molecular Reaction Dynamics
  160. Kinetics of the austenitization in the Fe-Mo-C ternary alloys during continuous heating
  161. Special Issue: Functional Advanced and Nanomaterials
  162. Colloidal synthesis of Culn0.75Ga0.25Se2 nanoparticles and their photovoltaic performance
  163. Special Issue: Functional Advanced and Nanomaterials
  164. Positioning and aligning CNTs by external magnetic field to assist localised epoxy cure
  165. Special Issue: Functional Advanced and Nanomaterials
  166. Quasi-planar elemental clusters in pair interactions approximation
  167. Special Issue: Functional Advanced and Nanomaterials
  168. Variable Viscosity Effects on Time Dependent Magnetic Nanofluid Flow past a Stretchable Rotating Plate
https://doi.org/10.1515/phys-2016-0013
Keywords for this article
Nonlinear PDEs; Generalized Kudryashov method; Exact solutions; Symmetrical hyperbolic Fibonacci function; The Biswas-Milovic equation; The Zakharov–Kuznetsov equation; The K(m,n) equation
Creative Commons
BY-NC-ND 3.0

Articles in the same Issue

  1. Regular articles
  2. Speeding of α Decay in Strong Laser Fields
  3. Regular articles
  4. Multi-soliton rational solutions for some nonlinear evolution equations
  5. Regular articles
  6. Thin film flow of an Oldroyd 6-constant fluid over a moving belt: an analytic approximate solution
  7. Regular articles
  8. Bilinearization and new multi-soliton solutions of mKdV hierarchy with time-dependent coefficients
  9. Regular articles
  10. Duality relation among the Hamiltonian structures of a parametric coupled Korteweg-de Vries system
  11. Regular articles
  12. Modeling the potential energy field caused by mass density distribution with Eton approach
  13. Regular articles
  14. Climate Solutions based on advanced scientific discoveries of Allatra physics
  15. Regular articles
  16. Investigation of TLD-700 energy response to low energy x-ray encountered in diagnostic radiology
  17. Regular articles
  18. Synthesis of Pt nanowires with the participation of physical vapour deposition
  19. Regular articles
  20. Quantum discord and entanglement in grover search algorithm
  21. Regular articles
  22. On order statistics from nonidentical discrete random variables
  23. Regular articles
  24. Charmed hadron photoproduction at COMPASS
  25. Regular articles
  26. Perturbation solutions for a micropolar fluid flow in a semi-infinite expanding or contracting pipe with large injection or suction through porous wall
  27. Regular articles
  28. Flap motion of helicopter rotors with novel, dynamic stall model
  29. Regular articles
  30. Impact of severe cracked germanium (111) substrate on aluminum indium gallium phosphate light-emitting-diode’s electro-optical performance
  31. Regular articles
  32. Slow-fast effect and generation mechanism of brusselator based on coordinate transformation
  33. Regular articles
  34. Space-time spectral collocation algorithm for solving time-fractional Tricomi-type equations
  35. Regular articles
  36. Recent Progress in Search for Dark Sector Signatures
  37. Regular articles
  38. Recent progress in organic spintronics
  39. Regular articles
  40. On the Construction of a Surface Family with Common Geodesic in Galilean Space G3
  41. Regular articles
  42. Self-healing phenomena of graphene: potential and applications
  43. Regular articles
  44. Viscous flow and heat transfer over an unsteady stretching surface
  45. Regular articles
  46. Spacetime Exterior to a Star: Against Asymptotic Flatness
  47. Regular articles
  48. Continuum dynamics and the electromagnetic field in the scalar ether theory of gravitation
  49. Regular articles
  50. Corrosion and mechanical properties of AM50 magnesium alloy after modified by different amounts of rare earth element Gadolinium
  51. Regular articles
  52. Genocchi Wavelet-like Operational Matrix and its Application for Solving Non-linear Fractional Differential Equations
  53. Regular articles
  54. Energy and Wave function Analysis on Harmonic Oscillator Under Simultaneous Non-Hermitian Transformations of Co-ordinate and Momentum: Iso-spectral case
  55. Regular articles
  56. Unification of all hyperbolic tangent function methods
  57. Regular articles
  58. Analytical solution for the correlator with Gribov propagators
  59. Regular articles
  60. A New Algorithm for the Approximation of the Schrödinger Equation
  61. Regular articles
  62. Analytical solutions for the fractional diffusion-advection equation describing super-diffusion
  63. Regular articles
  64. On the fractional differential equations with not instantaneous impulses
  65. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  66. Exact solutions of the Biswas-Milovic equation, the ZK(m,n,k) equation and the K(m,n) equation using the generalized Kudryashov method
  67. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  68. Numerical solution of two dimensional time fractional-order biological population model
  69. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  70. Rotational surfaces in isotropic spaces satisfying weingarten conditions
  71. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  72. Anti-synchronization of fractional order chaotic and hyperchaotic systems with fully unknown parameters using modified adaptive control
  73. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  74. Approximate solutions to the nonlinear Klein-Gordon equation in de Sitter spacetime
  75. Topical Issue: Uncertain Differential Equations: Theory, Methods and Applications
  76. Stability and Analytic Solutions of an Optimal Control Problem on the Schrödinger Lie Group
  77. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  78. Logical entropy of quantum dynamical systems
  79. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  80. An efficient algorithm for solving fractional differential equations with boundary conditions
  81. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  82. A numerical method for solving systems of higher order linear functional differential equations
  83. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  84. Nonlinear self adjointness, conservation laws and exact solutions of ill-posed Boussinesq equation
  85. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  86. On combined optical solitons of the one-dimensional Schrödinger’s equation with time dependent coefficients
  87. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  88. On soliton solutions of the Wu-Zhang system
  89. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  90. Comparison between the (G’/G) - expansion method and the modified extended tanh method
  91. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  92. On the union of graded prime ideals
  93. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  94. Oscillation criteria for nonlinear fractional differential equation with damping term
  95. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  96. A new method for computing the reliability of consecutive k-out-of-n:F systems
  97. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  98. A time-delay equation: well-posedness to optimal control
  99. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  100. Numerical solutions of multi-order fractional differential equations by Boubaker polynomials
  101. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  102. Laplace homotopy perturbation method for Burgers equation with space- and time-fractional order
  103. Topical Issue: Recent Developments in Applied and Engineering Mathematics
  104. The calculation of the optical gap energy of ZnXO (X = Bi, Sn and Fe)
  105. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  106. Analysis of time-fractional hunter-saxton equation: a model of neumatic liquid crystal
  107. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  108. A certain sequence of functions involving the Aleph function
  109. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  110. On negacyclic codes over the ring ℤp + uℤp + . . . + uk + 1 ℤp
  111. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  112. Solitary and compacton solutions of fractional KdV-like equations
  113. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  114. Regarding on the exact solutions for the nonlinear fractional differential equations
  115. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  116. Non-local Integrals and Derivatives on Fractal Sets with Applications
  117. Special Issue: Advanced Computational Modelling of Nonlinear Physical Phenomena
  118. On the solutions of electrohydrodynamic flow with fractional differential equations by reproducing kernel method
  119. Special issue on Information Technology and Computational Physics
  120. On uninorms and nullnorms on direct product of bounded lattices
  121. Special issue on Information Technology and Computational Physics
  122. Phase-space description of the coherent state dynamics in a small one-dimensional system
  123. Special issue on Information Technology and Computational Physics
  124. Automated Program Design – an Example Solving a Weather Forecasting Problem
  125. Special issue on Information Technology and Computational Physics
  126. Stress - Strain Response of the Human Spine Intervertebral Disc As an Anisotropic Body. Mathematical Modeling and Computation
  127. Special issue on Information Technology and Computational Physics
  128. Numerical solution to the Complex 2D Helmholtz Equation based on Finite Volume Method with Impedance Boundary Conditions
  129. Special issue on Information Technology and Computational Physics
  130. Application of Genetic Algorithm and Particle Swarm Optimization techniques for improved image steganography systems
  131. Special issue on Information Technology and Computational Physics
  132. Intelligent Chatter Bot for Regulation Search
  133. Special issue on Information Technology and Computational Physics
  134. Modeling and optimization of Quality of Service routing in Mobile Ad hoc Networks
  135. Special issue on Information Technology and Computational Physics
  136. Resource management for server virtualization under the limitations of recovery time objective
  137. Special issue on Information Technology and Computational Physics
  138. MODY – calculation of ordered structures by symmetry-adapted functions
  139. Special issue on Information Technology and Computational Physics
  140. Survey of Object-Based Data Reduction Techniques in Observational Astronomy
  141. Special issue on Information Technology and Computational Physics
  142. Optimization of the prediction of second refined wavelet coefficients in electron structure calculations
  143. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  144. Droplet spreading and permeating on the hybrid-wettability porous substrates: a lattice Boltzmann method study
  145. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  146. POD-Galerkin Model for Incompressible Single-Phase Flow in Porous Media
  147. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  148. Effect of the Pore Size Distribution on the Displacement Efficiency of Multiphase Flow in Porous Media
  149. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  150. Numerical heat transfer analysis of transcritical hydrocarbon fuel flow in a tube partially filled with porous media
  151. Special Issue on Advances on Modelling of Flowing and Transport in Porous Media
  152. Experimental Investigation on Oil Enhancement Mechanism of Hot Water Injection in tight reservoirs
  153. Special Issue on Research Frontier on Molecular Reaction Dynamics
  154. Role of intramolecular hydrogen bonding in the excited-state intramolecular double proton transfer (ESIDPT) of calix[4]arene: A TDDFT study
  155. Special Issue on Research Frontier on Molecular Reaction Dynamics
  156. Hydrogen-bonding study of photoexcited 4-nitro-1,8-naphthalimide in hydrogen-donating solvents
  157. Special Issue on Research Frontier on Molecular Reaction Dynamics
  158. The Interaction between Graphene and Oxygen Atom
  159. Special Issue on Research Frontier on Molecular Reaction Dynamics
  160. Kinetics of the austenitization in the Fe-Mo-C ternary alloys during continuous heating
  161. Special Issue: Functional Advanced and Nanomaterials
  162. Colloidal synthesis of Culn0.75Ga0.25Se2 nanoparticles and their photovoltaic performance
  163. Special Issue: Functional Advanced and Nanomaterials
  164. Positioning and aligning CNTs by external magnetic field to assist localised epoxy cure
  165. Special Issue: Functional Advanced and Nanomaterials
  166. Quasi-planar elemental clusters in pair interactions approximation
  167. Special Issue: Functional Advanced and Nanomaterials
  168. Variable Viscosity Effects on Time Dependent Magnetic Nanofluid Flow past a Stretchable Rotating Plate
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 27.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2016-0013/html
Scroll to top button