Anti-synchronization of fractional order chaotic and hyperchaotic systems with fully unknown parameters using modified adaptive control

M. Mossa Al-Sawalha; Ayman Al-Sawalha

doi:10.1515/phys-2016-0033

Article Open Access

Anti-synchronization of fractional order chaotic and hyperchaotic systems with fully unknown parameters using modified adaptive control

M. Mossa Al-Sawalha and Ayman Al-Sawalha

Published/Copyright: August 22, 2016

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 14 Issue 1

Abstract

The objective of this article is to implement and extend applications of adaptive control to anti-synchronize different fractional order chaotic and hyperchaotic dynamical systems. The sufficient conditions for achieving anti–synchronization are derived by using the Lyapunov stability theory and an analytic expression of the controller with its adaptive laws of parameters is shown. Theoretical analysis and numerical simulations are shown to verify the results.

Keywords: anti-synchronization; adaptive control; fractional order hyperchaos; fractional order chaos; unknown parameters

PACS: 05.45.-a; 47.52.+j; 89.75.-k

1 Introduction

We have seen some dramatic and amazing developments in the research of fractional order chaotic dynamics, particularly with respect to their interaction with the other fields of research and applications. There is now a developed science of fractional order chaos that has a vitally strong interaction between theory and experiment. This is a great leap compared to previously, in which theoretical work existed largely in the absence of substantial experimental realizations. This subject has gained much interest and appreciation in practical applications such as viscoelastic systems, electrode-electrolyte polarization, electromagnetic waves, etc. [1, 2]. Issues such as synchronization of fractional order chaotic systems in a broad variety of situations and the use of fractional order chaotic dynamics for various purposes are at the forefront of recent applications in nonlinear science. This topic encompasses a common link, which is uniting the knowledge of basic mathematical properties of fractional order chaos and specific practical considerations of various applications [3, 4]. A wide variety of approaches have been proposed for the synchronization of fractional order chaotic systems such as adaptive control, sliding mode control, linear active control technique, projective synchronization, and nonlinear active control [5, 30]. Another interesting phenomenon discovered is anti–synchronization (AS) which is noticeable in periodic oscillators. In the AS phenomenon, the state vectors of the synchronized systems have the same amplitude but opposite signs as those of the driving system. Thus, the sum of two signals are expected to converge to zero when AS appears. Several control methods have been applied to anti–synchronize chaotic systems [31–35]. Fortunately, some existing methods of anti–synchronizing of integer order can be generalized to anti-synchronize fractional order chaotic systems through some rigorous mathematical theory. However, in practical engineering situations, the parameters are probably unknown and may change from time to time. Therefore there is a vital need to effectively anti-synchronize two chaotic systems (identical and different) with unknown parameters. This is typically important in theoretical research as well as in practical applications. Among the aforementioned methods, the adaptive control strategy is an efficient control method to anti–synchronize fractional order chaotic chaotic systems. The adaptive control method is used when some or all parameters of the chaotic systems are unknown. The significant features of the adaptive control strategy include fast response, robustness against perturbations, good transient performance, and easy implementation in real applications. In (2013), Agrawal et. al [14] developed a novel adaptive synchronization scheme associated with the parameter update rule for identical and nonidentical fractional order chaotic systems with unknown parameters for the synchronization of fractional order as well as integer order chaotic systems. In spite of [14, 33–35], the epitome of this paper centers on fractional order chaos anti–synchronization between two fractional order chaotic systems, also the aforementioned method concerns synchronizing two fractional order chaotic system with low dimensional attractors characterized by one positive Lyapunov exponent. This feature limits the complexity of the fractional order chaotic dynamics. It is believed that fractional order chaotic systems with higher dimensional attractors have much wider applications. The rest of the paper is organized as follows. In section 2, we briefly describe the problem. In sections 3, we present the adaptive anti-synchronization scheme with a parameter update law for two different chaotic systems. Section 4, presents the adaptive anti-synchronization scheme with a parameter update law for two different hyperchaotic systems. The conclusion is given at the end.

2 Problem formulation

Preliminaries of fractional-order calculus

There are several definitions of fractional derivatives, the commonly used definition is the Riemann-Liouville definition, as follows:

aDtqzt=dndtnJtn−qzt,q>0,(1)

where n = ⌈q⌉, and

Jtϑψt=1Γϑ∫0tψυt−υ1−ϑdυ,(2)

where 0 < ϑ ≤ and Γ(.) is gamma function. The Caputo differential operator of fractional order q is defined as

cDtqzt=Jtn−qznt,q>0,(3)

where n = ⌈q⌉.

Lemma 1

[1, 14] In Riemann–Liouville derivatives ifp > q ≥ 0, m and n are integers such that 0 ≤ m − 1 ≤ p < m, 0 ≤ n − 1 < n, then we obtain

aDtqaDt−qft=aDtp−qft.(4)

Lemma 2

[1, 14] In Riemann–Liouville derivatives ifp > q ≥ 0, m and n are integers such that 0 ≤ m − 1 ≤ p < m, 0 ≤ n − 1 ≤ q < n, then we obtain

aDtpaDtqft=aDtp+qft−∑J=1naDtq−Jftt=a×t−a−p−JΓ1−p−J.(5)

Modified adaptive anti–synchronization

Consider the chaotic master system described by

Dtqx=f(x)+F(x)α,(6)

where x ∈ Ω₁ ⊂ Rⁿ is the state vector of system (6), α ∈ R^m is the unknown parameter vector of the system, f(x) is an n × 1 matrix, and F(x) is an n ∈ m matrix. Similarly, the slave system described by

Dtqy=g(y)+G(y)β+u,(7)

where y ∈ Ω₂ ⊂ Rⁿ is the state vector of system (7), β ∈ R^q is the unknown parameter vector of the system, g(y) is an n × 1 matrix, G(y) is an n × q matrix, and u ∈ Rⁿ is a control input vector. e = y + x is the anti–synchronization error vector. Our goal is to design a controller u such that the trajectory of the slave system (7) with initial conditions y₀ can asymptotically approach the master system (6) with initial conditions x₀ and finally implement anti–synchronization in the sense that limt→∞e=limt→∞y(t)+x(t)=0, where ∥⋅∥ is the Euclidean norm.

Theorem

If the nonlinear control function is selected as

U=−f(x)−F(x)α−g(y)−G(y)β+Dtq−1[F(x)(α−α~)+G(y)(β−β~)−Dtq−1ett−q−1−1Γ−q−1−ke](8)

and the adaptive laws of the parameters are taken as

α~˙=[F(x)]Te,β~˙=[G(y)]Te,(9)

whereα^=α−α~,β^=β−β~,k>0is a constant, q ∈ [0, 1] is the order of the derivative, andα~,β~are the estimated parameters of α and β, respectively.

Proof

From Eqs. (7) and (6) we get the error dynamical system as follows:

Dtqet=gy+G(y)β+f(x)+F(x)α+U.(10)

Inserting (8) into (10) yields the following:

Dtqe(t)=Dtq−1[F(x)(α−α~)+G(y)(β−β~)−(Dtq−1e(t))(t)−(q−1)−1Γ(−(q−1))−ke].(11)

If a Lyapunov function candidate is chosen as

V(e,α^,β^)=12[eTe+(α−α~)T(α−α~)+(β−β~)T(β−β~))](12)

the time derivative of V(e,α^,β^) along the trajectory of the error dynamical system (11) is

V˙(e,α^,β^)=[e˙Te+(α−α~)Tα~˙+(β−β~)Tβ~˙](13)

Using Lemma 2 in Eq. (13) we get

V˙(e,α^,β^)=([Dtq−1(Dtqe(t))+(Dtq−1e(t))t−q−1−1Γ−q−1]+α−α~Tα~˙+(β−β~)Tβ~˙)).(14)

From Eqs. (9) and (13), we get

V˙(e,α^,β^)=[Dtq−1(Dtq−1[F(x)(α~−α)+G(y)(β~−β)−(Dtq−1e(t))(t)−(q−1)−1Γ(−(q−1))−ke]+(Dtq−1e(t))(t)−(q−1)−1Γ(−(q−1))]T+(α−α~)Tα~˙+(β−β~)Tβ~˙,(15)

since ∀q ∈ [0, 1], (1 − q) > 0 and (q - 1) < 0. Now, using Lemma 1 and Eq. (9), Eq. (15) reduces to

V˙(e,α^,β^)=[(F(x)(α−α~)+G(y)(β−β~)−(Dtq−1e(t))(t)−(q−1)−1Γ(−(q−1))−ek)+(Dtq−1e(t))(t)−(q−1)−1Γ(−(q−1))]Te−(α−α~)T([F(x)]Te)−(β−β~)T([G(y)]Te)=[(α−α~)TF(x)T+(β−β~)TG(y)T−keT]e−(α−α~)T[F(x)]Te−(β−β~)T[G(y)]Te=−keTe≤0.(16)

Since V and V˙ are positive and negative semi-definite respectively, therefore, according to the Lyapunov stability theory [36], the response system (7) is both globally and asymptotically anti–synchronized to the drive system (6). This completes the proof. □

3 Adaptive anti–synchronization between two fractional-order chaotic systems

In order to achieve the behavior of anti–synchronization between two fractional-order chaotic systems using modified adaptive control, we take the fractional-order chaotic Lü [35] system to be the drive system and the fractional-order chaotic Liu system [22] to be the response system. The variables of the drive system are represented by the subscript 1 and the response system by the subscript 2. Both systems are described respectively by the following equations:

dαx1dαt=a1(y1−x1),dαy1dαt=−x1z1+c1y1,dαz1dαt=x1y1−b1z1,(17)

and

dαx2dαt=a2(y2−x2)+u1,dαy2dαt=b2x2−x2z2+u2,dαz2dαt=−c2z2+d2x22+u3,(18)

where, U = (u₁, u₂, u₃)^T is the control function to be designed. In order to determine the control functions to realize adaptive anti–synchronization between the systems in Eqs. (17) and (18), we add (17) to (18) and obtain

Dtq1e1(t)=a2(y2−x2)+a1(y1−x1)+u1,Dtq2e2(t)=b2x2−x2z2−x1z1+c1y1+u2,Dtq3e3(t)=−c2z2+d2x22+x1y1−b1z1+u3,(19)

where e₁ = x₂ + x₁, e₂ = y₂ + y₁, and e₃ = z₂ + z₁. Our goal is to derive the controller U with a parameter estimation update law such that Eqs. (18) globally and asymptotically anti-synchronize Eqs.(17).

Theorem 2

The fractional-order chaotic Liu system (18) can anti–synchronize the fractional-order Lü system (17) globally and asymptotically for any different initial condition with the following adaptive controller:

u1=−a2(y2−x2)−a1(y1−x1)+Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1],u2=−b2x2+x2z2+x1z1−c1y1+Dtq2−1[b~2x2+c~1y1−Dtq2−1e2t×t−q2−1−1Γ−q2−1−e2,u3=c2z2−d2x22−x1y1+b1z1+Dtq3−1[−c~2z2+d~2x22−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3],(20)

and parameter update rules

a^˙1=(y1−x1)e1,b^˙1=−z1e3,c^˙1=y1e2,a^˙2=(y2−x2)e1,b^˙2=x2e2,c^˙2=−z2e3,d^˙2=x22e3,(21)

where a^1,b^1,c^1,a^2,b^2,c^2, andd^2are estimates ofa₁, b₁, c₁, aM₂, b₂, c₂, and d₂, respectively.

proof

Applying the control law equation (20) to Eq. (19) yields the resulting closed-loop error dynamical system as follows:

Dtq1e1(t)=Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1],Dtq2e2(t)=Dtq2−1[b~2x2+c~1y1−(Dtq2−1e2(t))×(t)−(q2−1)−1Γ(−(q2−1))−e2],Dtq3e3(t)=Dtq3−1[−c~2z2+d~2x22−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3],(22)

where a~1=a1−a^1,b~1=b1−b^1,c~1=c1−c^1,a~2=a2−a^2,b~2=b2−b^2,c~2=c2−c^2, and d~2=d2−d^2.

Consider the following Lyapunov function candidate:

V=12(eTe+a~12+b~12+c~12+a~22+b~22+c~22+d~22),(23)

then the time derivative of V along the solution of the error dynamical system equation (22) gives

V˙=(eTe+a~1a~˙1+b~1b~˙1+c~1c~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+d~2d~˙2).(24)

Using Lemma 2 in Eq. (24) we get

V˙=([Dt1−q1(Dtq1e1(t))+(Dtq1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))]e1+([Dt1−q2(Dtq2e2(t))+(Dtq2e2(t))×(t)−(q2−1)−1Γ(−(q2−1))]e2+([Dt1−q3(Dtq3e3(t))+(Dtq3e3(t))×(t)−(q3−1)−1Γ(−(q3−1))]e3+a~1a~˙1+b~1b~˙1+c~1c~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+d~2d~˙2=([Dt1−q1(Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1])+(Dtq1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))]e1+([Dt1−q2(Dtq2−1[b~2x2+c~1y1−(Dtq2−1e2(t))×(t)−(q2−1)−1Γ(−(q2−1))−e2])+(Dtq2e2(t))×(t)−(q2−1)−1Γ(−(q2−1))]e2+([Dt1−q3(Dtq3−1[−c~2z2+d~2x22−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3])+(Dtq3e3(t))×(t)−(q3−1)−1Γ(−(q3−1))]e3+a~1a~˙1+b~1b~˙1+c~1c~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+d~2d~˙2,(25)

since ∀ q ∈ [0, 1], (1 - q) > 0 and (q - 1) < 0. Now, using Lemma 1, Eq. (25) reduces to

V˙=[a~2(y2−x2)+a~1(y1−x1)−e1]e1+[b~2x2+c~1y1−e2]e2+[−c~2z2+d~2x22−b~1z1−e3]e3+a~1(−(y1−x1)e1)+b~1(z1e3)+c~1(−y1e2)+a~2(−(y2−x2)e1)+b~2(−x2e2)+c~2(z2e3)+d~2(−x22e3),=−eTe≤0.(26)

Since V is positive definite and V˙ is negative definite in the neighborhood of the zero solution of the system equation (22), it follows that limt→∞et=0. Therefore system (18) can anti–synchronize system (17) asymptotically. This completes the proof. □

4 Numerical simulations

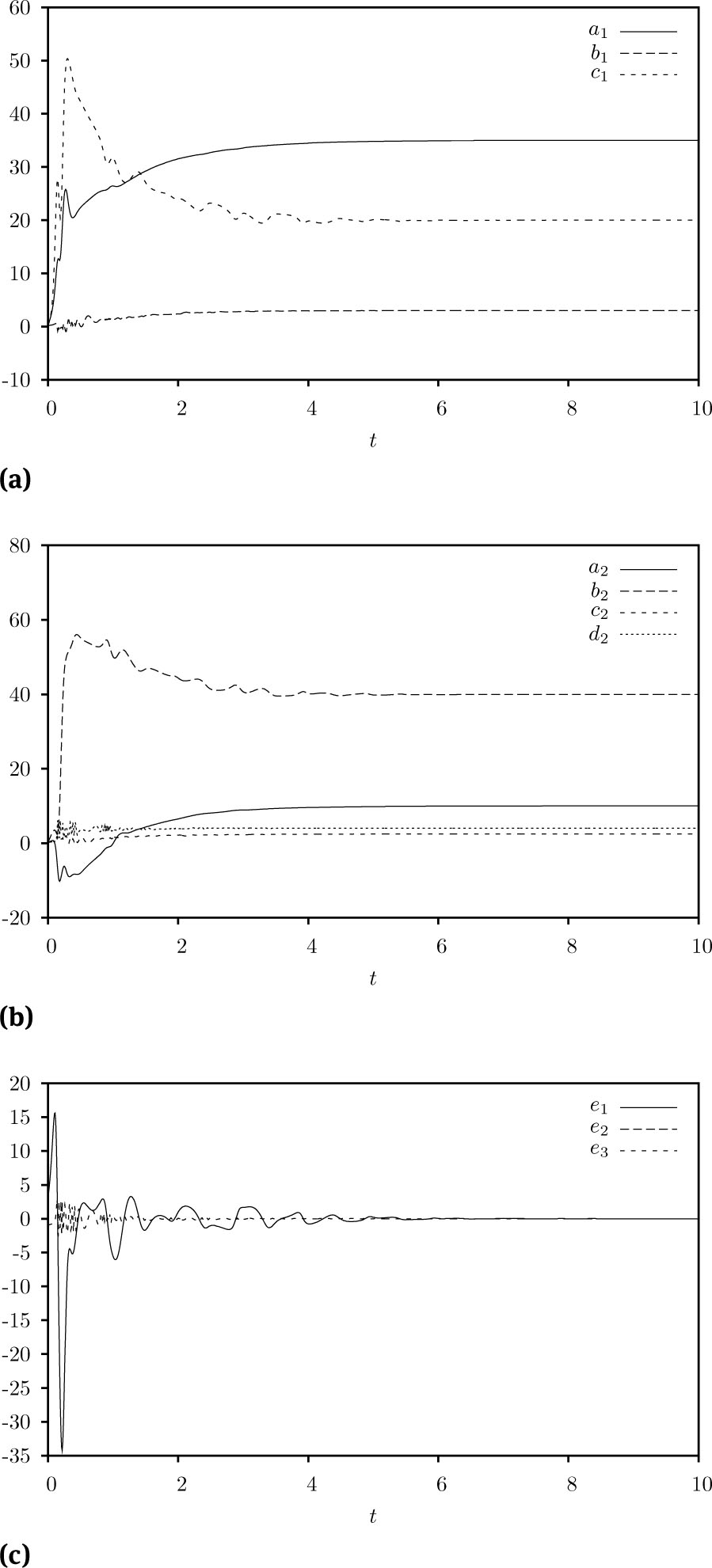
In the numerical simulations, the Adams-Bashforth-Moulton method is used to solve the systems. The fractional order is chosen as α = 0.95, and the unknown parameters are chosen as a₁ = 35, b₁ = 3, c₁ = 20, and a₂ = 10, b₂ = 40, c₂ = 2.5, and d₂ = 4, so that both systems exhibit a chaotic behavior. The initial values of the fractional-order drive system (17), the fractional-order response system (18) and the estimated parameters are arbitrarily chosen in the simulations as (x₁(0) = 0.2, y₁(0) = 0.6, z₁(0) = 1), (x₂(0) = 7, y₂(0) = 11, z₂(0) = 15), and a^1(0)=0.2,b^1(0)=0.2,c^1(0)=0.2 and a^2(0)=0.2,b^2(0)=0.2,c^2(0)=0.2,d^2(0)=0.2, respectively. Anti–synchronization of the systems (17) and (18) via the adaptive control law (20) and (21) are shown in Figs. (1)–(2). Fig. (1) displays the state trajectories of the drive system (17) and response system (18). Fig. (2) (a)–(b) show that the estimates a^1(t),b^1(t),c^1(t) and a^2(t),b^2(t),c^2(t),d^2(t) of the unknown parameters converge to a₁ = 35, b₁ = 3, c₁ = 20 and a₂ = 10, b₂ = 40, c₂ = 2.5, d₂ = 4 as t → ∞. Fig. (2) (c) displays the anti–synchronization errors of systems (17) and (18). Fig. (3) shows that the fractional order Liu system is controlled to be the fractional order Lü system.

Figure 1

State trajectories of drive system (17) and response system (18): (a): Signals x₁ and x₂; (b): signals y₁ and y₂; and (c): signals z₁ and z₂.

Figure 2

(a)–(b): Change in parameters a₁, b₁, c₁ and a₂, b₂, c₂, d₂ of the drive system (17) and the response system (18) with time t. (c): The error signals e₁; e₂; e₃ of the drive system (17) and the response system (18) under the controller (20) and the parameters update law (21).

$Figure 3 Fractional-order chaotic Lü system (solid line) and the controlled fractional-order Liu system (dotted line)$

Figure 3

Fractional-order chaotic Lü system (solid line) and the controlled fractional-order Liu system (dotted line)

5 Adaptive anti–synchronization between two fractional-order hyperchaotic systems

In order to achieve the behavior of anti–synchronization between two fractional-order chaotic systems using modified adaptive control, we take the fractional-order hyperchaotic Lorenz system [37] to be the drive system and the fractional-order hyperchaotic Chen system [38] to be the response system. The variables of the drive system are represented by the subscript 1 and the response system by the subscript 2. Both of the systems are described respectively by the following equations:

dαx1dαt=a1(y1−x1)+w1,dαy1dαt=c1x1−x1z1−y1,dαz1dαt=x1y1−b1z1,dαw1dαt=−y1z1+r1w1,(27)

and

dαx2dαt=a2(y2−x2)+w2+u1,dαy2dαt=r2x2−x2z2+c2y2+u2,dαz2dαt=x2y2−b2z2+u3,dαw2dαt=x2z2+d2w2+u4,(28)

where U = (u₁, u₂, u₃, u₄)^T is the control function to be designed. In order to determine the control functions to realize adaptive anti–synchronization between the systems in Eqs. (27) and (28), we add (27) to (28) and obtain

Dtq1e1(t)=a2(y2−x2)+w2+a1(y1−x1)+w1+u1,Dtq2e2(t)=r2x2−x2z2+c2y2+c1x1−x1z1−y1+u2,Dtq3e3(t)=x2y2−b2z2+x1y1−b1z1+u3,Dtq4e4(t)=x2z2+d2w2−y1z1+r1w1+u4,(29)

where e₁ = x₂ + x₁, e₂ = y₂ + y₁e₃ = z₂ + z₁, and e₄ = w₂ + w₁. Our goal is to derive the controller U with a parameter estimation update law such that Eqs. (28) globally and asymptotically anti-synchronize Eqs.(27).

Theorem 3

The fractional-order hyperchaotic Lorenz system (28) can anti–synchronize with the fractional-order Chen system (27) globally and asymptotically for any different initial condition with the following adaptive controller:

u1=−a2(y2−x2)−w2−a1(y1−x1)−w1+Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1],u2=−r2x2+x2z2−c2y2−c1x1+x1z1+y1+Dtq2−1[r~2x2+c~2y2+c~1x1−(Dtq2−1e2(t))×(t)−(q2−1)−1Γ(−(q2−1))−e2],u3=−x2y2+b2z2−x1y1+b1z1+Dtq3−1[−b~2z2−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3],u4=−x2z2−d2w2+y1z1−r1w1+Dtq4−1[d~2w2+r~1w1−(Dtq4−1e4(t))×(t)−(q4−1)−1Γ(−(q4−1))−e4],(30)

and parameter update rules

a^˙1=(y1−x1)e1,b^˙1=−z1e3,c^˙1=x1e2,r^˙1=w1e4,a^˙2=(y2−x2)e1,b^˙2=−z2e3,c^˙2=y2e2,r^˙2=x2e2,d^˙2=w2e4,(31)

where a^1,b^1,c^1,r^1,a^2,b^2,c^2,r^2, andd^2are estimates ofa}₁, b₁, c₁, r₁, a₂, b₂, c₂, r₂, andd₂ respectively.

Proof

Applying the control law equation (30) to Eq. (29) yields the resulting closed-loop error dynamical system as follows:

Dtq1e1(t)=Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1],Dtq2e2(t)=Dtq2−1[r~2x2+c~2y2+c~1x1−(Dtq2−1e2(t))×(t)−(q2−1)−1Γ(−(q2−1))−e2],Dtq3e3(t)=Dtq3−1[−b~2z2−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3],Dtq4e4(t)=Dtq4−1[d~2w2+r~1w1−(Dtq4−1e4(t))×(t)−(q4−1)−1Γ(−(q4−1))−e4],(32)

where a~1=a1−a^1,b~1=b1−b^1,c~1=c1−c^1,r~1=r1−r^1,a~2=a2−a^2,b~2=b2−b^2,c~2=c2−c^2,r~2=r2−r^2, and d~2=d2−d^2

Consider the following Lyapunov function candidate:

V=12(eTe+a~12+b~12+c~12+r~12+a~22+b~22+c~22+r~22+d~22),(33)

then the time derivative of V along the solution of the error dynamical system equation (32) gives

V˙=(eTe+a~1a~˙1+b~1b~˙1+c~1c~˙1+r~1r~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+r~2r~˙2+d~2d~˙2).(34)

Using Lemma 2 in Eq. (34) we get

V˙=([Dt1−q1(Dtq1e1(t))+(Dtq1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))]e1+([Dt1−q2(Dtq2e2(t))+(Dtq2e2(t))×(t)−(q2−1)−1Γ(−(q2−1))]e2+([Dt1−q3(Dtq3e3(t))+(Dtq3e3(t))×(t)−(q3−1)−1Γ(−(q3−1))]e3+([Dt1−q4(Dtq4e4(t))+(Dtq4e4(t))×(t)−(q4−1)−1Γ(−(q4−1))]e4+a~1a~˙1+b~1b~˙1+c~1c~˙1+r~1r~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+r~2r~˙2+d~2d~˙2=([Dt1−q1(Dtq1−1[a~2(y2−x2)+a~1(y1−x1)−(Dtq1−1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))−e1])+(Dtq1e1(t))×(t)−(q1−1)−1Γ(−(q1−1))]e1+([Dt1−q2(Dtq2−1[r~2x2+c~2y2+c~1x1−(Dtq2−1e2(t))×(t)−(q2−1)−1Γ(−(q2−1))−e2])+(Dtq2e2(t))×(t)−(q2−1)−1Γ(−(q2−1))]e2+([Dt1−q3(Dtq3−1[−b~2z2−b~1z1−(Dtq3−1e3(t))×(t)−(q3−1)−1Γ(−(q3−1))−e3])+(Dtq3e3(t))×(t)−(q3−1)−1Γ(−(q3−1))]e3+([Dt1−q4(Dtq4−1[d~2w2+r~1w1−(Dtq4−1e4(t))×(t)−(q4−1)−1Γ(−(q4−1))−e4])+(Dtq4e4(t))×(t)−(q4−1)−1Γ(−(q4−1))]e4+a~1a~˙1+b~1b~˙1+c~1c~˙1+r~1r~˙1+a~2a~˙2+b~2b~˙2+c~2c~˙2+r~2r~˙2+d~2d~˙2,(35)

since ∀ q ∈ [0, 1], (1 - q) > 0 and (q - 1) < 0. Now, using Lemma 1, Eq. (35) reduces to

V˙=[a~2(y2−x2)+a~1(y1−x1)−e1]e1+[c~2y2+c~1x1−e2]e2+[−b~2z2−b~1z1−e3]e3+[r~2w2+r~1w1−e4]e4+a~1(−(y1−x1)e1)+b~1(z1e3)+c~1(−x1e2)+r~1(−w1e4)+a~2(−(y2−x2)e1)+b~2(z2e3)+c~2(−y2e2)+r~2(−x2e3)+d~2(−w2e4),=−eTe≤0.(36)

Since V is positive definite and V˙ is negative definite in the neighborhood of the zero solution of the system equation (32), it follows that limt→∞et=0. Therefore system (28) can anti–synchronize system (27) asymptotically. This completes the proof. □

6 Numerical simulations

In the numerical simulations, the Adams-Bashforth-Moulton method is used to solve the systems. The fractional order is chosen as α = 0.97, and the unknown parameters are chosen as a₁ = 10, b₁ = 8/3, c₁ = 28, r₁ = -1 and a₂ = 35, b₂ = 3, c₂ = 12, r₂ = 0.5, d₂ = 7, so that both of the systems exhibit a hyperchaotic behavior. The initial values of the fractional-order drive system (27), the fractional-order response system (28) and the estimated parameters are arbitrarily chosen in simulations as (x₁(0) = 2, y₁(0) = 2, z₁(0) = 2, w₁(0) = -2), (x₂(0) = 20, y₂(0) = 10, z₂(0) = 10, w₂(0) = -15), a^1(0)=10,b^1(0)=10,c^1(0)=10,r^1(0)=10, and a^2(0)=10,b^2(0)=10,c^2(0)=10,r^2(0)=10 respectively. Anti–synchronization of the systems (27) and (28) via the adaptive control law (30) and (31) are shown in Figs. (4)–(5). Fig. (4) displays the state trajectories of the drive system (27) and the response system (28). Fig. (5) (a)–(b) shows that the estimates a^1(t),b^1(t),c^1(t),r^1(t) and a^2(t),b^2(t),c^2(t),r^2(t),d^2(t) of the unknown parameters converge to a₁ = 10, b₁ = 8/3, c₁ = 28, r₁ = -1 and a₂ = 35, b₂ = 3, c₂ = 12, r₂ = 0.5, d₂ = 7 as t → ∞. Fig. (5) (c) displays the anti-synchronization errors of systems (27) and (28). Fig. (6) shows that the fractional-order hyperchaotic Chen system is controlled to be the fractional-order hyperchaotic Lorenz system.

Figure 4

State trajectories of drive system (27) and response system (28): (a): Signals x₁ and x₂; (b): signals y₁ and y₂; (c): signals z₁ and z₂ and (d): signals w₁ and w₂.

Figure 5

(a)–(b): Changing parameters a₁, b₁, c₁, r₁ and a₂, b₂, c₂, r₂, d₂ of the drive system (27) and the response system (28) with time t. (c): The error signals e₁, e₂, e₃, e₄ of the drive system (27) and the the response system (28) under the controller (30) and the parameters update law (31).

$Figure 6 Fractional-order hyperchaotic Lorenz system (solid line) and the controlled fractional-order hyperchaotic Chen system (dotted line) in x − y − z projection.$

Figure 6

Fractional-order hyperchaotic Lorenz system (solid line) and the controlled fractional-order hyperchaotic Chen system (dotted line) in x − y − z projection.

7 Conclusion

In this paper, we have investigated the anti–synchronization of two different fractional order chaotic and hyperchaotic systems with uncertain parameters. Theoretical analysis was performed to demonstrate the effectiveness of the proposed control strategy. However, we would like to highlight that, in contrast to our method, the active control (cf. [35]) and H_∞ approach (cf. [33, 33]) anti-synchronization are based on exactly known system parameters. As a matter of fact, in real physical systems or experimental situations some system parameters cannot be exactly known in advance so chaos control and anti-synchronization with uncertain parameters are universal and have received significant attention for their potential applications in prior work. Thus it is much more attractive and challenging to realize the anti–synchronization of two different fractional order chaotic and/or hyperchaotic systems with unknown parameters. We strongly believe that there is high potential in this method and future work is planned to include cost and noise analysis.

Acknowledgements

The authors are grateful to the anonymous referees for their useful comments on the earlier draft of this paper.

References

[1] Podlubny I., Fractional Differential Equations. Academic Press, New York (1999).Search in Google Scholar

[2] Hilfer R., Applications of Fractional Calculus in Physics. World Scientific, New Jersey (2001).10.1142/3779Search in Google Scholar

[3] Xiangjun W., Hongtao L., Shilei S., Synchronization of a new fractional-order hyperchaotic system, Phys. Lett. A., 2009, 373, 2329-2337.10.1016/j.physleta.2009.04.063Search in Google Scholar

[4] Sha W., Yongguang Y., Miao D., Hybrid projective synchronization of chaotic fractional order systems with different dimensions, Physica A., 2010, 389, 4981-4988.10.1016/j.physa.2010.06.048Search in Google Scholar

[5] Choon K.A., Output feedback H_∞ synchronization for delayed chaotic neural networks, Nonlinear. Dyn., 2010, 59, 319-327.10.1007/s11071-009-9541-9Search in Google Scholar

[6] Choon K.A., Takagi-Sugeno fuzzy receding horizon H_∞ chaotic synchronization and its application to the Lorenz system, Nonlinear Analysis: Hybrid Systems.,2013, 9, 1-8.10.1016/j.nahs.2013.01.002Search in Google Scholar

[7] Yonghui S., Jinde C., Adaptive synchronization between two different noise-perturbed chaotic systems with fully unknown parameters, Physica A., 2007, 376, 253-265.10.1016/j.physa.2006.10.039Search in Google Scholar

[8] Ju H. P., Adaptive synchronization of hyperchaotic Chen system with uncertain parameters, Chaos Soliton & Fract., 2005, 26, 959-964.10.1016/j.chaos.2005.02.002Search in Google Scholar

[9] Shihua C., Jinhu L., Parameters identification and synchronization of chaotic systems based upon adaptive control, Phys. Lett. A., 2002. 299, 353-358.10.1016/S0375-9601(02)00522-4Search in Google Scholar

[10] Junan L., Xiaoqun W., Xiuping H., Jinhu L., Adaptive feedback synchronization of a unified chaotic system, Phys. Lett. A., 2004 329, 327-333.10.1016/j.physleta.2004.07.024Search in Google Scholar

[11] Jian H., Chaos synchronization between two novel different hyperchaotic systems with unknown parameters. Nonlinear. Anal. T.M.A., 2008, 69, 4174-4181.10.1016/j.na.2007.10.045Search in Google Scholar

[12] Al-Sawalha M. M., Noorani M. S. M., Adaptive anti-synchronization of two identical and different hyperchaotic systems with uncertain parameters. Commun. Nonlinear. Sci., 2010, 15, 1036-1047.10.1016/j.cnsns.2009.05.037Search in Google Scholar

[13] Huaguang Z., Wei H., Zhiliang W., Tianyou C., Adaptive synchronization between two different chaotic systems with unknown parameters, Phys. Lett. A., 2006, 350, 363-366.10.1016/j.physleta.2005.10.033Search in Google Scholar

[14] Agrawal S. K., Das S., A modified adaptive control method for synchronization of some fractional chaotic systems with unknown parameters, Nonlinear. Dyn., 2013, 73, 907-919.10.1007/s11071-013-0842-7Search in Google Scholar

[15] Zhen W., Xia H., Hao S., Control of an uncertain fractional order economic system via adaptive sliding mode, Neurocomputing, 2012, 83, 83-88.10.1016/j.neucom.2011.11.018Search in Google Scholar

[16] Zhe G., Xiaozhong L., Integral sliding mode control for fractional-order systems with mismatched uncertainties, Nonlinear Dyn., 2013, 72, 27-35.10.1007/s11071-012-0687-5Search in Google Scholar

[17] Yong X., Hua W., Di L., Hui H., Sliding mode control of a class of fractional chaotic systems in the presence of parameter perturbations, Journal of Vibration and Control, 2015, 21, 1-14.Search in Google Scholar

[18] Mohamed Z., Nejib S., Haitham S., Synchronization of the unified chaotic systems using a sliding mode controller, Chaos Soliton & Fract., 2009, 42, 3197-3209.10.1016/j.chaos.2009.04.051Search in Google Scholar

[19] Wafaa J., Noorani M. S. M., Al-sawalha M.M., Anti-Synchronization of Chaotic Systems via Adaptive Sliding Mode Control, Chin. Phys. Lett., 2012, 29, 120505.10.1088/0256-307X/29/12/120505Search in Google Scholar

[20] Wafaa J., Noorani M. S. M., Al-sawalha M.M., Robust active sliding mode anti-synchronization of hyperchaotic systems with uncertainties and external disturbances, Nonlinear Analysis: Real World Applications., 2012, 13, 2403-2413.10.1016/j.nonrwa.2012.02.006Search in Google Scholar

[21] Lin P., Wuneng Z., Jianán F., Dequan L., Synchronization and anti-synchronization of new uncertain fractional-order modified unified chaotic systems via novel active pinning control, Commun. Nonlinear. Sci., 2010 15, 3754-3762.10.1016/j.cnsns.2010.01.025Search in Google Scholar

[22] Sachin B., Varsha D. G., Synchronization of different fractional order chaotic systems using active control, Commun. Nonlinear Sci., 2010, 15, 3536-3546.10.1016/j.cnsns.2009.12.016Search in Google Scholar

[23] Al-Sawalha M. M., Noorani M. S. M., Chaos anti-synchronization between two novel different hyperchaotic systems, Chin. Phys. Lett., 2008, 25, 2743.10.1088/0256-307X/25/8/003Search in Google Scholar

[24] Al-Sawalha M. M., Noorani M. S. M., Anti-synchronization between two different hyperchaotic systems, Journal of uncertain systems., 2009, 3, 192-200.Search in Google Scholar

[25] Agrawal S. K., Srivastava M., Das S., Synchronization of fractional order chaotic systems using active control method, Chaos Soliton & Fract., 2012, 45, 737-752.10.1016/j.chaos.2012.02.004Search in Google Scholar

[26] Agrawal S. K., Das S., Function projective synchronization between four dimensional chaotic systems with uncertain parameters using modified adaptive control method, Journal of process control., 2014, 24, 517-530.10.1016/j.jprocont.2014.02.013Search in Google Scholar

[27] Jianrui C., Licheng J., Jianshe W., Xiaodong W., Projective synchronization with different scale factors in a driven-response complex network and its application in image encryption, Nonlinear Anal. Real World Appl., 2010, 11, 3045-3058.10.1016/j.nonrwa.2009.11.003Search in Google Scholar

[28] K. S. Sudheer, M. Sabir, Function projective synchronization in chaotic and hyperchaotic systems through open-plus-closed-loop coupling, Chaos., 2010, 20, 013115-5.10.1063/1.3309019Search in Google Scholar PubMed

[29] Hongyue D., Qingshuang Z., Changhong W., Mingxiang L., Function projective synchronization in coupled chaotic systems, Nonlinear Anal. Real World Appl., 2010, 11, 705-712.10.1016/j.nonrwa.2009.01.016Search in Google Scholar

[30] Zhenbo L., Xiaoshan Z., Generalized function projective synchronization of two different hyperchaotic systems with unknown parameters, Nonlinear Anal. Real World Appl., 2011, 12, 2607-2615.10.1016/j.nonrwa.2011.03.009Search in Google Scholar

[31] Al-Sawalha M. M., Noorani M. S. M., On anti-synchronization of chaotic systems via nonlinear control, Chaos Soliton & Fract., 2009, 42, 170-179.10.1016/j.chaos.2008.11.011Search in Google Scholar

[32] Al-Sawalha M. M., Noorani M. S. M., Anti-synchronization of two hyperchaotic systems via nonlinear control, Commun. Nonlinear. Sci., 2009 14, 3402-3411.10.1016/j.cnsns.2008.12.021Search in Google Scholar

[33] C. K. Ahn, Adaptive H_∞ Anti-Synchronization for Time-Delayed Chaotic Neural Networks, Progress of Theoretical Physics, 122, 1402 (2009)10.1143/PTP.122.1391Search in Google Scholar

[34] Choon K. A., An H_∞ approach to anti-synchronization for chaotic systems, Phys. Lett. A., 2009, 373, 1729-1733.10.1016/j.physleta.2009.03.032Search in Google Scholar

[35] Hadi T., Erjaee G. H., Phase and anti-phase synchronization of fractional order chaotic systems via active control, Commun. Nonlinear. Sci., 2011, 16, 4079-4088.10.1016/j.cnsns.2011.02.015Search in Google Scholar

[36] A. M. Liapunov, Stability of Motion. Elsevier/Academic Press, New York/London (1966).Search in Google Scholar

[37] Xing Y. W., Jun M. S., Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control, Commun. Nonlinear. Sci., 2009, 14, 3351-3357.10.1016/j.cnsns.2009.01.010Search in Google Scholar

[38] Yan P. W., Guo. D. W., Synchronization between Fractional-Order and Integer-Order Hyperchaotic Systems via Sliding Mode Controller, Journal of Applied Mathematics, 2013, 5, 151025-5.10.1155/2013/151025Search in Google Scholar

Received: 2015-9-14

Accepted: 2016-5-6

Published Online: 2016-8-22

Published in Print: 2016-1-1

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 3.0 License.