Abstract
A simple physical model of atomic structure and reactivity is extracted from quantum mechanics using widely known facts and relations but no expert knowledge of quantum chemistry. The Aufbau model is included and extended to account for the role of electron dynamics and energy degeneracy of the atomic ground states. The periodically variable reactivity is found to arise due to dynamical constraints on electron motion which lead to degeneracy (coincidence or near-coincidence) in the atomic energy spectrum. Verification is found in a strong correlation between energy degeneracy and reactivity with the inert gas atoms found to display least degeneracy. Chemical bonding follows as a means of relaxing atomic reactivity and reducing energy degeneracy. This can be achieved by permanent electron rearrangement among atomic centers (ionic bonding) or by oscillatory electron motion between atoms (covalent bonding). Ionic bonding is directly related to the variable stability of atomic structures, not only of neutral atoms but also of atomic ions formed by permanent electron redistribution. The most stable ions then form nondegenerate molecular structures by electrostatic interaction in neutral ionic clusters. The covalent bonding mechanism is instead fundamentally dynamical and interatomic since it depends directly on the facility (rate and spatial extent) with which electrons can move between atomic centers in a molecule. Energy degeneracy is found to imply dynamical constraint on electron motion which is reduced by covalent bonding, normally, but not always, to form a nondegenerate molecular ground state. Facilitation of interatomic electron motion, and the corresponding decrease in degeneracy of the ground and lowest energy excited states, thus become the covalent bonding mechanism. Equilibrium molecular geometries optimally balance this attraction against interatomic repulsions of electrostatic and steric (Pauli) nature which dominate at short range. The fundamental role of electron dynamics in atomic properties and bonding is reflected in a corresponding importance of not only ground state energy but the spectrum of low energy states.
Introduction
The long history of chemistry clearly shows an early focus on the atoms as independent elements and building blocks of molecules and substances. With the advent of the Periodic Table about 150 years ago, 1 it became possible to understand atomic properties as periodically variable with the atomic number of the atom. 2 Most atoms are individually reactive and rarely found in nature in gaseous form but sometimes in the form of pure elementary substances and more often as molecules in multi-atomic substances stabilized by some form of chemical bonding. There are, however, a small set of inert (or noble) atoms that are nearly always found in such gaseous form with independently moving particles. Thus it was clear from the early years of chemistry, after the composition of atoms of central nuclei and surrounding electrons had been determined [Thomson, 3 Rutherford 4 ], that some electronic structures of atoms, those of the inert gas atoms, were exceptionally stable while all others were reactive to a generally strong but very variable degree. Before the arrival of quantum mechanics, atomic structures and their periodically varying properties could not be understood by first principle, but an empirical rule was deduced and drawn upon in early modelling of chemical bonding [e.g. by Lewis, 5 Langmuir 6 ]: Inert-gas-like electronic structures of atoms are particularly stable. This rule, and its corollary, electronic structures of atoms which are not inert-gas-like are reactive, became, in a retrospective view, a form of “empirical quantum mechanics of atoms” that was extracted from the Periodic Table and used to understand chemical bonding and molecule formation.
The early models of chemical bonding and molecule formation could be rationalized by the use of this stability rule which singled out neutral atoms of nuclear charge + Ze with Z = 2 (helium), 10 (neon), 18 (argon), 36 (krypton) … as particularly stable. One simply noted that the stability must be related to the number of electrons Ne (= 2, 10, 18, 36 … for the inert gas atoms) more than to the charge of the nucleus. The special electronic stability applies to atomic ions as well if the number of electrons is 2, 10, 18 etcetera. Thus one could achieve stability by forming molecules such that, by transfer of electrons between atoms, a cluster of atomic ions would form where all ions had 2, 10, 18, … electrons. Valence numbers, historically related to how many electrons an atom would need to gain or lose to reach an inert gas electronic structure, were found to explain a major part of the specificity of the chemical bonding in molecule formation. This “empirical quantum mechanics” of atoms suffices to provide a fundamental understanding of ionic bonding. The electron transfer mechanism traditionally used for ionic bonding works well to explain many stable molecules but not for some of the most important, e.g. H2, N2, O2. In such molecules the valence numbers are not summing to zero, as +1 and −1 in HF, but are by symmetry the same, i.e. covalent.
The early notion of covalent bonding was that it reflected, not a transfer of electrons between atomic centers, but a sharing of electrons (Lewis 7 ). It became popular (and still is) to graphically represent the two electrons in H2 not to permanently transfer between the protons to form either H+H− or H−H+, but to form H:H, where the two electrons (as dots) are taken to be shared equally between the two protons. Thus, both hydrogen atoms have equal claim to the stable helium electronic structure. Similarly, the electronic structures of N2 and O2 were taken to display 6 and 4 shared electrons, respectively, allowing these N and O -atoms to take on some of the stability of Ne.
Without the use of any formal quantum mechanics it was in this way possible to develop an understanding of two mechanisms of chemical bonding, the ionic (electron transfer) and the covalent (electron sharing), which had great predictive power for molecule formation. The arrival and rapid development of quantum mechanics in the early 1900’s caused the very simple models above to be refined and extended with increasing input of quantum mechanics. Lewis 5 , 7 , 8 incorporated the idea of electron pairing which led, with the help of Langmuir, 6 , 9 to the famous octet rule, Lewis electron dot diagrams and later to geometry prediction by the valence shell electron pair repulsion (VSEPR) method 10 popularized by Gillespie and Nyholm. 11 , 12 All of this development accounted for quantum mechanics only implicitly and empirically, mainly through the known properties of atoms.
After the arrival of computational quantum mechanics to chemistry in the late 1920’s, Pauling 13 , 14 , 15 introduced an empirical form of the quantum-mechanical valence bond (VB) theory, first used by Heitler and London for H2, 16 wherein local bonds are formed between pairs of atoms. These bonds are represented by small wave functions involving only the bonding electrons while the other electrons (for molecules larger than H2) remain represented by atomic configurations. The interatomic molecular wave functions serve to bridge and bond atoms while the other nonbonding electrons contribute repulsion between bonded atoms. In this analysis quantum mechanics was directly drawn upon. It provided the atomic orbital geometries and the hybridization of them to extend in new directions contributed greatly to the success of Pauling’s empirical VB theory. 17 To a comforting degree the more empirical octet rule-VSEPR and the semi-empirical VB models agree, showing that intuitive and approximate forms of quantum mechanics can help chemists understand fundamental aspects of chemical bonding and molecule formation. These models remain in general use.
The relatively great success, and corresponding longevity, of these simple intuitive (octet rule, VSEPR and VB) models of bonding, molecular stability and geometry, has now been complemented by an even greater success of computational quantum chemistry 18 in providing “first principle predictions” of molecular ground states and properties. It would be reasonable to also expect quantum chemistry to produce better understanding and more refined physical models of bonding but, unfortunately, this development has lagged behind high expectations. The access to rigorous and accurate quantum chemical methods has certainly helped to understand, 19 , 20 but not greatly to revise and improve, the simple models above, nor has it resolved the historical debate over the best physical interpretation of the computational results.
Evidently numerical mastery has not so far overcome the inherent subtlety of the quantum effects that produce bonding. The Schrödinger equation clearly “knows about” chemical, and in particular covalent, bonding but its numerical answers rarely come with clear-cut physical explanations. The old bonding models are still used in essentially unchanged form. There is much discussion and disagreement (see below) over whether energy analysis or dynamical analysis (or both, as we suggest) should be the chosen way to more fully understand chemical bonding. With rare exceptions energy analysis is chosen, given its dominant role in main-stream quantum chemistry, but there is still a lingering question whether the electrostatic interactions 21 or the kinetic energy variations should be regarded as the key to bonding. The answer must account for the paradoxical role of the virial theorem (an exact theorem showing that when free atoms bind to form a molecule at its lowest energy geometry then the total kinetic energy rises but the total potential energy falls by twice as much) 22 which at first inspection seems to clearly favor electrostatics but, on closer inspection, does not. Further debate relates to whether electron densities are the natural vehicles 23 for a bonding analysis or wave functions are essential. A recent review of the role of quantum mechanics in covalent bonding finds the mechanism in the interference effects arising among the contributions to the wave function, expanded in atomic basis functions, from different atoms in the molecule. 24 Quantum mechanics allows different perspectives on the physical origin of bonding. They can all be formally valid but vary in clarity and practical utility. Indisputable facts, like the virial theorem, may even confuse until the analysis has reached sufficient depth to reveal the detailed synergism of the interaction of electrons with nuclei in molecules. 25 , 26
In describing our dynamical perspective on reactivity and bonding below we shall try to resolve, or at least mitigate, the uncertainties and difficulties by drawing on important qualitative features of quantum mechanics while using only simple intuitive arguments from the full quantum mechanical theory of atoms and molecules. The emphasis will be on atoms, the periodic table and the origin of the periodicity of atomic reactivity. In our view, understanding the nature of the strain of the electronic structure of reactive atoms, and the reason why this strain appears to be absent for inert gas atoms, will help us better understand the mechanisms of both ionic and covalent bonding. Our reasoning will be qualitative and explanatory rather than numerically predictive. No deeper mathematical or computational experience with quantum chemistry, beyond that provided by a good quality university study of chemistry (see e.g. ref. 27] and ref. 28]), will be required. We hope to take the empirical models of atoms, and their bonding to molecules, into quantum mechanics by physical reasoning. Clarifying this link between quantum mechanics and atomic properties and molecule formation should afford the reader a more fundamental understanding of atomic and molecular chemistry. The physical picture provided is, in all essential features, fully consistent with the results of quantum chemistry and offers an explanation and unification of the several theories of chemical bonding already present in the field.
The quantum-mechanical hydrogen atom – state diffusivity
Quantum mechanics applied to the electronic structure, particularly of the ground states, of atoms and molecules, is a deep and complex subject. Fortunately, there is a helpful ladder of simple and very useful systems and approximations which take us to the important chemical concepts of atomic reactivity and chemical bonding. Much of what we need to know is already illustrated by the simple hydrogen atom H which is long since solved and understood within quantum mechanics by analytical mathematics. A graphical view of the difference between classical and quantum mechanics with respect to ground state diffusivity is provided in Fig. 1 for one-dimensional motion in confining potentials.
The key role of quantum diffusivity
The hydrogen atom H is composed of a proton and an electron which are charged +e and −e, respectively. The Coulomb interaction between these particles is V(r) = −C/r, where r is the separation between particles and C = 1389 kj/mol × Å. Generally, we shall use atomic units a.u. in which the coulombic charge–charge interaction of two particles in vacuum of charges Z 1 e and Z 2 e is.
Classically a model of two point charges (they are both small enough that we can neglect any individual particle size) would have a collapsed ground state – about like a neutron. In reality a hydrogen atom has a spherical ground state with the radius of the electron distribution around the nucleus being about half an Ångström or 0.5 × 10−10 m. The existence of a hydrogen atom ground state of this small, but still very considerable, size must be understood as a quantum effect. Classically the “internal atomic states” would be phase space points of given positions x, y, z of the electron with respect to the proton at the origin and momenta p x , p y , p z , but in quantum mechanics states are described by wave functions ψ(x,y,z) and they are diffuse (delocalized) in both coordinate and momentum. How diffuse must they be? This can be appreciated from the Heisenberg uncertainty principle for a one-dimensional particle motion:
Here Δx and Δp are uncertainty intervals in the coordinate x and momentum p. This principle tells us that a quantum state of a one-dimensional particle motion does not correspond to a classical phase space point x, p but to an area in x, p – space roughly proportional to the minimum uncertainty area, ≈Δx × Δp, and to Planck’s constant h. Similarly the electron moving in three dimensions has a ground state corresponding to a six-dimensional phase space volume ≈ Δx Δy Δz × Δp x Δp y Δp z which is proportional to h 3. Not surprisingly this diffusivity also applies to excited energy eigenstates so the first lesson of quantum mechanics is that states in general, and our energy eigenstates in particular, acquire the form of space filling volumes in phase space. In an everyday metaphor “If classical mechanics builds a system from point-like grains of sand then quantum mechanics builds it from bricks”. This requirement of state diffusivity in quantum mechanics is absolutely fundamental in the understanding of atomic structure and chemical bonding.
Now we note that the uncertainty in momentum Δp is directly related to the kinetic energy KE as follows:
Here m is the mass of the particle (e.g. the electron) and we used the fact that the average momentum vanishes, <p> = 0. It follows that localization of the electron in space forces up the kinetic energy so the diffusivity of the ground state of hydrogen is a compromise between localization in x, y, z to minimize electrostatic energy and delocalization in the same variables to minimize kinetic energy. The uncertainty principle in (2), and its relation to kinetic energy in (3), shows us that if we let “diffusivity” be represented by the uncertainty Δx then a lower bound on the kinetic energy can be found as
In three dimensions (3D) we find that for independent motion in the three coordinates x, y, z, as appropriate for, e.g., a particle-in-a-box or in spherically symmetric harmonic potentials, the three motions can be described individually as in the 1D case above and the total kinetic energy satisfies:
For lower symmetry potentials the uncertainties in the three coordinates should be dealt with in a coupled fashion to minimize the lower bound on kinetic energy but we can see for the potentials above that the minimal kinetic energy is a sum of three 1D components. The minimal kinetic energy KEmin scales for the cubical box of volume V = L 3 with the confinement length L as
while a uniform spherical average (the electron is contained in a ball centered on the nucleus) of the electron-nucleus attraction in the H atom (Z = 1), and more generally in a one-electron atomic ion (Z > 1), is
Thus we see that at small L (tight confinement and high particle density, it will turn out) the kinetic energy dominates over the Coulomb attraction but at large L the reverse is true. At some in-between value of L the energy is minimal and the drive to confine the electron to gain binding energy from the Coulomb attraction is optimally balanced by the quantum mechanical cost in terms of rising kinetic energy. In this way the hydrogen atom gets its finite size and this balance between Coulombic and kinetic energies, between confinement and diffusivity, goes on in all ground state atoms.
The condition that quantum states of low energy must be diffuse, spread in phase space, explains why the hydrogen atom, and all other atoms after also accounting for fermion statistics, do not collapse to points. We note that increased diffusivity in coordinate space tends to lower the kinetic energy while localization tends to raise it. The rise in kinetic energy as the localization of an electron around the nucleus is increasingly tight eventually overwhelms the lowering of potential energy achieved. We note also that the cost of localization in kinetic energy is inversely proportional to the mass of the particle. Thus the light electron is far more affected by the “drive to diffuse” than the proton which is 1836 times heavier. This mass ratio is even greater for heavier atomic nuclei. It is therefore customary in quantum chemistry to use the “clamped nuclei approximation” (widely known as the Born-Oppenheimer (BO) approximation) which takes the nuclei in atoms and molecules to be stationary when determining the ground or excited states of the electron motion. 29 The small mass of the electron is the most important reason for the “quantum character of chemistry” but it is not the only reason. As we shall see below, the quantum character is of a very particular kind.
The origin of periodic atomic properties – the shell structure of hydrogenic atoms
The quantum mechanical requirement of diffusivity prevents electronic structures around atoms from collapsing, producing instead finite sized atoms as an optimal balance with the contractive electrostatic forces. Next, we consider the origin of atomic reactivity. Again the simple hydrogen atom can tell a fundamental part of the story rather well. 30 According to analytical quantum mechanics the hydrogen atom has a spectrum of bound energy eigenstates (of energy less than zero relative to the ionization threshold and the electron unable to escape from the proton) which can be identified by five quantum numbers n, l, m, s, m s . The energies ε n of the corresponding atomic orbitals (AOs) only depend on the principal quantum number n which goes from 1, 2, … to infinity:
where the atomic unit (a.u.) of energy is the Hartree equal to 2625.6 kJ/mol. The quantum number l is the total angular momentum quantum number and m is the quantum number describing the orientation of the angular momentum, both of which refer to the rotation of the electron around the proton. Their ranges are l = 0, 1, … n − 1, m = −l, −l +1, … , +l. Finally, s is the spin angular momentum quantum, which is 1/2, and m s refers to the two available directions of the electron spin, often called spin up and down (m s = ±1/2), respectively. We note the huge amount of degeneracy (number of states of the same energy) in the hydrogen spectrum. The degeneracy in each shell d n is 2 for n = 1 (m s = ±1), 8 for n = 2 (l = 0, m s = ±1, l = 1, m l = −1, 0, 1 and m s = ±1) and in general we find d n = 2n 2.
Degeneracy is a major feature of the spectrum of the hydrogen atom H with important related consequences also for all other atoms. As we shall see below ground state degeneracy is associated with reactivity and molecule formation is closely associated with “reduction of degeneracy”. The inert gas atoms are different from other atoms in that they have nondegenerate ground states and no excited states close in energy (on a scale of chemical bond energies) to the ground state, i.e. there is no significant near-degeneracy.
In quantum mechanics energy eigenstates are related directly to particle dynamics and degeneracy means that the particle dynamics is hindered. Eigenstates of the same energy (perfect degeneracy) are then dynamically separable and decoupled. Energy conservation cannot explain why parts of the Hilbert space of wave functions are dynamically disconnected (divisible into nontrivial parts which are intact (do not mix) under the dynamics of the system). The answer must be found in the presence of symmetries, conservation laws or barriers which restrain the dynamics. Eigenstates which are near-degenerate are generally coupled but wave packet motion among them occurs on a timescale proportional to the inverse of the energy difference between them, i.e. slowly if the energy gaps between the energy eigenstates are small. If there is no degeneracy and no near-degeneracy then the system is expected to be dynamically fully connected (“ergodic” in nomenclature taken over from classical mechanics), implying rapid dynamical relaxation and chemical stability. See the illustration in Fig. 2 below.
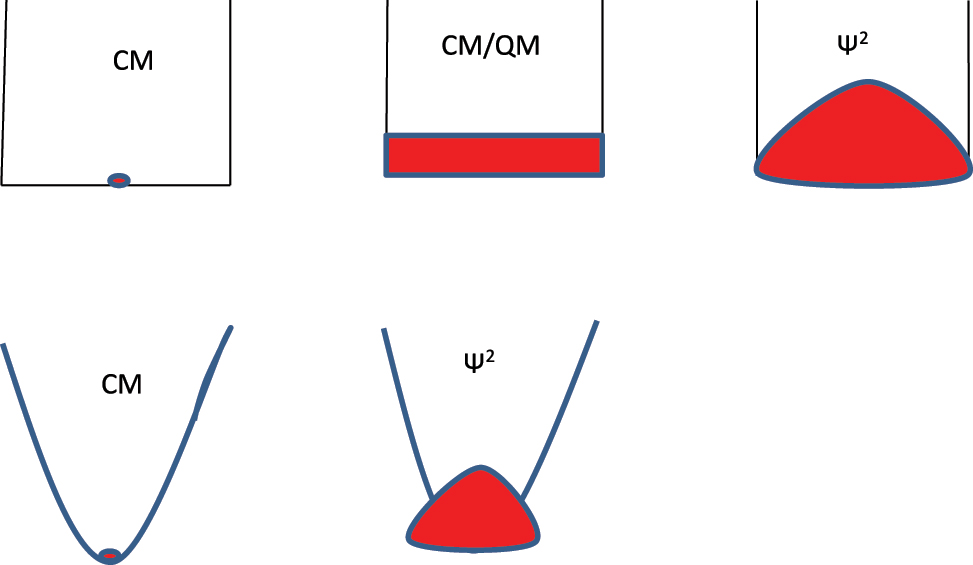
Locality of classical mechanics (CM) and diffusivity of quantum mechanics (QM) is illustrated in graphical images of ground states. The graphs of 1D potentials are in x, E where E is energy and the extent of states in red are in x, E for all but those marked ψ2 which show probability densities as function of x. The main points to note are: (1) classical ground states are point-like and infinitely degenerate in the particle in box case while nondegenerate for a potential of unique point of minimum potential energy; (2) importing quantum mechanics into classical phase space by the classical – quantum correspondence principle assigns a phase-space volume h to a quantum state and leads to the second graph which shows the diffuse and nondegenerate nature of the box ground state; (3) applying correct wave function QM adds a repulsion to a hard wall and pushes up the ground state energy as shown in the third graph; (4) a more typical potential (e.g. a harmonic potential) will have a unique classical ground state as in the fourth graph; (5) the diffuse character of the quantum ground state delocalizes it around the classical minimum and raises the energy by zero point motion. Note also that the particle tunnels into a soft wall as shown in the last graph.

A spectrum of six energy eigenvalues is shown with, on the left, two energy levels of degeneracy 2 and 4. In the middle we have added a “weak coupling” splitting the degenerate states but leaving a near-degeneracy of the two and four states. On the right we have strengthened the coupling to produce a fully coupled (ergodic) system with a smooth progression of energy levels showing no tendency towards degeneracy. Since relaxation rates are proportional to the gaps between neighboring energy eigenvalues they are maximal on the right, slower in the middle case and absent within the degenerate states on the left. The reactivity is highest on the left where small external perturbations can split the degeneracy. It then decreases as we go to the right but remains significant in the “near-degenerate” case in the middle while it is minimal in the nondegenerate case on the right.
As an example we consider the case of two nearest-neighbor states in the spectrum of energy eigenstates of e. g. an atom and introduce an external coupling between these states. The original uncoupled Hamiltonian, the coupled Hamiltonian and the energy eigenvalues before and after the coupling has been turned on are found as follows:
In the case of perfect degeneracy we see that the new energies are
In the limit of weak coupling,
The lower state is moved down and the higher state up by the same amount α 2/Δε while in the case of degeneracy when Δε = 0 the shift down and up is by |α|. Also in the case of near-degeneracy Δε > 0 the response becomes proportional to α in the strong coupling limit when the perturbation is stronger than the splitting |α| > Δε. This kind of weak coupling, considered in equation (10) for near-degenerate states, will arise between two atoms in the limit of large separations where we see that the response to the perturbation is weakened by the factor α/Δε in the weak coupling limit. This can be understood as a lowering of the reactivity when we go from full degeneracy Δε = 0 to near-degeneracy Δε > 0. Nevertheless the contribution to reactivity remains as we go from full degeneracy, as in the simplified Aufbau model, to more accurate quantum chemical approximations. As the atoms approach more closely the coupling strength is likely to reach into the strong coupling region where the response of degenerate and near-degenerate pairs of states is much the same. This will allow us to assess reactivity of atoms by a simplified analysis.
A simple illustration of degeneracy, near-degeneracy and ergodicity of energy level spectra is found in Fig. 2. The splitting of two neighboring energy eigenstates by a coupling, as discussed in equations (9) and (10) above, is illustrated in Fig. 3.
We can see that degeneracy and reactivity (responsiveness to external perturbation) are in quantum mechanics closely related to each other and in turn to constraints acting on the particle dynamics to produce reactivity. We shall see below that chemical bonding takes free atoms towards less degeneracy and in covalent bonding also towards more fully coupled and global dynamics.
Hydrogenic atoms
If we imagine atoms constructed of noninteracting electrons, so-called hydrogenic atoms, then this great degree of energy degeneracy for the smallest atom H would persist and may even increase for larger atoms. Recall from introductory university chemistry that we, by the Aufbau ansatz, can place zero, one or two electrons in each one-electron hydrogenic orbital but no more due to the Pauli exclusion principle that each electron shall occupy a unique one-electron state, i.e. spin-orbital, in the hydrogenic atom. The one-electron states obtained for a nucleus of charge +Ze are the same as those of the hydrogen atom but the energies are scaled by a factor Z 2 and the physical extent is decreased by the factor 1/Z. It can be seen that degeneracy signals reactivity since multiple states of equal energy can be both filled and unfilled in the same shell of given n allowing an external symmetry breaking perturbation to strongly influence the ground state structure. This responsiveness to external perturbation can then facilitate interactions with external fields or other atoms. The structure would thereby be unstable and reactive.
The Aufbau model is particularly simple, and exact, for hydrogenic atoms. The dependence of orbital energy on l is simply eliminated and the orbital energy is – Z 2/2n 2. The hydrogenic ground state degeneracies d 0 (atom) are for the first few elements.
We immediately realize that there are only a few nondegenerate ground states among the “hydrogenic atoms”. For electron numbers N
e
= 2, 10, 28…, in the notation
Thus, hydrogenic atoms would show “periodicity” similar, but not identical, to our periodic table for small atoms, becoming increasingly different for higher atomic number. We also note that “inert gas character” can arise despite the system being decoupled by spin- and angular momentum-conservation, i.e. ergodic (fully coupled and without hindrances) dynamics is not a prerequisite for stable states to appear. Such states can appear also due to uniform occupation of degenerate states leaving the structure non-degenerate. Although they are of interest theoretically, hydrogenic atoms are, for higher atomic number Z, unrealistically strongly bound and contracted in size. For better understanding of real atoms we need to account for electron-electron repulsion which introduces a very important “screening mechanism” in the electronic structure of atoms.
The Aufbau model – an empirical mean-field model of atoms
What is meant by “the Aufbau model”? – Aufbau means “build-up” and the model retains a shell structure of states related to, but significantly different from, that of the hydrogenic atoms discussed above. 31 , 32 Here we shall extend the hydrogenic model retaining the one-electron character of hydrogenic atoms but adding screening of the electron-nucleus attraction allowing the model to predict realistic one-electron structures of many-electron atoms including the effect of electron-electron repulsion. The Aufbau model thus accounts empirically and qualitatively for repulsion among the electrons and tells us which of these spin-orbital states, named by hydrogenic quantum numbers n, l, m l , s, m s , are occupied by electrons in the ground states of the neutral atoms. These “Aufbau rules” deviate significantly from the rules of the hydrogenic atoms since the orbital energies now include an account for the electron-electron repulsion. The “Aufbau orbital energies” are not predicted quantitatively, but rough estimates can be obtained and physical reasons are often provided for the order in which they are filled, i.e., from lowest to higher energies in a given atom. We shall show that these Aufbau rules will also allow us to determine “Aufbau degeneracy” and sometimes they also indicate “near-degeneracy” which, as noted above, plays an important role in understanding the properties of the atom. We have recently explored the possibility of obtaining a “measure of atomic reactivity” and included a measure based on “ground state degeneracy” as estimated by use of the Aufbau model. 33 It was found to agree well with other measures based on atomic first ionization energies or hydride atomization energies.
The hydrogenic atoms discussed above are “periodic” with respect to reactivity-stability due to the variable degeneracy of their ground states. As we now turn to consider real interacting electrons we may at first expect all of the simplicity and periodicity of the atoms to disappear due to strong and complex electron–electron repulsion but, remarkably, most of it remains, but in modified form. A mean-field (uncorrelated individual electrons moving independently in the average field of all electrons) treatment of the motions of the electrons in the atom suffices to capture the main effects of electron-electron repulsion allowing us to use the strong simplifications of the traditional Aufbau model without encountering disabling errors. Apparently, the electron-nucleus interaction still dominates and spherical symmetry is still a good approximation for the motion of individual electrons.
In its simplest form, the “mean-field” approximation replaces the detailed interactions arising with electrons at correlated specific locations by an assumption that each electron can be taken to interact with the average electron density (the mean field) formed by all other electrons. This approximation was brought into quantum chemistry by Hartree and then refined by Fock to include an exact account of the Pauli principle which forces the full wave function to be antisymmetric with respect to interchange of two electrons. In this way a beautiful “Hartree-Fock theory” of electronic structure 18 was formed which has become the foundation of modern quantum chemistry. In the presence of two or more electrons of the same spin the form of the Hartree-Fock wave function includes an “exchange correlation effect” 30 which is fundamentally related to wave functions rather than densities. It leads to significant reductions in atomic energies and a preference for “high spin Aufbau configurations”. We shall keep this in mind but leave the full treatment of the corresponding “Hund’s rules” out of our simplified Aufbau model. Similarly, the spin dependence of electron-electron interactions, and the construction of atomic eigen-states of given total spin, is an important topic worthy of further study but not fundamental to our discussion due to the weakness of the spin-spin interaction, in particular for the lighter atoms. In our empirical mean-field model of atoms we thus leave aside both the treatment of total spin states and the treatment of spin dependent “exchange correlation” and use a simpler one-electron approximation of “electron screening” as described below. Likewise we do not account for coupling of orbital angular momentum states into many-electron states of given total angular momentum, nor for the spin–orbit coupling of such many-electron states. They correspond to small energy gaps compared to the energies related to atomic reactivity and chemical bonding mechanisms that we are focusing on here.
Simple central potential representation of screening in an atom
The elaborated Aufbau model of atomic structure that we employ here is inherently of “qualitative mean-field” type. The mechanism here referred to as “screening” and its effect on the order in which subshells are filled in the atoms are normally discussed in textbooks in terms of “shielding”, “penetration” and “effective charge.” 27 , 28 , 30 The main addition we make below is to explicitly describe simple estimates of the corresponding “effective potential” experienced by the electrons.
The key idea is that a given electron experiences the “other electrons” as a spherically symmetric “shield” around the nucleus effectively reducing the charge of the nucleus. The “electronic countercharge” inside the radial position r of the given electron can be directly subtracted from the nuclear charge while the countercharge outside the given electron is much less effective in reducing the nuclear charge. Ignoring correlations, we assume that the electrons in an atom move independently as if they were in a potential of the form.
where the effective atomic number Z eff is decreased from the atomic number Z by screening (electron–electron repulsion) so that it goes from the full atomic number Z at r = 0 (the origin) to Z − N e + 1 at r = ∞, i.e. from unscreened (as in the hydrogenic model) to fully screened nuclear charge (reduced by all other electrons, i.e. N e − 1 in number) with increasing separation. In the case of a neutral atom the number of electrons N e is equal to the atomic number, i.e. N e = Z, so the effective charge approaches the value in the hydrogen atom at large r,
This shows that the orbital energies return towards values for the hydrogen atom for the outermost electrons in the neutral atom, but never all the way, as we shall see below. One reasonable, but in no way unique, form of Z eff is displaying “exponential screening” 34 as follows:
where k is adjusted to fit data, such as orbital energies and the inverse of the atomic radius. Note that the second term in the potential accounts for “screening” by the N e − 1 “other” electrons. These other electrons screen effectively only if they are inside the position r of our given electron. Thus the number of effective other electrons contributing to screening goes between zero at the center of the atom r = 0, to N e − 1 asymptotically for large r outside the atom.
This “single exponential” representation of screening in atoms can be made more accurate by going to multiple exponential representations where, for example, each shell of electrons is represented by an individual exponential with k decreasing as we go from inner towards outer shells. For the helium atom there is only a single screening electron in the inner most shell so the single exponential representation should be good. Figure 4 below illustrates the two components of the potential, Coulomb and screened Coulomb, in this case. The main point is to demonstrate that the screened component, which increasingly dominates for larger atoms, makes the total potential of shorter range, thereby increasing the energy of high l orbitals relative to lower l orbitals. Much of the empirically known behavior of atoms can be related to this effect of the screened component of the one-electron potential. The s-orbitals reach in close to the nucleus and get an added attraction from the less screened nucleus, while p-, d- and higher l orbitals get increasingly pushed away from this inner region and attraction from the screened component of the potential is correspondingly diminished (Fig. 4).
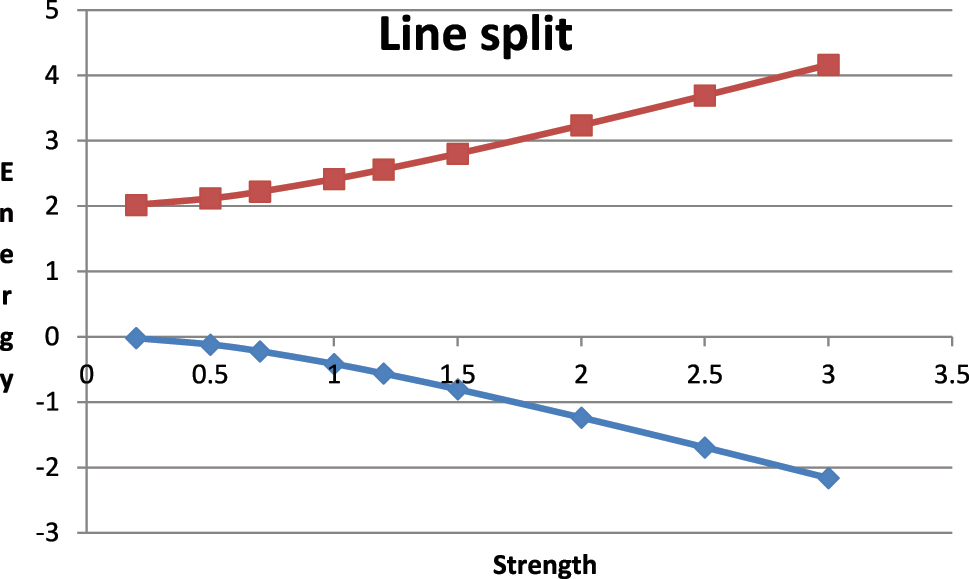
The splitting of a near-degenerate pair of energy levels by a coupling of strength α as in equations (9) and (10) above is shown. The energies without coupling are 0 and 2 so that Δε/2 is 1.
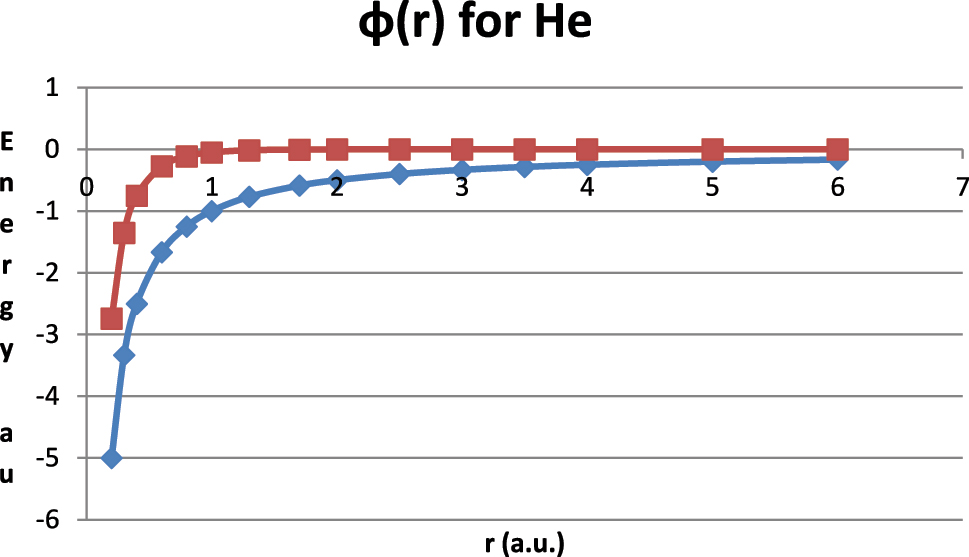
The coulombic potential ϕ C (r) = −1/r (diamonds) and the screened coulombic component ϕ SC(r) = −exp (−kr)/r (squares) for the helium atom (assuming k = 3 as an average of 2 for H and 4 for hydrogenic He for simplicity) are shown. Our screened one-electron-potential for helium is the sum of these components. Note that for r < 1/k the two components are similar while for r > 1/k the Coulomb potential persists while the screened potential rapidly approaches zero, i.e. the two components are long and short ranged in r, respectively. For larger atoms (larger Z) the screened component is multiplied by Z − 1 and the total one-electron potential becomes increasingly dominated by its innermost (small r) part.
We shall use this “screened atomic potential” for the purpose of understanding the effects of electron–electron repulsion on the Aufbau orbital energies. This potential has simplified “mean-field character” but it does correctly exclude “self-interaction” (of an electron with itself) in a global approximate way. If we don’t specifically say otherwise, we shall take the atom to be neutral in our discussion below. Recalling the hydrogenic orbital energies ε H,n (Z) we assume that the mean-field orbitals in a real atom are given by an average (average A is <A>) over the corresponding screened energy expression, i.e.
The precise form of this average will not be specified but we expect it to be an average over electron-nucleus separation r reflecting the distribution of an electron in an orbital of type n, l.
For the moment we need not specify the optimal form of the function Z eff (Z;r) any further. We expect it to change smoothly in a monotonic fashion between its two limits as related to the electron density around the nucleus. Its decrease in magnitude with r describes the increasing screening of the nucleus due mainly to inner electrons. The gist of it is that for small r the potential is roughly “hydrogenic” and unscreened (≈−Z/r) while for larger r screening sets in and it approaches the potential in the hydrogen atom (≈−1/r). Generally, as we go to heavier atoms, this means that the inner electrons are strongly bound, nearly as strongly as in the hydrogenic atom, while the outermost populated orbitals have roughly the same energy since Z eff(r) for the outermost region of the neutral atoms has approached the limiting value 1. The reasonable validity of such a simple model as we have proposed brings with it degeneracy related to the spherical symmetry of the potential and the lack of dependence on spin (Hund’s rules are neglected here). Thus, periodicity of properties follows from the model. The model is good, but not perfect, so deviations are expected but, as we shall see, the perfect Aufbau degeneracies turn into “near-degeneracies” in reality, which bring much the same consequences. In this way the model will be able to explain the periodicity of reactivity displayed in our celebrated empirical forms of the Periodic Table.
How screening splits the shell structure to Madelung form
We recall that for the Coulomb potential the orbital energies depend only on the principal quantum number n. In our Aufbau model the screening mechanism created an effective central potential which is of different radial shape since the screening is more effective the further out from the nucleus we go. In order to see the effect of this change of shape we need to be reminded of how a rising rotational share of the orbital motion of the electron influences the radial distribution of the electron. Despite their fundamental differences in other respects, this understanding can be extracted from the classical motions of the planets around our sun, or satellites around the earth. In the case of no rotation the satellite will fall on a straight line towards the center of the earth. If the orbital motion instead is entirely rotational then the same distance will be maintained to the earth as the satellite revolves around the earth. If there is both rotational and radial motion then the distance to the earth will oscillate, more widely the lower the fraction of rotational motion. In our quantum mechanical model of the atoms l is proportional to the share of rotation in the motion, so l = 0 means that the motion is all radial but the direction of the axis on which it moves is completely unknown so the s-orbitals are spherically symmetric. As we increase l the rotational motion increases and the electron withdraws from the innermost and outermost regions around the nucleus to approach (but never fully reach) the case of a constant distance for a purely rotational classical particle motion. Thus l tells us about the share of rotational motion of the electron and its widely varying (low l) or most sharply constrained (highest l) distribution of radial positions around the nucleus.
The deviation of the order (lowest to higher energy) of the one-electron energies of our mean-field model from the corresponding hydrogenic energies is due to the screening represented in our effective atomic potential by the variable atomic number Z and the corresponding effective atomic number Z
eff(r), which in turn depends on how the electron is positioned with respect to the distance to the nucleus r. For a Coulomb potential (Z
eff(r) independent of r) we know that there is a balance between inner and outer contributions to the energy such that the total orbital energy depends only on n and not on l. The question is what will happen if Z
eff(r) decreases as we increase r. Here it is important to note that since the energy contribution should go like
The “average” in the average effective atomic number in equation (14) must clearly be dependent on both n and l,
Aufbau coupling between degeneracy and reactivity
It is important to note that the screening mechanism, accounted for empirically in the Aufbau model, breaks the full l, m l , s, m s -degeneracy of the pure Coulomb potential in the hydrogenic model but retains m l , m s -degeneracy. In doing so it should decrease the atomic reactivity according to our analysis above. Is there any evidence of this in known behaviors of atoms and molecules? There is, if we add the effect of “near-degeneracy” and consider the change in character of molecules formed from first and second row central atoms. It is clear from our effective charge analysis of l-dependent orbital energies that the variation of the effective charge number Z eff (Z;r) for neutral atoms becomes greater with increasing atomic number Z and the increase in number of screening electrons N e − 1 = Z − 1. Thus the l-dependence starts out weak for small atoms and grows as we go to heavier atoms, e.g. by going from the 2nd row (Li – Ne) to the 3rd row (Na – Ar). Similarly the reactivity should generally decrease with increasing Z. We can see this in the prevalence of hybridized molecular structures such as sp, sp2 and sp3 when the central atom is light and the valence orbitals nearly degenerate, while with heavier central atoms the structures revert towards pure p-character since the valence s-orbital is too far below the valence p-orbital in energy. Familiar examples are H2O with bond angle 105° indicating mainly sp3 character (109.5°) while H2S has bond angle 92° indicating mainly p2 character (90°). Similarly NH3 with bond angle 97° and pH3 with bond angle 94° indicate a shift from hybridized to unhybridized structures as we go from 2nd to 3rd row central atoms. The increased splitting between 3s and 3p orbital energies as compared 2s and 2p is a reason for this reduction in mixing of orbitals to achieve hybridization. This increased splitting of orbitals of the same principal quantum number n but different orbital angular momentum l is also a reason why d-orbitals play a lesser, but still important, role in molecular structure. They only arise in the valence shell for the atoms heavier than neon at Z = 10 where the splitting of ns, np and nd – energies is already relatively large. There are clearly other factors at work, e.g. increasing presence of nonbonding electrons, but we expect and see evidence of decreased reactivity with increased principal quantum number of the outer electrons of atoms. This is in accord with our analysis of the influence of degeneracy on reactivity.
Another related feature is the reactivity bestowed on “low–l –electrons” due to their presence at relatively large r compared to their energy. Thus the outermost electrons in the inert gas atoms, except helium (1s), are generally of ns, np-character with the highest populated n-value, and lowest l-value, assuring low binding energy and presence at the surface of the atom. When some, or nearly all, such outermost ns, np-orbitals are unfilled we have an open valence shell ready to receive, or lose, electrons to approach the nearest inert gas configuration. We conclude that both energies and spatial distributions select outermost ns, np-orbitals to be the chemically operative part of the electronic structure of the atom.
The Aufbau rules for orbital population
We recall first that in the hydrogenic atoms (without electron-electron interaction) only the shells defined by a given principal quantum number n are of different one-electron energies rising uniformly with n as –Z 2/(2n 2). Accounting for electron-electron repulsion screens the nuclear potential and yields orbital energies which depend on both n and l. We don’t have a simple expression for these realistic orbital energies but we have well known empirical rules allowing us to order the subshell energies – with one proviso: the rules apply to the valence electrons of neutral atoms. For positive atomic ions, as we may consider in a process of building up the neutral atom by adding one electron at a time, we expect the rules to revert back towards the hydrogenic rules, since the screening mechanism is weaker. The Aufbau rules, first proposed by Madelung, 35 for the choice of outermost occupied n, l-subshell can be formulated as follows:
Minimize n + l among as yet not fully occupied subshells;
Minimize n among the available subshells n, l all of the same minimal n + l-value.
These “subshell ordering” rules are in full accord with what we have learned about the l-dependence of the Aufbau orbital energies but we should note that, despite their elegance and utility, they have not been derived and their status is mostly that of a convenient mnemonic for the observed order of the outermost n, l-subshells in the neutral atom ground state (see ref. 36]). Here we shall explain them as a consequence of the screening mechanism in atoms which changes the potential in the one-electron model of the atom from coulombic form Z/r to a more sharply nuclear centered form such as, e.g. [(Z−1)e −kr+1]/r for a neutral atom, as discussed above. In the traditional Aufbau model there is also another rule, generally referred to as Hund’s rule, as follows:
Hund’s rule for atomic ground states in one-electron representation:
The degeneracy, that often arises when populating atomic subshells according to the Madelung rules, is broken by a dependence on total spin such that the ground state is obtained by assigning electrons to spin-orbitals so as to maximize the resultant total spin.
Aufbau approximation: … by aligning individual electron spins in singly occupied orbitals all up or all down.
The Hund’s rule degeneracy is given by 2S + 1 where S is the total spin achieved by aligning all the electrons in singly occupied orbitals while the Aufbau estimate is just 2, reflecting the all spins up or all down options. We note that the Aufbau approximation will underestimate the ground state degeneracy when two or more electrons are singly occupying orbitals, but give a reasonable overall view of its variation.
The Hund’s rule is not explained at the level of “non-interacting electrons in a central screened potential”, the Madelung level, that we use here, but requires explicit description of the electron-electron repulsion as in, e.g., Hartree-Fock theory. The rule is based on the presence of “electron separation” due to the Pauli Principle, both the anti-symmetry of the many-electron wave function and the occupation of spatially separated atomic orbitals. We keep this rule in mind but it is a “higher level effect” not fully accounted for here. The full and correct treatment of spin-coupling effects on atomic energy eigenstate energy involves creation of many-electron “multiplet” (singlet, doublet, triplet etcetera) states while our simple one-electron Aufbau model deals with each electron as independent (a doublet with spin up or down). Our model is not completely consistent since the Pauli Principle, which we must include in it, is a “many-electron mechanism”, but we assume that any inconsistencies relating to spin-coupling are small enough that they will not have significant impact on our mainly qualitative reasoning here.
There are a few exceptions to these normal Aufbau rules which are applied in succession, i.e. first the Madelung rules and then the Hund’s rule. The most notable exceptions relate to particular strength of Hund’s rule, i.e. electron separation or weakened l-dependence and return towards hydrogenic ordering. They are of interest as illustrations of competing mechanisms at work but the Madelung rules above, or the corresponding graphical version of them, generally apply for the reasons discussed.
We see that, in our mean-field model, the periodicity is to a significant degree retained from the hydrogenic model of atoms but altered to account for the screening mechanism due to electron-electron repulsion so that the energies become l-dependent. We can now see that the existence and periodic variation in reactivity of atoms can be ascribed to two physical facts:
The diffusivity of the quantum states of electrons;
The good (but not perfect) validity of a mean-field model of the atoms with independent electrons in a spherically symmetric potential of screened Coulomb type.
Both these facts are of quantum-mechanical nature. The first prevents the collapse of atoms predicted classically and the second produces the Periodic Table as a consequence of the coupling of quantization to the dynamics of the electrons. The high symmetry of the model means that not only energy, but also angular momentum and spin, are exactly conserved quantities for each electron in the Aufbau model. In reality they are only approximately conserved. Only the total angular momentum of all electrons is rigorously conserved but not the individual contributions from each electron. Thus the approximate (but reasonably valid) “Aufbau dynamics” is highly constrained by mean-field one-electron symmetry and “nonergodic” in the sense that the quantum motion of individual electrons is decomposable into subspaces of different angular momentum and spin. This kind of “dynamical decomposability” (implying the presence of “constraints on dynamics beyond energy conservation”, e.g. conservation of electron spin and orbital angular momentum) is the origin of the reactivity of the model atoms as reflected also in the degeneracies of the energy eigenstates. Such decomposability is present in all atoms, also in the inert gas atoms, but it is associated with an energy strain (reactivity) which is strongly dependent on the electron population of the different subspaces. If the highest occupied states in each subspace are of much the same energy, and the gaps to unoccupied states are large, then the atom will be stable (inert) while if these highest energies in each subspace (subspace “Fermi energies” or chemical potentials) are showing large variation, including small gaps between occupied and unoccupied levels, then the atom will be correspondingly reactive. Since the atomic orbital energies in the screened Aufbau model depend on the quantum numbers n, l, which define subshells, we expect the atom to be stable if it contains only filled or empty subshells in its ground state Aufbau population. Presence of open subshells indicates degeneracy and atomic instability which in turn makes the atom ready for molecule formation.
The periodic table
Given that our Aufbau model, embellished with a quantum mechanical degeneracy analysis, and the long established Periodic Table agree in known essential features, it is reasonable to consider how our quantum-mechanical mechanisms of the Aufbau model impact issues of interpretation of the Periodic Table. The connection is broad and some of the impact, is obvious, so we focus on a single, perhaps most important, issue at present: The role of energy degeneracy in determining the reactivity of an atom or atomic ion. Our Aufbau analysis above suggests that the reactivity present is directly related to the degree of degeneracy present in the ground state structure. Recall that this relationship has recently been explored in connection with a search for a “measure of atomic reactivity” and found to agree quite well with experimental realities. 33
Let us recall how the atomic ground state degeneracy is determined in the Aufbau model at two levels: 1. According to the Madelung rules d M (A) and 2. After application of the Hund’s rule as well d MH (A). For hydrogen H we have the subshell structure 1s 1 and the spin degeneracy gives d M (H) = dMH(H) = 2. For boron B we have 1s 22s 22p 1 and d M (B) = dMH(B) = 6. For nitrogen we have 1s 22s 22p 3 and d M (N) = 8 (three singly occupied orbitals) + 12 (one doubly occupied, one singly occupied and one empty orbital) = 20. But applying Hund’s rule in the Aufbau approximation reduces degeneracy by aligning the spins to be all up or all down in the three singly occupied 2p-orbitals so we get dMHA(N) = 2, while the proper spin coupling raises this number to dMH(N) = 4 (S = 3/2). We note that the presence of three, rather than one, Aufbau degeneracy numbers relates to the extension by Hund’s rule of the model to account for the effect of the “exchange effect”, i.e. the consequence of wave function anti-symmetry for the electron–electron repulsion. For electrons of the same spin (either up or down) this exchange effect reduces the repulsion if there is any spatial overlap between the orbitals of the two electrons. This means that it is favorable (energy reduction) to align electron spins if several orbitals of the same one-electron orbital energy are available for occupation. For the case of two or more unpaired electrons with aligned spin the proper Hund’s rule ground states are multi-configurational and not part of the simple Aufbau analysis (single configurations only).
For the first 20 elements we get the following Madelung (M), Madelung-Hund (MH) and Aufbau approximation of the Madelung-Hund (MHA) degeneracies (Table 1).
Ground state Aufbau structures and degeneracies are shown at the Madelung (M), Madelung-Hund (MH) and Madelung plus Aufbau approximate Hund (MHA) levels for the first 20 atoms.
| Atom | Structure | dM | dMH | dMHA |
|---|---|---|---|---|
| H | 1s1 | 2 | 2 | 2 |
| He | 1s2 | 1 | 1 | 1 |
| Li | 1s22s1 | 2 | 2 | 2 |
| Be | 1s22s2 | 1 | 1 | 1 |
| B | 1s22s22p1 | 6 | 6 | 6 |
| C | 1s22s22p2 | 15 | 9 | 6 |
| N | 1s22s22p3 | 20 | 4 | 2 |
| O | 1s22s22p4 | 15 | 9 | 6 |
| F | 1s22s22p5 | 6 | 6 | 6 |
| Ne | 1s22s22p6 | 1 | 1 | 1 |
| Na | 1s22s22p63s1 | 2 | 2 | 2 |
| Mg | 1s22s22p63s2 | 1 | 1 | 1 |
| Al | 1s22s22p63s23p1 | 6 | 6 | 6 |
| Si | 1s22s22p63s23p2 | 15 | 9 | 6 |
| P | 1s22s22p63s23p3 | 20 | 4 | 2 |
| S | 1s22s22p63s23p4 | 15 | 9 | 6 |
| Cl | 1s22s22p63s23p5 | 6 | 6 | 6 |
| Ar | 1s22s22p63s23p6 | 1 | 1 | 1 |
| K | 1s22s22p63s23p64s1 | 2 | 2 | 2 |
| Ca | 1s22s22p63s23p64s2 | 1 | 1 | 1 |
Here we see an apparent strong correlation between degeneracy and reactivity, i.e. the inert gas atoms have nondegenerate ground states and the chemically most reactive atoms, as judged by their presence in strongly bound molecules, e.g. C and O, have the highest degeneracy values in the Aufbau model. Nitrogen is highly degenerate at the Madelung level but less so after the Hund’s rule has been applied. We note that the simplified Aufbau treatment of Hund’s rule is generally correct (no spin alignment) but underestimates the degeneracy for high spin ground states like those for N and P and C and O. This error will increase for heavier atoms with even higher spin ground states. It may be surprising that also beryllium, magnesium and calcium have nondegenerate ground states. These atoms are not normally considered to be inert, but this is likely to be related to the presence of additional near-degeneracy, i.e. in the form of ground state neighboring 2p, 3p and 4p states, respectively (with relatively small ns → np splitting). We also note that the outermost s-electrons in Be, Mg and Ca are held relatively loosely (low ionization energy) compared to the strongly bound outer electrons in the inert gases. Thus, there is additional near-degeneracy to higher excited states, and corresponding reactivity, not seen in the table. Nevertheless, the lack of “perfect degeneracy” for the alkaline earth atoms in the Aufbau model suggests a lack of reactivity by comparison with the other non-inert atoms. We return to this expectation in the discussion of molecules below.
For heavier atoms interesting exceptions to the Aufbau rules arise and relativistic effects start to play a significant role. Given our introductory aims here we leave these effects for future study. The basic principles illustrated here for the first 20 elements remain operative for all elements.
Beyond this general perspective of correlation between degeneracy and reactivity we shall focus on one key aspect of the reactivity issue, i.e. the least reactive inert gas structures and their placement in the orderly design of the Periodic Table. 2 From the point of view of periodicity of properties it would seem logical to have a group (column) with He at the top followed by Ne, Ar, Kr, Xe, Rn below. This is put in question by the known electronic structures of the valence shells which are of type ns 2 np 6, n = 2, 3, 4, 5, 6 for all the heavier inert gas atoms but 1s 2 for helium. Thus, with respect to orbital structure, helium is at the top of Group 2 followed below by the alkaline earth atoms. This may well seem unacceptable to many devotees of the Periodic Table in its more empirical and “chemical” forms.
The analysis of the quantum origin of atomic structure by the Aufbau model above tells us unequivocally that structural inertness of atoms is related to “strong non-degeneracy” of the ground state, i.e. to the uniqueness of the ground state and its separation from any excited states by a “chemically large” energy not readily recouped in various chemical bonding mechanisms. This is then the defining criterion of “inert gas” and it happens that different valence shell structures can produce such inertness, i.e. 1s2 and ns2 np6, n = 2, 3, 4, 5, 6. The smallest inert gas atom He is different because it does not have access to p-orbitals in its valence shell. In a sense the property “reactivity” is thereby not fully periodic. It seems most reasonable to let the two atoms H and He be at top of Groups 1 and 2 but mark the uniqueness of the K-shell atoms some way, e.g. by lifting this first short row one empty row above the remaining longer rows. These two first elements are by necessity different since the valence shell has only two available orbital-states and cannot therefore reproduce behaviors involving eight outermost ns and np – states as seen for all other elements. In this way of presenting the Periodic Table the inert gas position is always at the end of the regular row and the inertness is to be associated with the jump in largest principal quantum number n that occurs in the populated subshells as we go from the inert gas atom at the end of the row and the alkali-atom at the start of the next row below. It so happens that these inert “end-of-row atoms” do not fall in a single column due to the oddity of the first row with only two atoms. This seems a small price in graphical elegance to pay for the closer adherence of the Periodic Table to underlying electronic structure.
Our Aufbau analysis of the Periodic Table leads us to the dominant importance of the nature of the electronic ground state. Not only the ground state energy is important but also its energy degeneracy, which can be strongly nondegenerate, near-degenerate, or degenerate to variable degree. See a related discussion by Schwarz and Rich on page 437 in Ref. 36]. We conclude that both hydrogen and helium should be understood as fundamentally different from all following elements for which normal forms of the Periodic Table are more consistent with the underlying electronic structures. Hydrogen can be seen as the first alkali atom as well as the first halogen atom, i.e. one electron less than an inert gas structure. If it seems odd to see helium placed above beryllium, even with one empty row to the heavier elements, we must remember that beryllium and other alkaline earths below are similar to helium in that the ground state is nondegenerate but much different from helium since they have six empty spin-orbitals of p -type in the valence shell. These orbitals are higher in energy but not “chemically separated”. Thus bonding mechanisms can draw upon their presence with the result that alkaline earth atoms are not inert despite their nondegenerate ground state structures. The near-degenerate p-orbitals allow the onset of metallic binding to arise in clusters like Ben with sufficiently large n.
Chemical bonding mechanisms
The historical development of chemistry, and the central role of the Periodic Table in it, leaves no doubt that chemical bonding is closely related to the properties of the atoms. The explanatory picture of the atoms presented above suggests that degeneracy or near-degeneracy of atomic ground states creates reactivity and leads immediately to two mechanisms available for stabilization by molecule formation:
Redistribution of electrons among atoms to form molecules composed of stable (non-degenerate inert gas like) atomic ions held together by Coulomb attraction between unlike charges (Ionic bonding)
Ground state degeneracy reduction by removal of dynamical constraints to relax the “decomposability” of the electron dynamics by facilitating delocalization of electron motion over bonded atoms (Covalent bonding)
These two, purely ionic and purely covalent, mechanisms have strikingly different dynamical character of permanent electron displacement and oscillatory electron motion between bonded atoms, respectively. Nevertheless, they both reduce degeneracy in the molecular structures formed. Generally, bonds between atoms of different species will show partial presence of both these bonding mechanisms.
Ionic bonding
The ionic bonding mechanism is familiar and has long been understood to have a clear atomic basis. It is entirely dependent on quantum effects but, in its most basic form, only reliant on atomic quantum mechanics as represented in the Periodic Table and the corresponding variation of atomic properties. The variation in atomic stability systematically described in the Periodic Table is simply recognized to extend to atomic ions of low charge. In particular, the ions of the same number of electrons as the inert gas atoms, 2, 10, 18 …, are then expected to be particularly stable as well, e.g. H− and Li+ (He-like), O2−, F−, Na+ and Mg2+ (Ne-like), with non-degenerate ground states. Ionic bond energies can be estimated reasonably, at least for singly charged ions, by atomic ionization energies I
1(A) and electron affinities E
a
(A) for relevant atoms A and Coulomb interaction energies combined with ionic radii
A standard table (SI Chemical Data, 6th ed., Wiley) suggests that the ionic radii are
The simplest interpretation is that the ions are hard spheres. The Coulomb interaction between two spherical and non-overlapping singly charged ions at this distance is obtained as
It is clear that the ionic bonding mechanism provides a very significant binding energy and will stabilize the ion pair at separations up to about 6 Å. For a structure including an O2− ion one would have to include an extra promotion cost in energy to optimally confine the second added electron.
It follows from the analysis above that in simple, but reasonable, terms there is an ionic bonding mechanism that can be understood to be a consequence of the periodically varying properties of atoms. If we allow electrons to be transferred among reactive atoms to form pairs or small clusters of ions of inert gas electronic structure then these “ionic molecules” can be stabilized by the Coulomb interaction between the ions. In order for such stability to arise the atoms must be complementary, i.e. such that the cost of creating the positive ions is not too much greater than the electron affinities of the anions. According to empirical experience, the positive and negative ions appearing in such “ionic structures” can be identified as “inert gas like atomic ions” like Na+ and Cl−. With such complementarity the cluster (or molecule) of atomic ions always forms a non-degenerate “cluster ground state” and the cost of ion creation at great separation can be repaid in lowered (more negative) Coulomb interaction energy so as to make the cluster the most stable equilibrium structure. We note that this simplified ionic bonding mechanism can be extended from monovalent ions, as in our example above, to multiply charged ions where the “promotion” in the case of an ion like O2− would include its confinement to a finite physical size.
We conclude from this, generally accepted analysis, that there is an ionic bonding mechanism of “atomic character” in the sense that all the quantum effects responsible are found already in the Periodic Table on the assumption that its rule of “particular electronic stability” of inert gas atoms can be extended to atomic ions of low charge, and the interaction mechanism of the bonding is in essence of electrostatic character. From the point of view of our degeneracy analysis we note also that this mechanism takes reactive atoms of degenerate ground states and turns them into atomic ions of nondegenerate ground states and then, by Coulomb interaction, into a nondegenerate “ionic molecule”. Thus ionic bonding fits the general rule that bonding takes separate atoms from ground state degeneracy towards “molecular non-degeneracy”.
Seen in this way the ionic bonding mechanism is both simple and intuitive and it fits well with early bonding models drawing upon the concept of valency and electron redistribution. At an introductory level of discussion there is no pressing need to consider electron dynamics between ions in such structures. The empirical quantum mechanics of the Periodic Table suffices to understand the ionic mechanism of bonding with a simple extension to include low charge ions in the rule of particular inert gas atom stability. No great disputes about the nature of ionic bonding have, to our knowledge, a significant presence in the literature. A problem of another sort should be recognized: the ionic molecules discussed above are not very prominent in nature since they are inherently reactive to form larger ionic clusters and ionic crystals, as illustrated in the case of NaCl by the fact that we primarily know of it in its solid crystal form as table salt. In order to understand the more prevalent species and stabilities of the molecular universe of chemistry we have to turn to the other, more subtle, form of chemical bonding.
Covalent bonding
The covalent bonding mechanism, on the other hand, has confronted chemists with the need for a molecular form of quantum mechanics not readily extracted from the Periodic Table or the quantum mechanics of atoms. While the ionic bonding mechanism can be understood in terms of the quantum mechanics of atoms, including atomic ions, and the classical electrostatic interaction of ball shaped such ions, the covalent bonding mechanism relates to the quantum mechanics of both individual atoms and ions but also fundamentally to “polyatomic quantum effects”. For this reason there is a sharp rise in dependency on quantum effects when we consider covalent bonding and a similar rise in subtlety, and in disagreement among chemists regarding the physical explanation of the mechanism.
Covalent bonding can, in small molecules like H2 + and H2, immediately be seen to be associated with electron motion between the nuclei. In the normal energy analysis of quantum chemistry this interatomic motion is reflected in the delocalization of the molecular wave function over the two nuclei. In a one-electron model there is a splitting of the atomic ground state orbitals into a bonding and antibonding pair of molecular orbitals with the energy splitting proportional to the frequency of interatomic oscillation. This “dynamical view” of the covalent bonding mechanism, adopted by R. Feynman in a “two-state analysis of bonding” in 1965 37 in his Lectures on Physics (Section 10.2), is closely related to the kinetic energy analysis of Hellmann and Ruedenberg (1933 38 and 1962 22 ) but avoids the apparent paradox of the virial theorem encountered in the latter. The alternative dynamical interpretation of covalent bonding has also been used to understand the “non-bonding theorem” of the Thomas-Fermi density functional theory 39 and recommended as a complement to energy analysis in a series of studies of covalent bonding. 40 , 41 , 42 , 43 , 44
In an energy analysis the virial theorem seems, at first, to prove conclusively that the electrostatic interactions must be the source of the covalent bonding, since, by comparison with the far separated atoms, the kinetic energy change is positive at equilibrium separation and the potential energy change is negative and twice as large. Closer inspection shows, 22 however, that the energy analysis is confused by the presence of a second mechanism, a contraction of the electron density around the nuclei, which is a corollary of covalent bonding for Coulomb interacting electrons and nuclei, but not the mechanism of bonding. The dynamical view of bonding has no such disagreement with the virial theorem. For H2 +, for example, it has been recently shown 44 that if the electron is prevented from interatomic motion then the localized ground state has the energy of the antibonding molecular orbital (MO) and the delocalization energy associated with interatomic electron motion accounts for the full drop in energy from the antibonding to the bonding MO. We emphasize that this view of covalent bonding in H2 + is independent of whether we use a fixed exponent minimal basis set which cannot account for the “orbital contraction mechanism” or the optimized exponent version of the basis which accounts for the contraction. The latter basis gives better bonding mainly by reducing the Pauli repulsion associated with atomic basis overlap. In a “dynamical analysis” the covalent bonding is the result of interatomic electron motion and the need to distinguish “interatomic delocalization” and “atomic contractive” mechanisms of kinetic energy change does not arise at the most fundamental level of explanation.
The dynamical view of the covalent bonding mechanism also connects readily with the degeneracy analysis of atomic reactivity. In the simplest case of H2 + the separate atom limit, with no interatomic electron motion, has a degeneracy of 4 (left or right localized with spin up or down). As we couple the localized atomic orbitals, to form molecular orbitals, we split the orbitals into bonding and antibonding MOs with an energy gap proportional to the frequency of interatomic electron oscillation. For large separation R this energy gap is very small and the ground state MO is near-degenerate but for R close to the equilibrium value Re the energy gap has grown to a value comparable to that of a chemical bond and we would no longer say that the bonding MO is near-degenerate. In this way quantum mechanics “interpolates” between localized (dynamically decomposed) and delocalized (ergodic, fully dynamically coupled) ground state structures. As noted by Feynman 37 the electron oscillation between protons is understood in terms of the two MOs, bonding and antibonding, even though only one of them is occupied in the ground state. The “stationarity” of the bonding ground state is a statistical feature of quantum mechanics (a time-averaged oscillation). The electron in H2 + is moving in the vicinity of a proton and occasionally between protons. Since the spin can be up or down the ground state has degeneracy two but if we consider the case of H2 the extra electron must be added with opposite spin direction so the ground state is nondegenerate.
As we go from H2 + to H2 the complication of electron correlation must be accounted for. If we ignore it and use Hartree-Fock theory in simplest form, then the molecule is well described around the equilibrium bond length but dissociates incorrectly. The quantum-chemical Valence Bond (VB) theory recovers a sound and accurate bond energy curve by simply eliminating the so-called ionic configurations H+H− and H−H+ from the Hartree-Fock determinant. The remaining covalent configurations describe a molecule where two electrons correlate their oscillation between atoms to reduce the probability of both being at one of them. The interatomic motion is still the source of bonding, but it is in the form of correlated two-electron motion. The VB theory may seem “fully correlated” in keeping the electrons at different atoms but the overlap of the atomic basis functions allow them to coexist spatially enough to account for interatomic motion. It is well known (e.g. by configuration interaction (CI) calculations) that not only are both angular and in-out (atomic) correlations completely neglected in the VB theory, but the degree of left-right (interatomic) correlation present is overestimated. A more accurate (e.g. CI) calculation shows that this correlation is in reality somewhere between the Hartree-Fock and VB proposals but tending towards the VB model in the large bond length limit. 43
Electron sharing?
Most chemists have been taught that covalent bonding arises as a consequence of electrons being “shared” between bonded atoms. Graphically this “electron sharing mechanism” is illustrated by the shared electrons being placed as dots (or crosses) between the bonded atoms. In the case of H2 + and H2 we can use the notation (H·H)+ and H:H to represent two protons with one and two shared electrons between them, respectively. How are we to understand this “sharing” of electrons so as to agree with modern theory of covalent bonding? Given the long history of this Lewis dot picture of covalent bonding we must be careful not to omit the lessons of quantum mechanics for the simplicity of a traditional classical view of the electronic structure represented by these two graphs. It is distinctly incorrect to think that the shared electrons are sitting still at the bond midpoint. Nor is it correct to think that the bond energy is due to the electrostatic interaction of such static “shared electrons” with the neighboring protons. According to quantum mechanics, low mass electrons in their ground state are not sitting still but always moving and confinement to a small volume around the bond midpoint, which will have the character of a potential maximum, is costly in terms of energy. Instead, we must realize that the shared electrons are mobile between the two protons and pass through the region around the bond midpoint as a transition state on its oscillation between the two regions around the nuclei. It is this oscillation between nuclei which is the key to covalent bonding and the bond energy is directly related to the frequency of the oscillation and to the energy splitting of the two atomic states of the separate atoms which meet and couple most strongly in the region around the bond midpoint. The extra electron density which is found around the bond midpoint is important because it speeds up the passage of the electrons over the potential barrier between the atoms, not because it produces an electrostatic bond energy contribution. The latter contribution is small by comparison, and the dominant contribution is of a kinetic energy nature.
In the case of H2 we should note also that the “electron pairing” which is illustrated in this molecule, and common in many others, should not be interpreted too literally. It may seem from the graphical representation as if the electrons form a geometrically confined pair. We may then, after learning that the electrons do not sit still but move, assume that they move as a pair between the bonded atoms. This would be grossly in error. In Hartree-Fock theory, which provides the foundation for quantum chemistry, the two paired electrons move independently between the bonded atoms. They are no more geometrically confined to each other than being in the same orbital would imply. In fact, this “independent electron assumption” is increasingly in error as the bond length R between the atoms increases and asymptotically the molecule dissociates to form two neutral atoms excluding the “ionic configurations” H− H+ and H+ H−. This means that for large R the electron motion is “correlated” such as to keep the two electrons on different atoms, i.e. far from geometrically confined to be close. Fortunately this kind of electron correlation was well described by the Valence Bond theory of Heitler and London 16 already in 1927.
The detailed resolution of the covalent bonding mechanism is an active field of research with most studies performed for wide ranges of molecules within the “energy decomposition analysis” (EDA) which dominates quantum chemistry. 45 , 46 , 47 We believe there is much to recommend the alternative dynamical analysis, particularly as a complement to the normal focus on energy and other apparently “static” properties. While the roles played by potential and kinetic forms of energy, as coupled by scaling laws reflected in the virial theorem, continue to be debated, the idea that covalent bonding requires valence electrons to be able to move between bonded atoms, and molecular segments, is yet unopposed, if possibly by rarely being considered. 44 Moreover, the dynamical picture has clear physical implications in terms of extra stability found when the electrons are able to move not only between pairs of atoms but in chains and rings of atoms as in aromatic hydrocarbon molecules. Finally, the metallic binding in solid metal structures bears witness that stabilization may follow from interatomic electron mobility on a macroscopic scale. The quantum dynamics of electronic motion in molecular structures may seem to present quantum chemistry with new computational challenges but the connection between already familiar energy analysis and the alternative dynamical analysis is very close in quantum mechanics. The rewards in terms of the clarification of the origin of bonding should readily justify the efforts to become familiar with both the energy picture and the dynamical perspective on the mechanism of covalent bonding.
Aufbau analysis of change in energy degeneracy by molecule formation
A key feature of the present analysis is the bridge between energy and dynamics formed by the energy degeneracy of the ground state of both atoms and molecules. Even without explicit consideration of quantum dynamics of electrons, we can probe the character of the dynamics by exploring the energy degeneracy. From the perspective of degeneracy analysis, we note that the molecular ground states are nearly always nondegenerate, like the inert gas atoms. In rare cases the molecular ground state is still degenerate but always (so far as we know) less so than the corresponding separate atoms. Thus, the molecule formation can be seen as a very efficient mechanism for degeneracy reduction, or equivalently for “reactivity reduction”. The stability of the commonly occurring molecules can therefore be associated, not only with their low ground state energy, but also with their nondegenerate ground state. Using our simple Aufbau Madelung (dM) and Madelung-Hund (dMH) degeneracies this can be illustrated by the important reaction of water formation from the atomic elements:
The reduction in degeneracy is from 60 using only the Madelung rules, or from 36 when adding the Hund’s rule, to 1. Interestingly, the very familiar exception of O2, which is readily seen to be triply degenerate in its ground state (a triplet state) due to two singly occupied π-orbitals in a simple MO analysis, again involves the strongly reactive oxygen atom but now illustrates that, on a few occasions, a very stable molecule may still have a degenerate ground state:
Here the molecular orbital set contains 8 MOs of which the four lower are bonding and doubly filled while the higher antibonding ones start with two degenerate antibonding π*-orbitals. With no restrictions on spin, other than the Pauli Principle, there would be two doubly filled orbital configurations and four singly filled configurations of the same energy. Adding Hund’s rule in its simplified Aufbau form would yield dMHA = 2 but the correct number is dMH = 3 as shown, given that a triplet state is of that multiplicity. The Aufbau form of Hund’s rule does not include the m s = 0 component of the triplet and underestimates the degeneracy. As noted above the one-electron Aufbau treatment neglects higher order effects related to spin states of multiplicity 2S + 1 ≥ 3.
It is important to note that this reaction to form a degenerate molecule O2 still produces a massive reduction in degeneracy, i.e. from 225 to 6 according to the Madelung rules and from 81 to 3 according to the full set of Aufbau rules including the correction for the missing triplet component. Still, one may well wonder whether the remaining degeneracy of ground state O2 makes it more reactive than the usual molecule with a nondegenerate ground state. Perhaps such an extra molecular reactivity, associated with degeneracy of the ground state, is important in the explanation of the unique role molecular oxygen plays in the lifecycles of living organisms.
The semi-inert alkaline earth metal atoms
A stand-out feature of the listed Aufbau degeneracies above is the non-degeneracy of the ground states of the alkaline earth metal atoms Be, Mg, Ca. This non-degeneracy is shared only with the inert gas atoms and may raise expectations of similar inertness of these two groups of atoms, inert gas and alkaline earth metal atoms. This similarity is, however, only partial as can be understood from the ready formation of metallic binding among the latter. The difference between these groups can be understood as a consequence of their quite different degree of near-degeneracy. The inert gas atoms are not only non-degenerate with respect to the ground state but they are also without near-degeneracy. Thus, their inertness is two-pronged: non-degenerate ground state and lack of near-degenerate excited states. The alkaline earth metal atoms have “near-degenerate excited states”, i.e. unoccupied orbitals in the same atomic shell reached by an ns → np promotion. The promotion energy is relatively small for Be rising for the larger alkali earth atoms but always remaining small compared to chemical bonding energies. In fact, the non-degeneracy of the ground state still leaves a significant mark on the reactivity of the alkali earth metal atoms. This can be seen in the weak bonding of the dimers which has drawn considerable attention 48 , 49 for the challenge it poses to quantum chemists. As an example, we note that the beryllium dimer has a bond energy of 2.7 kcal/mol in comparison with 0.08 kcal/mol for He2 and 20.4 kcal/mol for Li2. 48 This dramatic bond energy variation reflects the different degrees of degeneracy and the corresponding effect on the nature of the bonding in these three dimers. There is essentially no degeneracy available in the formation of He2, only near-degeneracy for Be2, and both forms of degeneracy for Li2. The challenge posed to modern methods of quantum chemistry by the weak bonding in the beryllium dimer has recently been explored. 49 The same weakness (bond energies in the range 1–4 kcal/mol), stemming in our perspective from the non-degenerate (closed shell) ground state of the atom, persists for the whole group of alkali earth metal dimers. 48 The term “semi-inert” that we have used for the alkaline earth atoms is meant to convey this partial inertness due to the nondegenerate ground state and reflected in weak dimer bonding. The presence of near-degeneracy then introduces reactivity which allows strong metallic binding to arise for larger clusters of these atoms.
The interatomic repulsion in molecules – equilibrium geometries
The discussion of bonding above has focused on the key attractive mechanisms, which do indeed dominate and cause the formation of stable molecules. The stabilities and geometries of these molecules can, however, only be understood if we also account for the repulsive mechanisms which balance the attractions at equilibrium geometry and prevent the collapse of the molecule to a larger atom (the united atom limit). The numerical methods of quantum chemistry 18 generally do a very good job of representing these repulsions. Our limited aim here is to extract some physical insight into the nature of the repulsive mechanisms in molecule formation to complement the focus on attractions above.
Interatomic electrostatic interactions
The intramolecular electrostatic interactions play a crucial role in determining molecular geometries and also in the computations of molecular quantum chemistry. There are three different types of such interactions: i) electron-nucleus (e-n) attraction, ii) electron–electron (e–e) repulsion and iii) nucleus–nucleus (n–n) repulsion. This is also in the order of their importance. The e-n attraction is the sole reason for the existence of atoms and the only form of potential energy in a hydrogen atom. For larger atoms the e–e repulsions are added with important consequences (screening and correlation) as discussed above. We note that it is the e–e interaction of “two-body” type that turns electronic structure determination into a complex many-body problem dominated by approximations meant to reduce the full complexity. The now dominant use of Gaussian basis sets in the variational search for ground states was proposed in 1950 (by S. F. Boys 50 ) and popularized in the 1960s in order to exploit analyticity to reduce the burden of numerically calculating and storing the needed electron repulsion integrals. The n-n repulsions only arise for molecules or other multi-atomic systems. They prevent the collapse of the molecule in the united atom limit but otherwise, for molecules expanded beyond their equilibrium geometry, play a less important role due to “screening”. This term here refers to the fact that individual atoms in the expanded molecule are surrounded by neutralizing electrons and the electrostatic interactions between thus neutralized atoms are generally small except at quite small atomic separations.
Quantum effects play an important role in reducing the electrostatic interactions of electrons. We have already noted that the “quantum diffusivity” of the electron eliminates the classical collapse of the hydrogen atom. The general principle is that point charges interact more strongly by coulombic potentials than do diffuse charge distributions. The interaction of a diffuse electron with a point-like nuclear charge remains finite in the limit of zero separation. Similarly, the interaction of two electrons is “softened” by each electron being diffuse. It follows that there is a natural order of short range interaction strength where the n-n interaction diverges (stabilizing the molecule at contracted geometries), the e-n interaction remaining finite reaching hydrogenic atom energies in the R = 0 limit, and the e-e energies being weaker still but strong enough to require accurate representation.
Another way to look at the electrostatic interactions in a molecule is to subdivide them into “interatomic subsets” by associating subsets of the electrons with corresponding atoms so that the e–n and e–e interactions can be similarly subdivided into “within atom” and “between atom” components. This is natural to do for expanded molecular geometries but less so for near equilibrium geometries of stable molecules. The “atoms in molecules” are not uniquely definable and the interatomic forces are not of simple pairwise form. Nevertheless, the perspective of molecules as interacting atoms is intuitively appealing and frequently used. 20 , 23 It leads, e.g., to an understanding of the relatively short range of electrostatic interactions in an expanding neutral molecule due to the predominance of the atomic screening mechanism. An exception must be made here for ionic and highly polar covalent molecules where the electrostatic interactions are of longer range since the screening, in the presence of significant charge transfer among atomic centers, is then incomplete.
The Pauli repulsion
The repulsions between like charged particles, like the electron-electron and nucleus-nucleus repulsions discussed above, are so obvious and easy to understand that they often hide the, very different but equally important, Pauli repulsion acting in the formation of molecules. This type of repulsion is of considerably higher subtlety. Perhaps the easiest way to realize what it is all about is to note that the basic mechanism of “bonding by increased diffusivity”, or by electron delocalization, in covalent bonding also encounters an opposing localization as the atoms move closer to form a tightly bound molecule. For the far separated atoms diffusivity is small since the electrons are confined at separate atomic centers. As we move the atoms closer this confinement is relaxed as the electrons are increasingly able to move between atomic centers but at the same time the total molecular space available to the electrons decreases. Thus, there is competition between a dynamical decrease in confinement and a geometrical increase in confinement. The former is the origin of covalent bonding while the latter is the origin of Pauli repulsion.
The concept of Pauli repulsion is associated with the effect of the Pauli Principle which states that permissible many-electron wave functions must be antisymmetric with respect to pairwise particle exchange. The Pauli principle forces electrons in the Aufbau model of atoms, or similar orbital-based quantum chemical theories, to be assigned unique spin-orbitals identified by quantum numbers n, l, m l , m s for each electron. This requirement drives the hydrogenic, or Aufbau, or Hartree-Fock, orbital energies occupied by additional electrons upward in energy in the one-electron spectrum of states. This process is completely fundamental in the modeling of atomic structure, being the backbone of the Aufbau model, but it also gives rise to an interatomic repulsion in molecules. It is often said that this type of Pauli repulsion is dominant in the interaction of inert gas atoms, e.g. in the case of He-He. We can understand this suggestion if we note that in the “united atom limit” of the helium dimer, He–He → Be, two electrons have had to go from a 1s helium orbital to a 2s – orbital of beryllium. This increases energy and is reflected in Pauli repulsion between the helium atoms. This repulsion is directly related to the overlap of the He 1s – orbitals of the two atoms. This type of “overlap repulsion” is not only present for inert gas atoms but for atoms and molecules in general. From a physical point of view, it is important to note that the Pauli principle and the corresponding “Pauli repulsion” can be associated with three distinct, but closely related, types of effects:
Orthogonalization repulsion arising when electrons of equal spin are spatially coincident and require orthogonal orbital representation (normal Pauli repulsion);
Steric (or excluded volume) repulsion when spatially separated atoms or molecules with electrons of equal spin approach and keep these electrons in volumes which do not overlap.
Molecular space contraction – Atomic basis set overlap correction.
The first two mechanisms are generally recognized as “Pauli repulsion” but not distinguished. We do so here to emphasize that two different sub-mechanisms can be drawn upon (and mixed) relating to rising kinetic energy and excluded volume, respectively. and we add the “basis set overlap repulsion” as a third steric repulsion mechanism.
The orthogonalization energy effect (1) is dominant in the Aufbau model of ground state atoms while the steric repulsion (2) is exemplified in the interaction of ground state helium or other inert gas atoms, which basically serves to keep their electron densities apart. This is often modeled in statistical mechanics by the use of “hard sphere interaction models” which naturally include the concept of “excluded volume”. Finally, the atomic basis set overlap correction is ubiquitous in quantum chemistry but normally not associated with the term “Pauli repulsion”. It reflects the geometrical contraction of the molecule as it forms from far separated atoms. All three repulsions are of geometrical origin and therefore fundamentally related. They are not directly related to the electron dynamics found to be the origin of covalent attraction but an indirect relationship is present. The excluded volume effect is clearly associated with localized electron dynamics while fully delocalized electron dynamics would result in coincident electrons and the “orthogonalization” form of Pauli repulsion. In general, the total repulsion is a mixture of all the three stated forms as listed above.
The Pauli repulsion described above is typically of longer range than the electrostatic interactions for nonpolar molecules and comparable in range to the dominant delocalization attraction. Both the attractive and repulsive mechanisms of covalent bonding relate to the requirement for “diffusivity” of quantum states. The attraction is due to the facilitation of interatomic electron motion and corresponding reduction of degeneracy while the repulsion is due to reduction in configurational (or phase) space as the molecular geometry becomes tighter. We shall give an illustration of the expected relation between these two mechanisms in determining molecular stability in accord with ground state degeneracy.
Degeneracy analysis of small molecule stability: H2 +, H2, He2 + and He2
Let us consider the four molecules H2 +, H2, He2 + and He2 which can be most simply represented in a minimal basis treatment using the two atomic 1s orbitals to form a pair of bonding and antibonding molecular orbitals. The ground state structures are then formed by occupying these two molecular orbitals sequentially with one to four electrons. We consider the degeneracy change from the separate atom initial state to the molecular equilibrium state (if there is one). In the case of H2 + we have initial degeneracy 4 (electron right or left, spin up or down) and final degeneracy 2 (spin up or down) for the molecule. For H2 the initial degeneracy is still 4 (left spin up or down, right spin up or down) but now we have a nondegenerate final state (a bonding electron pair). Proceeding to He2 + we get again an initial degeneracy 4 and final 2. For He2 we start with a nondegenerate state and end with one also since the degeneracy will not change as the two helium atoms approach each other. There is no stable molecule formed. The degeneracy reduction is by a factor 4 for H2, 2 for H2 + and He2 + and 1 for He2. The corresponding bond energies are similar (432, 269 and 227, 0 kJ/mol) reflecting the electron population of bonding relative to antibonding molecular orbitals (twice the bond order). This perspective of several low lying states being degenerate in the separate atom limit, then near-degenerate as the molecule starts to form, and finally chemically split in energy around bond equilibrium, offers insight into the mechanism of bonding and the change in stability of this small set of molecules. We note that the repulsion in H2 + is that between the charges of the two protons and the molecular space contraction (3). For H2 an electron-electron repulsion is added. Only for He2 + and He2 there is proper Pauli repulsion of types (1) and (2) which for He2 is effective enough to completely cancel normal covalent bonding. There is an anti-correlation between degeneracy and Pauli repulsion. The availability of degenerate states is used to minimize Pauli repulsion. When there is no such degeneracy the Pauli repulsion is dominant.
Conclusions
Quantum mechanics made its way into chemistry, without chemists knowing it, first around 1870 in an empirical form, when the atoms were found to show predictable properties as systematized by the Periodic Table. About 50 years later it became understood how the Periodic Table could in principle be derived from the newly discovered quantum mechanics. Atomic and molecular quantum mechanics was over the last 100 years developed first mainly by physicists, but then also by chemists who have produced a form of “quantum chemistry” of great accuracy and applicability. The numerical methods are now extremely refined and available in comprehensive program packages. Our analysis above of atomic reactivity and molecule formation is meant to be complementary to the methods and results of modern quantum chemistry, i.e. by focusing on the physical and mechanistic origin of the atomic reactivity and chemical bonding reflected in the experimentally or computationally obtained results. We have tried to show that the required space-momentum uncertainty, or diffuseness, of quantum states and the inherent dynamical nature of quantization leads to systematic behaviors of individual atoms and of the molecules they form by chemical bonding. These inherently “quantum” mechanisms are related to the character of the energy eigenstates of the system (local or delocalized?) and the character of the spectrum of energy eigenvalues (degeneracy, near-degeneracy or chemical separation?). Thus, the atomic properties are related, not only to the ground state but, to the nature of the energy level spectrum just above it. This broader view of the low energy eigenstates casts new light on the basis of periodicity in the electronic structure and other properties of atoms.
The atomic structure and the property variations displayed in the Periodic Table are related to the persistence of one-electron decoupling of electron dynamics due to spherical symmetry of the whole atom. The interaction of individual electrons with the nucleus retains a high order “one-electron spherical symmetry” while the electron-electron interaction reduces this symmetry to a lower order “many-electron spherical symmetry”. Since the strength of the electron-nucleus interaction is dominant, and the electron-electron interaction weaker, the higher order one-electron symmetry is approximately retained in the many-electron structures of atoms. This fortunate simplification is the origin of the one-electron Aufbau model of atoms. The approximate decoupling due to spherical symmetry leads to many degeneracies in the Aufbau model, often changed to near-degeneracies in experimental reality. The ground state electron populations of some atoms will nevertheless, despite assumed decoupling, lead to nondegenerate Aufbau ground states of exceptional stability. Most stable of these are the inert gas atoms which rarely (but sometimes, particularly the heavier atoms Kr, Xe) participate in any kind of chemical bonding. Another group of “semi-inert” atoms are merely reluctant to dimerize (the alkaline earth atoms) due to a nondegenerate ground state, but rely on near-degenerarate states to turn on metallic binding in larger clusters. In general, the atomic ground states show degeneracy, and thereby reactivity, in accord with empirical evidence systematized in the Periodic Table.
Molecule formation of two or more atoms relaxes reactivity, and lowers degeneracy of bonded atoms, generally to produce a nondegenerate molecular ground state. This is achieved by electron redistribution among the atoms, or by interatomic electron motion in the ionic and covalent bonding mechanisms, respectively. These two mechanisms are both of atomic and quantum-mechanical origin but of different character, one being essentially static and the other dynamical. The essence of ionic bonding can be seen by extending the Periodic Table from neutral atoms to atomic ions. The motion of the valence electrons can then, to a good approximation, be taken to be localized to individual atomic ions. The mechanism of covalent bonding takes us more fundamentally to the properties of atomic clusters in which electrons can move between atomic centers. In heterogeneous molecules these mechanisms are both present. We then expect the bond energy to receive significant contributions from both the ionic mechanism of permanent charge redistribution and the covalent mechanism of interatomic electron motion.
Our analysis above should be seen as a way to understand the quantum-mechanical origin of the stability of atoms and molecules without need for detailed mathematics or accurate numerical calculation. Chemists should, with this analysis, be able to see the foundation of atomic and molecular chemistry more clearly. The Aufbau model of ground state atomic structure turns out to provide more insight if we also consider the approximative picture of energy degeneracy that it offers. The baseline of common understanding could then be extended beyond the Periodic Table combined with Lewis, VSEPR and empirical VB modeling to a level including basic quantum mechanics and the key role of electron dynamics as reflected in the degeneracy of its energy eigenvalue spectrum.
It is important to emphasize that this qualitative analysis in terms of electron dynamics and its representation in energy degeneracy is optional and does not invalidate earlier analysis of just the ground state. Energy decomposition analysis and the role of the virial theorem remain relevant. We have simply pointed out that quantization is inherently coupled to particle dynamics and dynamics is most clearly expressed in a multistate analysis of the spectrum of energy eigenstates. This analysis should help clarify the still debated origin of atomic reactivity and chemical bonding. Quantum chemists have the tools to probe in detail the validity of our approximate analysis and guide it in sequential improvement. There are important questions to answer by quantum-chemical computation such as: Can new computational results for not only ground states, but also their degeneracy, provide the claimed insight into reactivity versus stability of atoms and molecules? Can it be verified that covalent bonding fundamentally relates to relaxation of dynamical constraints seen computationally in reduction of degeneracy, and physically in increased electron mobility between bonded atoms? The “common knowledge” empirical evidence drawn upon in our qualitative analysis above should certainly be put to detailed quantitative testing.
Acknowledgments
I acknowledge generous help in the form of discussion and suggestions from George Bacskay.
-
Research ethics: Not applicable.
-
Informed consent: Not applicable.
-
Author contributions: The author has accepted responsibility for the entire content of the manuscript and approved its submission.
-
Use of Large Language Models, AI and Machine Learning Tools: None.
-
Conflict of interest: The author declares no conflict of interest.
-
Research funding: None declared.
-
Data availability: Not applicable.
References
1. Kaji, M. D. I. Mendeleev’s Concept of Chemical Elements and the Principles of Chemistry. Bull. Hist. Chem. 2002, 27, 4–16; https://doi.org/10.70359/bhc2002v027p004.Search in Google Scholar
2. Scerri, E. R. The Periodic Table – a Very Short Introduction, 2nd ed.; Oxford University Press: Oxford, U.K, 2019.10.1093/actrade/9780198842323.001.0001Search in Google Scholar
3. Thomson, J. J. On the Structure of the Atom: An Investigation of the Stability and Periods of Oscillation of a Number of Corpuscles Arranged at Equal Intervals Around the Circumference of a Circle: With Application to the Theory of Atomic Structure. Phil. Mag. S 1904, 6 (7), 237–265.10.1080/14786440409463107Search in Google Scholar
4. Rutherford, E. The Scattering of α and β Particles by Matter and the Structure of the Atom. Phil. Mag. 1911, 21, 669–688.10.1080/14786440508637080Search in Google Scholar
5. Lewis, G. N. The Atom and the Molecule. J. Am. Chem. Soc. 1916, 38, 762–785; https://doi.org/10.1021/ja02261a002.Search in Google Scholar
6. Langmuir, I. The Arrangement of Electrons in Atoms and Molecules. J. Am. Chem. Soc. 1919, 41, 868–934; https://doi.org/10.1021/ja02227a002.Search in Google Scholar
7. Lewis, G. N. Valence and the Structure of Atoms and Molecules; American Chemical Society Monograph Series: New York, NY, USA, 1923.Search in Google Scholar
8. Zhao, L.; Schwarz, W. H. E.; Frenking, G. The Lewis Pair Bonding Model: The Physical Background a Century Later. Nat. Rev. Chem. 2019, 3, 35–47; https://doi.org/10.1038/s41570-018-0052-4.Search in Google Scholar
9. Langmuir, I. Types of Valence. Sci. 1921, 54, 54–67; https://doi.org/10.1126/science.54.1386.59.Search in Google Scholar PubMed
10. Sidgwick, N. V.; Powell, H. M. Bakerian Lecture: Stereochemical Types and Valency Groups. Proc. Roy. Soc. A 1940, 176, 153–180.10.1098/rspa.1940.0084Search in Google Scholar
11. Gillespie, R. J.; Nyholm, R. S. Inorganic Stereochemistry. Q. Rev. Chem. Soc. 1957, 11, 339; https://doi.org/10.1039/qr9571100339.Search in Google Scholar
12. Gillespie, R. J. Fifty Years of the VSEPR Model. Coord. Chem. Rev. 2008, 252, 1315–1327; https://doi.org/10.1016/j.ccr.2007.07.007.Search in Google Scholar
13. Pauling, L. The Shared-Electron Chemical Bond. Proc. Natl. Acad. Sci. U. S. A. 1928, 14, 359–362; https://doi.org/10.1073/pnas.14.4.359.Search in Google Scholar PubMed PubMed Central
14. Pauling, L. The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond. J. Am. Chem. Soc. 1931, 3225–3237; https://doi.org/10.1021/ja01360a004.Search in Google Scholar
15. Pauling, L.; Wheland, G. W. The Nature of the Chemical Bond. V. The Quantum-Mechanical Calculation of the Resonance Energy of Benzene and Naphthalene and the Hydrocarbon Free Radicals. J. Chem. Phys. 1933, 1, 362–374; https://doi.org/10.1063/1.1749304.Search in Google Scholar
16. Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach den Quantenmechanik. Z. Phys. 1927, 44, 455–472; https://doi.org/10.1007/bf01397394.Search in Google Scholar
17. Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960.Search in Google Scholar
18. Helgaker, T.; Jörgensen, P.; Olsen, J. Molecular Electronic Structure Theory; Wiley: Chichester, UK, 2000.10.1002/9781119019572Search in Google Scholar
19. Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models of Main-Group Compounds. Chem. Rev. 2019, 119, 8781–8845; https://doi.org/10.1021/acs.chemrev.8b00722.Search in Google Scholar PubMed
20. Frenking, G.; Shaik, S. The Chemical Bond – Fundamental Aspects of Chemical Bonding; Wiley VCH: Weinheim, Germany, 2014.10.1002/9783527664658Search in Google Scholar
21. Burdett, J. K. Chemical Bonds: A Dialog; Wiley: Chichester, England, 1997.Search in Google Scholar
22. Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376; https://doi.org/10.1103/revmodphys.34.326.Search in Google Scholar
23. Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Oxford University Press: USA, 1994.Search in Google Scholar
24. Frenking, G. The Influence of Quantum Theory on Chemistry. Pur. Appl. Chem. 2025, https://doi.org/10.1515/pac-2025-0536.Search in Google Scholar
25. Schwarz, W. H. E.; Frenking, G.; Pan, S. Clarification of Some Bonding Concepts: Virial Theorem, Electron Pair Repulsion, and Rotational Barriers. J. Comp. Chem. 2025, 46, e70085; https://doi.org/10.1002/jcc.70085.Search in Google Scholar PubMed PubMed Central
26. Ruedenberg, K. Atoms and Bonds in Molecules as Synergisms of Interactions Between Electrons and Nuclei. J. Chem. Phys. 2022, 157, 21090; https://doi.org/10.1063/5.0124417.Search in Google Scholar PubMed
27. Burrows, A.; Holman, J.; Parsons, A.; Pilling, G.; Price, G. Chemistry3- Introducing Inorganic, Organic and Physical Chemistry; Oxford University Press: Oxford, England, 2009.Search in Google Scholar
28. Raff, L. M. Principles of Physical Chemistry; Prentice Hall: Upper Saddle River, NJ, USA, 2001.Search in Google Scholar
29. Grinter, R. The Quantum in Chemistry: An Experimentalist’s View; Wiley: Chichester, England, 2005. Section 6.3.Search in Google Scholar
30. Keeler, J.; Wothers, P. Chemical Structure and Reactivity: An Integrated Approach, 2nd ed.; Oxford University Press: Oxford, 2014. Section 2.3.10.1093/hesc/9780199604135.001.0001Search in Google Scholar
31. Kragh, H. S. Niels Bohr and the Quantum Atom – The Bohr Model of Atomic Structure 1913-1925; Oxford University Press: Oxford, 2012.10.1093/acprof:oso/9780199654987.001.0001Search in Google Scholar
32. Scerri, E. S. The Periodic Table. Its Story and its Significance; Oxford University Press: Oxford, 2007.Search in Google Scholar
33. Nordholm, S. From Electronegativity Towards Reactivity – Searching for a Measure of Atomic Reactivity. Mol. 2021, 26, 3680–3704; https://doi.org/10.3390/molecules26123680.Search in Google Scholar PubMed PubMed Central
34. Eek, W.; Nordholm, S.; Bacskay, G. B. The Screened Atomic Potential – a Simple Explanation of the Aufbau Model. Chem. Educator 2006, 11, 235–242.Search in Google Scholar
35. Madelung, E. Die Mathematische Hilfsmittel der Physikers, 3rd ed.; Springer: Berlin, 1936; p. 359.10.1007/978-3-662-02177-4_2Search in Google Scholar
36. Schwarz, W. H. E.; Rich, R. L. Theoretical Basis and Correct Explanation of the Periodic System: Review and Update. J. Chem. Ed. 2010, 87, 435–443; https://doi.org/10.1021/ed800124m.Search in Google Scholar
37. Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, Quantum Mechanics, Vol. III; Addison-Wesley Publishing Company: Reading, MA, USA, 1965; pp. 10-1–10-12.Search in Google Scholar
38. Hellmann, H. Zur Rolle der Kinetischen Elektronenergie für die zwischen Atomäre Kräfte. Z. Phys. 1933, 85, 180–190; https://doi.org/10.1007/bf01342053.Search in Google Scholar
39. Nordholm, S. Analysis of Covalent Bonding by Non-Ergodic Thomas-Fermi Theory. J. Chem. Phys. 1987, 86, 363–369; https://doi.org/10.1063/1.452572.Search in Google Scholar
40. Nordholm, S.; Bäck, A.; Bacskay, G. B. The Mechanism of Covalent Bonding: Analysis Within the Hückel Model of Electronic Structure. J. Chem. Ed. 2007, 84, 1201–1203.10.1021/ed084p1201Search in Google Scholar
41. Nordholm, S.; Eek, W. Ergodicity and Rapid Electron Delocalization – the Dynamical Mechanism of Atomic Reactivity and Covalent Bonding. Int. J. Quant. Chem. 2011, 111, 2072–2088; https://doi.org/10.1002/qua.22490.Search in Google Scholar
42. Nordholm, S.; Bacskay, G. B. The Role of Quantum Dynamics in Covalent Bonding – a Comparison of Thomas-Fermi and Hückel Models. In Advances in Quantum Theory; Cotaescu, I. I., Ed.; InTech: Rijeka, Croatia, 2012; pp. 107–152.10.5772/36698Search in Google Scholar
43. Nordholm, S.; Bacskay, G. B. The Basics of Covalent Bonding in Terms of Energy and Dynamics. Mol. 2020, 25, 2667–2701; https://doi.org/10.3390/molecules25112667.Search in Google Scholar PubMed PubMed Central
44. Nordholm, S. Analysis of Bonding by Quantum Chemistry – Resolving Delocalization Stabilization in a Mechanistic Basis and New Hückel Model. J. Phys. Chem. A 2023, 3449–3471; https://doi.org/10.1021/acs.jpca.2c08497.Search in Google Scholar PubMed PubMed Central
45. Esterhuysen, C.; Frenking, G. The Nature of the Chemical Bond Revisited. an Energy Partitioning Analysis of Diatomic Molecules E2 (E = N-Bi, F-I), CO and BF. Theor. Chem. Acc. 2004, 111, 381–389; https://doi.org/10.1007/s00214-003-0535-2.Search in Google Scholar
46. Levine, D. S.; Head-Gordon, M. Clarifying the Quantum Mechanical Origin of the Covalent Bond. Nat. Commun. 2020, 11, 4893–4900; https://doi.org/10.1038/s41467-020-18670-8.Search in Google Scholar PubMed PubMed Central
47. Bacskay, G. B. Orbital Contraction and Covalent Bonding. J. Chem. Phys. 2022, 156, 204122. https://doi.org/10.1063.0090196.10.1063/5.0090196Search in Google Scholar PubMed
48. Bao, J. J.; Gagliardi, L.; Truhlar, D. G. Weak Interactions in Alkaline Earth Metal Dimers by Pair Density Functional Theory. J. Phys. Chem. Lett. 2019, 10, 799–805; https://doi.org/10.1021/acs.jpclett.8b03846.Search in Google Scholar PubMed
49. Bacskay, G. B. The Electronic Structure and Bonding in Some Small Molecules. Mol. 2025, 30, 1154–1175. https://doi.org/10.3390/molecules30051154.Search in Google Scholar PubMed PubMed Central
50. Boys, S. F. Electronic Wave Functions – I. A General Method of Calculation for the Stationary States of Any Molecular System. Proc. R. Soc. London Ser. A 1950, 200, 542–554.10.1098/rspa.1950.0036Search in Google Scholar
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles in the same Issue
- Frontmatter
- IUPAC Recommendations
- Experimental methods and data evaluation procedures for the determination of radical copolymerization reactivity ratios from composition data (IUPAC Recommendations 2025)
- IUPAC Technical Reports
- Kinetic parameters for thermal decomposition of commercially available dialkyldiazenes (IUPAC Technical Report)
- FAIRSpec-ready spectroscopic data collections – advice for researchers, authors, and data managers (IUPAC Technical Report)
- Review Articles
- Are the Lennard-Jones potential parameters endowed with transferability? Lessons learnt from noble gases
- Quantum mechanics and human dynamics
- Quantum chemistry and large systems – a personal perspective
- The organic chemist and the quantum through the prism of R. B. Woodward
- Relativistic quantum theory for atomic and molecular response properties
- A chemical perspective of the 100 years of quantum mechanics
- Methylene: a turning point in the history of quantum chemistry and an enduring paradigm
- Quantum chemistry – from the first steps to linear-scaling electronic structure methods
- Nonadiabatic molecular dynamics on quantum computers: challenges and opportunities
- Research Articles
- Alzheimer’s disease – because β-amyloid cannot distinguish neurons from bacteria: an in silico simulation study
- Molecular electrostatic potential as a guide to intermolecular interactions: challenge of nucleophilic interaction sites
- Photophysical properties of functionalized terphenyls and implications to photoredox catalysis
- Combining molecular fragmentation and machine learning for accurate prediction of adiabatic ionization potentials
- Thermodynamic and kinetic insights into B10H14 and B10H14 2−
- Quantum origin of atoms and molecules – role of electron dynamics and energy degeneracy in atomic reactivity and chemical bonding
- Clifford Gaussians as Atomic Orbitals for periodic systems: one and two electrons in a Clifford Torus
- First-principles modeling of structural and RedOx processes in high-voltage Mn-based cathodes for sodium-ion batteries
- Erratum
- Erratum to: Furanyl-Chalcones as antimalarial agent: synthesis, in vitro study, DFT, and docking analysis of PfDHFR inhibition
Articles in the same Issue
- Frontmatter
- IUPAC Recommendations
- Experimental methods and data evaluation procedures for the determination of radical copolymerization reactivity ratios from composition data (IUPAC Recommendations 2025)
- IUPAC Technical Reports
- Kinetic parameters for thermal decomposition of commercially available dialkyldiazenes (IUPAC Technical Report)
- FAIRSpec-ready spectroscopic data collections – advice for researchers, authors, and data managers (IUPAC Technical Report)
- Review Articles
- Are the Lennard-Jones potential parameters endowed with transferability? Lessons learnt from noble gases
- Quantum mechanics and human dynamics
- Quantum chemistry and large systems – a personal perspective
- The organic chemist and the quantum through the prism of R. B. Woodward
- Relativistic quantum theory for atomic and molecular response properties
- A chemical perspective of the 100 years of quantum mechanics
- Methylene: a turning point in the history of quantum chemistry and an enduring paradigm
- Quantum chemistry – from the first steps to linear-scaling electronic structure methods
- Nonadiabatic molecular dynamics on quantum computers: challenges and opportunities
- Research Articles
- Alzheimer’s disease – because β-amyloid cannot distinguish neurons from bacteria: an in silico simulation study
- Molecular electrostatic potential as a guide to intermolecular interactions: challenge of nucleophilic interaction sites
- Photophysical properties of functionalized terphenyls and implications to photoredox catalysis
- Combining molecular fragmentation and machine learning for accurate prediction of adiabatic ionization potentials
- Thermodynamic and kinetic insights into B10H14 and B10H14 2−
- Quantum origin of atoms and molecules – role of electron dynamics and energy degeneracy in atomic reactivity and chemical bonding
- Clifford Gaussians as Atomic Orbitals for periodic systems: one and two electrons in a Clifford Torus
- First-principles modeling of structural and RedOx processes in high-voltage Mn-based cathodes for sodium-ion batteries
- Erratum
- Erratum to: Furanyl-Chalcones as antimalarial agent: synthesis, in vitro study, DFT, and docking analysis of PfDHFR inhibition

