Abstract
The problem of micropolar fluid flow over a nonlinear stretching convective vertical surface in the presence of Lorentz force and viscous dissipation is investigated. Due to the nature of heat transfer in the flow past vertical surface, Cattaneo-Christov heat flux model effect is properly accommodated in the energy equation. The governing partial differential equations for the flow and heat transfer are converted into a set of ordinary differential equations by employing the acceptable similarity transformations. Runge-Kutta and Newton’s methods are utilized to resolve the altered governing nonlinear equations. Obtained numerical results are compared with the available literature and found to be an excellent agreement. The impacts of dimensionless governing flow pertinent parameters on velocity, micropolar velocity and temperature profiles are presented graphically for two cases (linear and nonlinear) and analyzed in detail. Further, the variations of skin friction coefficient and local Nusselt number are reported with the aid of plots for the sundry flow parameters. The temperature and the related boundary enhances enhances with the boosting values of M. It is found that fluid temperature declines for larger thermal relaxation parameter. Also, it is revealed that the Nusselt number declines for the hike values of Bi.
1 Introduction
Micropolar fluids has come into prominence because of the conventional Newtonian fluids cannot accurately represent the features of fluid flow in various engineering applications namely polymeric fluids, paints and colloidal solutions, biology etc. A class of fluids has also considering its microstructure is known as micropolar fluids. Micropolar fluids are physically represent fluids in which the deformation of the particles omitted in the fluids and consisting of a suspension of rigid, spherical particles in a viscous medium. Initially, Eringen [1, 2] has been reported an analysis of theory of micropolar fluids which provided a mathematical model for its non-Newtonian flows in his studies. An analysis of boundary-layer theory for a micropolar fluid has extended by Peddieson and McNitt [3]. Heat transfer flow in a polar fluid towards a non-isothermal stretching surface with suction and blowing have been numerically investigated by Hassanien and Gorla [4]. For the formulation of mathematic model they are utilizing the Erigen theory of micropolar fluids. Rama Subba Reddy [5] have investigated the problem of mixed convection boundary layer on unsteady micropolar flow over a vertical plate and reveals that the friction factor and rate of heat transfer enhances to the improve of buoyancy force. Hady [6] studied an analytical solution of heat transfer in micropolar fluid over a non-isothermal permeable stretching sheet. The flow characteristics of micropolar fluid in moving wedge and flat plate have been analyzed by Ishak et al. [7]. By the same authors [8] have presented to the heat transfer analysis on micropolar fluids in a stretching surface. Mixed convection flow of a micropolar fluid towards a non-linear stretching surface investigated Hayat et al. [9]. The series solution retained by imposing HAM to the transformed coupled non-linear ordinary differential equations. The problem of micropolar fluid filled a porous channel was discussed by Sajid et al. [10]. Heat transfer on micropolar fluid flow over a stretchable melting surface was discussed by Animasaun [11].
Magnetohydrodynamics (MHD) has several momentous applications in the fields of aerospace engineering, medicine and geo and astrophysics. Several equipments including turbulent pumps, bearings, MHD generators and boundary layer control flow are influenced due to the interaction between the electrically conducting liquid and magnetic field. Ashraf and Batool [12] studied the magnetohydrodynamic flow and heat transfer behavior of a micropolar fluid past a stretchable disk. It is predict that the fluid flow of magnetic field strengthen the skin friction coefficient. Mahmoud and Waheed [13] studied heat transfer flow in micropolar fluid through a stretching sheet in the presence of magnetic field. Heat generation effect on steady hydromagnetic flow of micropolar fluid over a moving surface was presented by Gnaneswara Reddy [14]. Viscous dissipation effect for the convection flow of a micropolar fluid towards a stretching surface is examined by El-Aziz [15]. Gnaneswara Reddy and Venugopal Reddy [16] have reported the interaction of Joule heating on magnetohydrodynamic peristaltic transport of a Nanofluid. The interaction of heat transfer and hydromagnetic on a rotating micropolar fluid was recently analyzed by Mehmood et al. [17]. Gnaneswarara Reddy [18, 19] have reported the effect of viscous dissipation on steady MHD flow over stretched surface. The peristaltic transport of Jeffrey nanofluid over an asymmetric channel with magnetic field investigated recently Gnaneswara Reddy and Makinde [20]. Makinde and Animasaun [21] have investigated the heat transfer analysis on MHD bioconvection of nanofluid in paraboloid of revolution. Koriko et al. [22] have studied the effect MHD micropolar fluid flow along a vertical surface.
The classical Fourier’s [23] heat conduction is amongst the best utilized models in classical physics and which is used for the description of heat transfer transport mechanism in various associated situations. The one of major limitation for parabolic energy equation for temperature is that unique disturbance and simultaneously it dispute the principle of causality throughout whole medium. Fourier’s law of heat conduction is modified in context of thermal relaxation by Cattaneo [24]. Hyperbolic type energy equation exists in presence of Cattaneo’s expression. Christov [25] improved the heat conduction analysis of Cattaneo [24] by introducing thermal relaxation time along with Oldroyd’s upper-convicted derivative, in order to attain the material invariance of the model. Cattaneo–Cheristov heat flux model is the modified Fourier’s form which gives thermal relaxation time. Cattaneo-Christov model with influence of thermal convection was studied by Straughan [26]. Uniqueness of Cattaneo-Christov heat flux model for flow of incompressible fluids has been analyzed Tibullo and Zampoli [27]. Han et al. [28] reported the Cattaneo-Christov heat flux model on boundary layer flow of a Maxwell fluid. Mustafa [29] investigated the interaction of Cattaneo–Christov heat flux model for rotating flow of a Maxwell fluid with heat transfer. The problem of Cattaneo-Christov heat flux model on Viscoelastic Flow over an exponentially stretching surface is recently discussed khan et al. [30]. Impact of temperature dependent thermal conductivity fluid and Cattaneo–Christov heat flux flow of over a surface is examined Hayat et al. [31].
In view of the above cited studies and applications, still no study on the Cattaneo-Christov heat flux and MHD convection flow of micropolar fluid towards nonlinear stretched surface. The convective condition is also considered in the energy boundary conditions. The dimensionless nonlinear partial differential equations are transformed into ordinary differential equations by utilizing suitable similarity transformations and are solved numerically. A detailed parametric study is presented graphically to explore the interaction of various controlling flow physical parameters on velocity, micro-rotation and temperature distribution. Also the friction factor and local Nusselt number are plotted and analyzed for emerging dynamical parameters.
2 Mathematical Analysis
Consider a two-dimensional free convection flow of a viscous and an incompressible electrically conducting micropolar fluid induced by a nonlinear stretching surface. The physical model of the present flow problem is shown in Fig. 1. It is also further considered a general power-law surface velocity distribution uw = axn with a > 0. There is a non-uniform applied magnetic field of strength B(x) =
and the relevant boundary conditions for the present model are
where the components u and v are the velocities along x-and y-axis respectively, k is the vortex viscosity, ρ is the fluid density, μ is the dynamic viscosity, g is the gravitational acceleration, β is the thermal expansion coefficient, v is the kinematic viscosity, y* =
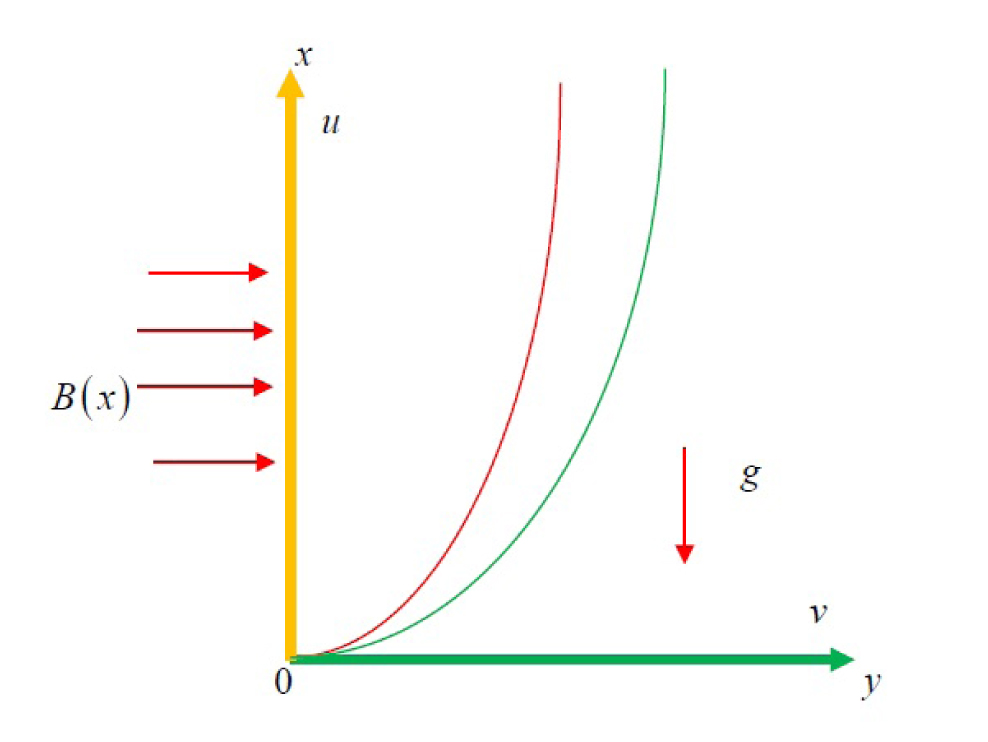
Schematic diagram of the flow problem
Define the following similarity transformations and variable quantities:
It is obvious that the continuity equation (1) is automatically satisfied. The remaining governing flow equations (2) – (4) and corresponding boundary conditions (5), which are reduced to the following dimensionless, coupled ordinary differential equations
and the reduced conditions are:
where primes indicates differentiation with respect to η, K the micro polar parameter, λ the mixed convection parameter, Grx the thermal buoyancy parameter, Rex the local Reynolds number, M the Hartman number, Pr the Prandtl number, y the thermal relaxation parameter, Ec the Eckert number, and Bi the Biot number.
For physical quantities of interest, the local friction factor coefficient Cf with surface shear stress τw and local Nusselt number Nux with surface heat flux qw are given by
where the quantities τw and qw are given by
By incorporating the similarity transformations and quantities in to Equations (11) and (12), the reduced dimensionless skin friction coefficient and local Nusselt number are given by
where Rex =
3 Numerical Solution
The final dimensionless ordinary differential equations (7) – (9) with the boundary restrictions (10) are not possible to find the exact solutions due to the equations are highly nonlinear and coupled. Hence there equations are resolved numerically with Runge-Kutta based shooting method. Initially, the set of nonlinear ordinary differential equations (7), (8) and (9) converted to first order ordinary differential equations, by using the following procedure:
with the corresponding boundary conditions
First guess the values of undefined initial conditions y3(0), y5(0) and y7(0) which are involved in equations (17) – (19). Once all initial conditions are found then we solve the equations (17) – (19) are integrated by using Runge-Kutta fourth order method with the successive iterative step length is 0.01.
The validation of the present obtained results for -f"(0) by comparing with the earlier published works when Pr = 1, ε = 0, and y = 0 is presented in Table 1. It can conclude a nice agreement of the present results with the existed literature of Cortell [32] and Waqas et al. [33]. This provides the validity of the present obtained results along with the accuracy of the numerical technique we used in the present study. It is seen that the friction factor is an enhancement for the uplifting values of M.
Comparative of the present numerical results of −f ″(0) for the variations of n and M with the published literature when Pr = 0.7, ϵ = 0, and y = 0.
| Cotell [32] | Waqas et al. [33] | Present results | ||
|---|---|---|---|---|
| 1 | 0.5 | 0.86595 | 0.86596 | 0.865956 |
| 1.0 | 1.09705 | 1.09705 | 1.097058 | |
| 2.0 | 1.75371 | 1.75372 | 1.753714 | |
| 3.0 | 2.74458 | 2.74459 | 2.744580 | |
| 2 | 0.5 | 0.95029 | 0.95028 | 0.950290 |
| 1.0 | 1.10152 | 1.10153 | 1.101523 | |
| 2.0 | 1.57268 | 1.57268 | 1.572680 | |
| 3.0 | 2.42941 | 2.42940 | 2.429416 |
4 Results and Discussion
The dimensionless velocity, micro-rotation velocity and temperature distributions are presented graphically in Figs. 2–14 to the effect of various pertinent dynamical parameters such as magnetic field parameter M, material parameter K, mixed convection parameter λ, boundary parameter m0, thermal relaxation parameter y, Prandtl number Pr, Eckert number Ec, and Biot number Bi. For numerical computations acquiring, we have utilize fixed values of the dimensionless numbers for this study: M = 1.0, K = 0.5, λ = 0.3, Pr = 2.0, Ec = 0.1, y = 0.5, m0 = 0.5, Bi = 0.5. The solid (Green color) and dashed (Red color) lines signify the profiles of linear and non-linear stretching surface respectively.
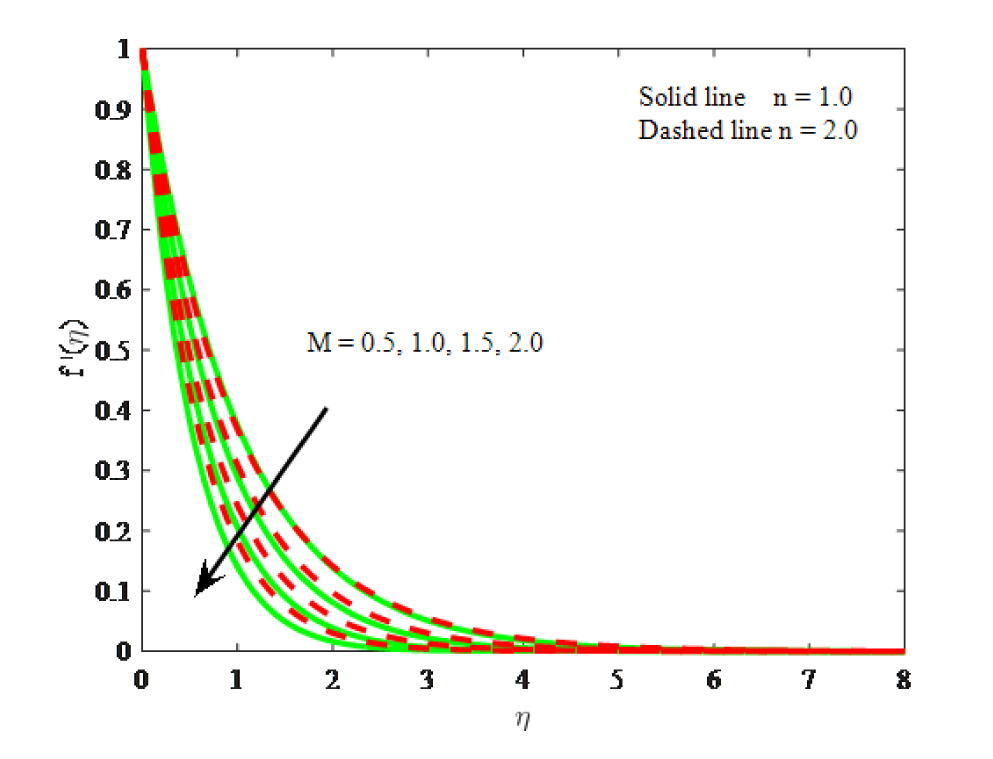
Impact of M on velocity
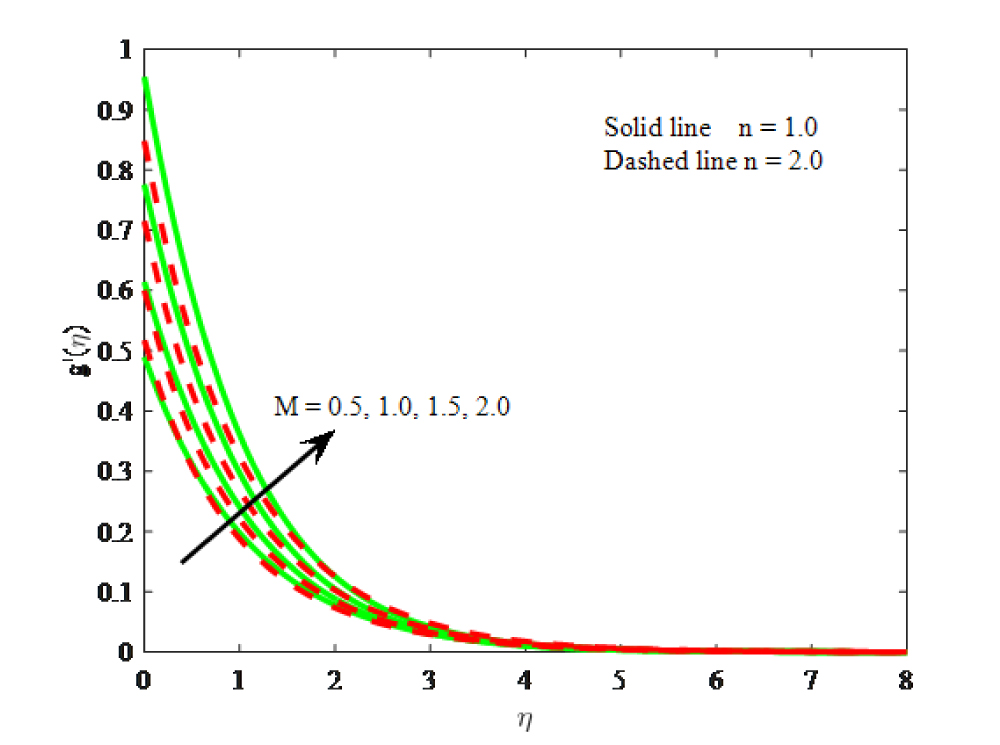
Impact of M on micro-rotation velocity
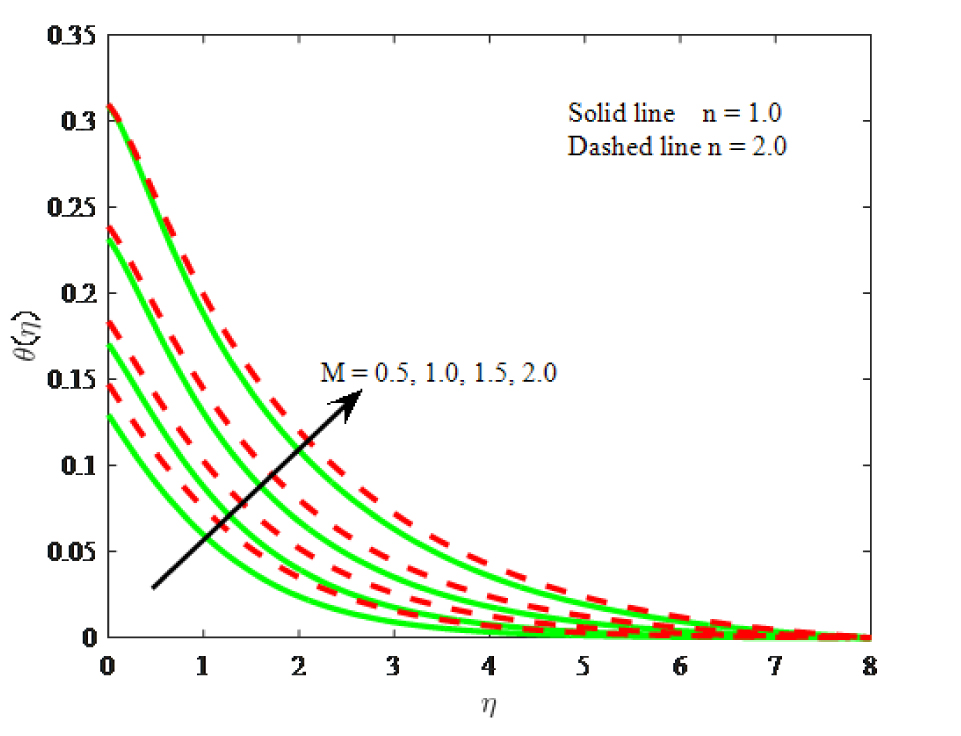
Impact of M on temperature
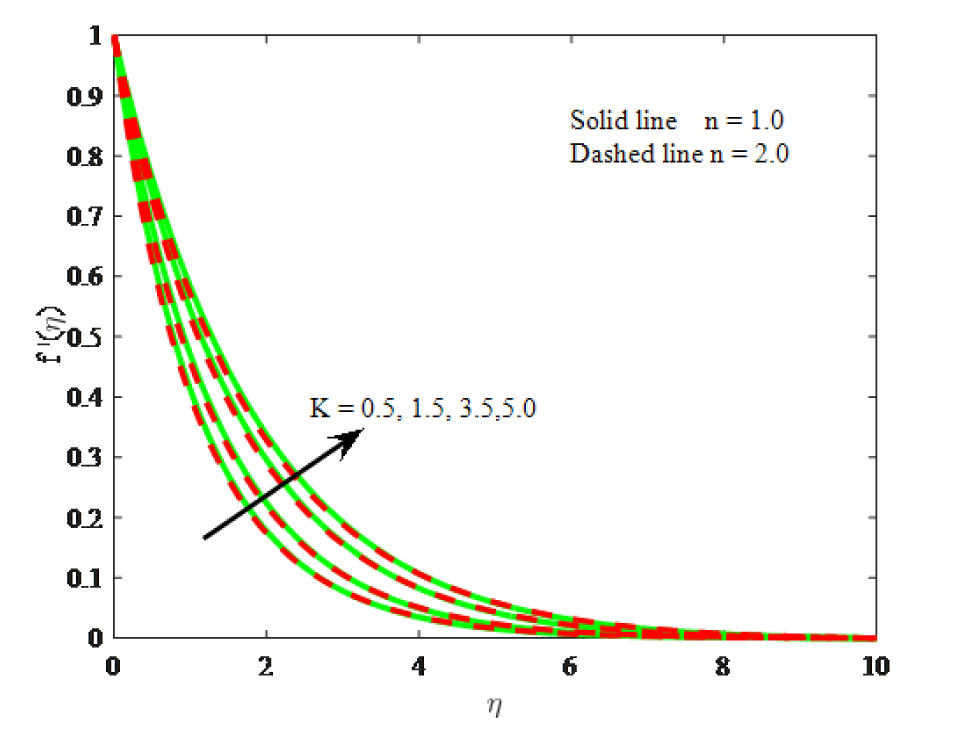
Impact of K on velocity
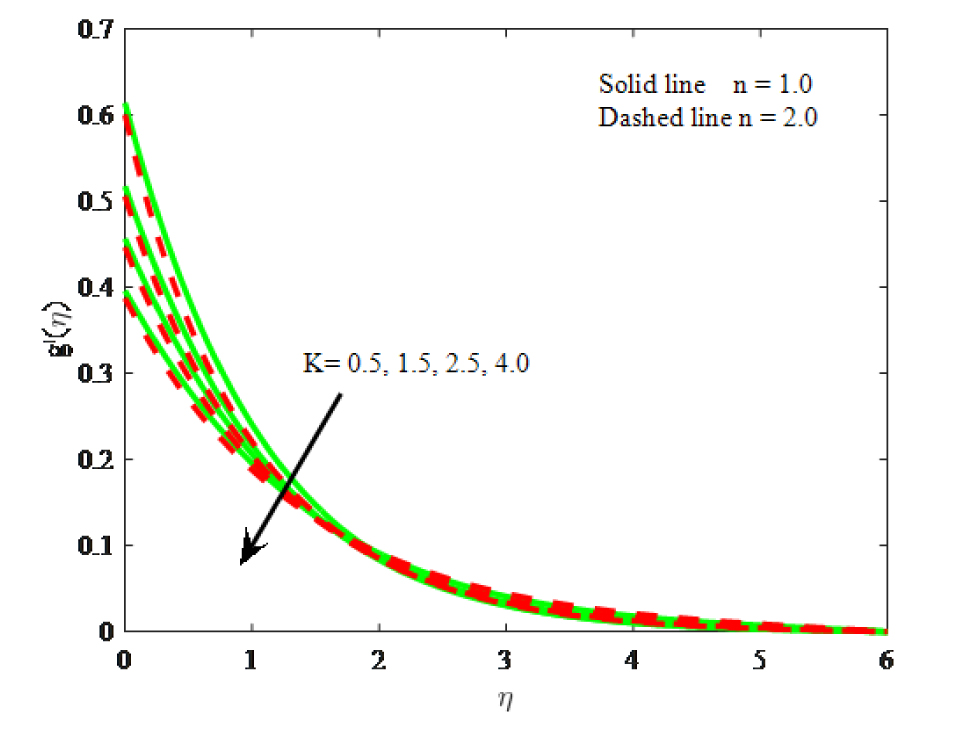
Impact of K on micro-rotation velocity
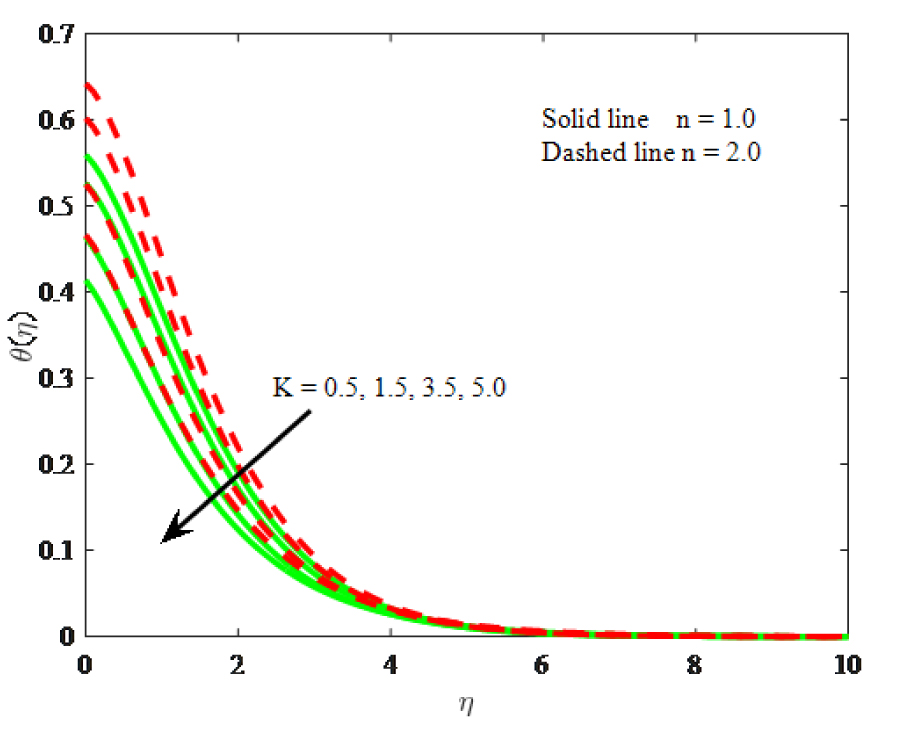
Impact of K on temperature
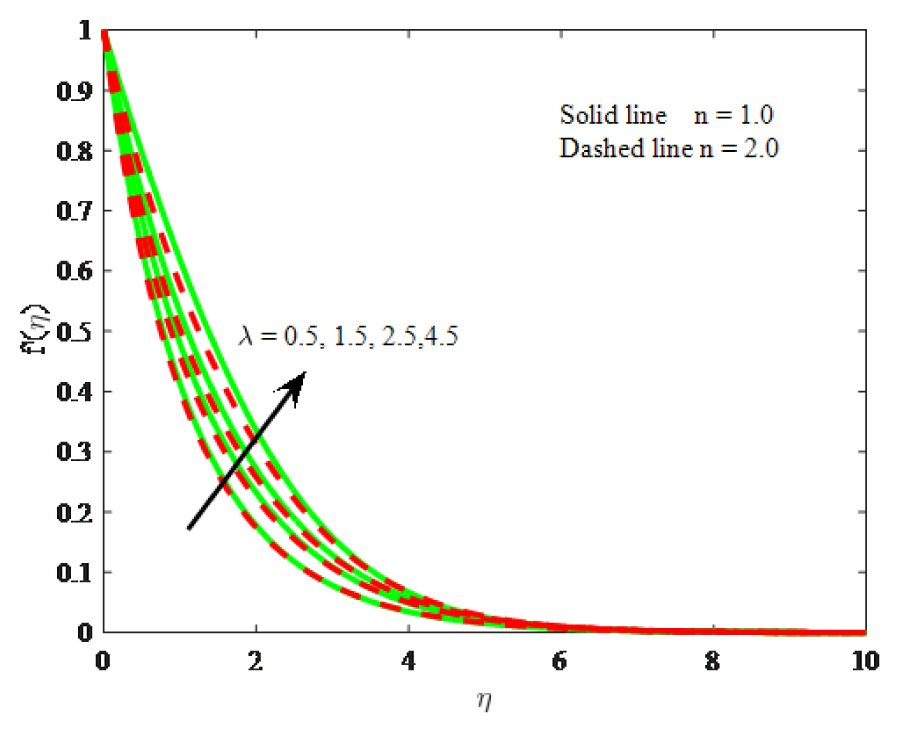
Impact of λ on velocity
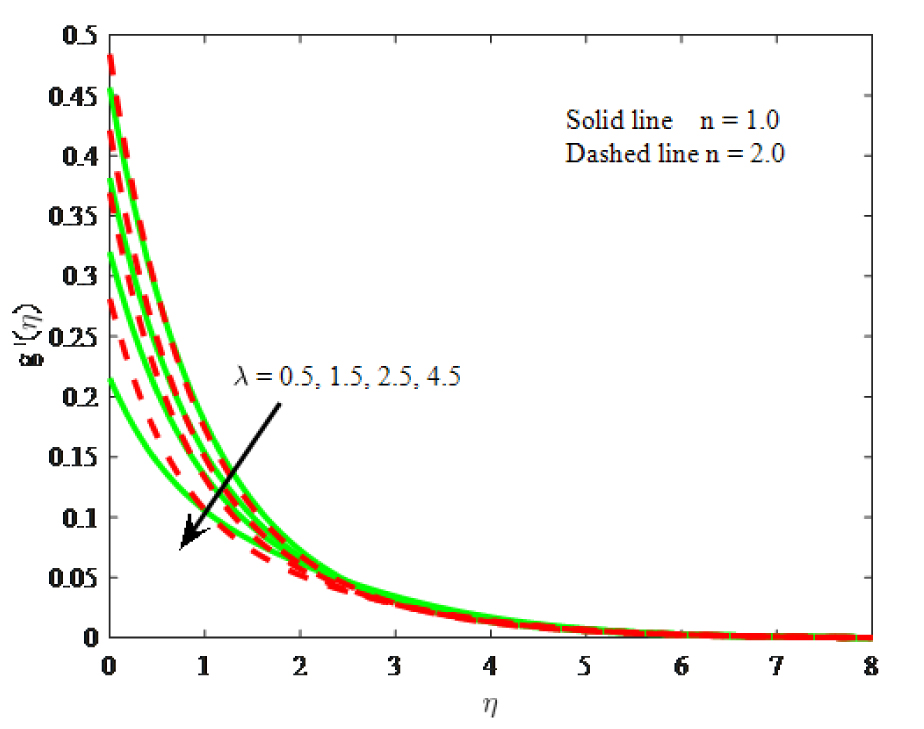
Impact of λ on micro-rotation velocity
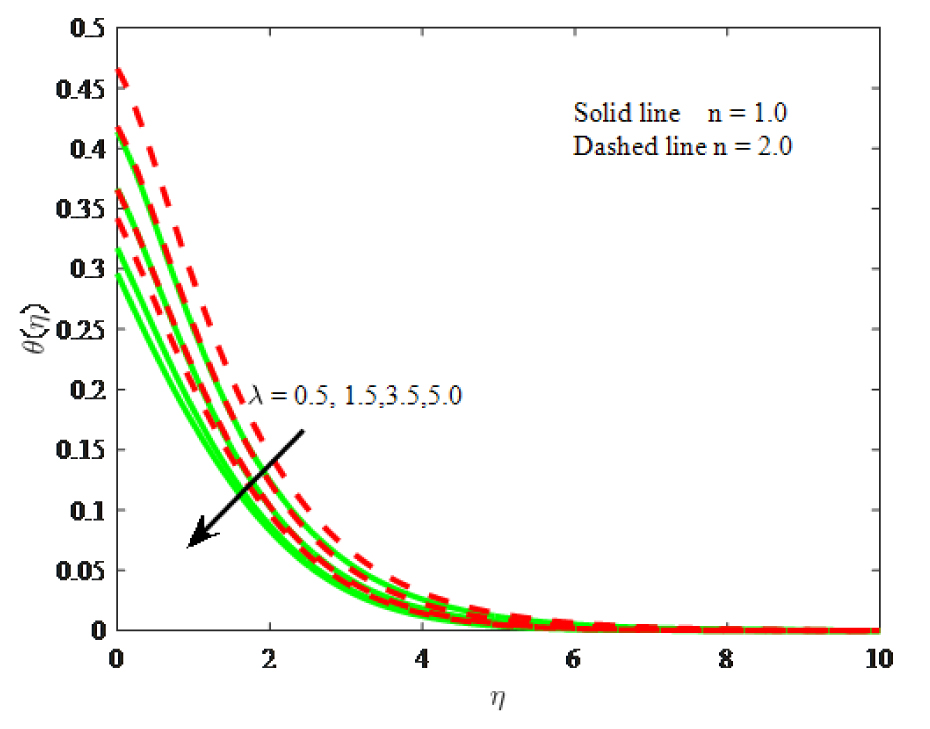
Impact of λ on temperature
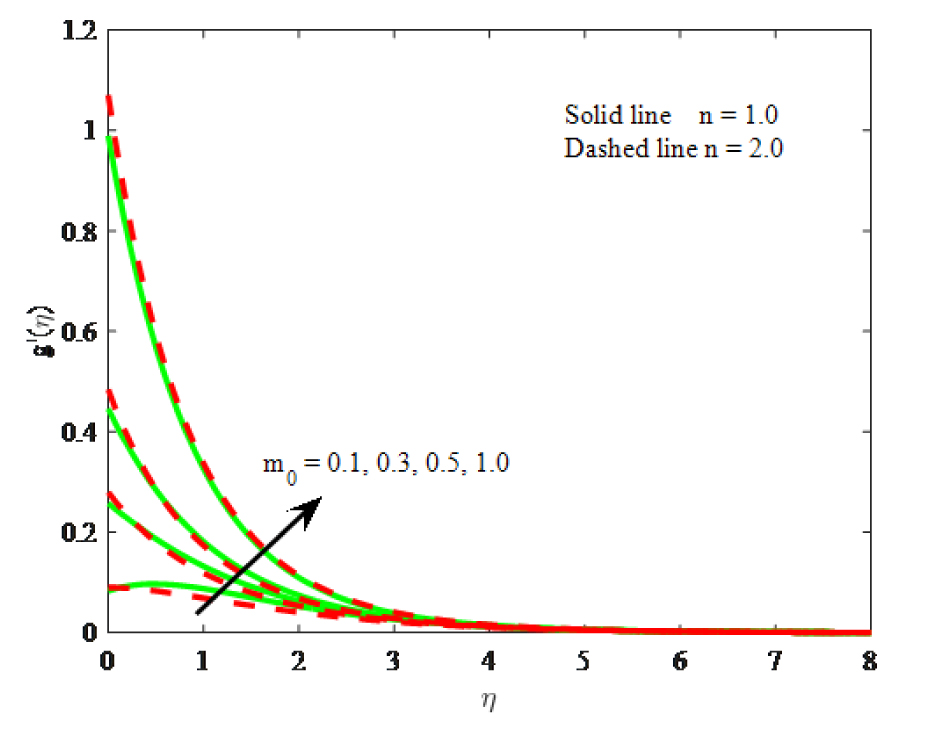
Impact of m0 on micro-rotation velocity
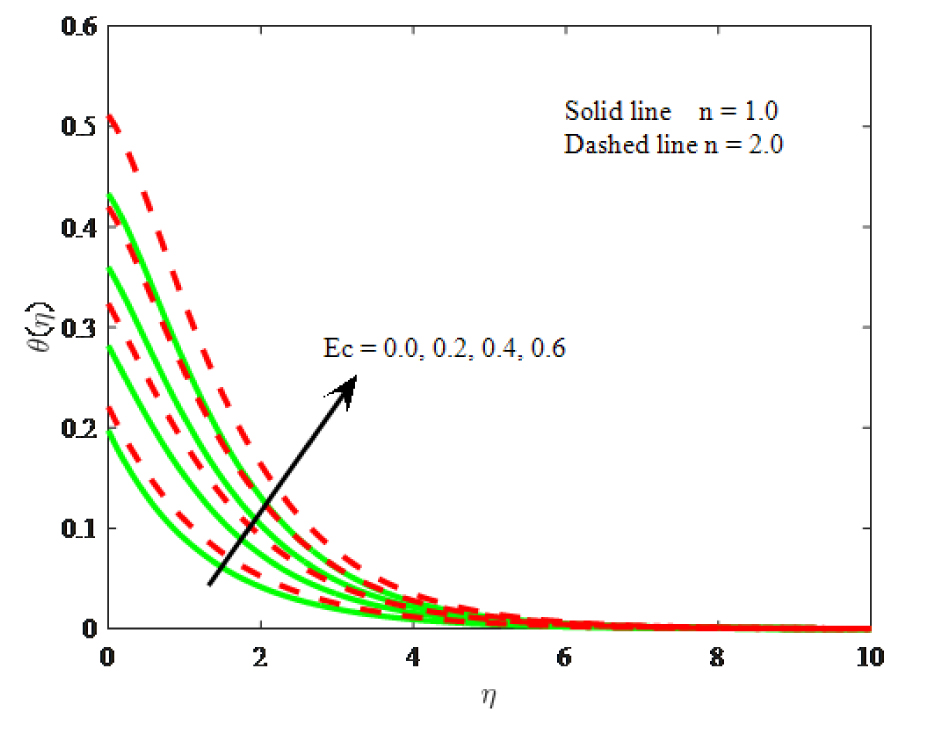
Impact of Ec on temperature
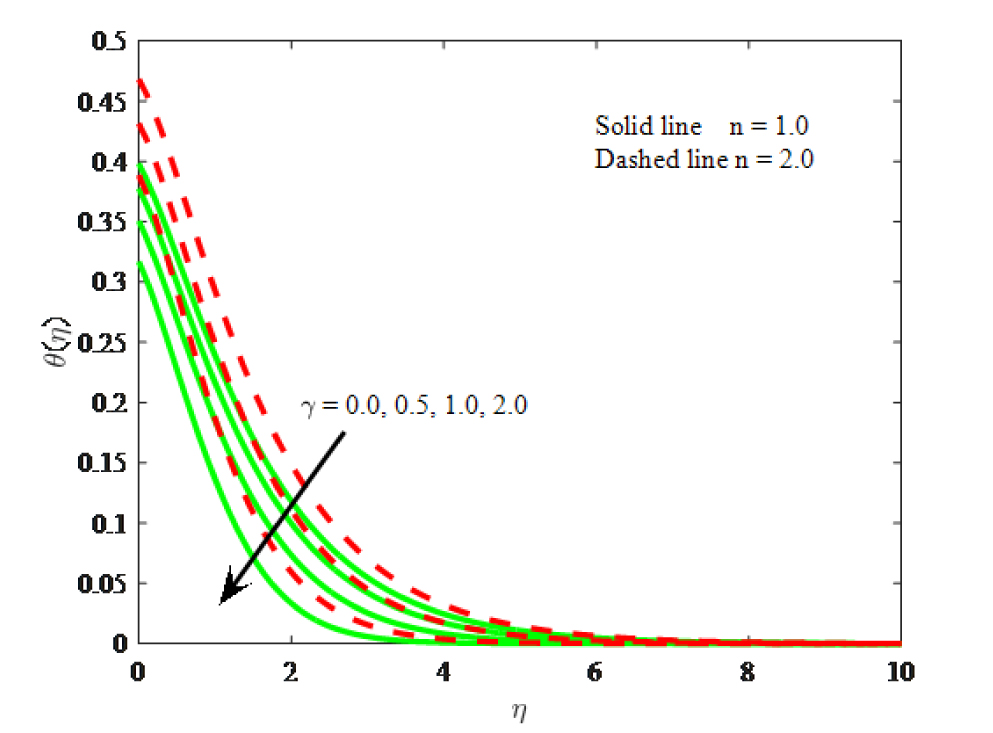
Impact of y on temperature
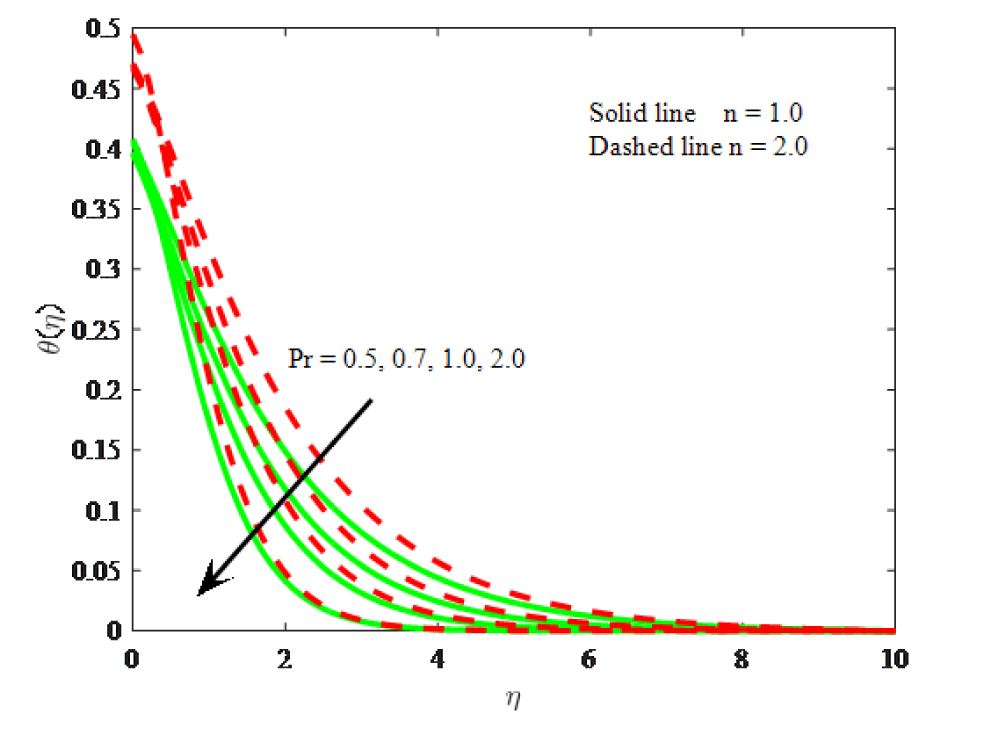
Impact of Pr on temperature
The influence of magnetic field parameter on velocity, mirco-rotation and dimensionless temperature are described in Figs. 2–4 respectively. It is revealed from Fig. 2 that for escalating values of magnetic field parameter decreases the magnitude of velocity distribution and reduced the related boundary layer thickness. This is due to an increase in magnetic field on the fluid flow produces a resistance fore and which is called the Lorentz force. Generally, escalating the values of Mgenerates Lorentz force in the flow, which is capable of declining the flow velocity by acting in the opposite direction of the flow. From Fig. 3 we can found that the mirco-rotation velocity distribution is rises with boosting values of M. The fluid temperature enhances with the boosting values of M and this is evident from Fig. 4. As a consequence, the heat will be generated in the flow field, due to which a hike in the fluid temperature is also perceived and simultaneously increased the thickness thermal boundary layer. Furthermore, the impact of magnetic field parameter on mirco-rotation and temperature is similar trend but the opposite for the velocity. It is further noticed that thermal and micro-rotation velocity boundary layers of linear stretching are low by the Lorentz force when compared with the non-linear stretching surface.
Figs. 5–7 depict the flow, micro-rotation velocity and temperature fields for different values of K. It is manifest that velocity distribution increased for higher values micropolar parameter. Because larger values of micropolar parameter which corresponds to the low viscosity and enhance the velocity. It can be found that initially angular velocity reduces by increasing of K while the opposite behavior to the free stream velocity. Temperature distribution is diminishes with the larger values of micropolar parameter. Furthermore, the micro-rotation velocity and energy boundary layers of linear stretching are opposite for the micropolar parameter when compared with the non-linear stretching surface.
Figs. 8– 10 illustrate the velocity, micro-rotation velocity and thermal distribution respectively for various values convection parameter λ. From Fig. 8, the velocity boosts with increasing values of mixed convection parameter λ. Because increase in mixed convection parameter to enhance the buoyancy force and this is evident in the progressive increase in the flow velocity. The angular velocity is decreases there is rise in the buoyancy parameter. It is noticed that the temperature diminishes with enhancing the mixed convection parameter λ. The impacts of micropolar parameter K and mixed convection parameter λ have similar on the three common profiles. The effect of boundary parameter m0 on the angular velocity is portrays in Fig. 11. The angular velocity is enhanced for larger boundary parameter m0.
Fig. 12 is drawn to observe the variation in temperature distribution under the action of Eckert number Ec. The temperature increases for larger values Eckert number. The increase in the buoyancy force due to an increase in the viscous dissipation parameter rise the temperature. Also, at this effect the fluid temperature is small for the linear while compared to the non-linear. Fig. 13 demonstrates the effect of thermal relaxation parameter (y) on dimensionless fluid temperature profile. It can be seen that the fluid temperature and energy boundary layer diminished for larger values of thermal relaxation parameter y. This is due to reason that for larger thermal relaxation parameter the particles of the material require more opportunity to transfer heat to its adjacent particles. It is found that the heat transfers quickly throughout the objects for y = 0. Also, the temperature is lower for Cattaneo-Christov heat flux model when compared with Fourier’s law. In addition, the energy boundary layer thickness is higher for the non-linear stretching surface. Fig. 14 is sketched to study the impact of Prandtl number Pr on dimensionless temperature field. It is concluding that both the thermal boundary layer thickness and temperature diminish to the enhancing values of Prandtl number (Pr = 0.5, 0.7, 1.0, 2.0). It is also seen that accumulation perception temperature is considerable larger at Pr = 0.5 when compared with Pr = 2.0. This is due to reason that thermal diffusivity increases for diminishing values of Pr. Fig. 15 is plotted for the variations of Biot number Bi on temperature profiles. Increasing values of Biot number boosts the dimensionless temperature. Because the Biot number contains the heat transfer coefficient and which enhances for larger values of Biot number. It is further revealed that the temperature is high for the non-linear stretching surface.
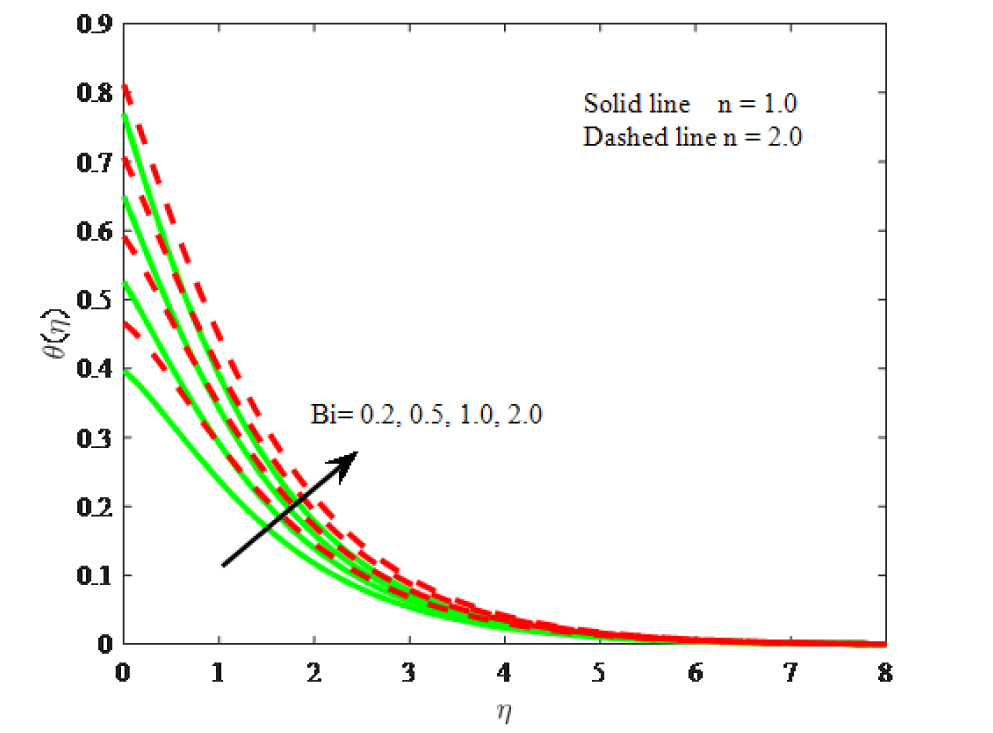
Impact of Bi on temperature
Finally, the physical quantities of interest such as the skin friction coefficient and Nusselt number for sundry values of dimensionless governing flow field parameters are plotted in Figs. 16 – 18 respectively. Impacts of Ec and Bi on skin friction coefficient is depicted in Fig. 16. It is found that raising the values of Biot number and Eckert number enhances the friction factor. Also, the friction factor is more for the linear stretching surface. Fig. 17 displays the impact of Ec and Bi on the Nusselt number. It is revealed that the Nusselt number declines for the hike values of Bi. Fig. 18 illustrates the variation in Nusselt number for the influence of Ec and y. It is manifest that boosting values of diminishes the reduced Nusselt number.
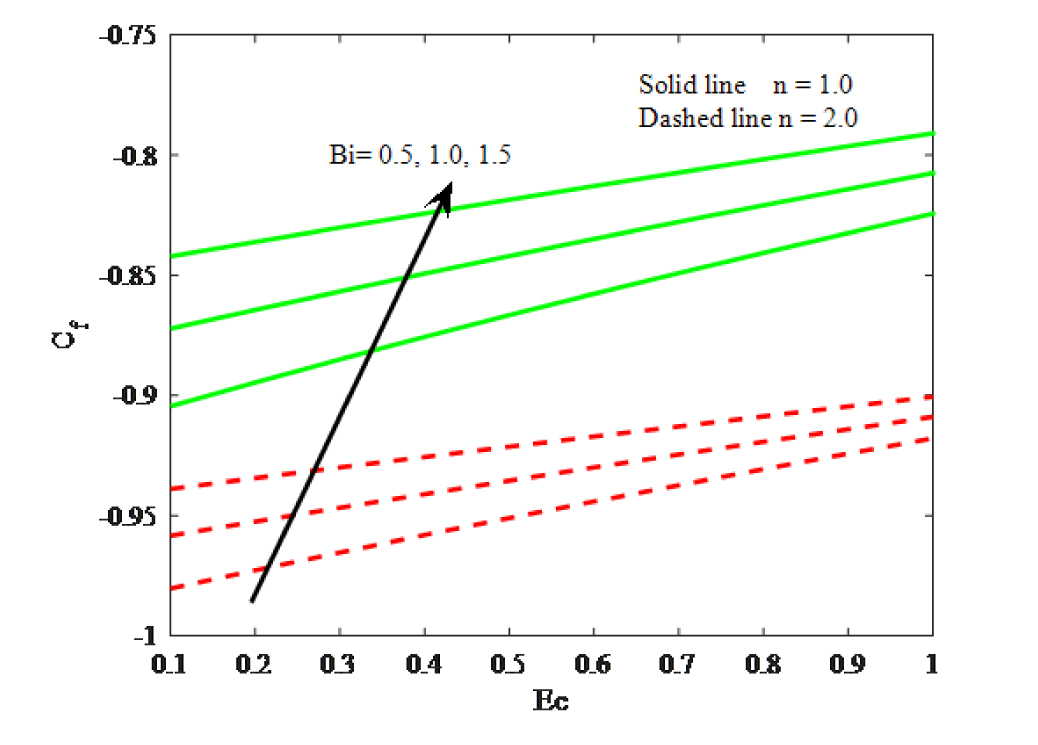
Impacts of Ec and Bi on friction factor
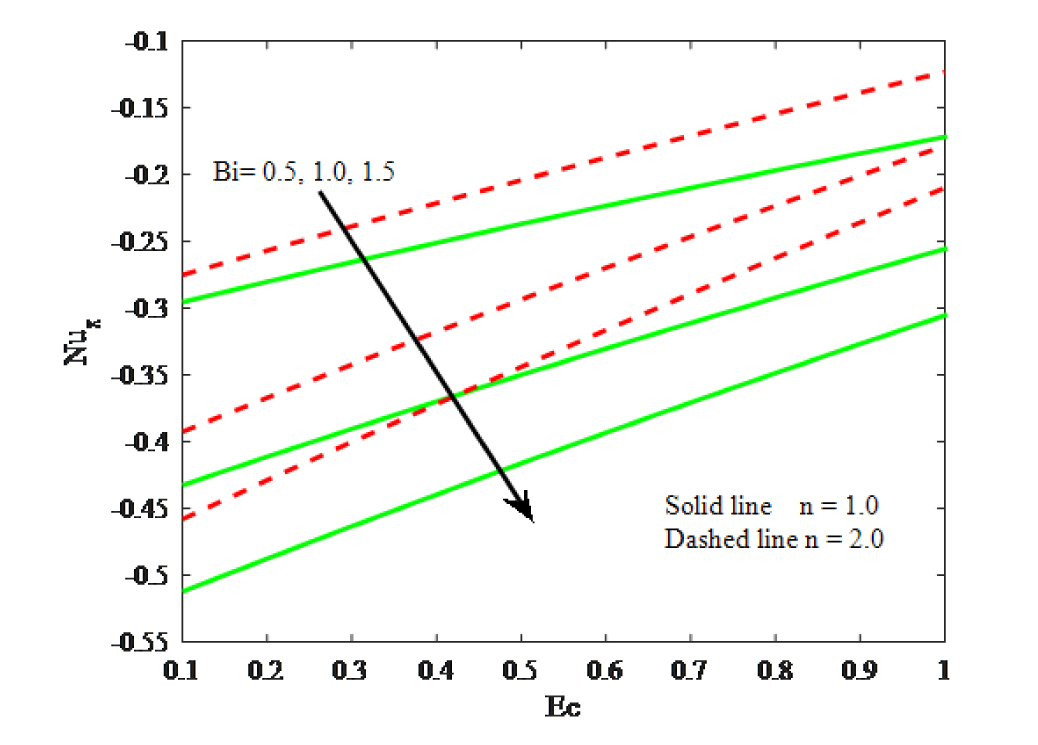
Impacts of Ec and Bi on Nusselt number.
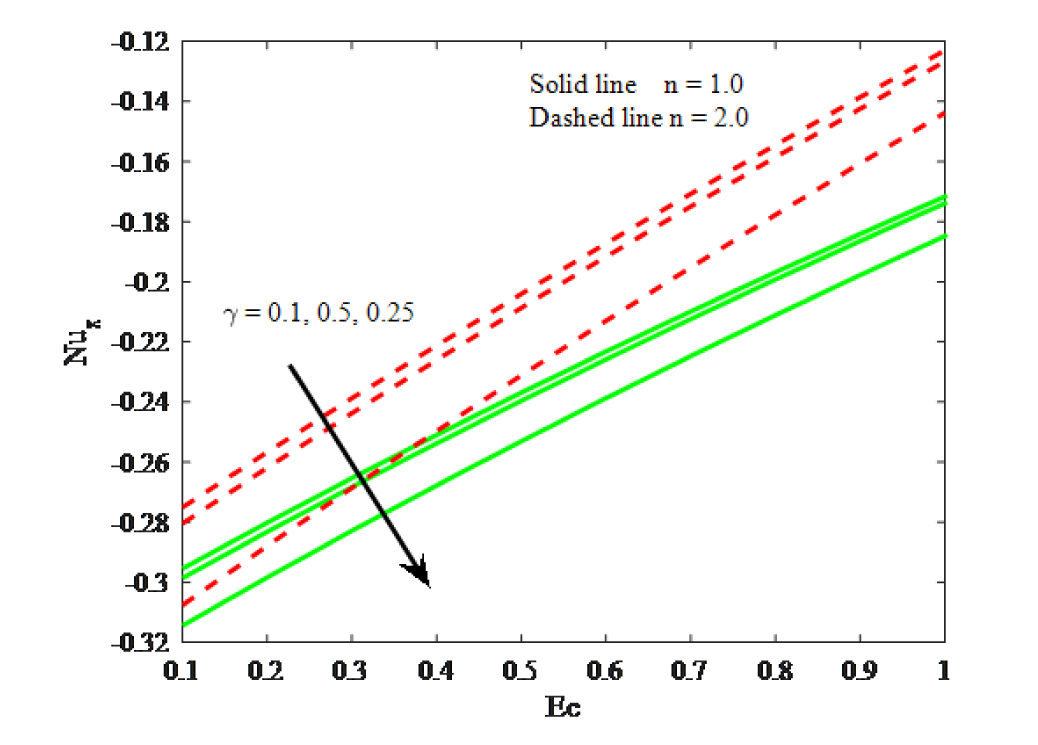
Impacts of Ec and y on Nusselt number
5 Conclusions
A Numerical investigation has been carried out for analyzing MHD flow of a micropolar fluid past a nonlinear stretched sheet with Cattaneo-Christov heat flux and viscous dissipation. The dimensionless governing equations are solved numerically using Runge–Kutta based shooting technique. The main findings of the present study are:
Temperature increases with the hike values of M.
Thermal and micro-rotation velocity boundary layers of linear stretching are low by the Lorentz force when compared with the non-linear stretching surface.
Fluid velocity enhanced for escalating values of K.
Angular velocity is enhanced for larger boundary parameter m0.
Temperature and energy boundary layer diminished for larger values of thermal relaxation parameter y.
Nusselt number declines for the hike values of Bi.
Acknowledgement
The author wishes to express their sincere thanks to reviewers for their precious suggestions and comments to improve the presentation of the manuscript.
Nomenclature
- Bi
Biot number
- Cf
local friction factor co-efficient
- cp
specific heat at constant pressure
- Ec
Eckert number
- Grx
thermal buoyancy parameter
- g
Gravitational acceleration
- hf
convective heat transfer coefficient
- j
Micro inertia
- K
micropolar parameter
- κ
vortex viscosity
- k∞
thermal conductivity of ambient fluid
- M
Hartman number
- m0
boundary parameter
- N
micro-rotation velocity
- Nux
Nusselt number
- Pr
Prandtl number
- qw
surface heat flux
- Rex
local Reynolds number
- T
temperature of the fluid
- Tf
convective fluid temperature
- Tw
stretching sheet temperature
- T∞
temperature far away from the stretching sheet
- u
velocity of the fluid along the x-axis
- ν
velocity of the fluid along the y-axis
- ρ
fluid density
- μ
dynamic viscosity
- β
thermal expansion coefficient
- v
kinematic viscosity
- y*
spin gradient viscosity
- α
thermal diffusivity
- λ
mixed convection parameter or buoyancy parameter
- y
thermal relaxation parameter
- τw
surface shear stress
References
[1] A.C. Eringen, Theory of micropolar fluids, J. Math. Anal. Appl. 16 (1966) 1–18.10.21236/AD0469176Suche in Google Scholar
[2] A.C. Eringen, Theory of thermomicrofluids, J. Math. Anal. Appl. 38 (1972) 480–4 96.10.1016/0022-247X(72)90106-0Suche in Google Scholar
[3] Peddieson J, McNitt RP. Boundary-layer theory for a micropolar fluid. Recent Adv. Eng. Sci. 1970; 5: 405–426.Suche in Google Scholar
[4] Hassanien IA, Gorla RSR. Heat transfer to a micropolar fluid from a non-isothermal stretching sheet with suction and blowing. Acta Mech. 1990; 84: 191–199.10.1007/BF01176097Suche in Google Scholar
[5] Gorla RSR. Unsteady mixed convection in micropolar boundary layer flow on a vertical plate. Fluid Dynamics Research. 1995; 15(4): 237–250.10.1016/0169-5983(95)94957-USuche in Google Scholar
[6] Hady FM. Short communication on the solution of heat transfer to micropolar fluid from a non-isothermal stretching sheet with injection. Int. J. Num. Meth. Heat Fluid Flow. 1996; 6: 99–104.10.1108/09615539610131299Suche in Google Scholar
[7] Ishak A, Nazar R, Pop I. Moving wedge and flat plate in a micropolar fluid. Int.J. Eng. Sci. 2006; 44: 1225–1236.10.1016/j.ijengsci.2006.08.005Suche in Google Scholar
[8] Ishak A, Nazar R, Pop I. Heat transfer over a stretching surface with variable surface heat flux in micropolar fluids. Phys. Lett. A. 2008; 372: 559–561.10.1016/j.physleta.2007.08.003Suche in Google Scholar
[9] Hayat T, Abbas Z, Javed T. Mixed convection flow of a micropolar fluid over a non-linear stretching sheet. Phys. Lett. A. 2008; 372: 637–647.10.1016/j.physleta.2007.08.006Suche in Google Scholar
[10] Sajid M, Abbas Z, Hayat T. Homotopy analysis for boundary layer flow of a micropolar fluid through a porous channel. Appl. Math. Model. 2009; 33: 4120–4125.10.1016/j.apm.2009.02.006Suche in Google Scholar
[11] Isaac Lare Animasaun, Melting heat and mass transfer in stagnation point micropolar fluid flow of temperature dependent fluid viscosity and thermal conductivity at constant vortex viscosity, Journal of the Egyptian Mathematical Society 25 (2017) 79–85.10.1016/j.joems.2016.06.007Suche in Google Scholar
[12] Ashraf M, Batool K. MHD flow and heat transfer of a micropolar fluid over a stretchable disk. J. Theor. Appl. Mech. 2013; 51(1): 25-38.Suche in Google Scholar
[13] Mahmoud MAA, Waheed SE. MHD flow and heat transfer of a micropolar fluid over a stretching surface with heat generation (absorption) and slip velocity. J Egypt Math Soc. 2012; 12: 20–27.10.1016/j.joems.2011.12.009Suche in Google Scholar
[14] Gnaneswara Reddy M. Heat generation and radiation effects on steady MHD free convection flow of micropolar fluid past a moving surface. Journal of Computational and Applied Research in Mechanical Engineering. 2013; 2(2): 1–10.Suche in Google Scholar
[15] El-Aziz M.A. Mixed convection flow of a micropolar fluid from an unsteady stretching surface with viscous dissipation. J. Egypt. Math. Soc. 2013; 21:385–394.10.1016/j.joems.2013.02.010Suche in Google Scholar
[16] Gnaneswara Reddy M, Venugopal Reddy K. Influence of Joule heating on MHD peristaltic flow of a nanofluid with compliant walls. Procedia Engineering. 2015; 127: 1002–1009.10.1016/j.proeng.2015.11.449Suche in Google Scholar
[17] Mehmood R, Nadeem S, Masood S. Effects of transverse magnetic field on a rotating micropolar fluid between parallel plates with heat transfer. J. Magn.Magn. Mater. 2016; 401: 1006–1014.10.1016/j.jmmm.2015.10.102Suche in Google Scholar
[18] Gnaneswara Reddy M. Effects of Thermophoresis, viscous dissipation and Joule heating on steady MHD flow over an inclined radiative isothermal permeable surface with variable thermal conductivity. Journal of Applied Fluid Mechanics. 2014; 7(1): 51–61.Suche in Google Scholar
[19] Gnaneswara Reddy M. Influence of thermal radiation, viscous dissipation and hall current on MHD convection flow over a stretched vertical flat plate. Ain Shams Engineering Journal. 2014; 5: 169–175.10.1016/j.asej.2013.08.003Suche in Google Scholar
[20] Gnaneswara Reddy M, Makinde OD. Magnetohydrodynamic peristaltic transport of Jeffrey nanofluid in an asymmetric channel. Journal of Molecular Liquids. 2016; 223: 1242–1248.10.1016/j.molliq.2016.09.080Suche in Google Scholar
[21] Makinde OD, Animasaun IL, Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. International Journal of Thermal Sciences. 2016; 109: 159–171.10.1016/j.ijthermalsci.2016.06.003Suche in Google Scholar
[22] Olubode Kolade Koriko, Tosin Oreyeni, Adeola John Omowaye, Isaac Lare Animasaun, Homotopy Analysis of MHD Free Convective Micropolar Fluid Flow along a Vertical Surface Embedded in Non-Darcian Thermally-Stratified Medium, Open Journal of Fluid Dynamics, 2016, 6, 198–221.10.4236/ojfd.2016.63016Suche in Google Scholar
[23] Fourier JBJ. Theorie Analytique De La Chaleur, Paris, 1822.10.1017/CBO9780511693229Suche in Google Scholar
[24] Cattaneo C. Sulla conduzione del calore, Atti Semin Mat. Fis. Univ. Modena Reggio Emilia.1948; 3: 83–101.10.1007/978-3-642-11051-1_5Suche in Google Scholar
[25] Christov CI. On frame indifferent formulation of the Maxwell-Cattaneo model of finite speed heat conduction. Mech. Res. Commun. 2009; 36: 481–486.10.1016/j.mechrescom.2008.11.003Suche in Google Scholar
[26] Straughan B. Thermal convection with the Cattaneo-Christov model. Int. J. Heat Mass Transf. 2010; 53: 95–98.10.1016/j.ijheatmasstransfer.2009.10.001Suche in Google Scholar
[27] Tibullo V, Zampoli V. A uniqueness result for the Cattaneo-Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011; 38: 77–99.10.1016/j.mechrescom.2010.10.008Suche in Google Scholar
[28] Han S, Zheng L, Li C, Zhang X. Coupled flow and heat transfer in Viscoelastic fluid with Cattaneo–Christov heat flux model. Appl. Math. Lett. 2014; 38: 87–93.10.1016/j.aml.2014.07.013Suche in Google Scholar
[29] Mustafa M. Cattaneo–Christov heat flux model for rotating flow and heat transfer of upper-convicted Maxwell fluid. AIP Adv. 2015; 5: 047109.10.1063/1.4917306Suche in Google Scholar
[30] Ahmad Khan J, Mustafa M, Hayat T, Alsaedi A. Numerical study of Cattaneo-Christov heat Flux model for Viscoelastic flow due to an exponentially stretching surface. PLoS ONE. 2015; 10(9): e0137363. 10.1371/journal.pone.0137363.Suche in Google Scholar PubMed PubMed Central
[31] Hayat T, Khan MI, Farooq M, Alsaedi A, Waqas M, Yasmeen T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016; 99: 702–710.10.1016/j.ijheatmasstransfer.2016.04.016Suche in Google Scholar
[32] Cortell R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007; 184: 864–873.10.1016/j.amc.2006.06.077Suche in Google Scholar
[33] Waqas M, Farooq M, Khan M, Alsaedi A, Hayat T, Yasmeen T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. International Journal of Heat and Mass Transfer. 2016; 102: 766–772.10.1016/j.ijheatmasstransfer.2016.05.142Suche in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- A New Computational Technique for the Generation of Optimised Aircraft Trajectories
- Modelling of Imbibition Phenomena in Fluid Flow through Heterogeneous Inclined Porous Media with different porous materials
- Double dispersion effects on non-Darcy free convective boundary layer flow of a nanofluid over vertical frustum of a cone with convective boundary condition
- F1 style MGU-H applied to the turbocharger of a gasoline hybrid electric passenger car
- Nonlinear control systems - A brief overview of historical and recent advances
- An analytical method with Padé technique for solving of variational problems
- Influence of Lorentz force, Cattaneo-Christov heat flux and viscous dissipation on the flow of micropolar fluid past a nonlinear convective stretching vertical surface
Artikel in diesem Heft
- Frontmatter
- A New Computational Technique for the Generation of Optimised Aircraft Trajectories
- Modelling of Imbibition Phenomena in Fluid Flow through Heterogeneous Inclined Porous Media with different porous materials
- Double dispersion effects on non-Darcy free convective boundary layer flow of a nanofluid over vertical frustum of a cone with convective boundary condition
- F1 style MGU-H applied to the turbocharger of a gasoline hybrid electric passenger car
- Nonlinear control systems - A brief overview of historical and recent advances
- An analytical method with Padé technique for solving of variational problems
- Influence of Lorentz force, Cattaneo-Christov heat flux and viscous dissipation on the flow of micropolar fluid past a nonlinear convective stretching vertical surface


