Abstract
In this paper, a numerical analysis is performed to investigate the effects of double dispersion and convective boundary condition on natural convection flow over vertical frustum of a cone in a nanofluid saturated non-Darcy porous medium. In addition, Brownian motion and thermophoresis effects have taken into consideration, and the uniform wall nanoparticle condition is replaced with the zero nanoparticle mass flux boundary condition to execute physically applicable results. For this complex problem, the similarity solution does not exist and hence suitable non-similarity transformations are used to transform the governing equations along with the boundary conditions into non-dimensional form. The Bivariate Pseudo-Spectral Local Linearisation Method (BPSLLM) is used to solve the reduced non-similar, coupled partial differential equations. To test the accuracy of proposed method, the error analysis and convergence tests are conducted. The effect of flow influenced parameters on non-dimensional velocity, temperature, nanoparticle volume fraction, regular concentration field as well as on the surface drag, heat transfer, nanoparticle and regular mass transfer rates are analyzed.
1 Introduction
Several studies have been reported in the literature by focusing on combined heat and mass transfer in Darcian porous media. However, Darcy law is reasonable for the flows through porous media with low permeability. At higher flow rates, there is a departure from the linear law and inertial effects become important and it can be considered through an additional velocity square term in the momentum equation, which is known as Forchheimer’s extension of Darcy’s law. A detailed review of convective heat and mass transfer in Darcian and non-Darcian porous media, to mention few, can be found in Nield and Bejan [1], Murthy et al. [2], Kairi and Murthy [3] and Nield and Kuznetsov [4] (also see the citations therein). In recent years, free and mixed convective heat transfer in nanofluids using an approach of a thermal or momentum boundary layer is an emerging area of research due to the high thermal conductivity of nanofluids. Initially, the term nanofluid suggested by Choi [5] and it describes as a liquid suspension containing nanometer-sized particles. Experimental studies have shown that the thermal conductivity of the base fluid enhanced by 10-50% with a small volumetric fraction of nanoparticles (Das [6], Xuan and Li [7], Eastman et al. [8]). One can find a basic theory and mathematical modeling of nanofluids in the book by Das et al. [9] and a paper by Buongiorno [10]. A literature review on the heat transfer enhancement by nanofluids including two different nanofluid models has been presented by Das et al. [11], Kakac and Pramuanjaroenkij [12], and Nield and Bejan [1]. The analytical investigation of free convection flow of nanofluid saturated porous medium with thermophoresis and Brownian motion has been given by Nield and Kuznetsov [13,14].
The study of both free and mixed convective flows over a full cone and vertical frustum of a cone has been presented by various researchers because of its real time applications in engineering and industrial problems such as cooling of electronic gadgets, heat exchangers, etc. The problem of free convective flow over a vertical frustum of a cone has been investigated by Na and Chiou [15] in two cases: (i) frustum of a cone with uniform wall temperature, and (ii) frustum of a cone subjected to constant wall heat flux. A non-similar boundary layer analysis for the double diffusive convection over vertical wavy frustum of a cone in porous media has been examined by Cheng [16]. By using Forchheimer-extended Darcy law, Noghrehabadi et al. [17] examined the free convective flow near a vertical cone embedded in a nanofluid saturated porous medium. Patrulescu et al. [18] studied the mixed convective boundary layer flow of a nanofluid over vertical truncated cone by employing Tiwari-Das nanofluid model. Different real time applications have been suggested by several authors to investigate the convective flows over vertical frustum of a cone/full cone (to mention few, see Shinmura [19], Hamilton et al. [20], McCutcheon et al. [21] and Nakamura et al. [22]).
It is seen from the literature that the uniform wall temperature or flux conditions does not valid in some industrial and engineering systems. For instance, material processing, geothermal systems, and in the design of thermal insulation, it has been observed that free convection can induce thermal stresses that lead to critical structural damage in the piping systems of nuclear reactors. To over come this, the heat transfer analysis with more realistic and general representation in the form of convective boundary condition attracted the interest of many researchers (see Aziz [23]). This type of analysis frequently appears in engineering and industrial processes such as transpiration cooling process, material drying, etc. Makinde and Aziz [24] numerically investigated the influence of convective boundary condition on MHD mixed convective heat and mass transfer along a vertical plate embedded in a porous medium and reported that the velocity and temperature enhance with an increase of the convective heat transfer parameter. The effect of magnetic field on free convective and thermally stratified flow of a nanofluid in non-Darcy porous medium under convective boundary condition has been studied by Murthy et al. [25].
The effects of thermal and solutal dispersion in non-Darcy porous medium are essential due to the existence of inertia effects (see Nield and Bejan [1]). Kairi et al. [26] studied the thermal and solutal dispersion effects on non-Darcy free convective flow of a non-Newtonian fluid from a vertical flat plate with uniform wall temperature and concentration and showed that the heat transfer rate enhances with an enhancement in thermal dispersion parameter in both the aiding and opposing flow cases. Telles and Trevisan [27] presented the hydrodynamic dispersion effect on free convective heat and mass transfer near to vertical surfaces in a porous medium. The effects of double dispersion and variable viscosity on free convection flow of non-Newtonian fluid with heat and mass transfer over a vertical cone embedded in a non-Darcy porous medium has been presented by Kairi [28]. RamReddy [29] examined the thermal and solutal dispersion effects on free convection heat and mass transfer flow over a vertical cone and showed that the skin friction coefficient, Nusselt number and Sherwood numbers increase with the increase of thermal dispersion parameter.
According to the author’s knowledge, the present study has not been discussed in the literature. The non-similarity solutions obtained by using Bivariate Pseudo-Spectral Local Linearization Method (BPSLLM), have been presented to investigate the effects of thermal dispersion, solutal dispersion, non-Darcy parameter and Biot number on non-dimensional flow, heat and mass transfer characteristics through graphs.
2 Analysis
Consider the steady, laminar two-dimensional natural convection heat and mass transfer over a vertical frustum of a cone embedded in a nanofluid saturated non-Darcy porous medium as shown in Fig.1. The geometry of the problem is chosen such that x̄-axis is along the surface and ȳ-axis normal to the surface of vertical frustum of a cone with the origin O at the vertex of the full cone. Let x̄0 is the distance of the leading edge of the vertical frustum of a cone measured from the origin O. The solutal concentration on the surface of the vertical frustum of a cone is C̄w, while the temperature, solutal concentration and the nanoparticle volume fraction of nanofluid at ambient medium are T̄∞, C̄∞, and φ̄∞ respectively. The zero nanaoparticle mass flux boundary condition
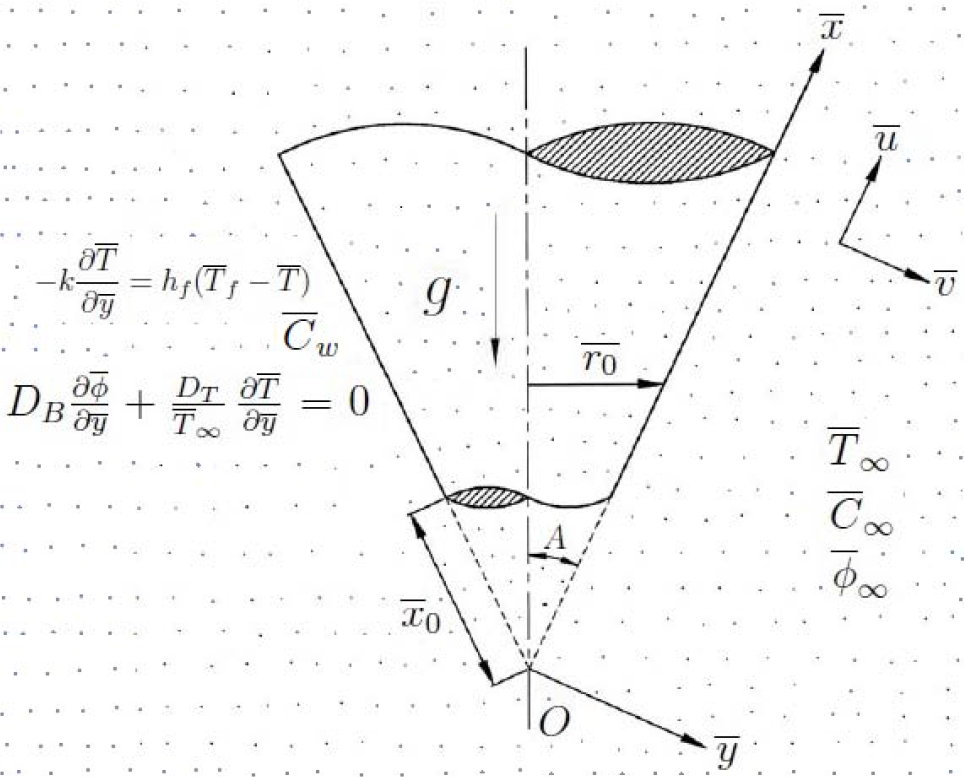
Geometry of the problem
Implementing the boundary layer and Oberbeck-Boussinesq approximations, the governing equations with momentum equation based on the Darcy-Forchheimer model (see Nield and Bejan [1]), can be written as:
where ū and v̄ are the velocity components along the x̄ and ȳ axes, respectively, T̄ is the temperature, φ̄ is the nanoparticle volume fraction, C̄ is the solutal concentration, g is the gravitational acceleration, Kp is the permeability, b is the empirical constant associated with the Forchheimer porous inertia term, and ε is the porosity. Further, d is the pore diameter,
The boundary conditions are
where hf is the convective heat transfer coefficient and the subscripts w and ∞ indicate the conditions at the wall, and at the outer edge of the boundary layer respectively.
Introducing the following dimensionless variables
where
Using the above non-similar variables (7) into Eqs. (1)-(5) along with the stream function ψ such that
where
The boundary conditions become
where the prime indicates differentiation with respect to η,
The shearing stress, local heat, nanoparticle and regular mass fluxes to indicate the surface drag, the heat, nanoparticle and regular mass transfer rates, respectively, can be obtained from
where ke = (k + kd) and De = (Dm + Dd) are the effective thermal and solutal conductivities of the porous medium, in which kd and Dd are the dispersion thermal and solutal conductivities.
The non-dimensional shear stress
where
3 Bivariate pseudo-spectral local linearisation method
Initially, Motsa [31] introduced the Local Linearisation Method (LLM) to find the solution of a coupled non-linear system of ordinary differential equations. Later, Motsa and Animasaun [32] extended this LLM along with the spectral collocation method to find the solution of the system of partial differential equations in both the space and time directions. Now, we present a bivariate pseudo-spectral local linearisation method (BPSLLM) to find the solution of the governing system of nonlinear partial differential equations (8)-(11) together with the boundary conditions (12) in three steps: (i) first we use an innovative linearisation and decoupling technique based on the quasi-linearisation technique to linearise all the equations(8)-(11) together with the boundary conditions (12) about one dependent variable at a time in the sequential order f, θ, γ and S, (ii) next we use Chebyshev pseudo-spectral collocation method to convert the resulting system of the iterative sequence of linearized partial differential equations into a system of linear algebraic equations in a matrix form, and (iii) finally we solve the system of equations iteratively in matrix form by taking a reasonable initial approximations.
First, we linearise the Eqs. (8)-(11) about f, θ, γand S, respectively, gives
where
Next, the pseudo-spectral collocation method is employed to discretize both the η and ξ domains. Before the numerical method is applied, the domains of η and ξ respectively are transformed to [-1, 1] and [-1, 1] under suitable linear transformations. For numerical implementation, the semi-infinite domain is truncated to η ∈ [0, η∞] and transformed to ζ ∈ [-1, 1]. Similarly, ξ ∈ [0, ξ∞] is transformed to τ ∈ [-1, 1]. In this process, η∞ is a limited value that is proposed to aid the numerical method at infinity and ξ∞ is the largest value of ξ used in the numerical simulations. Further, the Chebyshev-Gauss-Lobatto type of discretization points used in this study, are given below
The approximate solutions are assumed to be defined in terms of bivariate Lagrange interpolation polynomial of the form
which interpolates f (η, ξ) at the collocation points defined by equation (19). Similar expressions are used to define approximate functions for θ ( η, ξ) , γ(η, ξ) and S(η, ξ). The functions Lm(ζ ) and Lj(τ) are known as the characteristic Lagrange cardinal polynomials. Following [333435], we define the derivatives of the unknown functions with respect to η and ξ at the collocation points ζk and τi as follows:
where di,j (i,j = 0, 1,..., Nτ) are entries of the standard Chebyshev differentiation matrix
Similar expressions are obtained for derivatives of the other dependent variables with respect to η and ξ. Applying the pseudo-spectral method in both η and ξ gives
where
Equations (25) can be written in matrix form
for i = 0, 1,..., M, and where
The matrix form of Eqs. (26)-(28) can be obtained in a similar manner. To obtain the approximate solutions, the system of equations in matrix form solved iteratively by starting with a suitable initial approximations.
4 Results and Discussion
In this section, we present the numerical results obtained by solving Eqs. (8)-(11) using the method discussed in the last section for various values of physical parameters. The present computational work has been carried by taking the number of collocation points in η-direction Nx = 60, ξ -direction Nτ = 15, and Lx = 20 and Lt = 2 are used to aid the numerical approximations at infinity in η and ξ directions, respectively. We remark that the BPSLLM algorithm has been implemented in MATLAB machine software. To test the convergence of iteration scheme, we take the norm of difference in the values of two successive iterations. The algorithm is assumed to have converged when the norms are less than a given tolerance level (є = 10-10). The error norms at (r + 1)th iteration are defined as
Figures 2a-2d depict the variation of the norm of residual errors of the four governing equations (8)-(11) across ξ at different iterations levels of the BPSLLM. It can be seen from Figs. 2a-2d that the residual errors decrease with an increase in the number of iterations in all cases. This is an indication for convergence of the solutions. Furthermore, the small residual errors, which are obtained after a few iterations, are a clear sign of the accuracy of the solution method used to solve the governing PDEs. The residual error results validate the accuracy of the results generated in this study.
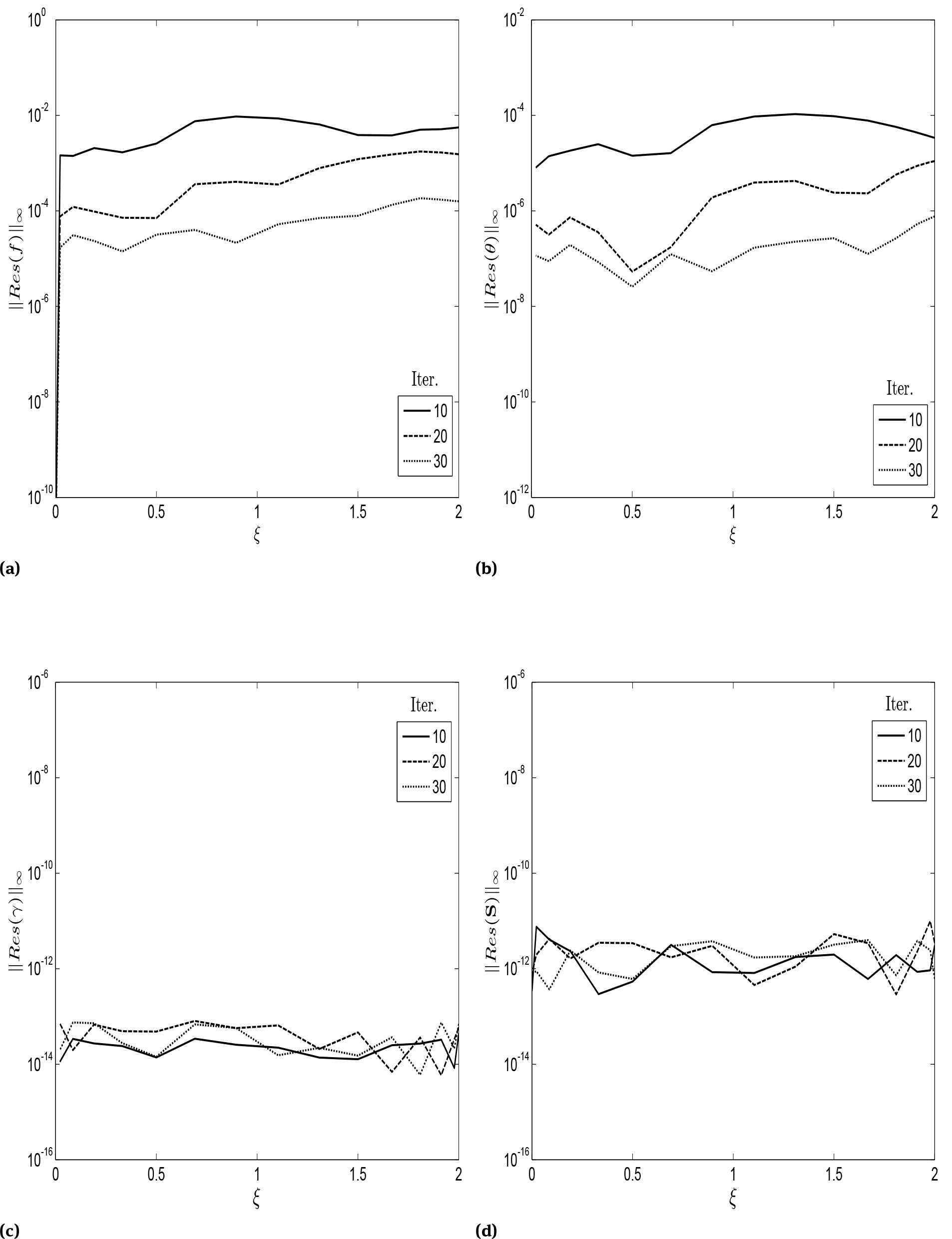
Residual error over iterations when Pr = 1.0, Sc = 0.6, Gr = 1.0, ε = 1.0, Da = 0.5, Fs = 1.0, Bi = 1.0, Ds = 0.2, Dc = 0.3, Nr = 0.5, Nc = 1.0, Le = 10, Nb = 0.2 and Nt = 0.3
The values of non-dimensional velocity, temperature, nanoparticle volume fraction and regular concentrations along with the skin friction coefficient, heat transfer, nanoparticle and regular mass transfer rates have been computed and presented graphically. In order to analyze the effects of non-Darcy parameter, Biot number, thermal and solutal dispersions on the flow profiles, the computations are carried out for the values of Pr = 1.0, Sc = 0.6, Le = 10.0, Nc = 1.0, Nr = 0.5, Gr = 5.0, ε = 0.8, Da = 0.5, Nt = 0.5 and Nb = 0.2. These values are fixed through the entire discussion unless specified separately. The current results of the skin friction f″(ξ, 0) and Nusselt number -θ′(ξ, 0) at ξ = 0 are compared with the results reported by Na and Chiou [15], Kays and Crawford [36], Lin and Chen [37] and Yih [38]. These comparisons are found to be in very good agreement as shown in Table 1.
Comparison values of f″(0, 0) and -θ′(0, 0) when Nt = 0.0, Nc = 0.0, Nr = 0.0, Sc = 1.0, Le = 1.0, 0.0 < Nb ≪ 1.0, Gr = 1.0, ε = 1.0, Da = 1.0, Ds = 0.0, Dc = 0.0, Bi ≫ 1.0.
| f″(0, 0) | -θ′(0, 0) | ||||||
|---|---|---|---|---|---|---|---|
| Pr | [38] | Present | [15] | [36] | [37] | [38] | Present |
| 0.1 | 1.2144 | 1.21446092 | - | 0.1640 | 0.1627 | 0.1629 | 0.16275771 |
| 1.0 | 0.9084 | 0.90819121 | 0.4010 | 0.4010 | 0.4009 | 0.4012 | 0.40103314 |
| 10.0 | 0.5927 | 0.59283234 | 0.8269 | 0.8270 | 0.8258 | 0.8266 | 0.82684304 |
| 100.0 | 0.3559 | 0.35587198 | 1.5493 | 1.5500 | 1.5490 | 1.5493 | 1.54948223 |
| 1000.0 | 0.2049 | 0.19648946 | - | 2.8000 | 2.8035 | 2.8035 | 2.79895143 |
The effects of mono-diffusion and double-diffusion of regular and nanofluids on the dimensionless velocity, temperature, nanoparticle volume fraction and regular concentration are depicted in Figs. 3a-3d. It is identified that the non-dimensional velocity and temperature are higher for mono-diffusion and double-diffusion nanofluids than regular fluids in the respective boundary layers. As expected that, the nanoparticle volume fraction of mono-diffusion regular fluid (Nr = Nb = Nt = Nc = 0) is zero. Also, it can be seen that the regular concentration is higher for regular fluids in the both mono and double diffusion. The similar observations have been reported by Akbar et al. [39] where they analyzed the effects of double-diffusive on the steady boundary layer flow of a nanofluid over a porous stretching surface.
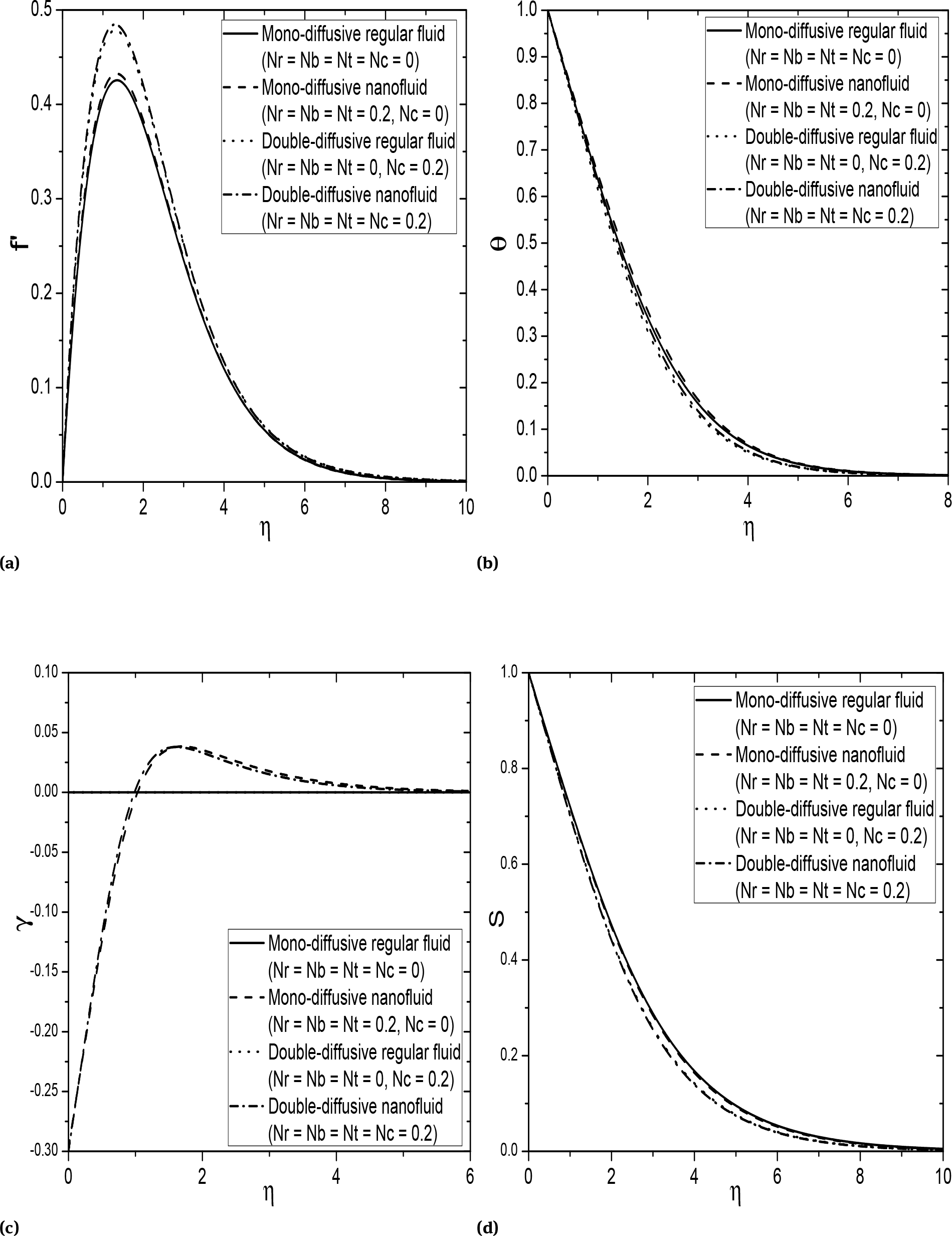
Effects of mono- and double-diffusion of regular and nanofluids on dimensionless (a) velocity, (b) temperature, (c) nanoparticle concentration and (d) regular concentration for ξ = 1.5, Fs = 0.5, Bi = 1.0, Ds = 0.2, Dc = 0.3.
4.1 Effects of non-Darcy parameter (Fs) and Biot number (Bi)
The variation of the dimensionless velocity, temperature, nanoparticle volume fraction and regular concentration shown in Figs. 4a-4d for different values of non-Darcy parameter (Fs) and Biot number (Bi ), respectively. In these figures, all the other parameters are taken to be fixed. It is observed that, an increase in the Biot number leads to increase the momentum and thermal boundary layer thickness and decrease the nanoparticle and regular concentration boundary layer thickness. We can see that, the velocity and nanoparticle volume fraction profiles decrease with the non-Darcy parameter, when it rises from Fs = 0 (Darcy flow) to Fs = 1 (non-Darcy flow). Conversely, non-Darcy parameter Fs enhance the temperature, and regular concentration profiles. The reason for the above behavior is that, the enhancement of non-Darcy parameter, i.e., Forchheimer term increase the pressure drop related to drag force. That is, for a fixed velocity with large Forchheimer’s coefficient produce a large pressure drop due to drag forces. In the same way, when the non-Darcy parameter increases with a fixed pressure drop, velocity would decreases. This relation between the non-Darcy term and velocity is shown in Fig.4a. The same behavior has been reported by Cheng et al. [40] where they studied non-Darcy effects on natural convection in a saturated porous medium using experimental setup.
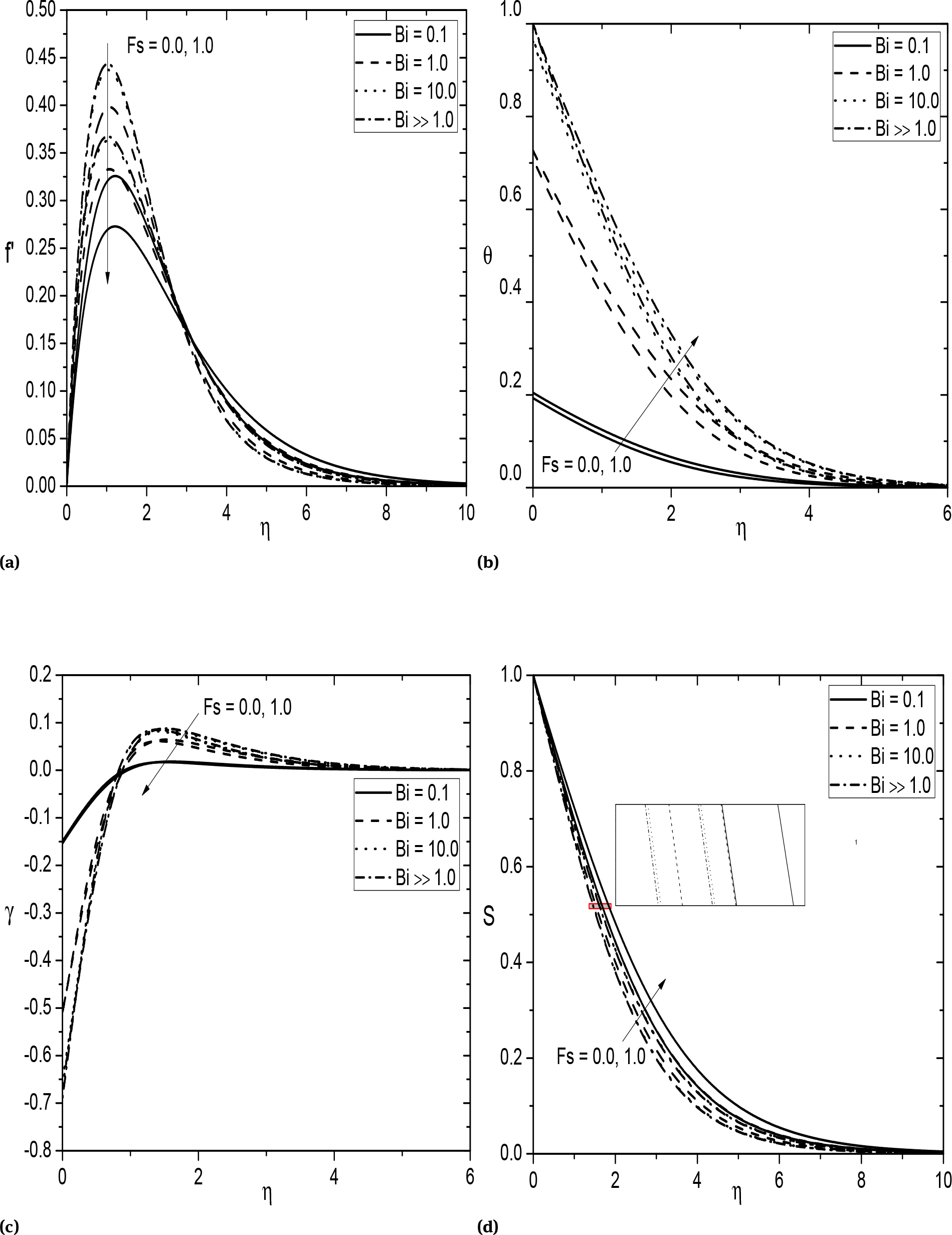
Effect of Fs and Bi on (a) velocity, (b) temperature, (c) nanoparticle volume fraction, and (d) regular concentration for Ds = 0.2, Dc = 0.3.
Figures 5a-5d represent the streamwise variation of ξ on non-dimensional skin friction, heat transfer rate, nanoparticle and regular mass transfer rates for various values of Biot number (Bi ) in two cases of Fs = 0.0 (Darcy flow) and Fs = 1.0 (non-Darcy flow), respectively. As the Biot number tends to infinity it reaches the isothermal surface (i,e., it becomes wall condition). The internal thermal resistance of a vertical frustum of a cone is more than the thermal resistance of boundary layer for high Biot number in reality. These figures depict that, an increase of Biot number enhance the magnitude of skin friction coefficient, heat transfer rate and mass transfer rate but reduces the nanoparticle mass transfer rate. As mentioned above, an increase of non-Darcy parameter reduces the velocity profiles and enhances the temperature profiles, and thus it decreases the surface drag, rate of heat, and regular mass transfer rates. Further, the values of skin friction and nanoparticle Sherwood number along vertical plate case (i.e., ξ = 0) are higher than those of over full cone (i.e., ξ ≫ 1) and, the nusselt and regular Sherwood numbers along vertical plate case (i.e., ξ = 0) are less than those of over full cone (i.e., ξ ≫ 1).
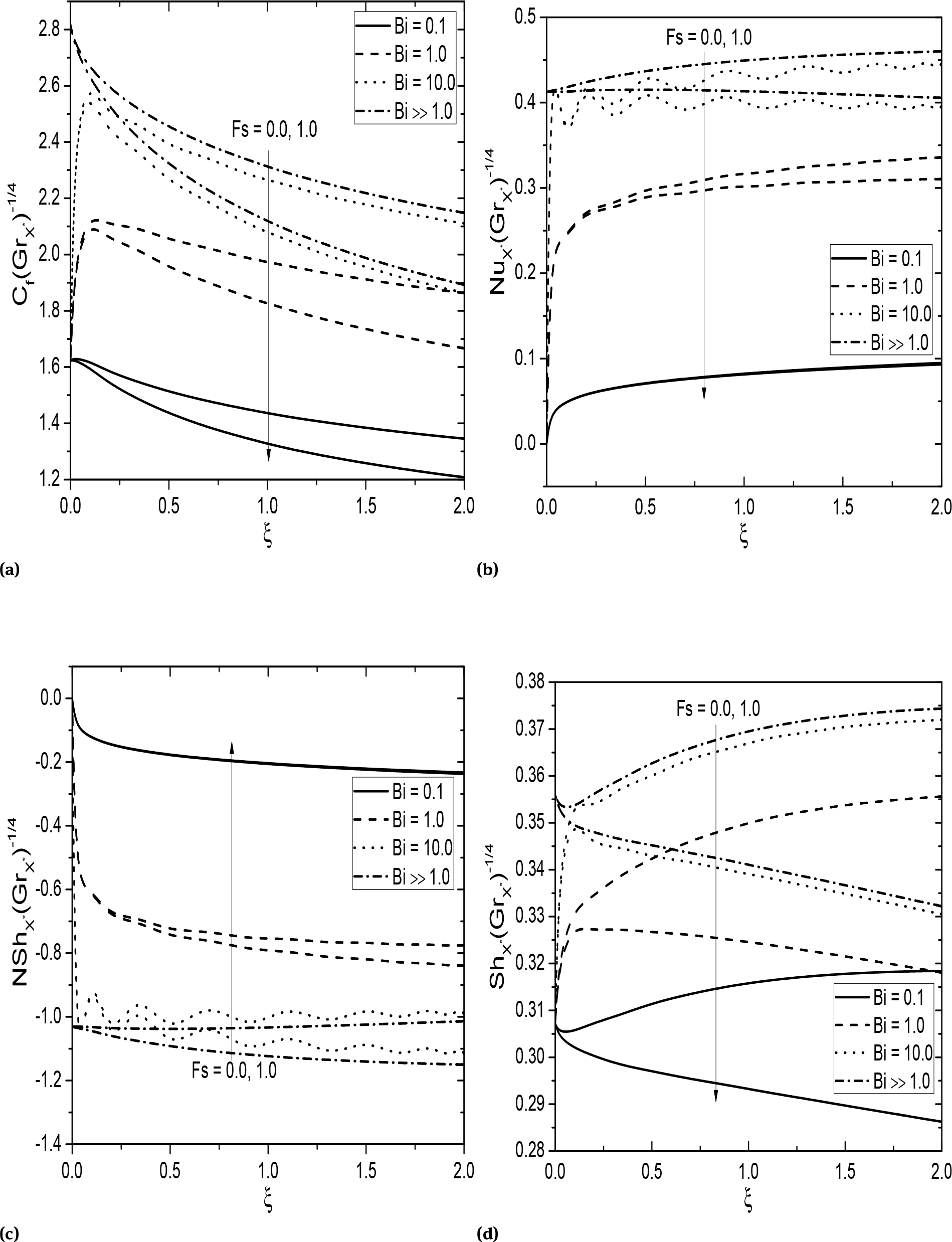
Effect of Fs and Bi on (a) skin friction, (b) heat transfer rate, (c) nanoparticle mass transfer rate, and (d) mass transfer rate Ds = 0.2, Dc = 0.3.
4.2 Effects of thermal dispersion parameter (Ds) and solutal dispersion parameter (Dc)
The effects of thermal dispersion (Ds) and solutal dispersion (Dc) on non-dimensional velocity, temperature, nanoparticle volume fraction and regular concentration displayed in Figs. 6a-6d across the boundary layers. Since Ds = 0 and Dc = 0, implies the case of nanofluid without thermal dispersion and solutal dispersion. The velocity is more in the presence of thermal dispersion and less that of in the absence of thermal dispersion. Taking thermal dispersion effect in the energy equation leads to conduction over convection. That is, supplementing dispersion effects to the energy equation gives thermal conduction more dominance. We can observe from Fig. 6b that the thermal boundary layer thickness improves with the enhancement of thermal dispersion coefficient near to the surface, but the opposite behavior can observed far away from the surface of the vertical frustum of a cone. This sudden change is due to the presence of non-isothermal boundary condition (CBC). The nanoparticle volume fraction profiles enhance with the thermal dispersion parameter near to the surface and negligible influence on regular concentration profiles in the boundary layers. On the other hand, increasing the solutal dispersion parameter leads to increase the thickness of momentum and regular concentration boundary layers. But, it is observed that the thermal and nanoparticle volume fraction boundary layer thickness slightly reduced with the increasing value of solutal dispersion parameter. As explained above, considerable influence of thermal and solutal dispersion effects on the thermal and concentration boundary layers is noticed, respectively.
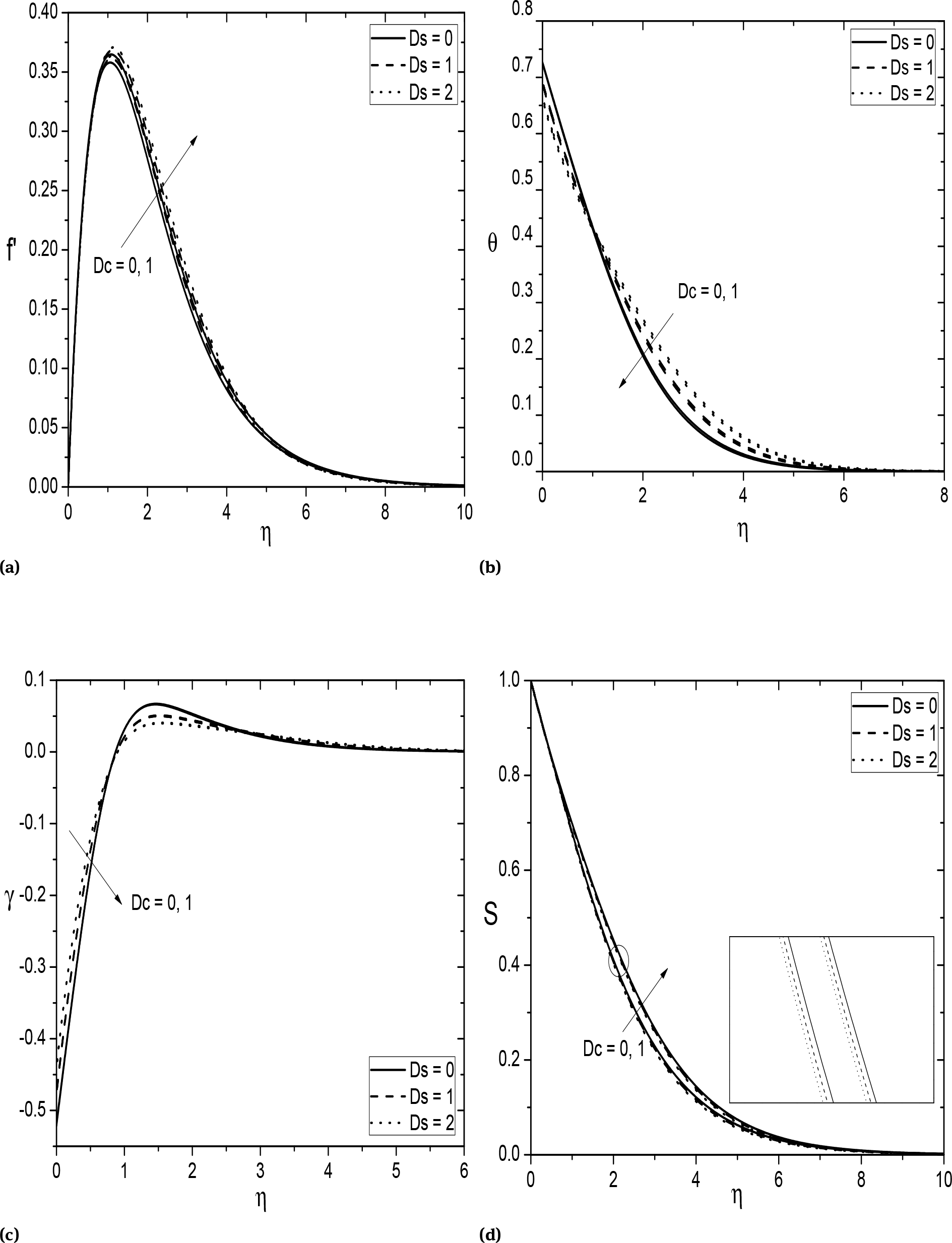
Effect of Ds and Dc on (a) velocity, (b) temperature, (c) nanoparticle volume fraction, and (d) regular concentration for Fs = 0.5, Bi = 1.0.
Figures 7a-7d prepared to explore the physical significance of thermal dispersion (Ds) and solutal dispersion (Dc) effects on the streamwise variations of surface drag, rate of heat, nanoparticle and regular mass transfers across the vertical frustum of a cone. As expected that, the strengthening of thermal dispersion parameter leads to reduce the surface drag and nano-mass transfer rate as shown in Fig. 7a and Fig. 7c, and enhance the heat transfer rate and regular mass transfer rate as shown in Fig. 7b and Fig. 7d. Further, it can be seen that the presence of solutal dispersion slightly enhance the surface drag and rate of heat but a large variation is observed in regular mass transfer rate. The opposite behavior is noticed in the nanoparticle mass transfer rate with solutal dispersion parameter. Moreover, the skin friction and the nanoparticle mass transfer rate produce large values along vertical plate (i.e., ξ = 0) than those of over full cone (i.e., ξ ≫ 1) and, the rate of heat and regular mass transfer rate along vertical plate case (i.e., ξ = 0) are less than those of over full cone (i.e., ξ ≫ 1).
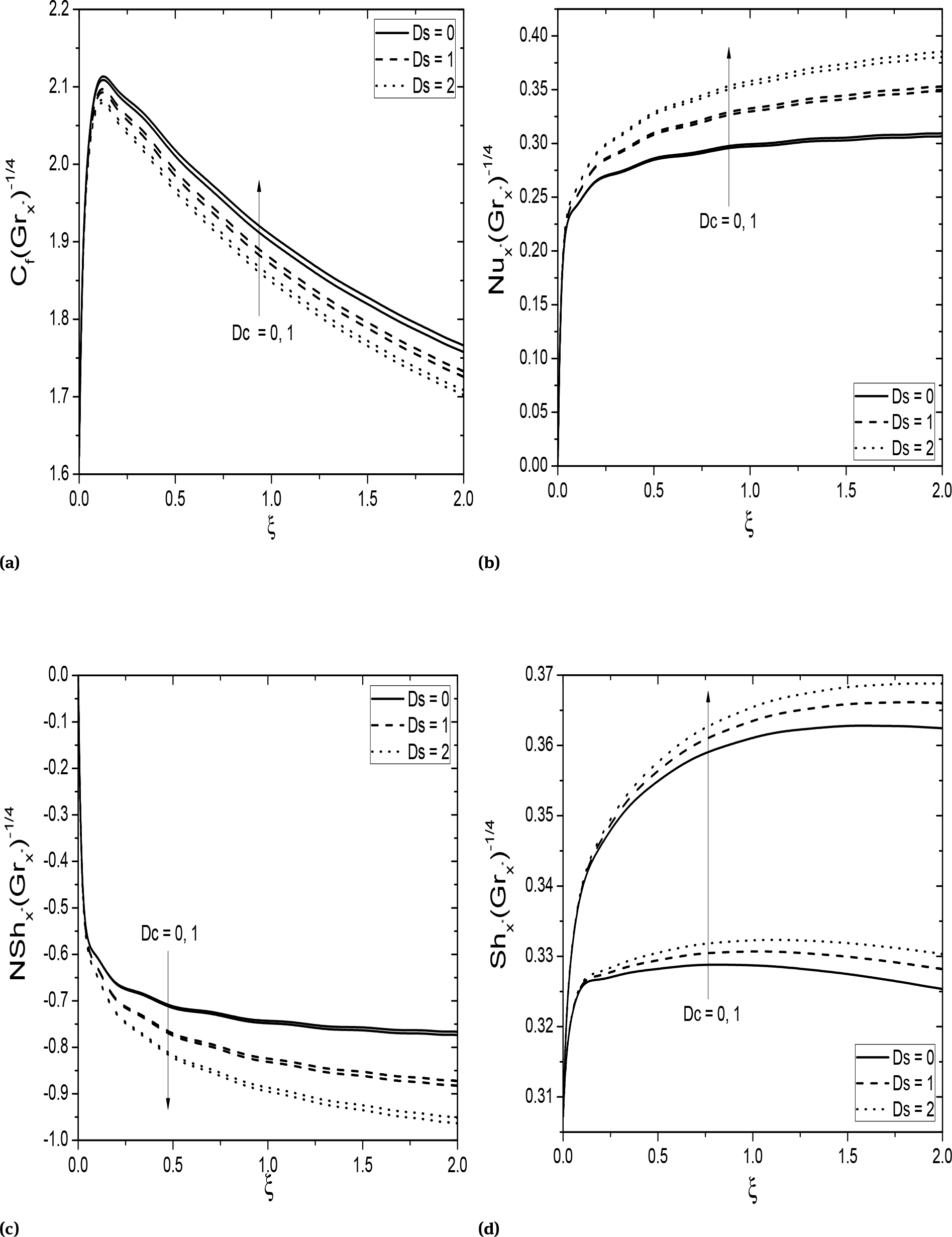
Effect of Ds and Dc on (a) skin friction, (b) heat transfer rate, (c) nanoparticle mass transfer rate, and (d) mass transfer rate Fs = 0.5, Bi = 1.0.
Further, the Figs. 8a-8d plotted to show the effect of streamwise coordinate (ξ) on dimensionless velocity, temperature, nanoparticle volume fraction and regular concentration. It is seen from Fig. 8a that the velocity diminishes with the rise of streamwise coordinate. Initially, there is a zero temperature when ξ = 0. But, we can see the improvement of temperature profiles near to the surface of a cone as ξ raises from 0 to 2. In the similar way, the nanoparticle volume fraction is improved with respect to ξ as shown in Fig. 8c. But, we can observe an opposite behaviour in the case of regular concentration profiles. That is, the strengthen values of streamwise coordinate causes reduce the regular concentration as given in Fig. 8d.
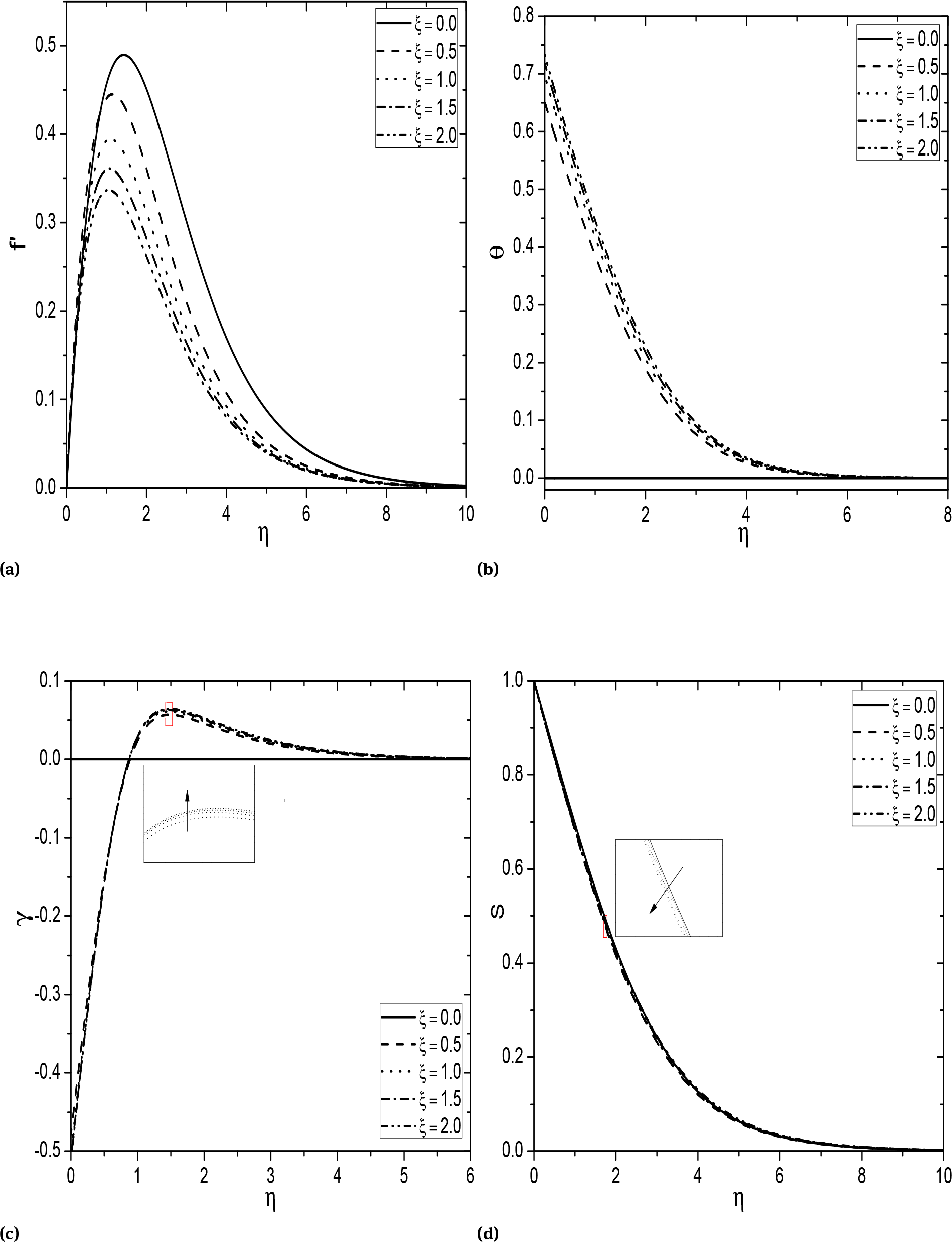
Variation of ξ on (a) velocity, (b) temperature, (c) nanoparticle concentration and (d) regular concentration for Fs = 0.5, Bi = 1.0, Ds = 0.2, Dc = 0.3.
5 Conclusions
In this article, a newly introduced numerical approach named as Bivariate Pseudo Spectral Local Linearisation Method (BPSLLM) has been used for solving highly nonlinear and coupled system of partial differential equations that model a non-Darcy natural convection flow of a nanofluid over a vertical frustum of cone in the presence of double dispersion effects and convective boundary condition. The non-dimensional velocity, temperature, nanoparticle volume fraction and regular concentration profiles are presented and the skin friction coefficient, heat transfer rate, nanoparticle and regular mass transfer rates are discussed for various values of non-Darcy parameter, Biot number and double dispersion parameters. The major findings emerging from this study are as follows:
The main conclusion is that the velocity, temperature, surface drag, heat and regular mass transfer rates enhance with the Biot number. Moreover, the nanoparticle volume fraction diminishes near to the surface of a vertical frustum of cone and far away from cone it shows the reverse trend in the both Darcy and non-Darcy flows.
For a fixed small value of Biot numer (non-isothermal surface), the temperature, nanoparticle mass transfer rate, nanoparticle volume fraction and regular concentration profiles increase, whereas the velocity, skin friction, rate of heat and regular mass transfer rate decrease with non-Darcy parameter.
An enhancement in the thermal dispersion parameter leads to increase the thickness of momentum, nanoparticle volume fraction boundary layers and heat transfer rate.
An increasing value of solutal dispersion parameter enhance the momentum, regular concentration boundary layer thickness, and heat and regular mass transfer rates.
The non-dimensional velocity and regular concentration decrease, and the temperature and nanoparticle volume fraction increase with the streamwise coordinate ξ (0 ≤ ξ ≤ 2).
The residual error analysis shown that, the convergence and effectiveness of bivariate pseudo-spectral local linearisation method for this kind of complicated flow problems.
References
[1] Nield DA, Bejan A. Convection in porous media. 4th Ed., Springer-Verlag, New York 2013.10.1007/978-1-4614-5541-7Suche in Google Scholar
[2] Murthy PVSN, Sutradhar A, RamReddy C. Double-diffusive free convection flow past an inclined plate embedded in a non-Darcy porous medium saturated with a nanofluid. Transport in Porous Media 2013, 98(3), 553-564.10.1007/s11242-013-0160-zSuche in Google Scholar
[3] Kairi RR, Murthy PVSN. Soret effect on free convection from a melting vertical surface in a non-Darcy porous medium. Journal of Porous Media 2013, 16(2), 97-104.10.1615/JPorMedia.v16.i2.20Suche in Google Scholar
[4] Nield DA, Kuznetsov AV. An historical and topical note on convection in porous media. Journal of Heat Transfer 2013, 135(6), 061201.10.1115/1.4023567Suche in Google Scholar
[5] Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles: Developments and applications of non-Newtonian flows. ASME FED 1995, 231, 99-103.Suche in Google Scholar
[6] Das S. Temperature dependence of thermal conductivity enhancement for nanofluid. Journal of Heat Transfer 2003, 125(4), 567-574.10.1115/1.1571080Suche in Google Scholar
[7] Xuan Y, Li Q. Investigation on convective heat transfer and flow features of nanofluids. Journal of Heat Transfer 2003, 125, 151-155.10.1115/1.1532008Suche in Google Scholar
[8] Eastman JA, Choi SUS, Li S, Yu W, Thompson LJ. Anomalously increased effective thermal conductivity of ethylene glycol-based nanofluids containing copper nanoparticles. Applied Physics Letters 2001, 78(6), 718-720.10.1063/1.1341218Suche in Google Scholar
[9] Das SK, Choi SUS, Yu W, Pradeep T. Nanofluids: Science and Technology. Wiley Interscience, New Jersey 2007.10.1002/9780470180693Suche in Google Scholar
[10] Buongiorno J. Convective transport in nanofluids. ASME Journal of Heat Transfer 2006, 128, 240-250.10.1115/1.2150834Suche in Google Scholar
[11] Das SK, Stephen US. A review of heat transfer in nanofluids. Advances in Heat Transfer 2009, 41, 81-197.10.1016/S0065-2717(08)41002-XSuche in Google Scholar
[12] Kakac S, Pramuanjaroenkij A. Review of convective heat transfer enhancement with nanofluids. International Journal of Heat and Mass Transfer 2009, 52, 3187-3196.10.1016/j.ijheatmasstransfer.2009.02.006Suche in Google Scholar
[13] Nield DA, Kuznetsov AV. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer 2009, 52(25), 5792-5795.10.1016/j.ijheatmasstransfer.2009.07.024Suche in Google Scholar
[14] Nield DA, Kuznetsov AV. The Cheng-Minkowycz problem for the double-diffusive natural convective boundary layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer 2011, 54(1), 374-378.10.1016/j.ijheatmasstransfer.2010.09.034Suche in Google Scholar
[15] Na TY, Chiou JP. Laminar natural convection over a frustum of a cone. Applied Scientific Research 1979, 35, 409-421.10.1007/BF00420389Suche in Google Scholar
[16] Cheng CY. Non-similar solutions for double diffusive convection near a frustum of a wavy cone in porous media. Applied Mathematics and Computation 2007, 194(1), 156-167.10.1016/j.amc.2007.04.074Suche in Google Scholar
[17] Noghrehabadi A, Behseresht A, Ghalambaz M, Behseresht J. Natural convection flow of nanofluids over vertical cone embedded in non-Darcy porous media. Journal of thermophysics and heat transfer 2013, 27(2), 334-341.10.2514/1.T3965Suche in Google Scholar
[18] Patrulescu FO, Groşan T, Pop I. Mixed convection boundary layer flow from a vertical truncated cone in a nanofluid. International Journal of Numerical Methods for Heat and Fluid Flow 2014, 24(5), 1175-1190.10.1108/HFF-11-2012-0267Suche in Google Scholar
[19] Shinmura T. Heat exchanger, EP 0694747 A2, 1996.Suche in Google Scholar
[20] Hamilton RE, Fagan TJ, Kennedy PG, Woodward WS. Closed loop liquid cooling for semiconductor RF simplifier modules, US005901037, 1999.Suche in Google Scholar
[21] McCutcheon JW, Narum TN, Soo PP, Liu YJ. Flexible heat sink, US006919504B2, 2005.Suche in Google Scholar
[22] Nakamura J, Kusunoki K, Matsushita M, Watanabe M, Sawada I, Fukada H, Tohi S. Plate heat exchanger used as evaporator or condenser, WO2010013608, 2010.Suche in Google Scholar
[23] Aziz A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Communications in Nonlinear Science and Numerical Simulation 2009, 14(4), 1064-1068.10.1016/j.cnsns.2008.05.003Suche in Google Scholar
[24] Makinde OD, Aziz A. MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition. International Journal of Thermal Sciences 2010, 49(9), 1813-1820.10.1016/j.ijthermalsci.2010.05.015Suche in Google Scholar
[25] Murthy PVSN, RamReddy C, Chamkha AJ, Rashad AM. Magnetic effect on thermally stratified nanofluid saturated non-Darcy porous medium under convective boundary condition. International Communications in Heat and Mass Transfer 2013, 47, 41-48.10.1016/j.icheatmasstransfer.2013.06.001Suche in Google Scholar
[26] Kairi RR, Narayana PAL, Murthy PVSN. The effect of double dispersion on natural convection heat and mass transfer in a non-Newtonian fluid saturated non-Darcy porous medium. Transport in a Porous Media 2009, 76, 377-390.10.1007/s11242-008-9252-6Suche in Google Scholar
[27] Telles RS, Trevisan OV. Dispersion in Heat and Mass Transfer Natural convection Along Vertical Boundaries in Porous Media. International Journal of Heat and Mass Transfer 1993, 36, 1357-1365.10.1016/S0017-9310(05)80103-6Suche in Google Scholar
[28] Kairi RR. Viscosity and Dispersion Effects on Natural Convection From a Vertical Cone in a Non-Newtonian Fluid Saturated Porous Medium. Thermal Sciences 2001, 15, S307-S316.10.2298/TSCI110614124KSuche in Google Scholar
[29] RamReddy C. Effect of Double Dispersion on Convective Flow over a Cone. International Journal of Nonlinear Science 2013, 15(4), 309-321.Suche in Google Scholar
[30] Kuznetsov AV, Nield DA. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. International Journal of Thermal Sciences 2014, 77, 126-129.10.1016/j.ijthermalsci.2013.10.007Suche in Google Scholar
[31] Motsa SS. A New Spectral Local Linearization Method for Nonlinear Boundary Layer Flow Problems. Journal of Applied Mathematics 2013, ID 423628.10.1155/2013/423628Suche in Google Scholar
[32] Motsa SS, Animasaun IL. A new numerical investigation of some thermo-physical properties on unsteady MHD non-Darcian flow past an impulsively started vertical surface. Thermal Sciences 2015, 19, 249-258.10.2298/TSCI15S1S49MSuche in Google Scholar
[33] Canuto C, Hussaini MY, Quarteroni A, Zang TA. Spectral Methods in Fluid Dynamics, Springer-Verlag, Berlin 1988.10.1007/978-3-642-84108-8Suche in Google Scholar
[34] Trefethen LN. Spectral Methods in MATLAB. SIAM 2000.10.1137/1.9780898719598Suche in Google Scholar
[35] Weideman JA, Reddy SC. A MATLAB differentiation matrix suite. ACM Transactions on Mathematical Software (TOMS) 2000, 26(4), 465-519.10.1145/365723.365727Suche in Google Scholar
[36] Kays WM, Crawford ME. Convective Heat and Mass transfer. 3rd ed., McGraw-Hill, New York 1980, 402.10.1115/1.3607663Suche in Google Scholar
[37] Lin HT, Chen CC. Mixed convection on vertical plate for fluids of any Prandtl number. Wärme-und Stoffübertragung 1988, 22, 159-168.10.1007/BF01052981Suche in Google Scholar
[38] Yih KA. Effect of radiation on natural convection about a truncated cone. International Journal of Heat and Mass Transfer 1999, 42(23), 4299-4305.10.1016/S0017-9310(99)00092-7Suche in Google Scholar
[39] Akbar N, Khan Z, Nadeem S, Khan W. Double-diffusive natural convective boundary-layer flow of a nanofluid over a stretching sheet with magnetic field. International Journal of Numerical Methods for Heat and Fluid Flow 2016, 26, 108-121.10.1108/HFF-01-2015-0019Suche in Google Scholar
[40] Cheng P, Ali CL, Verma AK. An experimental study of non-Darcian effects in free convection in a saturated porous medium. Letters in Heat and Mass Transfer 1981, 8(4), 261-265.10.1016/0094-4548(81)90040-0Suche in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- A New Computational Technique for the Generation of Optimised Aircraft Trajectories
- Modelling of Imbibition Phenomena in Fluid Flow through Heterogeneous Inclined Porous Media with different porous materials
- Double dispersion effects on non-Darcy free convective boundary layer flow of a nanofluid over vertical frustum of a cone with convective boundary condition
- F1 style MGU-H applied to the turbocharger of a gasoline hybrid electric passenger car
- Nonlinear control systems - A brief overview of historical and recent advances
- An analytical method with Padé technique for solving of variational problems
- Influence of Lorentz force, Cattaneo-Christov heat flux and viscous dissipation on the flow of micropolar fluid past a nonlinear convective stretching vertical surface
Artikel in diesem Heft
- Frontmatter
- A New Computational Technique for the Generation of Optimised Aircraft Trajectories
- Modelling of Imbibition Phenomena in Fluid Flow through Heterogeneous Inclined Porous Media with different porous materials
- Double dispersion effects on non-Darcy free convective boundary layer flow of a nanofluid over vertical frustum of a cone with convective boundary condition
- F1 style MGU-H applied to the turbocharger of a gasoline hybrid electric passenger car
- Nonlinear control systems - A brief overview of historical and recent advances
- An analytical method with Padé technique for solving of variational problems
- Influence of Lorentz force, Cattaneo-Christov heat flux and viscous dissipation on the flow of micropolar fluid past a nonlinear convective stretching vertical surface


