Abstract
Nonlinear surface-plasmon polaritons (NSPPs) in nanophotonic waveguides excite with dissimilar temporal properties due to input field modifications and material characteristics, but they possess similar nonlinear spectral evolution. In this work, we uncover the origin of this similarity and establish that the spectral dynamics is an inherent property of the system that depends on the synthetic dimension and is beyond waveguide geometrical dimensionality. To this aim, we design an ultralow loss nonlinear plasmonic waveguide, to establish the invariance of the surface plasmonic frequency combs (FCs) and phase singularities for plasmonic peregrine waves and Akhmediev breather. By finely tuning the nonlinear coefficient of the interaction interface, we uncover the conservation conditions through this plasmonic system and use the mean-value evolution of the quantum NSPP field commensurate with the Schrödinger equation to evaluate spectral dynamics of the plasmonic FCs (PFCs). Through providing suppressed interface losses and modified nonlinearity as dual requirements for conservative conditions, we propose exciting PFCs as equally spaced invariant quantities of this plasmonic scheme and prove that the spectral dynamics of the NSPPs within the interaction interface yields the formation of plasmonic analog of the synthetic photonic lattice, which we termed synthetic plasmonic lattice (SPL).
1 Introduction
Synthetic lattice (SL) [1] provides a platform for photonic structures to couple the integral degree of freedom of light such as orbital angular momentum and FC with geometrical dimensions of the waveguide to form higher-order synthetic space [2, 3]. This multidimensional property observes both theoretically and experimentally in various physical systems from photonics [4, 5] and cold atoms [6] to non Hermitian systems [7] and topological circuits [8]. SL also provides artificial gauge fields for a bosonic structure, which yields control over spectral and temporal behaviors of light and hence is valuable for topological lasing [9, 10], breaking time-reversal symmetry [11], etc.
Recently, SL with the periodic-boundary condition is introduced to the reconstruction of the FCs [12], to control the light manipulation in a nonlinear waveguide [13] and to induce a synthetic Hall effect for photons [14]. In previous investigations, these lattices are constructed as photonic structures with negligible dissipation and dispersion, whose internal degree of light acts as a synthetic dimension. Besides, plasmonic structures act as nanoscopic nonlinear waveguides that transport surface-plasmon polaritons (SPPs) instead of photons. Nonlinear SPP (NSPP) wave propagation is a well-explored topic within these media both in the presence and absence of gain [15–17]. It is also well-known that the combination of nonlinear response and gain amplification can be exploited to excite and sustain nonlinear waves such as different classes of solitons. As these hybrid interfaces possess the same nonlinearity and dispersion, there must be similarities such as the internal degree of freedom between these nonlinear waves. As spatiotemporal profiles of these NSPPs are quite dissimilar, these hidden similarities should be beyond waveguide geometrical dimensionality and may be related to synthetic dimension.
Consequently, natural questions that may arise are whether we can propose an SL for plasmonic nanostructures, and what would be the consequence of this synthetic plasmonic lattice (SPL)? Quite generally, constructing an SPL using an internal degree of freedom of SPPs has not yet been investigated and this concept should be a subject of potential applications from quantum nanophotonics [18] to ultrafast-nanoplasmonics [19]. Note that our work is conceptually novel, as we introduce the concept of synthetic dimension to dissipative nanophotonic structures such as plasmonic waveguides, and also this work is methodologically novel, as we develop a framework based on quantum nonlinear averaging of SPP field, to uncover the similarities between various NSPPs, and to discover the invariants of a plasmonic scheme in a loss-compensated waveguide. Finally, we propose a general nonlinear plasmonic waveguide configuration that comprises a tunable nonlinear layer situated on top of a plasmonic scheme with vanishing loss; consequently, our work can be extended to other low-loss hybrid nanostructures. We justify SL formation within a nonlinear plasmonic structure in three steps, namely, (i) first, we elucidate the robust PFCs propagation, (ii) we uncover the conservative conditions, and (iii) we introduce loss suppression and careful nonlinearity modification as dual requirements to generate robust PFCs and to form SPL.
1.1 Physical picture of our scheme
In this work, we aim to uncover the mutual propagation properties between plasmonic peregrine wave and Akhmediev breather. The key result of this work is that in a plasmonic waveguide with suppressed loss and tunable nonlinear coefficient, PFCs act as an invariant across different types of nonlinear waves and we interpret them in terms of a synthetic dimension to construct an SPL. Consequently, our work introduces two novel concepts to nonlinear plasmonic nanostructures, namely, (i) unveiling PFCs as synthetic dimension, and (ii) exploiting this synthetic dimension to form an SPL. To elucidate these concepts, we design a nonlinear graphene nanostructure that fulfills conservation conditions and can be exploited to validate our results.
2 Model
To uncover the invariant parameters of NSPPs, we suggest a nonlinear plasmonic nanostructure as it is shown in Figure 1. This scheme is a general extension to nonlinear hybrid plasmonic configurations that comprise a nonlinear medium situated on top of a plasmonic layer. In order to achieve the robust PFCs, establish the conservation conditions, and construct the SPL, we require a nonlinear waveguide with vanishing loss and tunable nonlinearity. In what follows, we elucidate the key essential components of each layer that validate the invariance of PFCs yielding formation of SPL.
![Figure 1:
Nonlinear plasmonic waveguide configuration for exciting invariant PFC and constructing SPL. Our suggested scheme comprises a plasmonic scheme placed as the bottom layer and a nonlinear medium situated on top. This nonlinear waveguide should possess tunable nonlinearity and vanishing loss. χ
(3)(ω) is the nonlinear coefficient of the medium, α
L = 0 is its linear absorption coefficient, and we assume α
M ≔ Im[
ɛ
(k, ω)] as suppressed loss of the plasmonic layer.](/document/doi/10.1515/nanoph-2021-0163/asset/graphic/j_nanoph-2021-0163_fig_001.jpg)
Nonlinear plasmonic waveguide configuration for exciting invariant PFC and constructing SPL. Our suggested scheme comprises a plasmonic scheme placed as the bottom layer and a nonlinear medium situated on top. This nonlinear waveguide should possess tunable nonlinearity and vanishing loss. χ (3)(ω) is the nonlinear coefficient of the medium, α L = 0 is its linear absorption coefficient, and we assume α M ≔ Im[ ɛ (k, ω)] as suppressed loss of the plasmonic layer.
2.1 Nonlinear material description
Various materials possess optical nonlinearity that may serve as the upper layer of our nonlinear plasmonic scheme. However, we consider a nonlinear medium that simultaneously fulfills two criteria, namely, (i) possesses suppressed linear absorption and (ii) the nonlinear parameter related to this layer is tunable. This nonlinear medium supports different classes of nonlinear waves such as Akhmedive breather and peregrine wave and provides opportunities to excite and generate robust FCs, which are required to construct an SPL.
2.2 Plasmonic layer description
Besides, our proposed plasmonic layer should possess ultra-low Ohmic loss for our wavelength of interest. Although various ultralow loss schemes can serve as the bottom layer, our scheme is double-layer graphene that can be modeled as substrate-graphene–dielectric–graphene multilayer, as it is indicated in Figure 1. We introduce gain to the bottom graphene layer by trigger laser irradiation through a photoinverted scheme and adjust a suitable laser power to suppress the Ohmic-loss of the waveguide through gain-loss competition. Our ultralow loss plasmonic scheme is an extension to previous researches [15–17], for which we exploit the gain-induced loss compensation in double-layer graphene structure (see Section S.2 of the supplementary information) instead of employing negative-index metamaterial structure.
2.3 General description of excitation
To sum up, we propose a nonlinear plasmonic waveguide that fulfills suppressed interface losses and modified nonlinearity as dual requirements for conservative conditions and supports different classes of NSPP waves such as plasmonic Akhemediev breather and peregrine waves. Robust PFCs excite as a consequence of these plasmonic fields that act as invariants of the system and can be interpreted in terms of synthetic dimension. The existence of this synthetic dimension would yield apparition of plasmonic counterparts of synthetic lattice that we termed as SPL.
3 Approach
We present our quantitative approach towards robust NSPP propagation in three steps. First, we present the key parameters required to describe our nonlinear waveguide. Next, we describe the SPP field excitation in our scheme. Finally, we elucidate the Fourier evolution of NSPP fields.
3.1 Essential parameters related to scheme
We quantitatively model our nonlinear waveguide in terms of the parameters related to the nonlinear medium and plasmonic scheme. We consider the nonlinear coefficient of the upper layer as χ (3)(ω), its linear absorption is α L = 0 and we further assume that the suppressed linear absorption and enhanced nonlinear coefficient are simultaneously achievable through adjusting a control parameter of the system. Besides, our proposed plasmonic structure is double-layer graphene, the bottom layer possesses gain and the upper graphene is lossy. We consider the susceptibility of the lossy graphene as χ (L)(k, ω) [20], gain-assisted graphene as χ (G)(k, ω) [21] and evaluate the effective susceptibility of the coupled system as χ (C)(k, ω).[1] Consequently, we achieve the dielectric function of the double-layer graphene as ɛ (k, ω) = 1 − χ (C)(k, ω) V (k); V (k) the coupling matrix between two layers. This double layer excites SPP for det{ ɛ (k, ω)} = 0 [22], and ultra low-loss SPP field propagates for Im[det{ ɛ (k, ω)}] = 0. The combination of the nonlinear material and this graphene nanostructure provides a nonlinear plasmonic waveguide that fulfills conservative conditions and hence is suitable to excite invariant PFCs.
3.2 Surface plasmon-field excitation
The graphene structure-nonlinear medium interface hence excite stable SPP with reciprocal chromatic dispersion
3.3 Spectral evolution of nonlinear SPP
The evolution of the SPP field then depends on two nonlinear parameters, i.e. dispersion
We note that the NSPP propagation within the nonlinear medium-graphene interface is similar to previous works [15–17] as both systems possess group-velocity dispersion and self-phase modulation. However, this work differs from our previous works due to exploiting NSPP similarities to establish conservation conditions, introduce frequency comb as a synthetic dimension, and constructing SPL.
3.4 Simulation parameters and scheme feasibility
Now, we introduce the simulation parameters to justify invariant PFCs excitation. In our scheme stable NSPP with ω
SPP = 1.57 eV propagates with group velocity dispersion
To simulate SPP propagation in this nonlinear plasmonic system, we assume (i) SPP waves propagate as far plasmonic fields, (ii) the plasmonic phases are constant (i.e.
4 Results
We present the results of this paper in three sections: first, we investigate the temporal and spectral dynamics of the plasmonic peregrine and Akhmediev breather phases within the interaction interface in Section 4.1. Next, in Section 4.2 we evaluate the spatial-spectral evolution of the energy flux and number of plasmon modes to achieve the conservative parameters of the system. Finally, we map the robust spectral dynamics to a synthetic photonic lattice in Section 4.3.
4.1 Robust FCs generation
The excited and propagated NSPPs are described by
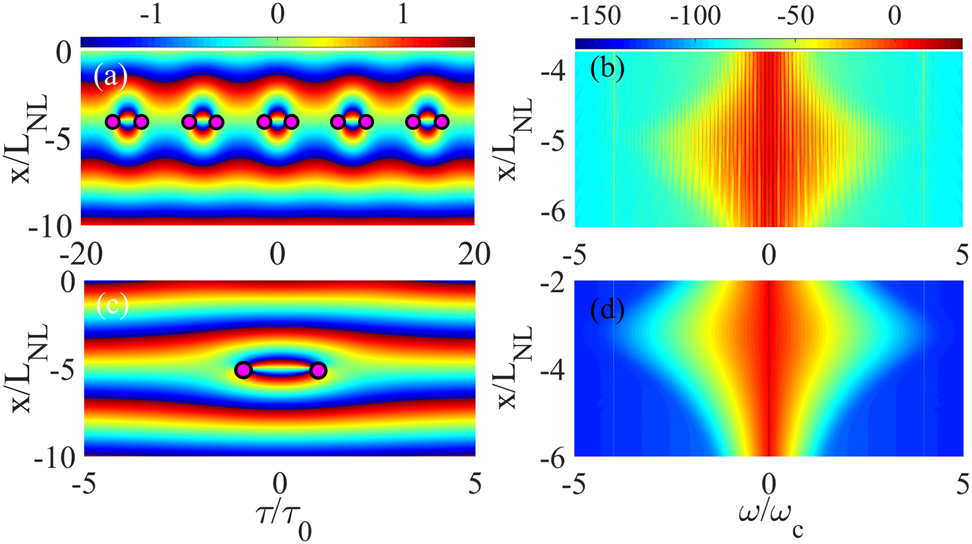
Panel (a) represents the phase dynamics of NSPPs through Akhmediev breather formation and panel (b) denotes corresponding spectral analysis. Panel (c) depicts the phase dynamics of NSPP through plasmonic peregrine wave and panel (d) represents its spectral evolution. For this figure P 0 = 10 μW, τ 0 = 10 μs, δω = 1 MHz, u N = 0.08 MHz. Panels (a) and (b) are plotted for modulation parameter a = 0.32 and for panels (c) and (d) we choose a = 0.5. Magenta dots in panels (a) and (c) represent the coordinates of PSs. Other parameters are given in the text.
Various nonlinear plasmonic phases such as periodic (Figure 2(a)) and single PSs (Figure 2(c)) are excited by tuning the modulation parameter through plasmonic Akhmediev breather and peregrine wave formation, respectively. Figure 2(b) and (d) demonstrate that the FCs correspond to these PSs generate for both NSPP excitation and these quantities are invariant against input field modulation. Consequently, PSs are the similar features of the exciting nonlinear waves, for peregrine wave and Akhmediev breather. For a characteristic frequency ω ch = 10 MHz, robust FCs up to ω comb ≈ 3ω ch are achieved through plasmonic PS. Consequently, similar frequency comb generation and their stable propagation through interaction interface are referred to as invariant of NSPPs. The FCs |ω| < 2ω ch can propagate for a few propagation lengths −5.5L NL < x < −4L NL and hence would produce a robust plateau, as it is shown clearly in Figure 2(b) and (d), which we exploit this square to design a plasmonic version of SL.
4.2 Invariants of nonlinear system
The formation of robust PFCs and their robustness against external field modulation can be elucidated through the apparition of hidden invariants of this nonlinear system, which we termed invariant parameters. One of the key theoretical results of this work is that the PFCs act as invariant features across different types of nonlinear waves excitation. PFCs are invariant of this plasmonic system if we fulfill two conditions simultaneously, namely, (i)
We note that our robust FCs propagate for characteristic length
and number of stable plasmon modes as
The dynamical evolution of the PFC, their robustness, and conservative conditions hence are limited by the nonlinear coefficient
This equation establishes that the apparition of conservation within a plasmonic system is independent of the SPP field dispersion/dissipation. The conservation of PFCs across different classes of NSPPs is an essential step to justify the invariance of FCs within our system (see Section S.3 A2 of supplementary information for more details). In what follows, we describe the nonlinear spectral evolution of the NSPP field in the presence of conserved
To describe the NSPP evolution, we should solve nonlinear Schrödinger equation considering conservative conditions and by assuming nonlinearity as Eq. (4), which is challenging due to the plasmonic field being propagated within the dispersive interface. To remedy this limitation, we consider SPP field as electromagnetic waves that can be quantized through interaction interface and use the quantum SPP approach that is independent of interface dispersion. Here we consider the NSPP field as time-harmonic profile
for
4.2.1 Discussion on the universality of FCs
In this work, we uncover the invariants only for plasmonic peregrine wave and Akhemediev breather, which means that our approach falls short of providing a universal description of nonlinear SPPs and frequency comb generation. Here, PFCs propagation and SPL formation are highly limited by loss suppression and nonlinear modification.[4] Consequently, our predicted effects would depend on robust PFC generation and conservation conditions, and hence are device-dependent. The extension of stable FC formation to other classes of solitons needs careful investigations and goes beyond the scope of this work.
4.3 Nonlinear spectral dynamics and synthetic lattice formation
In this section, first, we achieve the output spectral envelope function of the NSPP waves for peregrine and Akhmediev breather cases with and without the existence of conservatives, to establish the invariance of PFCs in our hybrid system that can be interpreted as a synthetic dimension. Next, we exploit this synthetic space to construct an SPL.
To investigate the spectral dynamics and evaluate the output envelope profiles of the NSPPs, we assume SPP field as
![Figure 3:
Spectral evolution of NSPPs through the interaction interface: panel (a) is the spectral phase variation ϕ(x, ω) panel (b) represents the logarithmic spectral harmonic intensity of the plasmonic breather as a function of perturbation frequency. Panel (c) denotes the phase variation and (d) is spectral logarithmic power density for plasmonic peregrine wave excitation. In both panels (b) and (d) the blue dotted-dashed line represents the input field and red solid-line denotes the NSPP excitation in the presence of invariants [Eq. (4)]. Despite the dissimilar phase variation, excited FCs are the invariant of the nonlinear system. See the text for more details.](/document/doi/10.1515/nanoph-2021-0163/asset/graphic/j_nanoph-2021-0163_fig_003.jpg)
Spectral evolution of NSPPs through the interaction interface: panel (a) is the spectral phase variation ϕ(x, ω) panel (b) represents the logarithmic spectral harmonic intensity of the plasmonic breather as a function of perturbation frequency. Panel (c) denotes the phase variation and (d) is spectral logarithmic power density for plasmonic peregrine wave excitation. In both panels (b) and (d) the blue dotted-dashed line represents the input field and red solid-line denotes the NSPP excitation in the presence of invariants [Eq. (4)]. Despite the dissimilar phase variation, excited FCs are the invariant of the nonlinear system. See the text for more details.
Our results hence indicate that in a nonlinear waveguide fulfilling the vanishing loss and tunable nonlinearity,
4.3.1 Qualitative description
Qualitatively, we prove that PFCs are invariant of excited NSPPs and they propagate as discrete frequency components with equal frequency spacing
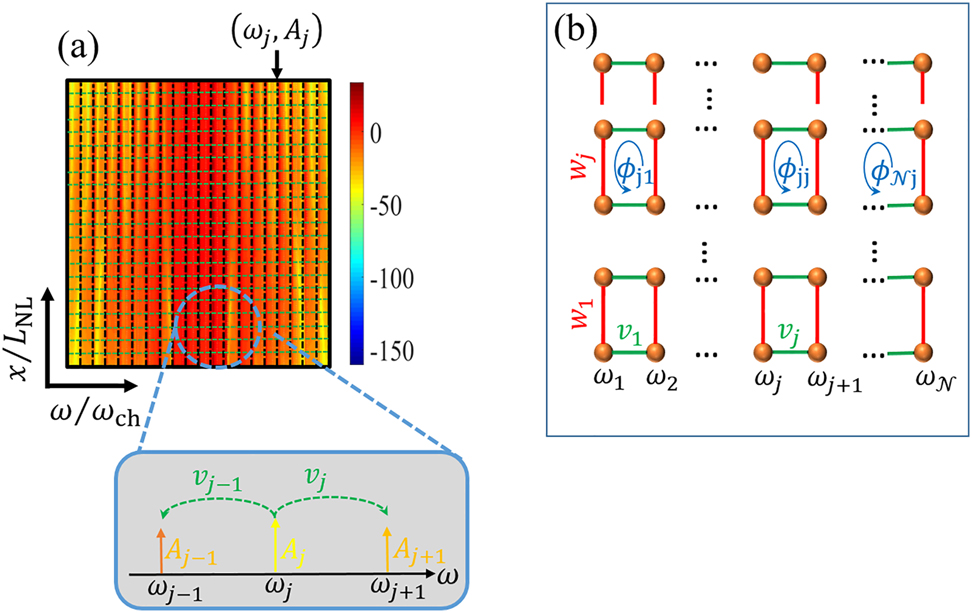
Mapping between the stable FCs to a synthetic dimension: panel (a) represents the power spectrum of the spectral harmonic side-bands for |ω| < 2ω ch and −5.5L NL < x < −4L NL correspond to robust propagation of FCs. The inset of this figure represents the correlation between the FCs. Panel (b) is the qualitative description of the synthetic lattice corresponding to frequency comb excitation.
4.3.2 Quantitative description
We assume PFCs excite with frequency components ω
n
= ±nδ, and with propagation constant ξ
n
= ξ
NL + Δξ
L;
We write the Hamiltonian of SPL in x–ω plane in terms of hoppings w i,j and v i,j in the most general case[6]
and consider the evolution of this lattice along the interaction interface as
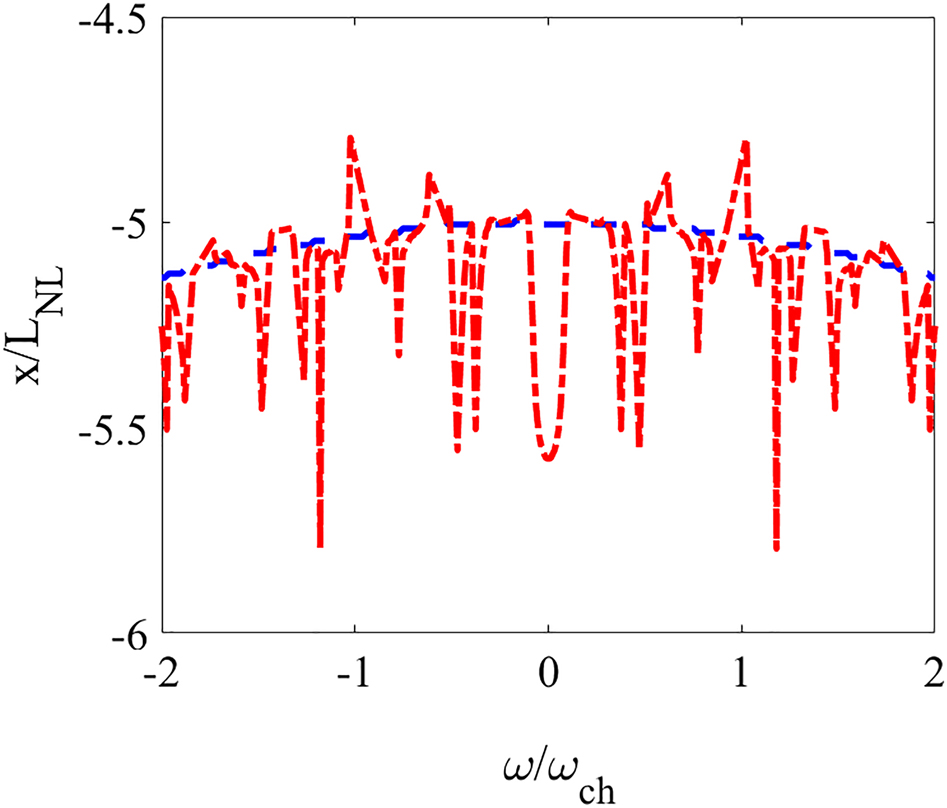
Observation of anomalous phase hopping, and nonzero phase trajectories through different NSPP field excitation: Dashed blue curve is the trajectory of nonzero phase hoppings ϕ i,j ≠ 0 for the plasmonic rogue wave formation, and red dashed-dotted curve is the corresponding phase trajectory for the breather formation.
5 Conclusions
To sum up, we exploit the spectral SPP field evolution to discover the hidden invariant parameter of the nonlinear plasmonic wave systems. The key theoretical result of this work is that in a plasmonic waveguide with suppressed loss and tunable nonlinear coefficient, PFCs act as an invariant across different types of nonlinear waves and are interpreted in terms of a synthetic dimension to construct an SPL. Invariant PFCs apparition and SPL formation are based on assumptions related to nonlinear waveguides and assumptions related to the SPP field. For the SPP field, we assume far-field approximation, neglect its phase variation, and consider the effect of evanescent coupling through mean-field averaging. For plasmonic configuration, we assume the interface with low dispersion and controllable nonlinearity. Our loss compensation scheme and field propagation methodology in our proposed scheme is then an extension to the ultra low-loss plasmonic scheme represented in [15–17] that the gain compensated graphene structure play the role of the metamaterial layer. In particular, we uncover that the FCs and PSs are similar features for plasmonic peregrine waves and Akhmediev breather.
Next, we prove that the linearized nonlinear coefficient provides similar PFCs that can be interpreted as the internal degrees of freedom and thereby act as synthetic dimensions. Qualitatively, we achieve this finely tuned nonlinearity as control parameters. Our analysis thereby indicates that dual requirement of the vanishing losses, linearizing the interface nonlinearity, and the existences of robust FCs with preserved number of excitation are requirements to constructing an SPL. We quantitatively describe the robust FCs generation through quantum NSPP field formalism commensurate with the Schrödinger approach and we also perform the mean-value averaging to achieve the Fourier dynamics of NSPPs in the presence of conservative conditions. Our approach justifies the existence of the anomalous hopping phase through characteristic reciprocal trajectories, which depend on input field modulation and can be exploited to various effects, from nonuniform magnetic flux to anomalous gauge field.
-
Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: None declared.
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
[1] L. Yuan, Q. Lin, M. Xiao, and S. Fan, “Synthetic dimension in photonics,” Optica, vol. 5, pp. 1396–1405, 2018. https://doi.org/10.1364/optica.5.001396.Suche in Google Scholar
[2] L. Yuan, Y. Shi, and S. Fan, “Photonic gauge potential in a system with a synthetic frequency dimension,” Opt. Lett., vol. 41, pp. 741–744, 2016. https://doi.org/10.1364/ol.41.000741.Suche in Google Scholar
[3] A. Dutt, M. Minkov, I. A. Williamson, and S. Fan, “Higher-order topological insulators in synthetic dimensions,” Light Sci. Appl., vol. 9, pp. 1–9, 2019. https://doi.org/10.1038/s41377-020-0334-8.Suche in Google Scholar PubMed PubMed Central
[4] T. Ozawa, H. M. Price, A. Amo, et al.., “Topological photonics,” Rev. Mod. Phys., vol. 91, p. 015006, 2019. https://doi.org/10.1103/revmodphys.91.015006.Suche in Google Scholar
[5] D. Smirnova, D. Leykam, Y. Chong, and Y. Kivshar, “Nonlinear topological photonics,” Appl. Phys. Rev., vol. 7, p. 021306, 2020. https://doi.org/10.1063/1.5142397.Suche in Google Scholar
[6] N. R. Cooper, J. Dalibard, and I. B. Spielman, “Topological bands for ultracold atoms,” Rev. Mod. Phys., vol. 91, p. 015005, 2019. https://doi.org/10.1103/revmodphys.91.015005.Suche in Google Scholar PubMed PubMed Central
[7] Y. Song, W. Liu, L. Zheng, Y. Zhang, B. Wang, and P. Lu, “Two-dimensional non-Hermitian skin effect in a synthetic photonic lattice,” Phys. Rev. Appl., vol. 14, p. 064076, 2020. https://doi.org/10.1103/physrevapplied.14.064076.Suche in Google Scholar
[8] S. Imhof, C. Berger, F. Bayer, et al.., “Topolectrical-circuit realization of topological corner modes,” Nat. Phys., vol. 14, p. 925, 2018.https://doi.org/10.1038/s41567-018-0246-1.Suche in Google Scholar
[9] G. Harari, M. A. Bandres, Y. Lumer, et al.., “Topological insulator laser: theory,” Science, vol. 359, p. 4003, 2018. https://doi.org/10.1126/science.aar4003.Suche in Google Scholar PubMed
[10] M. A. Bandres, S. Wittek, G. Harari, et al.., “Topological insulator laser: experiments,” Science, vol. 359, p. 4005, 2018. https://doi.org/10.1126/science.aar4005.Suche in Google Scholar PubMed
[11] Y. Lumer, M. A. Bandres, M. Heinrich, et al.., “Light guiding by artificial gauge fields,” Nat. Photonics, vol. 13, p. 339, 2019. https://doi.org/10.1038/s41566-019-0370-1.Suche in Google Scholar
[12] J. G. Titchener, B. Bell, K. Wang, A. S. Solntsev, B. J. Eggleton, and A. A. Sukhorukov, “Synthetic photonic lattice for single-shot reconstruction of frequency combs,” APL Photonics, vol. 5, p. 030805, 2020. https://doi.org/10.1063/1.5144119.Suche in Google Scholar
[13] K. Wang, B. A. Bell, A. S. Solntsev, D. N. Neshev, B. J. Eggleton, and A. A. Sukhorukov, “Multidimensional synthetic chiral-tube lattices via nonlinear frequency conversion,” Light Sci. Appl., vol. 9, p. 1, 2020. https://doi.org/10.1038/s41377-020-0299-7.Suche in Google Scholar PubMed PubMed Central
[14] S. Kim, D. B. Sohn, C. W. Peterson, and G. Bahl, “On-chip optical non-reciprocity through a synthetic Hall effect for photons,” APL Photonics, vol. 6, p. 011301, 2021.10.1063/5.0034291Suche in Google Scholar
[15] S. Asgarnezhad-Zorgabad, P. Berini, and B. C. Sanders, “Polaritonic frequency-comb generation and breather propagation in a negative-index metamaterial with a cold four-level atomic medium,” Phys. Rev. A, vol. 99, p. 051802, 2019. https://doi.org/10.1103/physreva.99.051802.Suche in Google Scholar
[16] S. Asgarnezhad-Zorgabad, R. Sadighi-Bonabi, B. Kibler, Ş, K. Özdemir, and B. C. Sanders, “Surface-polaritonic phase singularities and multimode polaritonic frequency combs via dark rogue-wave excitation in hybrid plasmonic waveguide,” New J. Phys., vol. 22, p. 033008, 2020. https://doi.org/10.1088/1367-2630/ab7259.Suche in Google Scholar
[17] S. Asgarnezhad-Zorgabad and B. C. Sanders, “Nonlinear frequency conversions via weak surface polaritonic wave breaking in a hybrid plasmonic waveguide,” Opt. Lett., vol. 45, pp. 5432–5435, 2020. https://doi.org/10.1364/ol.402282.Suche in Google Scholar
[18] A. Reserbat-Plantey, I. Epstein, I. Torre, et al.., “Quantum nanophotonics in two-dimensional materials,” ACS Photonics, vol. 8, p. 85, 2021. https://doi.org/10.1021/acsphotonics.0c01224.Suche in Google Scholar
[19] N. Maccaferri, S. Meuret, N. Kornienko, and D. Jari-wala, “Speeding up nanoscience and nanotechnology with ultrafast plasmonics,” Nano Lett., vol. 20, p. 5593, 2020. https://doi.org/10.1021/acs.nanolett.0c02452.Suche in Google Scholar PubMed
[20] Z. Jalali-Mola and S. Jafari, “Electromagnetic modes from Stoner enhancement: graphene as a case study,” J. Magn. Magn Mater., vol. 471, p. 220, 2019. https://doi.org/10.1016/j.jmmm.2018.09.040.Suche in Google Scholar
[21] A. F. Page, F. Ballout, O. Hess, and J. M. Hamm, “Nonequilibrium plasmons with gain in graphene,” Phys. Rev. B, vol. 91, p. 075404, 2015. https://doi.org/10.1103/physrevb.91.075404.Suche in Google Scholar
[22] Z. Jalali-Mola and S. Jafari, “Kinked plasmon dispersion in borophene-borophene and borophene-graphene double layers,” Phys. Rev. B, vol. 98, p. 235430, 2018. https://doi.org/10.1103/physrevb.98.235430.Suche in Google Scholar
[23] S. Asgarnezhad-Zorgabad, R. Sadighi-Bonabi, and B. C. Sanders, “Excitation and propagation of surface polaritonic rogue waves and breathers,” Phys. Rev. A., vol. 98, p. 013825, 2018. https://doi.org/10.1103/physreva.98.013825.Suche in Google Scholar
[24] B. A. Ferreira, B. Amorim, A. J. Chaves, and N. M. R. Peres, “Quantization of graphene plasmons,” Phys. Rev. A, vol. 101, p. 033817, 2020. https://doi.org/10.1103/physreva.101.033817.Suche in Google Scholar
[25] M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge, England, Cambridge University Press, 1999.10.1119/1.19344Suche in Google Scholar
[26] Y. Lai and H. A. Haus, “Quantum theory of solitons in optical fibers. I. Time-dependent Hartree approximation,” Phys. Rev. A., vol. 40, p. 844, 1989. https://doi.org/10.1103/physreva.40.844.Suche in Google Scholar PubMed
Supplementary Material
The online version of this article offers supplementary material (https://doi.org/10.1515/nanoph-2021-0163).
© 2021 Zahra Jalali-Mola et al., published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Review
- Femtosecond laser micromachining for integrated quantum photonics
- Research Article
- Synthetic plasmonic lattice formation through invariant frequency comb excitation in graphene structures
- Nearly total optical transmission of linearly polarized light through transparent electrode composed of GaSb monolithic high-contrast grating integrated with gold
- Super-regular femtosecond laser nanolithography based on dual-interface plasmons coupling
- Inverse design of grating couplers using the policy gradient method from reinforcement learning
- Exfoliated Bi2Te3 nanoparticle suspensions and films: morphological and nonlinear optical characterization
- Experimental demonstration of broadband negative refraction at visible frequencies by critical layer thickness analysis in a vertical hyperbolic metamaterial
- Sensitive THz sensing based on Fano resonance in all-polymeric Bloch surface wave structure
- Photonic crystal nanobeam cavities with lateral fins
- Spectral tuning of diamond photonic crystal slabs by deposition of a thin layer with silicon vacancy centers
- Tailoring of plasmonic functionalized metastructures to enhance local heating release
- Fourier-component engineering to control light diffraction beyond subwavelength limit
Artikel in diesem Heft
- Frontmatter
- Review
- Femtosecond laser micromachining for integrated quantum photonics
- Research Article
- Synthetic plasmonic lattice formation through invariant frequency comb excitation in graphene structures
- Nearly total optical transmission of linearly polarized light through transparent electrode composed of GaSb monolithic high-contrast grating integrated with gold
- Super-regular femtosecond laser nanolithography based on dual-interface plasmons coupling
- Inverse design of grating couplers using the policy gradient method from reinforcement learning
- Exfoliated Bi2Te3 nanoparticle suspensions and films: morphological and nonlinear optical characterization
- Experimental demonstration of broadband negative refraction at visible frequencies by critical layer thickness analysis in a vertical hyperbolic metamaterial
- Sensitive THz sensing based on Fano resonance in all-polymeric Bloch surface wave structure
- Photonic crystal nanobeam cavities with lateral fins
- Spectral tuning of diamond photonic crystal slabs by deposition of a thin layer with silicon vacancy centers
- Tailoring of plasmonic functionalized metastructures to enhance local heating release
- Fourier-component engineering to control light diffraction beyond subwavelength limit

