Computation of the Thermal Residual Stresses in SiC/SiC Composites with Multi-Layered Interphases by Using ANN with the Structure of Random Forest

Introduction

Ceramic matrix composites (CMCs) with continuous fibre reinforcement exhibit attractive properties for thermal-structural applications, including low density, high strength and non-brittle mechanical behaviour. These applications mainly cover nozzles, leading edges, thermal protection systems and thrusters in aerospace engineering [1, 2, 3]. Others are involved in brakes, heat shields, outer flaps of turbojet engines and hot gas path components. It is now well established that the mechanical behaviour of fibre-reinforced CMCs depend strongly on the interphase between the fibres and the matrix [4, 5]. The CMCs display brittle mechanical behaviour when the fibre/matrix bond is too strong and non-brittle behaviour in the presence of a weak fibre/matrix bond. This trend is usually observed in the SiC/SiC composites with a pyrocarbon (PyC) interphase.

The low-oxidation resistance of pyrocarbon has led the researchers to develop alternative interphases with a view to the structural application of CMCs at high temperatures. Recently, CMCs with multi-layered interphases that have both oxidation resistance and high strength have been developed [6, 7]. The multi-layered interphases consist of alternating sublayers of two different materials, for instance, PyC and anti-oxidative silicon carbide (SiC) associated in a sequence of n PyC/SiC layers (denoted as (PyC/SiC)_n) [8, 9]. The multi-layered interphases are usually obtained using the chemical vapour infiltration (CVI) process [10, 11]. During the CVI process, the thicknesses of layers are controllable.

In CMCs with multi-layered interphases, thermal residual stresses (TRS) are often generated upon cooling from processing to room temperatures due to extensive mismatch of the coefficients of thermal expansion (CTE) between the constituents (fibre, interphase and matrix).The distribution of TRS, resulting in the cracks and separations in the matrix and interphases, has a significant influence on the mechanical behaviour and lifetime of CMCs. Complicated architecture and material heterogeneity of the multi-layered interphases constitute the challenge to understand the effect of TRS in CMCs. To achieve an excellent thermal–mechanical performance of CMCs, it is necessary to analyse and adjust the thicknesses of the multi-layered interphases for an optimized TRS distribution.

During past three decades, considerable research has been carried out to understand and design the composites according to desired performance. A common method is micromechanical model, which provides overall behaviours of the composites through a finite element analysis of a unit cell model [12, 13]. Due to the complex multi-layered microstructure and large heterogeneity of multi-phase materials of the CMCs with multi-layered interphases, a detailed finite element model of the unit cell usually involves large number of elements and the computational costs are quite high. Generalization of the relationship between the multi-layered interphases thicknesses and the TRS of the composite using this finite element procedure is extremely difficult. This is because of the fact that, a new finite element mesh has to be set up for each new situation and an iterative finite element analysis has to be carried out. This is extremely time consuming, computationally expensive and also involves very large number crunching operations.

Artificial neural network (ANN) is the first widely used technique of machine learning. However, ANN still has several limitations, such as over-fitting, the ability of generalization is not strong and the number of the nodes of the hidden layer is difficult to choose. These limitations have hindered the further application of the ANN. In order to overcome the defects of ANN algorithm, many hybrid training algorithms which combines evolution algorithms (EAs) and ANN are presented to reduce the forecast error and improve the accuracy of the model. The genetic algorithm [14, 15] and differential evolution algorithm [16] have been regarded as the effective EAs for improving the ANN algorithm.

Motivated by the thoughts of Random Forest (RF), this paper presents a new approach of the combination of random neural networks. The new approach is that while training the single neural network, the training samples are randomly selected by the method of Bagging, and the number of the nodes of the hidden layer is randomly selected within the certain range by a new empirical formula. The final output of the combination of neural network discriminates the test sample by a simple average method for regression. The introduction of two randomness increases the random differences between individual neural network.

The intention of the present paper is to evaluate the contribution of multi-layered (PyC/SiC)_n interphases on the TRS of unidirectional SiC/SiC composites. A framework on the integrating finite element computation and Random Forest-artificial neural network (RFANN) algorithm is proposed to compute TRS. The methodology utilizing the finite element method to calculate the TRS distribution and employing the RFANN to approximate the non-linear relationship between the thicknesses of multi-layered (PyC/SiC)_n interphases and the TRS is developed. To illustrate the detailed procedure and processes, a case study is used to implement the developed methodology.

Finite element analysis of TRS

Finite element model of the sic/sic composites with multi-layered (PyC/SiC)_n interphases

The SiC/SiC composites with multi-layered (PyC/SiC)_n interphases are usually fabricated from SiC-based Hi-Nicalon fibre tows via CVI process. In the present study, square fibres arrays are used to model the unidirectional SiC/SiC composites. Six layers of interphases are distributed around the fibres. Note that in this study a perfect interface between different constituents is assumed for simplifying the modelling. In fact, the state of interface would affect the load transfer and result in different mechanical properties of composite. Details about the interface modelling can be found in Refs. [20, 21, 22]. In the longitudinal direction, the fibre axes have been assumed to be parallel and of equal lengths. The unit cell of composite (as shown in Figure 1) is used in the present finite element analysis. Characteristic geometric parameters of the Reticulated Vitreous Carbon (RVC) model are given: ϕ^f is fibre diameter, d₁–d₆ are thicknesses of the interphase layers, d_m is the thickness of the matrix layer.

Figure 1:

Geometry of the RVC model.

The RVC model is meshed using the 3D twenty-node, thermal-structural coupled element (SOLID 96) of ANSYS finite element software [23], as depicted in Figure 2.

Figure 2:

Finite element model of the RVC.

The analytical model is assumed as a perfect elastic body without plastic deformation. The structural and thermal boundary conditions are given as follows:

1. Nodes on the boundary surfaces are free to move but have to remain planar in a parallel way to preserve the compatibility with adjacent cells.

2. The initial stresses of all nodes are assumed as zero at the sintering temperature, and TRS generated in the succeeded cooling process.

3. The model is cooled from sintering temperature to room temperature, with a uniform temperature field. In practice, temperature of the model is decreased by ΔT and ANSYS finite element software is used to calculate the TRS in the model.

Comparison with experimental results

Due to the complexity of the CVI fabrication process of multi-layered interphases, most of the available experimental results and numerical values evaluated by other numerical methods in the literatures are focused on the CMCs with single-layered interphase. Hence, in this section, numerical tests are dealt with to evaluate TRS of CMCs with single-layered interphase. These results are compared with experimental data and other available numerical results to show the validity of the model.

A unidirectional carbon fibre-reinforced SiC CMC with single-layered molybdenum disiticide (MoSi₂) interphase is studied. Residual axial and hoop thermal stresses in C/MoSi₂/SiC composites fabricated with T300 carbon fibre have been measured experimentally [7]. The finite element models of the unit cell of C/MoSi₂/SiC composite with various interphase/matrix thicknesses are created.

Material properties of the constituents are taken from Ref. [10] and are given in Table 1. Two thermal loading states are prescribed. The unit cell is assumed initially at a uniform temperature of 1,000 °C (state 1). Then in state 2, the temperature is uniformly set to 0 °C.

Table 1:

Properties of the constituents.

Constituents	Elastic moduli (GPa)				Poisson ratio		CTEs (10−6/°C)
	EXX	EZZ	GXY	GYZ	νXY	νYZ	αXX	αZZ
Carbon fibre	22	220	7.75	4.8	0.4	0.12	27	0
SiC fibre	200	200	80	80	0.12	0.12	3	3
MoSi2 interphase	310	310	124	124	0.25	0.25	8.4	8.4
PyC interphase	12	30	4.3	2	0.4	0.12	28	2
SiC matrix	350	350	145.8	145.8	0.2	0.2	4.6	4.6

Table 2 lists the average values of the numerically obtained TRS against experimental results in Ref. [10]. It can be seen that the numerical results are globally in agreement with the experimental ones.

Table 2:

Comparison of numerical results with experimental ones.

Interphase/matrix thickness (μm)		Axial stresses (MPa)		Hoop stresses (MPa)
		Interphase	Matrix	Interphase	Matrix
0.3/2.1	Numerical analysis	1,287	158	162	−910
	Experimental results	1,190	140	230	−740
1/2.1	Numerical analysis	935	127	146	−903
	Experimental results	820	140	180	−670
0.3/2.5	Numerical analysis	1,610	109	1,548	232
	Experimental results	1,490	120	1,420	210
1/2.5	Numerical analysis	1,026	87	1,603	215
	Experimental results	890	120	1,430	190

As the examination of residual axial and hoop thermal stresses of C/MoSi₂/SiC gives only a limited view of the prediction accuracy, a unidirectional SiC fibre-reinforced SiC CMC with MoSi₂ interphase (SiC/MoSi₂/SiC) studied in Ref. [24] is also taken into account. The diameter of SiC fibre is 14 μm. The thicknesses of interphase and matrix are 0.5 and 1.6 μm, respectively. Material properties of the constituents are given in Table 1. Figure 3 shows the residual radial thermal stresses (the units of the stress are all in GPa) distributions for 1/4 RVC of SiC/MoSi₂/SiC. Meanwhile, the present numerical results are compared with numerical values evaluated by cylinder model in Ref. [24]. It can be seen that the predicted profiles coincide well with the numerical results reported in the literature.

Figure 3:

Residual radial thermal stresses distribution for 1/4 RVC of SiC/MoSi₂/SiC.

The finite element computation has well demonstrated the ability in simulating the TRS of SiC/SiC composites. However, due to the complex multi-layer microstructure and large heterogeneity of multi-phase materials of the SiC/SiC composite, a detailed finite element model involves large number of elements and the computational cost is high. For instance, the finite element model shown in Figure 2 involves 10,312 elements and the computation time of one calculation is nearly 6 s. Thus, in the following sections, a framework integrating finite element computation and RFANN algorithm is proposed to compute TRS with high-computational efficiency.

Case description

In this paper, a unidirectional SiC/SiC composite with six layers of (PyC/SiC) interphases is presented. For each constituent, the elastic and CTE [12] are listed in Table 2. During the CVI process, the layer thicknesses have to be properly controlled since the thickness variation of each layer will change the material microstructure and affect the effective properties of the composite as well. Hence, the thicknesses of interphases are selected as the design parameters. Usually, the layers thicknesses should be regular values without many decimal places for reducing the complexity of the CVI fabrication process. In addition, the lower bounds of thicknesses of interphase layers should be bigger than 0.2 μm for oxidation resistance considerations. The upper bounds of thicknesses of interphase layers are defined as 0.8 μm.

Hybrid strategy based on RF and ANN

In this study, the training cases are generated by finite element simulations. It can be known that large-scale computations would be involved if all the levels of every parameter are studied. Therefore, a novel method combining the ANN into RF structure is proposed to find out the relationship between the parameters and TR using small amount of simulations.

The hybrid strategy defined ANN with the structure of RF. Figure 4 shows the flowchart related to the strategy.

Figure 4:

Flowchart of the hybrid strategy based on ANN and RF.

In the ANN, Each neuron in the structure is defined using three quantities: an input, an output and a transfer function. The transfer function is a sigmoid function which is adequate for continuous variable processing [26]. W_ij and W_jk are the weight matrix representing all possible connections between the neuron outputs, hidden layer and the neuron inputs indexed by k (k=1), i (i=1, 2,…,6), and j represents the number of neurons in hidden layer. The input layer of each ANN consists of six neurons representing the thicknesses of six interphase layers.

However, it is quite difficult to choose the number of neurons in hidden layer: if the number is too small, the ANN may not be trained well; on the other hand, if the number is too large, the trained ANN may turn up over-fitting and result in complicated implementation and computation. In the past, the traditional way is k-fold cross-validation [27], but this method always consumes much time. On the other hand, the generalization ability of single ANN training often performs not well.

Motivated by those problems, we come up with a novel method, combining the ANN into RF structure. This combination of RFANN consists of several ANNs with different number of neurons in hidden layers, which are chosen randomly in a certain boundary. Each ANNs, we use the random sampling to select the training set and we adopt the simple majority vote method to obtain the output for classification; for regression, we adopt the simple average method to obtain the answer. Unlike the method above, the algorithm tends to provide good generalization performance at extremely fast learning speed.

The design steps are stated as the following in Figure 5.

Figure 5:

The flow diagram for the training phase of RFANN.

Step 1: Initializing k ANNs. The input layer of each ANN consists of six neurons representing the interphase layers thicknesses and each ANN has different hidden neurons.

Step 2: For every ANN, we divide the data set with bootstrap sampling method [28] into two sets: training set and testing set.

Step 3: The training set of the ANN is used to train this ANN, the number of hidden neurons is chose by the formula below:

where a is a random number from 1 to 10, m is the number of nodes in the output layer and n is the number of nodes in the input layer. Unlike traditional method to choose the number of hidden neurons, in this algorithm, we choose the number in a direct way with certain boundary. The other parameters in every ANN are set with same figure.

Step 4: With the trained ANNs, the testing set of the ANN is used to predict, and the outcome of it is named h_i.

Step 5: Using the simple majority vote (for classification) or simple average method (for regression), we can obtain the final result H.

Results and discussion

ANNRSM training

We firstly trained the ANN in a traditional way, the activation function is sigmoid (x)=1/(1 + exp(−x)), and the hidden neurons are simply chosen as three. With 4,089 steps, the reached threshold is 0.009861560223. In our case, one training process as that shown in figures blow takes within 1 s. Figures 6 and 7 illustrate responses of the TRS and the generated neural network.

Figure 6:

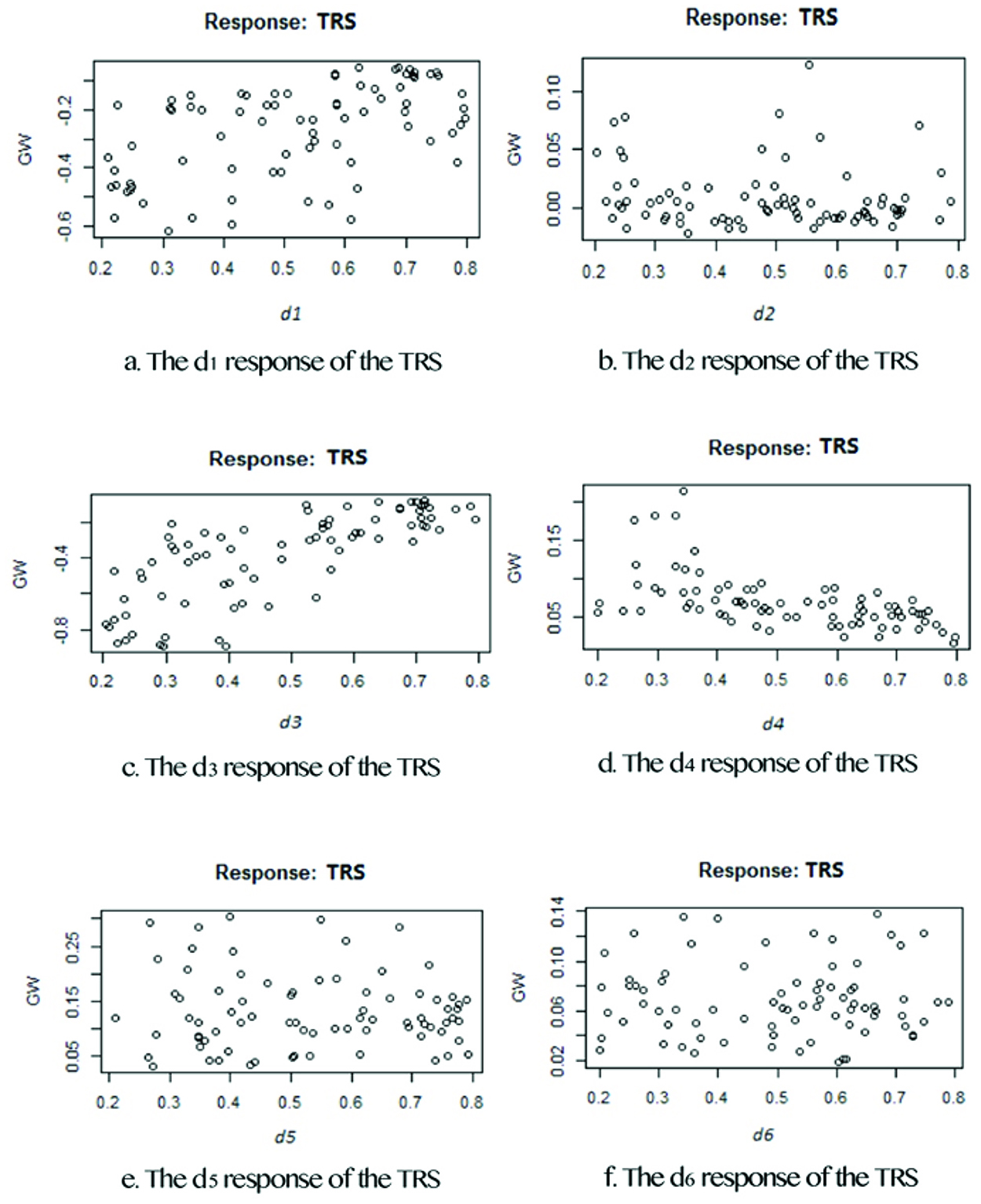
The response of TRS.

Figure 7:

The generated neural network.

Estimation of the RFANN

In order to demonstrate the RFANN’s ability to generalize the training data, we sampled 80 % of data set for training and 20 % for testing, 70 % training and 30 % testing, 60 % training and 40 % testing, respectively. The FEM’s and only one ANN’s results in the same test environment are compared. Figure 8 shows the comparison of the FEM’s, ANN’s and RFANN’s results.

Figure 8:

Results of testing.

In those figures, we can easily find that the RFANN is more close to the FEM and more adaptive compared with ANN.

Conclusions

In this study, an integrated methodology based on finite element analysis, RFANN algorithm is presented to compute the TRS in SiC/SiC composites with multi-layered interphases. This integrated methodology can effectively find out the highly non-linear relationship between the multi-layered interphases thicknesses and the TRS of the SiC/SiC composites and store this relationship in RFANN. The results show that the proposed methodology could estimate the TRS of different design solutions. The developed methodology in this paper can help compute the TRS and thus can greatly reduce the simulation time and make it possible to search for the optimal design in the whole design space.