Abstract
In distributed computing environments, the collaboration of nodes for predictive analytics at the network edge plays a crucial role in supporting real-time services. When a node’s service becomes unavailable for various reasons (e.g., service updates, node maintenance, or even node failure), the rest of the available nodes connot efficiently replace its service due to different data and predictive models (e.g., machine learning [ML] models). To address this, we propose decision-making strategies rooted in the statistical signatures of nodes’ data. Specifically, these signatures refer to the unique patterns and behaviors within each node’s data that can be leveraged to predict the suitability of potential surrogate nodes. Recognizing and acting on these statistical nuances ensures a more targeted and efficient response to node failures. Such strategies aim to identify surrogate nodes capable of substituting for failing nodes’ services by building enhanced predictive models. Our resilient framework helps to guide the task requests from failing nodes to the most appropriate surrogate nodes. In this case, the surrogate nodes can use their enhanced models, which can produce equivalent and satisfactory results for the requested tasks. We provide experimental evaluations and comparative assessments with baseline approaches over real datasets. Our results showcase the capability of our framework to maintain the overall performance of predictive analytics under nodes’ failures in edge computing environments.
1 Introduction and background
1.1 Emergence of edge computing (EC)
The advancement in communication technologies has paved the way for significant progress in artificial intelligence (AI). This surge is primarily due to the colossal volume of data generated by mobile and Internet of Things (IoT) devices that can now be effectively transmitted and accumulated. One major offshoot of these developments is EC. EC is a novel computing paradigm that shifts the computation closer to the source of data generation, right at the network’s edge, near sensors and end users. This approach ensures optimal use of resources and enables services that require real-time decision-making, delay-sensitive responses, and are context-aware [1].
1.2 Synergy between AI and EC
As AI solutions often require substantial data processing capabilities and appreciate minimal latency for real-time services, the integration of AI and EC is emerging swiftly. This amalgamation can primarily be categorized into two segments: “AI for edge,” which aspires to enhance EC using AI techniques, and “AI on edge,” which perceives EC as a utility for the efficient deployment of AI systems [2]. A plethora of “AI on Edge” applications have already shown success, offering a wide range of predictive services such as anomaly detection, regression, classification, and clustering. Notably, by harnessing “AI on Edge,” considerable costs associated with data transmission to the Cloud can be saved [3].
The union of AI and EC has indeed heralded a new era of technology. By pushing AI capabilities to the edge, we are not only decentralizing intelligence but also ensuring that decision-making is faster, more efficient, and less reliant on distant data centers. However, as with all nascent integrations, some challenges need to be addressed, especially when delving deeper into predictive analytics within the EC framework.
1.3 Predictive analytics in EC environments: Challenges and limitations
Predictive analytics, relying heavily on machine learning (ML) models, have found significant applications in domains such as smart cities and sustainable agriculture. In smart cities, technology is leveraged to enhance city services and the overall quality of life for its inhabitants, with tasks such as traffic predictions, energy consumption estimations, and aiding transportation companies in anticipating potential route issues. In sustainable agriculture, ML models are invaluable during both the pre-production (predicting crop yields, and soil property assessments) and production phases (disease and weed detection, and soil nutrient management). These ML models transition from raw data processing to advanced tasks like regression and classification [4].
However, when applied in the EC context, several challenges emerge. Conventional ML systems designed for “AI on Edge” applications typically have each edge node (or node for short) accessing its local data and containing ML models trained solely with these data. Despite nodes potentially operating under similar conditions and gathering data from like environments, the unique statistical characteristics of their data render their models noninterchangeable. In realistic EC scenarios, where nodes might fail due to connectivity issues or security breaches, the current system design means that functioning nodes cannot readily take over the predictive tasks of their failing counterparts [5].
1.4 A novel approach to enhance reliability in EC
The challenges highlighted necessitate the presence of “surrogate nodes” or “substitute nodes” that can efficiently process requests from failing nodes. The current paradigm of localized training (training each node’s models with only its local data) does not cater to this need. Furthermore, the idea of having a centralized backup, such as a Cloud server, is untenable in EC due to the sheer volume of internode data transfers, which contradicts the principles of EC.
Our proposed solution targets the heart of this issue: we aim to enhance the adaptability of models on neighboring nodes. The goal is to enable these nodes to efficiently handle “unfamiliar” data from failing nodes. This is achieved by actively sharing and integrating statistical signature information during the training process. However, the realization of this vision presents its own set of challenges:
Determining the best surrogate node(s) when a node failure arises.
Formulating context-aware strategies for nodes to extract and share relevant data signatures from potential failure-prone counterparts.
Ascertain the type and amount of data that should be shared to ensure the surrogate nodes perform on par with the original nodes.
To address these intricacies, we offer a comprehensive framework. This design integrates strategies to extract and combine data statistics from peer nodes, creating resilient models that maintain predictive performance even during node failures. Through rigorous testing using varied real-world datasets in diverse distributed computing scenarios, our framework showcases its capability to preserve and, in some instances, surpass the performance levels of systems without node failures, outshining traditional centralized approaches.
1.5 Limitations of traditional approaches in EC contexts
Historically, numerous strategies have been employed to tackle the challenges posed by node failures. Some of the pioneering efforts [6,7] adopted a straightforward approach: replications and backups. The primary philosophy behind this was to maintain duplicate versions or replicas of the nodes. In this setup, systems would operate under the assumption that the principal node remains functional. In the event of the main node’s failure, the replicas would step in to ensure continuity. However, such a strategy is resource-intensive. Creating and preserving these replicas demands a significantly higher allocation of bandwidth, storage, and computational resources, making it a less favorable solution in EC contexts.
Another well-established method to circumvent node failures is through the process of checkpointing [8,9, 10,11]. In this approach, systems periodically generate and save snapshots (termed as checkpoints) of the nodes’ states. When a node encounters a failure, the system can resort to the most recent snapshot to restore the node to its last operational state. While conceptually sound, this method comes with its own set of drawbacks. It can be taxing in terms of storage and bandwidth usage, particularly when these snapshots are stored centrally. Furthermore, certain types of node failures, such as those arising from power outages or network disruptions, that render a node entirely inaccessible cannot be remedied simply by restoring a previous state. In such scenarios, an entirely new node would be needed to replace the failed one, utilizing the saved snapshot.
Contrastingly, the framework we introduce in this article proposes a novel perspective on the problem. Our approach is rooted in the idea of developing generalized models on nodes, equipping them with the capability to assist their neighboring nodes during instances of failure. This method stands out by offering a unique solution that does not heavily lean on resource consumption, and instead, focuses on enhancing the inherent capacities of the nodes.
The article is organized as follows: Section 2 reports on the related work and our technical contribution; Section 3 formulates our problem; Section 4.1 introduces the rationale of our framework; Section 5 reports on the experimental setup, performance evaluation, and comparative assessment; Section 6 discusses the results and remaining problems; and Section 7 concludes the article.
2 Related work and contribution
In the burgeoning domain of EC, resilience is paramount. Defined as the “ability of a system to provide an acceptable level of service in the presence of challenges” [12], resilience is pivotal when facing challenges in EC, such as those brought about by external attacks or internal failures [13,14, 15,16]. A compromised node in an EC system threatens the very service it delivers.
While achieving resilience can involve resource-intensive methods like storage backup or additional network capacity [17], the unpredictable nature of system status adds layers of complexity to ensuring availability, responsiveness, and resistance to external events [18]. Herein lies the uniqueness of our contribution: instead of the general goal of system resilience, we delve into the nuanced challenge of resilience in the face of failing nodes, particularly those providing predictive services using ML models.
Our inspiration stems from several works in the field. For instance, the feasibility of “familiarizing” models has roots in adversarial training, where the models’ robustness is enhanced by introducing adversarial examples during the training process [19,20,21]. In a similar vein, domain adaptation seeks to transition algorithms between source and target domains, addressing the divergence between training and testing data [22,23]. Our work draws from this, aiming to create models capable of processing requests from both local and failing nodes.
The landscape of resilience in EC is dotted with related endeavors. Samanta et al.’s auction mechanism, for instance, balances users’ demand and task offloading to edge servers, fostering tolerance against execution failures [24]. Similarly, efforts have been made to address data stream processing failures [25] and real-time messaging architecture to counteract message losses [26]. Our framework distinguishes itself by its focus on model adaptability and universality in EC environments, aiming for broader fault tolerance and resilience.
In conclusion, our work represents a significant extension of our initial findings in [27]. Our approach, deeply rooted in the current literature and driven by the pressing challenges of the field, introduces novel strategies for information extraction and node invocation. By addressing node failure in EC with enhanced predictive models, we make strides toward a more resilient EC landscape. Our main contributions are as follows:
A comprehensive framework to identify the optimal surrogate node during node failures;
Innovative strategies for effective information extraction, bolstering model generalizability;
A guidance mechanism facilitating node invocation and load balancing during failures;
Exhaustive experimental results that underscore the advantages of our approach against traditional methods.
3 Rationale and problem definition
Table 1 provides a nomenclature used in this article. Consider an EC system with
Nomenclature
| Parameter | Notation | |
|---|---|---|
|
|
Independent (input) and dependent variables (output) | |
|
|
Input data dimensionality | |
|
|
Number of nodes | |
|
|
Set of global and adjacency strategies | |
|
|
Node with index
|
|
|
|
Local dataset on node
|
|
|
|
Mixture of
|
|
|
|
Sample mixing rate | |
|
|
Selected subset of
|
|
|
|
Number of data clusters | |
|
|
The
|
|
|
|
Number of input–output pairs and probability of sampling a point from
|
|
|
|
Local model of node
|
|
|
|
Enhanced model on
|
|
|
|
Global model trained with all nodes’ data | |
|
|
Neighboring/peer nodes of node
|
|
|
|
Node adjacency list for node
|
|
|
|
Average vectors of top-
|
Our rationale is based on the idea of training enhanced substitute models on nodes by introducing our strategies used in case of failures. In each strategy
Problem 1: We seek the best mixture of enhanced models
Let us focus on
Then, we use
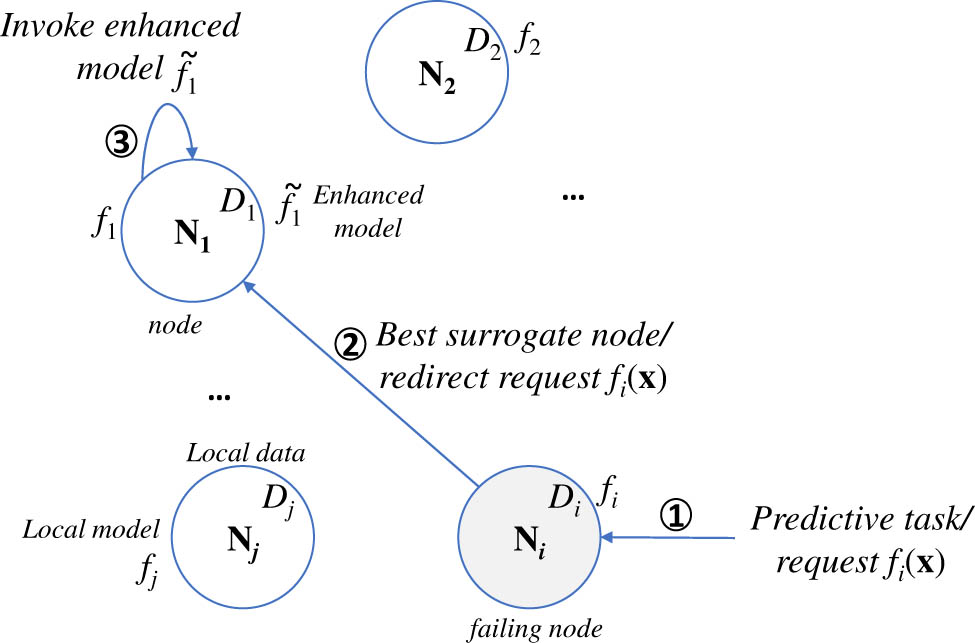
Node
In order to provide more insight on our rationale, we elaborate on the statistical learning capability of the enhanced model
where
where
Remark 1
One could come up with the following question: “Why should we adopt enhanced models instead of replicating local models?” The introduction of enhanced models to support failing nodes should be argued against the use of replicated local models, as it seems that the latter could be used to achieve the same goal. That is, if we equip each node with the replica of its neighboring nodes’ local models, when node failures occur, the requests from the failing node could be directed to its neighboring nodes and processed with the replica of the failing node’s local model. This is very close to the works that utilize data replication and backups to achieve resilience to node failures. However, this is not the straightforward solution/approach to our problem, where we would need to replicate local models (instead of data) due to the following fundamental reasons:
(R1) Each node could be equipped with a large number of local models, while the number of nodes can also be huge, thus replicating all of them several times would be very costly. Recall that an analytics task consists of a series of interrelated/workflow-based ML models being in a specific sequence to provide a predictive service. (R2) It would make the maintenance of models exponentially more difficult (due to, e.g., concept drifts, obsolete data, and new data dimensionality). As each time the models are updated, the same replication process (now including also model re-training and adaptation beforehand) is needed to be carried out again. (R3) Such a replication strategy means all the nodes are treated equally. This disregards the valuable inter-node relationships, which are discovered and taken into account as we show in the experiments (and, this helps to achieve efficient collaboration between nodes). (R4) In principle, the local models are directly and heavily dependent on the nodes’ local data. Hence, (e.g., non-parametric) models, which during deployment and inference require access to the data in order to provide predictive services (like
4 Predictive model resilience strategies
Evidently, the performances of the enhanced models are directly linked to the quality of the enhanced training dataset

Node
4.1 Global sampling (GS) strategy
GS is based on a random sampling node
4.2 Guided sampling strategies
GS gives a relatively average summary of
4.2.1 Nearest centroid guided (NCG) strategy
In NCG strategy, we quantize only the input space
with
4.2.2 Centroid guided (CG) strategy
In CG strategy, instead of selecting the nearest pairs to centroids
4.2.3 Weighted guided (WG) strategy
The unfamiliar samples
Hence, given a rate
4.3 Strategies based on information adjacency
The strategies we have introduced so far treat all the
Grouping together the nodes with similarly distributed data seems to be a sensible option, as by only letting the models have controlled access to less “unfamiliar” data within the group, we expect them to be less affected by instances that are more likely to be in nodes from foreign groups that will damage their performance. However, the effect of grouping is heavily affected by the adopted grouping method. Hence, the improper grouping may even negatively impact the models’ predictability. We then investigate how grouping helps under different circumstances and compare the possible gain in performance instead of turning to grouping strategies completely. In this context, we introduce strategy variants based on this information adjacency that leverage inherent or latent information embedded within the nodes’ data to achieve grouping for each of the strategies above. These adjacency variants function exactly the same as their counterparts except that, when generating the enhanced training data
Since grouping strategies value the similarities of the nodes’ data (statistical distances) more than the physical distance (though sometimes they are closely related), we revoked the 1-hop restriction on them. Nodes in the same group are not necessarily reachable to each other within 1 time of data exchange. The topology of the grouping is demonstrated in Figure 3. The nodes adjacency list

Two (groupings) adjacency lists of nodes
4.3.1 Adjacency global sampling (AGS) strategy
In AGS, a neighboring node
4.3.2 Adjacency nearest centroid guided (ANCG) and adjacency centroid guided (ACG) strategies
In ANCG, we take the average vectors
Similarly, in ACG, we obtain the Hausdorff distance between the sets of the centroids of the node
4.3.3 Adjacency weighted guided (AWG) strategy
The AWG strategy is a hybrid of ACG and AGS. Specifically, first, we obtain the Hausdorff distance between the sets of centroids
4.4 Model-driven data (MD) strategy
The MD strategy is proposed as a different one from the above data-driven strategies, where nodes do not need to disseminate real data among them. The rationale of MD is that node
In short, the fabricated input,
The adjacency model-driven (AMD) strategy depends on the distances of the mean vector
A node
5 Experimental evaluation
5.1 Datasets
The GNFUV [30] dataset was collected during the experiments of our project GNFUV5.1
[1]. The dataset contains readings of temperature and humidity from sensors mounted on four unmanned surface vehicles (USVs) monitoring the sea surface in a coastal area in Athens, Greece. The local data
The last dataset is the Combined Cycle Power Plant (CCPP) [32], which contains four types of environmental sensor readings like temperature and pressure. With these readings, the power plant’s total output power is predicted. We proceeded with clustering these data using Gaussian Mixture Model (GMM) into several clusters. UMAP[33] was also used to reduce the clustering results to three dimensions for viewing them intuitively, as shown in Figure 4). Therefore, the clustered data were assigned to

The visualization of the best clustering results we got on CCPP dataset (3 clusters).
5.2 Experimental scenarios
With the GNFUV, Accelerometer and CCPP datasets, we obtain three scenarios: (i) a distributed computing system that has spatiotemporally correlated data across its nodes (hereinafter referred to as GNFUV scenario), (ii) a distributed computing system that has natural data split across its nodes, but the correlation between nodes’ data is relatively weaker (hereinafter referred to as Accelerometer scenario), and (iii) a distributed computing system that has randomly split data across its nodes (hereinafter referred to as CCPP scenario).
GNFUV dataset was collected when the USVs were moving along their parallel routes (as shown in Figure 5). By being spatially close, USVs were moving along adjacent routes and thus were more likely to collect spatiotemporally correlated contextual data. Hence, the nodes that have their data collected by USVs from directly adjacent routes are considered to be adjacent forming their adjacency lists

The trajectories of the USVs building GNFUV dataset.
For both the accelerometer and CCPP datasets, as there are three nodes for these two scenarios, we found that each node has only one adjacent node in their lists
Specifically, for the CCPP dataset, as shown in Figure 4, there are patterns of separation of different nodes’ data, thus forming almost separable clusters. In addition, for the Accelerometer dataset, as shown in Figure 6, all three nodes’ data are centered around the origin 3D point

The distribution of different all nodes’ Accelerometer data in (right) 3D plane; (left) 2D plane over the two principal components using UMAP.
For predictive models, we adopt the supervised learning support vector regression (SVR) model
5.3 Model performance assessment
Upon nodes (e.g., USVs) failure, our framework seeks the most appropriate surrogate node
For each node
Figure 7 shows the results of the enhanced model

GNFUV: Sensitivity analysis of the
5.4 Deployment of our scenarios
5.4.1 Decision-making and assignment resilience policy
We have first identified the best strategy
We introduce a directed graph

GNFUV: Directed graph
With the directed graph, the system is fully operable in EC environments where node failures happen. To further better understand the benefits brought by our approach, we evaluated the system’s performance with full, half, and no guidance at all with node failing probability
Random substitute assignment: The request is assigned to a randomly chosen nonfailing node, which locally processes the task using its local model. This is a baseline policy to investigate what happens without the graph guidance of our approach and without invoking the enhanced models on substitute nodes (zero guidance).
Random substitute assignment with best enhanced model: The request is assigned to a randomly chosen nonfailing node, which locally processes the task using its best enhanced model given the provided graph (half guidance).
Guided substitute assignment: The request is assigned to the most appropriate substitute node as per graph, which locally processes the task using its best enhanced model as per graph (full guidance).
Remark 2
In Figure 8, none of the edges is associated with WG. Compared to other strategies, WG did not achieve a single best on arbitrary pairs of failing
5.4.2 Predictive accuracy assessment
The prediction accuracy results of the aforementioned resilience policies are shown in Figure 9 against node failure probability

GNFUV: System performance against node failure probability
One could observe that the system’s predictability with the guided substitute assignment always out performs the Cloud-based policy even when
Moreover, when
5.4.3 Load impact
We investigated the impact of the substitute assignment policies on the number of invocations on each node, i.e., extra load. Figure 10 shows that with the full guidance policy, node extra loads are relatively balanced. Although we expect node imbalance given tasks workloads; requests to failing node

GNFUV: Extra load per node in the system with full guidance assignment policy and half/zero guidance policy.
5.5 Incorporating the adjacency strategies
From the results in Section 5.3, we obtained insights into the framework’s feasibility and potential based on the first four global strategies (global strategies refer to
5.5.1 Predictive accuracy
The evaluation process, settings, and metrics remain the same as the experiments in Section 5.3. Figures 11, 12 and 13 show the sensitivity analysis regarding the predictive performance across global and adjacency strategies against ratio

Accelerometer: Sensitivity analysis of the

CCPP: Sensitivity analysis of the

GNFUV: Sensitivity analysis of the
For node
In CCPP scenario, node
The performances of the enhanced models of GNFUV’s node
5.5.2 Improved decision-making and assignment resilience policies
For each scenario, we provide the optimal directed graphs

Directed graphs
For Accelerometer and CCPP,
As for the holistic performance of the framework against possible node failures shown in Figure 15, there are several latent but important things worth mentioning. The starting point of all three lines (hereinafter referred to as starting point) in each subplot represents the average error of the system when no node failure occurs.

Framework fault-tolerant predictive performance against node failure probability
5.5.3 Load impact
We can observe some load imbalance in all scenarios in Figure 16 when we also incorporate the adjacency strategies. As mentioned before, this problem could be alleviated by not always using the best substitute node with some trade-offs of performance, which is left in our future research agenda.

Extra load per node in the system with full guidance assignment policy and half/zero guidance policy for all the scenarios adopting global and adjacency strategies.
6 Discussion
6.1 Impact of information adjacency strategies
The discrepancy in the gain from introducing information adjacency, as shown in the experimental results for different scenarios, highlights that the effectiveness of nodes' grouping through this method is heavily dependent on the efficiency of the process for acquiring the lists
It is worth mentioning that, though strategies
6.2 Model maintenance
One of the most important functionalities our framework could provide is effective model maintenance. As in dynamically changing distributed ML systems, the ML models should not remain static because of certain changes in the underlying data (like concept drifts). Instead, such systems should have the ability to keep up with the data changes by recognizing new patterns introduced by concept drifts in, e.g., data streams and retraining them with instances that follow these patterns. We expect that the proposed graph-based guidance (i.e., the directed graphs) to hold for the most part as it is built by excavating inter-nodes’ data relationships. When the system detects meaningful drifts in a node’s data, novel instances should be efficiently sent to whichever nodes have enhanced models that require data from the changing node for model maintenance. In the current stage, our framework focuses on guidance building in the case of node failures and only considers the best substitute node and strategy. In fact, facilitated by the flexibility of the framework, through intelligently grouping nodes and allocating enhanced models invocation, it is possible to make a node failure tolerant system that only requires each of the nodes to maintain one or two models with slight performance trade-offs as compared to a system that operates on an “all best” strategy (i.e., follow the directed graph strictly) when node failure occurs. Such a system is well suited for model maintenance as the process only requires the transferring of a few novel instances and the retaining of several models. The investigation of this mechanism is included in our future research agenda.
7 Conclusions
We propose a predictive model resilience framework relying on strategies to build enhanced models handling requests on behalf of failing nodes. Our framework seeks the best strategy for pairs of failing and substitute nodes to guide invocations upon failures. The best strategies are represented via directed graphs. We assess the system performance over certain node assignment guidance policies and compared it with baseline approaches over real data in distributed computing scenarios. In ideal setups, our framework maintains the system’s predictability performance higher than the baselines even with high failure probability and offers flexibility in load balancing problems. Even in adverse environments, our framework still showed valuable potential. In the future, we plan to expand our framework in terms of (i) intelligent node grouping and enhanced model allocation while providing multiple options for node balancing, (ii) novel pattern detection and model maintenance mechanisms, and (iii) expansion on non-convex optimization (like Deep Learning) regression and classification tasks.
Acknowledgements
The authors would like to thank the Saudi Prime Minister (Crown Prince Mohammad Bin Salman), the Royal Saudi Air Force, Major General Abdulmonaim ALharbi, Senior Engineer Mohammad Aleissa, Saudi Arabia, and the Saudi Arabian Cultural Bureau in the United Kingdom for their support and encouragement.
-
Funding information: The authors state no funding is involved.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: Dr. Christos Anagnostopoulos is the Editor-in-Chief of Open Computer Science but was not involved in the review process of this article.
-
Data availability statement: The datasets used in this article are publicly available.
References
[1] J. Ren, Y. Pan, A. Goscinski, and R. A. Beyah, “Edge computing for the internet of things,” IEEE Netw., vol. 32, no. 1. pp. 6–7, 2018. 10.1109/MNET.2018.8270624Search in Google Scholar
[2] S. Deng, H. Zhao, W. Fang, J. Yin, S. Dustdar, and A. Y. Zomaya, “Edge intelligence: The confluence of edge computing and artificial intelligence,” IEEE Internet Things J., vol. 7, no. 8. pp. 7457–7469, 2020. 10.1109/JIOT.2020.2984887Search in Google Scholar
[3] W. Shi, J. Cao, Q. Zhang, Y. Li, and L. Xu, “Edge computing: Vision and challenges,”. IEEE Internet Things J., vol. 3, no. 5. pp. 637–646, 2016. 10.1109/JIOT.2016.2579198Search in Google Scholar
[4] M. A. Jan, et al. “An AI-enabled lightweight data fusion and load optimization approach for internet of things,” Future Gener. Comput. Syst., vol. 122, pp. 40–51, 2021. 10.1016/j.future.2021.03.020Search in Google Scholar PubMed PubMed Central
[5] J. Wang, S. Pambudi, W. Wang, and M. Song, “Resilience of iot systems against edge-induced cascade-of-failures: A networking perspective,” IEEE Internet Things J., vol. 6, no. 4. pp. 6952–6963, 2019b. 10.1109/JIOT.2019.2913140Search in Google Scholar
[6] A. Borg, J. Baumbach, and S. Glazer, “A message system supporting fault tolerance,” ACM SIGOPS Operating Systems Review, vol. 17, no. 5. pp. 90–99, 1983. 10.1145/773379.806617Search in Google Scholar
[7] B. Cully, G. Lefebvre, D. Meyer, M. Feeley, N. Hutchinson, and A. Warfield, “Remus: High availability via asynchronous virtual machine replication,” In Proceedings of the 5th USENIX symposium on networked systems design and implementation, pp. 161–174. San Francisco, 2008. Search in Google Scholar
[8] J. Sherry, P. X. Gao, S. Basu, A. Panda, A. Krishnamurthy, C. Maciocco, et al. “Rollback-recovery for middleboxes,” In Proceedings of the 2015 ACM Conference on Special Interest Group on Data Communication, pp. 227–240, 2015. 10.1145/2785956.2787501Search in Google Scholar
[9] M. Mudassar, Y. Zhai, and L. Lejian, “Adaptive fault-tolerant strategy for latency-aware IoT application executing in edge computing environment,” IEEE Internet Things J., vol. 9, no. 15. pp. 13250–13262, 2022. 10.1109/JIOT.2022.3144026Search in Google Scholar
[10] M. Siavvas, and E. Gelenbe, “Optimum interval for application-level checkpoints,” In 2019 6th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2019 5th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), pp. 145–150, 2019. 10.1109/CSCloud/EdgeCom.2019.000-4Search in Google Scholar
[11] Y. Harchol, A. Mushtaq, V. Fang, J. McCauley, A. Panda, and S. Shenker, “Making edge-computing resilient,” In Proceedings of the 11th ACM Symposium on Cloud Computing, SoCC ’20, pp. 253–266, New York, NY, USA. Association for Computing Machinery, 2020. 10.1145/3419111.3421278Search in Google Scholar
[12] J. P. Sterbenz, D. Hutchison, E. K. Çetinkaya, A. Jabber, J. P. Rohrer, M. Schller, et al., “Resilience and survivability in communication networks: Strategies, principles, and survey of disciplines,” Comput. Netw., vol. 54, no. 8. pp. 1245–1265, 2010. Resilient and Survivable networks.10.1016/j.comnet.2010.03.005Search in Google Scholar
[13] K. A. Delic, “On resilience of IoT systems: The internet of things (ubiquity symposium),” Ubiquity, 2016 February:1–7. 10.1145/2822885Search in Google Scholar
[14] J. Beutel, K. Römer, M. Ringwald, and M. Woehrle, “Deployment Techniques for Sensor Networks,” pp. 219–248, 2009. 10.1007/978-3-642-01341-6_9Search in Google Scholar
[15] M. M. H. Khan, H. K. Le, M. LeMay, P. Moinzadeh, L. Wang, Y. Yang, et al., “Diagnostic power tracing for sensor node failure analysis,” In Proceedings of the 9th ACM/IEEE international conference on information processing in sensor networks, pp. 117–128, 2010. 10.1145/1791212.1791227Search in Google Scholar
[16] S. Shao, X. Huang, H. E. Stanley, and S. Havlin, “Percolation of localized attack on complex networks,” New J. Phys., vol. 17, no. 2. p. 023049, 2015. 10.1088/1367-2630/17/2/023049Search in Google Scholar
[17] S. N. Shirazi, A. Gouglidis, A. Farshad, and D. Hutchison, “The extended cloud: Review and analysis of mobile edge computing and fog from a security and resilience perspective,” IEEE J. Sel. Areas Commun., vol. 35, no. 11. pp. 2586–2595, 2017. 10.1109/JSAC.2017.2760478Search in Google Scholar
[18] S. Kounev, P. Reinecke, F. Brosig, J. T. Bradley, K. Joshi, V. Babka, et al., “Providing Dependability and Resilience in the Cloud: Challenges and Opportunities,” pp. 65–81. Springer Berlin Heidelberg, Berlin, Heidelberg, 2012. 10.1007/978-3-642-29032-9_4Search in Google Scholar
[19] A. Shafahi, M. Najibi, Z. Xu, J. Dickerson, L. S. Davis, and T. Goldstein, “Universal adversarial training,” AAAI Conference on Artificial Intelligence, vol. 34, no. 04. pp. 5636–5643, 2020. 10.1609/aaai.v34i04.6017Search in Google Scholar
[20] E. Wong, L. Rice, and J. Z. Kolter, “Fast is better than free: Revisiting adversarial training,” CoRR, abs/2001. vol. 03994, 2020. Search in Google Scholar
[21] T. Bai, J. Luo, J. Zhao, B. Wen, and Q. Wang, “Recent advances in adversarial training for adversarial robustness,” CoRR, vol. abs/2102.01356, 2021. 10.24963/ijcai.2021/591Search in Google Scholar
[22] H. Daumé III, “Frustratingly easy domain adaptation,” arXiv:http://arXiv.org/abs/arXiv:0907.1815, 2009. Search in Google Scholar
[23] A. Farahani, S. Voghoei, K. Rasheed, and A. R. Arabnia, “A brief review of domain adaptation,” Advances in Data Science and Information Engineering, pp. 877–894, 2021. 10.1007/978-3-030-71704-9_65Search in Google Scholar
[24] A. Samanta, F. Esposito, and T. G. Nguyen, “Fault-tolerant mechanism for edge-based iot networks with demand uncertainty,” IEEE Internet Things J., vol. 8, no. 23. pp. 16963–16971, 2021. 10.1109/JIOT.2021.3075681Search in Google Scholar
[25] D. Takao, K. Sugiura, and Y. Ishikawa, Approximate fault-tolerant data stream aggregation for edge computing,” In Big-Data-Analytics in Astronomy, Science, and Engineering: 9th International Conference on Big Data Analytics, BDA 2021, Virtual Event, December 7–9, 2021, Proceedings, Berlin, Heidelberg, Springer-Verlag, pp. 233–244, 2021. 10.1007/978-3-030-96600-3_17Search in Google Scholar
[26] C. Wang, C. Gill, and C. Lu, “Frame: Fault tolerant and real-time messaging for edge computing,” In 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), pp. 976– 985. IEEE, 2019a. 10.1109/ICDCS.2019.00101Search in Google Scholar
[27] Q. Wang, J. M. Fornes, C. Anagnostopoulos, and K. Kolomvatsos, “Predictive model resilience in edge computing,” Accepted on IEEE 8th World Forum on Internet of Things 2022. 10.1109/WF-IoT54382.2022.10152282Search in Google Scholar
[28] C. Chatfield, “Model uncertainty, data mining and statistical inference,” Journal of the Royal Statistical Society. Series A (Statistics in Society), vol. 158, no. 3. pp. 419–466, 1995. 10.2307/2983440Search in Google Scholar
[29] A. E. Raftery, D. Madigan, and J. A. Hoeting, “Bayesian model averaging for linear regression models,” J. Am. Stat. Assoc., vol. 92, no. 437. pp. 179–191, 1997. 10.1080/01621459.1997.10473615Search in Google Scholar
[30] N. Harth, and C. Anagnostopoulos, “Edge-centric efficient regression analytics,” In 2018 IEEE EDGE, pp. 93–100. IEEE, 2018. 10.1109/EDGE.2018.00020Search in Google Scholar
[31] G. S. Sampaio, A. R. de Aguiar Vallim Filho, L. S. da Silva, and L. A. da Silva, “Prediction of motor failure time using an artificial neural network,” Sensors, vol. 19, no. 19. p. 4342, 2019. 10.3390/s19194342Search in Google Scholar PubMed PubMed Central
[32] P. Tüfekci, “Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods,” Int J. Electr. Power Energy Syst., vol. 60, pp. 126–140, 2014. 10.1016/j.ijepes.2014.02.027Search in Google Scholar
[33] L. McInnes, J. Healy, and J. Melville, “UMAP: Uniform manifold approximation and projection for dimension reduction,” 2018. 10.21105/joss.00861Search in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- AFOD: Two-stage object detection based on anchor-free remote sensing photos
- A Bi-GRU-DSA-based social network rumor detection approach
- Task offloading in mobile edge computing using cost-based discounted optimal stopping
- Communication network security situation analysis based on time series data mining technology
- The establishment of a performance evaluation model using education informatization to evaluate teacher morality construction in colleges and universities
- The construction of sports tourism projects under the strategy of national fitness by wireless sensor network
- Resilient edge predictive analytics by enhancing local models
- The implementation of a proposed deep-learning algorithm to classify music genres
- Moving object detection via feature extraction and classification
- Listing all delta partitions of a given set: Algorithm design and results
- Application of big data technology in emergency management platform informatization construction
- Evaluation of Internet of Things computer network security and remote control technology
- Solving linear and nonlinear problems using Taylor series method
- Chinese and English text classification techniques incorporating CHI feature selection for ELT cloud classroom
- Software compliance in various industries using CI/CD, dynamic microservices, and containers
- The extraction method used for English–Chinese machine translation corpus based on bilingual sentence pair coverage
- Material selection system of literature and art multimedia courseware based on data analysis algorithm
- Spatial relationship description model and algorithm of urban and rural planning in the smart city
- Hardware automatic test scheme and intelligent analyze application based on machine learning model
- Integration path of digital media art and environmental design based on virtual reality technology
- Comparing the influence of cybersecurity knowledge on attack detection: insights from experts and novice cybersecurity professionals
- Simulation-based optimization of decision-making process in railway nodes
- Mine underground object detection algorithm based on TTFNet and anchor-free
- Detection and tracking of safety helmet wearing based on deep learning
- WSN intrusion detection method using improved spatiotemporal ResNet and GAN
- Review Article
- The use of artificial neural networks and decision trees: Implications for health-care research
Articles in the same Issue
- Regular Articles
- AFOD: Two-stage object detection based on anchor-free remote sensing photos
- A Bi-GRU-DSA-based social network rumor detection approach
- Task offloading in mobile edge computing using cost-based discounted optimal stopping
- Communication network security situation analysis based on time series data mining technology
- The establishment of a performance evaluation model using education informatization to evaluate teacher morality construction in colleges and universities
- The construction of sports tourism projects under the strategy of national fitness by wireless sensor network
- Resilient edge predictive analytics by enhancing local models
- The implementation of a proposed deep-learning algorithm to classify music genres
- Moving object detection via feature extraction and classification
- Listing all delta partitions of a given set: Algorithm design and results
- Application of big data technology in emergency management platform informatization construction
- Evaluation of Internet of Things computer network security and remote control technology
- Solving linear and nonlinear problems using Taylor series method
- Chinese and English text classification techniques incorporating CHI feature selection for ELT cloud classroom
- Software compliance in various industries using CI/CD, dynamic microservices, and containers
- The extraction method used for English–Chinese machine translation corpus based on bilingual sentence pair coverage
- Material selection system of literature and art multimedia courseware based on data analysis algorithm
- Spatial relationship description model and algorithm of urban and rural planning in the smart city
- Hardware automatic test scheme and intelligent analyze application based on machine learning model
- Integration path of digital media art and environmental design based on virtual reality technology
- Comparing the influence of cybersecurity knowledge on attack detection: insights from experts and novice cybersecurity professionals
- Simulation-based optimization of decision-making process in railway nodes
- Mine underground object detection algorithm based on TTFNet and anchor-free
- Detection and tracking of safety helmet wearing based on deep learning
- WSN intrusion detection method using improved spatiotemporal ResNet and GAN
- Review Article
- The use of artificial neural networks and decision trees: Implications for health-care research

