Dynamics of an eco-epidemic model with Allee effect in prey and disease in predator

Bipin Kumar; Rajesh Kumar Sinha

doi:10.1515/cmb-2023-0108

Article Open Access

Dynamics of an eco-epidemic model with Allee effect in prey and disease in predator

Bipin Kumar and Rajesh Kumar Sinha

Published/Copyright: December 29, 2023

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Computational and Mathematical Biophysics Volume 11 Issue 1

Abstract

In this work, the dynamics of a food chain model with disease in the predator and the Allee effect in the prey have been investigated. The model also incorporates a Holling type-III functional response, accounting for both disease transmission and predation. The existence of equilibria and their stability in the model have also been investigated. The primary objective of this research is to examine the effects of the Allee parameter. Hopf bifurcations are explored about the interior and disease-free equilibrium point, where the Allee is taken as a bifurcation point. In numerical simulation, phase portraits have been used to look into the existence of equilibrium points and their stability. The bifurcation diagrams that have been drawn clearly demonstrate the presence of significant local bifurcations, including Hopf, transcritical, and saddle-node bifurcations. Through the phase portrait, limit cycle, and time series, the stability and oscillatory behaviour of the equilibrium point of the model are investigated. The numerical simulation has been done using MATLAB and Matcont.

Keywords: eco-epidemic model; equilibrium point; stability analysis; Hopf bifurcation; transcritical bifurcation

MSC 2010: 34D20; 92B05; 92D25; 34C23; 37Gxx

1 Introduction

In ecology and eco-epidemiology, mathematical modelling plays an important role. In the current situation, the world suffers from various epidemic crises like COVID, dengue, plague, flu, and various zoonotic diseases. Eco-epidemiology is a relatively new area in mathematical modelling that deals with ecological and epidemiological issues simultaneously [10,31]. Our understanding of epidemic models has greatly improved as a result of the innovative work done by Kermack and McKendrick, opening the door for the investigation of a newly created interdisciplinary area called eco-epidemiology [11]. To better understand the dynamics of disease within communities, this field connects components of ecology and epidemiology. There is a wealth of literature in the field of human-related epidemiology that applies the ideas of the Kermack-McKendrick model. Research on diseases like HIV [3], rabies [27], the mumps virus [24], and the SARS-coronavirus [4] are a few famous examples. These research have improved our knowledge of how diseases spread and are controlled in human societies. By creating mathematical models that depict the spread of diseases among interacting populations, Hadeler and Freedman [17] have significantly improved our understanding of the subject. Their research has illuminated how illnesses might spread across intricate ecological networks. By examining subjects like species persistence and Hopf bifurcation within epidemic models, Mukherjee [25] has added to our understanding. This study has shed important light on the mechanisms of disease persistence and the crucial junctures at which important shifts in ecological and epidemiological systems take place. Ecological species sizes are important in ecological studies and are influenced by a variety of ecological and epidemiological factors. Predatory behaviour, intraspecific and interspecific competition, and various types of species interaction are the ecological aspects. The transmission of infectious diseases is one of the major epidemiological issues [28]. Researchers are interested in studying infectious diseases in their natural environment. The effects of infectious diseases should be considered in the study of dynamical systems [26]. The first predator-prey model was given by Lotka and Volterra for two species and is the simplest model of predator-prey interactions. The predator-prey model was developed independently by Lotka in 1925 and Volterra in 1926 [9,37], the general form of the simplest Lotka-Volterra model is given as follows:

(1a) d z d t = α z − β z w

(1b) d w d t = γ z w − δ w ,

where z is the number of prey population, w is the predator population, β and γ are the positive interaction parameters, and α and δ are the birth rate of prey and natural death rate of predator respectively. The first three-species food chain model was given by Hasting and Powell in 1991. The author investigated the dynamics of the model without the Allee effect, and the model was found to be very chaotic in long-term behaviour when the biologically valid parameters were taken [19]. After this, further research were carried out on dynamical properties of food chain model without Allee and with a different type of functional responses [1]. In 2016, KP Das introduced the Eco-epidemic model involving three-species, excluding the Allee effect. According to Das’s publication, the presence of chaotic dynamics is observed as the population of infected predators increases. It is shown that occurrence and chaos control are due to half saturation [13,14]. The Allee effect was first introduced by Warder Clyde Allee in 1930s. The Allee effect is crucial for describing the population growth rate in population biology, and when the population density is low, the Allee effect is a biological phenomenon that results in a positive relationship between population size and per capita growth rate [15,34]. Mathematical expression of Allee term with logistic growth given as:

(2) d N d t = r N 1 − N K N A − 1 ,

where A is the Allee parameter, K is carrying capacity and r is the intrinsic growth rate.

The Allee effect has currently received considerable attention in research communities due to its significant effect on population dynamics. The phenomenon, often referred to as the Allee effect [2], explains the positive association between the per capita growth rate and population density. The emergence of this phenomenon may be related to many different factors, including challenges in locating compatible partners in territories with low populations, a rise in susceptibility to predation, negative effects resulting from mating among closely related individuals, the insufficient presence of defensive mechanisms against predators, and other contributing factors. The Allee effect is often classified into two primary categories: strong and weak instances. The phenomenon referred to as a significant Allee effect, sometimes termed critical dispensation, occurs when a population attains a critical size or threshold. Once the barrier has been overcome, the per capita growth rate transitions from negative to positive and gradually approaches the carrying capacity. On the other hand, the weak Allee effect does not demonstrate a discernible threshold. Both manifestations of the Allee effect, whether they are powerful or mild, have noteworthy implications for the dynamics of populations. The Allee concept is briefly discussed in the studies by Arancibia-Ibarra and Flores [6] and Sarangi and Raw [30]. The earlier discovery has prompted the recognition that the co-occurrence of diseases and the Allee effect may have a collective influence on the sustainability and potential extinction of species. In order to clarify the biological importance of the Allee effect, notable instances such as the island fox [5] and the African wild dog [12] may be examined. The ecological and eco-epidemiological models have been published with the Allee effect by the authors [22,23,32]. These articles examine the effects of the Allee effect, which causes Hopf bifurcation and chaos.

The Allee effect can change interior equilibria and is capable of influencing internal attraction. In addition, coexistence is possible at endemic state, and under appropriate parametric situations, the infection may be suppressed [20]. The chaotic behaviour of the ecological model decreases with the increase in severity of the Allee effect [22]. Recently, researchers did work on the effects of double Allee on eco-epidemic model [30]. In predator-prey interactions, the choice of functional response plays a crucial role. The predator-prey functional response quantifies the rate at which predators consume prey per unit of time. Mathematical analyses of ecological, epidemiological, and eco-epidemiological systems rely on various functional responses, including the Holling type-I functional response [29], the Holling type-II functional response [33], and the ratio-dependent functional response, Among these, the predator-prey interaction with ratio-dependent functional response is often considered the most effective approach [7]. In this study, we investigate an eco-epidemic model that incorporates the Allee effect in prey and disease in predators. The model is initially based on the Holling type-II functional response for both predation and disease transmission, as described in the study by Shaikh and Das [32]. However, in our research, we introduce the Holling type-III functional response to the model to study its dynamics.

In this current study, we examine the dynamic behaviour of a system, specifically focusing on the examination of equilibrium states and their stability. In addition, we conduct a comprehensive analysis of bifurcation phenomena within the system. In Section 2, model formulation is discussed. In Section 3, theoretical studies such as positivity and boundedness of model 4 are studied. In Section 4, the conditions for the existence of equilibrium points have been analysed. Stability analysis about all possible equilibrium and bifurcation analysis is discussed in Section 5, in which Hopf bifurcation about the Allee parameter is obtained. In Section 6, numerical study has been done, and the dynamical properties, such as equilibria and their stability, as well as the periodic behaviour of the model, look exactly the same as the analytical study for the restricted conditions. Finally, the result discussion, the biological significance of the model, and future research have been discussed in Section 7.

2 Model description

This model is a modification of the article published by Shaikh and Das [32]. The predator is divided into two compartments, susceptible S and infected predator I , respectively, and the prey population density is denoted by N . The prey population grows logistically with carrying capacity k and the intrinsic growth rate R . Furthermore, the population of prey exhibits the Allee effect. The disease is transmitted by predators horizontally. Infected predator cannot catch and kill the prey population as parasite infection decreases the host’s stamina and locomotive efficiency [14]. We use Holling type-III functional response for predation and disease transmission mechanism.

The model with the above assumptions takes the following form:

(3a) d N d T = R N 1 − N K N L − 1 − A N 2 S B 1 + N 2

(3b) d S d T = C 1 A N 2 S B 1 + N 2 − λ S 2 I B 2 + S 2 − D 1 S

(3c) d I d T = λ S 2 I B 2 + S 2 − D 2 I ,

where we take the initial restrictions N ( 0 ) ≥ 0 , S ( 0 ) ≥ 0 , and I ( 0 ) ≥ 0 for the further analysis; the parameter L denotes the Allee threshold value, whereas λ , B 1 , D 1 , and D 2 denote the rates of disease transmission, the half saturation constant, and the rates of natural mortality of susceptible and infected predators, respectively. The parameter C 1 ∈ ( 0 , 1 ) denotes the rate of conversion of prey biomass into susceptible predator. By using the following transformations: x = N K , y = S K , I 1 = I K , and t = R T , respectively, the model (3) has transformed into a non-dimensional model (4) as follows:

(4) d x d t = x ( 1 − x ) ( θ x − 1 ) − α x 2 y 1 + b 1 x 2 = x f 1 ( x , y , I 1 ) d y d t = r x 2 y 1 + b 1 x 2 − β y 2 I 1 1 + b 2 y 2 − d 1 y = y f 2 ( x , y , I 1 ) d I 1 d t = β y 2 I 1 1 + b 2 y 2 − d 2 I 1 = I 1 f 3 ( x , y , I 1 ) ,

with initial condition x ( 0 ) ≥ 0 , y ( 0 ) ≥ 0 , and I 1 ( 0 ) ≥ 0 , where

θ = K L , α = A K 2 B K , r = C 1 A 1 K 2 B 1 R , d 2 = D 2 R , d 1 = D 1 R , b 1 = K 2 B 1 , and b 2 = K 2 B 2 .

3 Theoretical studies of model (4)

3.1 Existence and positivity

Theorem 3.1

For the system described in equation (4) every solution associated with initial conditions where x ( 0 ) ≥ 0 , y ( 0 ) ≥ 0 , and I 1 ( 0 ) ≥ 0 exists and unique in the interval [ 0 , ε ] , where 0 < ε < ∞ and x ( t ) ≥ 0 , y ( t ) ≥ 0 , and I 1 ≥ 0 for all t in this interval.

Proof

Since the given function x f 1 , y f 2 , and I 1 f 3 are continuous and locally Lipschitzian on R + 3 , which implies that the solution ( x ( t ) , y ( t ) , I 1 ( t ) ) exists and unique on [ 0 , ε ] , where 0 < ε < ∞ [18]. Furthermore, by integrating the model (4) with respect to the initial conditions, we obtain the following solutions:

x ( t ) = x ( 0 ) e ∫ 0 t f 1 ( x ( s ) , y ( s ) , I 1 ( s ) ) d s ≥ 0 ,

y ( t ) = y ( 0 ) e ∫ 0 t f 2 ( x ( s ) , y ( s ) , I 1 ( s ) ) d s ≥ 0 ,

I 1 ( t ) = I 1 ( 0 ) e ∫ 0 t f 3 ( x ( s ) , y ( s ) , I 1 ( s ) ) d s ≥ 0 ,

where x ( 0 ) = x 0 ≥ 0 , y ( 0 ) = y 0 ≥ 0 , and I 1 ( 0 ) ≥ 0 . Hence, the theorem proved.□

3.2 Boundedness of the solution

Theorem 3.2

In R + 3 , all the solution of model (4) are uniformly bounded.

Proof

Let us assume p = x + y + I 1 , and by differentiating it, we obtain

(5) d p d t = d x d t + d y d t + d I 1 d t

and taking the value of d x d t , d y d t , and d z d t from model (4), we have

d p d t = x ( 1 − x ) ( θ x − 1 ) − α x 2 y 1 + b 1 x 2 + r x 2 y 1 + b 1 x 2 − d 1 y − d 2 I 1 , d p d t + μ p = [ x ( 1 − x ) ( θ x − 1 ) + μ x ] − α x 2 y 1 + b 1 x 2 + r x 2 y 1 + b 1 x 2 − ( d 1 − μ ) y − ( d 2 − μ ) I 1 , ≤ x [ ( ( θ + 1 + μ ) − θ x ) x ] − ( d 1 − μ ) y − ( d 2 − μ ) I 1 , ≤ 1 + θ θ μ + ( θ + 1 ) 4 θ = ϕ .

If ϕ > min ( d 1 , d 2 ) and using upper bound ( 1 + θ ) / θ of x, we defined ϕ > 0 such that

d p d t + μ p ≤ ϕ ∀ t ∈ ( 0 , t b )

with the theory of differential inequality (Grönwall’s inequality) [8] we obtain

0 < p ( x , y , I 1 ) ≤ ϕ μ ( 1 − e − μ t ) + p ( x ( 0 ) , y ( 0 ) , I 1 ( 0 ) ) e − μ t .

and we have 0 < p < ϕ μ for t → ∞ . Hence, it is clear that all solutions of the system will remain in the region

□ τ = ( x , y , I 1 ) ∈ R + 3 : p ≤ ϕ μ for all time .

4 Equilibria and their existence

The equilibrium points of system (4) are obtained by solving the equations d x d t = 0 , d y d t = 0 , and d I 1 d t = 0 . We are getting the trivial equilibrium point E 0 ( 0 , 0 , 0 ) , which always exists. Two axial equilibrium points E 1 ( 1 , 0 , 0 ) and E 2 ( 1 θ , 0 , 0 ) always exists. Another equilibrium point that is the boundary equilibrium point E 3 ( x * , y * , 0 ) exists under the condition r > b 1 d 1 , p ≤ 1 , and p ≥ 1 θ , where x * = d 1 ( r − b 1 d 1 ) = p (say) and y * = ( 1 + b 1 p 2 ) ( 1 − p ) ( θ p − 1 ) α p . Next, the system has the interior equilibrium points ( x * , y * , I 1 * ) , where y * = d 2 β − b 2 d 2 and I 1 * = r x * 2 1 + b 1 x 2 − d 1 1 + b 2 y * 2 β y * provided x * < d 1 r − d 1 b 1 , r > b 1 d 1 , β > b 2 d 2 , and x * is calculated from equation (6) as follows:

(6) f ( x ) = − θ b x 4 + ( θ + 1 ) b x 3 − ( θ + b ) x 2 − ( α p − ( θ + 1 ) ) x − 1 = 0

Using Descartes’ rule of signs, equation (6) could have two positive roots if α > θ + 1 y * . This is because there are two sign changes in this case. If the condition fails, then three possibilities exist: (i) no positive root; (ii) two positive roots; and (iii) four positive roots (Figure 1).

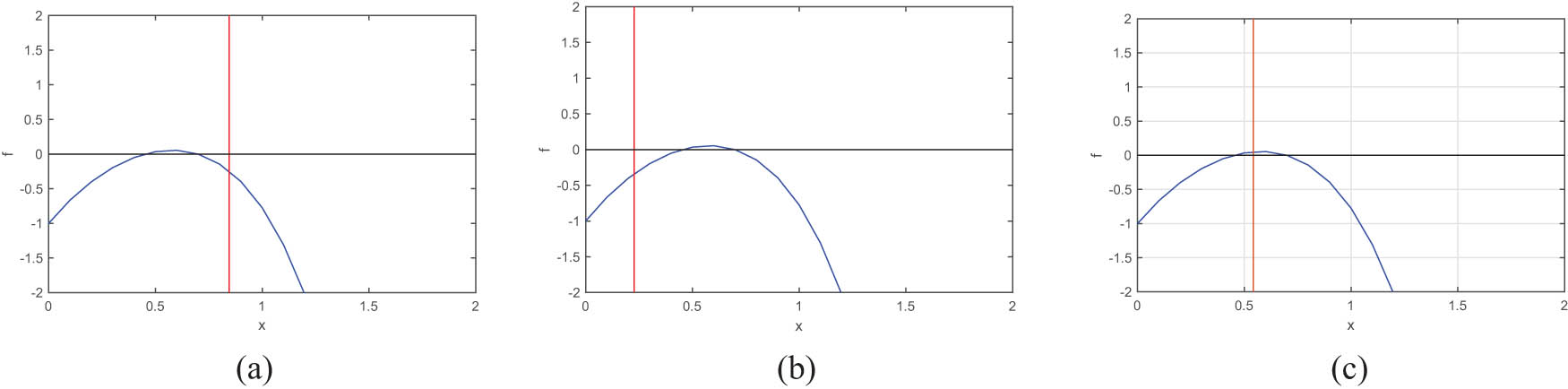
$Figure 1 These figures show the positive roots of equation (6). The blue curve represents the graph of f ( x ) f\left(x) vs x x for the equation (6). The red line represents the line x * = d 1 r − d 1 b 1 {x}^{* }=\sqrt{\frac{{d}_{1}}{r-{d}_{1}{b}_{1}}} . For the positive roots of the equation (6), it holds that x * < d 1 r − d 1 b 1 {x}^{* }\lt \sqrt{\frac{{d}_{1}}{r-{d}_{1}{b}_{1}}} , so from the above figure, it is clear that (a) shows two feasible roots, (b) shows zero feasible roots, and (c) shows one feasible root, respectively. The parameters are taken from Table 1.$

Figure 1

These figures show the positive roots of equation (6). The blue curve represents the graph of f ( x ) vs x for the equation (6). The red line represents the line x * = d 1 r − d 1 b 1 . For the positive roots of the equation (6), it holds that x * < d 1 r − d 1 b 1 , so from the above figure, it is clear that (a) shows two feasible roots, (b) shows zero feasible roots, and (c) shows one feasible root, respectively. The parameters are taken from Table 1.

5 Stability of equilibria and local bifurcation

For the local stability of the equilibrium point, we need to first find Jacobian matrix about the equilibrium point and then find the eigenvalue of the matrix. Now Jacobian matrix for model (4) is defined as follows:

(7) J * = A 11 A 12 A 13 A 21 A 22 A 23 A 31 A 32 A 33 ,

where

A 11 = ∂ f 1 ∂ x = − 3 θ x 2 + 2 x ( θ + 1 ) − 1 − 2 α x y ( 1 + b 1 x 2 ) 2 , A 12 = ∂ f 1 ∂ y = − α x 2 ( 1 + b 1 x 2 ) A 13 = ∂ f 1 ∂ I 1 = 0 , A 21 = ∂ f 2 ∂ x = − 2 r x y ( 1 + b 1 x 2 ) 2 , A 22 = ∂ f 2 ∂ y = r x 2 ( 1 + b 1 x 2 ) − 2 β y I 1 ( 1 + b 2 y 2 ) 2 − d 1 A 23 = ∂ f 2 ∂ I 1 = − β y 2 1 + b 2 y 2 , A 31 = ∂ f 3 ∂ x = 0 , A 32 = ∂ f 3 ∂ y = − 2 β y I 1 ( 1 + b 2 y 2 ) 2 , A 33 = ∂ f 3 ∂ I 1 = β y 2 1 + b 2 y 2 − d 2 .

The Jacobian matrix of model (4) about trivial equilibrium is:

(8) J ( E 0 ) = − 1 0 0 0 − d 1 0 0 0 − d 2 ,

where − 1 , − d 1 , and − d 2 are eigenvalues, respectively, and are all negative; hence, E 0 = ( 0 , 0 , 0 ) is always in asymptotically stable equilibrium.

Theorem 5.1

The equilibrium point E 1 = ( 1 , 0 , 0 ) is stable if θ > 1 and d 1 > r 1 + b 1 ; otherwise, unstable.

Proof

Jacobian matrix about E 1 ( 1 , 0 , 0 )

(9) J ( E 1 ) = 1 − θ − α 1 + b 1 0 0 r 1 + b 1 − d 1 0 0 0 − d 2 .

Here, all eigenvalues are negative if θ > 1 and d 1 > r 1 + b 1 . Hence, the axial equilibrium E ( 1 , 0 , 0 ) is asymptotically stable.□

Theorem 5.2

Disease-free equilibrium E 3 = ( x * , y * , 0 ) is locally stable if A 11 < 0 , A 33 < 0 , and A 12 . A 21 < 0 .

Proof

The Jacobian matrix of model (4) about Disease-free equilibrium is:

(10) J = A 11 A 12 A 13 A 21 A 22 A 23 A 31 A 32 A 33 ,

where

A 11 = a = − 3 θ p 2 + 2 p ( θ + 1 ) − 1 − α p q ( 1 + p 2 b 1 ) 2 , A 12 = a 12 = − α p 2 ( 1 + p 2 b 1 ) , A 13 = a 13 = 0 , A 21 = 2 r p q ( 1 + p 2 b 1 ) 2 , A 22 = − r p 2 ( 1 + p 2 b 1 ) − d 1 , A 23 = − β q 2 ( 1 + q 2 b 2 ) , A 31 = 0 , A 32 = 0 , A 33 = c = β q 2 ( 1 + q 2 b 2 ) − d 2 , where x * = p = d 1 r − b 1 d 1 and y * = q = ( 1 + b 1 p 2 ) ( 1 − p ) ( θ p − 1 ) α p

(11) J = a A 12 0 A 21 0 A 23 0 0 A 33

The one eigenvalue of the above Jacobian matrix is A 33 < 0 , and the other two eigenvalues can be calculated from the equation λ 2 − a λ − A 12 A 21 = 0 , i.e.,

(12) λ 1 , 2 = a ± a 2 + 4 A 12 A 21 2

where both roots of equation (12) are negative if it satisfies the following conditions:

A 21 A 12 < 0 and A 11 < 0 , i.e., if these conditions are satisfied then disease-free equilibrium point is locally asymptotically stable.□

5.1 Stability analysis of coexistence equilibrium

Theorem 5.3

The interior equilibrium point of model (4) is locally asymptotically stable if the following conditions hold: a 1 > 0 , a 3 > 0 , and a 1 a 2 − a 3 > 0 .

Proof

Jacobian matrix about the coexistence equilibrium:

(13) J = A 11 A 12 0 A 21 A 22 A 23 0 A 32 0 ,

where

A 11 = ∂ f 1 ∂ x = − 3 x 2 + 2 x ( θ + 1 ) − 1 − 2 α x y ( 1 + b 1 x 2 ) , A 12 = ∂ f 1 ∂ y = − α x 2 ( 1 + b 1 x 2 ) , A 13 = 0 , A 21 = ∂ f 2 ∂ x = 2 r x y ( 1 + b 1 x 2 ) ,

A 22 = ∂ f 2 ∂ y = r x 2 ( 1 + b 1 x 2 ) − 2 β y I 1 ( 1 + b 2 y 2 ) − d 1 , A 23 = − β y 2 1 + b 2 y 2 , A 31 = 0 , A 32 = ∂ f 3 ∂ y = − 2 β y I 1 ( 1 + b 2 y 2 ) 2 ,

A 33 = ∂ f 3 ∂ I 1 = β y 2 1 + b 2 y 2 − d 2 .

The characteristic equation of the matrix is:

(14) λ 3 + a 1 λ 2 + a 2 λ + a 3 = 0 ,

where

a 1 = − ( A 11 + A 22 ) , a 2 = A 11 A 22 − A 32 A 23 − A 12 A 21 , a 3 = − ( A 32 A 11 A 23 ) ,

and λ is the eigenvalue. According to the Routh-Hurwitz criterion, stability conditions are a 1 > 0 , a 3 > 0 , and a 1 a 2 > a 3 . If the equilibrium point satisfies these conditions, the equilibrium point will be locally asymptotically stable.□

5.2 Bifurcation analysis

Definition 5.4

Bifurcation: Bifurcation occurs when the dynamical behaviour of a system, such as equilibrium stability and number of equilibrium, changes as a result of a small change in a parameter. The parameter at which the behaviour changes is called the bifurcation point [35].

5.2.1 Hopf bifurcation

Definition 5.5

A Hopf bifurcation is a type of local bifurcation in dynamical systems where a stable equilibrium point becomes unstable and periodic (oscillatory) behaviour emerges as a parameter changes [35].

Theorem 5.6

The model (4) shows Hopf bifurcation around a disease-free equilibrium point if θ exceeds its critical value, i.e.,

(15) θ = θ h = α p q + ( 1 + p 2 b 1 ) 2 + 2 p ( 1 + p 2 b 1 ) 2 − 3 p 2 ( 1 + p 2 b 1 ) 2 + 2 p ( 1 + p 2 b 1 ) 2

Proof

The eigenvalues of the model (4) about the disease-free equilibrium is defined in Theorem 5.2, where λ 1 and λ 2 are the complex eigenvalues and λ 3 is the real eigenvalue. The complex eigenvalues λ 1 and λ 2 are purely imaginary if and only if there is a critical value of θ = θ h . By differentiating the real part of the complex eigenvalue about θ and equating with zero, we obtain θ h as follows:

θ = θ h = α p q + ( 1 + p 2 b 1 ) 2 + 2 p ( 1 + p 2 b 1 ) 2 − 3 p 2 ( 1 + p 2 b 1 ) 2 + 2 p ( 1 + p 2 b 1 ) 2 .

Furthermore, for i = 1 , 2 , the real part Re d λ i d θ = − 3 p 2 + 2 p ≠ 0 , which satisfy the transversality condition. So the system experience Hopf bifurcation around E 4 ( x * , y * , 0 ) for some critical value of the parameter θ = θ h .

Numerically, it can also be proven by setting the parameters as follows: α = 0.79 , θ = 2.5 , β = 0.16 , r = 1 , d 1 = 0.6868 , d 2 = 0.71 , b 1 = 0.015 , and b 2 = 0.010158 . There exists a single boundary equilibrium, denoted as E b ( x , y , 0 ) = ( 0.7589 , 0.363096 , 0 ) , for these parameters. The corresponding eigenvalues are ( − 0.363643 + 0.339455 i , − 0.363643 − 0.339455 i , − 0.697620932 ) . This equilibrium point is stable, as all the real parts of the Jacobian matrix are negative. In addition, the eigenvalues of the Jacobian matrix at the Hopf bifurcation point, θ = 1.4458113 , are approximately ( 0.215560238 i , − 0.2155600238 i , − 0.7095630693 ) . This signifies that the equilibrium point becomes unstable as the eigenvalues have opposite signs. The stability is lost at θ = 1.4458113 . The transversality condition is satisfied as Re ( d λ d θ ) = − 0.1875 ≠ 0 . Hence, Hopf bifurcation is proved for the given parameters.□

Theorem 5.7

Hopf bifurcation about the interior equilibrium E ( x * , y * , I 1 * ) of model 4 occurs whenever the Allee parameter attains the threshold value θ = θ h b in the domain D h b = θ h b

D h b = θ h b ∈ R + : H ( θ h b ) = [ a 1 ( θ ) a 2 ( θ ) − a 3 ( θ ) ] θ = θ h b = 0 with a 2 ( θ h b ) > 0 , d H ( θ ) d θ θ = θ h b ≠ 0 .

Proof

The characteristic equation for a matrix J * is given as follows:

(16) λ 3 + a 1 λ 2 + a 2 λ + a 3 = 0 ,

In this equation, λ represents the eigenvalues of the matrix J * and a 1 , a 2 , and a 3 are coefficients defined in the proof of Theorem 5.3. We have ( a 1 a 2 − a 3 ) ∣ θ = θ h b = 0 . In addition, from equation (16), we have ( λ 2 + a 2 ) ( λ + a 1 ) , which gives three roots: λ 1 = i a 2 , λ 2 = − i a 2 , and λ 3 = − a 3 . The generally form the roots of (16) are λ 1 = p ( θ ) + i b ( θ ) , λ 2 = p ( θ ) − i b ( θ ) , λ 3 = − a 1 ( θ ) for all values of λ . By differentiating characteristic equation (16), we have

(17) d λ d θ = − ( λ 2 a 1 ˙ + λ a 2 ˙ + a 3 ˙ ) 3 λ 2 + 2 a 1 λ + a 2

and by substituting, λ = i a 2 in equation (17), we have

d λ d θ = a 3 ˙ − a 2 a 1 ˙ + i a 2 ˙ a 2 2 ( a 2 − i a 1 a 2 ) ,

after rationalisation, we have

(18) d λ d θ = a 3 ˙ − ( a 2 a 1 ˙ + a 2 a 1 ˙ ) 2 ( a 1 2 + a 2 ) + i a 2 ( a 1 a 3 ˙ + a 2 a 2 ˙ − a 1 a 2 a 1 ˙ ) 2 a 2 ( a 1 2 + a 2 ) = − − d H d θ 2 ( a 1 2 + a 2 ) + i a 2 a 2 ˙ 2 a 2 − a 1 a 2 d H d θ 2 a 2 ( a 1 2 + a 2 ) ,

From equation (18), we clearly see that all the criteria for the Hopf bifurcation satisfy for the domain assumed in the that theorem. Here, d Re ( λ ) d θ θ h b = − d H d θ 2 ( a 1 2 + a 2 ) ≠ 0 , and by monotonicity restriction in the real part of the complex root d R ( λ ) d θ ≠ 0 [38], the transversality condition d H d θ ≠ 0 ensures the existence of Hopf bifurcation.□

5.2.2 Transcritical bifurcation

Definition 5.8

A transcritical bifurcation refers to a particular type of bifurcation that occurs in dynamical systems. This phenomenon occurs when two equilibrium points, each having opposite stability characteristics, undergo a switch in their stability features when a parameter is varied.

Theorem 5.9

The model (4) has transcritical bifurcation around the axial equilibrium E 1 ( 1 , 0 , 0 ) at θ = θ [ t c ] , where θ [ t c ] = 1 and r 1 + b 1 ≠ d 1 .

Proof

The model (4) undergoes a transcritical bifurcation around the axial equilibrium if it meets the criteria outlined by Sotomayor, stated as follows: (i) W T f θ ( E 1 , θ ) = 0 , (ii) W T [ D f θ ( E 1 , θ ) v ] ≠ 0 , and (iii) W T [ D 2 f ( E 1 , θ ) ( v , v ) ] ≠ 0 . From matrix (9), we clearly see that one of the eigenvalue will be zero iff D e t ( J 1 ) = 0 , which implies that θ [ t c ] = 1 and the other two nonzero eigenvalues are − d 2 , − ( 1 + b 1 ) d 1 + r 1 + b 1 . We find eigenvectors v and w with a zero eigenvalue corresponding to matrix J and J T . Then, we obtain v = ( 1 , 0 , 0 ) T and w = − ( 1 + b 1 ) d 1 + r α , 1 , 0 T . We have

( i ) W T f θ ( E 1 , θ ) = 0 , ( i i ) W T [ D f θ ( E 1 , θ ) v ] = − − ( 1 + b 1 ) d 1 + r α ≠ 0 ,

and

( i i i ) W T [ D 2 f ( E 1 , θ ) ( v , v ) ] = − 2 − ( 1 + b 1 ) d 1 + r α ≠ 0

if d 1 ≠ r 1 + b 1 and all conditions of Sotomayor’s are satisfied. Hence, the system experiences transcritical bifurcation.□

Theorem 5.10

For the interior equilibrium point, saddle-node bifurcation occurs at θ = 3.302872 for the fixed parameters shown in Table 1.

Table 1

This table shows the fixed parameters set denoted by set (A)

α	β	r	d 1	d 2	b 1	b 2
0.5	0.061	0.5	0.05	0.06	0.5	0.6

Proof

The number of interior equilibrium points changed as the bifurcation parameter value θ varied. From bifurcation Figure 2, we easily see that two equilibriums come together, collide, and annihilate each other at limit point θ = 3.302872 . At the limit point, there is exactly one equilibrium. There are no equilibria before it, and after the limit point, two equilibria occur (Figure 2).□

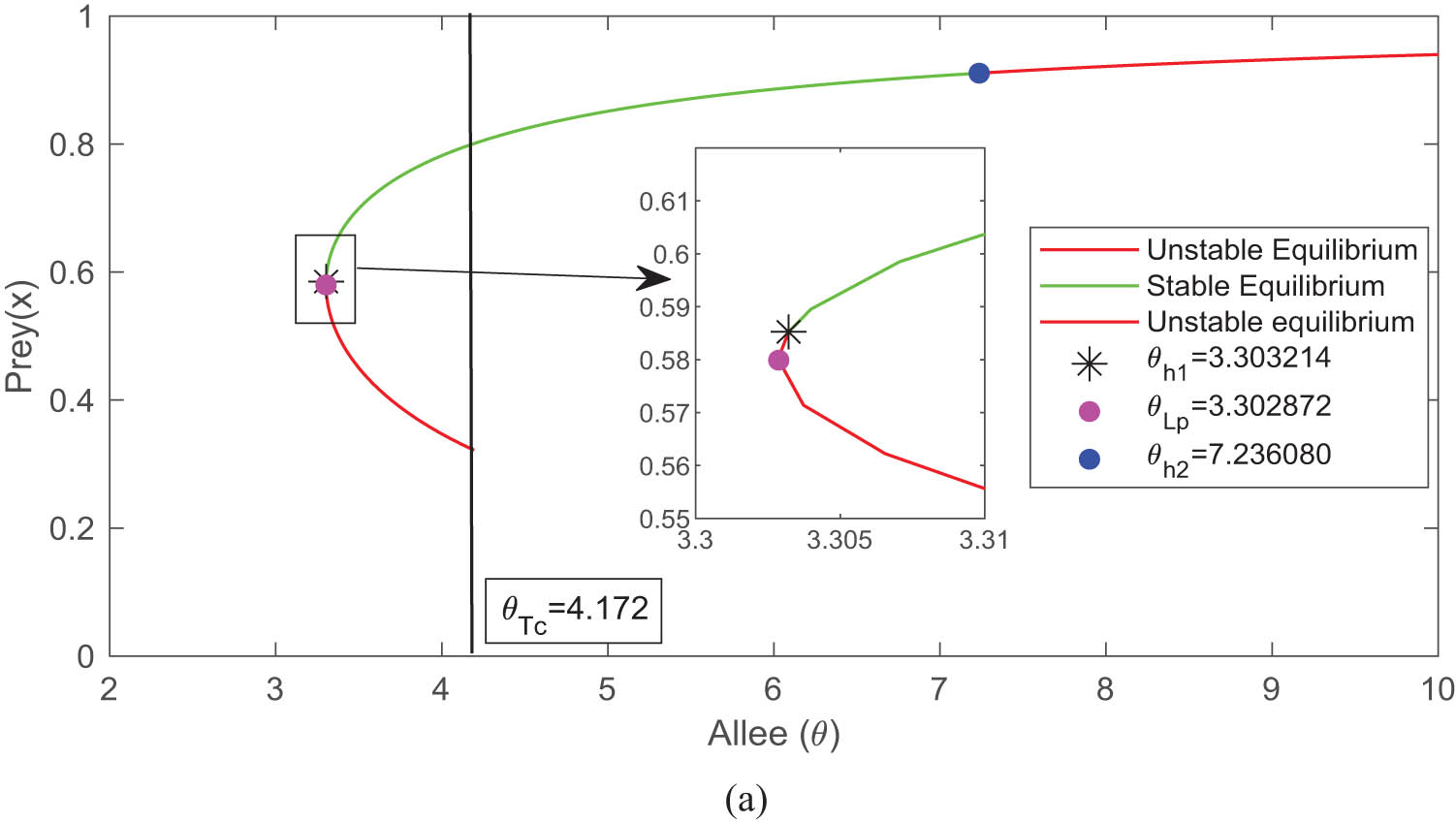
$Figure 2 This is the one parametric bifurcation diagram, where the Allee considered as a bifurcations parameter. This diagram shows that Hopf bifurcations are occurs at θ = θ h 1 = 3.303214 \theta ={\theta }_{h1}=3.303214 , and θ = θ h 2 = 7.236080 \theta ={\theta }_{h2}=7.236080 , Also saddle node and transcritical bifurcation obtained at θ = θ L P = 3.302872 , \theta ={\theta }_{LP}=3.302872, and θ = θ t c = 4.172 \theta ={\theta }_{tc}=4.172 respectively. Taking all parameters same as fixed set A in Table 1 and initial condition x 0 = 0.97 {x}_{0}=0.97 , y 0 = 1.56 {y}_{0}=1.56 , and I 1 ( 0 ) = 6.3 {I}_{1}\left(0)=6.3 .$

Figure 2

This is the one parametric bifurcation diagram, where the Allee considered as a bifurcations parameter. This diagram shows that Hopf bifurcations are occurs at θ = θ h 1 = 3.303214 , and θ = θ h 2 = 7.236080 , Also saddle node and transcritical bifurcation obtained at θ = θ L P = 3.302872 , and θ = θ t c = 4.172 respectively. Taking all parameters same as fixed set A in Table 1 and initial condition x 0 = 0.97 , y 0 = 1.56 , and I 1 ( 0 ) = 6.3 .

6 Numerical simulation

In this section, we describe the dynamics of model (4) numerically, for which we have used the mathematical tools Matlab and Maple. The Runge-Kutta fourth order method is used to describe the dynamical behaviour of the model. The analytical and numerical studies give exactly the same results, which means that the study of dynamical behaviour like equilibria and their stability, as well as some local bifurcations, in both analytical and numerical studies gives the same results for the valid set of parameters. We have fixed the parameters set (1) for further numerical simulation.

In order to conduct more numerical simulations, we maintain the fixed parameters and investigate the impact of the Allee parameter by varying its value. This part focuses on the examination of the dynamical properties, including stability and bifurcation, of the model with respect to its equilibrium points. By using the Maple software (mathematical tool), we have verified the analytical results numerically. Now we have plotted one-dimensional bifurcation diagram using the bifurcation parameter Allee ( θ ) with the help of the Matcont toolbox.

To study a Hopf bifurcation point more closely, you can indeed plot various visual representations of the system’s behaviour, including phase portrait, limit cycle, and time series. A limit cycle is a closed trajectory in the phase space, representing the oscillatory behaviour. This can help you visualise the system’s periodic motion. The time series plots show how the system’s behaviour evolves over time and can illustrate the transition to oscillatory behaviour at the Hopf bifurcation point. This article investigates bifurcation diagrams, limit cycles, and time series plots in the next subsections.

6.1 Bifurcation diagram

Figure 2 describes two interior equilibria for 3.302872 < θ < 4.172 , one of which is stable and the other is unstable. There is one stable interior equilibrium for 4.172 < θ < 7.236080 , and one unstable interior equilibrium for θ > 7.236080 . The limit point bifurcation occurred at θ = θ L P = 3.302872 . In Figure 2, it is evident that there are no interior equilibria before reaching the value of θ L P . However, as we cross the limit point θ L P , the system exhibits two interior equilibria. This observation indicates that there is a change in the number of equilibria as the parameter θ varies, which is a characteristic of a saddle-node bifurcation. The black line (line drown at θ t c = 4.172 ) depicts transcritical bifurcation, as two equilibrium points exist before the black line and one equilibrium point after the black line. In addition, at θ = 7.236080 , supercritical Hopf bifurcation occurs because the first Lyapunov coefficient is − 4.469271 e − 03 < 0 , and at θ = 3.3032143 , subcritical Hopf bifurcation occurs because the first Lyapunov coefficient is 7.104523 e − 03 > 0 . Figure 3a and b shows that the interior equilibrium points change their stability and arise a limit cycle or oscillatory behaviour at Hopf points. After θ = 7.236080 , the amplitude of the limit cycle increases as θ increases. At θ = 3.303214 , stability changes, and the limit cycle burns at that point, but before it, there is no interior point, so it does not show any dynamical behaviour.

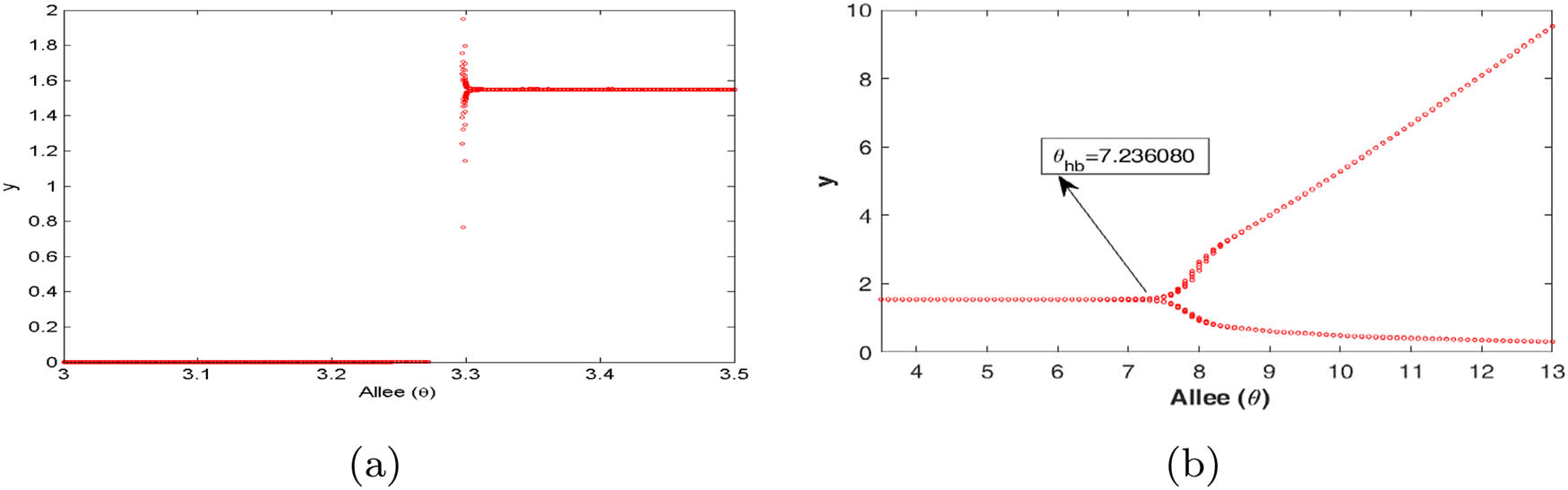
$Figure 3 (a and b) Bifurcation diagrams with θ \theta as the bifurcation parameter for different intervals: 3 < θ < 3.5 3\lt \theta \lt 3.5 and 3.5 < θ < 20 , 3.5\lt \theta \lt 20, respectively. These diagrams clearly illustrate that the stability of the equilibrium point shifts from a stable state to an oscillatory state at points θ = 7.236080 \theta =7.236080 and θ = 3.303214 , \theta =3.303214, respectively. All other parameters are the same as those in Table 1.$

Figure 3

(a and b) Bifurcation diagrams with θ as the bifurcation parameter for different intervals: 3 < θ < 3.5 and 3.5 < θ < 20 , respectively. These diagrams clearly illustrate that the stability of the equilibrium point shifts from a stable state to an oscillatory state at points θ = 7.236080 and θ = 3.303214 , respectively. All other parameters are the same as those in Table 1.

6.2 Limit cycle and time series at Hopf bifurcation points

Figures 4, 5, 6 are drawn for the fixed parameters set (A) given in Table 1 and the Hopf bifurcation points θ h 1 = 3.303214 and θ h 2 = 3.303214 , respectively.

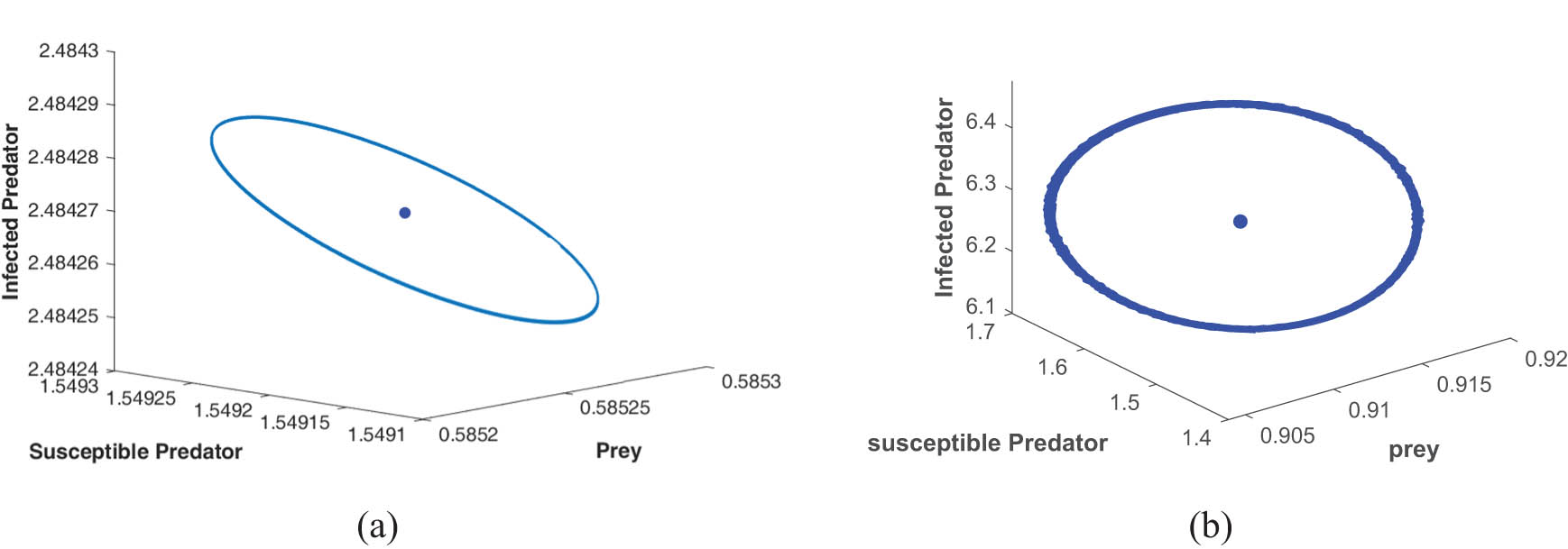
$Figure 4 (a) Limit cycle at Hopf point θ h 1 = 3.303214 {\theta }_{h1}=3.303214 , and (b) limit cycle behaviour at second Hopf bifurcation point θ h 2 = 7.236080 {\theta }_{h2}=7.236080 .$

Figure 4

(a) Limit cycle at Hopf point θ h 1 = 3.303214 , and (b) limit cycle behaviour at second Hopf bifurcation point θ h 2 = 7.236080 .

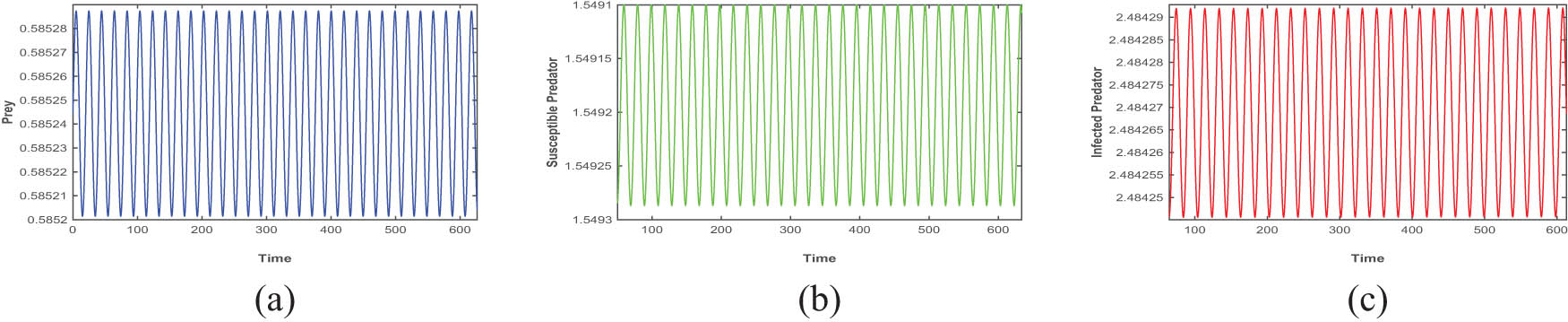
$Figure 5 The figures (a), (b), and (c) are time series plots that ensure periodic oscillation of the model (4) at Hopf point θ = 3.3032143 \theta =3.3032143 .$

Figure 5

The figures (a), (b), and (c) are time series plots that ensure periodic oscillation of the model (4) at Hopf point θ = 3.3032143 .

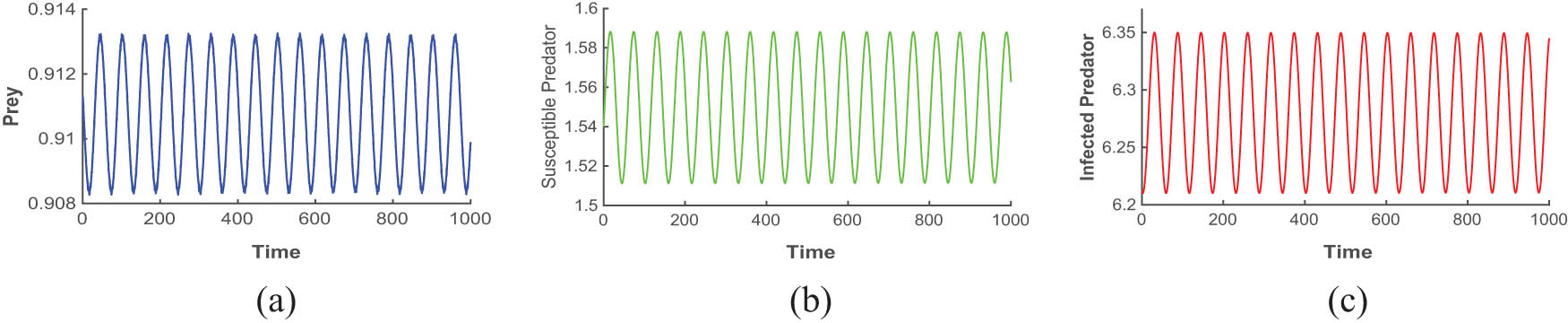
$Figure 6 The figures (a), (b), and (c) are time series plots that ensure periodic oscillation of the model (4) at Hopf point θ h 2 = 7.236080 {\theta }_{h2}=7.236080 .$

Figure 6

The figures (a), (b), and (c) are time series plots that ensure periodic oscillation of the model (4) at Hopf point θ h 2 = 7.236080 .

Figures 4, 5, and 6 depict the periodic oscillations of model (4). This periodic oscillation suggests that the species in the ecosystem exhibit cyclic fluctuations, indicating that their populations are not permanently stable and do not face immediate extinction. Instead, these oscillations imply that the species remains in existence over time despite the recurrent population fluctuations. Hence, we can say from the figure that all the species of prey, susceptible predator, and infected predator exist in the form of recurrent population fluctuations.

6.3 Phase portrait in the different region of the Allee parameter

The phase portraits are plotted for the different region of the Allee parameter, and the all other parameters are the same as fixed. Figure 2 shows three Allee parameter region 3.302872 < θ < 4.172 , 4.172 < θ < 7.236080 , and θ > 7.236080 .

In Figure 7, it is depicted that after passing the second Hopf bifurcation point, marked as θ h 2 = 7.236080 , the system exhibits periodic oscillations. When we increment the value of θ in the system, we observe that the amplitude of the limit cycle also undergoes an increase. Figure 8 represents two phase portraits Figure 8(a) for 3.302872 < θ < 4.172 , which shows that two interior exist in which one is locally stable and other is unstable, Figure 8(b) for 4.172 < θ < 7.236080 shows that one stable interior equilibrium exists. The equilibrium point is denoted by dot in the given figures. Figures 9(a) and 10(a) illustrate that for the given parameters, all nearby trajectories converge towards the equilibrium point. This indicates that both the axial and disease-free equilibrium points are asymptotically stable. The Allee parameter destabilised the disease-free equilibrium as it converted stable (Figure 10) to oscillatory behaviour (Figure 11).

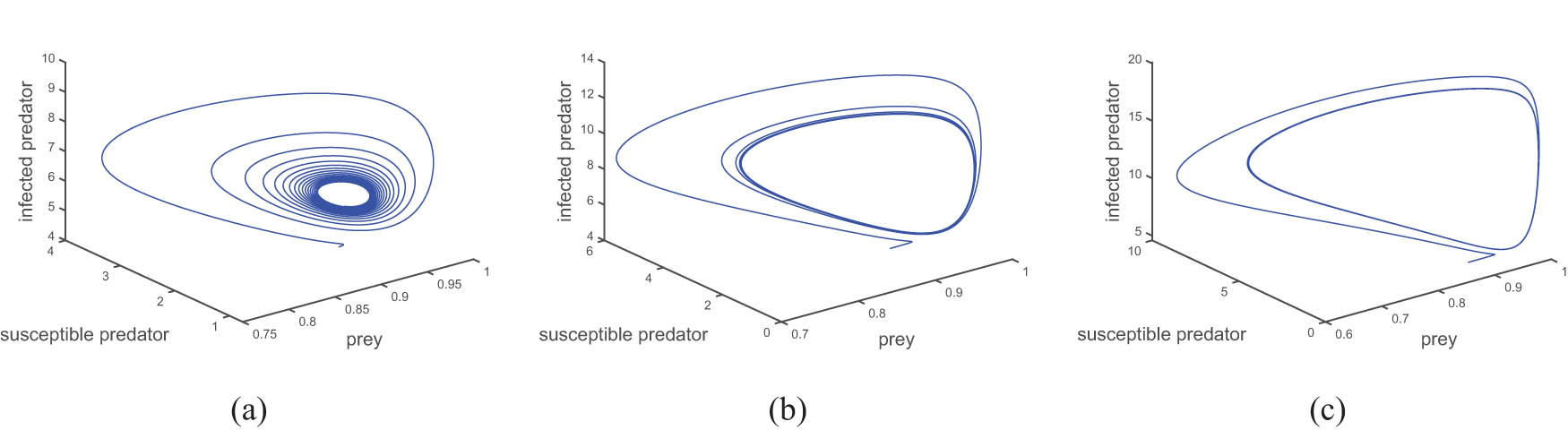
$Figure 7 This figure shows the limit cycle behaviour after Hopf bifurcation point ( h 2 ) \left({h}_{2}) at (a) θ = 10.1 \theta =10.1 , (b) θ = 12 \theta =12 , and (c) θ = 17 \theta =17 , respectively. All other parameters are the same as those in Table 1.$

Figure 7

This figure shows the limit cycle behaviour after Hopf bifurcation point ( h 2 ) at (a) θ = 10.1 , (b) θ = 12 , and (c) θ = 17 , respectively. All other parameters are the same as those in Table 1.

$Figure 8 (a) The phase portrait indicates that there are two interior equilibria, one of which is stable and the other is unstable. Furthermore, it demonstrates that the trivial equilibrium is stable when θ = 3.5 \theta =3.5 . In addition, (b) the phase portrait for θ = 4.5 \theta =4.5 reveals that only one stable equilibrium point exists, while all other parameters remain the same as those in the fixed parameters set in Table 1.$

Figure 8

(a) The phase portrait indicates that there are two interior equilibria, one of which is stable and the other is unstable. Furthermore, it demonstrates that the trivial equilibrium is stable when θ = 3.5 . In addition, (b) the phase portrait for θ = 4.5 reveals that only one stable equilibrium point exists, while all other parameters remain the same as those in the fixed parameters set in Table 1.

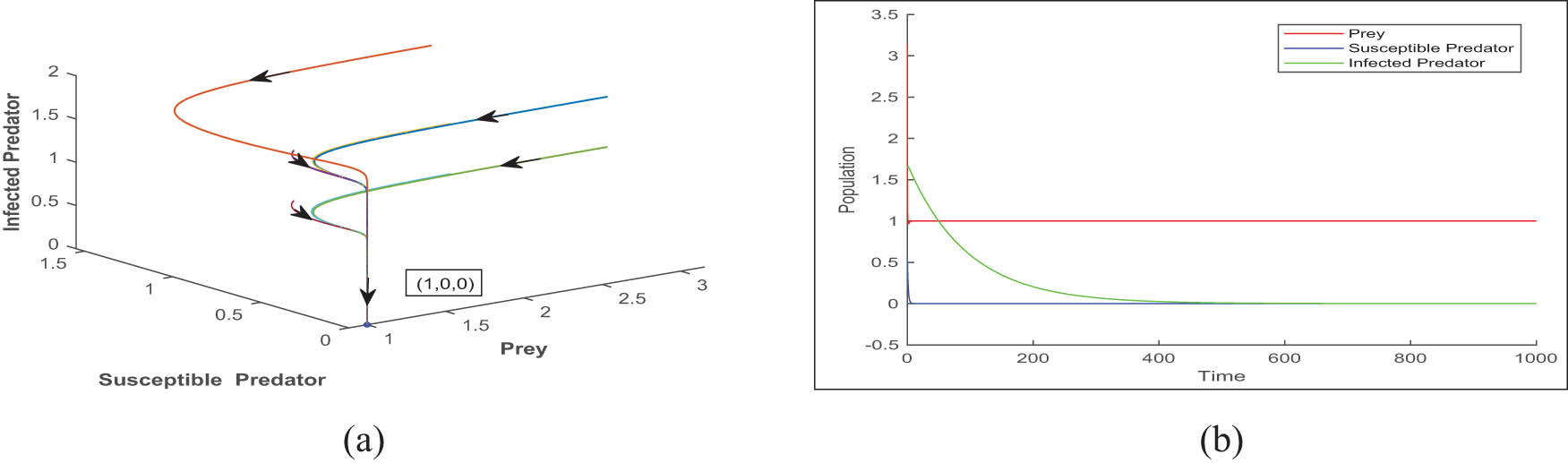
$Figure 9 (a) A phase portrait showing that the axial equilibrium E 1 ( 1 , 0 , 0 ) {E}_{1}\left(1,0,0) is stable. (b) A time series plot with initial conditions x 0 = 3.15 {x}_{0}=3.15 , y 0 = 0 . 202 {y}_{0}=0.202 , I 1 ( 0 ) = 1.7 {I}_{1}\left(0)=1.7 and the parameter values α = 0.5 \alpha =0.5 , θ = 3 \theta =3 , β = 0.142 \beta =0.142 , r = 0.0372 r=0.0372 , d 1 = 0.7 {d}_{1}=0.7 , d 2 = 0.01056 {d}_{2}=0.01056 , b 2 = 0.75 {b}_{2}=0.75 , and b 1 = 0.2 {b}_{1}=0.2 .$

Figure 9

(a) A phase portrait showing that the axial equilibrium E 1 ( 1 , 0 , 0 ) is stable. (b) A time series plot with initial conditions x 0 = 3.15 , y 0 = 0 . 202 , I 1 ( 0 ) = 1.7 and the parameter values α = 0.5 , θ = 3 , β = 0.142 , r = 0.0372 , d 1 = 0.7 , d 2 = 0.01056 , b 2 = 0.75 , and b 1 = 0.2 .

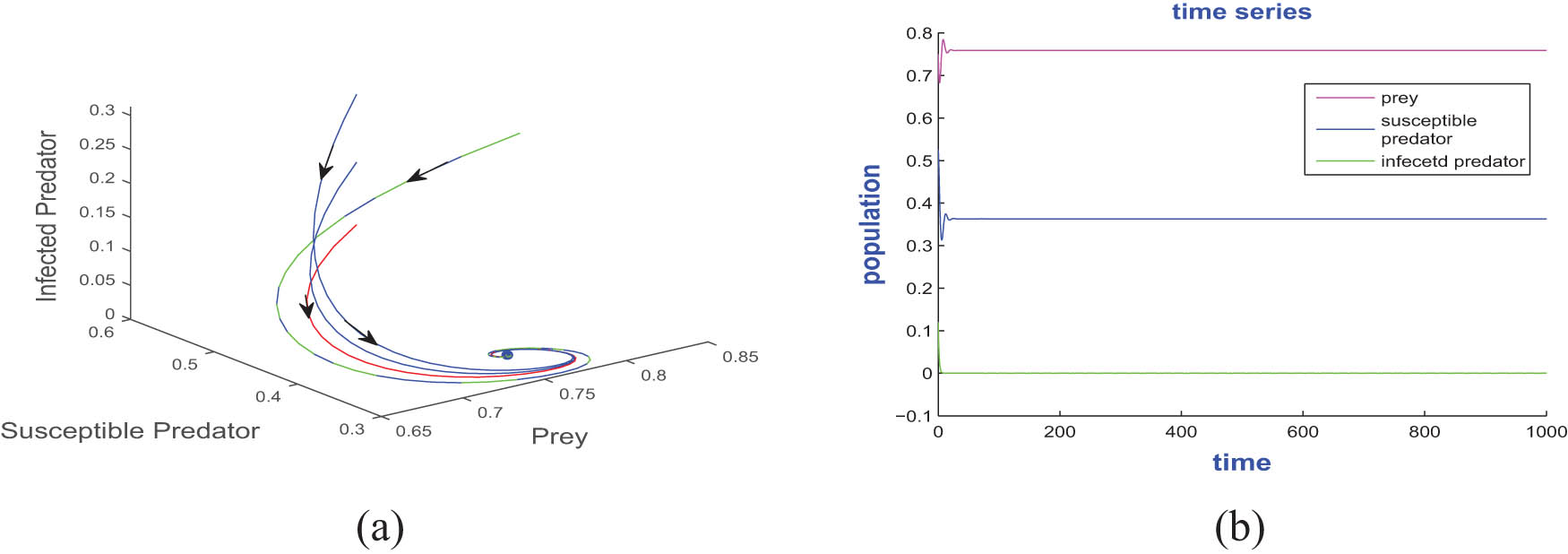
$Figure 10 (a) A phase portrait showing that the disease-free equilibrium point E 2 ( x * , y * , 0 ) {E}_{2}\left({x}^{* },{y}^{* },0) is stable; and (b) a time series plot with the parameter values as α = 0.79 , θ = 2.5 , β = 0.16 , r = 1.2 , d 1 = 0.6868 , d 2 = 0.71 , b 2 = 0.015 \alpha =0.79,\theta =2.5,\beta =0.16,r=1.2,{d}_{1}=0.6868,{d}_{2}=0.71,{b}_{2}=0.015 , and b 1 = 0.010158 {b}_{1}=0.010158 .$

Figure 10

(a) A phase portrait showing that the disease-free equilibrium point E 2 ( x * , y * , 0 ) is stable; and (b) a time series plot with the parameter values as α = 0.79 , θ = 2.5 , β = 0.16 , r = 1.2 , d 1 = 0.6868 , d 2 = 0.71 , b 2 = 0.015 , and b 1 = 0.010158 .

$Figure 11 (a) A phase portrait for the Hopf threshold value θ = 1.4458113 \theta =1.4458113 that shows the limit cycle. (b) A time series plot that shows the periodic oscillation of the disease-free population, taking other parameters that are the same as Figure 10.$

Figure 11

(a) A phase portrait for the Hopf threshold value θ = 1.4458113 that shows the limit cycle. (b) A time series plot that shows the periodic oscillation of the disease-free population, taking other parameters that are the same as Figure 10.

Now discuss the phase portrait about the axial and boundary equilibrium points for different sets of parameters mentioned in the caption of Figure 9 and 10, respectively.

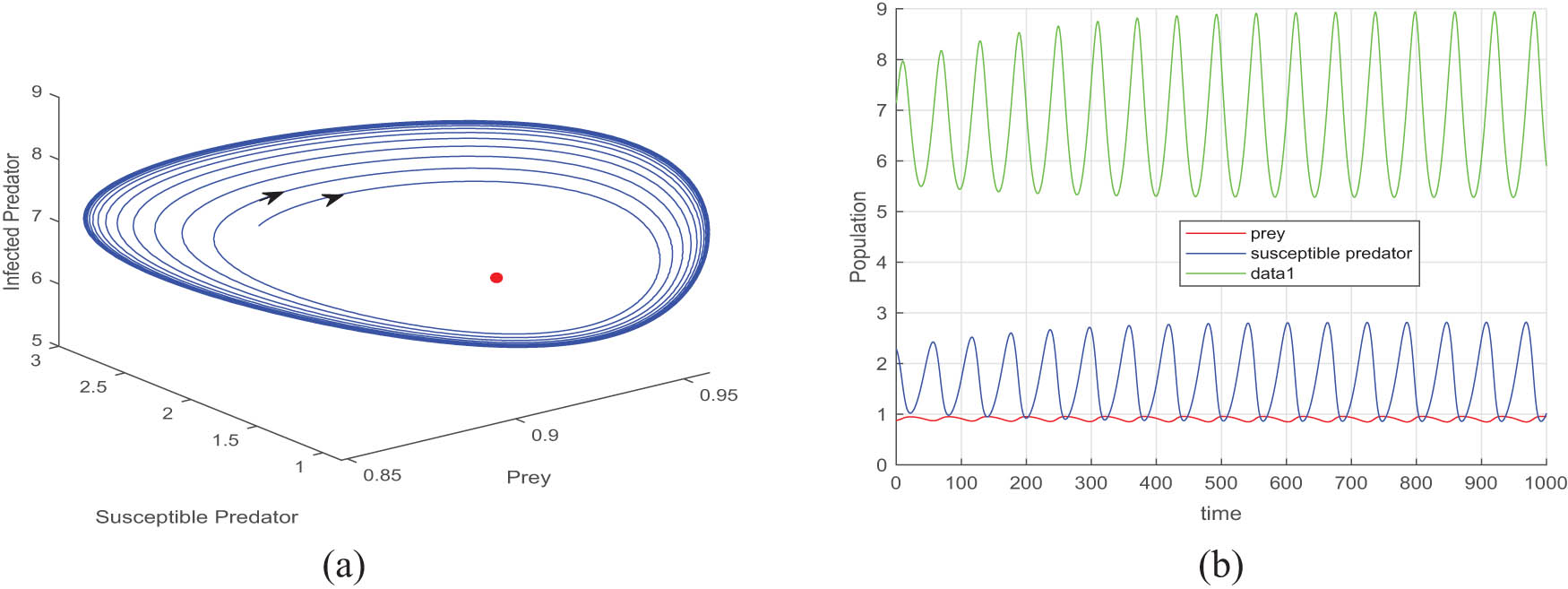
$Figure 12 (a) The stable limit cycle behaviour around the unstable equilibrium point, and (b) the periodic oscillation for the same. Taken θ = 8 \theta =8 , and all other parameters are the same as those in Table 1.$

Figure 12

(a) The stable limit cycle behaviour around the unstable equilibrium point, and (b) the periodic oscillation for the same. Taken θ = 8 , and all other parameters are the same as those in Table 1.

7 Discussion and conclusions

The Allee effect has huge impact on the eco-epidemiological model and also gives a good understanding of ecology and epidemiological issues. This article investigated all possible biologically feasible steady states of model (4) and also studied the stability of model (4) for every feasible equilibrium state. The ability for all species to coexist in a stable or oscillatory manner is dependent upon a set of parametric restrictions, with the Allee effect playing a significant part throughout the system. The Allee effect can destabilise the system; see the bifurcation diagram 2. The stability of the model about the interior equilibrium points switches, and the system appeared to be Hopf bifurcation, where the Allee effect plays an important role as a bifurcation parameter (Figure 2). The asymptotic stability of the system was examined for all possible equilibrium states. The investigation has been conducted on the presence of Hopf bifurcation in nearby areas of both the disease-free and interior equilibrium states. Figures 5 and 6 shows that all species exist together in oscillatory motion in presence of the Allee effect and diseases. All the species (prey, susceptible predator, and infected predator) co-exists and stable together for the Allee parameter θ = 4.5 (Figure 8). The survival of predators can also be facilitated when prey populations experience the Allee effect. The Allee effect has a notable impact on the stability of equilibrium points in ecosystems where multiple species coexist. The one-dimensional bifurcation analysis has been studied, where the Allee effect is taken as a bifurcation parameter. The diagram describes the different types of local bifurcation such as Hopf bifurcations, transcritical bifurcation, and saddle-node bifurcation (Figure 2). This article is primarily focused on comparing it with article [32]. The study by Shaikh and Das [32] shows that the Allee effect controls the chaotic behaviour of the model. In the present article, the chaotic oscillation is not obtained for the Allee parameter. Our model illustrates only stable and oscillating behaviour. The functional response change the dynamics of the model as chaotic oscillation is not obtained in the present article. Most of the results are similar to that of the article by Shaikh and Das [32]. The stability and oscillatory behaviours of the disease-free equilibrium point are shown in the phase portraits in Figures 10 and 11, respectively. Furthermore, limit cycle and periodic oscillation behaviours at Hopf bifurcation points about interior equilibrium point are shown in the phase portraits in Figures 4–6 respectively. The purpose of this article is to make important contributions to the progress of research in ecology, eco-epidemiology, and other related fields, especially when it comes to protecting biodiversity and putting effective management plans into action. In further research efforts, it is possible to investigate the possibility of incorporating gestation delay as a means of enhancing the existing model. Significantly, the examination of pattern-forming instabilities in reaction-diffusion systems is now emerging as a significant and interesting area of study [39]. With the help of important recent work [16,21,36], the researchers may modify this model using delay differential equation for a more realistic model, as well as modify this model using fractional operators as part of future work.

Acknowledgments

The authors express their gratitude to the reviewers for their valuable comments and suggestions. Additionally, appreciation is extended to the editor for their insightful input. The authors would like to thank their friends Saddam Hussain and Amit Kumar for their indispensable assistance throughout the preparation of this paper.

Funding information: This research received no specific grant from any funding agency and commercial or nonprofit sectors.
Author contributions: Bipin Kumar conceived the idea, conducted analyses and simulations, and drafted the manuscript. Rajesh kumar Sinha conceptualized the flow for the entire draft of the manuscript, verified all the results and edited the draft.
Conflict of interest: The authors declare that they have no conflict of interest.
Ethical approval: This research did not require any ethical approval.
Informed consent: Informed consent has been obtained from all individuals included in this study.
Data availability statement: Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

[1] Ali, N., Haque, M., Venturino, E., & Chakravarty, S. (2017). Dynamics of a three species ratio-dependent food chain model with intra-specific competition within the top predator. Computers in Biology and Medicine, 85, 63–74. 10.1016/j.compbiomed.2017.04.007Search in Google Scholar PubMed

[2] Allee, W. C. (1927). Animal aggregations. The Quarterly Review of Biology, 2(3), 367–398. 10.1086/394281Search in Google Scholar

[3] Anderson, R., Medley, G., May, R., & Johnson, A. (1986). A preliminary study of the transmission dynamics of the human immunodeficiency virus (HIV), the causative agent of aids. Mathematical Medicine and Biology: A Journal of the IMA, 3(4), 229–263. 10.1093/imammb/3.4.229Search in Google Scholar PubMed

[4] Anderson, R. M., Heesterbeek, H., Klinkenberg, D., & Hollingsworth, T. D. (2020). How will country-based mitigation measures influence the course of the covid-19 epidemic? The Lancet, 395(10228), 931–934. 10.1016/S0140-6736(20)30567-5Search in Google Scholar PubMed PubMed Central

[5] Angulo, E., Roemer, G. W., Berec, L., Gascoigne, J., & Courchamp, F. (2007). Double Allee effects and extinction in the island fox. Conservation Biology, 21(4), 1082–1091. 10.1111/j.1523-1739.2007.00721.xSearch in Google Scholar PubMed

[6] Arancibia-Ibarra, C., & Flores, J. (2021). Dynamics of a Leslie-Gower predator-prey model with Holling type ii functional response, Allee effect and a generalist predator. Mathematics and Computers in Simulation, 188, 1–22. 10.1016/j.matcom.2021.03.035Search in Google Scholar

[7] Arditi, R., & Ginzburg, L. R. (2012). How species interact: altering the standard view on trophic ecology. Oxford University Press. 10.1093/acprof:osobl/9780199913831.001.0001Search in Google Scholar

[8] Birkhoff, G., & Rota, G. (1982). Ordinary differential equation, Boston: Ginn. and co. Search in Google Scholar

[9] Brauer, F., Castillo-Chavez, C., & Castillo-Chavez, C. (2012). Mathematical models in population biology and epidemiology (Vol 2). Springer. 10.1007/978-1-4614-1686-9Search in Google Scholar

[10] Brearley, G., Rhodes, J., Bradley, A., Baxter, G., Seabrook, L., Lunney, D., …, McAlpine, C. (2013). Wildlife disease prevalence in human-modified landscapes. Biological Reviews, 88(2), 427–442. 10.1111/brv.12009Search in Google Scholar PubMed

[11] Chattopadhyay, J., & Arino, O. (1999). A predator-prey model with disease in the prey. Nonlinear Analysis, 36, 747–766. 10.1016/S0362-546X(98)00126-6Search in Google Scholar

[12] Courchamp, F., Clutton-Brock, T., & Grenfell, B. (2000). Multipack dynamics and the Allee effect in the African wild dog, Lycaon pictus. In Animal Conservation Forum (Vol. 3, pp. 277–285). Cambridge University Press. 10.1017/S1367943000001001Search in Google Scholar

[13] Das, K. P. (2016a). Complex dynamics and its stabilization in an eco-epidemiological model with alternative food. Modeling Earth Systems and Environment, 2(4), 1–12. 10.1007/s40808-016-0224-5Search in Google Scholar

[14] Das, K. P. (2016b). Disease-induced chaotic oscillations and its possible control in a predator-prey system with disease in predator. Differential Equations and Dynamical Systems, 24(2), 215–230. 10.1007/s12591-015-0249-7Search in Google Scholar

[15] Drake, J. M., & Kramer, A. M. (2011). Allee effects. Nature Education Knowledge, 3(10), 2. Search in Google Scholar

[16] Ghanbari, B. (2021). On the modeling of an eco-epidemiological model using a new fractional operator. Results in Physics, 21, 103799. 10.1016/j.rinp.2020.103799Search in Google Scholar

[17] Hadeler, K., & Freedman, H. (1989). Predator-prey populations with parasitic infection. Journal of Mathematical Biology, 27(6), 609–631. 10.1007/BF00276947Search in Google Scholar PubMed

[18] Hale, J. K. (1971). Functional differential equations. In Analytic theory of differential equations (pp. 9–22). Springer. 10.1007/BFb0060406Search in Google Scholar

[19] Hastings, A., & Powell, T. (1991). Chaos in a three-species food chain. Ecology, 72(3), 896–903. 10.2307/1940591Search in Google Scholar

[20] Kumar, U., Mandal, P. S., & Venturino, E. (2020). Impact of Allee effect on an eco-epidemiological system. Ecological Complexity, 42, 100828. 10.1016/j.ecocom.2020.100828Search in Google Scholar

[21] Kumar, V., & Kumari, N. (2021). Bifurcation study and pattern formation analysis of a tritrophic food chain model with group defense and Ivlev-like nonmonotonic functional response. Chaos, Solitons & Fractals, 147, 110964. 10.1016/j.chaos.2021.110964Search in Google Scholar

[22] Mandal, S., Al Basir, F., & Ray, S. (2021). Additive Allee effect of top predator in a mathematical model of three species food chain. Energy, Ecology and Environment, 6(5), 451–461. 10.1007/s40974-020-00200-3Search in Google Scholar

[23] Mccann, K., & Yodzis, P. (1995). Bifurcation structure of a three-species food-chain model. Theoretical Population Biology, 48(2), 93–125. 10.1006/tpbi.1995.1023Search in Google Scholar

[24] Mohammadi, H., Kumar, S., Rezapour, S., & Etemad, S. (2021). A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to mumps virus with optimal control. Chaos, Solitons & Fractals, 144, 110668. 10.1016/j.chaos.2021.110668Search in Google Scholar

[25] Mukherjee, D. (2010). Hopf bifurcation in an eco-epidemic model. Applied Mathematics and Computation, 217(5), 2118–2124. 10.1016/j.amc.2010.07.010Search in Google Scholar

[26] Mukhopadhyay, B., & Bhattacharyya, R. (2005). Dynamics of a delay-diffusion prey-predator model with disease in the prey. Journal of Applied Mathematics and Computing, 17(1), 361–377. 10.1007/BF02936062Search in Google Scholar

[27] Murray, J., & Seward, W. (1992). On the spatial spread of rabies among foxes with immunity. Journal of Theoretical Biology, 156(3), 327–348. 10.1016/S0022-5193(05)80679-4Search in Google Scholar

[28] Saenz, R. A., Hethcote, H. W., & Gray, G. C. (2006). Confined animal feeding operations as amplifiers of influenza. Vector-Borne & Zoonotic Diseases, 6(4), 338–346. 10.1089/vbz.2006.6.338Search in Google Scholar PubMed PubMed Central

[29] Sahoo, B., & Poria, S. (2014). Diseased prey predator model with general Holling type interactions. Applied Mathematics and Computation, 226, 83–100. 10.1016/j.amc.2013.10.013Search in Google Scholar PubMed PubMed Central

[30] Sarangi, B., & Raw, S. (2023). Dynamics of a spatially explicit eco-epidemic model with double Allee effect. Mathematics and Computers in Simulation, 206, 241–263. 10.1016/j.matcom.2022.11.004Search in Google Scholar

[31] Sen, M., Banerjee, M., & Morozov, A. (2015). A generalist predator regulating spread of a wildlife disease: Exploring two infection transmission scenarios. Mathematical Modelling of Natural Phenomena, 10(2), 74–95. 10.1051/mmnp/201510206Search in Google Scholar

[32] Shaikh, A. A., & Das, H. (2020). An eco-epidemic predator-prey model with Allee effect in prey. International Journal of Bifurcation and Chaos, 30(13), 2050194. 10.1142/S0218127420501941Search in Google Scholar

[33] Skalski, G. T., & Gilliam, J. F. (2001). Functional responses with predator interference: Viable alternatives to the Holling type ii model. Ecology, 82(11), 3083–3092. 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2Search in Google Scholar

[34] Stephens, P. A., Sutherland, W. J., & Freckleton, R. P. (1999). What is the Allee effect? Oikos, 185–190. 10.2307/3547011Search in Google Scholar

[35] Strogatz, S. H. (2018). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering. CRC Press. 10.1201/9780429399640Search in Google Scholar

[36] Vinoth, S., Sivasamy, R., Sathiyanathan, K., Rajchakit, G., Hammachukiattikul, P., Vadivel, R., & Gunasekaran, N. (2021). Dynamical analysis of a delayed food chain model with additive Allee effect. Advances in Difference Equations, 2021(1), 1–20. 10.1186/s13662-021-03216-zSearch in Google Scholar

[37] Wangersky, P. J. (1978). Lotka-Volterra population models. Annual Review of Ecology and Systematics, 9, 189–218. 10.1146/annurev.es.09.110178.001201Search in Google Scholar

[38] Wiggins, S., Wiggins, S., & Golubitsky, M. (2003). Introduction to applied nonlinear dynamical systems and chaos (Vol 2). Springer. Search in Google Scholar

[39] Yadav, R., Mukherjee, N., & Sen, M. (2022). Spatiotemporal dynamics of a prey-predator model with Allee effect in prey and hunting cooperation in a Holling type iii functional response. Nonlinear Dynamics, 107, 1397–1410. 10.1007/s11071-021-07066-ySearch in Google Scholar

Received: 2023-08-12

Revised: 2023-10-26

Accepted: 2023-11-16

Published Online: 2023-12-29

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/cmb-2023-0108

Keywords for this article

eco-epidemic model; equilibrium point; stability analysis; Hopf bifurcation; transcritical bifurcation

Creative Commons

BY 4.0