Flutter investigation and deep learning prediction of FG composite wing reinforced with carbon nanotube

Aseel J. Mohammed; Hatam K. Kadhom

doi:10.1515/cls-2022-0218

Artikel Open Access

Flutter investigation and deep learning prediction of FG composite wing reinforced with carbon nanotube

Aseel J. Mohammed und Hatam K. Kadhom

Veröffentlicht/Copyright: 3. Januar 2024

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Curved and Layered Structures Band 11 Heft 1

Abstract

The flutter of a composite wing reinforced with functionally graded carbon nanotubes (CNTs) has been investigated. A rectangular plate models a supersonic wing with cantilever boundary conditions. To determine displacement fields of a moderately thick plate, shear deformation theory is used. Using the Hamilton principle, a first-order piston theory was used to simulate supersonic airflow. This study examines four types of CNT thickness. Also, four different CNT distribution patterns are investigated. In a two-layer asymmetric composite, the effects of patch mass, mass distribution, fiber orientation angle, and distribution of CNTs were examined. Moreover, the results are compared and verified with other studies. A greater mass ratio led to a smaller flutter boundary, while a longer added mass increased the flutter boundary. A variation in the distribution pattern in CNT fiber orientation results in a distinct behavior of the flutter boundary for asymmetric composites with increasing orientation angles. The artificial neural network is utilized to predict the damping ratio, and the results showed great accuracy compared to the study results. Hyperparameter tuning is employed for better optimizing the predictive models.

Keywords: flutter instability; functionally graded composite sheet; carbon nanotube; monolayer sheet; extended added mass

1 Introduction

In the last few decades, along with the dramatical rise in the use of composite materials in the fields of mechanics, construction, aerospace industries, and many other modern industries, research and research in this regard and the optimization of their mechanical properties have also expanded a lot [1,2]. In this regard, carbon nanotubes (CNTs) are suggested as a reinforcement. CNTs have excellent and significant mechanical properties such as stiffness, strength, and very high thermal conductivity compared to filler materials. Next to a low density, these characteristics can make their use as reinforcement in composites a very good choice [3,4]. These materials can be found as single-walled CNT (SWCNT) or multi-walled CNT (MWCNT) [5,6].

SWCNTs consist of a graphene layer wrapped in a cylindrical shape, while MWCNTs are obtained from two or more concentric single walls with different diameters. Functionally graded (FG) materials reinforced with CNTs are obtained by applying different distribution functions on CNTs [7].

There have been a number of studies investigating the free vibration of CNT-reinforced FG composite sheets (functionally graded carbon nanotubes [FG-CNTs]). FG-CNT composite multilayers with thin to relatively thick thicknesses were investigated for vibration in the study of Alibeigloo and Emtehani [8]. As FG thick rectangular plates reinforced with CNTs vibrate freely under free tension, Nami and Janghorban [9] employed a novel method. Civalek and Avcar [10] studied the FG-CNTs on non-rectangular sheets. They concluded that the tilted sheets’ natural frequency changes with the distribution pattern of CNTs.

Aeroelasticity examines the interaction of elastic, inertial, and aerodynamic forces. The use of CNT materials in aeroelastic stability issues, which is an important factor in the design of modern, flexible wings, can optimize the design of the wing. The flutter phenomenon is one of the most important issues in aeroelastic stability and is involved with airplane flights. This destructive phenomenon is the self-excited vibration of the system, which has been investigated in many studies [11]. Natarajan et al. [12] utilized FEM to investigate the characteristics of flutter instability in a sheet made of functionally graded material (FGM). The aeroelastic properties of the FG sheet reinforced with CNTs and exposed to ultrasonic flow were investigated by Guo et al. [13]. The theory of the Kirchhoff sheet was used to approximate the thin sheet. Sankar et al. [14] studied the flutter properties of a rectangular sandwich sheet by applying high-order shear theory to the structure. They used CNTs to reinforce two sandwich sheets, and the FEM was used to solve the problem. Zhang et al. [15] studied the aeroelastic properties and active control of flutter for nonlinear sandwich beams using a piezoelectric sensor/actuator pair. In another work, Song et al. [16] investigated the active control of the buckling of aerothermal sheets.

Investigating the effect of added mass concentrated on the sheet was first proposed to design electrical systems [17]. Alibeigloo and Kari [18] studied extended added mass on the free vibrations of composite sheets. Their research showed that the fundamental frequency increases by augmenting the composite layers or the aspect ratio. Lin et al. [19] investigated a wing’s static instability and aerodynamics with an external tank. In this research, by using Hamilton’s principle to derive the governing equations of the problem and considering the infinite aerodynamic pressure, the effect of the installation location of the added mass on the wing on the flutter instability boundary and divergence was studied. Peiró et al. [20] investigated the effect of extended one-dimensional added mass on the flutter speed of a composite sheet of a single head. Using the piston theory to approximate the ultrasonic flow and the classical sheet theory to approximate the structure, they studied the effect of added mass density and its position on the occurrence of flutter. The governing equations are depicted in Section 2 based on previous studies [21–31]. Also, the machine learning predictions are presented and compared with previous studies [32–38].

Based on a precise three-dimensional (3D) shell model, Brischetto [39] analyzed the free vibrations of SWCNTs. Using isotropic cylinders with specific equivalent thickness and Young’s modulus definitions, the study attempts to determine the natural frequencies of SWCNTs. Various one-dimensional beam analyses are also compared with this 3D shell model to show their limitations. The research also explores SWCNT behavior by calculating vibration modes for different chiralities, lengths, and geometries. For modeling complex structures made of anisotropic materials, particularly those with variable geometries, Tornabene et al. [40] proposed the equivalent single layer method. To analyze a wide range of structural shapes, they use an isogeometric mapping technique. Through the use of the Hamiltonian principle, governing equations are presented for the structural behavior and solved numerically with two-dimensional generalized differential quadrature. Stacking sequences, material types, and boundary conditions are studied to determine the effect of different factors on the vibration response of doubly curved shell structures. The results are validated through comparisons with 3D finite-element simulations. A study of FGM constructed from circular cylindrical shells by Mercan et al. [41] investigates the free vibration response. For these cylindrical FGM shells, the governing equation of motion is numerically solved by discrete singular convolution. Material properties follow a volume fraction power law in the thickness direction, based on Love’s first approximation shell theory. Based on a combination of boundary conditions, material characteristics, and geometric parameters, the researchers calculate vibration frequencies. Based on the results of this study, we can conclude that the approach used and the results obtained are valid and consistent with the findings of other researchers. A first-order shear deformation theory (FSDT) simulation was performed by Sofiyev et al. [42] by combining axial/lateral load conditions with axial/hydrostatic loading conditions. It is investigated the effects of uniform reinforcement distribution on carbon nanotube reinforced composite conical shells (CNTRC-CSs) and FG reinforcement on CNTRC-CSs. For the purpose of determining critical loading conditions, the fundamental equations are derived and solved analytically. It examines how geometric parameters, loading parameters, distribution type, CNT volume fraction, and distribution method affect structural responses initially. Kiani et al. [43] examined the natural frequencies of a polymeric matrix reinforced with uniform or FG-CNTs. This panel’s mechanical properties are determined by a refined rule of mixtures. A virtual strain expression and kinetic energy expression are derived using Hamilton’s principle. A study is conducted to analyze how CNT volume fractions and patterns affect the free vibration of panels.

In the present work, considering the previous activity in the field of vibrations and flutter of sheets reinforced with CNTs, as well as the research conducted on the mass added to the sheet, the flutter of FG relatively thick composite sheets reinforced with nanotubes is investigated. Carbons are paid along with the added mass. This research uses the FSDT to model the sheet, and the first-order piston theory is used to approximate the ultrasonic flow. The displacement field and sheet rotation functions are expressed based on Chebyshev polynomials. The influence of different distributions of CNTs and the location and size of the added mass on the flutter boundary have been investigated. Also, a machine learning algorithm is employed to propose a predictive model. The model is evaluated by using the data from the modeling. The computational costs of both methods are compared as well.

2 Theory and governing equations

Figure 1 depicts the top view of the sheet. Also, the specifications of the sheet are mentioned in Figure 1. The ultrasonic airflow is along the x-axis. The dimensions of the expanded mass are specified by c and d, and the position of its center by x m and y m .

Figure 1

Sheet geometry with extended added mass.

Figure 2 is a cross-sectional view of a composite multilayer sheet with thickness. t k is the thickness of the kth layer.

Figure 2

Cross-sectional view of the composite multilayer sheet.

2.1 Mechanical properties

The distribution patterns of CNTs along the thickness can be uniform or FG. Four types of distribution of sheets reinforced with CNTs are used (uniform, decreasing–increasing, increasing–decreasing, and decreasing distributions). The volume percentage of CNTs as a function of thickness is presented in the study of Zhang et al. [21]. V CN * indicates the total volumetric percentage of CNTs.

The general method of mixtures has been used to estimate the properties of reinforcing materials with CNTs. According to this method, Young’s and shear modulus can be written as follows:

(1) E 11 = η 1 V CN E 11 CN + V m E m ,

(2) η 2 E 22 = V CN E 22 CN + V m E m ,

(3) η 3 G 12 = V CN G 12 CN + V m G m .

In these equations, E 11 CN , E 22 CN , and G 12 CN are Young’s modulus and the shear modulus of SWCNT, respectively. E m and G m are Young’s and shear modulus of the equivalent spherical field and η 1 , η 2 , and η 3 are the effective parameters of the properties reinforced with CNTs. There is a relation between the volume percentage of CNT reinforcement ( V CN ) and the volume percentage of the background ( V m ), which is expressed in the following equation:

(4) V CN + V m = 1 .

Mass density and effective Poisson’s ratio of FGMs reinforced with CNTs are given as follows [7]:

(5) ρ = V CN ρ CN + V m ρ m ,

(6) v 12 = V CN * v CN + V m v m .

And in that, ρ CN , v CN ρ m , and v m are the density and Poisson’s ratio for the CNT reinforcement, respectively.

2.2 Structure modeling

The FSDT has been applied to the FG sheet. The displacement field of the sheet on displacements and rotations of the middle plane of the sheet will be in the form of Eq. (5) [10]:

(7) u ( x , y , z , t ) = z ϕ x ( x , y , t ) ,

(8) v ( x , y , z , t ) = z ϕ y ( x , y , t ) ,

(9) w ( x , y , z , t ) = w 0 ( x , y , t ) .

The components of in-plane and out-of-plane shear strains are expressed as follows:

(10) ε xx ε yy γ xy = ZK , γ xz γ yz = γ 0 ,

where K and γ 0 are defined as follows:

(11) K = ∂ ϕ x ∂ x ∂ ϕ y ∂ y ∂ ϕ x ∂ y + ∂ ϕ y ∂ x ,

(12) γ 0 = ϕ x + ∂ w 0 ∂ x ϕ y + ∂ w 0 ∂ y .

The general linear stress–strain relationship is expressed as follows:

(13) σ xx σ yy σ xy τ xz τ yz = Q 11 Q 12 0 0 0 Q 12 Q 22 0 0 0 0 0 Q 33 0 0 0 0 0 Q 44 0 0 0 0 0 Q 55 ε xx ε yy γ xy γ xz γ yz ,

where the components of Q are defined as follows:

(14) Q 11 = E 11 1 − v 12 v 21 , Q 22 = E 22 1 − v 12 v 21 , Q 12 = v 21 E 11 1 − v 12 v 21 , Q 33 = G 12 , Q 44 = G 13 , Q 55 = G 13 .

E 11 and E 22 are the effective Young’s modulus of sheets reinforced with CNTs in the local coordinates of the material. G 12 , G 13 , and G 23 are shear modulus and v 12 and v 21 are Poisson’s ratios. Eq. (10) shows the strain energy of the sheet as follows:

(15) U = 1 2 ∫ 0 a ∫ 0 b ε T S ε d y d x .

The parameters in Eq. (15) are defined as follows:

(16) ε = K γ 0 ,

(17) S = D 11 D 12 D 13 0 0 D 21 D 22 D 23 0 0 D 31 D 32 D 33 0 0 0 0 0 A 44 S A 45 S 0 0 0 A 45 S A 55 S = D 0 0 A S ,

(18) D ij = ∑ i = 1 k ∫ tk yk + 1 Q ̅ ij k z 2 d z ,

(19) A ij s = K ∑ i = 1 k ∫ t k t k + 1 Q ̅ ij k d z .

Bending stiffness D ij is defined for i,j = 1,2,3, and transverse shear stiffness A ij s for i, j = 4, 5. K equals 0.833 [22,23]. Reduced transition stiffnesses for the kth layer or Q ̅ ij are expressed in the following equation:

(20) [ Q ̅ ] = [ T ] − 1 [ Q ] [ T ] − T ,

where the transfer matrix T is in the following form:

(21) [ T ] = cos 2 θ sin 2 θ 2 sin θ cos θ 0 0 sin 2 θ cos 2 θ − 2 sin θ cos θ 0 0 − sin θ cos θ sin θ cos θ cos 2 θ − sin 2 θ 0 0 0 0 0 cos θ − sin θ 0 0 0 sin θ cos θ .

θ is the rotation angle of the kth layer. Eq. (22) is a function of kinetic energy for the scale plate

(22) Θ p = 1 2 ∫ − h 2 h 2 ∫ 0 a ∫ 0 b ρ ( z ) ( u ̇ 2 + v ̇ 2 + w ̇ 2 ) d y d x d z .

And using the equation of displacement, the kinetic energy of the sheet can be rewritten as follows:

(23) Θ p = 1 2 ∫ 0 a ∫ 0 b ( I 0 ( w ̇ 2 ) + I 2 ( ϕ ̇ x 2 + ϕ ̇ y 2 ) ) d y d x ,

where

(24) ( I 0 , I 2 ) = ∫ − h / 2 h / 2 ρ ( z ) · ( 1 , z 2 ) d z .

The kinetic energy of the extended mass added on the upper surface of the sheet is equal to

(25) Θ m = 1 2 ∫ x m − c 2 x m + c 2 ∫ y m − d 2 y m + d 2 γ m w ̇ 2 + h 2 3 ϕ ̇ x 2 + h 2 3 ϕ ̇ y 2 d y d x ,

where γ m is equal to the mass density added per unit area. Considering that only the effect of mass is considered for the added mass, the total kinetic energy is equal to

(26) Θ = Θ p + Θ m .

The energy equations are rewritten using 22 dimensionless parameters. The dimensionless ratios of AR, H, LR, WR, and MR are aspect ratio, thickness ratio, length ratio, width ratio, and mass ratio, respectively,

(27) X ̅ = x a , Y ̅ = y b , W ̅ = w a , AR = a b , H = h a , LR = c a , WR = d b , MR = γ m ρ h .

The kinetic energy of the sheet and the added extended mass using dimensionless relations are rewritten as follows:

(28) Θ ̅ p = 1 2 ∫ 0 1 ∫ 0 1 ( I 0 ( w ̅ 2 ) + I 2 a 2 ( ϕ ̇ x 2 + ϕ ̇ y 2 ) ) d X ̅ d Y , ̅

(29) Θ ̅ m = 1 2 ∫ y m / b − WR / 2 y m / b + WR / 2 ∫ x m / b − WR / 2 x m / b + LR / 2 γ m w ̇ 2 ̅ + H 2 3 ϕ ̇ x 2 + H 2 3 ϕ ̇ y 2 d X ̅ d Y ̅ .

And the total kinetic energy is equal to

(30) Θ ̅ = Θ ̅ p + Θ ̅ m .

The strain energy of the sheet is also rewritten as Eq. (31) in the dimensionless state:

(31) U ̅ = 1 2 ∫ 0 1 ∫ 0 1 ε ̅ T S ε ̅ d X ̅ d Y . ̅

The parameters related to this equation are also rewritten as follows:

(32) ε ̅ = K ̅ γ ̅ 0 / a ,

(33) K ̅ = ∂ ϕ x ∂ X ̅ AR ∂ ϕ y ∂ Y ̅ AR ∂ ϕ y ∂ Y ̅ + ∂ ϕ y ∂ X ̅ ,

(34) γ ̅ 0 = ϕ x + H · ∂ w ̅ 0 ∂ X ̅ ϕ y + H · AR· ∂ w ̅ 0 ∂ Y ̅ .

Hamilton’s principle is used to obtain the equation of motion for the reinforced structure system with CNTs

(35) ∫ 0 t [ δ ( Θ ̅ − U ̅ ) + δ W ̅ ] d t = 0 ,

where W ̅ is the work done by external loads and is according to the following equation:

(36) W ̅ = ∫ 0 1 ∫ 0 1 Δ p w ̅ d X ̅ d Y , ̅

Δ p is the aerodynamic pressure. The flow direction is along the x-axis, which is shown in Figure 1. Eq. (38) is the aerodynamic pressure Δ p [24]:

(37) Δ p = 2 q ∞ β ∞ M ∞ 2 − 2 M ∞ 2 − 1 a u ∞ ∂ w ̅ ∂ t + ∂ w ̅ ∂ X ̅ ,

where q ∞ is calculated as follows:

(38) q ∞ = ρ ∞ U ∞ 2 2 , β ∞ = M ∞ 2 − 1 .

In Eq. (38), M ∞ is the Mach number in free flow. Dimensionless aerodynamic pressure is introduced as λ = 2 q ∞ a 3 / β ∞ D 11 . In this case that M ∞ = 1 , we have [ ( M ∞ 2 − 2 ) / ( M ∞ 2 − 1 ) ] 2 μ / β ∞ → μ / M ∞ , where μ = ρ ∞ a / ρ h .

2.3 Mode shape functions

To analyze the flutter problem, the hypothetical mode shape method has been used. According to Eqs. (39)–(41), the structural system’s displacement field and rotation functions can be written as dual series of Chebyshev polynomials multiplied by the boundary function that satisfies the basic geometric boundary conditions [25,26]

(39) w ̅ ( X ̅ , Y ̅ , t ) = F w ( X ̅ , Y ̅ ) ∑ i = 1 n ∑ j = 1 m ω ̅ ij ( X ̅ , Y ̅ ) a ij ( t ) = ϖ T ( X ̅ , Y ̅ ) a ( t ) , ϕ x ( X ̅ , Y ̅ , t ) ,

(40) ϕ x ( X ̅ , Y ̅ , t ) = F ϕ x ( X ̅ , Y ̅ ) ∑ i = 1 n ∑ m = 1 m φ ι m ( X ̅ , Y ̅ ) b ι m ( t ) = φ T ( X ̅ , Y ̅ ) b ( t ) , ϕ y ( X ̅ , Y ̅ , t ) ,

(41) ϕ y ( X ̅ , Y ̅ , t ) = F ϕ y ( X ̅ , Y ̅ ) ∑ p = 1 n ∑ q = 1 m ψ pq ( X ̅ , Y ̅ ) c pq ( t ) = ψ T ( X ̅ , Y ̅ ) c ( t ) ,

where m and n are the numbers of modes in the x and y directions, and the column vectors ω ̅ , φ , and ψ are the shape of the hypothetical modes. a, b, and c are the generalized coordinate vector.

The boundary functions must satisfy the geometric boundary conditions of the sheet. The geometric boundary conditions for a one-clamped sheet can be considered as simply supported in the x direction and simply supported-clamped in the y direction (Figure 1). Based on this, we have

(42) y = 0 → clamped boundary condition ( x = 0 , x = a , y = b ) → free boundary condition .

As a result, the boundary functions of a sheet can be written as relation (34):

(43) F x ( X ̅ , Y ̅ ) = F ϕ x ( X ̅ , Y ̅ ) = F ϕ y ( X ̅ , Y ̅ ) = Y ̅ .

The mode functions are described in the following equations:

(44) ω ̅ ij = ( X ̅ , Y ̅ ) = P i ( X ̅ ) P j ( Y ̅ ) ,

(45) φ ι m ( X ̅ , Y ̅ ) = P ι ( X ̅ ) P m ( Y ̅ ) ,

(46) ψ pq ( X ̅ , Y ̅ ) = P p ( X ̅ ) P q ( Y ̅ ) ,

where P s ( χ ) is equal to the sth ( χ = X ̅ , Y ̅ ) one-dimensional Chebyshev polynomial and is expressed in the form of cosine functions and in the form of Eq. (36):

(47) P s ( χ ) = cos [ ( s − 1 ) arccos ( 2 χ − 1 ) ] ; ( s = 1 , 2 , 3 , … ) .

Chebyshev polynomial series as an admissible function for the shape of the modes have two advantages. First, they are a complete and orthogonal set in the interval [−1,1]. Furthermore, Chebyshev’s polynomial and its derivatives are expressed in a straightforward and simple manner, which simplifies the coding procedure [27,28,29].

2.4 Eigenvalues of differential equation

Eq. (37) is derived by applying Hamilton’s principle to the linear motion equation of the system

(48) M X ̈ ( t ) + C Δ p X ̇ ( t ) + ( K + K Δ p ) X ( t ) = 0 .

In order to simplify the stability analysis, the differential Eq. (38) can be written in the state space form:

(49) Z ̇ ̅ = [ A ] Z , ̅

where

(50) Z ̅ = { X T X ̇ T } T ,

(51) [ A ] = [ 0 ] [ I ] − [ M ] − 1 [ K ] − [ M ] − 1 [ K ] .

The eigenvalues of the matrix [A] are obtained in the form of Eq. (52) in the form of a complex number.

(52) Ω r + i ω ,

where i = − 1 , Ω r indicates the damping ratio of the system, and ω is the specific frequency of the system.

Flutter for the system occurs when two special frequencies meet and become one [30] or when the value of the damping ratio becomes positive [31]. At the limit of the flutter, the dimensionless aerodynamic pressure is critical and is presented as λ cr .

3 Results and discussion

The flutter of the FG-CNTs with added mass is investigated and analyzed.

3.1 Validation

To verify the accuracy of the results, validation is performed on the data of other research. Table 1 provides a summary of properties.

Table 1

Properties in the structural systems

Filler material	SWCNT	CNT with V CNT * = 0.12	CNT with V CNT * = 0.17
E m = 2.5 GPa	E 11 CNT = 5.646 TPa	η 1 = 0.137	η 1 = 0.142
ρ m = 1,150 kg / m 3	E 33 CNT = 7.080 TPa	η 2 = 1.022	η 2 = 1.626
ν m = 0.34	G 12 CNT = 1.944 TPa	η 3 = 0.715	η 3 = 0.7 η 2
	ν 12 CNT = 0.175 TPa
	ρ CNT = 1,400 kg / m 3

The shear modulus is assumed to be G 12 = G 13 and G 23 = 1.2 G 12 . The aerodynamic parameter µ is considered equal to 0.01 [30].

The natural frequencies for a sheet reinforced with CNTs around the joint were compared for validation. For this purpose, the natural frequencies of the sheet, with AR = 1 , H = 0.1 , and V CNT * = 0.17 with two uniform and decreasing–increasing patterns were obtained and compared with Lei et al. [31]. Figure 3 shows the first four natural frequencies of this comparison.

Figure 3

The validation of natural frequency with Lei et al. [31] for (a) uniform and (b) decreasing–increasing distribution.

Evidently, the results of the present work matches well with the validation case. In order to validate the aerodynamics of the problem, the critical boundary of the flutter was investigated for an isosceles circular sheet of a square-shaped airfoil. This study was compared with Weiliang and Dowell’s research [32]. The results are shown in Table 2 and show how well the results match.

Table 2

Flutter boundary for a square sheet with a round shape of AR = 1

Parameter	Weiliang and Dowell [32]	The present study
λ cr	49.00	46.82

3.2 Investigation of flutter boundary

This section investigates how parameters such as extended mass and the composite sheet reinforced with CNTs of a one-side clamped on the flutter boundary affect the results. In the first step, we study the effect of different distribution patterns of CNTs on the flutter boundary. For this purpose, in each case, the pattern of distribution changes and other parameters are kept constant.

Figure 4 shows the changes in a specific frequency regarding dimensionless aerodynamic pressure for the first two vibration modes of the square sheet. In this case, the distribution of CNTs along the thickness has been chosen according to a uniform pattern. The added square mass with MR = 0.8 and LR = WR = 0.45 is installed in the center of the sheet with x m / a = y m / b = 0.5 . For the sheet with H = 0.1 , AR = 1 and V CN * = 17 have been assumed. It is clear that the first two modes of vibration meet at the dimensionless aerodynamic pressure of λ cr = 22.98 , and at this point, the fluttering has occurred for the system.

Figure 4

The specific frequency changes of the reinforced composite sheet with uniform distribution of CNTs according to dimensionless aerodynamic pressure.

Figure 5 shows the flutter boundary for the first two vibration modes of the sheet with added mass and the decreasing–increasing distribution pattern. In this case, flutter occurred in the dimensionless aerodynamic pressure of λ cr = 14.66 for the system. Comparing Figures 4 and 5, it can be seen that flutter occurred earlier for the sheet with an increasing–decreasing distribution than a uniform distribution.

Figure 5

The specific frequency changes of the composite sheet reinforced with CNTs increasing–decreasing distribution in terms of dimensionless aerodynamic pressure.

In Figures 6 and 7, which respectively show the flutter boundary for decreasing and increasing–decreasing distribution patterns, flutter occurs at λ cr = 25.48 for the decreasing pattern and at λ cr = 45.18 for the increasing–decreasing pattern.

Figure 6

The specific frequency changes of composite sheet reinforced with the distribution of CNTs, decreasing distribution in terms of dimensionless aerodynamic pressure.

Figure 7

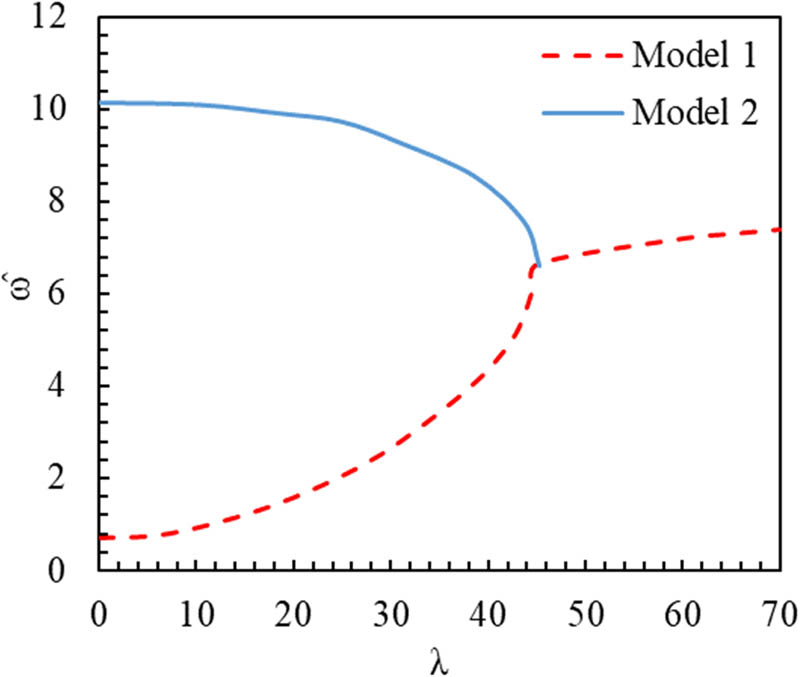
The specific frequency changes of composite sheet reinforced with the distribution of CNTs increasing–decreasing distribution in terms of dimensionless aerodynamic pressure.

By comparing Figures 4–7, it can be seen that the limit of flutter is the lowest for the decreasing–increasing pattern than the others, the highest for the increasing–decreasing distributional pattern, and the stability for the decreasing and uniform patterns is very close to each other. It can also be seen in these figures that the specific frequency in the flutter boundary for the case of uniform distribution occurred in ω ˆ = 3.528 , decreasing–increasing in ω ˆ = 8.982 , increasing–decreasing in ω ˆ = 6.588 , and decreasing in ω ˆ = 6.831 . The specific frequency is the highest for the decreasing–increasing pattern, followed by decreasing, increasing–decreasing and uniform patterns.

Figure 8 shows the change in the damping ratio according to the increase in the dimensionless aerodynamic pressure. Flutter occurs when the first two vibration modes’ damping ratio deviates from zero. In this figure, which is drawn for a uniform distribution and in different mass ratios, with the increase of the MR mass ratio and the heavier added mass compared to the base sheet from 0.15 to 1.2, the flutter boundary decreases and occurs sooner for the system.

Figure 8

Flutter boundary of the reinforced composite sheet with uniform distribution of CNTs according to different mass ratios.

In Figure 9, the dimensionless aerodynamic pressure is shown as the effect of LR on flutter. The dimensionless length of the added mass for four different distribution patterns of CNTs varies from 0.1 to 0.9 in this figure. In all four distribution patterns, it is clear the flutter limit rises with the increase in the length of the added mass for all four distribution patterns. It can also be seen that the limit of flutter in all LR values is higher for the decreasing pattern than for the increasing–decreasing pattern. For the increasing–decreasing pattern, it is higher than the two decreasing–increasing and uniform patterns.

Figure 9

Flutter boundary of the composite CNT sheets in terms of LR.

The distance of the added mass from the attacking edge on the flutter boundary in terms of dimensionless aerodynamic pressure is plotted in Figure 10 for four distribution patterns. For each distribution pattern, the changes are different, but in all the values of x m / a , the decreasing distribution is always the highest, and the increasing–decreasing distribution are the lowest to reach flutter instability.

$Figure 10 Flutter boundary of CNTs in terms of x m / a {x}_{m}/a .$

Figure 10

Flutter boundary of CNTs in terms of x m / a .

Figure 11 depicts how distance of the added mass from the root in terms of dimensionless aerodynamic pressure changes flutter boundary. For the uniform pattern, the flutter boundary is reduced with the distance of the added mass from the root of the sheet. However, for the three decreasing–increasing, decreasing, and increasing–decreasing patterns with the rising distance of the added mass from the edge of the root, initially, the flutter boundary increases and then drops.

$Figure 11 Flutter boundary of CNTs in terms of y m / b {{\rm{y}}}_{m}/b .$

Figure 11

Flutter boundary of CNTs in terms of y m / b .

Figures 12 and 13 show the distance variation from the root edge for three sheets with added mass that differ only in the size of WR. Figure 12 is based on the increasing–decreasing pattern, and Figure 13 is drawn based on the uniform pattern. As is clear in each diagram, with the increase in the distance y m / b from 0.3 to 0.7, the flutter boundary decreases. For the decreasing–increasing pattern, with the increase of WR from 0.15 to 0.35 for all values of y m / b , the flutter boundary has increased. For the uniform pattern in y m / b values less than 0.58, the sheet with WR = 0.3 5 provides the highest flutter stability boundary, and for y m / b values greater than 0.63, the sheet with WR = 0.15 has the highest flutter boundary.

$Figure 12 Flutter boundary of composite sheet reinforced by CNTs of decreasing–increasing distribution with different WRs in terms of y m / b {y}_{m}/b .$

Figure 12

Flutter boundary of composite sheet reinforced by CNTs of decreasing–increasing distribution with different WRs in terms of y m / b .

$Figure 13 Flutter boundary of composite sheet reinforced by uniformly distributed CNTs with different WRs in terms of y m / b {y}_{m}/b .$

Figure 13

Flutter boundary of composite sheet reinforced by uniformly distributed CNTs with different WRs in terms of y m / b .

In Figures 14 and 15, the value of the damping ratio is plotted in terms of dimensionless aerodynamic pressure, and the influence of lay-up with different angles for an asymmetric two-layer composite on the flutter boundary is investigated. Figure 14 is drawn for three different angles of the lay-up from the decreasing pattern, and as it is known, the flutter boundary is the highest in the lay-up [55/−55], and the flutter boundary is the lowest in the lay-up [25/−25]. For Figure 15, which is based on a uniform distribution pattern, the same result has been confirmed, and the lay-up [55/−55] has the highest flutter boundary and [25/−25] the lowest flutter boundary.

Figure 14

Flutter boundary of composite sheet reinforced by CNTs of decreasing distribution with different lay-ups according to dimensionless aerodynamic pressure.

Figure 15

Flutter boundary of composite sheet reinforced by distributed CNTs uniform with different lay-ups according to the dimensionless aerodynamic pressure.

4 Artificial neural networks (ANNs)

In order to analyze complex data sets and make predictions based on patterns and trends, ANNs are powerful tools. A number of materials, including composite materials, have been investigated by ANNs in recent years [33,34,35,36]. One such application is the investigation of FG composite wing reinforced with CNTs, which has become an area of interest due to its potential for improving strength and durability [33,37]. In this context, ANNs can be used to analyze experimental data and simulate the behavior of composite materials under different conditions, providing valuable insights into their mechanical properties and performance. This article explores the use of ANNs in the investigation of FG composite reinforced with CNTs, highlighting the predictive ability of the damping ratio using the present study’s data.

Python is used to implement the model. To propose the predictive model, the LR , WR , lay-up, x m / a , y m / b are selected as input parameters. The model is optimized by using hyperparameter tuning [38]. For this, Table 3 presents the parameters for the final proposed model.

Table 3

Parameters for the final ANN model

Parameters	Values
Input parameters	LR , WR , lay-up, x m / a , y m / b
Hidden layer	(400, 300, 200, 100, 50, 10)
Loss function	Mean squared error
Epochs	8,000
Batch size	4
Activation function	ReLU

The results of the present study produced 81 data for the damping ratio, 24 of which are considered for evaluation of the model. By selecting data randomly, we trained the model, and Figure 16 presents the model’s results. As seen in this figure, the model is evaluated using mean absolute error and R 2 .

Figure 16

The ANN model for predicting the damping ratio of the structure by using hyperparameter tuning.

As seen in Figure 16, the model performed very well, with an MAE of 1.64%. Also, to measure the model’s predictive capabilities, the coefficient of determination is used and is equal to 0.98. The computational costs of the ANN model are also compared with the modeling performed in the present study. It is concluded that the ANN model has satisfactory accuracy and operates very quickly. The ANN model takes almost less than 10% of the modeling time to reach the results. Therefore, it seems very applicable in designing processes since there is high demand for timely designs.

5 Conclusion

This research studied the extended added mass on the flutter boundary of FG-CNTs. Hamilton’s principle was applied to the rectangular plate with added mass in the ultrasonic flow, using the first-order shear theories for the plate and the first-order piston for the ultrasonic flow. The effect of mass ratio, location of added mass, dimensions of added mass, and different distribution patterns in CNTs reinforcing the sheet on the aeroelastic behavior of the sheet was investigated. As the mass ratio increases and the added mass becomes heavier compared to the base sheet, the flutter boundary decreases, and the flutter occurs earlier. Increasing the length of the added mass in the flow direction increases the flutter boundary and the range of stability. Compared to other patterns, the decreasing distribution in CNTs has the highest amount of changes in relation to the location and dimensions of the added mass and is more sensitive. By changing the location of the added mass perpendicular to the flow and by increasing the distance from the root of the sheet, the flutter boundary first increases and then decreases. By changing the location of the added mass in the direction of the flow, for different distribution patterns of CNTs, the behavior of the sheet will be different in reaching flutter instability. Flutter stability increases by increasing the angle of the lay-up of fibers in boundary asymmetric composites. Finally, the ANN model is utilized to predict the damping ratio. Hyperparameter tuning is utilized to predict optimize the model. The final results showed a model with an MAE of less than 2%. The computational costs of both models were compared, and the ANN model showed a fascinating performance in this regard.

Acknowledgements

The author would like to thank the University of Technology-Iraq, Baghdad, Iraq, for supporting present work.

Funding information: The authors did not receive any funding.
Author contributions: Aseel M: conceptualization, writing, revision. Hatam K: writing draft, date analysis, editing.
Conflict of interest: The authors declare that they have no conflict of interests.
Ethical approval: This work does not contain any experiments with human participants or animals undertaken.

References

[1] Vo-Duy T, Ho-Huu V, Nguyen-Thoi T. Free vibration analysis of laminated FG-CNT reinforced composite beams using finite element method. Front Struct Civ Eng. 2019 Apr;13:324–36.10.1007/s11709-018-0466-6Suche in Google Scholar

[2] Ramteke PM, Kumar V, Sharma N, Panda SK. Geometrical nonlinear numerical frequency prediction of porous functionally graded shell panel under thermal environment. Int J Non-Linear Mech. 2022 Jul 1;143:104041.10.1016/j.ijnonlinmec.2022.104041Suche in Google Scholar

[3] Nurazzi NM, Sabaruddin FA, Harussani MM, Kamarudin SH, Rayung M, Asyraf MR, et al. Mechanical performance and applications of CNTs reinforced polymer composites – A review. Nanomaterials. 2021 Aug;11(9):2186.10.3390/nano11092186Suche in Google Scholar PubMed PubMed Central

[4] Bakshi SR, Agarwal A. An analysis of the factors affecting strengthening in carbon nanotube reinforced aluminum composites. Carbon. 2011 Feb;49(2):533–44.10.1016/j.carbon.2010.09.054Suche in Google Scholar

[5] Yu W, Sisi L, Haiyan Y, Jie L. Progress in the functional modification of graphene/graphene oxide: A review. RSC Adv. 2020;10(26):15328–45.10.1039/D0RA01068ESuche in Google Scholar

[6] Baig N, Kammakakam I, Falath W. Nanomaterials: A Rev Synth methods, properties, recent progress. Chall Mater Adv. 2021;2(6):1821–71.10.1039/D0MA00807ASuche in Google Scholar

[7] Mustafa MA, Abdullah AR, Hasan WK, Habeeb LJ, Nassar MF. Two-Way Fluid-Structure Interaction Study of Twisted Tape Insert in a Circular Tube Having Integral Fins With Nanofluid. East-Eur J Enterp Technol. 2021 Jun;3(8):111.10.15587/1729-4061.2021.234125Suche in Google Scholar

[8] Alibeigloo A, Emtehani A. Static and free vibration analyses of carbon nanotube-reinforced composite plate using differential quadrature method. Meccanica. 2015 Jan;50:61–76.10.1007/s11012-014-0050-7Suche in Google Scholar

[9] Nami MR, Janghorban M. Free vibration of thick functionally graded carbon nanotube-reinforced rectangular composite plates based on three-dimensional elasticity theory via differential quadrature method. Adv Compos Mater. 2015 Sep;24(5):439–50.10.1080/09243046.2014.901472Suche in Google Scholar

[10] Civalek Ö, Avcar M. Free vibration and buckling analyses of CNT reinforced laminated non-rectangular plates by discrete singular convolution method. Eng Comput. 2022 Apr;38(Suppl 1):489–521.10.1007/s00366-020-01168-8Suche in Google Scholar

[11] Swain PK, Adhikari B, Maiti DK, Singh BN. Aeroelastic analysis of CNT reinforced functionally graded laminated composite plates with damage under subsonic regime. Compos Struct. 2019 Aug;222:110916.10.1016/j.compstruct.2019.110916Suche in Google Scholar

[12] Natarajan S, Kaleeswaran K, Manickam G. Functionally graded material panel flutter by cell-based smoothed finite elements. J Coupled Syst Multiscale Dyn. 2013 Jun;1(2):205–15.10.1166/jcsmd.2013.1014Suche in Google Scholar

[13] Guo H, Żur KK, Ouyang X. New insights into the nonlinear stability of nanocomposite cylindrical panels under aero-thermal loads. Compos Struct. 2023 Jan;303:116231.10.1016/j.compstruct.2022.116231Suche in Google Scholar

[14] Sankar A, Natarajan S, Zineb TB, Ganapathi M. Investigation of supersonic flutter of thick doubly curved sandwich panels with CNT reinforced facesheets using higher-order structural theory. Compos Struct. 2015 Sep;127:340–55.10.1016/j.compstruct.2015.02.047Suche in Google Scholar

[15] Zhang LW, Song ZG, Liew KM. Optimal shape control of CNT reinforced functionally graded composite plates using piezoelectric patches. Compos Part B: Eng. 2016 Feb;85:140–9.10.1016/j.compositesb.2015.09.044Suche in Google Scholar

[16] Song ZG, Li FM, Zhang W. Active flutter and aerothermal postbuckling control for nonlinear composite laminated panels in supersonic airflow. J Intell Mater Syst Struct. 2015 May;26(7):840–57.10.1177/1045389X14535013Suche in Google Scholar

[17] Li B, Amin AH, Ali AM, Isam M, Lagum AA, Sabugaa MM, et al. UV and solar-based photocatalytic degradation of organic pollutants from ceramics industrial wastewater by Fe-doped ZnS nanoparticles. Chemosphere. 2023 Jun;336:139208.10.1016/j.chemosphere.2023.139208Suche in Google Scholar PubMed

[18] Alibeigloo A, Kari MR. Forced vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third order shear deformation theory. Thin-Walled Struct. 2009 Jun;47(6–7):653–60.10.1016/j.tws.2008.11.006Suche in Google Scholar

[19] Lin H, Cao D, Xu Y. Vibration characteristics and flutter analysis of a composite laminated plate with a store. Appl Math Mech. 2018 Feb;39(2):241–60.10.1007/s10483-018-2297-6Suche in Google Scholar

[20] Peiró J, Galvanetto U, Chantharasenawong C. Assessment of added mass effects on flutter boundaries using the Leishman–Beddoes dynamic stall model. J Fluids Struct. 2010 Jul;26(5):814–40.10.1016/j.jfluidstructs.2010.04.002Suche in Google Scholar

[21] Zhang LW, Lei ZX, Liew KM. Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos Struct. 2015 Feb;120:189–99.10.1016/j.compstruct.2014.10.009Suche in Google Scholar

[22] Shen HS, Zhang CL. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Mater Des. 2010 Aug;31(7):3403–11.10.1016/j.matdes.2010.01.048Suche in Google Scholar

[23] Hassan A, Samawi KA, Nassar MF, Haddad R, Roostaie A, Sadeghzadeh SM. Synthesis of Cyclic Carbonate from Carbon Dioxide and Epoxides Using Bicobalt Complexes Absorbed on DFNS. Catal Lett. 2022 Nov;1:2900–9.10.1007/s10562-022-04130-zSuche in Google Scholar

[24] Chai Y, Song Z, Li F. Investigations on the aerothermoelastic properties of composite laminated cylindrical shells with elastic boundaries in supersonic airflow based on the Rayleigh–Ritz method. Aerosp Sci Technol. 2018 Nov;82:534–44.10.1016/j.ast.2018.09.040Suche in Google Scholar

[25] Zhou D, Cheung YK, Au FT, Lo SH. Three-dimensional vibration analysis of thick rectangular plates using Chebyshev polynomial and Ritz method. Int J Solids Struct. 2002 Dec;39(26):6339–53.10.1016/S0020-7683(02)00460-2Suche in Google Scholar

[26] Abo-Bakr HM, Abo-Bakr RM, Mohamed SA, Eltaher MA. Weight optimization of axially functionally graded microbeams under buckling and vibration behaviors. Mech based Des Struct Mach. 2023 Jan;51(1):213–34.10.1080/15397734.2020.1838298Suche in Google Scholar

[27] El Jery A, Salman HM, Al-Khafaji RM, Nassar MF, Sillanpää M. Thermodynamics Investigation and Artificial Neural Network Prediction of Energy, Exergy, and Hydrogen Production from a Solar Thermochemical Plant Using a Polymer Membrane Electrolyzer. Molecules. 2023 Mar;28(6):2649.10.3390/molecules28062649Suche in Google Scholar PubMed PubMed Central

[28] Prakash T, Ganapathi M. Supersonic flutter characteristics of functionally graded flat panels including thermal effects. Compos Struct. 2006 Jan;72(1):10–8.10.1016/j.compstruct.2004.10.007Suche in Google Scholar

[29] Shin WH, Oh IK, Han JH, Lee I. Aeroelastic characteristics of cylindrical hybrid composite panels with viscoelastic damping treatments. J Sound Vib. 2006 Sep;296(1–2):99–116.10.1016/j.jsv.2006.01.068Suche in Google Scholar

[30] Salman EA, Samawi KA, Nassar MF, Abdulkareem-Alsultan G, Abdulmalek E. 3D Hollow Spheres Comprising MXene/g-C3N4 Heterostructre for Efficient Polysulfide Adsorption and Conversion in High-Performance Li-S Batteries. J Electroanal Chem. 2023 Jun;945:117629.10.1016/j.jelechem.2023.117629Suche in Google Scholar

[31] Lei ZX, Zhang LW, Liew KM. Free vibration analysis of laminated FG-CNT reinforced composite rectangular plates using the kp-Ritz method. Compos Struct. 2015 Sep;127:245–59.10.1016/j.compstruct.2015.03.019Suche in Google Scholar

[32] saed kariem Alawamleh H, Amin AH, Ali AM, Abd Alreda B, Lagum AA, Pecho RD, et al. Solar light driven enhanced photocatalytic treatment of azo dye contaminated water based on Co-doped ZnO/g-C3N4 nanocomposite. Chemosphere. 2023 Jun;335:139104.10.1016/j.chemosphere.2023.139104Suche in Google Scholar PubMed

[33] Singh S, Junaid ZB, Vyas V, Kalyanwat TS, Rana SS. Identification of vacancy defects in carbon nanotubes using vibration analysis and machine learning. Carbon Trends. 2021 Oct;5:100091.10.1016/j.cartre.2021.100091Suche in Google Scholar

[34] Tran ZL, Truong TT, Nguyen-Thoi T. Optimization design of laminated functionally carbon nanotube-reinforced composite plates using deep neural networks and differential evolution. Int J Comput Methods. 2023 Jun;20(05):2250065.10.1142/S0219876222500657Suche in Google Scholar

[35] Eskandari E, Alimoradi H, Pourbagian M, Shams M. Numerical investigation and deep learning-based prediction of heat transfer characteristics and bubble dynamics of subcooled flow boiling in a vertical tube. Korean J Chem Eng. 2022 Dec;39(12):3227–45.10.1007/s11814-022-1267-0Suche in Google Scholar

[36] Garg A, Belarbi MO, Tounsi A, Li L, Singh A, Mukhopadhyay T. Predicting elemental stiffness matrix of FG nanoplates using Gaussian process regression based surrogate model in framework of layerwise model. Eng Anal Bound Elem. 2022 Oct;143:779–95.10.1016/j.enganabound.2022.08.001Suche in Google Scholar

[37] Heidary Z, Ramezani SR, Mojra A. Exploring the benefits of functionally graded carbon nanotubes (FG-CNTs) as a platform for targeted drug delivery systems. Comput Methods Programs Biomed. 2023 Aug;238:107603.10.1016/j.cmpb.2023.107603Suche in Google Scholar PubMed

[38] Alimoradi H, Eskandari E, Pourbagian M, Shams M. A parametric study of subcooled flow boiling of Al2O3/water nanofluid using numerical simulation and artificial neural networks. Nanoscale Microscale Thermophys Eng. 2022 Jul;26(2–3):129–59.10.1080/15567265.2022.2108949Suche in Google Scholar

[39] Brischetto S. A continuum elastic three-dimensional model for natural frequencies of single-walled carbon nanotubes. Compos Part B: Eng. 2014 May;61:222–8.10.1016/j.compositesb.2014.01.046Suche in Google Scholar

[40] Tornabene F, Viscoti M, Dimitri R, Reddy JN. Higher order theories for the vibration study of doubly-curved anisotropic shells with a variable thickness and isogeometric mapped geometry. Compos Struct. 2021 Jul;267:113829.10.1016/j.compstruct.2021.113829Suche in Google Scholar

[41] Mercan K, Demir Ç, Civalek Ö. Vibration analysis of FG cylindrical shells with power-law index using discrete singular convolution technique. Curved Layer Struct. 2016;3(1):82–90.10.1515/cls-2016-0007Suche in Google Scholar

[42] Sofiyev AH, Tornabene F, Dimitri R, Kuruoglu N. Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials. 2020 Feb;10(3):419.10.3390/nano10030419Suche in Google Scholar PubMed PubMed Central

[43] Kiani Y, Dimitri R, Tornabene F. Free vibration study of composite conical panels reinforced with FG-CNTs. Eng Struct. 2018 Oct;172:472–82.10.1016/j.engstruct.2018.06.006Suche in Google Scholar

Received: 2023-06-11

Revised: 2023-09-30

Accepted: 2023-11-08

Published Online: 2024-01-03

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/cls-2022-0218

Schlagwörter für diesen Artikel

flutter instability; functionally graded composite sheet; carbon nanotube; monolayer sheet; extended added mass

Creative Commons

BY 4.0