Determination of gamma-ray transmission factors of WO3–TeO2–B2O3 glasses using MCNPX Monte Carlo code for shielding and protection purposes
-
Ghada ALMisned
und Huseyin Ozan Tekin
Abstract
The aim of this study is to assess the individual gamma-ray transmission factors (TFs) and some fundamental gamma-ray attenuation properties of several types of glasses based on WO3–TeO2–B2O3 glasses system. MCNPX (version 2.7.0) is used for the calculation of TFs. Other critical parameters are determined using the Phy-X/PSD program. To determine the TFs of studied glasses, several medical radioisotopes are determined along with their characteristic gamma-ray energies. The superior values for the investigated parameters are found in glass sample S6. Furthermore, the exposure build-up factor and energy absorption build-up factor values for glass sample S6 were the lowest. S6 glass sample with the chemical composition 0.03833B + 0.26075O + 0.11591Zn + 0.52783Te + 0.05718W and a density of 3.3579 g/cm3 is found to have exceptional gamma-ray attenuation qualities, according to our findings. It can be concluded that the prospective attributes of WO3-doped glass systems and associated glass compositions would be beneficial for scientific community in terms of providing a clearer view for some advanced applications of these glass types.
1 Introduction
Photon–matter interaction, which allows us to examine the interior structure of a material, is a commonly used concept in the medical sector for the purposes of diagnosis and therapy [1,2]. Although the sort of energy created by the radioisotopes used for diagnosis and treatment is advantageous for research, it has, on the other hand, harmful effects on biological tissues [3,4]. For the best protection conditions against the hazardous consequences of ionizing radiation, it is essential to comprehend all the quantifiable shielding properties of materials that may absorb the given radiation energy [5]. Meanwhile, lead (Pb) is one of the most traditional materials used for shielding purposes in various radiation fields. However, Pb is a toxic element that has detrimental biological effects when it enters the body by breathing and skin absorption. Therefore, various ongoing research aim to extend the design of shielding materials made without Pb and Pb-based compounds. In recent years, various types of alternative materials such as polymers, glasses, concrete, building supplies, ceramics, etc. have all been used due to the enormous scientific motivation provided by these drawbacks of Pb. The development of radiation shielding materials with innovative and environmentally advantageous properties has been pursued. The removal of Pb from the design of glass materials, which are vital components of nuclear medicine units [6–10], is one of the primary objectives of researchers. It has been shown earlier [11–15] that glasses containing oxide-based additions possess intriguing shielding properties. In the meantime, it is difficult to achieve a glassy structure without a glass modifier. Hereby, borate is one of the most often used and effective materials for producing glass (B2O3). Strong tungsten–oxygen (W–O) bonding and a strong polarization capacity make tungsten-oxide (WO3) a fascinating material for application in glass technology [16]. To improve their mechanical and shielding characteristics, glasses often include WO3 such as telluride, borate, and phosphate glasses [16–19]. The telluride glass systems, particularly binary TeO2–WO3 glasses, on the other hand, are the subject of the most popular research [19,20]. Tellurite’s glass formation and thermal stability may be improved by adding ZnO [21]. As a result, researchers are focused on expanding the spectrum of shielding glass material groups and developing the ideal glass structure for this use. The creation of radiation shielding materials made of glass is the subject of extensive investigation. Glass systems like ZnO–TeO2, B2O3–P3O4–ZnO, and WO3–ZnO–PbO–B2O3 that include zinc oxide as one of its components have been studied recently for their radiation shielding characteristics [21–23]. Recent studies have examined how the addition of WO3 to the synthesis and nuclear safety features of the telluride glass system might significantly modify the nuclear shielding properties [24–26]. Particularly, if the radiation shielding parameters could be defined for each energy value generated by radioisotopes used in nuclear medicine, it would be simpler to decide the structure that can be employed for shielding and give the maximum degree of protection [27]. Radiation shielding operates on the attenuation principle, which states that a barrier material will stop or deflect particles while decreasing the efficacy of waves or rays. Moreover, it is crucial to investigate the tenth value layer, half value layer, effective atomic number, exposure build-up factor (EBF), and energy absorption build-up factor (EABF) of the sample glasses in terms of better understanding the overall attenuation behaviours of the shielding materials. To expand the earlier work [28], the unstudied shielding parameters of the WO3–TeO2–B2O3 composite system, whose structural, physical, and optical aspects have been thoroughly studied, but only a few of its shielding parameters have been explored, are reviewed in detail. Moreover, transmission factor (TF) values are determined for some well-known radioisotopes’ energies, which ranged from 0.0086 to 1.3325 MeV, to investigate the shielding capabilities using the Monte Carlo method. The results of this investigation may be utilized in future investigations or to assist researchers with similar scientific goals.
2 Materials and methods
2.1 Studied glass samples
The previous investigation’s findings served as the foundation for the current investigation’s objective, which was to expand the scope of those findings [28] by giving a deeper understanding of the monotonic effects of increasing WO3 contribution on unstudied gamma-ray attenuation parameters. Moreover, another purpose of the current investigation was also to explore the individual TF values of these glasses against various types of radioisotopes using advanced Monte Carlo simulation methods. The following are the physical features of the glasses studied:
S1: 0.04131B + 0.26492O + 0.12492Zn + 0.56885Te + 0W with density and molar volume (ρ = 5.4794 g/cm3 and molar volume [V m = 28.793 cm3/mol]).
S2: 0.04070B + 0.26407O + 0.12309Zn + 0.56049Te + 0.01165W with density and molar volume (ρ = 4.7368 g/cm3 and molar volume [V m = 33.465 cm3/mol]).
S3: 0.04010B + 0.26323O + 0.12127Zn + 0.55220Te + 0.02320W with density and molar volume (ρ = 4.2931 g/cm3 and molar volume [V m = 37.098 cm3/mol]).
S4: 0.03951B + 0.26239O + 0.11946Zn + 0.54401Te + 0.03463W with density and molar volume (ρ = 3.8798 g/cm3 and molar volume [V m = 41.050 cm3/mol]).
S5: 0.03892B + 0.26157O + 0.11768Zn + 0.53588Te + 0.04595W with density and molar volume (ρ = 3.6826 g/cm3 and molar volume [V m = 43.451 cm3/mol]).
S6: 0.03833B + 0.26075O + 0.11591Zn + 0.52783Te + 0.05718W with density and molar volume (ρ = 3.3579 g/cm3 and molar volume [V m = 47.875 cm3/mol]).
Table 1 lists the codes, weight fractions, and densities of these glasses. In this investigation, the following codes were applied to the chosen glasses [28].
Samples code, elemental weight fraction, density, and molar volume of (1−x)[0.7TeO2–0.3B2O3–0.3ZnO]−xWO3 (x = 0.00, 0.01, 0.02, 0.03, 0.04 and 0.05 mol% glasses)
| Samples code | Elemental weight fraction (wt%) | Density, ρ (g/cm3) [28] | Molar volume, V m (cm3/mol) [28] | ||||
|---|---|---|---|---|---|---|---|
| B | O | Zn | Te | W | |||
| S1 | 0.04131 | 0.26492 | 0.12492 | 0.56885 | 0 | 5.4794 | 28.793 |
| S2 | 0.04070 | 0.26407 | 0.12309 | 0.56049 | 0.01165 | 4.7368 | 33.465 |
| S3 | 0.04010 | 0.26323 | 0.12127 | 0.55220 | 0.02320 | 4.2931 | 37.098 |
| S4 | 0.03951 | 0.26239 | 0.11946 | 0.54401 | 0.03463 | 3.8798 | 41.050 |
| S5 | 0.03892 | 0.26157 | 0.11768 | 0.53588 | 0.04595 | 3.6826 | 43.451 |
| S6 | 0.03833 | 0.26075 | 0.11591 | 0.52783 | 0.05718 | 3.3579 | 47.875 |
2.2 Shielding parameters and gamma TFs
To achieve the goals of this study, six glasses containing tungsten trioxide, tellurium dioxide, and boron trioxide (WO3–TeO2–B2O3) were chosen from previous research [28]. As a means of keeping the photon energy range explored in this work at a much higher level, the gamma-ray energies of various radioisotopes (0.0086–1.3325 MeV) are utilized to determine TFs. However, the unexplored shielding characteristics of the glasses were assessed with the aid of the Phy-X/PSD (Photon Shielding and Dosimetry) software [11]. The gamma TFs were calculated using MCNPX 2.7.0 general-purpose Monte Carlo simulation program. The TFs of glasses (i.e., S1–S6) having diverse chemical compositions of WO3–TeO2–B2O3 were comprehensively evaluated and compared using several evaluation parameters [29–32]. During the computation of TFs for a wide number of radioisotopes, as shown in Table 2, each input file has been designed considering the elemental mass fractions, densities, and other related parameters of the glasses that are essential for an input determination. Figure 1 depicts the layout of the MCNPX simulation used to determine the gamma-ray transmission coefficient. The TF of the absorber was calculated by dividing the total radiation flux (F) by the radiation flux (I) after absorption process by attenuator material. To estimate the TF of the investigated glasses, the average gamma-ray flux in the F4 tally mesh was multiplied by the average gamma-ray flux in the uniform detection field. Two detecting fields, one in front and one behind the glass, were used to convert this formulation into MCNPX code. This formulation was translated into MCNPX [33] code by using two detecting fields, one in front of the glass and one behind the glass. Both the main gamma-ray intensity in front of the glass and the attenuated gamma-ray intensity behind the glass were measured and detected instantly.
Gamma ray energies of nuclear-type radioisotopes
| Radioisotopes | Gamma-ray energy (MeV) |
|---|---|
| 67Ga | 0.0086, 0.0093, 0.1840 |
| 57Co | 0.0144, 0.1221, 0.1365 |
| 111In | 0.0230, 0.1710, 0.2450 |
| 133Ba | 0.0532, 0.0796, 0.0810, 0.2764, 0.3029, 0.3560, 0.3838 |
| 201Tl | 0.0710, 0.1350, 0.1670 |
| 99mTc | 0.1405 |
| 51Cr | 0.3201 |
| 131I | 0.2843, 0.3645, 0.6370, 0.7229 |
| 58Co | 0.5110, 0.8108 |
| 137Cs | 0.6617 |
| 60Co | 1.1732, 1.3325 |

2-D and 3-D illustration of designed MCNPX setup (2-D and 3-D views are obtained from MCNPX Visual Editor VisedX22S).
3 Results and discussions
The direct contribution of structural changes to the absorption qualities of glass materials may be examined by calculating the radiation absorption characteristics of glass materials in accordance with specified parameters [34–45]. The term effective atomic number (Z eff) is of great interest for radiation researchers due to its role during the absorption process of initial photons in the material. It is worth mentioning that the gamma-ray radiation scattering and absorption are related to the Z eff values of the investigated glass samples. As seen in Figure 2, Z eff values changed as a function of incoming photon energy (MeV). As the photon energy increased, it was obvious that the Z eff values for the glass samples also altered. In the low-energy zone, the photoelectric effect predominates due to the photon–matter interaction. Consequently, the low-energy photons on the absorbing layer interact with the electrons in the orbit of the material medium, contributing their whole energy to this interaction and achieving complete absorption. In response to an increase in photon energy, electrons in this orbit are ejected, and photons with decreasing energy are released to generate secondary and subsequent collisions. In this situation, Compton scattering is the most prominent photon–matter interaction in the mid-energy region. Due to the k-absorption edge of Te (i.e., 0.31 keV), the Z eff values reached their maximum at 0.3 MeV on the graph. On the other hand, Z eff value exhibits a progressive rise when energies above 2.0 MeV are considered (Table 3). For the photon-exposed sample glasses, the effective electron number (N eff) changes in the same way as Z eff does [46–48]. The effective atomic number (Z eff) and the effective electron density (N eff) both show contradictory tendencies in their relationship with the energy of the incident photon (MeV), with values beginning to diverge in opposite directions around 0.04 MeV. For the photon-exposed sample glasses, the effective electron number (N eff) changes in the same way as Z eff does. This is mostly due to the correlation between the effective atomic number and the effective electron number. As is well known, the number of electrons a nucleus contains is proportional to its atomic number. As the atomic number grows, so does the number of electrons, which is the primary reason that elements with a high atomic number are better in their ability to absorb photons. The photon that reaches the atomic orbit contacts several times with a large number of electrons and is absorbed more efficiently and in less time as a consequence. The effective atomic number (Z eff) and the effective electron density (N eff) both show contradictory tendencies in their relationship with the energy of the incident photon (MeV), with values beginning to diverge in opposite directions around 0.03 MeV. The Z eff values (Figure 2) converge until 0.08 MeV, after which they diverge with a significant rise in the value difference. They continue in the same sequence until the very end, when S6 shows the highest values, followed by the remaining glasses in descending order until S1 reports the lowest values. At 0.04 MeV, the N eff values diverge, making it simpler to discern the S6–S1 values in decreasing order. Before proceeding, they momentarily swap to S1–S6 decreasing values (Figure 3). In Figure 4 one can see that the photon’s energy level correlates with the atomic equivalent number Z eq. This pattern is most notable for the rapid rise at 0.03 MeV, which is followed by a less abrupt increase at 0.07 MeV, with S1 having the lowest value and the other glasses rising steadily until S6 has the highest value. Meanwhile, the terms EBF and EABFs are crucial for assessment of photon absorption process considering the interacted and un-interacted photons with the absorber material. In this study, both the EBF and the EABF were calculated, and the results are presented in Figures 5 and 6 as a function of energy (MeV) over a range of mean free paths (from 0.5 to 40 mfp). Consistent increases in these quantities are seen for increasing photon energies, with the largest increases occurring at 0.04, 0.06, 0.08, 0.1, and 15 MeV. However, the EBF and EABF values alter significantly when the energy is increased up to 15 MeV, although they are less visible at shorter penetration depths. In general, with denser materials and a broader spectrum of incoming X-rays or gamma rays, larger mfp values result in photon accumulation. Energy ranges serve as the basis for EABF and EBF values. High values are visible in high energy, while low values are visible in low energy. This is caused by pair production at high energies, which results in the total absorption of photons, and the dominance of photoelectric processes at low energies. The energy of incident photons is decreased throughout this process, yet they are not entirely absorbed. Consequently, multiple scattering is generated by this mechanism, which leads to an accumulation of photons in the medium. Based on our results, S6 has the highest EBF and EABF values, while S1 has the lowest. To estimate the effective atomic number (Z eff) of the studied glasses, it is necessary to establish the radiation shielding parameters such as atomic cross-section (ACS) and electronic cross-section (ECS). Figure 7 illustrates the variation of the ACS as a function of the photon energy entering the system, whereas Figure 8 depicts the variation of the ECS. Out of the six glasses tested, S1 sample had the maximum attenuation of gamma rays, indicating that it is the most effective gamma-ray shield. To calculate the effective atomic number (Z eff) of the examined glasses, it is essential to know the radiation shielding parameters such as ACS and ECS. As can be seen in both figures, as the photon’s energy rises, both the ACS and ECS values decrease. Moreover, in every glass sample, the ACS values were greater than the ECS values. This is due to the fact that the likelihood of full atomic interaction in any given material is far greater than the probability of full electrical contact with incoming photons in any given material. In the last part of this study, the values of the gamma-ray TF were determined for each of the glass samples that were evaluated for a range of radioisotope energies between 0.0086 and 1.3325 MeV. Two different methods were used determine the glasses’ TF values. The TF factors of samples S1–S6 with varied glass thicknesses were measured first. These samples were put through a series of tests. Figure 9 depicts the TF of the examined glasses as a function of the radioisotope energy (MeV). Transmission increases as the energy of the radioisotope increases from 0.0086 to 1.3325 MeV. This is due to an increase in the number of photons capable of penetrating the opposite side of the material. Moreover, as shown in Figure 9, although transmission values reach their maximum at low glass thicknesses, TF values tend to decline as glass thickness increases. This indicates that the number of photons that travel through the glass at low thicknesses is higher, whereas this rate decreases as the thickness increases. At around 0.1 MeV, however, a distinct separation becomes apparent. Glass samples of varying thicknesses respond to gamma rays in different ways. As the energy level grows, these distinctions become more prominent. For all the analysed glass samples, the maximum attenuation values (and the lowest transmission values) were obtained at a thickness of 3 cm. This effect demonstrates that an increase in shield thickness will result in a greater attenuation of incoming gamma rays. Figure 10 depicts TFs as a function of radioisotope energy for various glass thicknesses (MeV). At different glass thicknesses, such as 0.5, 1.5, 2.5, and 3 cm, the TFs of all glass samples are changed.

Variations of effective atomic number (Z eff) with photon energy (MeV) for all S1–S6 glasses.
Effective atomic number (Z eff) values of all glasses
| Energy (MeV) | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|
| 0.015 | 73.92 | 47.50 | 48.57 | 49.58 | 50.53 | 51.43 |
| 0.02 | 73.93 | 47.53 | 48.63 | 49.67 | 50.63 | 51.55 |
| 0.03 | 73.93 | 47.56 | 48.69 | 49.75 | 50.74 | 51.67 |
| 0.04 | 73.74 | 50.95 | 51.19 | 51.42 | 51.66 | 51.89 |
| 0.05 | 73.74 | 50.87 | 51.11 | 51.35 | 51.58 | 51.82 |
| 0.06 | 73.74 | 50.74 | 50.97 | 51.21 | 51.45 | 51.69 |
| 0.08 | 73.94 | 51.11 | 52.11 | 53.03 | 53.90 | 54.72 |
| 0.1 | 73.94 | 50.49 | 51.51 | 52.47 | 53.36 | 54.20 |
| 0.15 | 73.93 | 48.26 | 49.30 | 50.26 | 51.17 | 52.03 |
| 0.2 | 73.91 | 45.80 | 46.78 | 47.71 | 48.59 | 49.42 |
| 0.3 | 73.87 | 42.00 | 42.82 | 43.60 | 44.36 | 45.09 |
| 0.4 | 73.82 | 39.86 | 40.54 | 41.21 | 41.85 | 42.48 |
| 0.5 | 73.78 | 38.68 | 39.27 | 39.86 | 40.43 | 40.99 |
| 0.6 | 73.76 | 37.99 | 38.53 | 39.06 | 39.58 | 40.09 |
| 0.8 | 73.72 | 37.26 | 37.74 | 38.21 | 38.67 | 39.13 |
| 1 | 73.70 | 36.90 | 37.35 | 37.79 | 38.22 | 38.65 |
| 1.5 | 73.67 | 36.68 | 37.10 | 37.51 | 37.92 | 38.32 |
| 2 | 73.68 | 36.96 | 37.38 | 37.79 | 38.20 | 38.61 |
| 3 | 73.71 | 37.92 | 38.36 | 38.79 | 39.22 | 39.64 |
| 4 | 73.73 | 38.91 | 39.37 | 39.82 | 40.26 | 40.70 |
| 5 | 73.75 | 39.79 | 40.27 | 40.73 | 41.19 | 41.64 |
| 6 | 73.76 | 40.53 | 41.02 | 41.49 | 41.96 | 42.42 |
| 8 | 73.78 | 41.69 | 42.20 | 42.69 | 43.17 | 43.65 |
| 10 | 73.80 | 42.54 | 43.05 | 43.55 | 44.05 | 44.53 |
| 15 | 73.82 | 43.85 | 44.38 | 44.90 | 45.41 | 45.91 |

Variations of effective electron density (electrons/g) with photon energy (MeV) for all S1–S6 glasses.

Variations of equivalent atomic number (Z eq) with photon energy (MeV) for all S1–S6 glasses.

Variation of EBF of investigated glasses at different mean free path values.

Variation of EABF of investigated glasses at different mean free path values.
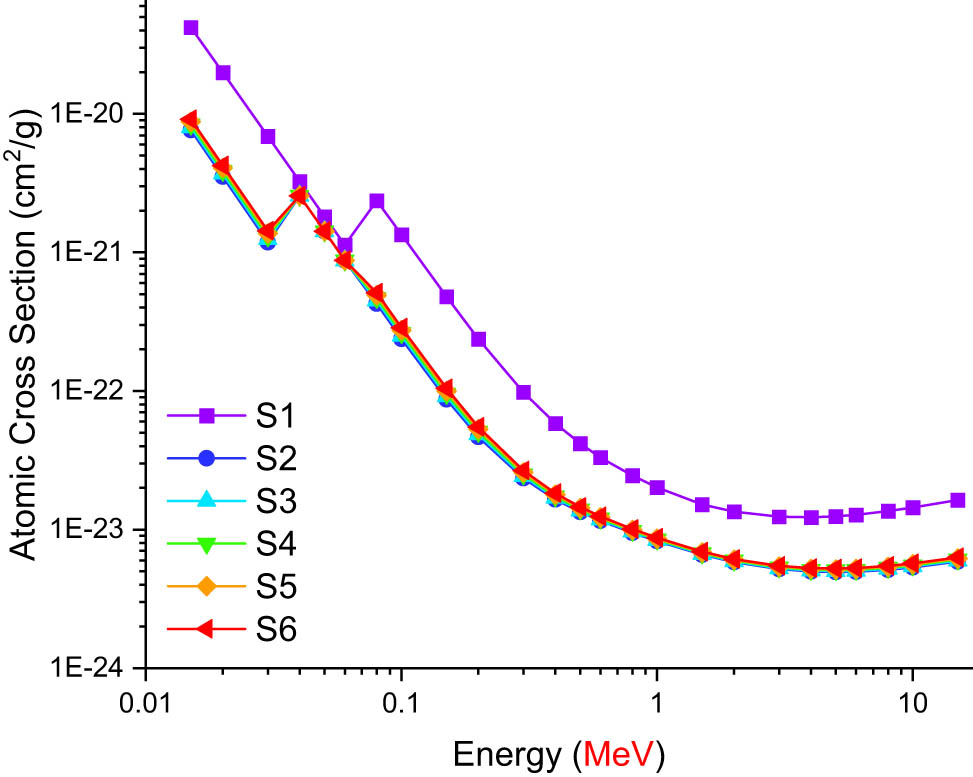
Variations of atomic cross-section with photon energy (MeV) for all S1–S6 glasses.

Variations of electronic cross-section with photon energy (MeV) for all S1–S6 glasses.

TFs of investigated glasses as a function of used radioisotope energy (MeV) at different glass thicknesses.

Comparison of the TFs as a function of used radioisotope energy (MeV) for different glass thicknesses.
4 Conclusion
The aim of the research was to broaden the scope of a previous study conducted on WO3–TeO2–B2O3 glasses in order to gain a better understanding of the effects of varying quantities of WO3 additive by calculating crucial gamma-ray absorption parameters and analysing its contribution to the absorption properties in a more comprehensive manner. Accordingly, some critical gamma-ray attenuation properties such as Z eff, N eff, Z eq, EBF, EABF, ACS, ECS, and TFs of six different glass samples were determined in a wide-range photon energy. In transmission tests using the MCNP code, the gamma-ray transmission ratios of the glasses investigated with a broad variety of radioisotopes were also evaluated. As WO3 concentration and molar volume increase, it has been observed that sample density decreases. In addition to confirming previously published gamma-ray absorption values, the findings of this investigation also demonstrated that the decrease in density caused by the higher WO3 ratio in the TeO2/WO3 translocation had a detrimental effect on all those parameters. The glass sample S1 (ZnO–B2O3–TeO2), which has the highest proportion of TeO2, is found to have the best shielding composition among the samples investigated in this investigation. According to the findings of this investigation, the density of the oxide type added to the glass composition plays an essential role in defining its absorption properties. Among the various translocated oxides, the percentage increase in the composition of the low-density oxide has the potential to generate a disadvantage by reducing the absorption capabilities.
-
Funding information: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0004.
-
Author contributions: Ghada ALMisned: writing, calculations, revision; Duygu Sen Baykal: calculations, writing, illustrations; Gokhan Kilic: calculations, writing; G. Susoy: calculations, writing, revision; Hesham M.H. Zakaly: calculations, writing; Antoaneta Ene: calculations, writing (The work of Antoaneta Ene and the APC were supported by Dunarea de Jos University of Galati, Romania through the grant no. RF 3621/2021.); Huseyin Ozan Tekin: writing, calculation, supervision, revision.
-
Conflict of interest: None.
-
Data availability statement: Data will be made available on request.
-
Ethical approval: The conducted research is not related to either human or animal use.
References
[1] Sodhi KS, Krishna S, Saxena AK, Sinha A, Khandelwal N, Lee EY. Clinical application of “Justification” and “Optimization” principle of ALARA in pediatric CT imaging: ‘How many children can be protected from unnecessary radiation?’ Eur J Rad. 2015;84:1752–7. 10.1016/j.ejrad.2015.05.030.Suche in Google Scholar PubMed
[2] Fahey FH, Goodking A, Treves ST, Grant FD. Nuclear medicine and radiation protection. J Radiol Nurs. 2016;35(1):5–11.10.1016/j.jradnu.2015.12.005Suche in Google Scholar
[3] Kaewkhao J, Pokaipisit A, Limsuwan P. Study on borate glass system containing with Bi2O3 and BaO for gamma-rays shielding materials: comparison with PbO. J Nucl Mater. 2010;399(1):38–40.10.1016/j.jnucmat.2009.12.020Suche in Google Scholar
[4] Singh N, Singh KJ, Singh K, Singh H. Comparative study of lead borate and bismuth lead borate glass systems as gamma-radiation shielding materials. Nucl Instrum Methods Phys Res B. 2004;225(3):305–9.10.1016/j.nimb.2004.05.016Suche in Google Scholar
[5] Abouhaswa AS, Tekin HO, Kavaz E, Perisanoglu U. Optical and nuclear radiation protection characteristics of lithium bismo-borate glasses: role of ZrO2 substitution. Radiat Phys Chem. 2021;183:109428.10.1016/j.radphyschem.2021.109428Suche in Google Scholar
[6] Tekin HO, Kassab LR, Issa SAM, Bordon CDS, Guclu EEA, da Silva Mattos GR, et al. Synthesis and nuclear radiation shielding characterization of newly developed germanium oxide and bismuth oxide glasses. Ceram Int. 2019;45(3):24664–74.10.1016/j.ceramint.2019.08.204Suche in Google Scholar
[7] Fares H, Jlassi I, Elhouichet H, Ferid M. Investigation of thermal, structural and optical properties of tellurite glass with WO3 adding. J Non-Cryst Solids 2014;396–307:1–7. 10.1016/j.jnoncrysol.2014.04.012.Suche in Google Scholar
[8] Singh VR, Badiger NM, Kaewkhao J. Radiation shielding competence of silicate and borate heavy metal oxide glasses: comparative study. J Non-Cryst Solids. 2014;404:167–73.10.1016/j.jnoncrysol.2014.08.003Suche in Google Scholar
[9] Abuzaid MM, Susoy G, Issa SA, Elshami W, Kilicoglu O, Tekin HO. Relationship between melting-conditions and gamma shielding performance of fluoro-sulfo-phosphate (FPS) glass systems: a comparative investigation. Ceram Int. 2020;46(10):15255–69.10.1016/j.ceramint.2020.03.065Suche in Google Scholar
[10] ALMisned G, Elshami W, Issa SA, Susoy G, Zakaly HM, Algethami M, et al. Enhancement of gamma-ray shielding properties in cobalt-doped heavy metal borate glasses: the role of lanthanum oxide reinforcement. Mater (Basel). 2021 Dec;14(24):7703.10.3390/ma14247703Suche in Google Scholar PubMed PubMed Central
[11] Şakar E, Özpolat ÖF, Alım B, Sayyed MI, Kurudirek M. Phy-X/PSD: development of a user friendly online software for calculation of parameters relevant to radiation shielding and dosimetry. Radiat Phys Chem. 2020;166:108496.10.1016/j.radphyschem.2019.108496Suche in Google Scholar
[12] Waly ES, Fusco MA, Bourham MA. Gamma-ray mass attenuation coefficient and half value layer factor of some oxide glass shielding materials. Ann Nucl Energy. 2016;96:26–30.10.1016/j.anucene.2016.05.028Suche in Google Scholar
[13] AbouDeif YM, Alqahtani MS, Massoud EE, Yaha IS, Yousef E. An evaluation of the radiation protection characteristics of prototyped oxide glasses utilising Phy-X/PSD software. J Instrum 2020;15(8):P08005. 10.1088/1748-0221/15/08/P08005.Suche in Google Scholar
[14] Sayyed MI, Laariedh F, Kumr A, Al-Buriahi MS. Experimental studies on the gamma photons-shielding competence of TeO2–PbO–BaO–Na2O–B2O3 glasses. Appl Phys A Mater Sci Process. 2020;126(1):1.10.1007/s00339-019-3182-8Suche in Google Scholar
[15] Pavani PG, Sadhana K, Mouli VC. Optical, physical and structural studies of boro-zinc tellurite glasses. Phys B Phys B. 2011;406(6–7):1242–7.10.1016/j.physb.2011.01.006Suche in Google Scholar
[16] Chen Q. WO3 concentration-dependent magneto-optical properties of Faraday rotating glasses and glass-ceramics. J Non-Cryst Solids. 2019;522:119584.10.1016/j.jnoncrysol.2019.119584Suche in Google Scholar
[17] Stalin S, Gaikwad DK, Al-Buriahi MS, Srinivasu C, Ahmed SA, Tekin HO, et al. Influence of Bi2O3/WO3 substitution on the optical, mechanical, chemical durability and gamma ray shielding properties of lithium-borate glasses. Ceram Int. 2021;47(4):5286–99.10.1016/j.ceramint.2020.10.109Suche in Google Scholar
[18] ElBatal HA, Abdelghany AM, ElBatal FH, EzzElDin FM. Gamma rays interactions with WO3-doped lead borate glasses. Mater Chem Phys. 2012;134(1):542–8.10.1016/j.matchemphys.2012.03.032Suche in Google Scholar
[19] Kaur A, Khanna A, Sathe VG, Gonzalez F, Ortiz B. Optical, thermal, and structural properties of Nb2O5–TeO2 and WO3–TeO2 glasses. Phase Transit. 2013;86(6):598–619.10.1080/01411594.2012.727998Suche in Google Scholar
[20] Tanaka K, Narazaki A, Hirao K. Large optical second-order nonlinearity of poled WO3–TeO2 glass. Opt Lett. 2000 Feb;25(4):251–3.10.1364/OL.25.000251Suche in Google Scholar PubMed
[21] Issa SA, Sayyed MI, Kurudirek M. Study of gamma radiation shielding properties of ZnO–TeO2 glasses. Bull Mater Sci. 2017;40(4):841–57.10.1007/s12034-017-1425-xSuche in Google Scholar
[22] Abouhaswa AS, Peris U, Tekin HO, Kavaz E, Henaish AMA. Nuclear shielding properties of B2O3–Pb3O4–ZnO glasses: multiple impacts of Er2O3 additive. Ceram Int. 2020;46(17):27849–59. 10.1016/j.ceramint.2020.07.283.Suche in Google Scholar
[23] Al-Hadeethi Y, Sayyed MI, Nune M. Radiation shielding study of WO3–ZnO–PbO–B2O3 glasses using Geant4 and Phys-X: a comparative study. Ceram Int. 2021;47(3):3988–93.10.1016/j.ceramint.2020.09.263Suche in Google Scholar
[24] Al-Hadeethi Y, Sayyed MI. A comprehensive study on the effect of TeO2 on the radiation shielding properties of TeO2–B2O3–Bi2O3–LiF–SrCl2 glass system using Phy-X/PSD software. Ceram Int. 2020;46(5):6136–40. 10.1016/j.ceramint.2019.11.078.Suche in Google Scholar
[25] Pullaiah G, Rao KV, Jamalaiah BC, Madhu N, Nutalapati V. Spectroscopic and luminescent properties of Ce3+-doped TeO2–WO3–GeO2 glasses. Mater Sci Eng B. 2022;284:115879. 10.1016/j.mseb.2022.115879.Suche in Google Scholar
[26] Alzuhair AZ, Alqahtani MS, Alkulib AJ, Hussein KI, Reben M, Yousef E. Structural and shielding properties of the tellurite-tungsten glass matrix with addition zinc fluoride. Chalcogenide Lett. 2022;19(3):187–95.10.15251/CL.2022.193.187Suche in Google Scholar
[27] Erdemir RU, Kilic G, Sen Baykal D, ALMisned G, Issa SAM, Zakaly HMH, et al. Diagnostic and therapeutic radioisotopes in nuclear medicine: determination of gamma-ray transmission factors and safety competencies of high-dense and transparent glassy shields. Open Chem. 2022;20(1):517–24.10.1515/chem-2022-0167Suche in Google Scholar
[28] Alzahrani JS, Sharma A, Nazrin SN, Alrowaili ZA, Al-Buriahi MS. Optical and radiation shielding effectiveness of a newly fabricated WO3 doped TeO2–B2O3 glass system. Radiat Phys Chem. 2022;193:109968. 10.1016/j.radphyschem.2022.109968. ISSN 0969-806X.Suche in Google Scholar
[29] Almateri M, Agar O, Altunsoy EE, Kilicoglu O, Sayyed MI, Tekin HO. Photon and neutron shielding characteristics of samarium doped lead alumino borate glasses containing barium, lithium and zinc oxides determined at medical diagnostic energies. Results Phys. 2019;12:2123–8.10.1016/j.rinp.2019.01.094Suche in Google Scholar
[30] Elshami W, Akudjedu TN, Abuzaid M, David LR, Tekin HO, Cavli B, et al. The radiology workforce’s response to the COVID-19 pandemic in the Middle East, North Africa and India. Radiography. 2021 May;27(2):360–8.10.1016/j.radi.2020.09.016Suche in Google Scholar PubMed PubMed Central
[31] Almatari M, Agar O, Altunsoy E, Kilicoglu O, Sayyed M, Tekin HO. Photon and neutron shielding characteristics of samarium doped lead alumino borate glasses containing barium, lithium and zinc oxides determined at medical diagnostic energies. Results Phys. 2019;12:2123–8.10.1016/j.rinp.2019.01.094Suche in Google Scholar
[32] Tekin HO, ALMisned G, Rammah YS, Susoy G, Ali FT, Sen Baykal D, et al. Mechanical properties, elastic moduli, transmission factors, and gamma-ray-shielding performances of Bi2O3–P2O5–B2O3–V2O5 quaternary glass system. Open Chem. 2022;20(1):314–29.10.1515/chem-2022-0145Suche in Google Scholar
[33] Computer Code Collection RS. MCNPX User’s Manual Version 2.4.0. Monte Carlo N-Particle Transport Code System for Multiple and High Energy Applications; 2002.Suche in Google Scholar
[34] Tekin HO, ALMisned G, Susoy G, Ali FT, Baykal DS, Ene A, et al. Transmission factor (TF) behavior of Bi2O3–TeO2–Na2O–TiO2–ZnO glass system: a Monte Carlo simulation study. Sustainability (Basel). 2022;14(5):2893.10.3390/su14052893Suche in Google Scholar
[35] Tekin HO, Issa SAM, Kavaz E, Guclu EEA. The direct effect of Er2O3 on bismuth barium telluro borate glasses for nuclear security applications. Mater Res Express. 2019;6(11):115212.10.1088/2053-1591/ab4cb5Suche in Google Scholar
[36] Mahmoud IS, Issa SAM, Saddek YB, Tekin HO, Kilicoglu O, Alharbi T, et al. Gamma, neutron shielding and mechanical parameters for vanadium lead vanadate glasses. Ceram Int. 2019;45:14058–72.10.1016/j.ceramint.2019.04.105Suche in Google Scholar
[37] Tekin HO, Kassab LR, Kilicoglu O, Magalhães ES, Issa SA, da Silva Mattos GR. Newly developed tellurium oxide glasses for nuclear shielding applications: an extended investigation. J Non-Cryst Solids. 2020;528:119763.10.1016/j.jnoncrysol.2019.119763Suche in Google Scholar
[38] Sayyed MI, Kumar A, Tekin HO, Kaur R, Singh M, Agar O, et al. Evaluation of gamma-ray and neutron shielding features of heavy metals doped Bi2O3–BaO–Na2O–MgO–B2O3 glass systems. Prog Nucl Energy. 2020;118:103118.10.1016/j.pnucene.2019.103118Suche in Google Scholar
[39] Rammah YS, Kumar A, Mahmoud KA, El-Mallawany R, El-Agawany FI, Susoy G, et al. SnO reinforced silicate glasses and utilization in gamma radiation shielding applications. Emerg Mater Res. 2020;9(3):1000–8. 10.1680/jemmr.20.00150.Suche in Google Scholar
[40] Agar O, Kavaz E, Altunsoy EE, Kilicoglu O, Tekin HO, Sayyed MI, et al. Er2O3 effects on photon and neutron shielding properties of TeO2–Li2O–ZnO–Nb2O5 glass system. Results Phys. 2019;13:102277.10.1016/j.rinp.2019.102277Suche in Google Scholar
[41] Rashad M, Tekin HO, Zakaly HMH, Pyshkina M, Issa SAM, Susoy G. Physical and nuclear shielding properties of newly synthesized magnesium oxide and zinc oxide nanoparticles. Nucl Eng Technol. 2020;52(9):2078–84.10.1016/j.net.2020.02.013Suche in Google Scholar
[42] Sharma A, Sayyed MI, Agar O, Tekin HO. Simulation of shielding parameters for TeO2–WO3–GeO2 glasses using FLUKA code. Results Phys. 2019;13:102199.10.1016/j.rinp.2019.102199Suche in Google Scholar
[43] Rammah Y, Issa SAM, Zakaly H, Tekin HO, Yousef E, Abouhaswa AS. B2O3–Bi2O3–Li2O3–Cr2O3 glasses: fabrication, structure, mechanical, and gamma radiation shielding qualities. J Aust Ceram Soc. 2021;57:1057–69. 10.1007/s41779-021-00599-w.Suche in Google Scholar
[44] Issa SAM, Tekin HO, Hessien MM, Rammah YS. Investigation of the elastic moduli, optical characteristics, and ionizing radiation attenuation capacity of specific strontium borosilicate glasses. J Aust Ceram Soc. 2022;58:495–510. 10.1007/s41779-022-00706-5.Suche in Google Scholar
[45] Tekin HO, Rammah YS, Hessien MM, Zakaly HMH, Issa SAM. Evaluating the optical and gamma-ray protection properties of bismo-tellurite sodium titanium zinc glasses. J Aust Ceram Soc. 2022 Mar;26(3):851–66.10.1007/s41779-022-00732-3Suche in Google Scholar
[46] ALMisned G, Akkurt I, Tekin HO, Erdamar IYD, Dogan SO. Gamma ray shielding properties of CeO2-added hydroxyapatite composite. J Aust Ceram Soc. 2022;58:1209–17. 10.1007/s41779-022-00763-w.Suche in Google Scholar
[47] Akkurt I. Effective atomic numbers for Fe–Mn alloy using transmission experiment. Chin Phys Lett. 2007;24(10):2812–4.10.1088/0256-307X/24/10/027Suche in Google Scholar
[48] Akkurt I. Effective atomic and electron numbers of some steels at different energies. Ann Nucl Energy. 2009;36-11(12):1702–5. 10.1016/j.anucene.2009.09.005.Suche in Google Scholar
© 2022 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Research Articles
- Modeling thixotropic break-down behavior of dense anaerobically digested sludge
- Structure of pumpkin pectin and its effect on its technological properties
- Free volumes in mixed-tacticity poly(3-hydroxybutyrate) determined by viscosimetry and their correlations with structural features and mechanical properties
- In-line measurement and modeling of temperature, pressure, and blowing agent dependent viscosity of polymer melts
- Determining the gas accumulation period using fluid inclusion observations: Xiang Zhong Basin, China
- Rheological thixotropy and pasting properties of food thickening gums orienting at improving food holding rate
- Evaluation of four different cogeneration cycles by using some criteria
- Effect of phosphogypsum and water-retaining in the stabilization and durability of stabilized mortars
- Determination of gamma-ray transmission factors of WO3–TeO2–B2O3 glasses using MCNPX Monte Carlo code for shielding and protection purposes
- Assessment of the usability conditions of Sb2O3–PbO–B2O3 glasses for shielding purposes in some medical radioisotope and a wide gamma-ray energy spectrum
- Exergy analyses of two and three stage cryogenic cycles
- Special Issue on Rheological Behavior and Engineering Stability of Rock Mass - Part I
- Mechanical properties of sandstone under hydro-mechanical coupling
- GIS-based landslide susceptibility mapping using frequency ratio and index of entropy models for She County of Anhui Province, China
- Reinforcement placement on mechanics and deformation of stepped reinforced retaining wall experimental study of characteristics
Artikel in diesem Heft
- Research Articles
- Modeling thixotropic break-down behavior of dense anaerobically digested sludge
- Structure of pumpkin pectin and its effect on its technological properties
- Free volumes in mixed-tacticity poly(3-hydroxybutyrate) determined by viscosimetry and their correlations with structural features and mechanical properties
- In-line measurement and modeling of temperature, pressure, and blowing agent dependent viscosity of polymer melts
- Determining the gas accumulation period using fluid inclusion observations: Xiang Zhong Basin, China
- Rheological thixotropy and pasting properties of food thickening gums orienting at improving food holding rate
- Evaluation of four different cogeneration cycles by using some criteria
- Effect of phosphogypsum and water-retaining in the stabilization and durability of stabilized mortars
- Determination of gamma-ray transmission factors of WO3–TeO2–B2O3 glasses using MCNPX Monte Carlo code for shielding and protection purposes
- Assessment of the usability conditions of Sb2O3–PbO–B2O3 glasses for shielding purposes in some medical radioisotope and a wide gamma-ray energy spectrum
- Exergy analyses of two and three stage cryogenic cycles
- Special Issue on Rheological Behavior and Engineering Stability of Rock Mass - Part I
- Mechanical properties of sandstone under hydro-mechanical coupling
- GIS-based landslide susceptibility mapping using frequency ratio and index of entropy models for She County of Anhui Province, China
- Reinforcement placement on mechanics and deformation of stepped reinforced retaining wall experimental study of characteristics

