Nearest Neighbour Particle-Particle Interaction in Fermionic Quasi One-Dimensional Flat Band Lattices

Simon Tilleke; Mirko Daumann; Thomas Dahm

doi:10.1515/zna-2019-0371

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Öffentlich zugänglich

Nearest Neighbour Particle-Particle Interaction in Fermionic Quasi One-Dimensional Flat Band Lattices

Simon Tilleke , Mirko Daumann und Thomas Dahm

Veröffentlicht/Copyright: 25. März 2020

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Zeitschrift für Naturforschung A Band 75 Heft 5

Abstract

In this paper, we have studied spinless fermions in four specific quasi one-dimensional systems that are known to host flat bands in the noninteracting limit: the triangle lattice, the stub lattice, the diamond lattice, and the diamond lattice with transverse hopping. The influence of the nearest neighbour interaction on the flat bands was investigated. We used exact diagonalization of finite size lattices employing the Lanczos technique and determine the single particle spectral functions of the interacting system. Our results are compared with mean field calculations. In the cases of the triangle lattice and the stub lattice we found that the flat bands become dispersive in the presence of a finite interaction. For the diamond lattice and the diamond lattice with transverse hopping, we demonstrated that the flat bands are robust under the influence of the interaction in certain parameter ranges. Such systems could be realised experimentally with cold atoms in optical lattices.

Keywords: Exact Diagonalization; Flat Band Systems; Many Particle Systems; Quasi One-Dimensional Systems; Spectral Functions

1 Introduction

Recently there has been an increased interest in flat band lattice systems. Such systems are characterised by the presence of completely dispersionless energy bands, which are accompanied by a macroscopic degeneracy, zero group velocity, and infinite effective mass. They also possess a macroscopic number of degenerate localised energy eigenstates. Flat bands appear in a variety of condensed matter systems [1], like the Landau levels of an electron gas, frustrated magnets [2], edge states of graphene [3], topological insulators [4], Weyl semimetals [5], unconventional superconductors [6], or optical lattices [7]. They can also emerge in strongly correlated electron systems [8]. Flat bands have been realised experimentally with photonic waveguide arrays [9], [10], exciton-polariton condensates [11], [12], cold atoms [13], [14], and on an appropriately doped Cu surface [15].

In a flat band system the influence of perturbations to the system like disorder or interactions can lead to interesting new phenomena. For example, interactions can lead to ferromagnetism [16], [17], topological magnons [18], [19], a fractional quantum Hall state [20], [21], [22], spin liquid states [23], or surface superconductivity with high critical temperature [24]. Disorder in flat band systems can give rise to an inverse Anderson transition (delocalization transition) [25], multifractal behaviour [26], or mobility edges with algebraic singularities [27]. However, most of these perturbations lift the degeneracy of the flat band.

In the present work we have studied several quasi one-dimensional flat band systems and ask whether the flat bands remain robust in the presence of an interaction between the particles. We show that in specific cases the flat band stays flat even in the presence of interaction. Such systems can be useful for information storage and also they might show many body localisation [28], [29], [30], because they possess stationary localised states in the presence of interaction. We restricted ourselves to spinless fermions on the quasi one-dimensional lattices shown in Figure 1. These lattices were shown to host flat bands previously [31]. We considered a nearest neighbour repulsive interaction between the particles. To determine the behaviour of these systems in the presence of interaction we performed numerical exact diagonalization of the many body Hamiltonian using the Lanczos technique. We compared these calculations with mean field calculations, which agree very well, when the interaction strength is weak.

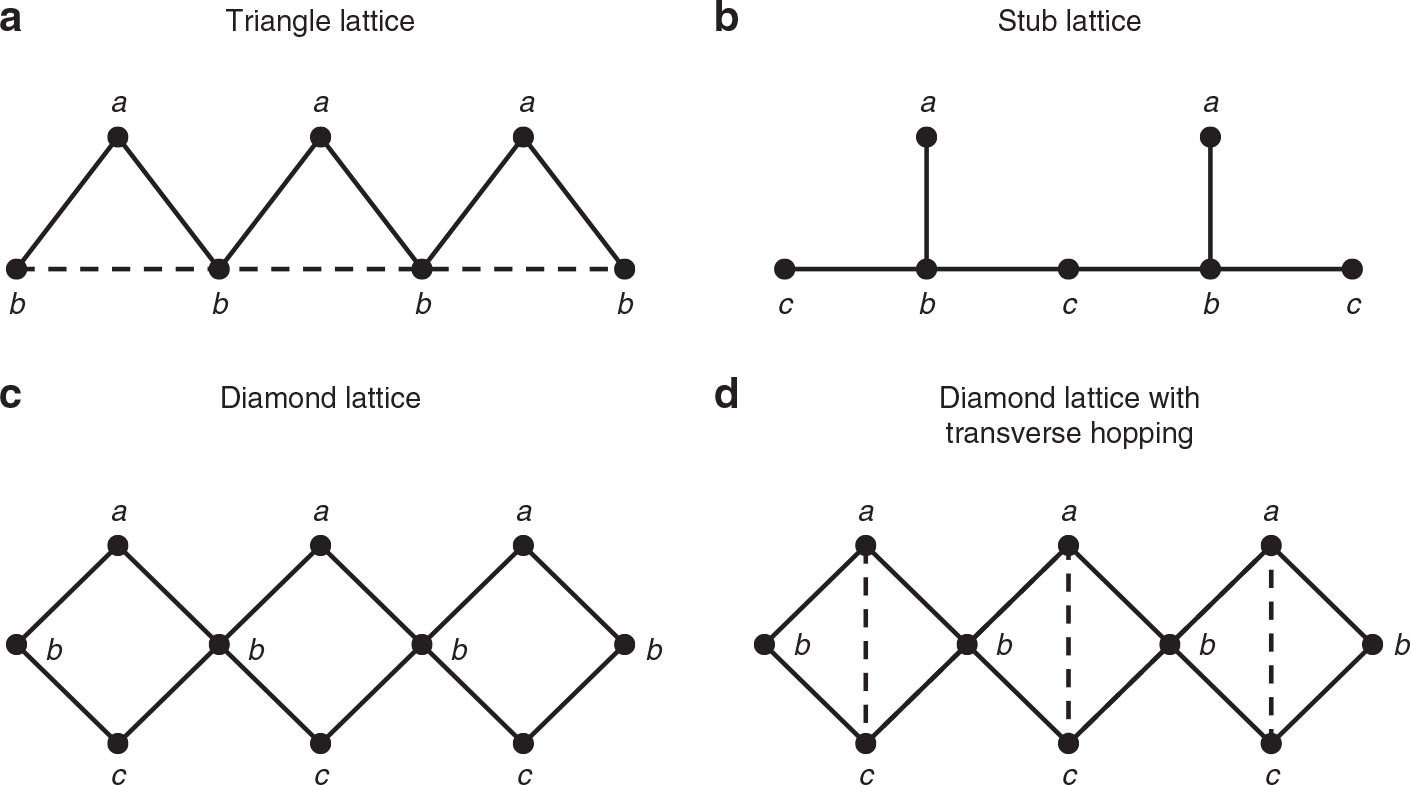
$Figure 1: Quasi one-dimensional lattices considered in this work: (a) triangle lattice, (b) stub lattice, (c) diamond lattice, and (d) diamond lattice with transverse hopping. The nearest neighbour hopping parameter t is denoted by solid lines in the lattices. The dashed lines correspond to a next nearest neighbour hopping parameter t′. The triangle lattice (a) possesses a flat band, when t′=t/2$t\prime=t/\sqrt{2}$. The diamond lattice in (d) possesses two dispersive and a flat band independent of the value of t′. The energy position of the flat band relative to the dispersive bands can be tuned by the parameter t′. A nearest neighbour repulsion of same strength V is considered on both solid and dashed bonds.$

Figure 1:

Quasi one-dimensional lattices considered in this work: (a) triangle lattice, (b) stub lattice, (c) diamond lattice, and (d) diamond lattice with transverse hopping. The nearest neighbour hopping parameter t is denoted by solid lines in the lattices. The dashed lines correspond to a next nearest neighbour hopping parameter t′. The triangle lattice (a) possesses a flat band, when t′=t/2. The diamond lattice in (d) possesses two dispersive and a flat band independent of the value of t′. The energy position of the flat band relative to the dispersive bands can be tuned by the parameter t′. A nearest neighbour repulsion of same strength V is considered on both solid and dashed bonds.

2 Models and Calculations

We investigated a tight-binding model having one fermionic state per lattice site. Hopping up to the next nearest neighbour is included, as shown in Figure 1. In addition, a nearest neighbour interaction acts between the particles. The Hamiltonian is given by

(1)H=−∑⟨iα,jβ⟩tiα,jβcjβ†ciα+V2∑⟨iα,jβ⟩n^jβn^iα,

where ciα† (ciα) creates (annihilates) a particle in unit cell i at lattice site α∈{a,b,c}. We consider lattices with N unit cells and periodic boundary conditions. V is the strength of the (next) nearest neighbour interaction and n^iα=ciα†ciα. Here, ⟨iα,jβ⟩ denotes a summation over all lattice sites (i,α) and (j,β) that are nearest or next nearest neighbours on the lattice, i.e. connected by solid and dashed bonds in Figure 1. tiα,jβ is the hopping parameter. For the lattices in Figure 1 it can only assume two values: tiα,jβ=t, if (i,α) and (j,β) are nearest neighbours, and tiα,jβ=t′, if (i,α) and (j,β) are next nearest neighbours. Note that due to the Pauli exclusion principle there is no on-site interaction between the particles.

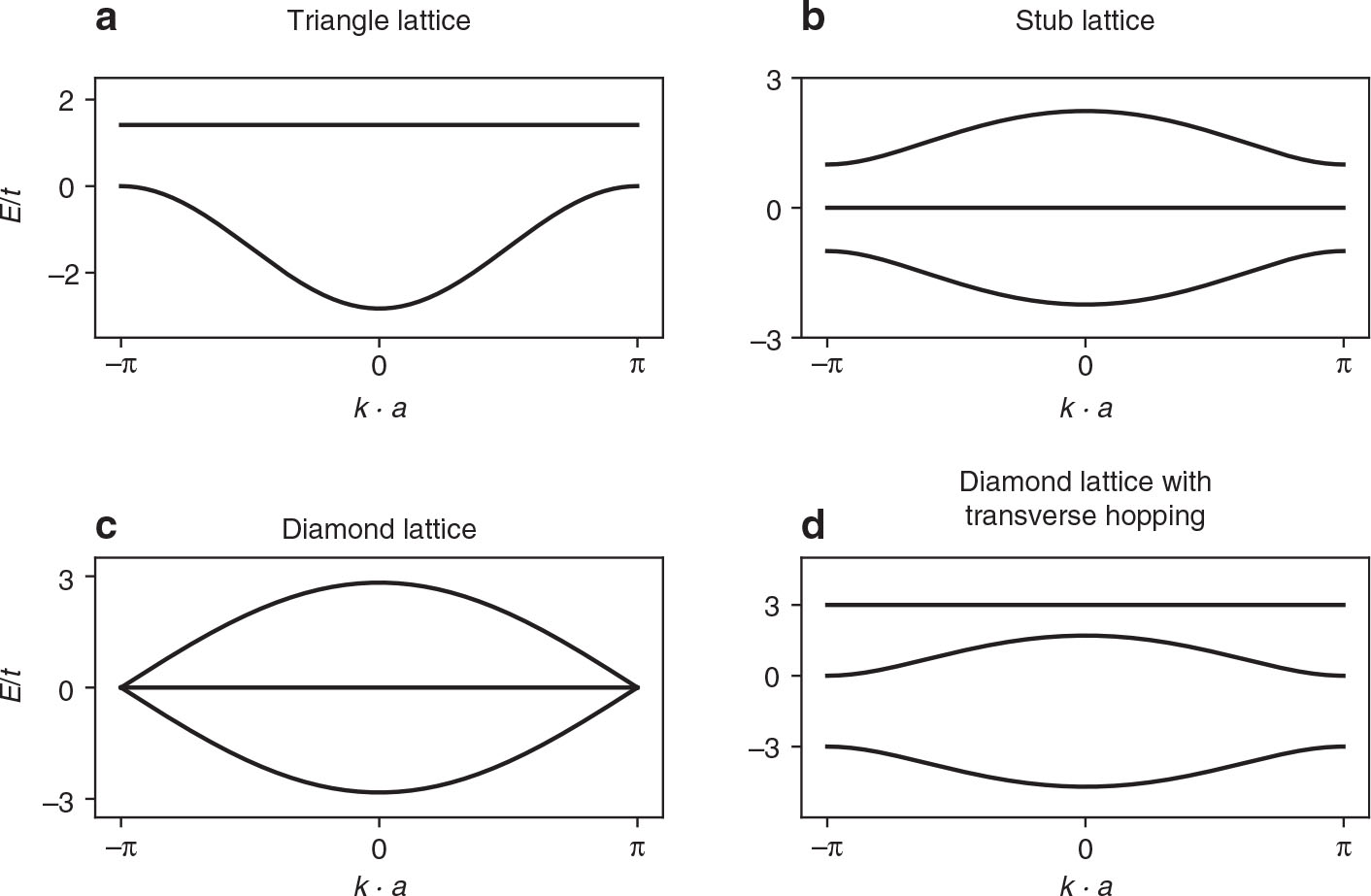
In Figure 2 we show the bare band structures corresponding to the lattices in Figure 1. All energies are given in units of the nearest neighbour hopping t. The triangle lattice in Figure 2a has two bands. The higher energy band becomes flat, when t′=t/2. This flat band is located at energy E=2t. Both bands are separated from each other by a gap. The stub lattice in Figure 2b has three bands, two dispersive ones and one flat band. The flat band is located at E = 0 in between the two dispersive bands and is separated from them by gaps. The diamond lattice in Figure 2c has two dispersive bands and one flat band at E = 0, too. However, in this case all bands merge at the Brillouin zone boundary. Both the noninteracting stub lattice and diamond lattice possess a particle-hole symmetry, which is broken by the interaction, however. In the diamond lattice with transverse hopping in Figure 2d the position of the flat band can be moved up or down relative to the two dispersive bands by variation of the next nearest neighbour hopping parameter t′. The flat band is located at E=t′. Also, a gap appears between the two dispersive bands, when t′ becomes nonzero.

$Figure 2: Bandstructures of the lattices in Figure 1, (a)–(d) corresponding to Figure 1. For the diamond lattice in (d) a transverse hopping t′=3t$t\prime=3t$ was chosen. For this value the flat band is the highest energy band.$

Figure 2:

Bandstructures of the lattices in Figure 1, (a)–(d) corresponding to Figure 1. For the diamond lattice in (d) a transverse hopping t′=3t was chosen. For this value the flat band is the highest energy band.

2.1 Mean Field Calculations

As a comparison with exact calculations a mean field approximation to the Hamiltonian (1) is useful. As we will see below, the mean-field approximation is a good approximation only for weak interaction strengths. However, it is simpler to calculate and serves as a reference. We look for homogeneous solutions, such that the ground state expectation value of the particle number operator nβ=⟨n^iβ⟩ becomes independent of unit cell index i and only depends on the orbital β. With this assumption the mean field Hamiltonian can be written

(2)HMF=E0−∑⟨iα,jβ⟩tiα,jβcjβ†ciα+∑iαVαMFn^iα,

where E₀ is a constant energy offset

(3)E0=−V2∑⟨iα,jβ⟩⟨n^jβ⟩⟨n^iα⟩=−V2∑⟨iα,jβ⟩nβnα.

Here, VαMF is an effective mean field potential that is seen by particles at α sites and given by

(4)VαMF=V∑βn.n.nβ,

where the sum runs over all neighbours of site α.

Within the mean field approximation the Hamiltonian H_MF describes a system of noninteracting fermions and can be diagonalised by transformation into momentum space. This way it can be brought into the form

(5)HMF=E0+∑kαεkαMFbkα†bkα.

where εkαMF are the energy eigenvalues and bkα† and bkα are the creation and annihilation operators of the corresponding eigenstates. The ground state of this system is given by

(6)|Φ⟩=(∏kαocc.bkα†)|0⟩,

where |0⟩ is the vacuum state and the product runs over the occupied lowest energy states. Both εkαMF and |Φ⟩ depend on the particle number expectation values n_β. Thus, a selfconsistent solution needs to be found, that fulfils

(7)nβ=⟨Φ|n^iβ|Φ⟩

These solutions are determined iteratively, i.e. one starts with a reasonable guess for n_β, calculates εkαMF and |Φ⟩ and obtains new values for n_β from (7). This procedure is repeated until a selfconsistent solution for n_β is found. With this solution the mean field bandstructure εkαMF can be analyzed for the existence of flat bands.

2.2 Exact Calculations Using the Lanczos Procedure

In an interacting many particle system, a band structure in the strict sense does not exist anymore. However, we can still examine the single particle excitations above the ground state of an interacting many particle system and ask whether they possess flat bands in the sense that the excitation energy is independent of momentum. For this purpose we calculated the single particle spectral function and looked for flat band structures.

To find the ground state of the system we used the Lanczos procedure [32]. In the Lanczos procedure one starts with a normalised random state vector and constructs an orthonormal basis by repeatedly applying the Hamiltonian. Within this basis the Hamiltonian is of tridiagonal form. After N_L steps one obtains an NL×NL tridiagonal matrix, whose eigenvalues and eigenvectors give an approximation for the full spectrum of the Hamiltonian. In particular, the extreme eigenstates of the Hamiltonian converge very quickly. The method is particulary efficient when the Hamiltonian is a sparse matrix as in the present tight-binding case. The Lanczos procedure is stopped, when the relative change of the ground state energy becomes less than ε=10−15.

In the presence of a flat band, the ground state of the Hamiltonian can be highly degenerate. For a noninteracting system this becomes clear from the bandstructures in Figure 2: if the band filling is chosen such that the flat band is only partially occupied, the particles in the flat band can be rearranged without changing the energy of the system. For this reason it is of interest here to also determine the degeneracy of the ground state. This can be done with the Lanczos procedure in the following way: after a ground state has been determined from a random start vector, the Lanczos procedure is repeated with a different random start vector. If the new ground state is linearly independent from the first ground state, the Lanczos procedure is repeated again until no new linearly independent ground state is found anymore. Technically, after each Lanczos run, one determines the rank of the matrix of all ground states found so far. If the rank does not change anymore, the procedure can be stopped.

2.3 Spectral Functions

The single particle spectral function Aα(k,E) gives the energy distribution of the system after a particle with momentum k and orbital α has been added to the system or, respectively, the energy spectrum after a particle with momentum k and orbital α has been removed from the system [33]. It can be calculated using the Lanczos procedure in the following way: let us define the Fourier transform of the annihilation operator

(8)dkα=1N∑j=0N−1e−ikjcjα.

We first determine the ground state |Φ⟩ of the system with M fermions numerically using the Lanczos procedure. We can then add or remove a particle with momentum k creating the states

(9)|Φkα+⟩=dkα†|Φ⟩ and |Φkα−⟩=dkα|Φ⟩.

Note, that the state |Φkα+⟩ is an M + 1 particle state and |Φkα−⟩ an M − 1 particle state, i.e. they belong to different subspaces of the full 2^N dimensional Hilbert space. We are now interested in determining the energy spectrum of the states |Φkα±⟩. To do so, we can again use the Lanczos procedure in the M + 1 particle subspace or the M − 1 particle subspace, respectively. In this case, the states |Φkα±⟩ are normalised and taken as start vectors for further Lanczos runs. The Lanczos procedure will then generate an orthonormal basis that is particularly well suited to expand the start vectors into the eigenstates of the Hamiltonian. After N_L Lanczos steps let |Ψj±⟩ with 1≤j≤NL be the eigenstates of the tridiagonal matrix and Ej± their corresponding eigenvalues. Then we can obtain an approximation for the spectral function using

(10)Aα±(k,E)=∑j=1NL|⟨Φkα±|Ψj±⟩|2πΓ[E±(EG−Ej±)]2+Γ2.

Here, E_G is the ground state energy of the M particle system (before the particle was removed or added) and Γ is a broadening parameter which helps to visualise the spectral function and is taken to be Γ = 0.05 here. The function Aα+(k,E) describes the particle excitations of the fermionic system at energies above the Fermi level, while Aα−(k,E) describes the hole excitations at energies below the Fermi level. To get a complete picture of both particle and hole excitations it is useful to calculate the sum

(11)Aα(k,E)=Aα+(k,E)+Aα−(k,E).

3 Results

In this section our results for the mean field bandstructure and the spectral function (11) are presented for the triangle lattice, stub lattice, and diamond lattices shown in Figure 1. In all cases the bandfilling was chosen in such a way that the flat band is half filled in the noninteracting case V = 0. In most cases a few hundred Lanczos iterations were sufficient to obtain accurate ground states and spectral functions.

3.1 Triangle Lattice

In this section the triangle lattice from Figure 1a with t′=t/2 is investigated. We considered 10 unit cells filled with 15 particles, such that in the noninteracting case the lower dispersive band is fully filled and the upper flat band is half filled.

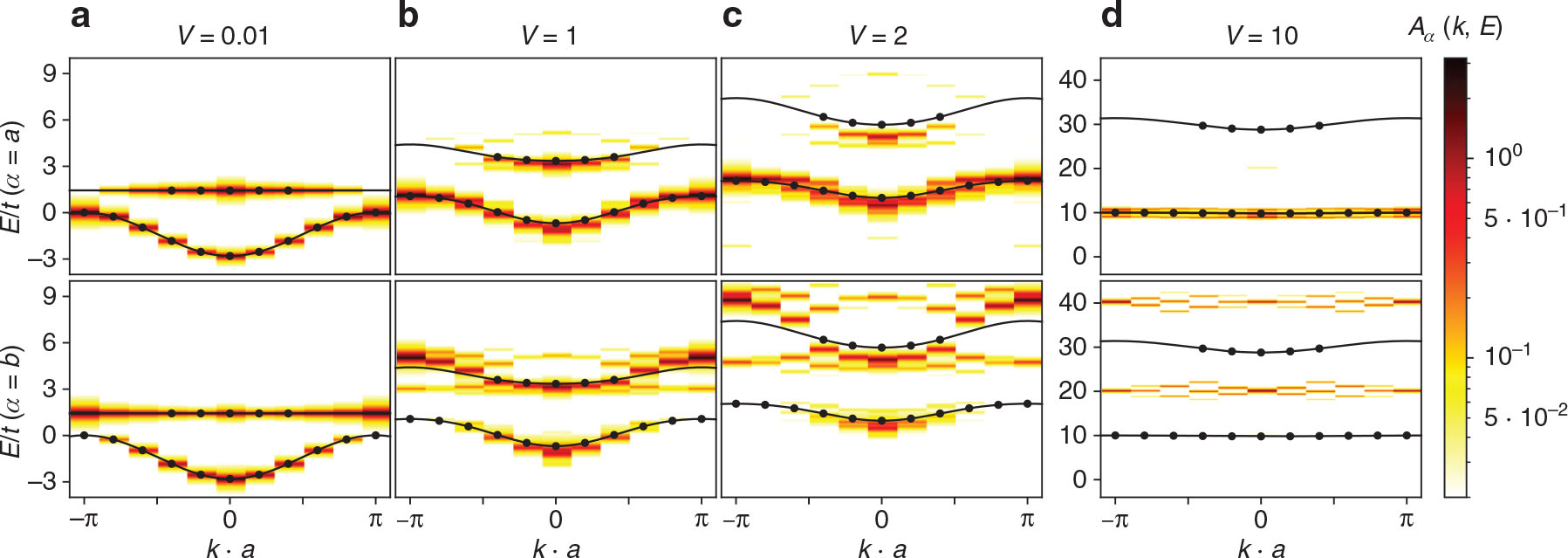
$Figure 3: Spectral functions Aα(k,E)${A_{\alpha}}(k,E)$ and mean field bandstructures for the triangle lattice with next nearest neighbour hopping t′=t/2$t\prime=t/\sqrt{2}$, 10 unit cells and 15 particles. Black solid lines show the mean field bandstructure and the black dots indicate the occupied states. The spectral function Aα(k,E)${A_{\alpha}}(k,E)$ is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=a$\alpha=a$ and the lower panel for α=b$\alpha=b$. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.$

Figure 3:

Spectral functions Aα(k,E) and mean field bandstructures for the triangle lattice with next nearest neighbour hopping t′=t/2, 10 unit cells and 15 particles. Black solid lines show the mean field bandstructure and the black dots indicate the occupied states. The spectral function Aα(k,E) is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=a and the lower panel for α=b. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.

The mean field band structures and spectral functions Aα(k,E) are shown in Figure 2. For V = 0 the ground state has a degeneracy of (105)=252, because five particles can be distributed over 10 available states in the flat band. For V = 0.01 this degeneracy is already lifted and the ground state becomes nondegenerate. In Figure 3a the mean field bandstructure appears flat, however a closer look at the numerical results shows that the flat band gained a tiny dispersion, which is responsible for the lifting of the degeneracy. The spectral function is seen to closely follow the mean field bandstructure. In Figure 3b for V = 1 the dispersion of the upper band becomes apparent in both mean field bandstructure and spectral function. There is similar intensity of the spectral function in both bands. This is due to the fact that the bands are linear combinations of both a and b lattice sites. In Figure 3c for V = 2 one can see that the exact spectral function starts to deviate from the mean field bandstructure. For the a sites, the spectral function gets stronger weight in the lower energy band. This can be understood from Figure 1a in the following way: each a site is connected to two b sites, while each b site is connected to two a and two b sites. Thus, at higher interaction strength the a sites become energetically more favorable. As a result, the lower energy band gains more weight on the a sites, while the higher energy band becomes more located at the b sites. This can be seen more clearly for V = 10 in Figure 3d. Here it is apparent that the band on the a sites becomes almost flat. The band on the b sites splits into two almost flat subbands. In this strong interaction limit, the a sites become fully occupied and the b sites are occupied half. The energy of an electron on an a site approaches 2V2=V. The splitting of the b band into two subbands can be understood qualitatively, if one considers a spontaneous breaking of translational invariance such that every other b site is fully occupied, while the sites in between are empty. Then, the energy of an occupied b site becomes 2V, while adding a particle to an empty b site costs an energy of 4V. This explains the splitting of the b band into two subbands at energies 2V and 4V.

Figure 4:

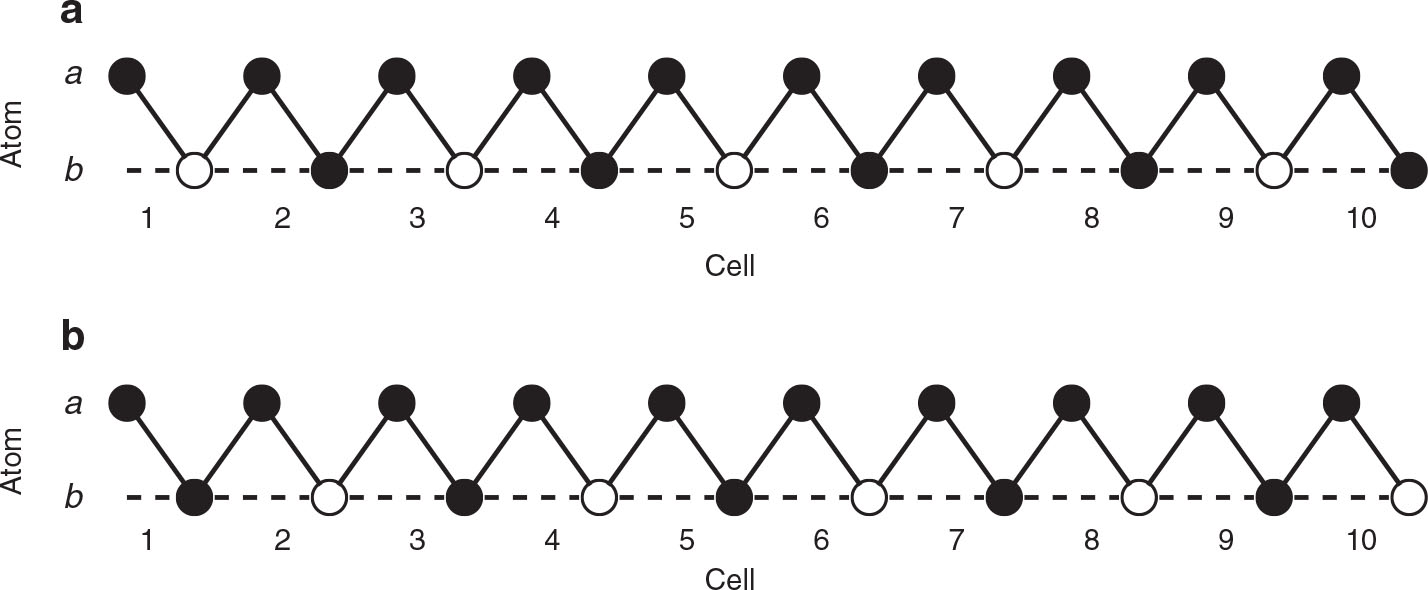
The two leading real space basis states that contribute most to the ground state wave function of the triangular lattice for V ≳ 10. In both states the a sites are fully occupied. In (a) the even numbered b sites are occupied, while in (b) the even numbered b sites are empty.

$Figure 5: Spectral functions Aα(k,E)${A_{\alpha}}(k,E)$ and mean field bandstructures for the stub lattice with 6 unit cells and 9 particles. Black solid lines show the mean field bandstructure and the black dots indicate the occupied states. The spectral function Aα(k,E)${A_{\alpha}}(k,E)$ is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=a$\alpha=a$, the center panel for α=b$\alpha=b$, and the lower panel for α=c$\alpha=c$. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.$

Figure 5:

Spectral functions Aα(k,E) and mean field bandstructures for the stub lattice with 6 unit cells and 9 particles. Black solid lines show the mean field bandstructure and the black dots indicate the occupied states. The spectral function Aα(k,E) is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=a, the center panel for α=b, and the lower panel for α=c. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.

To verify this qualitative picture we expanded the ground state wave function into the real space basis states. For large positive interaction strength V ≳ 10 it turns out that the ground state is essentially just a linear superposition of the two real space eigenstates shown in Figure 4. For V = 10 we found that both states contributed 46.9 % each to the ground state wave function. For V = 100 they even contributed 49.96 % each.

To summarise, for the triangular lattice the flat band becomes dispersive as soon as a repulsive nearest neighbour interaction is turned on. In the limit of strong interaction at three quarter filling, however, the interaction can block the motion of the particles and all bands become flat again.

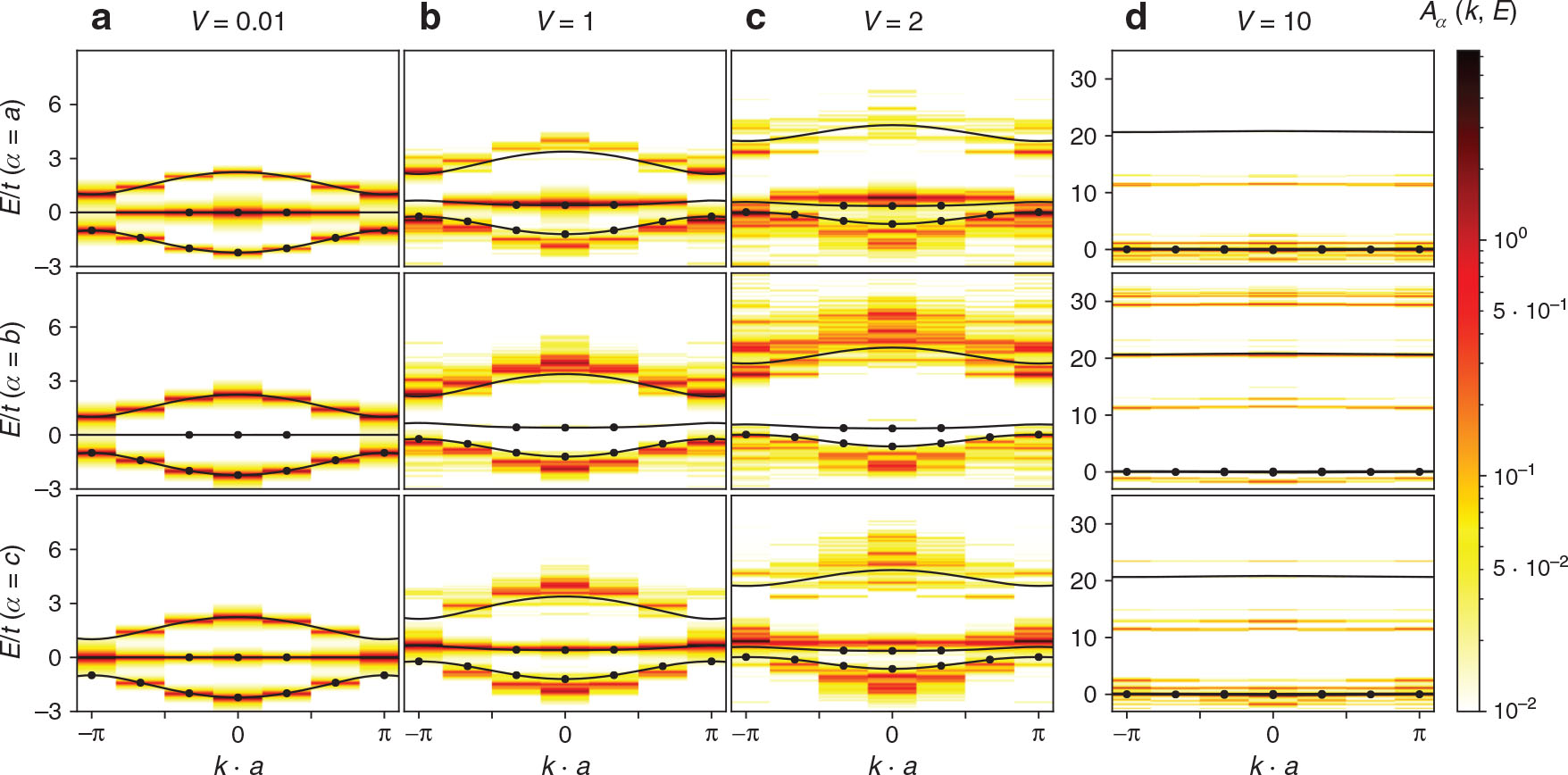
3.2 Stub Lattice

In this section the stub lattice from Figure 1b is studied. We considered six unit cells filled with nine particles, such that in the noninteracting case the lower dispersive band is fully filled, the flat band is half filled, and the upper dispersive band is empty.

The mean field band structures and spectral functions Aα(k,E) are shown in Figure 5. For V = 0 the ground state has a degeneracy of (63)=20, because three particles can be distributed over six available states in the flat band. For V = 0.01 this degeneracy is already lifted and the ground state becomes nondegenerate. Similarly as for the triangle lattice, in Figure 5a the mean field bandstructure appears flat, however the numerical results show that the flat band gained a tiny dispersion, which is responsible for the lifting of the degeneracy. The spectral functions have weight in the flat band in the α=a and α=c channels, but not in the α=b channel. This is due to the fact that the flat band is a superposition of states on the a and c sites. In Figure 5b for V = 1 the dispersion of the center band becomes apparent in both mean field bandstructure and spectral function. When the interaction strength is further increased, the spectral functions deviate from the mean field dispersions. In Figure 5c for V = 2 the energy distribution is very much blurred over a large range of energies. Well defined bands can hardly be seen in this case. In the strongly interacting limit V ≫ 1 the b sites become unfavourable, because they are connected to three sites each. Thus, the particles predominantly occupy the a and c sites to avoid the repulsion. For this reason excitations in the b channel appear at much higher energy than in the a and c channels.

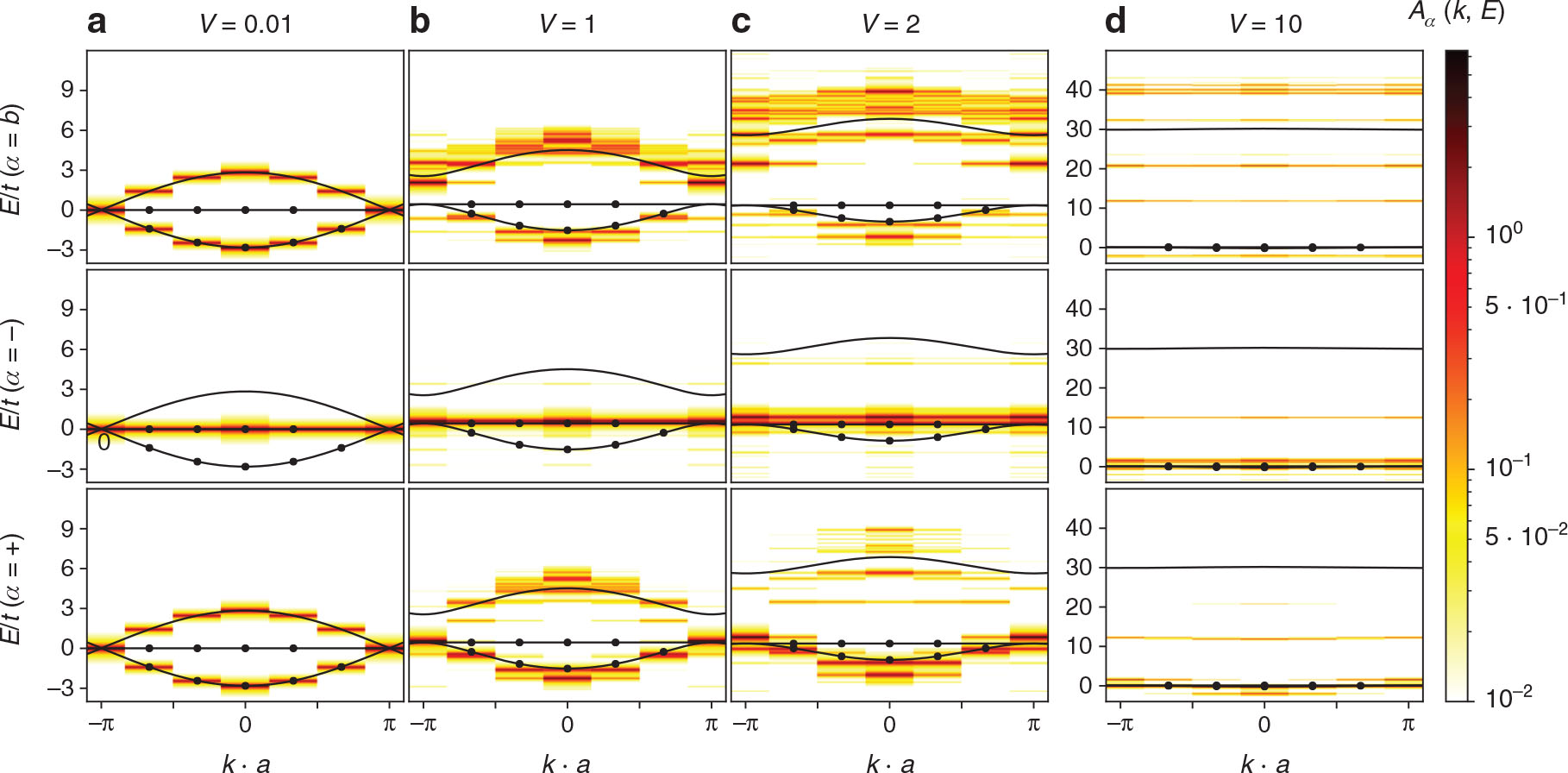
$Figure 6: Spectral functions Aα(k,E)${A_{\alpha}}(k,E)$ for α∈{b,−,+}$\alpha\in\left\{{b,-,+}\right\}$ and mean field bandstructures for the diamond lattice with six unit cells and nine particles. Black solid lines show the mean field bandstructure. The black dots indicate the occupied states. The spectral function Aα(k,E)${A_{\alpha}}(k,E)$ is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=b$\alpha=b$, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.$

Figure 6:

Spectral functions Aα(k,E) for α∈{b,−,+} and mean field bandstructures for the diamond lattice with six unit cells and nine particles. Black solid lines show the mean field bandstructure. The black dots indicate the occupied states. The spectral function Aα(k,E) is shown color coded on a logarithmic color scale. The upper panel shows the spectral function for lattice sites α=b, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 0.01, (b) V = 1, (c) V = 2, and (d) V = 10.

3.3 Diamond Lattice

In contrast to the triangle lattice and stub lattice, the diamond lattice possesses an additional mirror symmetry with respect to the main axis of the lattice. Thus, all energy eigenstates can be chosen as symmetric or antisymmetric states with respect to this axis. For this reason it is useful to define the following annihilation operators:

(12)dk+=12(dka+dkc)

and

(13)dk−=12(dka−dkc)

and calculate the corresponding spectral functions A±(k,E) instead of Aa(k,E) and Ac(k,E). As for the stub lattice, we considered six unit cells filled with nine particles, such that in the noninteracting case the lower dispersive band is fully filled, the flat band is half filled, and the upper dispersive band is empty.

The mean field band structures and spectral functions Aα(k,E) for α∈{b,−,+} are shown in Figure 6. For V = 0 the ground state has a degeneracy of (84)=70. This is because the six states of the flat band are degenerate with one state of the upper and lower band each at k = π. So five particles occupy the lowest five states in the lower dispersive band. The remaining four particles can then be distributed over the eight available degenerate states. In contrast to the triangle lattice and stub lattice, for V > 0 this degeneracy is only partially lifted and the ground state degeneracy becomes six, which is equal to the number of unit cells. This indicates that the system has a tendency to develop an inhomogeneous charge distribution in the ground state or in other words that the ground state is a superposition of 6 degenerate inhomogeneous states that are shifted with respect to each other.

$Figure 7: Spectral functions and mean field bandstructures for the diamond lattice with next nearest neighbour hopping t′=3t$t\prime=3t$, 10 unit cells, and 25 particles. The upper panel shows the spectral function for lattice sites α=b$\alpha=b$, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 1, (b) V = 1.7, (c) V = 1.9, and (d) V = 2.3.$

Figure 7:

Spectral functions and mean field bandstructures for the diamond lattice with next nearest neighbour hopping t′=3t, 10 unit cells, and 25 particles. The upper panel shows the spectral function for lattice sites α=b, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 1, (b) V = 1.7, (c) V = 1.9, and (d) V = 2.3.

As is seen in Figure 6 the flat band appears in the α = − channel and thus corresponds to those states that possess antisymmetric wave functions with respect to the mirror axis. The two dispersive bands appear to be linear combinations of the b and + channels. For V ≲ 1 the flat band remains flat in both mean field solution and spectral function. For V ≳ 2 in the exact calculation the flat band starts to split into two flat bands, seen in Figure 6c and d. In the strongly interacting limit V ≫ 1 the b sites become unfavourable, because they are connected to four sites each. Thus, the particles predominantly occupy the a and c sites to avoid the repulsion. For this reason the excitations in the b channel appear at much higher energy than in the a and c channels when V becomes large. In this limit all three bands become flat. The b band appears to split into 5 sub-bands at energies E≈nV with n∈{0,1,2,3,4}. These energies can be interpreted as coming from states at which a b site has 0, 1, 2, 3, or 4 occupied neighbouring a and c sites. The + and − bands become degenerate and split into two flat bands at energies E ≈ 0 and E≈V. The band at E ≈ 0 is coming from states in which the b sites are unoccupied. The band at E≈V, which has less intensity, can be interpreted as coming from states in which a single b site is occupied. For V = 10 we calculated the expectation value of the particle number on the b sites in the exact ground state and found it to be nb=0.09, i.e. there is still some occupation of b sites, which accounts for the band visible at E≈V in the + and − channels.

$Figure 8: Spectral functions and mean field bandstructures for the diamond lattice with next nearest neighbour hopping t′=−3t$t\prime=-3t$, 10 unit cells, and 5 particles. The upper panel shows the spectral function for lattice sites α=b$\alpha=b$, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 1, (b) V = 2, (c) V = 4, and (d) V = 10.$

Figure 8:

Spectral functions and mean field bandstructures for the diamond lattice with next nearest neighbour hopping t′=−3t, 10 unit cells, and 5 particles. The upper panel shows the spectral function for lattice sites α=b, the center panel for α = −, and the lower panel for α = +. The four columns show the results for interaction strengths (a) V = 1, (b) V = 2, (c) V = 4, and (d) V = 10.

To summarise, for the diamond lattice we found a flat band in the α = − channel that persists throughout the whole range of interaction strengths V. For V ≳ 2 this band starts to split into two separate flat sub-bands. The higher energy sub-band can be interpreted as coming from states with occupied b sites.

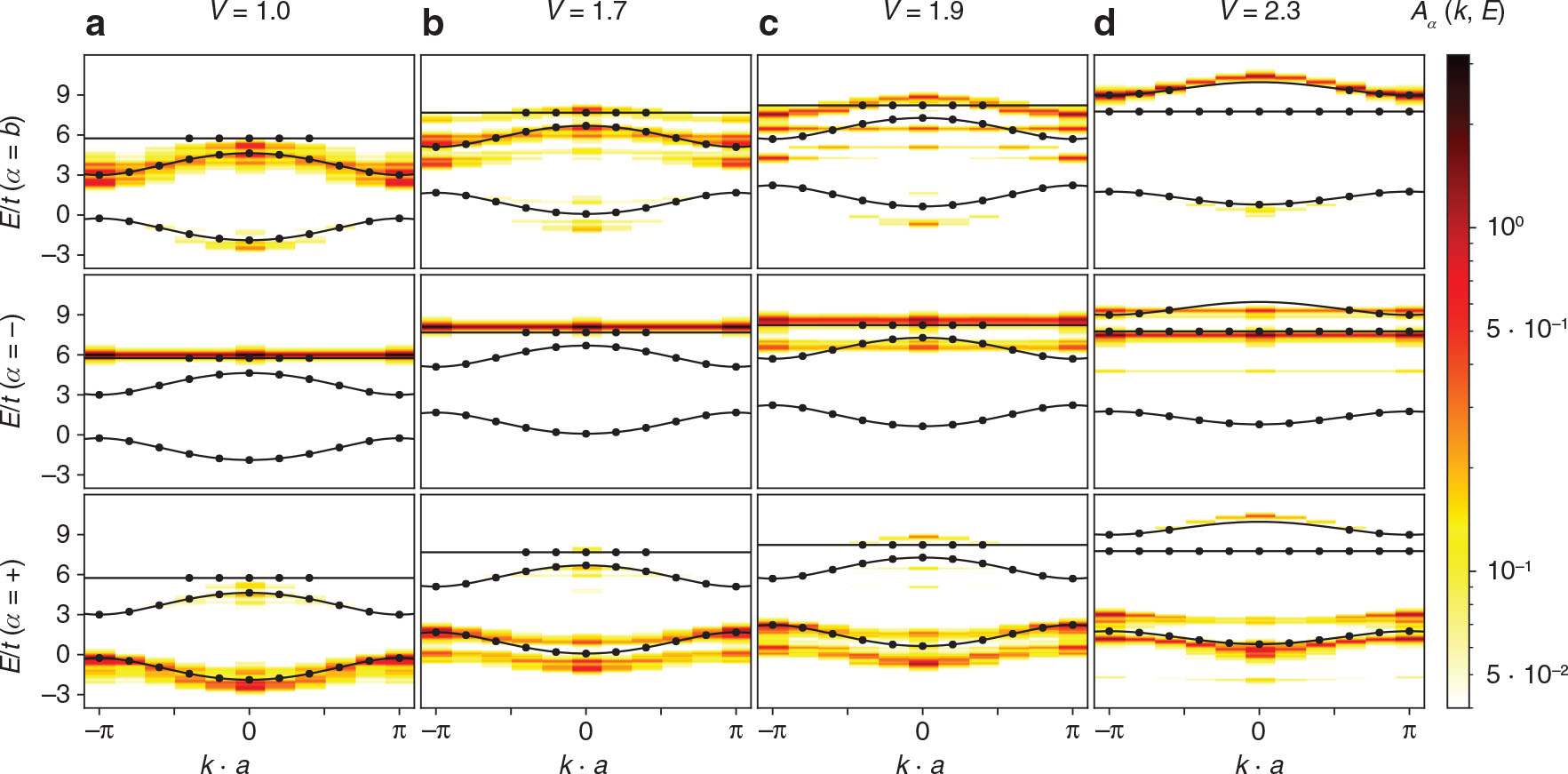
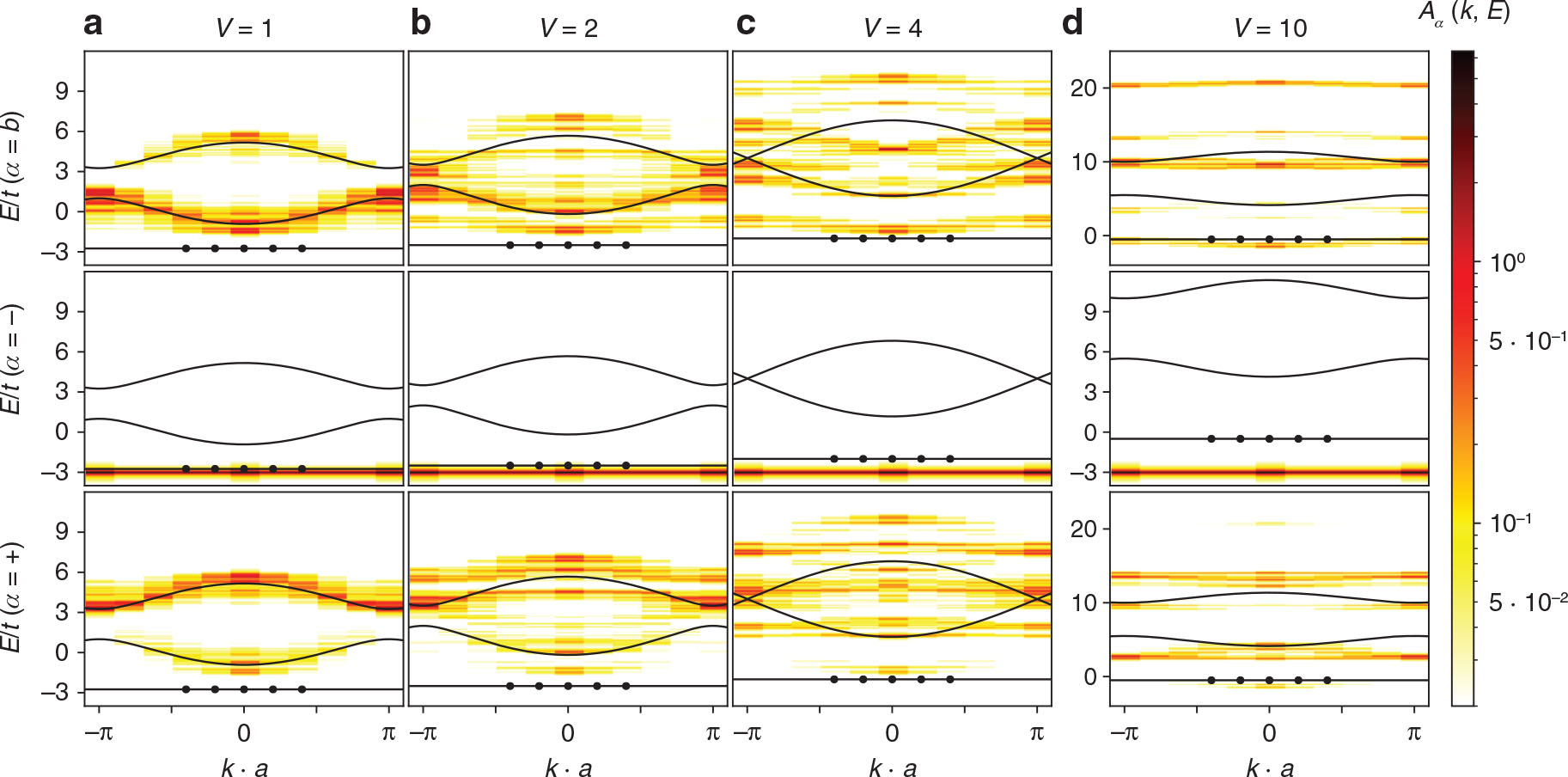
3.4 Diamond Lattice with Transverse Hopping

The diamond lattice with transverse hopping and an interaction between the a and c sites possesses the same mirror symmetry as the bare diamond lattice. Therefore the spectral functions for the +, −, and b channels are discussed also in this section.

In Figure 7 the spectral functions Aα(k,E) for t′=3t are shown. We considered 10 unit cells filled with 25 particles, such that in the noninteracting case the two dispersive bands are fully filled and the flat band is half filled. For V = 0 the ground state has a degeneracy of (105)=252, because five particles can be distributed over 10 available states in the flat band. In contrast to the triangle lattice and stub lattice, for V = 0.01 this degeneracy is not lifted, but remains unchanged up to a value of V ≈ 1.8. As for the bare diamond lattice, the flat band appears in the α = − channel. The lowest dispersive band mostly corresponds to the + channel, while the higher dispersive band mostly corresponds to the b channel. In the limit of large interaction strength V ≫ 1 the b sites become unfavourable, because they are connected to four sites each, while the a and c sites now possess three neighbours each. In this limit the a and c sites approach 100 % occupation, while the b sites approach 50 % occupation. For this reason the energy of the upper dispersive band increases more strongly with V than the energy of the flat band. Starting from V = 0 with increasing interaction strength the upper dispersive band thus moves toward the flat band. At a specific interaction strength (here around V = 1.8) the upper dispersive band starts to overlap with the flat band. For V = 1.8 we also found that the degeneracy of the ground state drops from 252 to 10, which is equal to the number of unit cells. When V is further increased above 2.1 the dispersive band becomes the highest energy band and the flat band is located between the two dispersive bands. For V > 2.1 the ground state becomes nondegenerate, then. In Figure 7b–d the spectral functions in the transition region are shown, where the two bands cross each other. While for V = 1.7 (Fig. 7b) the flat band is still flat, for V = 1.9 (Fig. 7c) the flat band splits into two sub-bands. For V = 1.9 the upper of these two sub-bands has stronger spectral weight. When V is further increased, the spectral weight is gradually transferred to the lower subband, as can be seen in Figure 7d.

In Figure 8 the spectral functions Aα(k,E) for t′=−3t are shown. In this case the flat band is the lowest energy band. We considered 10 unit cells filled with 5 particles, such that in the noninteracting case the two dispersive bands are empty and the flat band is half filled. For V = 0 the ground state has a degeneracy of (105)=252, because 5 particles can be distributed over 10 available states in the flat band. For V > 0 this degeneracy is not lifted, but remains unchanged for all values of V. In contrast to the case with t′=3t the dispersive bands do not cross the flat band. The flat band remains the lowest energy band for all interaction strengths V > 0. As can be seen in Figure 8 for the α = − channel the flat band remains flat and does not split.

To summarise, for the diamond lattice with t′=3t the flat band remains intact for V ≲ 1.8. For V ≳ 1.8 the flat band overlaps with one of the dispersive bands and splits into two sub-bands. For V ≳ 2.1 a dispersive band becomes the highest energy band. While the flat band is still flat, it becomes fully occupied and the highest dispersive band becomes half filled. As a result, the ground state of the system becomes nondegenerate then. In contrast, for t′=−3t the flat band remains intact over the full range of interaction strengths V > 0.

We have seen that under a finite interaction the flat band does not stay flat for the triangle lattice and stub lattice, while it has a robustness for the two diamond lattices. We suggest that the mirror symmetry of the diamond lattice plays an important role here to stabilise the flat band. The mirror symmetry guarantees the existence of energy eigenstates that are antisymmetric, i.e. have zeroes on the b sites. In such states the particles in different unit cells are effectively decoupled. Then, Wannier states localised in a single unit cell become eigenstates of the Hamiltonian. As a result, the flat band remains flat, even in the presence of interaction.

4 Summary and Conclusions

We have investigated spinless fermions in several quasi one-dimensional lattices that are known to host flat bands in the noninteracting limit. We studied the influence of a repulsive nearest neighbour interaction on the flat bands using both mean field approximation and exact diagonalisation by Lanczos technique.

For the triangle lattice and stub lattice we found that the flat band becomes dispersive, as soon as a finite interaction is turned on. For the three quarter filled triangle lattice the bands become flat again in the strongly interacting limit V → ∞.

For the bare diamond lattice we found that the flat band remains flat for all interaction strengths. For V ≳ 2 the flat band splits into two flat sub-bands. The ground state degeneracy becomes equal to the number of lattice sites as soon as a finite interaction strength is turned on.

For the diamond lattice with transverse hopping t′=3t we could identify three different regimes for the interaction strength with three qualitatively different ground states. With increasing interaction strength the upper dispersive band moves upward in energy relative to the other bands. In the first regime, the flat band is located above the upper dispersive band and remains intact as does the ground state degeneracy. In the second regime the flat band overlaps with the upper dispersive band and splits into two flat subbands. The ground state degeneracy drops and becomes equal to the number of lattice sites. In the third regime the upper dispersive band has moved up in energy so much that the flat band is no longer relevant at the Fermi level. As a result, the ground state is no longer degenerate.

For the diamond lattice with transverse hopping t′=−3t both the flat band and the ground state degeneracy remain intact for all interaction strengths and the flat band does not split.

Generally, for small interaction strengths V ≲ 1 the results from mean field approximation agree well with exact results from the Lanczos technique. For larger interaction strengths the spectral functions appear to be smeared out in energy or show splittings that are not reproduced by mean field approximation.

Acknowledgement

Financial support from the DFG via the research group FOR2692, Funder Id: http://dx.doi.org/10.13039/501100001659, grant number 397171440 is gratefully acknowledged. We would like to thank S. kleine Brüning and S. Kehrein for valuable discussions.

References

[1] D. Leykam, A. Andreanov, and S. Flach, Adv. Phys. X 3, 1473052 (2018).10.1080/23746149.2018.1473052Suche in Google Scholar

[2] O. Derzhko, J. Richter, and M. Maksymenko, Int. J. Mod. Phys. B 29, 1530007 (2015).10.1142/S0217979215300078Suche in Google Scholar

[3] K. Nakada, M. Fujita, G. Dresselhaus, and M. S. Dresselhaus, Phys. Rev. B 54, 17954 (1996).10.1103/PhysRevB.54.17954Suche in Google Scholar PubMed

[4] T. Paananen and T. Dahm, Phys. Rev. B 87, 195447 (2013).10.1103/PhysRevB.87.195447Suche in Google Scholar

[5] T. Paananen, H. Gerber, M. Götte, and T. Dahm, New J. Phys. 16, 033019 (2014).10.1088/1367-2630/16/3/033019Suche in Google Scholar

[6] S. Matsuura, P.-Y. Chang, A. P. Schnyder, and S. Ryu, New J. Phys. 15, 065001 (2013).10.1088/1367-2630/15/6/065001Suche in Google Scholar

[7] T. Paananen and T. Dahm, Phys. Rev. A 91, 033604 (2015).10.1103/PhysRevA.91.033604Suche in Google Scholar

[8] R.-Q. He and Z.-Y. Weng, Sci. Rep. 6, 35208 (2016).10.1038/srep35208Suche in Google Scholar PubMed PubMed Central

[9] R. A. Vicencio, C. Cantillano, L. Morales-Inostroza, B. Real, C. Meja-Cortés, et al., Phys. Rev. Lett. 114, 245503 (2015).10.1103/PhysRevLett.114.245503Suche in Google Scholar PubMed

[10] S. Mukherjee, A. Spracklen, D. Choudhury, N. Goldman, P. Öhberg, et al., Phys. Rev. Lett. 114, 245504 (2015).10.1103/PhysRevLett.114.245504Suche in Google Scholar PubMed

[11] N. Masumoto, N. Y. Kim, T. Byrnes, K. Kusudo, A. Löffler, et al., New J. Phys. 14, 065002 (2012).10.1088/1367-2630/14/6/065002Suche in Google Scholar

[12] F. Baboux, L. Ge, T. Jacqmin, M. Biondi, E. Galopin, et al., Phys. Rev. Lett. 116, 066402 (2016).10.1103/PhysRevLett.116.066402Suche in Google Scholar PubMed

[13] M. Aidelsburger, M. Lohse, C. Schweizer, M. Atala, J. T. Barreiro, et al., Nat. Phys. 11, 162 (2015).10.1038/nphys3171Suche in Google Scholar

[14] S. Taie, H. Ozawa, T. Ichinose, T. Nishio, S. Nakajima, et al., Sci. Adv. 1, e1500854 (2015).10.1126/sciadv.1500854Suche in Google Scholar PubMed PubMed Central

[15] M. R. Slot, T. S. Gardenier, P. H. Jacobse, G. C. P. van Miert, S. N. Kempkes, et al., Nat. Phys. 13, 672 (2017).10.1038/nphys4105Suche in Google Scholar PubMed PubMed Central

[16] H. Tasaki, Phys. Rev. Lett. 69, 1608 (1992).10.1103/PhysRevLett.69.1608Suche in Google Scholar PubMed

[17] J. S. Hofmann, F. F. Assaad, and A. P. Schnyder, Phys. Rev. B 93, 201116 (2016).10.1103/PhysRevB.93.201116Suche in Google Scholar

[18] X.-F. Su, Z.-L. Gu, Z.-Y. Dong, and J.-X. Li, Phys. Rev. B 97, 245111 (2018).10.1103/PhysRevB.97.245111Suche in Google Scholar

[19] X.-F. Su, Z.-L. Gu, Z.-Y. Dong, S.-L. Yu, and J.-X. Li, Phys. Rev. B 99, 014407 (2019).10.1103/PhysRevB.99.014407Suche in Google Scholar

[20] C. Weeks and M. Franz, Phys. Rev. B 85, 041104 (2012).10.1103/PhysRevB.85.041104Suche in Google Scholar

[21] K. Sun, Z. Gu, H. Katsura, and S. Das Sarma, Phys. Rev. Lett. 106, 236803 (2011).10.1103/PhysRevLett.106.236803Suche in Google Scholar PubMed

[22] E. J. Bergholtz and Z. Liu, Int. J. Mod. Phys. B 27, 1330017 (2013).10.1142/S021797921330017XSuche in Google Scholar

[23] S.-H. Lee, C. Broholm, W. Ratcliff, G. Gasparovic, Q. Huang, et al., Nature (London) 418, 856 (2002).10.1038/nature00964Suche in Google Scholar PubMed

[24] N. B. Kopnin, M. Ijäs, A. Harju, and T. T. Heikkilä, Phys. Rev. B 87, 140503 (2013).10.1103/PhysRevB.87.140503Suche in Google Scholar

[25] M. Goda, S. Nishino, and H. Matsuda, Phys. Rev. Lett. 96, 126401 (2006).10.1103/PhysRevLett.96.126401Suche in Google Scholar PubMed

[26] J. T. Chalker, T. S. Pickles, and P. Shukla, Phys. Rev. B 82, 104209 (2010).10.1103/PhysRevB.82.104209Suche in Google Scholar

[27] J. D. Bodyfelt, D. Leykam, C. Danieli, X. Yu, and S. Flach, Phys. Rev. Lett. 113, 236403 (2014).10.1103/PhysRevLett.113.236403Suche in Google Scholar PubMed

[28] R. Nandkishore and D. A. Huse, Annu. Rev. Cond. Mat. Phys. 6, 15 (2015).10.1146/annurev-conmatphys-031214-014726Suche in Google Scholar

[29] Y. Kuno, T. Orito, and I. Ichinose, New J. Phys. 22, 013032 (2020).10.1088/1367-2630/ab6352Suche in Google Scholar

[30] N. Roy, A. Ramachandran, and A. Sharma, arXiv preprint 1912.09951 (2019).Suche in Google Scholar

[31] M. Hyrkäs, V. Apaja, and M. Manninen, Phys. Rev. A 87, 023614 (2013).10.1103/PhysRevA.87.023614Suche in Google Scholar

[32] C. Lanczos, J. Res. Natl. Bur. Stand. 45, 255 (1950).10.6028/jres.045.026Suche in Google Scholar

[33] G. Rickayzen, Green’s Functions and Condensed Matter, Academic Press, London 1987.Suche in Google Scholar

Received: 2019-12-28

Accepted: 2020-02-20

Published Online: 2020-03-25

Published in Print: 2020-05-26

Artikel in diesem Heft

https://doi.org/10.1515/zna-2019-0371

Schlagwörter für diesen Artikel

Exact Diagonalization; Flat Band Systems; Many Particle Systems; Quasi One-Dimensional Systems; Spectral Functions