Approximate logic dendritic neuron model classification based on improved DE algorithm

3.1 Feature-guided adaptive DE algorithm

ALDNM can effectively cope with feature extraction and complex pattern classification tasks by simulating the logical operations and nonlinear information integration functions of neuronal dendrites. However, its performance is highly dependent on parameter settings and optimization [17]. Due to its strong global search capability, adaptability to nonlinear optimization problems, and simple algorithm, DE can effectively optimize the parameters of ALDNM [18]. However, traditional DE algorithms often face limitations, including Slow Convergence Speed (SCS), STLO, and insufficient population diversity in high-dimensional complex problems [19]. Therefore, this study first proposes an improved DE algorithm, namely FG-ADE, to enhance parameter optimization efficiency and classification performance. FG-ADE has made three major improvements based on the traditional DE algorithm, as shown in Figure 1.

Figure 1

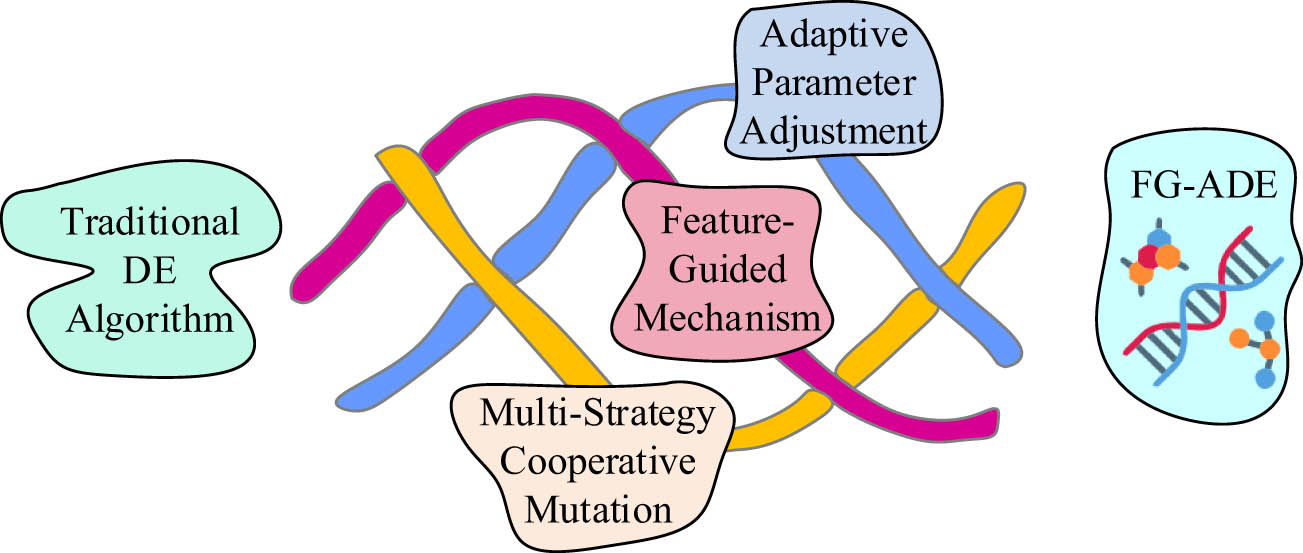
Three improvements of FG-ADE algorithm.

In Figure 1, the three core improvements are feature guidance mechanism, adaptive parameter adjustment, and multi-strategy collaborative mutation. Among them, the feature guidance mechanism dynamically adjusts the optimization direction to improve algorithm efficiency by extracting the fitness distribution and diversity information of the population. Adaptive parameter adjustment adjusts the values of control parameters according to different requirements during the search phase, achieving a balance between global exploration and local development. Multi-strategy collaborative mutation combines multiple mutation strategies to enhance the search ability of the population and accelerate the convergence process. The feature guidance mechanism is the first core improvement of FG-ADE. In this mechanism, population characteristic information is crucial. By analyzing population characteristic information, the current search status can be reflected, which can determine the next optimization direction. The core content is displayed in Figure 2.

Figure 2

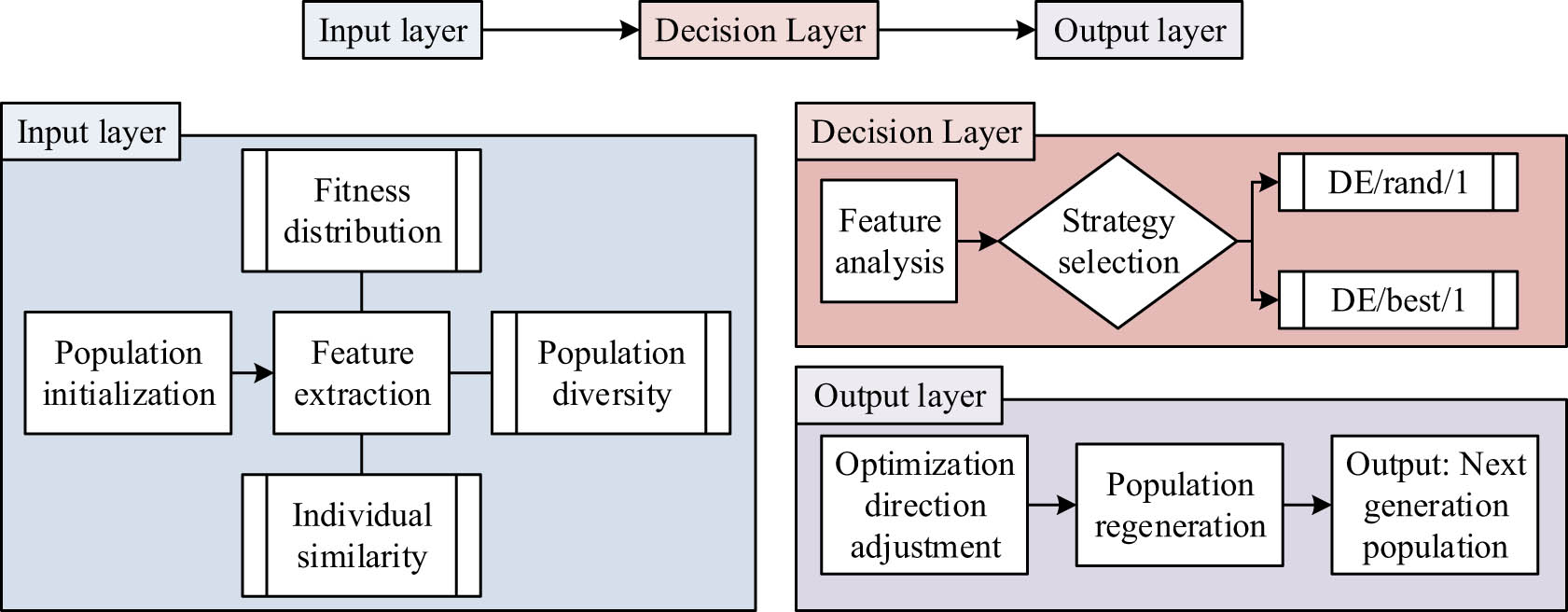
The core content of the feature steering mechanism.

In Figure 2, the core of the feature guidance mechanism mainly includes the extraction of population feature information, feature analysis, and dynamic strategy selection. Its essence is to dynamically adjust the optimization direction and mutation strategy by analyzing the fitness distribution, diversity information, and individual similarity of the population. Assuming the current population is P t = { x 1 t , x 2 t , .. . , x N t } , where t is the current iteration algebra, N is the population size, and x i t is the solution of the i th individual. The fitness of each individual is calculated based on the objective function to evaluate the quality of the solution. In the feature extraction stage, the first step is to calculate the mean fitness f ¯ t and variance σ f t of the population, as shown in equation (1).

In equation (1), f ¯ t can serve as an evaluation criterion for the global search direction, while σ f t is used to measure the diversity of the population. Meanwhile, to measure the similarity between individuals, the mean Euclidean distance between individuals in the population is defined as d t , as given by equation (2).

In equation (2), ∥ ⋅ ∥ is the Euclidean distance. The smaller the value of d t , the more concentrated the population may be, and a more advanced level of exploration may be needed. On the contrary, when d t is large, it indicates population dispersion and the need to enhance local development capabilities. In the feature analysis stage, an adaptive weight function ω ( x i t ) is defined based on the extracted population feature information, as shown in equation (3).

In equation (3), ε is a small constant that avoids the denominator being zero. The higher the ω ( x i t ) value, the stronger the individual’s superiority in the current population, and it is prioritized for mutation operations. Based on the above analysis, a mutation strategy can be dynamically selected. When the population diversity is high, a strategy with strong global search ability is chosen, such as DE/rand/1. When diversity decreases, the strategy with faster convergence speed is chosen, such as DE/best/1. Finally, the feature guidance mechanism guides individuals to search in a more optimal direction by dynamically adjusting the optimization direction Δ x i t , as shown in equation (4).

In equation (4), F is the scaling factor, x r t and x s t are randomly selected individuals, and x b t is the current optimal individual. The first term represents the global exploration direction based on random individuals, while the second term adjusts the speed at which individuals approach the optimal solution through adaptive weighting. The introduced adaptive parameter adjustment mechanism mainly targets the F and the crossover probability CR . F is the variation relationship with the iteration process, as shown in equation (5).

In equation (5), F max and F min are the preset minimum and maximum F . t and T are the current and total number of iterations. α is the adjustment index used to control the degree of nonlinearity of the scaling factor variation. The dynamic adjustment of CR is based on the diversity information of the population, as shown in equation (6).

In equation (6), CR base is the basic crossover probability, β is the adjustment coefficient, and σ f t and σ f 0 are the fitness variances of the current and initial populations. It can be known from equations (5) and (6) that the scaling factor gradually decreases with the number of iterations, achieving a smooth transition from the initial global search to the later local development. The crossover probability is dynamically adjusted based on the change in the variance of population fitness. When the variance decreases, the crossover probability is reduced to enhance the convergence stability. When the variance increases, the crossover probability is increased to maintain the search diversity. This mechanism can achieve an adaptive balance between global exploration and local convergence, and improve the optimization efficiency and robustness.

The multi-strategy collaborative mutation introduced in FG-ADE in this study is achieved by dynamically combining DE/rand/1 and DE/best/1 strategies. In the initial stage of optimization, DE/rand/1 is utilized to enhance global search capability, and in the later stage, DE/best/1 is gradually shifted to accelerate convergence. At the same time, by dynamically adjusting the selection probability based on the historical success frequency of statistical strategies, multiple mutation strategies work together to improve the optimization efficiency and adaptability of the algorithm. Combining the three major improvement designs, the final flow of the FG-ADE is exhibited in Figure 3.

Figure 3

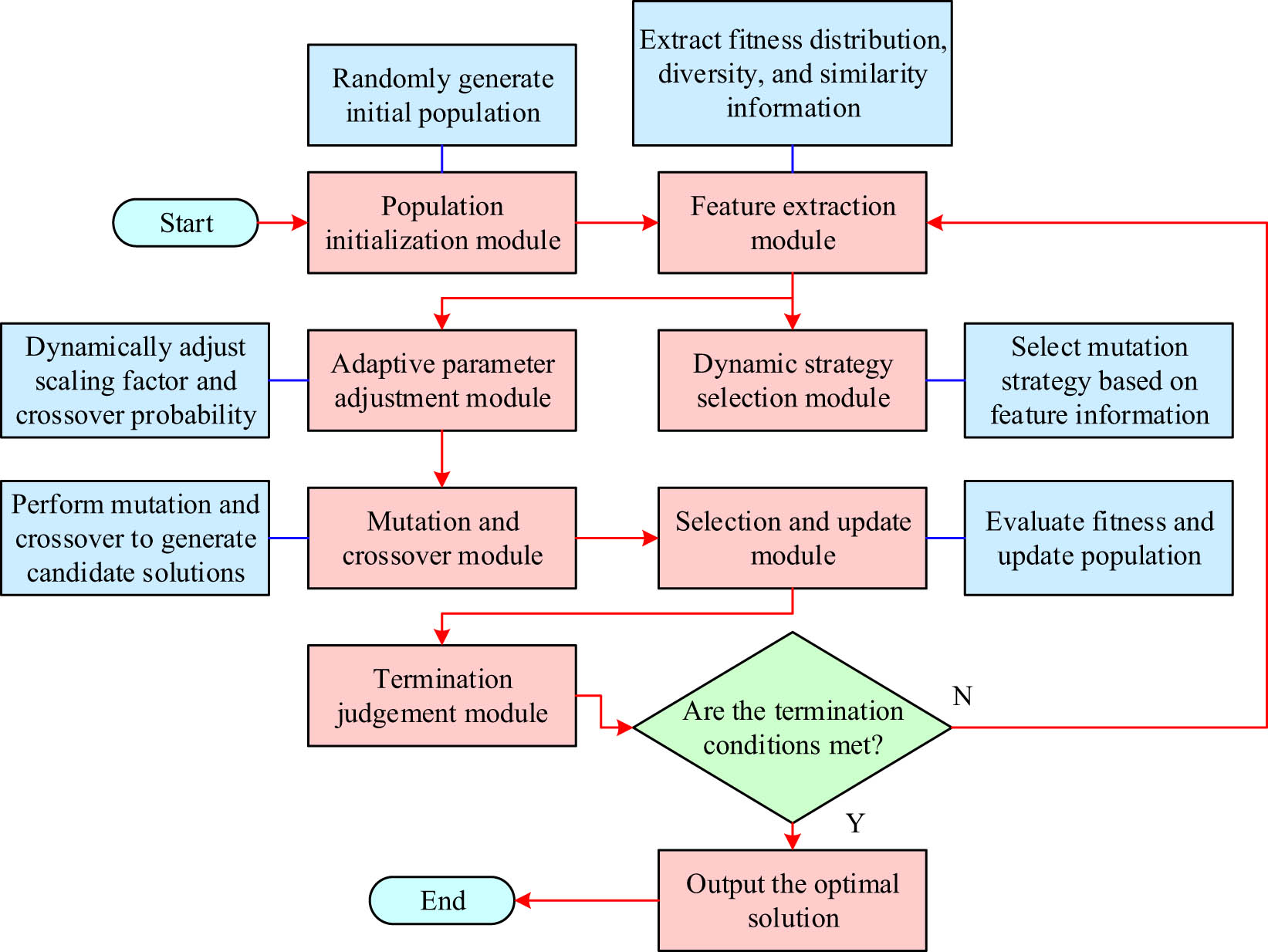
Flow diagram of FG-ADE algorithm.

In Figure 3, FG-ADE first generates an initial population through random initialization and extracts features such as fitness distribution and diversity information of the population. Subsequently, based on the feature-guided mechanism, the optimal mutation strategy is dynamically selected. Combined with the adaptive parameter adjustment mechanism, the scaling factor and crossover probability are flexibly set to balance global exploration and local development capabilities. Furthermore, multiple strategy collaborative mutation operations are utilized to generate new solutions, and individual selection and updating are completed through fitness evaluation. Finally, the optimal solution is output based on the optimization termination condition. The entire process can effectively improve the optimization efficiency of the algorithm through the synergistic effect of three major improvements.

3.2 ALDNM based on FG-ADE

The proposed FG-ADE algorithm solves the problems of SCS, STLO, and insufficient population diversity in traditional DE algorithms for high-dimensional complex problems by introducing a feature guidance mechanism, adaptive parameter adjustment, and multi-strategy collaborative mutation. Therefore, to improve the classification performance of ALDNM and address the shortcomings of low parameter optimization efficiency and STLO, this study applies FG-ADE to ALDNM. To achieve effective application of FG-ADE, it is necessary to first have a deep understanding of the working principle of ALDNM. The working principle of ALDNM is inspired by the dendritic structure of biological neurons, as shown in Figure 4.

Figure 4

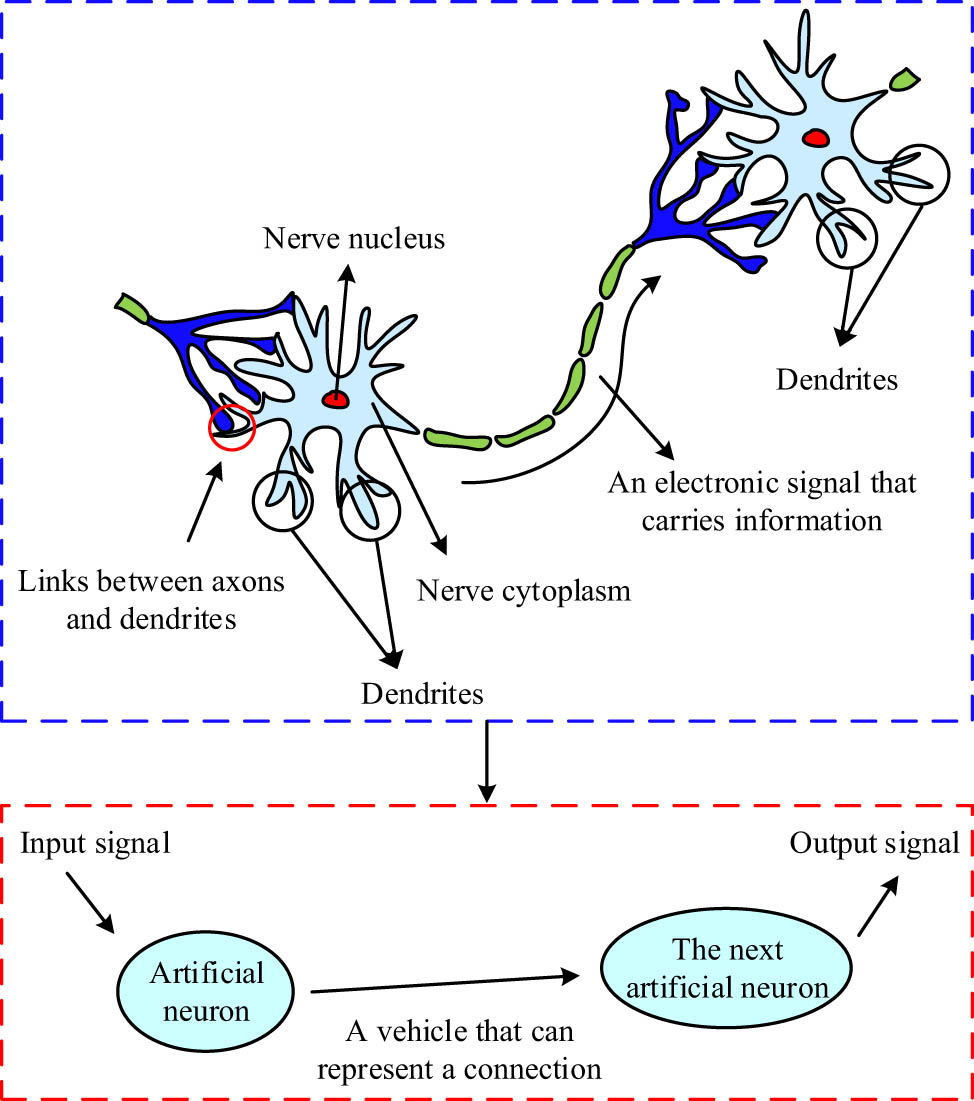
Working principle of the ALDNM.

In Figure 4, the working principle of biological neurons includes signal reception, integration, and transmission. The input signal enters the neuron through dendrites. Dendrites, as the main information receivers, screen and integrate signals from other neurons, and then transmit the processed signals to the cell body [20]. As the core processing unit of information, the cell body weighs and integrates the signals transmitted by dendrites, and transmits the output to the next neuron in the form of electronic signals through axons. Inspired by this, ALDNM not only simulates the working mechanism of biological neurons but also further combines specific mathematical logic operations and optimization processes to enhance classification and feature extraction capabilities. The specific structure of its model is shown in Figure 5.

Figure 5

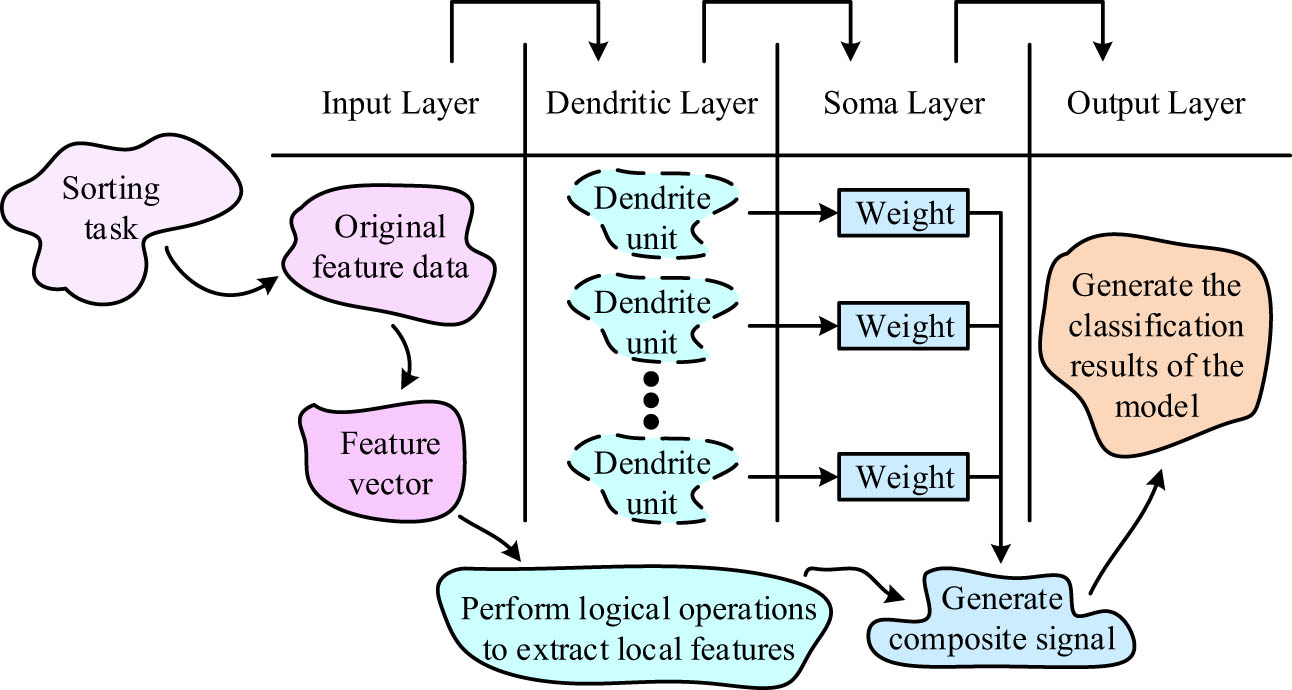
Schematic diagram of the ALDNM.

In Figure 5, ALDNM mainly consists of an input layer, dendritic layer, cytoplasmic layer, and output layer. The functions of each part highly correspond to the signal reception, integration, and transmission processes of biological neurons. In the input layer, the raw feature data are mapped into feature vectors, which are then subjected to logical operations and local feature extraction in the dendritic layer. After weighted integration by the cellular layer, the comprehensive signal is transmitted to the output layer, and the final classification result is generated through the activation function. Assuming the input feature vector is X = [ x 1 , x 2 , .. . , x n ] , where x i is the i th input feature and n is the feature dimension. At the dendritic layer, the logic unit performs nonlinear logic operations on the input signal to generate local feature outputs, as shown in equation (7).

In equation (7), z k is the output of the k -th dendritic unit. S k is the set of features involved in logical operations. ω i , k is the weight of the feature x i in dendritic units. In the cytoplasmic layer, the outputs of all dendritic units are weighted and integrated into a composite signal y , as shown in equation (8).

In equation (8), m represents the number of dendritic units, and v k is the weight of dendritic unit z k . Finally, the output layer generates the classification result o through the activation function, as shown in equation (9).

In equation (9), f act is the activation function, and θ is used to adjust the sensitivity of classification decisions. When applying the FG-ADE algorithm to ALDNM in this study, it mainly focuses on ω i , k , v k , and θ . FG-ADE dynamically adjusts the weight of each dendritic unit by extracting population feature information, achieving optimal configuration on a global scale, as shown in equation (10).

In equation (10), ω i , k t represents the weight of the t -th generation. ω r 1 , k and ω r 2 , k are a randomly selected weighted individual. ω best, k is the current optimal weight. FG-ADE dynamically adjusts v k through multi-strategy collaborative mutation, as shown in equation (11).

In equation (11), Δ v i · k is the weight increment updated through mutation strategy. Finally, FG-ADE dynamically optimizes the threshold θ through a feature-guided mechanism, as given by equation (12).

In equation (12), θ best is the current optimal threshold solution. Therefore, the process of using ALDNM based on FG-ADE for classification is shown in Figure 6.

Figure 6

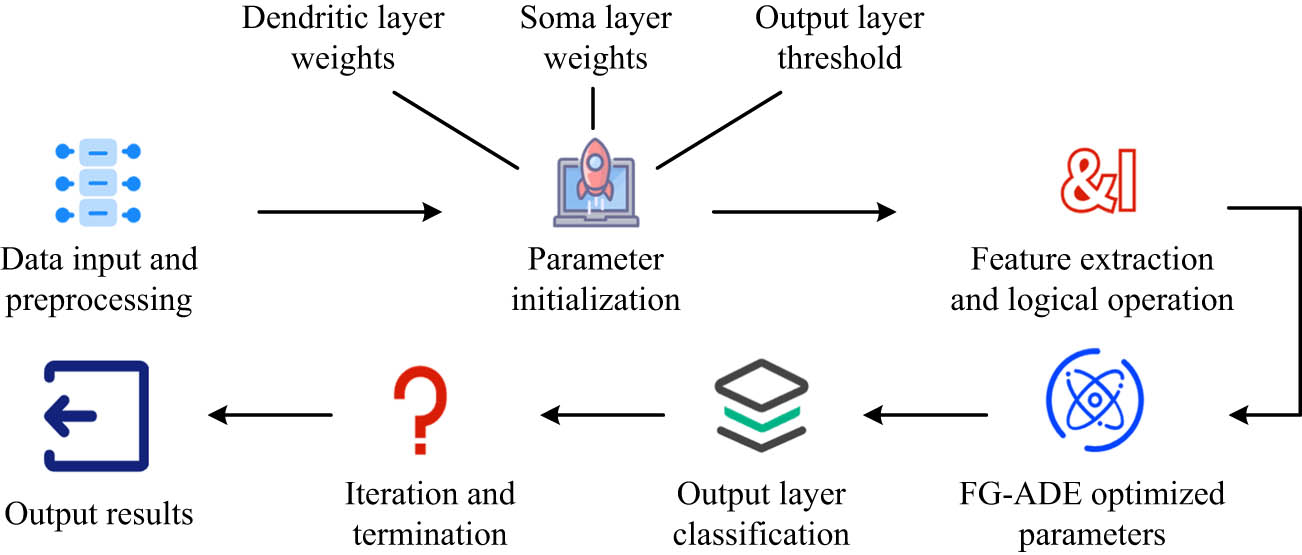
The flow of FG-ADE-based ALDNM used for classification.

In Figure 6, when performing classification tasks based on FG-ADE-optimized ALDNM, the input feature data are first mapped into feature vectors and passed to the dendritic layer to extract local features through logical operations. Subsequently, it weighs and integrates the outputs of dendritic units at the cellular level to generate a comprehensive signal. To improve model performance, FG-ADE adjusts dendritic layer weights, cell body layer weights, and output layer thresholds through feature-guided mechanisms and dynamic optimization strategies, balancing global search and local development capabilities to optimize classification performance. Finally, the model generates classification results through the output layer activation function and evaluates its performance based on test data to ensure excellent performance in complex classification tasks.

4.1 Performance verification and analysis of FG-ADE algorithm

The environmental experiments are listed in Table 1.

This study first conducts experiments on FG-ADE. In Table 1, the population size is set to 50, the maximum number of iterations is 100, and the initial values of the scaling factor and crossover probability are 0.5 and 0.7, which are dynamically adjusted during the optimization process. The mutation strategy initially adopts random mutation, and gradually shifts to the mutation strategy based on the optima in the later stage. To verify the optimization performance of FG-ADE, four baseline algorithms are selected for comparison: the traditional DE algorithm, the PSO-GA, the Chaotic Fruit Fly Optimization Algorithm (CFOA), and the Adaptive Whale Optimization Algorithm (AWOA). All algorithms are executed on the same hardware and software platform to ensure the fairness and reproducibility of the comparative experiments. The key parameter settings of the baseline algorithms are as follows: The traditional DE algorithm adopts the DE/rand/1/bin strategy, with the scaling factor set to 0.5 and the crossover probability set to 0.7, which are consistent with the initial settings in FG-ADE. In PSO-GA, the particle swarm component uses 30 particles, with an inertia weight of 0.7, and both the personal and social learning factors are set to 1.5. In the GA component, the crossover rate and mutation rate are set to 0.8 and 0.1, respectively. CFOA uses an initial population size of 30, a maximum flight distance of 10, and a step size factor of 0.5, with chaotic behavior introduced via a Logistic map. AWOA employs a linearly decreasing convergence factor from 2 to 0, and incorporates a spiral position update mechanism along with a jump search strategy, with a population size of 30 as well. The typical high-dimensional optimization test functions, namely Rastrigin, Rosenbrock, and Ackley functions, are selected as the test benchmarks for the experiment, as shown in Figure 7.

Figure 7

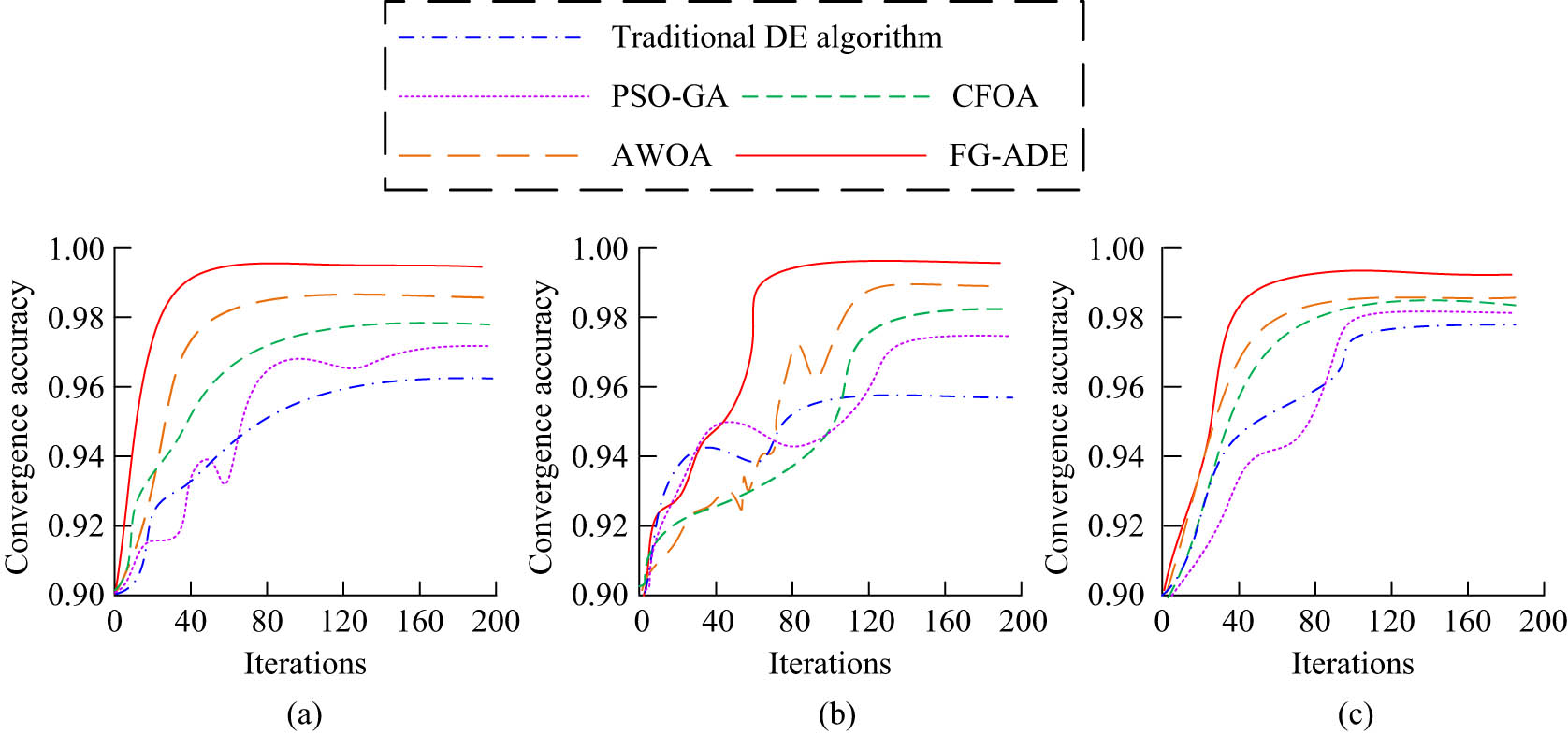
Performance comparison experiment results of FG-ADE. (a) Rastrigin. (b) Rosenbrock. (c) Ackley.

In Figure 7(a), on the Rastrigin function, the convergence speed of FG-ADE is significantly better than other algorithms, approaching the global optimal solution after about 40 iterations and maintaining stability, with a convergence accuracy of 0.994. In Figure 7(b), FG-ADE exhibits superior local development capability on the Rosenbrock function, with higher convergence accuracy than other algorithms, and reaches the optimal value of 0.997 after about 50 iterations. In Figure 7(c), on the Ackley function, FG-ADE has strong optimization ability in multi-modal complex problems, and its convergence speed and accuracy are also better than the compared algorithms. Therefore, FG-ADE performs better in high-dimensional nonlinear optimization problems. Furthermore, this study conducted ablation experiments on the FG-ADE algorithm, as shown in Table 2.

In Table 2, I1, I2, and I3 represent three improved designs: feature guidance mechanism, adaptive parameter adjustment, and multi-strategy collaborative mutation. As shown in Table 2, the complete FG-ADE model achieves the best performance in all evaluation metrics, with the lowest error of 0.001, the highest average fitness of 0.997, and the greatest population diversity of 0.856. Removing any single improvement will result in performance degradation, indicating that these three mechanisms have complementary and synergistic effects. It is worth noting that removing the feature-guided mechanism (I1) results in the largest decrease in population diversity, reaching 0.594, and the fitness value also significantly decreases. This is due to the lack of adaptive feedback on population status, which causes the mutation strategy to become less directed and increases the risk of premature convergence. Without the adaptive parameter adjustment mechanism (I2), the average fitness decreases to 0.992, as fixed parameters fail to accommodate the dynamic nature of the search process, especially in later stages. Eliminating the multi-strategy mutation mechanism (I3) reduces the algorithm’s ability to escape local optima, leading to lower diversity and less robust solutions. Due to the additional computation of population analysis and dynamic strategy selection required for each iteration, the complete FG-ADE has a slightly higher time cost of 3.5 s, but the performance improvement proves that the increase in computational overhead is reasonable. These findings highlight the crucial role of all three components in enhancing global search capacity, maintaining diversity, and improving convergence quality, particularly in high-dimensional optimization tasks.

4.2 Validation and analysis of ALDNM

For ALDNM based on FG-ADE, this study chooses the UCI Wine Dataset and MNIST Dataset as data sources. The former has a smaller data scale, containing 178 samples and 13 continuous features, which can be used to verify the performance and stability of the model in multi-class classification tasks. The latter has a larger data scale, containing 70,000 samples and 784 high-dimensional features, which is suitable for testing the classification ability of the model on complex high-dimensional features and large-scale data. To ensure the consistency and reproducibility of the experiments, all datasets are preprocessed prior to use. Specifically, missing values are handled using mean imputation, and all features are normalized using Min-Max scaling to the range [0, 1] to eliminate the impact of differing feature scales on model training.

The traditional DE-optimized ALDNM (M1), PSO-GA-optimized ALDNM (M2), and gradient descent-optimized ALDNM (M3) are used as comparison methods, while the research model is M0. Firstly, the model performance in classification tasks is validated, as exhibited in Figure 8.

Figure 8

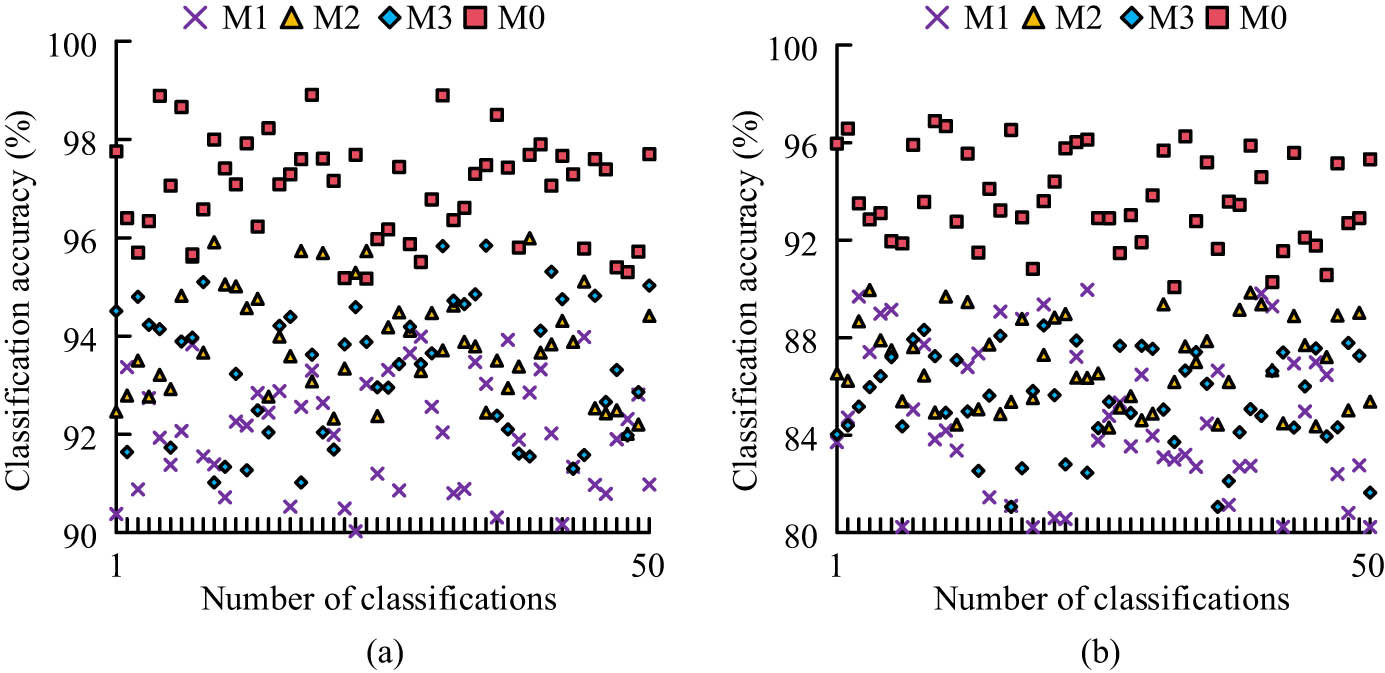
Comparison of model performance in classification tasks. (a) UCI Wine Dataset. (b) MNIST Dataset.

In Figure 8(a), in the UCI Wine Dataset, the classification accuracy of M1 fluctuates between 90 and 94% in 50 classification tasks, M2 fluctuates between 92 and 96%, M3 fluctuates between 91 and 96%, and M0 fluctuates between 95 and 99%. In a few classification tasks, M0 has lower classification accuracy than M2 or M3, but overall accuracy is higher. In Figure 8(b), in the MNIST Dataset, due to the large amount of data and high feature dimensions, the classification accuracy of all four models has decreased, but M0 still remains between 91 and 97%, showing the best performance. This study thoroughly analyzes the classification performance under different dimensions, as shown in Figure 9.

Figure 9

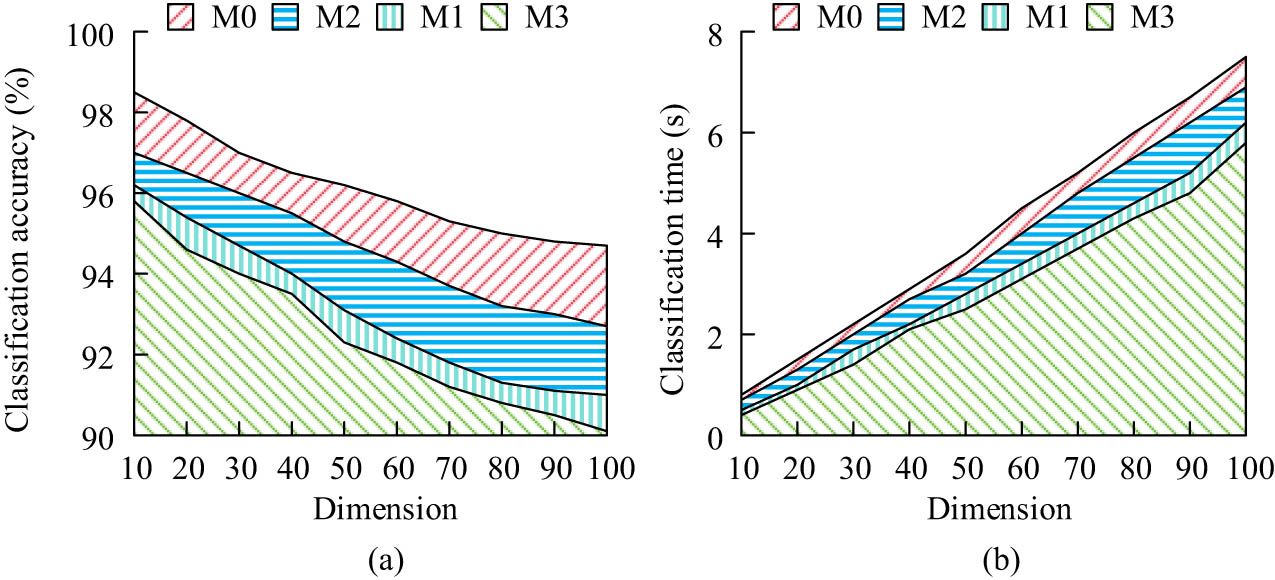
Classification performance in different dimensions: (a) Classification accuracy and (b) classification time.

In Figure 9(a), as the data dimension increases, the classification accuracy of all models decreases. However, M0 has the highest classification accuracy in all dimensions, reaching 98.5% when the dimension is 10 and maintaining 94.7% when the dimension reaches 100 dimensions. The accuracy of M1, M2, and M3 has decreased significantly, and their overall performance is far inferior to M0. In Figure 9(b), as the dimension increases, the time consumption of all models shows a gradually increasing trend. Compared to other models, M0 has a higher time consumption, but it remains within an acceptable range. At 100 dimensions, the completion time of the entire classification task for M0–M3 is 7.5, 6.2, 6.9, and 5.8 s, respectively. Overall, FG-ADE exhibits a good balance between accuracy and time consumption, and can still maintain strong classification performance in high-dimensional complex data. This study validates the robustness of the model in class imbalance problems by using the Credit Card Fraud Dataset from the UCI database and a Synthetic imbalance dataset as experimental data. The class imbalance problem is tested using three data processing methods: raw data, Synthetic Minority Over-sampling Technique (SMOTE), and undersampling. The results are shown in Figure 10.

Figure 10

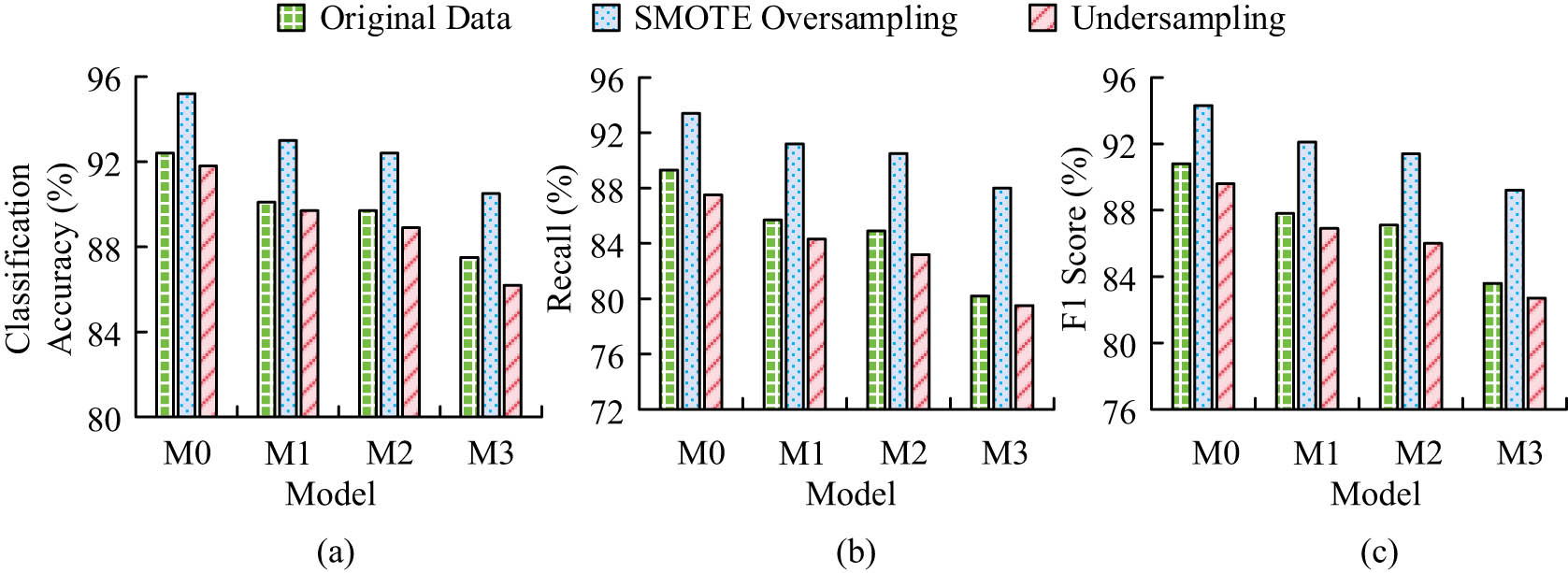
Robustness comparison in class imbalance problem: (a) Classification accuracy, (b) comparison of recall, and (c) comparison of F1.

In Figure 10(a), among the three data processing methods, M0 has the highest classification accuracy, reaching 95.2% under SMOTE, which is higher than M1’s 93.0, M2’s 92.4, and M3’s 90.5%. In Figure 10(b), M0 performs outstandingly in terms of recall rate, with 89.3, 93.4, and 87.5% under raw data, SMOTE, and undersampling, which are higher than the comparison model, indicating that M0 has a stronger recognition ability for minority categories. In Figure 10(c), the F1 score of M0 is the highest among the three data processing methods, at 90.8, 94.3, and 89.6%, further demonstrating its superior comprehensive performance in imbalanced data. Therefore, the results validate the robustness and optimization effectiveness of the FG-ADE algorithm in class imbalance problems. To further evaluate the practical feasibility of the FG-ADE model, a comparative analysis of computational efficiency and resource consumption is conducted under varying feature dimensions. All models are executed on the same hardware platform. For each model, the average runtime for completing a full classification task is recorded, along with CPU utilization and peak memory usage. The results for the 100-dimensional case are shown in Table 3.

As shown in Table 3, the FG-ADE model has an average runtime of 6.8 s on the 100-dimensional dataset. In comparison, the traditional DE algorithm requires 5.9 s, the PSO-GA model takes 6.3 s, and the Gradient Descent model finishes in 5.4 s. Regarding CPU utilization, FG-ADE reaches 82.4%, while the traditional DE, PSO-GA, and Gradient Descent models reach 79.1, 80.7, and 77.5%, respectively. In terms of peak memory usage, FG-ADE consumes 496 megabytes, compared to 463 megabytes for traditional DE, 475 megabytes for PSO-GA, and 458 megabytes for Gradient Descent. Overall, although FG-ADE incurs slightly higher computational costs, the increase remains moderate and within acceptable limits. Given its significantly better classification accuracy and robustness in high-dimensional scenarios, the additional computational investment is justified, demonstrating strong applicability and scalability in practical tasks.