Global Research Trends of Intuitionistic Fuzzy Set: A Bibliometric Analysis

Xiaorong He; Yingyu Wu

doi:10.1515/jisys-2017-0240

Artikel Open Access

Global Research Trends of Intuitionistic Fuzzy Set: A Bibliometric Analysis

Xiaorong He und Yingyu Wu

Veröffentlicht/Copyright: 11. September 2017

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Journal of Intelligent Systems Band 28 Heft 4

Abstract

Despite the fast growth of intuitionistic fuzzy publications, only a small part of these groundbreaking researches have significantly impacted the field. The main purpose of this paper was to identify and investigate the 100 most cited publications in the intuitionistic fuzzy field. Topic search based on the keyword “intuitionistic fuzzy” in the Science Citation Index and Social Sciences Citation Index databases was conducted to identify the 100 most cited articles. Bibliometric analysis methods were employed to describe these articles from different angles, such as the citation amount and rate, distribution among journals, institutions and countries/regions, author frequency, and citation distribution over time. This paper provides an insight on the characteristics of the highly cited intuitionistic fuzzy publications. The achievements of this study may provide useful information for researchers in the fields related to intuitionistic fuzzy.

Keywords: Intuitionistic fuzzy; bibliometrics; Web of science; citation

1 Introduction

With the increase in the complexity and uncertainty of the socio-economic environment, the difficulty of decision makers in dealing with decision-making problems is also significantly enhanced [117, 118]. It is difficult for decision makers to describe the decision-making object accurately and then make accurate decisions [31, 32]. Intuitionistic fuzzy set (IFS), introduced by Atanassov [1, 2], is an effective technique to deal with the decision maker’s subjective uncertainty and fuzziness of knowledge [110]. As an extension of the traditional fuzzy set [127], IFS has been widely used in various fields, such as computer science [113], mathematics, operations research and management science, engineering, and automation and control systems [111, 112, 114]. At present, IFS has become an important branch of fuzzy mathematics and it has been extended to hesitant fuzzy sets (HFSs) [116, 132], dual HFSs [123, 122, 133], and so on. The research on IFS has evolved rapidly over the last few decades. A lot of achievements of the research on its theory and application have been made by scholars around the world [125, 126].

Given the extensive application of IFS and the thousands of academic achievements that have been made, it is necessary to make a comprehensive overview of the current research status. In previous related studies, Yu and Shi [119] investigated the developmental track of IFS based on bibliometric analysis methods. The positions of crucial literatures are also determined via analyzing the citation network. Yu et al. [120] presented a scientometric review on IFS studies. Visualization technologies are also employed to show the influential authors and influential journals. It should be noted that the research object of these two studies are all the publications related to IFS included in Web of Science. Although each article contributes to the development of this discipline, only a small part of those groundbreaking researches have significantly impacted the field. Therefore, identifying and analyzing the critical researches are very helpful to understand the developmental track and trend of this discipline.

Some research has been conducted on the highly cited articles in various disciplines. For example, Garousi and Fernandes [28] identified the top 100 papers in the field of software engineering based on two indicators: total citations and citation rate. Ellul et al. [27] presented a bibliometric analysis and identified the top 100 highly cited papers in the field of emergency abdominal surgery. The formation and development of the key research topics in this field are well investigated. Tahim et al. [70] studied the evolutional trends and characteristics of the top 100 highly cited papers in facial trauma surgery. Recently, several bibliometric analyses-based publications appeared focused on the 100 highly cited papers in the field of spine [17, 22, 35] or radiology, nuclear medicine, and medical imaging [10, 38, 57, 58]. To the best of our knowledge, however, there has been no research focused on the most cited papers in the field of IFS.

The structure of this paper is organized as follows. Section 2 illustrates the bibliometric analysis methods and the document data. Section 3 presents the research findings and discussions. Section 4 concludes this paper.

2 Data Sources and Methods

IFS is a very popular research topic in the past decades. Tens of thousands of research publications appear in a Google Scholar search. In order to ensure the standardization and quality of research data, Web of Science is used to search related documents. The search strategy of this paper for retrieving IFS-related publications was defined as follows:

TC = (intuitionistic fuzzy);
Timespan = all years. Databases = (SCI -EXPANDED, SSCI). The retrieval time was April 7, 2017;
TC was referred to as the topic search.

A total of 1903 records are found based on the above search strategy. Furthermore, these records are ranked according to their citations. The top 100 records are selected for further analysis.

Bibliometric analysis methods [33, 115, 124] are used in this paper for the analysis of the top 100 most cited publications. The total citation and citation rate of these publications, features of the influential scholars, journals, institutions, and countries/regions are investigated.

3 Results and Analysis

The SCI (Science Citation Index) and SSCI (Social Sciences Citation Index) returned 1903 papers. The 100 most cited papers are shown in Table 1. The most frequent publication year was 2010 with 17 publications. The citation times ranged from 2564 for Atanassov [2] to 82 for Zhou and Wu [131]. The most cited publication in IFS was Atanassov’s 1986 article [2] in Fuzzy Sets and Systems. In this pioneering achievement, the author defined the concept of IFS, which is a generalization of the traditional fuzzy set and proved various properties of IFS. According to the statistical results from Web of Science, this paper was not cited since 3 years after its publication, and the citation rate is very low before 2000. However, this study has been widely cited in recent years, and the year with the most citations was 2016, with 539 citations. The second most highly cited publication was the 1989 paper by Atanassov and Gargov [6], which extended the IFS and introduced the notion of interval-valued IFS, inspired by the ordinary interval-valued fuzzy sets. Since its publication in 1989, it has received 826 citations and the most citations are generated in the past 10 years. Ranked the third place is a paper written by Xu and published in 2007 [90]. In this paper, the author presented a method for ranking the intuitionistic fuzzy values based on the score function and accuracy function. Furthermore, the author developed a series of intuitionistic fuzzy aggregation operators, such as intuitionistic fuzzy weighted averaging operator, intuitionistic fuzzy ordered weighted averaging operator, and intuitionistic fuzzy hybrid aggregation operator [90]. This publication has been consistently cited since 2008, and a total of 562 papers have cited this publication.

Table 1:

Top 100 Cited Papers in Intuitionistic Fuzzy.

Studies	Total no. of citations		Average citations per year		Studies	Total no. of citations		Average citations per year
Studies	No.	Rank	No.	Rank	Studies	No.	Rank	No.	Rank
Atanassov [2]	2564	1	85.47	1	Saadati and Park [63]	135	51	13.50	76
Atanassov and Gargov [6]	826	2	30.59	16	Szmidt and Kacprzyk [68]	135	52	9.64	92
Xu [90]	562	3	62.44	4	Xu [95]	133	53	22.17	31
Xu and Yager [101]	546	4	54.60	5	Mitchell [55]	132	54	12.00	85
Torra [74]	511	5	85.17	2	Li [40]	129	55	21.50	35
Maji et al. [53]	481	6	37.00	10	Xu and Yager [103]	128	56	18.29	47
Szmidt and Kacprzyk [66]	467	7	29.19	19	Takeuti and Titani [71]	125	57	3.91	100
Bustince and Burillo [14]	434	8	21.70	34	Ye [106]	124	58	17.71	50
Maji et al. [52]	409	9	29.21	18	Zeng and Li [128]	124	59	12.40	82
Atanassov [3]	387	10	14.33	69	Wang and Xin [77]	124	60	11.27	89
Deschrijver and Kerre [23]	368	11	28.31	22	Ye [108]	123	61	20.50	41
Xia and Xu [87]	332	12	66.40	3	Xu [91]	123	62	13.67	75
Herrera et al. [34]	321	13	29.18	20	Chen and Li [16]	121	63	40.33	9
Boran et al. [9]	316	14	45.14	8	Xu [98]	119	64	14.88	67
Xu [92]	306	15	34.00	13	Beliakov et al. [8]	116	65	23.20	28
Szmidt and Kacprzyk [67]	295	16	19.67	44	Wei [80]	116	66	16.57	57
Wei [81]	287	17	47.83	6	Wei [79]	116	67	14.50	68
Liu and Wang [50]	278	18	30.89	15	Liu and Jin [51]	112	68	28.00	23
Li and Chuntian [44]	278	19	19.86	43	Wei [83]	112	69	22.40	29
Atanassov [4]	273	20	12.41	81	Xu and Wang [89]	112	70	12.44	80
Li [39]	264	21	24.00	26	Çoker [18]	112	71	5.89	97
De et al. [21]	263	22	17.53	52	Tan [72]	109	72	21.80	32
Atanassov [5]	253	23	11.50	86	Li [43]	107	73	21.40	36
Deschrijver et al. [25]	249	24	20.75	40	Xu and Yager [104]	107	74	21.40	37
Xu and Yager [102]	243	25	30.38	17	Park et al. [61]	106	75	21.20	39
Burillo and Bustince [11]	228	26	11.40	87	Ye [107]	105	76	17.50	53
Xu [96]	222	27	37.00	11	Li et al. [45]	102	77	11.33	88
Grzegorzewski [30]	216	28	18.00	48	Gerstenkorn and Mańko [29]	100	78	4.00	99
Zhao et al. [130]	208	29	34.67	12	Ye [109]	98	79	19.60	45
Liang and Shi [48]	195	30	15.00	66	Zeng and Li [129]	97	80	19.40	46
Dubois et al. [26]	190	31	17.27	54	Li [41]	97	81	16.17	58
Hung and Yang [37]	189	32	15.75	61	Yu et al. [121]	96	82	24.00	27
Cornelis et al. [19]	186	33	15.50	62	Bustince and Burillo [13]	94	83	4.70	98
Vlachos and Sergiadis [75]	182	34	20.22	42	Rodríguez et al. [62]	93	84	46.50	7
Wei [82]	170	35	28.33	21	Li et al. [47]	92	85	15.33	63
Atanassov et al. [7]	167	36	15.18	65	Xu et al. [105]	92	86	15.33	64
Mitchell [54]	161	37	12.38	83	Wang [76]	91	87	13.00	77
Xu [97]	160	38	32.00	14	Shabir and Naz [64]	90	88	18.00	49
Tan and Chen [73]	157	39	26.17	25	Wei and Zhao [84]	89	89	22.25	30
Lin et al. [49]	154	40	17.11	56	Park et al. [60]	89	90	12.71	78
Bustince and Burillo [12]	154	41	7.33	95	Li et al. [46]	88	91	12.57	79
De et al. [20]	153	42	9.56	93	Hung and Wu [36]	87	92	6.21	96
Wang et al. [78]	152	43	21.71	33	Xu and Chen [99]	86	93	17.20	55
Park [59]	146	44	12.17	84	Li [42]	86	94	14.33	70
Xu [88]	145	45	16.11	59	Wei and Zhao [85]	85	95	21.25	38
Deschrijver and Kerre [24]	142	46	15.78	60	Xu [94]	84	96	14.00	71
Xu [93]	141	47	17.63	51	Montero et al. [56]	84	97	9.33	94
Xu and Xia [100]	138	48	27.60	24	Chen et al. [15]	83	98	13.83	72
Shu et al. [65]	138	49	13.80	74	Wei et al. [86]	83	99	13.83	73
Szmidt and Kacprzyk [69]	137	50	10.54	90	Zhou and Wu [131]	82	100	10.25	91

Takeuti and Titani [71] is the oldest publication in the top 100. The most recent publication was published by Rodríguez et al. [62], and looked at the state of the art and future directions of HFSs. The authors pointed out that special attention should paid to the coming HFS-based proposals. The second newest publication was the 2013 paper written by Chen and Li [16] In this paper, the authors first presented the interval-valued hesitant preference relations based on the combination of hesitant fuzzy preference relations and interval-valued HFSs. Some aggregation operators for aggregating interval-valued hesitant fuzzy information are also presented in this study [16].

The average citations per year were also included to describe these highly cited documents. Another ranking list of these 100 articles based on citation rate is also shown in Table 1. Atanassov [2] was again in the first place, with an average of 85.47 citations per year. Following were the 2010 paper by Torra [74] (85.17 citations per year) on HFSs and the 2011 paper by Xia and Xu [87] (66.40 citations per year), which proposed a series of hesitant fuzzy information aggregation operators and discussed their applications in decision making.

These top 100 most cited articles were published in 25 different journals. The most number of publications appeared in Fuzzy Sets and Systems (20), followed by Information Sciences (13), and Expert Syst. Appl. (9). The total ranking list according to the number of articles (TP) in the top 100 is shown in Table 2. Some other indicators such as the impact factor (IF) (2015), 5-year impact factor (5-IF), and citation numbers (TC) are also used to describe these journals. Fuzzy Sets and Systems did not only publish the most highly cited papers but also had the most citations (7585). IEEE Transactions on Fuzzy Systems had the highest IF (6.701) and 5-IF (7.198).

Table 2:

Journals with the Top 100 Cited Intuitionistic Fuzzy Articles.

Journal title	Journal title (abbreviation)	IF (2015)	5-IF	TP	TC
Fuzzy Sets and Systems	FSS	2.098	2.376	20	7585
Information Sciences	INS	3.364	3.683	13	1800
Expert Systems with Applications	ESWA	2.981	2.879	9	1169
Knowledge-Based Systems	KBS	3.325	3.433	7	898
Pattern Recognition Letters	PRL	1.586	2.002	7	1232
Computers & Mathematics with Applications	CMWA	1.398	1.873	5	1169
Applied Soft Computing	ASCO	2.857	3.288	4	568
International Journal of Intelligent Systems	IJIS	2.05	2.483	4	856
European Journal of Operational Research	EJOR	2.679	3.109	3	722
IEEE Transactions on Fuzzy Systems	TFS	6.701	7.198	3	940
International Journal of Approximate Reasoning	IJAR	2.696	2.655	3	704
International Journal of Uncertainty Fuzziness and Knowledge-Based Systems	IJUFKBS	1.0	1.004	3	421
Applied Mathematical Modelling	AMM	2.291	2.4	2	211
Chaos, Solitons & Fractals	CSF	1.611	1.628	2	251
Fuzzy Optimization and Decision Making	FODM	2.569	2.57	2	273
International Journal of General Systems	IJGS	1.677	1.244	2	674
Journal of Computer and System Sciences	JCSS	1.583	1.598	2	387
Mathematical and Computer Modelling	MCM	1.366	1.602	2	252
Control and Cybernetics	CC	0.3	0.773	1	135
Group Decision and Negotiation	GDN	1.312	1.394	1	84
IEEE Transactions on Systems Man and Cybernetics Part B Cybernetics	TSMC	6.22	6.184	1	107
International Journal of Computational Intelligence Systems	IJCIS	0.391	0.639	1	83
International Journal of Systems Science	IJSS	1.947	1.837	1	167
Journal of Symbolic Logic	JSL	0.51	0.517	1	125
Microelectronics Reliability	MR	1.202	1.285	1	138

The country/region that contributed the most papers in the top 100 was China, with 56 highly cited papers. Following was Spain with nine. Table 3 shows the ranking in IFS field by country/region. Figure 1 shows the global geographic distribution of the highly cited publications in IFS.

Table 3:

Countries/Regions of Origin of the 100 Most Cited IFS Articles.

Country/region	No.	Country/region	No.
China	56	Sweden	1
Spain	9	Saudi Arabia	1
USA	7	Pakistan	1
Poland	7	Italy	1
Bulgaria	6	Iran	1
Taiwan	5	Greece	1
India	5	Germany	1
South Korea	4	France	1
Belgium	4	Czech Republic	1
Turkey	2	Canada	1
Israel	2	Australia	1

Figure 1:

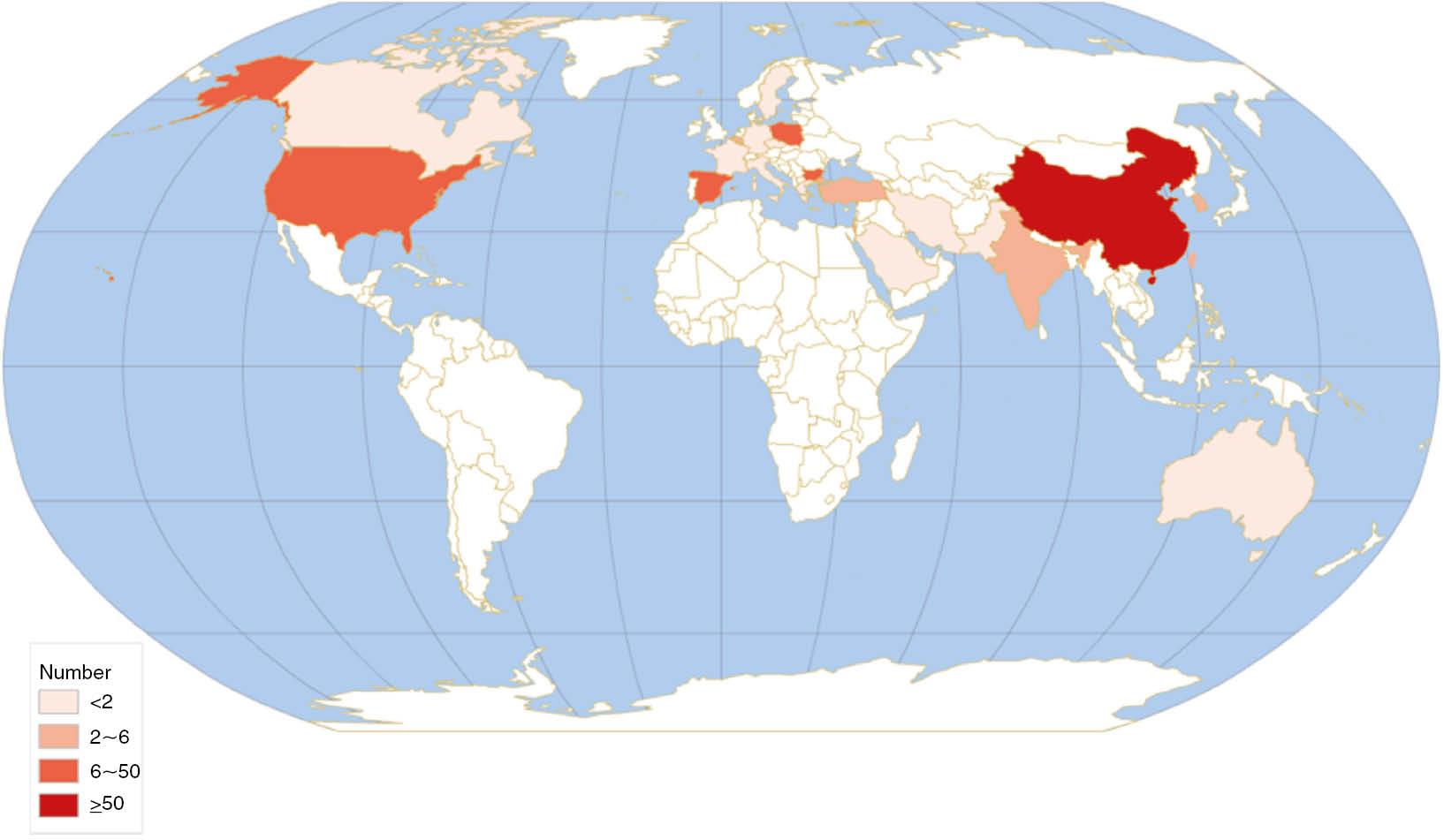
Global Geographic Distribution of the Highly Cited Publications in IFS.

The contributions of different institutions in IFS studies were investigated and the influential ones that have more than two highly cited papers are shown in Table 4. Southeast University in China contributed nine publications with 1324 citations, followed by Chongqing University Arts and Sciences in China with eight papers, Tsinghua University in China with seven papers, and PLA University of Science Technology in China with six papers.

Table 4:

Institutions with the Top 100 Cited IFS Articles (n≥2).

Institution	Country	No. of articles in top 100	No. of citations
Southeast University	China	9	1324
Chongqing University Arts and Sciences	China	8	1058
Tsinghua University	China	7	1913
PLA University of Science Technology	China	6	951
Polish Academy of Sciences	Poland	6	1440
Shanghai Jiao Tong University	China	6	1017
The Public University of Navarra	Spain	6	1110
Dalian Naval Academy	China	5	808
Fuzhou University	China	5	511
Iona College	USA	5	956
Bulgarian Academy of Sciences	Bulgaria	4	3944
Ghent University	Belgium	4	945
Indian Institute of Technology	India	4	1306
Pukyong National University	South Korea	4	476
Shaoxing University	China	4	450
Central South University	China	2	266
CSIC	Spain	2	604
Dalian University of Technology	China	2	432
Dong A University	South Korea	2	195
Elta Systems Ltd.	Israel	2	293
IPACT	Bulgaria	2	526
University of Jaen	Spain	2	414
University of Granada	Spain	2	414

Authors who contributed two or more of the 100 most cited IFS articles are shown in Table 5. Xu from Sichuan University, China, was the most productive author with 20 highly cited publications. As shown in Table 5, most of the authors work in China and Spain, although some scholars work in Bulgaria, Poland, India, South Korea, Belgium, and Israel.

Table 5:

Authors Who Contributed ≥2 of the 100 Most Cited IFS Articles.

Author	Institutions	Country	No. of articles	Position on author list (no. of articles)
Xu	Sichuan University	China	20	First (16), second (3), third (0), fourth (1)
Wei	Sichuan Normal University	China	8	First (8)
Li	Fuzhou University	China	8	First (8)
Bustince	The Public University of Navarra	Spain	6	First (3), second (2), third (1)
Atanassov	Bulgarian Academy of Sciences	Bulgaria	6	First (6)
Kacprzyk	Warsaw University of Technology	Poland	5	Second (4), fourth (1)
Ye	Shaoxing College of Arts and Sciences	China	4	First (4)
Yager	Iona College	USA	4	Second (4)
Szmidt	Polish Academic of Sciences	Poland	4	First (4)
Roy	Indian Institute of Technology	India	4	Second (1), third (3)
Park	Pukyong National University	South Korea	4	First (1), second (1), fourth (1)
Kerre	Ghent University	Belgium	4	Second (2), third (2)
Deschrijver	Ghent University	Belgium	4	First (3), second (1)
Burillo	The Public University of Navarra	Spain	4	First (1), second (3)
Zhao	Chongqing University of Arts and Sciences	China	3	Second (3)
Xia	Beijing Jiao Tong University	China	3	First (1), second (1), third (1)
Biswas	Indian Institute of Technology	India	3	Second (3)
Torra	Institution of Investigation and Intelligence Artificial	Spain	2	First (1), third (1)
Tan	Central South University	China	2	First (2)
Park	Pukyong National University	South Korea	2	Second (1), fourth (1)
Mitchell	Elta Systems Ltd	Israel	2	First (2)
Martinez	University of Jaen	Spain	2	Second (2)
Maji	Indian Institute of Technology	India	2	First (2)
Kwun	Dong A University	South Korea	2	Second (1), third (1)
Hung	National Hsinchu Teachers College	Taiwan	2	First (2)
Herrera	University of Granada	Spain	2	First (1), fifth (1)
De	Midnapore College	India	2	First (2)
Cornelis	Ghent University	Belgium	2	First (1), second (2)

4 Conclusions

Although citation analysis is not the only way to evaluate the quality of a scientific publication, it is an effective tool to help the scientific community determine the influential authors, journals, and articles. In this study, we identified and studied the 100 most cited IFS articles. Some important and interesting results were obtained. This analysis provided an insight into the historical developments in the intuitionistic fuzzy field.

Bibliography

[1] K. T. Atanassov, Intuitionistic Fuzzy Sets, VII ITKR’s Session, Deposed in Central Sci.- Techn. Library of Bulg. Acd. of Sci. Sofia (1983) 1677–1684.Suche in Google Scholar

[2] K. T. Atanassov, Intuitionistic fuzzy sets, Fuzzy Set. Syst.20 (1986), 87–96.10.1016/S0165-0114(86)80034-3Suche in Google Scholar

[3] K. T. Atanassov, More on intuitionistic fuzzy sets, Fuzzy Set. Syst. 33 (1989), 37–45.10.1016/0165-0114(89)90215-7Suche in Google Scholar

[4] K. T. Atanassov, New operations defined over the intuitionistic fuzzy sets, Fuzzy Set. Syst.61 (1994), 137–142.10.1016/0165-0114(94)90229-1Suche in Google Scholar

[5] K. T. Atanassov, Operators over interval valued intuitionistic fuzzy sets, Fuzzy Set. Syst.64 (1994), 159–174.10.1016/0165-0114(94)90331-XSuche in Google Scholar

[6] K. T. Atanassov and G. Gargov, Interval valued intuitionistic fuzzy sets, Fuzzy Set. Syst.31 (1989), 343–349.10.1016/0165-0114(89)90205-4Suche in Google Scholar

[7] K. T. Atanassov, G. Pasi and R. Yager, Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making, Int. J. Syst. Sci.36 (2005), 859–868.10.1080/00207720500382365Suche in Google Scholar

[8] G. Beliakov, H. Bustince, D. P. Goswami, U. K. Mukherjee and N. R. Pal, On averaging operators for Atanassov’s intuitionistic fuzzy sets, Inf. Sci.181 (2011), 1116–1124.10.1016/j.ins.2010.11.024Suche in Google Scholar

[9] F. E. Boran, S. Genç, M. Kurt and D. Akay, A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method, Expert Syst. Appl.36 (2009), 11363–11368.10.1016/j.eswa.2009.03.039Suche in Google Scholar

[10] W. Brinjikji, A. Klunder and D. F. Kallmes, The 100 most-cited articles in the imaging literature, Radiology269 (2013), 272–276.10.1148/radiol.13122242Suche in Google Scholar

[11] P. Burillo and H. Bustince, Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets, Fuzzy Set. Syst.78 (1996), 305–316.10.1016/0165-0114(96)84611-2Suche in Google Scholar

[12] H. Bustince and P. Burillo, Correlation of interval-valued intuitionistic fuzzy sets, Fuzzy Set. Syst.74 (1995), 237–244.10.1016/0165-0114(94)00343-6Suche in Google Scholar

[13] H. Bustince and P. Burillo, Structures on intuitionistic fuzzy relations, Fuzzy Set. Syst.78 (1996), 293–303.10.1016/0165-0114(96)84610-0Suche in Google Scholar

[14] H. Bustince and P. Burillo, Vague sets are intuitionistic fuzzy sets, Fuzzy Set. Syst.79 (1996), 403–405.10.1016/0165-0114(95)00154-9Suche in Google Scholar

[15] T. Y. Chen and C. H. Li, Determining objective weights with intuitionistic fuzzy entropy measures: a comparative analysis, Inf. Sci.180 (2010), 4207–4222.10.1016/j.ins.2010.07.009Suche in Google Scholar

[16] N. Chen, Z. S. Xu and M. Xia, Interval-valued hesitant preference relations and their applications to group decision making, Knowl.-Based Syst.37 (2013), 528–540.10.1016/j.knosys.2012.09.009Suche in Google Scholar

[17] J. Cohen, N. Alan, J. Zhou and D. Kojo Hamilton, The 100 most cited articles in metastatic spine disease, Neurosurg. Focus41 (2016), E10.10.3171/2016.5.FOCUS16158Suche in Google Scholar

[18] D. Çoker, An introduction to intuitionistic fuzzy topological spaces, Fuzzy Set. Syst.88 (1997), 81–89.10.1016/S0165-0114(96)00076-0Suche in Google Scholar

[19] C. Cornelis, G. Deschrijver and E. E. Kerre, Implication in intuitionistic fuzzy and interval-valued fuzzy set theory: construction, classification, application, Int. J. Approx. Reason.35 (2004), 55–95.10.1016/S0888-613X(03)00072-0Suche in Google Scholar

[20] S. K. De, R. Biswas and A. R. Roy, Some operations on intuitionistic fuzzy sets, Fuzzy Set. Syst.114 (2000), 477–484.10.1016/S0165-0114(98)00191-2Suche in Google Scholar

[21] S. K. De, R. Biswas and A. R. Roy, An application of intuitionistic fuzzy sets in medical diagnosis, Fuzzy Set. Syst.117 (2001), 209–213.10.1016/S0165-0114(98)00235-8Suche in Google Scholar

[22] R. De la Garza-Ramos, M. Benvenutti-Regato and E. Caro-Osorio, The 100 most-cited articles in spinal oncology, J. Neurosurg. Spine24 (2016), 810–823.10.3171/2015.8.SPINE15674Suche in Google Scholar

[23] G. Deschrijver and E. E. Kerre, On the relationship between some extensions of fuzzy set theory, Fuzzy Set. Syst.133 (2003), 227–235.10.1016/S0165-0114(02)00127-6Suche in Google Scholar

[24] G. Deschrijver and E. E. Kerre, On the position of intuitionistic fuzzy set theory in the framework of theories modelling imprecision, Inf. Sci.177 (2007), 1860–1866.10.1016/j.ins.2006.11.005Suche in Google Scholar

[25] G. Deschrijver, C. Cornelis and E. E. Kerre, On the representation of intuitionistic fuzzy t-norms and t-conorms, IEEE Trans. Fuzzy Syst.12 (2004), 45–61.10.1109/TFUZZ.2003.822678Suche in Google Scholar

[26] D. Dubois, S. Gottwald, P. Hajek, J. Kacprzyk and H. Prade, Terminological difficulties in fuzzy set theory – the case of “intuitionistic fuzzy sets”, Fuzzy Set. Syst.156 (2005), 485–491.10.1016/j.fss.2005.06.001Suche in Google Scholar

[27] T. Ellul, N. Bullock, T. Abdelrahman, A. G. Powell, J. Witherspoon and W. G. Lewis, The 100 most cited manuscripts in emergency abdominal surgery: a bibliometric analysis, Int. J. Surg.37 (2017), 29–35.10.1016/j.ijsu.2016.12.006Suche in Google Scholar

[28] V. Garousi and J. M. Fernandes, Highly-cited papers in software engineering: the top-100, Inform. Software Tech.71 (2016), 108–128.10.1016/j.infsof.2015.11.003Suche in Google Scholar

[29] T. Gerstenkorn and J. Mańko, Correlation of intuitionistic fuzzy sets, Fuzzy Set. Syst.44 (1991), 39–43.10.1016/0165-0114(91)90031-KSuche in Google Scholar

[30] P. Grzegorzewski, Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric, Fuzzy Set. Syst.148 (2004), 319–328.10.1016/j.fss.2003.08.005Suche in Google Scholar

[31] X. R. He and Y. Y. Wu, Independent hesitant fuzzy group decision making methods with application to person and post matching, J. Intell. Fuzzy Syst.33 (2017), 93–103.10.3233/JIFS-161159Suche in Google Scholar

[32] X. R. He, Y. Y. Wu and D. J. Yu, Intuitionistic fuzzy multi-criteria decision making with application to job hunting: a comparative perspective, J. Intell. Fuzzy Syst.30 (2016), 1935–1946.10.3233/IFS-151904Suche in Google Scholar

[33] X. He, Y. Wu, D. Yu and J. M. Merigó, Exploring the ordered weighted averaging operator knowledge domain: a bibliometric analysis, Int. J. Int. Syst.32 (2017), 1151–1166.10.1002/int.21894Suche in Google Scholar

[34] F. Herrera, L. Martınez and P. J. Sánchez, Managing non-homogeneous information in group decision making, Eur. J. Oper. Res.166 (2005), 115–132.10.1016/j.ejor.2003.11.031Suche in Google Scholar

[35] W. Huang, L. Wang, B. Wang, L. Yu and X. Yu, Top 100 cited articles on back pain research: a citation analysis, Spine41 (2016), 1683–1692.10.1097/BRS.0000000000001736Suche in Google Scholar

[36] W. L. Hung and J. W. Wu, Correlation of intuitionistic fuzzy sets by centroid method, Inf. Sci.144 (2002), 219–225.10.1016/S0020-0255(02)00181-0Suche in Google Scholar

[37] W. L. Hung and M. S. Yang, Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance, Pattern Recogn. Lett.25 (2004), 1603–1611.10.1016/j.patrec.2004.06.006Suche in Google Scholar

[38] H. J. Kim, D. Y. Yoon, E. S. Kim, K. Lee, J. S. Bae and J. H. Lee, The 100 most-cited articles in neuroimaging: a bibliometric analysis, NeuroImage139 (2016), 149–156.10.1016/j.neuroimage.2016.06.029Suche in Google Scholar PubMed

[39] D. F. Li, Multiattribute decision making models and methods using intuitionistic fuzzy sets, J. Comput. Syst. Sci.70 (2005), 73–85.10.1016/j.jcss.2004.06.002Suche in Google Scholar

[40] D. F. Li, TOPSIS-based nonlinear-programming methodology for multiattribute decision making with interval-valued intuitionistic fuzzy sets, IEEE Trans. Fuzzy Syst.18 (2010), 299–311.10.1109/TFUZZ.2010.2041009Suche in Google Scholar

[41] D. F. Li, Linear programming method for MADM with interval-valued intuitionistic fuzzy sets, Expert Syst. Appl.37 (2010), 5939–5945.10.1016/j.eswa.2010.02.011Suche in Google Scholar

[42] D. F. Li, A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems, Comput. Math. Appl.60 (2010), 1557–1570.10.1016/j.camwa.2010.06.039Suche in Google Scholar

[43] D. F. Li, Closeness coefficient based nonlinear programming method for interval-valued intuitionistic fuzzy multiattribute decision making with incomplete preference information, Appl. Soft Comput.11 (2011), 3402–3418.10.1016/j.asoc.2011.01.011Suche in Google Scholar

[44] D. F. Li and C. Chuntian, New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions, Pattern Recogn. Lett.23 (2002), 221–225.10.1016/S0167-8655(01)00110-6Suche in Google Scholar

[45] Y. Li, D. L. Olson and Z. Qin, Similarity measures between intuitionistic fuzzy (vague) sets: a comparative analysis, Pattern Recogn. Lett.28 (2007), 278–285.10.1016/j.patrec.2006.07.009Suche in Google Scholar

[46] D. F. Li, Y. C. Wang, S. Liu and F. Shan, Fractional programming methodology for multi-attribute group decision-making using IFS, Appl. Soft Comput.9 (2009), 219–225.10.1016/j.asoc.2008.04.006Suche in Google Scholar

[47] D. F. Li, G. H. Chen and Z. G. Huang, Linear programming method for multiattribute group decision making using IF sets, Inf. Sci.180 (2010), 1591–1609.10.1016/j.ins.2010.01.017Suche in Google Scholar

[48] Z. Liang and P. Shi, Similarity measures on intuitionistic fuzzy sets, Pattern Recog. Lett.24 (2003), 2687–2693.10.1016/S0167-8655(03)00111-9Suche in Google Scholar

[49] L. Lin, X. H. Yuan and Z. Q. Xia, Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets, J. Comput. Syst. Sci.73 (2007), 84–88.10.1016/j.jcss.2006.03.004Suche in Google Scholar

[50] H. W. Liu and G. J. Wang, Multi-criteria decision-making methods based on intuitionistic fuzzy sets, Eur. J. Oper. Res.179 (2007), 220–233.10.1016/j.ejor.2006.04.009Suche in Google Scholar

[51] P. Liu and F. Jin, Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making, Inf. Sci.205 (2012), 58–71.10.1016/j.ins.2012.04.014Suche in Google Scholar

[52] P. K. Maji, A. R. Roy and R. Biswas, An application of soft sets in a decision making problem, Comput. Math. Appl.44 (2002), 1077–1083.10.1016/S0898-1221(02)00216-XSuche in Google Scholar

[53] P. K. Maji, R. Biswas and A. Roy, Soft set theory, Comput. Math. Appl.45 (2003), 555–562.10.1016/S0898-1221(03)00016-6Suche in Google Scholar

[54] H. B. Mitchell, On the Dengfeng-Chuntian similarity measure and its application to pattern recognition, Pattern Recogn. Lett.24 (2003), 3101–3104.10.1016/S0167-8655(03)00169-7Suche in Google Scholar

[55] H. B. Mitchell, Pattern recognition using type-II fuzzy sets, Inf. Sci.170 (2005), 409–418.10.1016/j.ins.2004.02.027Suche in Google Scholar

[56] J. Montero, D. Gómez and H. Bustince, On the relevance of some families of fuzzy sets, Fuzzy Set. Syst.158 (2007), 2429–2442.10.1016/j.fss.2007.04.021Suche in Google Scholar

[57] M. E. O’Keeffe, T. N. Hanna, D. Holmes, O. Marais, M. F. Mohammed, S. Clark, P. McLaughlin, S. Nicolaou and F. Khosa, The 100 most-cited original articles in cardiac computed tomography: a bibliometric analysis, J. Cardiovasc. Comput. Tomogr.10 (2016), 414–423.10.1016/j.jcct.2016.07.013Suche in Google Scholar PubMed

[58] M. Pagni, N. R. Khan, H. L. Cohen and A. F. Choudhri, Highly cited works in radiology: the top 100 cited articles in radiologic journals, Acad. Radiol.21 (2014), 1056–1066.10.1016/j.acra.2014.03.011Suche in Google Scholar PubMed

[59] J. H. Park, Intuitionistic fuzzy metric spaces, Chaos Soliton. Fract.22 (2004), 1039–1046.10.1016/j.chaos.2004.02.051Suche in Google Scholar

[60] D. G. Park, Y. C. Kwun, J. H. Park and I. Y. Park, Correlation coefficient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision making problems, Math. Comput. Model.50 (2009), 1279–1293.10.1016/j.mcm.2009.06.010Suche in Google Scholar

[61] J. H. Park, I. Y. Park, Y. C. Kwun and X. Tan, Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment, Appl. Math. Model.35 (2011), 2544–2556.10.1016/j.apm.2010.11.025Suche in Google Scholar

[62] R. M. Rodríguez, L. Martínez, V. Torra, Z. S. Xu and F. Herrera, Hesitant fuzzy sets: state of the art and future directions, Int. J Intell. Syst.29 (2014), 495–524.10.1002/int.21654Suche in Google Scholar

[63] R. Saadati and J. H. Park, On the intuitionistic fuzzy topological spaces, Chaos Soliton. Fract.27 (2006), 331–344.10.1016/j.chaos.2005.03.019Suche in Google Scholar

[64] M. Shabir and M. Naz, On soft topological spaces, Comput. Math. Appl.61 (2011), 1786–1799.10.1016/j.camwa.2011.02.006Suche in Google Scholar

[65] M. H. Shu, C. H. Cheng and J. R. Chang, Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly, Microelectron. Reliab.46 (2006), 2139–2148.10.1016/j.microrel.2006.01.007Suche in Google Scholar

[66] E. Szmidt and J. Kacprzyk, Distances between intuitionistic fuzzy sets, Fuzzy Set. Syst.114 (2000), 505–518.10.1016/S0165-0114(98)00244-9Suche in Google Scholar

[67] E. Szmidt and J. Kacprzyk, Entropy for intuitionistic fuzzy sets, Fuzzy Set. Syst.118 (2001), 467–477.10.1016/S0165-0114(98)00402-3Suche in Google Scholar

[68] E. Szmidt and J. Kacprzyk, Using intuitionistic fuzzy sets in group decision making, Control Cybern.31 (2002), 1055–1057.Suche in Google Scholar

[69] E. Szmidt and J. Kacprzyk, A consensus-reaching process under intuitionistic fuzzy preference relations, Int. J Intell. Syst.18 (2003), 837–852.10.1002/int.10119Suche in Google Scholar

[70] A. Tahim, K. Patel, C. Bridle and S. Holmes, The 100 most cited articles in facial trauma: a bibliometric analysis, J. Oral Maxillofac. Surg.74 (2016), 2240.e1–2240.e14.10.1016/j.joms.2016.06.175Suche in Google Scholar PubMed

[71] G. Takeuti and S. Titani, Intuitionistic fuzzy logic and intuitionistic fuzzy set theory, J. Symb. Logic49 (1984), 851–866.10.2307/2274139Suche in Google Scholar

[72] C. Tan, A multi-criteria interval-valued intuitionistic fuzzy group decision making with Choquet integral-based TOPSIS, Expert Syst. Appl.38 (2011), 3023–3033.10.1016/j.eswa.2010.08.092Suche in Google Scholar

[73] C. Tan and X. Chen, Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making, Expert Syst. Appl.37 (2010), 149–157.10.1016/j.eswa.2009.05.005Suche in Google Scholar

[74] V. Torra, Hesitant fuzzy sets, Int. J Intell. Syst.25 (2010), 529–539.10.1002/int.20418Suche in Google Scholar

[75] I. K. Vlachos and G. D. Sergiadis, Intuitionistic fuzzy information – applications to pattern recognition, Pattern Recogn. Lett.28 (2007), 197–206.10.1016/j.patrec.2006.07.004Suche in Google Scholar

[76] P. Wang, QoS-aware web services selection with intuitionistic fuzzy set under consumer’s vague perception, Expert Syst. Appl.36 (2009), 4460–4466.10.1016/j.eswa.2008.05.007Suche in Google Scholar

[77] W. Wang and X. Xin, Distance measure between intuitionistic fuzzy sets, Pattern Recogn. Lett.26 (2005), 2063–2069.10.1016/j.patrec.2005.03.018Suche in Google Scholar

[78] Z. Wang, K. W. Li and W. Wang, An approach to multiattribute decision making with interval-valued intuitionistic fuzzy assessments and incomplete weights, Inf. Sci.179 (2009), 3026–3040.10.1016/j.ins.2009.05.001Suche in Google Scholar

[79] G. W. Wei, Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting, Knowl.-Based Syst.21 (2008), 833–836.10.1016/j.knosys.2008.03.038Suche in Google Scholar

[80] G. W. Wei, Some geometric aggregation functions and their application to dynamic multiple attribute decision making in the intuitionistic fuzzy setting, Int. J. Uncertain. Fuzz. Knowl.-Based Syst.17 (2009), 179–196.10.1142/S0218488509005802Suche in Google Scholar

[81] G. W. Wei, Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making, Appl. Soft Comput.10 (2010), 423–431.10.1016/j.asoc.2009.08.009Suche in Google Scholar

[82] G. W. Wei, GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting, Knowl.-Based Syst.23 (2010), 243–247.10.1016/j.knosys.2010.01.003Suche in Google Scholar

[83] G. W. Wei, Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making, Expert Syst. Appl.38 (2011), 11671–11677.10.1016/j.eswa.2011.03.048Suche in Google Scholar

[84] G. W. Wei and X. Zhao, Some induced correlated aggregating operators with intuitionistic fuzzy information and their application to multiple attribute group decision making, Expert Syst. Appl.39 (2012), 2026–2034.10.1016/j.eswa.2011.08.031Suche in Google Scholar

[85] G. W. Wei and X. Zhao, Some dependent aggregation operators with 2-tuple linguistic information and their application to multiple attribute group decision making, Expert Syst. Appl.39 (2012), 5881–5886.10.1016/j.eswa.2011.11.120Suche in Google Scholar

[86] G. W. Wei, X. Zhao and R. Lin, Some induced aggregating operators with fuzzy number intuitionistic fuzzy information and their applications to group decision making, Int. J. Comput. Int. Syst.3 (2010), 84–95.10.1080/18756891.2010.9727679Suche in Google Scholar

[87] M. M. Xia and Z. S. Xu, Hesitant fuzzy information aggregation in decision making, Int. J. Approx. Reason.52 (2011), 395–407.10.1016/j.ijar.2010.09.002Suche in Google Scholar

[88] Z. S. Xu, Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making, Fuzzy Optim. Decis. Ma.6 (2007), 109–121.10.1007/s10700-007-9004-zSuche in Google Scholar

[89] Z. S. Xu, Models for multiple attribute decision making with intuitionistic fuzzy information, Int. J. Uncertain. Fuzz15 (2007), 285–297.10.1142/S0218488507004686Suche in Google Scholar

[90] Z. S. Xu, Intuitionistic fuzzy aggregation operators, IEEE Trans. Fuzzy Syst.15 (2007), 1179–1187.10.1109/TFUZZ.2006.890678Suche in Google Scholar

[91] Z. S. Xu, A survey of preference relations, Int. J. Gen. Syst.36 (2007), 179–203.10.1080/03081070600913726Suche in Google Scholar

[92] Z. S. Xu, Intuitionistic preference relations and their application in group decision making, Inf. Sci.177 (2007), 2363–2379.10.1016/j.ins.2006.12.019Suche in Google Scholar

[93] Z. S. Xu, J. Chen and J. Wu, Clustering algorithm for intuitionistic fuzzy sets, Inf. Sci.178 (2008), 3775–3790.10.1016/j.ins.2008.06.008Suche in Google Scholar

[94] Z. S. Xu, A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making, Group Decis. Negot.19 (2010), 57–76.10.1007/s10726-009-9164-zSuche in Google Scholar

[95] Z. S. Xu, A method based on distance measure for interval-valued intuitionistic fuzzy group decision making, Inf. Sci.180 (2010), 181–190.10.1016/j.ins.2009.09.005Suche in Google Scholar

[96] Z. S. Xu, Choquet integrals of weighted intuitionistic fuzzy information, Inf. Sci.180 (2010), 726–736.10.1016/j.ins.2009.11.011Suche in Google Scholar

[97] Z. S. Xu, Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators, Knowl.-Based Syst.24 (2011), 749–760.10.1016/j.knosys.2011.01.011Suche in Google Scholar

[98] Z. S. Xu and J. Chen, An overview of distance and similarity measures of intuitionistic fuzzy sets, Int. J. Uncertain. Fuzz16 (2008), 529–555.10.1142/S0218488508005406Suche in Google Scholar

[99] Y. Xu and H. Wang, Approaches based on 2-tuple linguistic power aggregation operators for multiple attribute group decision making under linguistic environment, Appl. Soft Comput.11 (2011), 3988–3997.10.1016/j.asoc.2011.02.027Suche in Google Scholar

[100] Z. S. Xu and M. Xia, Induced generalized intuitionistic fuzzy operators, Knowl.-Based Syst.24 (2011), 197–209.10.1016/j.knosys.2010.04.010Suche in Google Scholar

[101] Z. S. Xu and R. R. Yager, Some geometric aggregation operators based on intuitionistic fuzzy sets, Int. J. Gen. Syst.35 (2006), 417–433.10.1080/03081070600574353Suche in Google Scholar

[102] Z. S. Xu and R. R. Yager, Dynamic intuitionistic fuzzy multi-attribute decision making, Int. J. Approx. Reason.48 (2008), 246–262.10.1016/j.ijar.2007.08.008Suche in Google Scholar

[103] Z. S. Xu and R. R. Yager, Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group, Fuzzy Optim. Decis. Ma.8 (2009), 123–139.10.1007/s10700-009-9056-3Suche in Google Scholar

[104] Z. S. Xu and R. R. Yager, Intuitionistic fuzzy Bonferroni means, IEEE Trans. Syst. Man Cybern. B Cybern.41 (2011), 568–578.10.1109/TSMCB.2010.2072918Suche in Google Scholar PubMed

[105] W. Xu, J. Ma, S. Wang and G. Hao, Vague soft sets and their properties, Comput. Math. Appl.59 (2010), 787–794.10.1016/j.camwa.2009.10.015Suche in Google Scholar

[106] J. Ye, Multi-criteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment, Expert Syst Appl.36 (2009), 6899–6902.10.1016/j.eswa.2008.08.042Suche in Google Scholar

[107] J. Ye, Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets, Appl. Math. Model.34 (2010), 3864–3870.10.1016/j.apm.2010.03.025Suche in Google Scholar

[108] J. Ye, Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment, Eur. J. Oper. Res.205 (2010), 202–204.10.1016/j.ejor.2010.01.019Suche in Google Scholar

[109] J. Ye, Cosine similarity measures for intuitionistic fuzzy sets and their applications, Math. Comput. Model.53 (2011), 91–97.10.1016/j.mcm.2010.07.022Suche in Google Scholar

[110] D. J. Yu, Multi-criteria decision making based on generalized prioritized aggregation operators under intuitionistic fuzzy environment, Int. J. Fuzzy Syst.15 (2013), 47–54.Suche in Google Scholar

[111] D. J. Yu, Decision making based on generalized geometric operator under interval-valued intuitionistic fuzzy environment, J. Intell. Fuzzy Syst.25 (2013), 471–480.10.3233/IFS-120652Suche in Google Scholar

[112] D. J. Yu, Prioritized information fusion method for triangular intuitionistic fuzzy set and its application to teaching quality evaluation, Int. J Intell. Syst.28 (2013), 411–435.10.1002/int.21583Suche in Google Scholar

[113] D. J. Yu, Group decision making under interval-valued multiplicative intuitionistic fuzzy environment based on Archimedean t-conorm and t-norm, Int. J Intell. Syst.30 (2015), 590–616.10.1002/int.21710Suche in Google Scholar

[114] D. J. Yu, Intuitionistic fuzzy theory based typhoon disaster evaluation in Zhejiang Province, China: a comparative perspective, Nat. Hazard.75 (2015), 2559–2576.10.1007/s11069-014-1450-7Suche in Google Scholar

[115] D. Yu, A scientometrics review on aggregation operator research, Scientometrics105 (2015), 115–133.10.1007/s11192-015-1695-2Suche in Google Scholar

[116] D. J. Yu, Hesitant fuzzy multi-criteria decision making methods based on Heronian mean, Technological and Economic Development of Economy23 (2017), 296–315.10.3846/20294913.2015.1072755Suche in Google Scholar

[117] D. J. Yu and L. Fang, Intuitionistic multiplicative aggregation operators with their application in group decision making, J. Intell. Fuzzy Syst.27 (2014), 131–142.10.3233/IFS-130984Suche in Google Scholar

[118] D. J. Yu and D. F. Li, Dual hesitant fuzzy multi-criteria decision making and its application to teaching quality assessment, J. Intell. Fuzzy Syst.27 (2014), 1679–1688.10.3233/IFS-141134Suche in Google Scholar

[119] D. J. Yu and S. S. Shi, Researching the development of Atanassov intuitionistic fuzzy set: using a citation network analysis, Appl. Soft Comput.32 (2015), 189–198.10.1016/j.asoc.2015.03.027Suche in Google Scholar

[120] D. J. Yu and H. C. Liao, Visualization and quantitative research on intuitionistic fuzzy studies, J. Intell. Fuzzy Syst.30 (2016), 3653–3663.10.3233/IFS-162111Suche in Google Scholar

[121] D. J. Yu, Y. Y. Wu and T. Lu, Interval-valued intuitionistic fuzzy prioritized operators and their application in group decision making, Knowl.-Based Syst.30 (2012), 57–66.10.1016/j.knosys.2011.11.004Suche in Google Scholar

[122] D. Yu, D. F. Li and J. M. Merigó, Dual hesitant fuzzy group decision making method and its application to supplier selection, Int. J. Mach. Learn. Cyb.7 (2016), 819–831.10.1007/s13042-015-0400-3Suche in Google Scholar

[123] D. J. Yu, W. Y. Zhang and G. Huang, Dual hesitant fuzzy aggregation operators, Technol. Econ. Dev. Eco.22 (2016), 194–209.10.3846/20294913.2015.1012657Suche in Google Scholar

[124] D. J. Yu, D. F. Li, J. M., Merigó and L. C. Fang, Mapping development of linguistic decision making studies, J. Intell. Fuzzy Syst.30 (2016), 2727–2736.10.3233/IFS-152026Suche in Google Scholar

[125] D. J. Yu, Z. S. Xu, W. Pedrycz and W. R. Wang, Information Sciences 1968–2016: a retrospective analysis with text mining and bibliometric, Inf. Sci. (2017, in press), https://doi.org/10.1016/j.ins.2017.08.031. [Epub ahead of print].10.1016/j.ins.2017.08.031Suche in Google Scholar

[126] D. J. Yu, Z. S. Xu, Y. Kao and C. T. Lin, The structure and citation landscape of IEEE Transactions on Fuzzy Systems (1994–2015), IEEE Trans. Fuzzy Syst. (2017, in press), doi: 10.1109/TFUZZ.2017.2672732. [Epub ahead of print].10.1109/TFUZZ.2017.2672732Suche in Google Scholar

[127] L. A. Zadeh, Fuzzy sets, Inf. Control8 (1965), 338–353.10.1016/S0019-9958(65)90241-XSuche in Google Scholar

[128] W. Zeng and H. Li, Relationship between similarity measure and entropy of interval valued fuzzy sets, Fuzzy Set. Syst.157 (2006), 1477–1484.10.1016/j.fss.2005.11.020Suche in Google Scholar

[129] S. Zeng and W. Su, Intuitionistic fuzzy ordered weighted distance operator, Knowl.-Based Syst.24 (2011), 1224–1232.10.1016/j.knosys.2011.05.013Suche in Google Scholar

[130] H. Zhao, Z. S. Xu, M. Ni and S. Liu, Generalized aggregation operators for intuitionistic fuzzy sets, Int. J Intell. Syst.25 (2010), 1–30.10.1002/int.20386Suche in Google Scholar

[131] L. Zhou and W. Z. Wu, On generalized intuitionistic fuzzy rough approximation operators, Inf. Sci.178 (2008), 2448–2465.10.1016/j.ins.2008.01.012Suche in Google Scholar

[132] W. Zhou and Z. S. Xu, Asymmetric hesitant fuzzy sigmoid preference relations in the analytic hierarchy process, Inf. Sci.358 (2016), 191–207.10.1016/j.ins.2016.04.003Suche in Google Scholar

[133] B. Zhu, Z. Xu and M. Xia, Dual hesitant fuzzy sets, J. Appl. Math.2012 (2012), Article ID 879629, 13 pages, http://dx.doi.org/10.1155/2012/879629.10.1155/2012/879629Suche in Google Scholar

Received: 2017-05-23

Published Online: 2017-09-11

Published in Print: 2019-09-25

This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Artikel in diesem Heft

https://doi.org/10.1515/jisys-2017-0240

Schlagwörter für diesen Artikel

Intuitionistic fuzzy; bibliometrics; Web of science; citation

Creative Commons

BY-NC-ND 3.0