High-temperature diffraction experiments and phase diagram of ZrO₂ and ZrSiO₄

2.1 Sample preparation

We used ZrSiO₄ and ZrO₂ powder reagents of 99.9% purity (Furu-uchi Chem. Cltd). For diffraction experiments, the pure ZrSiO₄ and ZrO₂ powders, a ZrSiO₄-platinum mixture and a ZrO₂-platinum mixture were used. The platinum mixtures were obtained by adding 20 wt% Pt. The pure powders and mixtures were pressed into cylindrical shape and sintered at T = 1400–1550 °C for 24 h. The sintered samples were shaped into a sphere with a diameter of 2 mm.

2.2 High-temperature diffraction experiments

High-temperature angular dispersive diffraction experiments of ZrSiO₄ and ZrO₂ were carried out at the BL04B2 beamline at the SPring-8 synchrotron radiation facility, using the laser heating and aerodynamic levitation technique [27], [28], [29]. The energy of the incident X-rays was 61.4 KeV (BL04B2). Each diffraction pattern was measured within about 3 min to avoid grain growth at high-temperature. A two-dimensional IP detector was used and diffraction profiles in wide azimuth angles were projected onto one dimension for Rietveld analysis. Using the Rietveld analysis program [31], we simulated a powder diffraction pattern of each specimen. The sample was set in a shallow nozzle where the sample was aerodynamically levitated. The levitated sample was then heated by a 100-W CO₂ laser. The temperature of the sample was monitored by a two-color pyrometer. The temperature was calibrated using the melting temperatures of ZrO₂ (2715 °C) and Al₂O₃ (2072(10) °C). Although error values on the experimental device are within 5 K, temperature fluctuations of about ±30 K were observed due to rotation of the spherical samples. Platinum was also used for temperature calibration for the diffraction experiments in the medium temperature range [29]. The unit cell parameters and volumes of pure ZrSiO₄, tetragonal and cubic ZrO₂ were determined as a function of temperature. High-temperature XRD experiments for ZrSiO₄ in the range from room temperature to 1200 °C were carried out at the Institute for Material Research, Tohoku University, Sendai, Japan. XRD powder patterns were measured using CuKα radiation at 40 kV and 20 mA by using a Rigaku Ultima III X-ray diffractometer and a high-temperature furnace. The temperature was calibrated using the thermal expansion ratio of α-Al₂O₃. Figure 1 shows the experimental results using synchrotron radiation and the aerodynamic levitation technique (data labeled “synchro”) and the laboratory diffraction methods (data labeled “lab”).

Figure 1:

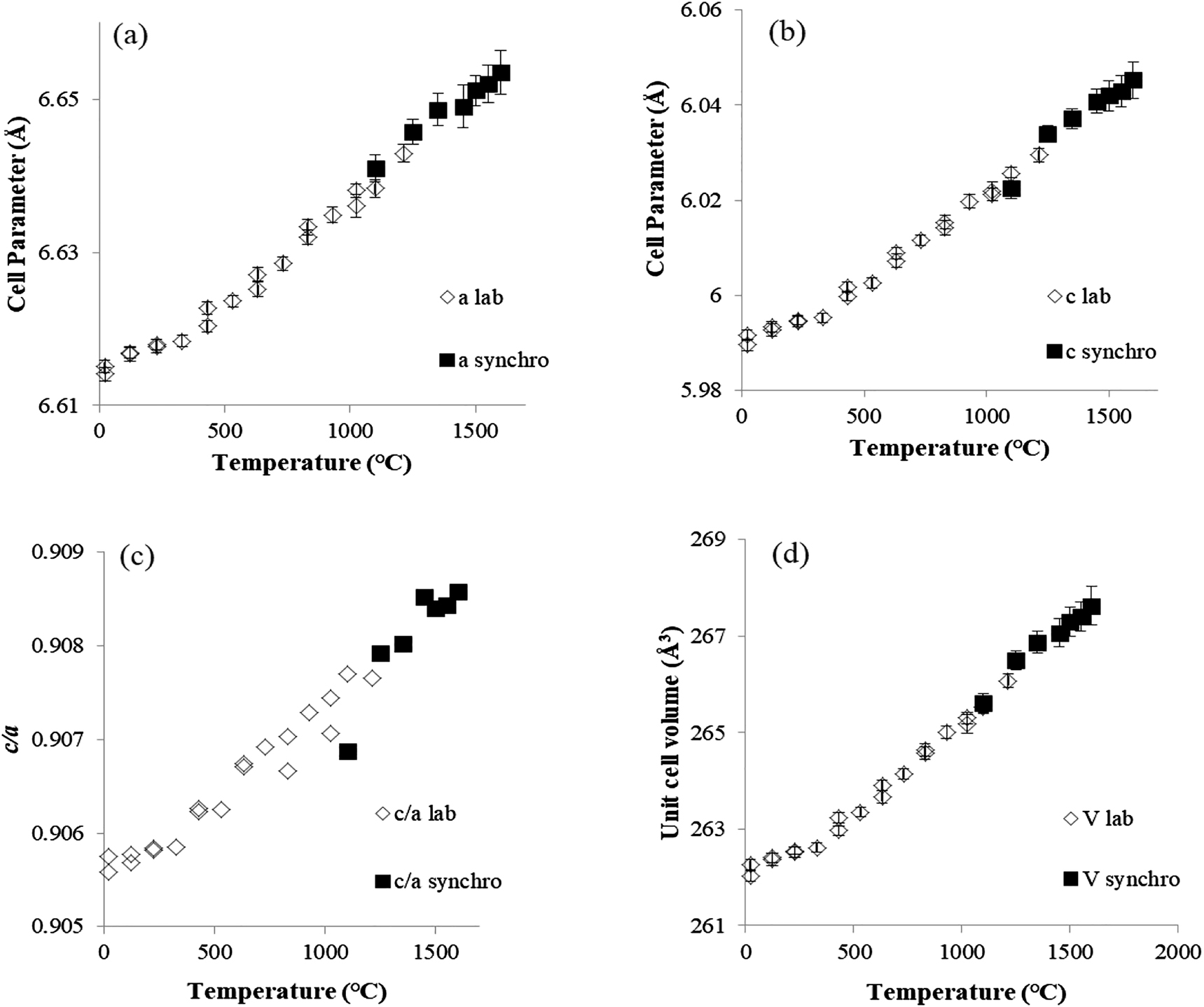
Temperature dependencies of unit cell parameters a (a) and c (b), c/a ratios (c) and unit cell volumes for ZrSiO₄ (d). Open diamonds and solid squares show the results using the laboratory diffraction method (lab) and the aerodynamic levitation technique at the synchrotron facility (synchro), respectively.

3.1 Temperature dependence of unit cell parameters and phase transitions of ZrSiO₄ and ZrO₂

The unit cell parameters, c/a ratios and unit cell volumes for ZrSiO₄ (space group I4₁/amd and Z = 4), tetragonal ZrO₂ (space groupe P4₂/nmc and Z = 2), and cubic ZrO₂ (space group F m 3   ‾ m and Z = 4) have been obtained at high-temperature. Powder XRD patterns indicate the decomposition of ZrSiO₄ to ZrO₂ and SiO₂ and the phase transition of ZrO₂ (Figure 2). The diffraction peaks of the cubic phase are not smooth, affected by the large grain growth. Each diffraction peak becomes rough with one-dimensional projection of spotty large intensity reflection points. The diffraction spots became larger because the diffraction center positions of the large grain size crystals were dispersed by the rotational motion of the specimen [29]. The unit cell parameters and volumes and c/a ratios of ZrSiO₄ and ZrO₂ are shown in Figures 1 and 3. A discontinuous change in unit cell parameters for ZrSiO₄ is not observed (Figure 1) and the c/a ratios for ZrSiO₄ increase with temperature (Figure 1c). The thermal expansion coefficient for the a axis direction is smaller than that for the c-axis direction, especially in ZrSiO₄, whereas the discontinuous change is observed in the unit cell parameters c for ZrO₂ (Figure 3a). ZrSiO₄ and ZrO₂ have different thermal expansion characteristics. The increase rates of the volumes of ZrSiO₄ and ZrO₂ are 0.11 and 0.13 Å³ per 100 K, respectively, the difference between both of which values is large. Thus it can be inferred that the sintered materials of ZrSiO₄ and ZrO₂ are probably weak against thermal stress. The boundary of these sintered materials should be easily cracked.

Figure 2:

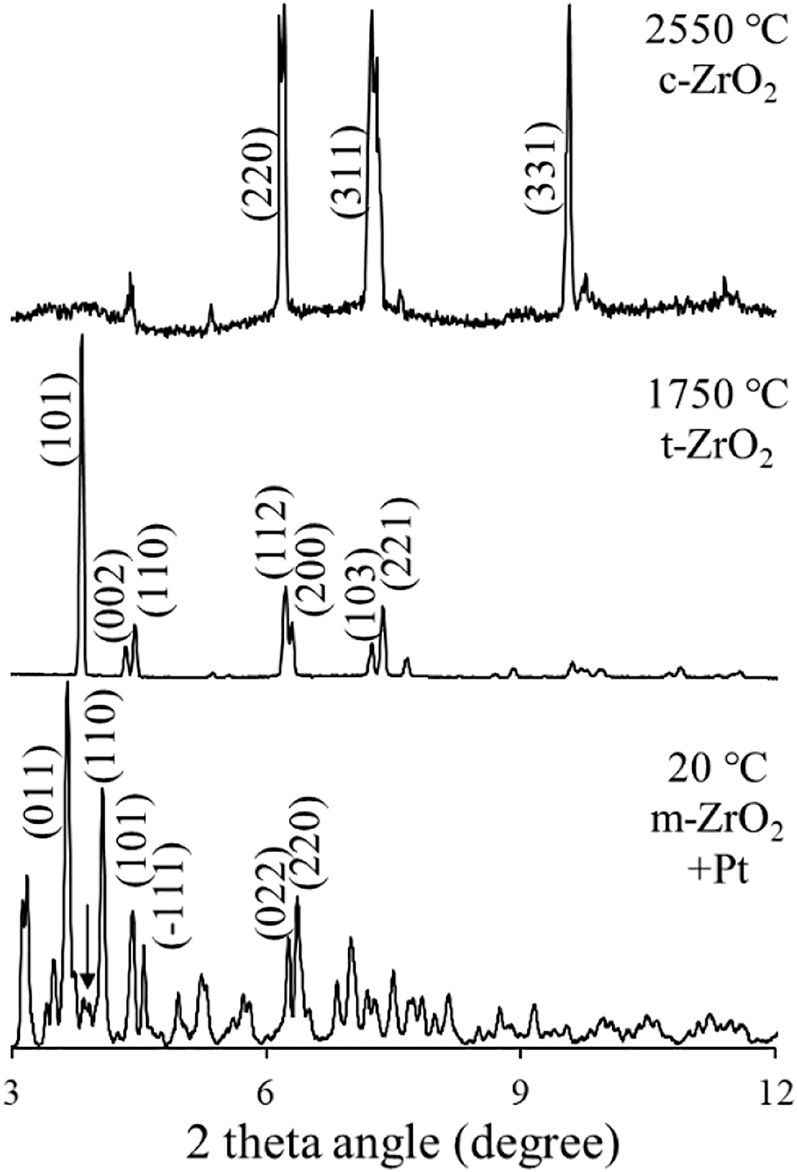
XRD patterns of ZrO₂ at various temperatures with representative indices (ZrO₂ monoclinic phase at 20 °C, tetragonal phase at 1750 °C and cubic phase at 2550 °C). The wavelength λ is 0.2019 Å.

Figure 3:

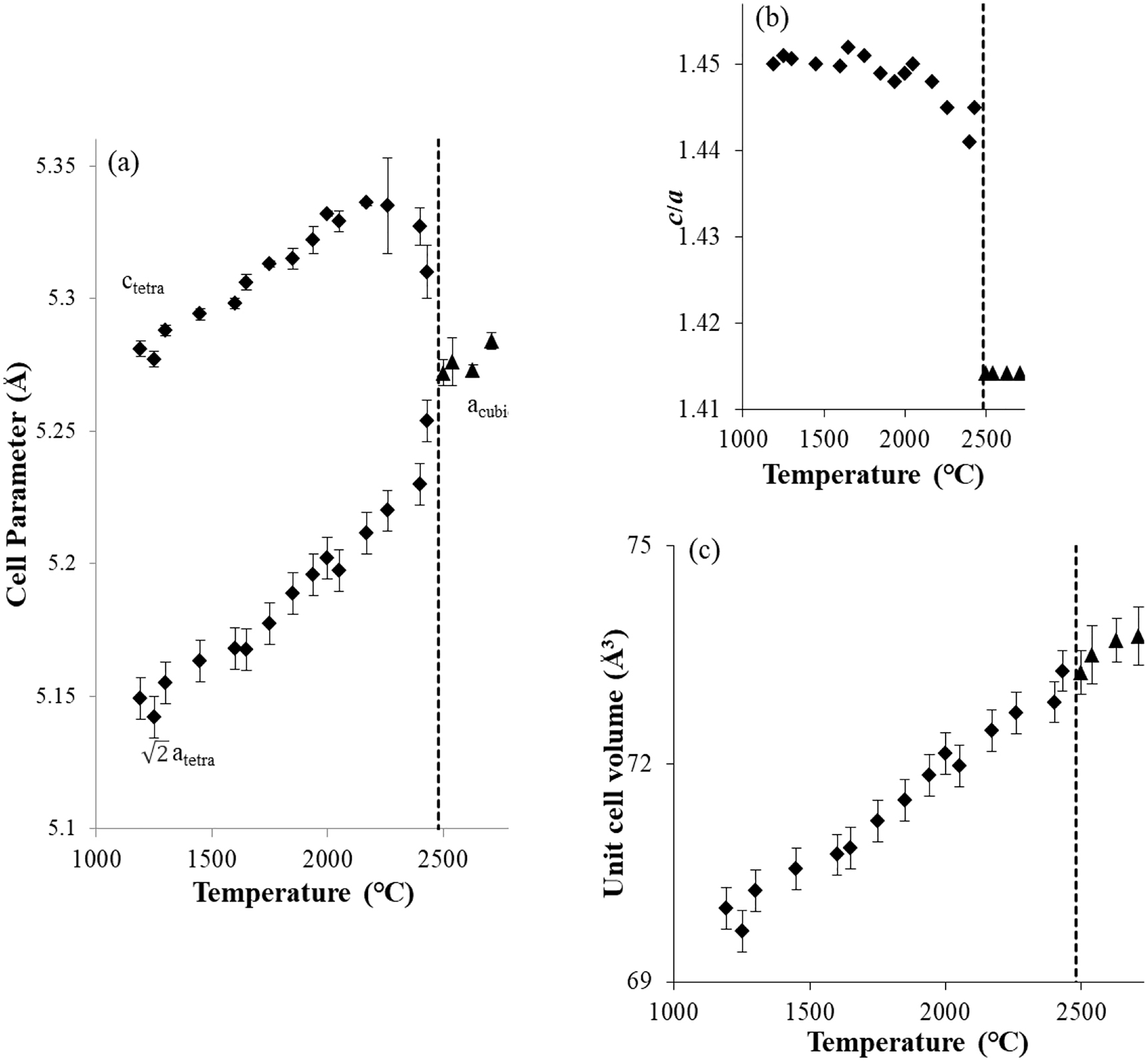
Temperature dependencies of unit cell parameters 2 a and c for pure ZrO₂ (a), c/a ratios for pure ZrO ₂ (b), and unit cell volumes for pure ZrO₂ (c). The diamonds and triangles represent the tetragonal and the cubic phase of ZrO₂, respectively.

The transition temperature of ZrO₂ from the tetragonal to the cubic phase is specified between 2430 and 2540 °C (Figure 3). The pre-transition behavior becomes obvious from around 2200 °C on in terms of expansion of the a axis and contraction of the unit cell parameter c. This phenomenon starts from considerably lower temperature than the phase transition points. A similar observation was made for HfO₂, which starts from around 1900 °C [29]. In ZrO₂, this change starts at a higher temperature and the temperature range of this behavior is narrower than in HfO₂.

A decrease of the unit cell volume has been observed at the transition point from the monoclinic phase to the tetragonal phase. The monoclinic-to-tetragonal phase boundary has a negative slope in the P-T phase diagram [1], [2], [3]. The slope of the coexistence line can be estimated based on the Clausius–Clapeyron equation, dP/dT = ΔS/ΔV. ΔV of ZrO₂ is negative because the high-temperature tetragonal phase has a higher density than the low temperature monoclinic phase. The tetragonal-to-cubic phase boundary remains unobserved in the P-T phase diagram although the phase boundary is assumed to be negative. A clear unit cell volume change is not observed at the transition point from the tetragonal to the cubic phase (Figure 3c). We propose from this observation that the slope of the phase boundary from the tetragonal to the cubic phase is not negative (Figure 4). In the P-T phase diagram of ZrO₂ proposed so far, the phase boundary from the tetragonal to the cubic phase has been shown with a negative slope. In-situ high pressure and high-temperature experiments [3] revealed that the tetragonal phase is stable up to the melting temperature below 12.5 GPa, and that there is no cubic phase in the high-temperature regime. The stoichiometric ZrO₂ does not show the cubic structure up to the melting temperature under high pressure. The phase boundary from tetragonal-to-cubic may have a positive slope. According to Ohtaka et al. [3], we propose a revised phase diagram (Figure 4) assuming that the cubic phase does not have a region extending into the high pressure range.

Figure 4:

Proposed P-T phase relationship for ZrO₂ based on the presented experiments and in-situ high pressure and high-temperature measurements [1], [2], [3]. The gray diamonds and black triangles represent the tetragonal and the cubic phase of ZrO₂, respectively.

3.2 Chemical composition and phase diagram in the ZrO₂-SiO₂ system

All recovered samples in our experiments were of pure white color, which excludes oxygen deficiency. Platinum powder gathered in small metal spheres. A representative SEM image of the quenched glass sample of the ZrSiO₄ melt at 1800 °C is shown in Figure 5. The volume ratio of glass to ZrO₂ crystals is relatively low in the lower temperature region after melting of zircon, whereas the volume ratio of glass increases at higher temperatures. The observed glass regions in the samples were less than 10 μm in width (Figure 5). The electron beam size for energy-dispersive X-ray spectrometry (EDS) analysis is 1 μm and the X-ray excitation region of the analytical point is larger than the beam size. Since the size of the measured points is mostly around 5 μm, the influence of fluorescent X-ray from the surrounding ZrO₂ gives a higher content of Zr than is really present depending on the location. The analytical ratios of SiO₂ to ZrSiO₄ are shown in Figure 6. The analytical ratios with the highest Si content at a temperature below 2200 °C are consistent with the liquidus curve. Considering the reaction time of solid and liquid and the effect of X-ray fluorescence from the surrounding ZrO₂, almost the same liquidus curve can be drawn between 1700 and 2200 °C. At 2300 and 2400 °C, we could not observe any liquid immiscibility area, as was proposed by Butterman and Foster [15]. The highest Si contents in glass are 53.3 and 49.1% for samples quenched from 2300 to 2400 °C, respectively, which are in the liquid immiscible area. The liquidus line in our phase diagram is basically consistent with the phase diagram proposed by Butterman and Foster [15] without a two liquids immiscible area. This area of two immiscible liquids at 2250–2430 °C, which is higher than the vaporization temperature of SiO₂, may have been proposed from the observation of compositional fluctuations in glass due to volatilization of the SiO₂ component from the liquid. We propose a new ZrO₂–SiO₂ phase diagram (Figure 6) based on the transition point of tetragonal-to-cubic ZrO₂ and the chemical analyses of the quenched glass.

Figure 5:

The representative SEM image of the quenched glass sample from ZrSiO₄ melt at T = 1800 °C. Dark and bright areas are glass and ZrO₂ crystals, respectively.

Figure 6:

Proposed phase diagram of the SiO₂–ZrO₂ system revised from Butterman and Foster [15]. The diamonds represent the chemical composition of quenched glasses obtained from several analytical points of recovered samples.