Ferromagnetism in Fe_3−x−yNi_xGeTe₂

1 Introduction

Metallic compounds with quasi two-dimensional crystal structures and itinerant magnetism attract considerable interest [1, 2]. In contrast to localized magnetism of unpaired electrons in 3d or 4f shells, itinerant magnetism is not an atomic phenomenon but caused by correlations between the conduction electrons. Magnetic fluctuations occurring in such itinerant magnetic systems are currently believed to be one key to unconventional superconductivity [3, 4]. Therefore the search for new materials with weak itinerant magnetism is well underway. A compound of recent awakening interest is the telluride Fe₃GeTe₂ which is metallic and ferromagnetic below T_C = 230 K with a relatively low saturation moment of 1.2 μ_B per iron atom [5]. Recent more detailed studies [6, 7] revealed strongly anisotropic ferromagnetism with moments aligned along the c axis as expected from the pronounced two-dimensional character of the crystal structure. Interestingly, the analogous nickel compound Ni₃GeTe₂ shows no magnetic ordering but is a Pauli paramagnetic metal [5]. In contrast to Fe₃GeTe₂, the nickel compound shows significant electron density in the van der Waals gap between the tellurium layers in the crystal structure. The partial occupancy of the additional site is accompanied by a nickel deficiency in the NiGe hexagons. Due to the differences in the magnetic behavior of the iron and nickel compounds interesting properties of the solid solutions Fe_3−xNi_xGeTe₂ are conceivable. These could occur if magnetic fluctuations persist while the ordering is suppressed. Furthermore Fe₃GeTe₂ has a composition range according to Fe_3−yGeTe₂ which also affects the Curie temperature [8]. Here we study the crystal structures and magnetic properties of the iron-deficient compounds Fe_3−yGeTe₂ and the solid solutions Fe_3−x−yNi_xGeTe₂.

2 Experimental section

Polycrystalline samples of Fe_3−yGeTe₂ with nominal y = 0, 0.2, 0.4 and Fe_3−x−yNi_xGeTe₂ with nominal x = 0.25, 0.5, 0.75, 1.0, 1.5 and y = 0.1 were synthesized from Fe, Ni, Ge and Te powder in alumina crucibles sealed in silica ampoules under argon atmosphere. In a first step the stoichiometric mixture was heated up to 898 K at a rate of 100 K h⁻¹ and kept at this temperature for 60 h. After cooling at a rate of 100 K h⁻¹ or 200 K h⁻¹ the samples were ground in a mortar and – except for Fe_3−yGeTe₂ with nominal y = 0.2 and 0.4 – sintered at 973 K for 60 h with a heating and cooling rate of 100 K h⁻¹, respectively. For nominal Fe_2.8GeTe₂ the sintering step was carried out like the first one.

X-ray powder diffraction analysis of the samples was performed on a STOE STADI P diffractometer using MoK_α1 radiation. Rietveld refinements were done using the Topas program package [9]. Energy-dispersive spectroscopy measurements were performed on a ZEISS EVO-MA 10 microscope. Data was collected using a BRUKER X-Flash 410-M detector and the software Quantax 200. Magnetic measurements of the powder samples were carried out with a Quantum Design SQUID-Magnetometer MPMS XL-5. Neutron powder diffraction analysis was realized at the Laboratory for Neutron Scattering and Imaging at the Paul Scherrer Institute (Villigen, Switzerland) with the High-Resolution Powder Diffractometer for Thermal Neutrons. Data was collected with a wavelength of 188.570 pm at 3–300 K. Data refinement was done with the Jana2006 program package [10].

3 Results and discussion

3.1 Crystal and magnetic structure

The crystallographic data obtained from Rietveld refinements of X-ray and neutron diffraction patterns are fully consistent with those given in refs. [5, 7]. Neutron patterns at 3 K and 300 K are shown in Fig. 1. Small impurities of Fe_2.25Te₂ (1.0 wt %) and Fe₃O₄ (0.8 wt %) are identified by Rietveld analysis. Fe₃GeTe₂ crystallizes in the hexagonal space group P6₃/mmc in its own structure type (Fig. 2), which contains Fe₃Ge layers similar to those present in Fe₂Ge [8, 9]. Fe₂Ge can be derived from the AlB₂-type structure with planar FeGe hexagons separated by additional iron atoms (Fe[FeGe]). Fe₂Ge is not stoichiometric but iron-deficient according to Fe_2−xGe (x ≈ 0.1–0.5) with Fe vacancies on the Fe2 site in the FeGe hexagons as it is the case in Fe_3−yGeTe₂. The Fe₃Ge sheets are well separated by a double layers of tellurium atoms at an interlayer distance of 815 pm.

Fig. 1:

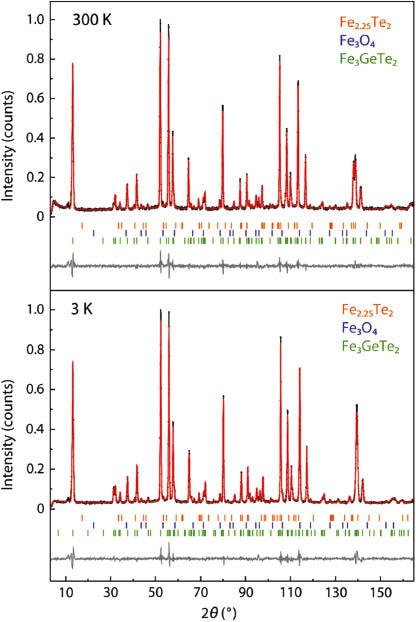
Neutron diffraction patterns (λ = 188.57 pm) of Fe₃GeTe₂ at room temperature and at 3 K with Rietveld fits.

Fig. 2:

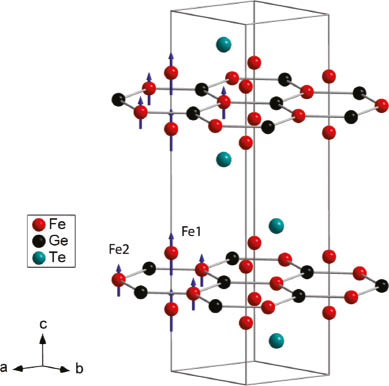
Crystal structure of Fe₃GeTe₂ with magnetic moments (μ_Fe1 = 1.75(6) μ_B, μ_Fe2 = 1.07(16) μ_B) aligned ferromagnetically along the crystallographic c axis.

The compositions of the samples Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂ were determined by EDX measurements. Samples of Fe_3−yGeTe₂ are homogeneous up to Fe_2.7GeTe₂. The iron vacancies cause a shrinking of the unit cell volume through smaller lattice parameters a even though the c axis increases slightly (Table 1, Fig. 3). Further reduction of the iron content down to 1.33 is possible by substitution with nickel. The lattice parameters a, c and the cell volumes of the solid solution Fe_3−x−yNi_xGeTe₂ decrease continuously but with smaller slopes than in Fe_3−yGeTe₂ because iron vacancies are now filled with nickel atoms. We point out that no nickel atoms are found in the van-der-Waals gap in our Fe_3−x−yNi_xGeTe₂ samples up to x = 1.32, as it is the case for the pure nickel compound Ni₃GeTe₂ [5].

Table 1

Lattice parameters a and c, unit cell volumes V, Curie temperatures T_C and saturation magnetizations μ^sat of Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂.

y (± 0.05)	x (± 0.05)	a (pm) (± 0.07)	c (pm) (± 0.3)	V (nm3) (± 0.0005)	TC (K) (± 1)	μsat (μB) (± 0.05 μB)
0.08	0	402.7	1632.8	0.2293	229	1.56
0.14	0	399.0	1636.0	0.2260	208	1.39
0.29	0	395.6	1639.5	0.2222	153	0.85
0.14	0.24	399.5	1630.9	0.2254	158	1.43
0.29	0.41	398.1	1629.6	0.2236	108	1.22
0.14	0.73	396.5	1627.4	0.2215	49	0.89
0.41	0.89	395.4	1625.2	0.2200	30	0.55
0.35	1.32	393.9	1620.2	0.2177	22	0.38
0.21	2.79	390.2	1602.2	0.2113	–	–

Fig. 3:

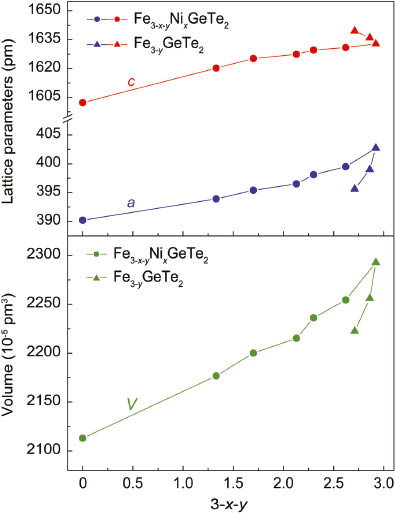
Lattice parameters (top) and unit cell volumes (bottom) of Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂.

3.2 Magnetic properties

The top panel of Fig. 4 shows magnetic susceptibilities of Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂ measured from 300 to 2 K at 20 kOe external fields (1 kOe = 7.96 × 10⁴ A m⁻¹). The zero points of the second derivatives (d2χdT2) reveal ferromagnetic Curie temperatures (T_C) which decrease continuously with the iron content from 229 K in Fe_2.92GeTe₂ down to 22 K in Fe_1.33Ni_1.32GeTe₂ (see Table 1). Thus magnetic ordering becomes successively suppressed as the iron vacancy concentration or the nickel content increases and is hardly detectable in Fe_1.33Ni_1.32GeTe₂. Isothermal magnetizations at 1.8 K confirm ferromagnetic ordering and the continuous decrease of the saturation moments from 1.56 μ_B in Fe_2.92GeTe₂ to 0.38 μ_B in Fe_1.33Ni_1.32GeTe₂ (Fig. 4 bottom). Coercive fields are small with values between 0.2 and 0.7 kOe which indicate that the materials are soft ferromagnets.

Fig. 4:

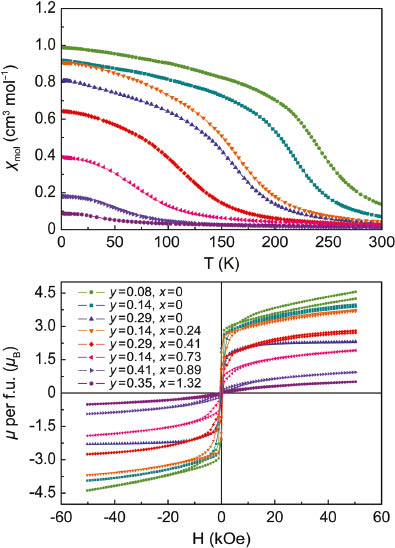
Magnetic susceptibilities measured at 20 kOe (top) and isothermal magnetizations at 1.8 K (bottom) of Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂.

The ferromagnetism of these compounds in terms of T_C and μ^sat is not proportional to the valence electron count but depends on the iron concentration, as depicted in Fig. 5. Nickel remains non-magnetic as it is known from other nickel tellurides with layered structures which are exclusively Pauli paramagnetic metals [5, 10, 11]. The suppression of magnetic ordering turns out to be more efficient by introducing iron vacancies. However, this is only possible up to Fe_2.7GeTe₂ where the ferromagnetism is still present.

Fig. 5:

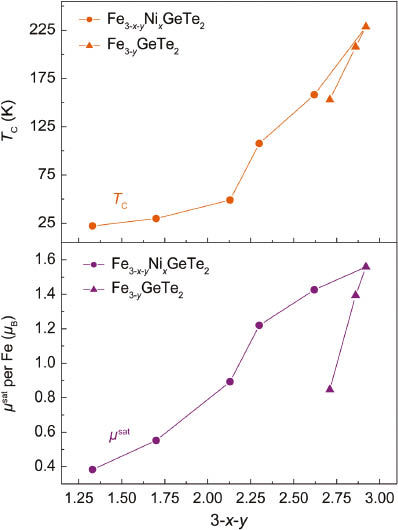
Curie temperatures T_C (top) and saturation magnetizations μ^sat (bottom) of Fe_3−yGeTe₂ and Fe_3−x−yNi_xGeTe₂ against the iron concentration.

4 Conclusion

Ferromagnetism in the compounds Fe_3−x−yNi_xGeTe₂ is suppressed through random dilution of the magnetic iron atoms by either vacancies (most efficient) or by non-magnetic nickel atoms. The Curie temperatures as well as the saturation moments decrease continuously as the magnetic coupling between the iron atoms becomes weaker. Similar suppression of magnetic ordering has also been observed in other layered tellurides, for example Fe_1.1−xNi_xTe (x = 0.02, 0.04, 0.08, 0.12) [12], as well as in the diluted antiferromagnet Mn_xZn_1−xPS₃ [13].