Lead phosphate oxyapatite, Pb₁₀(PO₄)₆O, with c-double superstructure

2.1 Sample preparation and characterization

PPO single crystals were grown from melt of a mixture of PbO (99.5 %; FUJIFILM Wako Pure Chemical Co., Japan) and NH₄H₂PO₄ (99.0 %; FUJIFILM Wako) reagents with a molar ratio of 2:1. The mixture was ground in an agate mortar and wrapped with a platinum foil to suppress evaporation of P₂O₅ component. The wrapping was then put in a latex balloon and hydrostatically pressed in water for several hours (500–600 kgf/cm²). The wrapping was encased in an alumina crucible with a lid, set inside a saggar and heated in air in an electric furnace. Preparation conditions were optimized by referring to thermogravimetry/differential thermal analysis (TG/DTA) and powder X-ray diffraction (pXRD) profiles. An association of Pb₄O(PO₄)₂ with PPO ¹¹ was allowed for the product.

TG/DTA data of the mixture were collected with a Rigaku ThermoPlus TG 8120 on both heating and consecutive cooling cycles (ΔT/min = 7 °C on both cycles) operated under air atmosphere. No inert gas-flow was applied to prevent unnecessary evaporation of P₂O₅ component. Maximum temperature was set at 1000 °C. TG/DTA profiles showed an endothermic peak at 945 °C on the heating cycle and consecutive weight loss (Figure 1). This weight loss lasted until T ≈ 800 °C on the cooling cycle. Exothermic peaks at 924 °C and 884 °C were apparent on the cooling cycle. The samples with various cooling conditions were examined with pXRD, and Pb₄O(PO₄)₂ predominated in most of the samples. Since the target compound was the majority phase only in the sample quenched from 920 °C, exothermic peaks at 924 °C and 884 °C correspond to crystallization of PPO and Pb₄O(PO₄)₂, respectively.

Figure 1:

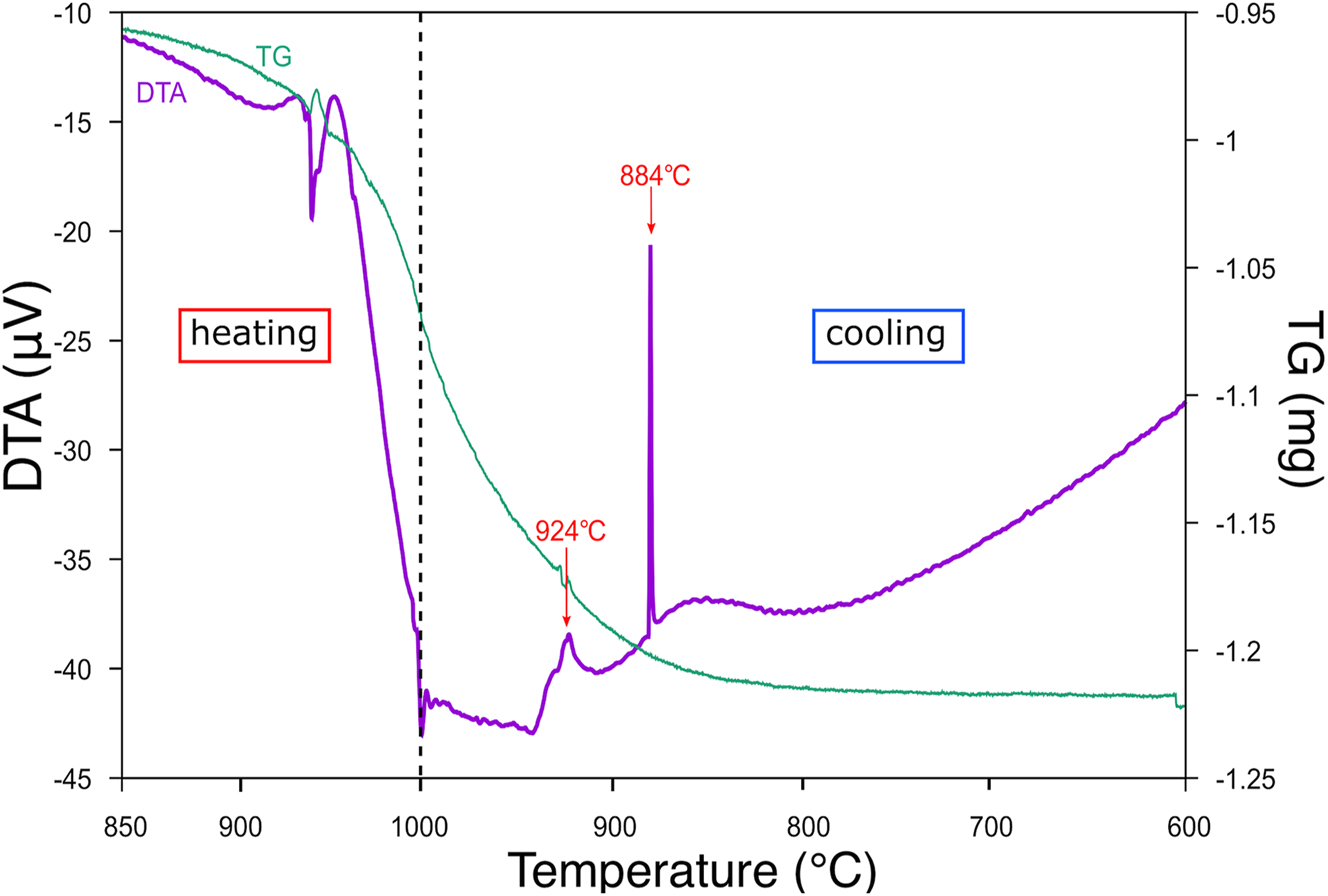
TG/DTA profiles of mixture of PbO and NH₄H₂PO₄ over 120−200 min. Purple line: DTA profile; green line: TG profile.

On preparations of the single crystal specimens used in the following experiments, the temperature was raised from room temperature to 1000 °C in 1 h. Temperature was slowly lowered to 920 °C at a rate of 1.2 °C/h, held at this temperature for 25 h, and then the crucible was taken out from the furnace and the wrapping was quenched by dropping it into water (batch 12). Preservation of a high temperature state of PPO was expected since the specimen was quenched together with a platinum foil within 15 s after opening the saggar. Slowly cooled specimens were also prepared for comparisons with cooling rate of 3 °C/h to 800 °C and then 20 °C/h to 500 °C (batch 9) or 6 °C/h from 1000 °C to 500 °C (batch 8). After that the furnace was cooled down by turning the power off. Quantitative chemical analyses (a JEOL JSM-6010LV with integrated EDS) showed no sign of Pb-deficiency and thus the empirical chemical formula of the specimens was Pb₁₀(PO₄)₆O.

Single-crystal specimens were picked out under polarizing optical microscope and examined with a Weissenberg camera and Cu Kα radiation (Figure 2). Ni-foil was used as a β-filter. On all the specimens there were apparent c-double superstructure reflections on the rotation photographs (rotated around c), and presence of mirror symmetry normal to the rotation axis was also apparent. On the other hand, diffraction spots on the 1st-layer Weissenberg photograph of a specimen from batch 8 could be successfully indexed with a and γ of the parent structure.

Figure 2:

Rotation photograph of specimen from batch12 (rotated 20° around c) using a Weissenberg camera. Cu Kα radiation and Ni-filter was used. Superstructure reflections were indicated by red arrows.

2.2 Data collection and data processing

High absorbance of Pb for X-ray and thus low diffraction intensities are intrinsic problem on X-ray investigations of Pb-bearing compounds. Therefore, complete data sets were collected on two specimens of different thermal histories to check if there was noteworthy difference on two refined structures. Specimens used on the following measurements were ground into spheres (d = 170 μm and 140 μm for specimens from batches 12 and 9, hereafter referred to as b12s2 and b9s1, respectively). The intensities of Bragg reflections and values of θ were measured on a Rigaku AFC-5S automated four-circle diffractometer. Graphite-monochromatized Mo Kα radiation and the ω-2θ scan method were employed for the data collection with scan width 1.5° + 0.35 tanθ and scan speed of 4° min⁻¹. Diffraction intensities of three standard reflections were monitored after every 200 reflections. Totals of 41092 reflections up to 2θ = 90° (b12s2) and 30861 reflections up to 2θ = 80° (b9s1) were measured for the full sphere of reciprocal space. Relationships found among Bragg positions and observed intensities from the parent lattice suggested Laue group 6/m. Possible space groups for superstructure will be discussed more rigorously in the next chapter. The least-squares fitting of the peak positions of 25 intense reflections in the range 43.2° < 2θ < 47.5° resulted in the cell dimensions a = 9.8151(15) Å and c = 14.8458(11) Å for b12s2 after calibration with Si. ¹⁵ Cell dimensions for b9s1, a = 9.8178(12) Å and c = 14.8478(10) Å, matched to the values within their combined standard uncertainties (s.u.s) (σ). See Table 1 for further crystallographic details and experimental conditions.

The intensity data were converted to |F_obs| and their s.u.s after applying Lorentz, polarization and spherical absorption corrections (μr = 5.81 for b12s2). These structure amplitudes were averaged for the Laue group to be assumed at respective structure refinement. Some weak [|F̄_obs| < 3σ(F̄_obs)] and ill-behaved (|F_obs|_max > 2.0|F_obs|_min among equivalents) reflections were removed from the data sets for respective point group to be assumed.

3.1 P6₃/m refinement of the parent structure

The structure was refined firstly in aristotype apatite structure with reindexed diffraction data as a foundation of the superstructure models. The least-squares program LSGCEX ¹⁶ was used for structure refinements with variables including one scale and one isotropic extinction factor (type I with the Lorentzian mosaic spread). ¹⁷ A simple weighting scheme with weights proportional to σ⁻² was employed. Conditions for structure refinements, such as choice of form factors, application of low-angle threshold for diffraction data, and applicable restraints in the superstructure refinements were also examined at this step. The refinement started from the atomic coordinates and anisotropic displacement parameters (ADPs) given for Pb₅(PO₄)₃Cl (OP-4 in ref. 5]) for the host structure and the z-coordinate of the X site with ADPs given in ref. 11]. Neutral form factors and low-angle threshold for diffraction data (0.25 ≤ sinθ/λ) were employed after examinations noted in ref. 5]. Neutral form factors for respective atoms and their anomalous dispersion terms were taken from International Tables for Crystallography, Vol. C. In the final iterations the occupation factor at the X site was fixed at 1/4 and all the other atomic sites were assumed fully occupied by respective elements. The least-squares calculation converged at R(F), R(F²) and wR(F) = 0.026, 0.037 and 0.029, respectively, for 538 independent reflections with 41 parameters. Minimum and maximum of Δρ were −3.10 e Å⁻³ at (0.01, 0.23, 0.75) and 4.39 e Å⁻³ at (0.99, 0.79, 0.81), respectively. Selected structural parameter values are listed in Table 3.

There was no notable difference between our structure and previously reported one for the parent structure. ¹¹ As can be seen in Table 3, mean square displacements (MSDs, <u²> Ų) of P⁵⁺ at B site were small and even smaller than those of Pb²⁺ at A sites in spite of their weights. Displacement ellipsoid at A2 site [at (0.00169(8), 0.24288(8), 1/4)] was larger and more anisotropic than that in OP-4; MSDs at the site were 1.3 and 3.2 times larger along <001> and <010>, respectively, in PPO and as a result the ellipsoid was flat in the yz-plane. These larger displacements, particularly along <010>, implies that the 2 × c modulation occurred in sizes of A2 triangles.

3.2 P 3 ‾ refinement of superstructure

The P 3 ‾ unit cell was taken by doubling c of the parent structure with no shift of origin. Abbreviations of atomic sites referred to the parent structure, i.e. A1a – A1d sites in P 3 ‾ structure correspond to the A1 site in the parent structure and these four sites will be referred to as ‘A1 sites’ when no distinction is needed. All the atomic sites in the host structure were assumed fully occupied from the considerations in §3.1. Displacements at O1–O3 sites were set isotropic and constrained to be equal for stable least-squares cycles. The same constraint applied on B sites. No further constraint or restraint was applied in the following calculations, except as noted. The P 3 ‾ refinement was started from the positional parameters and U_eq values (average for O1–O3) after the P6₃/m refinement except the X site. In the early stages of the refinement the X site was set vacant to find their locations as positive residuals in the channel. Displacement parameters at A sites were expanded to ADPs after convergence of the calculations with U_iso. The calculation with ADPs converged at R(F), R(F²) and wR(F) = 0.093, 0.098 and 0.117, respectively, for 1589 independent reflections with 64 parameters. Minimum and maximum of Δρ were −14.64 e Å⁻³ at (0.00, 0.95, 0.39) and 13.99 e Å⁻³ at (0.99, 0.79, 0.39), respectively. Similarly prominent (|Δρ| > 13 e Å⁻³) positive and negative residuals were found inside the A2 triangles around the c-axis. However, no particular positive residual attributable to presence of oxide anion was found on the axis.

In the next step oxide anions were introduced in the channel (at Wyckoff positions 1a, 1b and 2c) and refined the positions, ADPs, and their partitioning when necessary. Total number of channel site oxide anions was restrained to be 2.0. ADP values at X sites were taken from SrPr₄(SiO₄)₃O ¹⁸ and refined at final iterations. We examined all the possible X site positions and their combinations, and a structure with fully occupied X site at z = 0.192(15) was the only structure which yielded convergence of least-squares calculations with ADPs. The ADP ellipsoid at the X site was highly elongated along <001> as it was seen after P6₃/m refinement.

Sizes of A2 triangles in the refined P 3 ‾ superstructure had an order ‘ – small – large – large – small – ’ (our setting) along c with edge lengths (Å) of 3.933(6) and 4.308(4). The X site was thus located in between small and large A2 triangles and close to the smaller one. This model yields the structure refined in §3.1 for additional symmetry elements in P6₃/m space group and thus reasonable at first glance. However, the R-values did not change even after introducing the X site. Indeed, residual densities around the c-axis remained virtually unchanged even with the X site in the channel. Apart from the R-factors, the structure itself had a problem. Both of B1 and B2 sites were located at off-centric positions in their coordination polyhedra (O–B–O bond-angle variances were 33° in B1O₄ and 53° in B2O₄), and these BO₄ tetrahedra were distorted and different in sizes: volumes of B1O₄ and B2O₄ were 1.69(8) and 2.22(8) ų, respectively.

The structure was refined also with S helxl ¹⁹ to check if the specimen had been twinned. Two X sites with fixed ADP values from ref. 18] were set inside the channel to make the model topologically the same as the structure in ref. 10]. Only 0.25 ≤ sinθ/λ and |F̄_obs| > 3σ(F̄_obs) thresholds were applied for data truncation. Least-squares cycles converged at R1 = 0.055 without twin for 66 parameters and 1770 data. R1 reduced to 0.027 by applying [100/010/001̄] twin matrix with fractions of 0.50:0.50. Volumes of two BO₄ tetrahedra got closer (1.884 and 1.853 ų) but they were still highly distorted (O–B–O bond-angle variances were 32° and 34° with quadratic elongation indices 1.010 on both).

3.3 P 6 ‾ refinement of superstructure

We continued structure refinement, hereafter with P 6 ‾ space group. To allow long-range ordering in sizes and separations among A2 triangles in the superstructure, origin of the z-coordinate was shifted to z = −1/8 and thereafter the z-coordinate of A2a site was taken as z = 0 (Wyckoff position 3j). This structure has no inversion center but mirrors at z = 0 and 1/2. The preliminary refinement with no X site model converged at R(F), R(F²) and wR(F) = 0.029, 0.040 and 0.028, respectively, for 1705 reflections with 70 parameters. Minimum and maximum of Δρ were −5.08 e Å⁻³ at (0.23, 0.48, 0.51) and 18.73 e Å⁻³ at (0, 0, 0.47), respectively. Prominent positive residuals were found on the c-axis in the vicinity of A2c triangle at z = 1/2 and A2b triangle at z ≈ 1/4, while no prominent positive residual was found in the vicinity of A2a triangle at z = 0.

Next, we refined the structure with oxide anions in the channel. Oxide anions were introduced on the c-axis at z = 0.47 (X1), 0.19 (X2) and 0.27 (X3), in other words pairs of positions near the faces of A2b and A2c triangles, after results of difference Fourier synthesis. The same considerations applied on the structure refinement as noted in §3.2. Least-squares calculation with positions and occupation factors at three X sites as free variables resulted in unreasonably large occupancy at X1 site [72(13)%] in spite of small separation between two equivalent positions connected by a mirror plane at z = 1/2. Occupancies at X2 and X3 sites were approximately 1/3 and 1/6 of the value at X1 site after this calculation. Least-squares calculation became unstable when one more oxide anion site was introduced wherever possible in the channel: occupancy of one out of X2, X3 and X4 (additional) sites became negative and they moved across the border of cells. Therefore we limited number of X sites in the model to three, and occupancy at the X1 site was set at 1/2 in consecutive iterations. The total number of oxide anions exceeded 2.0 per cell in all the cases whenever possible, and therefore further restraint was applied on the total of occupancies at X2 and X3 sites to be 1/2. This calculation converged at R(F), R(F²) and wR(F) = 0.028, 0.037 and 0.027, respectively, for 1705 reflections with 74 parameters. Minimum and maximum of Δρ were −4.94 e Å⁻³ at (0.0, 0.74, 0.01) and 4.51 e Å⁻³ at (0.30, 0.10, 0.51), respectively. Δρ at (0, 0, 0.47) was reduced to 3.92 e Å⁻³. Any attempt to refine ADPs at X sites, however, was unsuccessful and therefore we employed the ADP values in ref. 18] in the final structure. In addition, ratios among occupancies at X sites [1/2, 30(2) % and 20 % at X1, X2 and X3 sites, respectively] after final iterations apparently differed from those without restraints. Occurrence of these minor inconsistencies indicated difficulty to picture a projection of various local structures by using three distinct X site positions even with ADPs. This also indicated potential ambiguities on positions and occupancies of X2 and X3 sites more than their s.u.s. Convergence of structure refinement with b9s1 data set was virtually the same with 1307 reflections and so was the structure: 28 out of 47 positional parameters (including z-coordinates of three X sites) matched to each other within their combined s.u.s and only two positional parameters (x of O3c and y of O3d) differed more than 3 times of combined s.u.s. These two specimens have different thermal histories but essentially the same structure, suggesting that the target compound crystallizes from melt in the superstructure and an occurrence of order-disorder phase transition is not likely. Crystal structure of PPO is shown in Figure 3. Structural parameter values for b12s2 are listed in Table 4. Selected bond distances and bond-valence sums are listed in Table 5. CIF file can be obtained from CCDC website on quoting the deposition number CSD 2363464.

Figure 3:

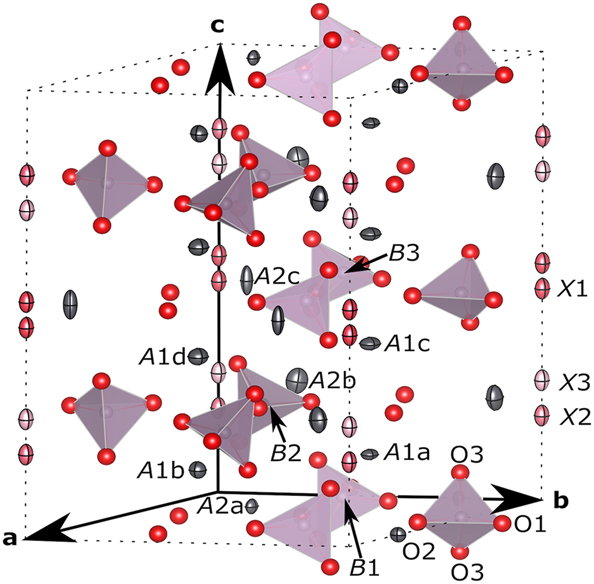
Orthographic view of the P 6 ‾ structure with atoms in 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1 and first neighbors of B sites in the range. Red balls: O1–O3 sites; red to pink ellipsoids on c: X sites; purple balls inside of purple tetrahedra: B sites; gray ellipsoids: A sites. All atoms, balls and ellipsoids are shown with 80 % probability. Colors of X site ellipsoids reflect difference of occupancies among those positions (thicker is larger). Figures 3–5 are all drawn with VESTA. ²³

Further least-squares cycles had done with SHELXL to compare convergence of iterations with twinned P 3 ‾ structure. Site occupancies and ADP values at X sites were fixed for stable least-squares cycles. Only 0.25 ≤ sinθ/λ and |F̄_obs| > 3σ(F̄_obs) thresholds were applied for data truncation. Least-squares cycles converged at R1 = 0.027 without twin for 73 parameters and 1887 data. Quadratic elongations and bond-angle variances were 1.004 and 9° (B1O₄), 1.001 and 5° (B2O₄), and 1.006 and 23° (B3O₄). No twin analysis was made for sufficiently low R1 value.

4.1 Space group

Refined P 3 ‾ structure with twin was topologically the same as that reported by Krivovichev & Engel ¹⁰ even equal fractions of domains, indicating that the structures of specimens in two studies were the same. Relationship among two domains was twofold rotation around c, therefore 0.5:0.5 ratio of domains meant that ‘averaged’ diffraction data had additional twofold symmetry around c*. The same enhancement of symmetry in reciprocal space occurs when diffraction data from a compound having P 6 ‾ space group are handled under 3 ‾ point group. While R1 values after SHELXL refinements were the same, refined P 3 ‾ structure was physically less reasonable than P 6 ‾ structure as far as we expect high rigidity of (PO₄)³⁻ complex anions. ⁵ Here we conclude that P 6 ‾ is the most appropriate space group of the compound. Krivovichev & Engel explored space group of the superstructure under supergroup-subgroup relationship regarding possible order-disorder transition of the specimen. However, identity of the structures of specimens b9s1 and b12s2 support crystallization of the compound from the melt in P 6 ‾ structure. This space group itself support absence of P6₃/m state for the composition under supergroup-subgroup consideration.

4.2 Long-range order in superstructure

Sizes of A2 triangles in the refined P 6 ‾ superstructure had an order ‘large – middle – small – middle – (large)’ along c with edge lengths (Å) of 4.359(3), 4.128(6) and 3.781(3) and virtually equal separations [3.663(4) – 3.760(4) Å]. So the area of the smallest triangle was 75 % of that of the largest one in the superstructure. BO₄ tetrahedra had little distortion with volumes of 1.99(5), 1.89(4) and 1.80(4) ų for B1O₄, B2O₄ and B3O₄ tetrahedra, respectively. B2O₄ tetrahedra were tilted in biaxial rotations with cooperative shift of O3c site with A2c site toward the c-axis. A2 sites were coordinated by O1–O3 sites in pentagonal pyramidal manner with basal plane parallel to c and A2c site was shifted toward the c-axis together with its pentagonal basal plane (Figure 4b). This cooperative shift, however, was not perfect: A2c site was 0.3 Å apart from O1c – O3d – O3d’ triangle (the isosceles triangle with acute apex at O1 site in the pentagon) toward the c-axis, while the separation of A2a site from O1a – O3a – O3a’ triangle toward the c-axis was 0.1 Å. As a result, edge lengths of O3 triangles normal to c changed rather smoothly [5.55(4) – 5.60(3) – 5.23(3) – 5.10(4) Å in halfway with increasing z] with 15 % reduction in areas. It seemed noteworthy here that A2 site positions in apatite structures hitherto published are located on, or shifted toward the c-axis a little from, the above-mentioned isosceles triangle and this is not a unique feature in lead apatites. Only exceptions were Cd₅(PO₄)₃Br, Cd₅(VO₄)₃Br and Cd₅(VO₄)₃I ²⁴ in which X anion seemed too large for the host structure.

Figure 4:

Geometry of coordination polyhedra around A2 sites and their sequence. For presentation of atoms please refer to the caption on Figure 3. (a) A2- and B-site atoms in the region 0 ≤ x ≤ 0.5, 0 ≤ y ≤ 0.5, 0 ≤ z ≤ 1 and their first neighbors. (b) Projection of A2aO₆ – B2O₄ – A2cO₆ array approximately in [ 2 ‾ 1 0]. Tilt of B2O₄ around direction normal to c and difference in sizes of A2O₆ pentagonal pyramids are visible. Dotted lines are for eye-guide.

Formation of bond with X1 site O²⁻ reduced charge of A2c site Pb²⁺ for the other Pb²⁺ – O²⁻ bonds and caused expansion of the pentagonal pyramid. This effect lengthened A2c – O2c distance more than the others since this elongation only rotated B3O₄ tetrahedron and had no effect on cell-edge lengths of the host structure. For this reason, B3O₄ tetrahedron was rotated 13° (approx.) on mirror normal to c with respect to B1O₄ tetrahedron (Figure 5).

Figure 5:

[0 0 1 ‾ ] projection of the A2 and O3 triangles with X sites and BO₄ tetrahedra on xy-plane. For presentation of atoms please refer to the caption on Figure 3. The unit cell boundaries are shown as dashed lines. Red and gray triangles are for eye-guide.

Since no superstructure had been reported on apatite-type Pb₉(PO₄)₆ which had no channel anion, ²⁵ occurrence of the long-range order should be attributed to a fractional number on X in the formula A1₂A2₃(BO₄)₃X_0.5. No superstructure is necessary for the composition when channel site oxide anions are located on every other A2 layers whether the site is split or not. In such a case sizes of A2 triangles will have a ‘ – large – small – ’ sequence no matter how different they are. This sequence did not occur in the real structure, probably because the host structure with such order can not be accomplished without large distortions of (PO₄)³⁻ complex anions. Long-range periodicity was necessary to vary the sizes of A2 triangles in the host structure only by rotations of rigid BO₄ units with least distortion.

4.3 Positions of X anions

The X1 site was located near the small A2c triangle, and either one of two X1 site positions [at z = 0.471(7) & 0.529(7)] was occupied by oxide anion in every unit cell. The X2 and X3 sites were close to the middle-size A2b triangle with similarly low occupancy factors, they were not equidistant from the A2b triangle though. Remaining two positions equivalent to the X1 site in the parent structure (near A2a at z = 0) were vacant. The edge length (Å) of the largest A2a triangle in PPO [4.359(3)] was close to those in Pb₉(PO₄)₆ [4.311(3)] and Pb₅(PO₄)₃Cl [OP-4; 4.3493(11)], indicating that the A2a-site Pb²⁺ were enough separated from each other to stand for repulsion among themselves including clouds of presumable 6s2 lone electron pairs. Estimated bond-valence sum (BVS) for O²⁻ at the center of the A2a triangle (1.0) is, as expected, far smaller than its formal valence. In contrast, the A2c triangle was far smaller (−25 % in areas) and have an appropriate size to accommodate O²⁻ near its center. Estimated BVS values for O²⁻ at the X1 site position were 1.8 ²⁰ or 2.0, ²¹ in other words the X1 site position suite to O²⁻ in the channel. So we consider shrinkage of A2c triangle due to attraction from X1 site O²⁻ as the main cause of the superstructure in the following discussion.

Calculated BVS values for O²⁻ at the center of A2c triangle were 1.9 ²⁰ or 2.1. ²¹ Based on the BVS values after ref. 20] and discussions on spatial distribution of stereoactive 6s2 electron orbitals of Pb^{2+ 13 , 14} we can deduce a consideration as follows. Stereoactive 6s2 electron orbitals of Pb²⁺ are pointing inside of the channel and these orbitals push O²⁻ apart from the triangle along <001>. Directions of 6s2 orbitals might be canted toward the opposite side, but their repulsion is still strong enough to compete against a demand to make the A2c triangle further smaller to accomplish ideal Pb²⁺ – O²⁻ bond lengths. In this sense size of the A2c triangle is the possible minimum in the structure and the BVS values for O²⁻ are still smaller than 2.0 at both the X1 site and the center of the triangle. On the other hand, the BVS values after ref. 21] implies that an arrangement of atoms around the X1 site position is quite reasonable. However, we have to notice that the A2c triangle had no reason to shrink other than attraction from the X1-site O²⁻. This implies that the ideal position for O²⁻ is a center of regular A2c triangle and that the A2c triangle is a little smaller than necessary. This leads a consideration such that the O²⁻ is pushed out from the triangle plane but keep Pb²⁺ – O²⁻ distance ideal to use up its charge. In other words, repulsion among 6s2 orbitals is not strong enough to compete against a demand to make Pb²⁺ – O²⁻ distance ideal. We can not conclude whether the size of the A2c triangle is a possible minimum for Pb²⁺ triangle or not, but presence of repulsion between 6s2 electron clouds and outer shell electrons of O²⁻ in the channel is very likely. This repulsion also explains the positions of X2 and X3 sites. Calculated BVS for O²⁻ at the center of A2b triangle was 1.3 but both X2 and X3 sites were located out from the triangle plane due to repulsion from 6s2 orbitals at A2b site.