Multiscale thermomechanical modeling of short fiber-reinforced composites

1 Introduction

The use of fiber-reinforced materials has grown rapidly in the recent years in many applications, including aircraft, yachts, sporting goods, and motor vehicles, beside a wide range of military applications. Fiber-reinforced materials are a broad and versatile class of materials, which include a wide range of fiber and matrix combinations that provide a large number of component design and manufacturing options. High strength-to-weight ratio, coupled with excellent durability, corrosion resistance, and low maintenance cost, is among the factors that make fiber-reinforced materials ideal for widespread applications.

Short fiber-reinforced composites enjoy the advantage of providing stiffness levels comparable to continuous fibers while at the same time being moldable into complex shapes. They are attractive in relatively low fabrication costs and constitute a major portion of the demand of composites in automotive, marine, and aeronautic applications. Figure 1 includes the composite window frame designed by the Boeing aircraft company [1].

Figure 1:

Composite window frame.

The particular benefits exhibited by metal matrix composites, such as increased specific strength and stiffness, improved high-temperature performance limits, and better wear-abrasion resistance, are dependent on the properties of the matrix alloy and of the reinforcing phase. A variety of metal matrix composite materials are used in automotive, space systems and satellites, medical, power semiconductors, sporting goods, and several military applications. Among the multiple uses are the space shuttle frames, Hubble telescope, bicycle frames, automotive pistons, brakes, and disks.

The properties of materials depend in a complex manner on the microstructure. The strength of a fiber-reinforced composite, for example, is determined by fracture criteria, themselves governed by a combination of microscopic phenomena. These include the plastic deformation of the matrix, the strength of the interface, and the distribution of the reinforcement within the composite. Therefore, predicting the strength of the composite from that of its constituent phases is generally challenging.

In the aviation industry, airworthiness specifications require an evaluation of the principal structural elements under cyclic mechanical and thermal loading as expected in service. The thermomechanical behavior of short fiber-reinforced composites has been investigated at high working temperature [2, 3]. However, the investigation was limited to varying mechanical loading at uniform temperature or constant mechanical loading under temperature time history. In addition, particle-reinforced composites [4, 5] have been studied under uniaxial tensile loading. However, these investigations were limited to mechanical uniaxial loading. In practical applications, short fiber-reinforced composites are subjected to cyclic mechanical loading coupled by simultaneous varying temperatures. Furthermore, it is difficult to align the short fibers during processing in a typical production environment.

Cavalcante et al. [6] modeled heterogeneous materials with macroscopically uniform microstructures using either the concepts of statistical homogeneity based on “representative volume” element or periodicity based on repeating unit cell. This research demonstrated that a micromechanics model plays a key role in understanding how the local properties of constituent phases and their arrangement influence the macroscopic structural behavior. The purpose of this paper is to predict the overall response of short fiber-reinforced composites under cyclic mechanical and thermal loading and to investigate the influence of the short fiber’s aspect ratio, volume fraction, and spatial orientation.

2 Thermomechanical constitutive relations

2.1 Representative volume

A representative volume element is the smallest possible volume that contains the necessary microstructure details such that the response of these elements under appropriate boundary conditions is identical to that of the material at large. The representative volume consists of matrix and short fiber phases and whose fibers are uniformly distributed, well bonded with the matrix, and identical in material and shape. A representative volume is not in a neighborhood close to the boundary. It contains sufficiently large number of short fibers to reflect the microstructure of materials yet is small enough compared to the macroscopic scale. The representative volume is selected to embody the overall response of the structure [6–8]. The shape of the short fibers is assumed to be ellipsoid, and the particulate-reinforced composite is one of its particular cases.

Throughout this paper, scalars and integers are represented by italic letters, vectors and second-order tensors by lower-case boldface letters, and fourth-order tensors by upper-case boldface letters. To describe the orientation of short fibers, two coordinate systems were defined. A global coordinate system (x₁, x₂, x₃) and a local coordinate system (x₁′, x₂′, x₃′) in which the x₃′ axis coincides with the major axis of the ellipsoidal fiber were introduced (Figure 2). The local and global systems are related by the transformation: x=βx′, where β is the transformation matrix, whose components are functions of the angles θ and φ.

Figure 2:

Schematic illustration of the global and local coordinate systems.

The distribution of the possible fiber orientation in the representative volume can be defined by a statistical density function ρ(θ, φ). In this study, a reduced density function ρ(θ) was considered for simplicity, which corresponds to a 2D case or a 3D axis symmetrical distribution.

2.4 Cyclic hardening effect of metal matrix

Because the properties of a metal matrix composite in the plastic range are mainly dependent on the properties of the matrix, then attention is paid to the cyclic thermo-elastic-plastic constitutive relationship of the matrix. For a time-independent metal-matrix material, the strain increment can be decomposed into a mechanical part and a thermal part: dε=dεe+dεp+dεT=dεep+dεT=Mep:dσ+mdT(9)

Where, M_ep is the fourth-order instantaneous effective compliance tensor of the material.

It is a well established fact that most metallic materials exhibit the Bauschinger effect, which can be described by kinematic hardening. The formulation of the Bauschinger effect is based on introducing the so-called back-stress, b, to compute the stresses and strains after plastic flow. The back-stress describes the shift of the center of the yield surface.

The linear combined hardening model [15] was selected to describe the cyclic work-hardening behavior of the matrix materials. According to the J₂-flow theory [16], the yield condition can be expressed by

(10)f(σ,σs,b)=12(σ′-b′):(σ′-b′)-13σs2=0 (10)

Where, σ_s denotes the instantaneous radius of the yield surface and σ′ and b′ are the deviatoric tensors of σ and b.

Defining the cumulative plastic strain ε̅_p, dε¯p=23dεp:dεp,σ_s is obtained as follows:

(11)σs=(1-w)σs,0+wY(ε¯p) (11)

Where σ_s,0 is the initial yield stress, w is the isotropic hardening coefficient, and Y(ε̅_p) is the result in terms of the isotropic hardening model. It should be noted that σ_s and Y(ε̅_p) are functions of ε̅_p.

In the case of uniaxial cyclic loading, ε̅_p=ε_p, and the constitutive curve of the material is shown in Figure 3. Each monotonic loading branch is numbered as k, k=1, 2, 3 … n-1, n. When the material reaches plasticity, for example on the nth loading branch, Y(ε̅_p) is updated through the hardening coefficient H and the hardening exponent X of the material.

Figure 3:

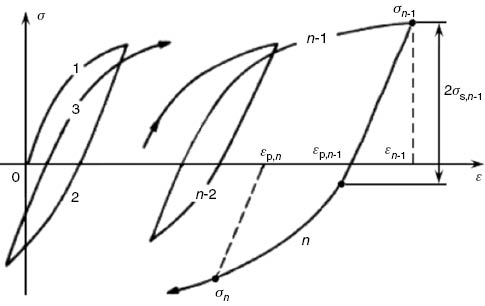
Constitutive curve of the material under uniaxial cyclic loading.

(12)Yn(ε¯p)=|σn|=|σn−1+(-1)n+1(2σs,n-1+H|εp,n-εp,n-1|X)| (12)

The material plastic modulus E_ep, which is a function of ε̅_p, is defined under unidirectional loading as E_ep=dσ/dε_p. Therefore, the expression of the instantaneous effective compliance tensor of a material could be written as

(13)Mep=M+94Eepσs2(σ′-b′)(σ′-b′) (13)

To obtain an expression to determine the back-stress deviatoric tensor b′ during the cyclic loading process, the increment of b′ can be written as

(14)db′=23[dY(ε¯p)-dσs]n (14)

Where n is the unit tensor normal to the material yield surface, and Eq. (14) can be solved to obtain

(15)b′=b′0+(1-w)H(Δε¯p)Xσ′σeq (15)

Where, b′0 is the initial back-stress deviatoric tensor at the beginning of each monotonic loading branch and the equivalent (Von-Mises) stress is σeq=32σ′:σ′.

3 Numerical simulation

To express tensors in FORTRAN program, they were transformed into the form of matrices. It is assumed that the uniaxial cyclic loading is strain controlled for both mechanical and thermal loading.

Because there are unknown quantities in both the average stress and strain increments, the global constitutive relations of the representative volume are simplified:

P=cfMf:B¯f+cmMm:Bm

According to Equation (16), a set of equations was formed and solved to obtain the components not specified in the matrices. The average stress and strain increments of the matrix and fiber-reinforced phases were then calculated through the previous formulas. When the matrix reached the nonlinear range, an iterative procedure was required and the average stress increment of the matrix in the ith step is given by

where B^¯mi-1 and b^¯mi-1 are defined above, and the initial increments could be calculated through the method used for the linearly elastic range. The iterative procedure is continued until the convergence criterion is satisfied.

where γ is the allowable value for error. When a new loading step is applied, the above iterative procedure is repeated.

4 Examples of the proposed model and discussion

Lagoudas et al. [17] have compared the results of the periodic hexagonal array (PHA) model, the self-consistent model, and the Mori-Tanaka model when a multiaxial proportional loading (σ₃₃=2σ₁₃) was applied on a composite system with aluminum matrix and unidirectional distributed silicon carbide whiskers. The whisker reinforcement had a volume fraction of 24% in the composite, and the other parameters chosen for the numerical calculations are as follows: aluminum, elastic modulus E_m=72 GPa, Poisson ratio ν_m=0.33, σ_s,0=70 MPa and H=14.5 MPa, and SiC, E_f=430 GPa, and ν_f=0.25. In Figure 4, the numerical results of the proposed model are compared to the results of the PHA, Mori-Tanaka, and self-consistent models included in Ref. [17], and a good correlation is shown.

Figure 4:

Comparison between the proposed model and other numerical models.

Figure 5 shows a comparison between the published experimental results [18] and the present numerical results. The composite used in the experiment was Al-6061 alloy reinforced by SiC whiskers with volume fraction of 28%. This experiment was conducted under strain control for mechanical strain range from -0.006 to 0.006 at 300°C. Because some of the composite material parameters had not been included in the publication, these parameters were selected to enable using the proposed model: E_m=72 GPa, ν_m=0.33, w=0.7; E_f=430 GPa, ν_f=0.2. The curve presenting the results of this model was similar to the experimental results, except that the published results showed slight nonlinearity in the response. Better correlation to the experimental results can be achieved using the improved hardening model.

Figure 5:

Comparison between calculated stress-strain responses and experimental results under isothermal loading: (A) experimental results and (B) calculated results of the proposed model.

The following is a discussion of the influence of volume fraction, aspect ratio, and distribution of the spatial orientation of the fiber-reinforced phases on the stress-strain response of composites under cyclic strain control loading at room temperature.

Figure 6 illustrates the effect of volume fraction of the fiber-reinforced phases on the total stress-strain response of the composite. The composite was Al+3.5% Cu reinforced by SiC fibers, whose geometry was taken to be spherical. The aspect ratio of spherical fibers is 1:1:1 and their orientation distribution has no effect on the macroscopic response of composites. The volume fractions of the reinforcements were 0%, 6%, and 20%. Monotonic strain-controlled loading ranging from 0 to 0.009 was applied. The material properties were E_m=70 GPa, ν_m=0.33, σ_s,0=175 MPa, H=90 MPa, X=0.25, w=0.4; E_f=450 GPa, ν_f=0.17.

Figure 6:

Stress-strain response of composite with different volume fractions of reinforcement.

Apparently, in Figure 6, the total elastic modulus and the initial yield stress of composites increased with the fiber volume fraction. Increasing the fiber volume fraction improves the capability of the composite to support the loading, and more strain energy could be consumed under equal plastic strain. This improves the impact energy absorption characteristic, which is desired in certain civilian and military applications.

Figure 7 displays the different average stress-strain response curves of composites with different aspect ratios (1:1:1 and 1:1:5) and in different spatial orientation distributions of the short fiber-reinforced phases. The composite was Al-2124 reinforced by SiC fibers, with the volume fraction of 13%. The material properties were E_m=70 GPa, ν_m=0.33, σ_s,0=205 MPa, H=220 MPa, X=0.5; E_f=450 GPa, ν_f=0.17. The short fiber orientation distributions were unidirectional, distributed in the loading direction, cosine distribution ρ(θ)=cos(3θ/2), and random distribution. The response of the unidirectional short fiber composite is shown in Figure 7A and the response of the cosine and random distributions are shown in Figure 7B and C, respectively.

Figure 7:

Stress-strain response of composite with different fiber aspect ratios: (A) unidirectional distribution, (B) cosine distribution, and (C) random distribution.

Two cycles of strain-controlled loading ranging from -0.008 to 0.008 were considered, and the coefficient of isotropic hardening was defined as w=0.2 to accelerate the stabilization of the cyclic loops. The reinforcement effect of particles was weaker than elliptical fibers with an aspect ratio of 1:1:5 as shown in Figure 7A. Higher elastic modulus and yield strength were found with a larger aspect ratio in the loading direction. The aspect ratio of cosine-distributed short fibers did not have much influence in reinforcement as unidirectionally distributed ones because only a part of the reinforcing short fibers had their major axes along the loading direction. When the short fibers were randomly distributed, the reinforcement effect of ellipsoidal fibers to the overall response of the composite was similar to the reinforcement effect of particles, as shown in Figure 7C. Increasing the volume fraction is more efficient and easier than controlling the orientation of the fibers in short fiber composites to improve its load-carrying capacity.

Finally, we analyzed the properties of composites under coupled thermomechanical loading. Two types of thermomechanical loading, in-phase (maximum tensile strain at maximum temperature) and out-of-phase (maximum compressive strain at maximum temperature), were adopted to simulate the loading history. The total strain varied from -0.01 to 0.01, and the temperature range was 90°C–210°C. The used composite was Al/SiC, and its properties were functions of temperature: E_m=74657[1-(T+273)³/933³] MPa, ν_m=0.33, m_m=2.35×10^-5+2.476×10^-8T K^-1; E_f=450 GPa, ν_f=0.17.

Figure 8 illustrates the stress-strain response for the in-phase and out-of-phase loading history. In addition, the stress-strain response for the case of isothermal loading at the average thermal loading temperature (150°C) is shown in Figure 8 as reference for comparison. When the stress-strain responses for the in-phase and out-of-phase loading history were compared to that of the isothermal loading, the response curve of in-phase loading was much flatter than that of isothermal loading and the corresponding stress was lower for the identical strain at the plastic stage. The out-of-phase loading demonstrated the opposite phenomenon. These results can be explained by the fact that heat expansion compensates part of the mechanical strain and the thermal contraction requires less compressive mechanical strain. Furthermore, the decrease in the elastic modulus with increasing temperature also contributed to the observed results.

Figure 8:

Stress-strain response under isothermal and thermomechanical loading: (A) in-phase and (B) out-of-phase.

5 Conclusions

There is a good correlation between the results of the proposed model and the predicting results of the PHA model, the Mori-Tanaka model, and the self-consistent model. In addition, a good agreement was found when the results of applying the proposed model to aluminum matrix composites were compared to relevant published experimental results. The linear combined hardening model was used in the simulation and the response might be improved using a better cyclic hardening model.

The macroscopic properties of composites are dependent on the fiber’s architecture and spatial orientation, especially the volume fraction of fibers. The reinforcement effect of particles is weaker than elliptical fibers, especially when unidirectional fibers are distributed in the loading direction. Increasing the fiber volume fraction improves the capability of short fiber composites to support the loading, in particular when more ellipsoidal fibers are used in the loading direction.

The numerical simulation of in-phase and out-of-phase thermomechanical loading history resulted in distinctly different stress-strain responses, which indicate the significant influence of thermal loading time history in the case of large temperature variation. The stress-strain response of the in-phase loading history was much flatter than that of isothermal loading at the average thermal loading temperature (150°C).