A quantum chemical perspective of photoactivated biological functions

2.1 Light harvesting & energy conversion

The terms light harvesting (LH) and energy conversion in photosynthetic systems refer to two distinct but sequential processes used in the so-called light-phase of photosynthesis. Both are essential for transforming sunlight into chemical energy, but they involve different molecular components, timescales, and physical principles. Light harvesting is the initial step of photosynthesis in which photons are captured and funneled to the reaction center (RC). Energy conversion refers instead to the transformation of the harvested excitation energy into a stable chemical form via charge separation and electron transport in the reaction center. Both these sequential processes are realized in photosystems, multisubunit membrane protein supercomplexes containing at the core, the RC and at peripheries, the LH antennas ^{22 , 23} (see Fig. 1).

Fig. 1:

Representation of photosystem II (PSII): (a) the composition in terms of antennas and reaction center (RC). (b) The monomer of the major antenna, the trimeric LHCII and the arrangement of its pigments, Chlorophyll a (light green), Chlorophyll b (green) and carotenoids (Lutein in orange and neoxanthin in violet); (c) The reaction center and the arrangement of the set of pigments involved in the primary electron transfer reaction (Chlorophyll a in light green, Pheophytin in cyano and β-Carotene in yellow).

The core structures of RCs are highly conserved in photosynthetic organisms. Instead, a wide diversity of antenna systems is found, and in many cases, the classification of these organisms is closely linked to the specific types of antenna complexes they possess. ^{13 , 14 , 24} In all cases, the antenna system does not carry out chemical reactions; instead, it absorbs light and uses energy transfer processes to move the excitation energy in space toward the core of the photosystem and ultimately to the reaction center. This physical process relies on excitonic coupling between pigments, which are typically bound to proteins in highly specific arrangements. In addition to chlorophylls, which are the primary pigments in plants and other oxygenic photosynthetic organisms, a variety of other antenna pigments are employed across different photosynthetic systems. Bacteriochlorophylls serve a similar light-harvesting role in most anoxygenic photosynthetic bacteria, while bilins, linear, open-chain tetrapyrrole pigments, are characteristic of antenna complexes known as phycobilisomes present in read algae and cyanobacteria. Furthermore, all known native photosynthetic organisms possess ancillary pigments known as carotenoids (see Fig. 1). In oxygenic species, carotenoids typically feature ring structures at both ends of the conjugated backbone, and many contain oxygenated functional groups. These pigments play critical roles not only in light harvesting but also structural stabilization of antenna complexes and photoprotection. ^{25 , 26} Because sunlight is a relatively dilute energy source, the number of antennas associated with each reaction center is large. Under stress conditions, such as high light intensity, these antennas can absorb more energy than the system can effectively utilize, potentially causing photodamage. To mitigate this, both antenna complexes and reaction centers are equipped with regulatory, protective, and repair mechanisms. ^{27 , 28 , 29}

The reaction center is a multisubunit protein complex where charge separation (CS) takes place. In the RC of photosystem II (PSII), the set of pigments responsible for the conversion of excitation energy into CS is composed by four chlorophylls and two pheophytins (see 1(c)). Moroever, various additional cofactors are present including carotenoids, quinones and the oxygen-evolving complex (OEC). To avoid energy loss through recombination (where the electron is transferred back and the energy is converted into heat and rapidly dissipated), the system employs a rapid series of secondary electron transfer steps. These steps outcompete recombination by spatially separating charge across the membrane within less than a nanosecond. Subsequent slower processes stabilize and convert this charge separation into usable chemical energy. ^{23 , 30}

Despite the detailed structural and spectroscopic studies we have achieved so far for photosystems, several fundamental questions remain open. A central issue is how EET occurs with such high efficiency across complex pigment–protein architectures under physiological conditions. ^{31 , 32 , 33} Furthermore, how protein dynamics and structural fluctuations modulate energy landscapes and guide energy flow through these networks is still not fully resolved. This includes the role of the environment in dynamically tuning pigment site energies and couplings. Regarding electron transfer in reaction centers, one major puzzle is why ET proceeds asymmetrically through only one branch, despite the structural symmetry of cofactors. The role of the protein environment in tuning redox potentials and controlling ET dynamics through local electrostatics, hydrogen bonding, and conformational fluctuations is also not fully understood.

2.2 Photoreception & signalling

The terms photoreception and signaling are closely related in the context of light-activated biological processes, but they refer to distinct stages in the sequence of events. Photoreception is the initial detection and absorption of light by a protein embedding a chromophore which acts as a switch. Signaling instead refers to the cascade of biochemical and physiological events following the initial photoreception, and ultimately leading to a biological response.

The mechanisms used for photoreceptor and for signalling vary across organisms and functions. ^{34 , 35 , 36 , 37} Typical examples are light-induced photoisomerization of the embedded chromophore or light-induced electron transfer. Typical examples of signaling mechanisms are instead conformational changes that modulate the binding affinity or enzymatic activity of the system.

To explain in more details, here we focus on two largely diffused photoreceptors, Phytochromes and Cryptochromes.

Phytochromes are light-sensitive proteins in plants (and some bacteria and fungi) that act as photoreceptors for red and far-red light. They play a central role in regulating light-dependent development and behavior. ^{34 , 38} Phytochromes function as reversible molecular switches. For example, in plants they are used to sense the red/far-red light ratio, which varies with canopy cover, time of day, and seasons. This allows plants to distinguish between light conditions and activate/promote different behaviors. Phytochromes are typically homodimers where each monomer is composed of a generally conserved photosensory module made of three domains (PAS–GAF–PHY). The photosensory module embeds a chromophore, a linear tetrapyrrole (bilin) covalently attached to the GAF domain via a cystein residue (see Fig. 2). By absorbing light, the chromophore undergoes a Z → E isomerization of a double bond. This causes a conformational change in the protein, particularly in the PHY tongue, activating downstream signaling.

Fig. 2:

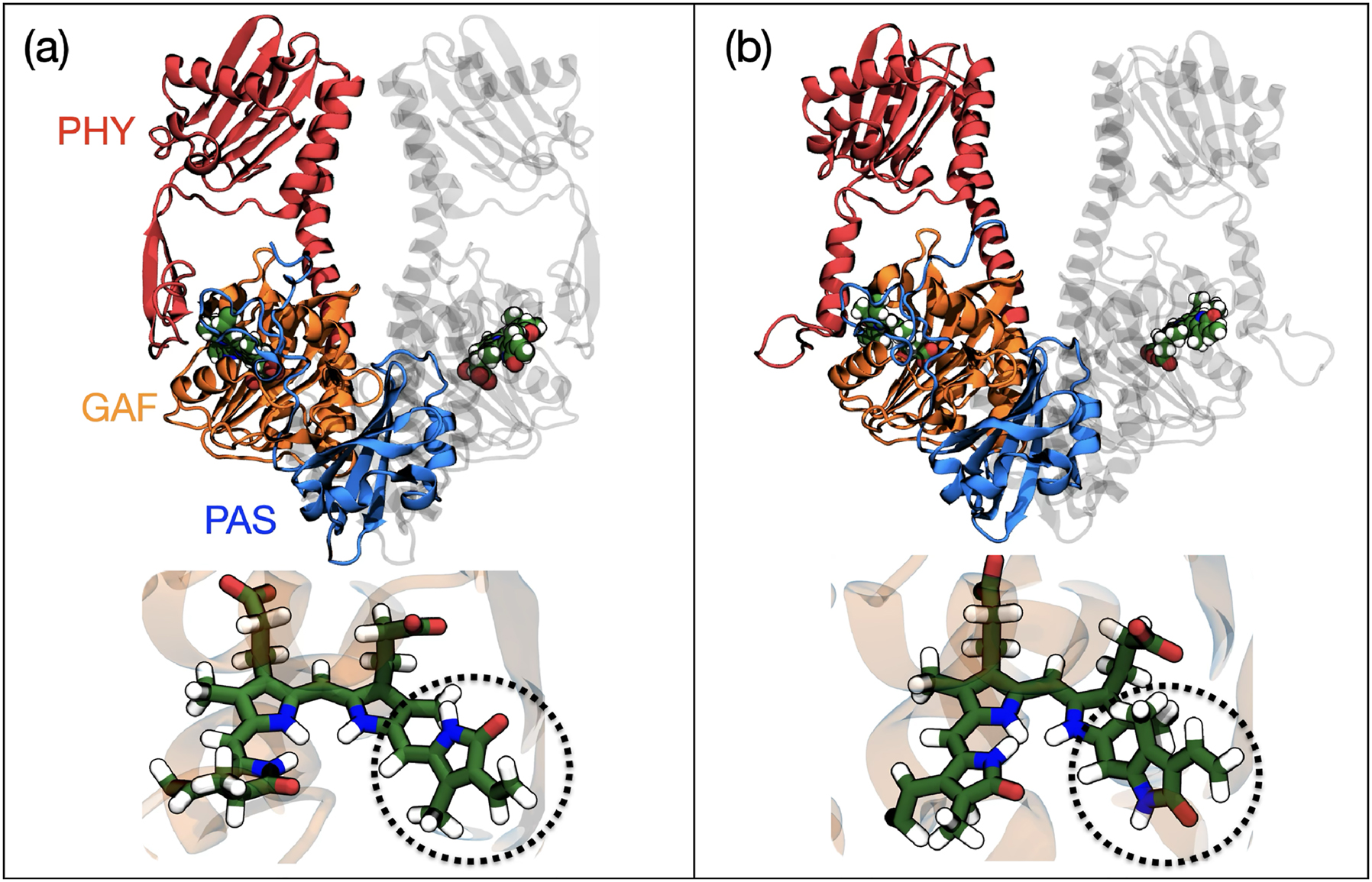
Schematic representation of the (a) dark and (b) light activated states of Phytochrome in the Deinococcus bacterium and the embedded bilin. The dotted circle indicates the region of the molecule where photoisomerization occurs.

A different mechanism of action is represented by the blue-light photoreceptors known as cryptochromes (CRY). Cryptochromes are photo sensory receptors that regulate several vital biological functions such as growth, development and flowering as well as the regulation of the circadian clock in plants and animals. ¹⁸ Structurally, CRY contains a conserved N-terminal photolyase-related domain that binds to flavin adenine dinucleotide (FAD) and a C-terminal domain of variable length. Upon blue light irradiation, electron transfer from a close-by tryptophan to flavin occurs allowing a fast (hundreds of fs) initial charge separation and subsequent stabilization of the radical species through a chain of tryptophans (see Fig. 3). These stabilized radical pairs are thought to serve in triggering a conformational change. This change results in the formation of homodimers or heterodimers with CRY-interacting proteins.

Fig. 3:

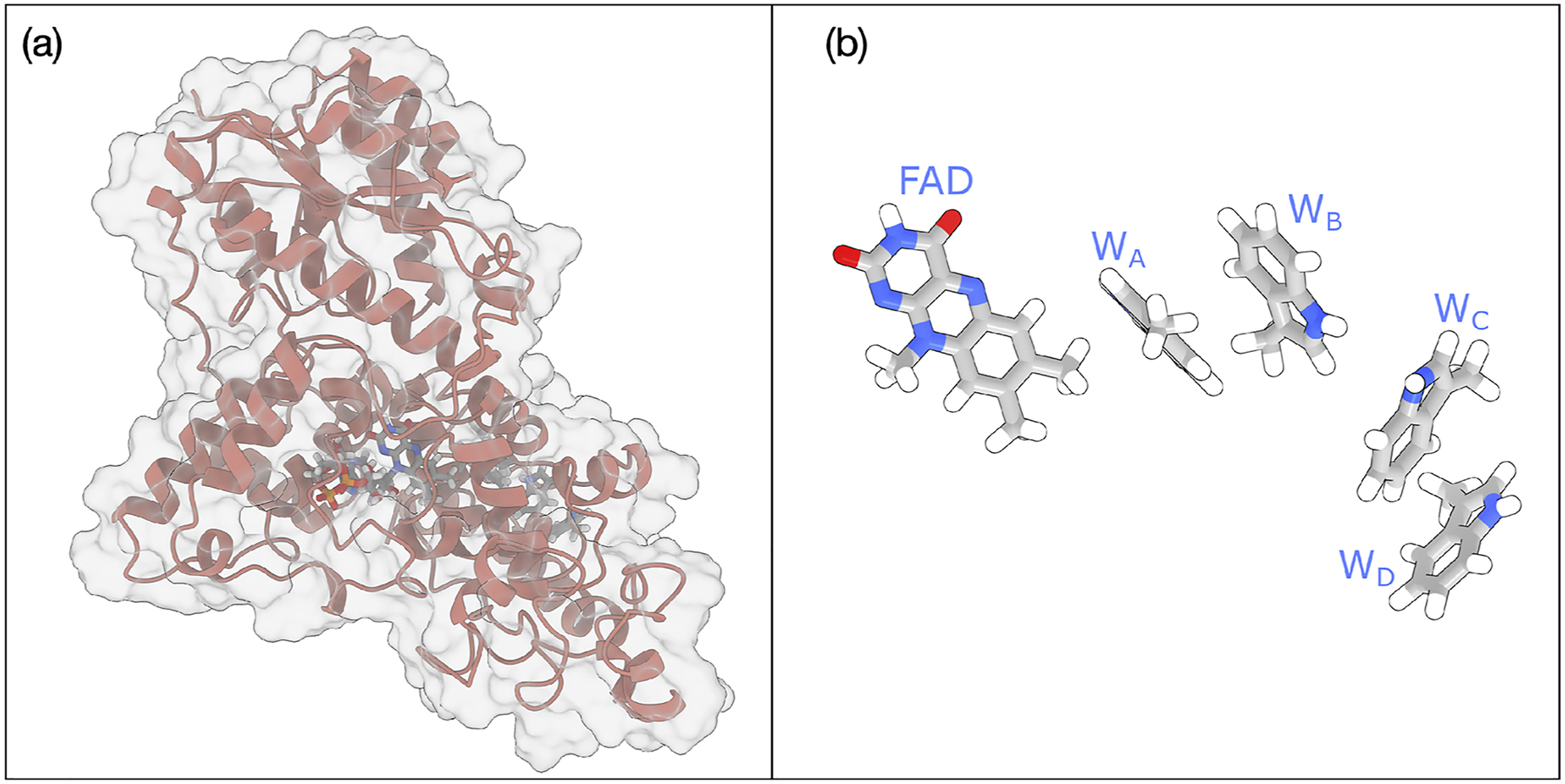
Schematic representation of (a) Cryptochrome 4 widely thought to be responsible for the magneto-reception of migratory birds and (b) the FAD and the four tryptophan residues involved in the ET chain.

Cryptochromes have also been proposed as actors in magnetoreception, a mechanism to underlie spatial orientation in migratory birds relative to Earth’s magnetic field. ³⁹ In the proposed cryptochrome-based model, blue light absorption by the FAD cofactor initiates photoreduction, generating a light-induced radical pair. The magnetic sensitivity arises from the spin-dependent dynamics of this radical pair, which influence downstream biochemical or neuronal responses involved in orientation and navigation.

Despite the significant progress achieved so far, the mechanistic understanding of photoreceptors at molecular level remains incomplete. One major open question concerns the ultrafast photochemical events, such as isomerization and charge rearrangement, that follow photon absorption and occur on femtosecond to picosecond timescales. ⁴⁰ How these events are influenced by the protein environment, including hydrogen bonding and electrostatics, remains poorly defined. Another key challenge is elucidating how localized changes at the chromophore site are converted into global conformational changes that activate downstream signaling domains. The structural pathways that mediate this allosteric communication, and whether conserved dynamic motifs exist across photoreceptor families, are still not fully resolved.

3.1 Energy transfer

Computational studies of energy transfer in photosystems rely on a hierarchy of methods, from quantum chemistry for accurate pigment-level descriptions, to exciton models and open quantum system theory for energy migration, and molecular simulations to incorporate environmental dynamics.

At the pigment level, quantum chemical methods such as time-dependent Density Functional Theory (TDDFT), multiconfigurational approaches, or semiempirical models are employed to compute excitation energies of the single pigments (also called site energies) and electronic couplings between these excitations. ^{41 , 42 , 43 , 44 , 45} It is crucial that the chosen QM method accurately captures not only the excitation energy associated with the electronic transition of interest but also its underlying electronic character. For instance, in the case of chlorophylls, single-reference methods such as TDDFT are generally adequate due to the relatively straightforward nature of their lowest-energy excitation, e.g. the one involved in the light-harvesting. In contrast, for other classes of pigments such as carotenoids, multireference methods are often required to account for the more complex electronic structure involved in their excited states.

To account for the influence of the protein matrix and surrounding environment, these calculations are typically done within a hybrid QM/MM framework. While electrostatic embedding is often sufficient for capturing the primary environmental effects, a more accurate and physically complete description is achieved with polarizable embedding. ^{5 , 46 , 47} Mutual polarization between the chromophores and their environment can significantly influence site energies and, more critically, the excitonic couplings. This is particularly important because a polarizable environment can mediate the Coulomb interaction between transition densities, thereby altering the electronic couplings that govern energy transfer dynamics.

Once the site energies and electronic couplings are determined, they can be used to construct a Frenkel exciton Hamiltonian. ⁴⁸ In this framework, a system composed of N pigment molecules is considered, where each pigment (or site) is modeled as a two-level system – either in its ground or excited electronic state and inter-site charge transfer is neglected. Under these assumptions, the excitonic Hamiltonian takes the form:

where ɛ _n is the excitation (site) energy of pigment n and V _nm the electronic coupling between sites n and m, usually arising from Coulombic interaction.

The coupling can be primarily attributed to Coulomb interactions between transition densities localized in the two chromophores. When the separation between the two chromophores is large compared to their spatial extent, the Coulombic coupling can be approximated by the dipole–dipole interaction (from now on atomic units will be used):

where μ _m and μ _m are the transition dipole moments of chromophores n and m, R _nm = R _n  − R _m is the vector connecting the two chromophores and R _nm = |R _nm | the distance between them. In this equation, ϵ _∞ denotes the optical dielectric constant, which accounts for the response of the environment surrounding the two chromophores, modeled as a continuum dielectric medium. In more accurate treatments, environmental effects are incorporated through polarizable embedding QM/MM approaches, which account for the modulation of transition densities and the screening of their Coulomb interactions. ^{42 , 49} In addition to Coulomb interactions, the coupling should also contain contributions from exchange interactions. ⁵⁰ However, these contributions are typically much weaker and decay more rapidly with distance compared to the Coulombic terms, and are therefore often neglected.

By diagonalizing the excitonic Hamiltonian H ^exc we obtain the excitons, i.e. the delocalized electronic excitation states that arise from coupling between local excitations on pigment sites. These excitonic states are expressed as linear combinations of site-localized states:

where |K⟩ is the K-th exciton state (with energy E _K ) and c _nK is the coefficient giving the contribution of site n to exciton K. If the coupling V _nm is small compared to energetic difference |ɛ _n  − ɛ _m |, excitons are localized, and |K⟩ ≈ |n⟩. On the contrary, if coupling dominates, excitons are delocalized over many sites and carry wave-like character.

Starting from the excitonic Hamiltonian, different dynamical theories can be applied to simulate the energy transfer processes, ^{51 , 52} ranging from Förster and Redfield theory to more advanced treatments like modified Redfield or numerically exact methods such as the Hierarchical Equations of Motion. To apply these models it is necessary to add the effects of nuclear motions of both the pigments and the external protein and solvent. Generally these motions are approximated in terms of a ”bath” of quantum harmonic oscillators which are coupled to the electronic degrees of freedom of the pigments through the electron-bath coupling. The electron-bath coupling quantifies how the energy levels of electronic states are modulated by nuclear motions. It introduces both dephasing (loss of quantum coherence) and relaxation (redistribution of population among excitonic states) and it governs the transition between coherent and incoherent regimes of energy transfer. A stronger electron-bath coupling with respect to the electronic couplings lead to incoherent energy transfer, while weaker electron-bath coupling support coherent (wave-like) excitation transport.

Mathematically, a Hamiltonian of the form:

is used, where H ^bath is the bath of quantum oscillators, and H ^exc-bath is the coupling between the excitonic system and the bath.

The effects of electron-bath coupling are accounted for in terms of the spectral density function J(ω), which describes how strongly the electronic system couples to different vibrations in the system. The spectral density can be defined in terms of the autocorrelation function of the excitation energy fluctuations. Let δɛ(t) = ɛ(t) − ⟨ɛ⟩ be the fluctuation of the excitation energy of a pigment around its mean value, caused by nuclear motions. The autocorrelation function of these fluctuations is:

Then, the spectral density J(ω) is related to the imaginary part of the Fourier transform of the quantum correlation function, but in many simulations and semi-classical approximations, it is directly constructed from the classical autocorrelation function as: ⁵³

where β = 1 k B T is the inverse temperature. This definition is especially useful when extracting spectral densities from molecular dynamics simulations: the excitation energy ɛ(t) of a pigment is calculated along a trajectory, and its time correlation function is computed and Fourier transformed. ⁵⁴

Alternatively, spectral densities can be computed using normal-mode analysis, as proposed in semiclassical approaches. ⁵⁵ This method assumes that both the ground and excited-state potential energy surfaces share the same harmonic shape but differ in their equilibrium geometries. Under this approximation, the spectral density is given by:

where ω _k and λ _k are the frequency and the reorganization energy along the kth normal mode, respectively. The reorganization energy along each normal mode is determined using the expression λ k = f k 2 / 2 ω k 2 , where f _k is the excited-state gradient at the Franck-Condon point (vertical gradient). ^{49 , 55}

Electron-bath coupling is central to understanding and modeling EET because it governs how the vibrations modulates electronic excitations, thereby influencing the balance between coherent and incoherent transport, relaxation rates, and spectroscopic signatures.

Another fundamental quantity in shaping excitonic behavior and energy transfers is the static disorder due to the fluctuations in the interactions with the environment. To illustrate its fundamental impact, we can compare how static disorder influences the Förster and Redfield regimes. ^{51 , 56}

In the Förster regime, where electronic coupling is weak, the rate of energy transfer from site i to site j is given by:

where the integral represents the spectral overlap between the donor fluorescence spectrum Φ _i (ω) and the acceptor absorption spectrum A _j (ω). Static disorder modifies the rate primarily by broadening and reshaping these spectra, thereby altering the extent of spectral overlap and, consequently, the efficiency of energy transfer.

In the opposite limit, e.g. when the coupling is strong, a Redfield regime applies and the transfer is between exciton states: ⁵⁷

where K, L denote the exciton states involved in the transfer, c _iK and c _iL are the corresponding excitonic coefficients and ω _KL = (ω _L  − ω _K ) their energy difference. In this case, the effects of the static disorder is through the composition of the excitons represented by the excitonic coefficients.

In many cases, neither the Förster nor the Redfield regime alone adequately describes excitation energy transfer, necessitating a hybrid Redfield–Förster approach. In this framework, the excitonic Hamiltonian is partitioned into blocks, each representing a group of strongly coupled pigments. Within each block, strong couplings lead to exciton delocalization, while weaker inter-block couplings are treated perturbatively and drive energy transfer between blocks. ^{49 , 58} As a result of this partitioning, exciton states are localized within individual blocks. Energy relaxation among excitons within the same block is described using Redfield theory, capturing coherent population dynamics among delocalized states. In contrast, inter-block transfers are treated with the Generalized Förster (GF) approach, where transitions occur incoherently between excitons. The EET rate from exciton K to L, belonging to different blocks, is given by:

In this context, disorder can influence energy transfer by combining the effects typically associated with both the Redfield and Förster regimes. Moreover, it can perturb the partitioning of the system into blocks of strongly coupled pigments, potentially altering the definition and stability of excitonic compartments.

Neglecting static disorder in EET simulations can therefore result not only in quantitative inaccuracies but also in qualitative artifacts. To properly account for these effects, it is necessary to recalculate the excitonic Hamiltonian over an ensemble of system configurations, typically sampled from a sufficiently long molecular dynamics (MD) trajectory – potentially extending to the microsecond timescale. However, achieving such timescales with fully QM or even hybrid QM/MM methods is computationally prohibitive. As a result, most studies rely on classical MD simulations using molecular mechanics (MM) force fields to generate the structural ensembles required for statistically meaningful modeling of disorder. ⁴³

3.2 Photochemistry

The computational approaches commonly used to study photoreceptors differ from those described in the previous section for antenna complexes. In this context, the key event is usually an ultrafast, localized photochemical reaction, such as a photoisomerization, occurring on a single chromophore. ^{59 , 60 , 61 , 62 , 63} To accurately describe such light-induced dynamics, the most suitable and widely adopted method is mixed quantum–classical nonadiabatic dynamics. ^{64 , 65 , 66 , 67}

Within this framework, the nuclei are treated classically, evolving according to Newtonian mechanics on a given potential energy surface (PES), while the electronic subsystem is described quantum mechanically through the time-dependent Schrödinger equation:

where M _I is the mass of nucleus I, R _I (t) is the time-dependent position of nucleus I, E _j (R) is the potential energy of the j-th adiabatic electronic state at nuclear geometry R.

Expanding |Ψ(t)⟩ in the adiabatic basis {|ψ _j (R(t))⟩}, the wavefunction becomes:

Substituting into the Schrödinger equation leads to the coupled equations for the electronic amplitudes A _j (t):

where d _jk = ⟨ψ _j |∇ _R |ψ _k ⟩ is the nonadiabatic coupling vector between adiabatic states j and k, and R ̇ is the nuclear velocity. The nonadiabatic coupling vectors, which quantify the coupling between the nuclear and electronic degrees of freedom, become significant in regions where electronic states are nearly degenerate, such as near avoided crossings or conical intersections, allowing for transitions between electronic states

Among the most commonly used formulations of the mixed quantum–classical methods is the trajectory-based approach known as fewest switches surface hopping (FSSH) which was originally developed by Tully. ⁶⁸ The method allows probabilistic hops between PESs to account for nonadiabatic transitions, ensuring a statistically correct description of population transfer among electronic states. Upon a hop, the nuclear kinetic energy is adjusted (typically by rescaling the velocities along the direction of nonadiabatic coupling) to conserve total energy. If there is insufficient kinetic energy to perform the hop (i.e., the hop is “frustrated”), the trajectory continues on the current surface. FSSH has been successfully applied to investigate ultrafast photoactivation mechanisms in photoreceptors such as rhodopsins ^{69 , 70} and phytochromes. ^{71 , 72} In these studies the effects of protein or solvent environments are generally included using within a QM/MM framework.

The success of independent-trajectory methods like surface hopping can be explained recalling that in many photochemical processes, quantum nuclear effects such as interference, tunneling, and zero-point energy can often be neglected. However, quantum decoherence, e.g. the loss of coherence between wave packets evolving on different potential energy surfaces, cannot always be ignored. ⁷³

Because surface hopping treats nuclear motion classically and electronic transitions probabilistically, individual trajectories do not represent the real physical behavior. To recover statistically meaningful quantum observables, such as state populations or branching ratios, averaging over many trajectories is essential (see Fig. 4). The ensemble is needed to reproduce quantum populations through the aggregate of stochastic surface switches (hops), to capture the diversity of initial conditions (e.g., nuclear geometries, velocities) due to quantum zero-point energy and thermal distributions, and to compensate for approximations, such as the absence of nuclear quantum effects or decoherence corrections, by statistical sampling.

Fig. 4:

Comparison between the dynamics of (a) a quantum mechanical wave packet and (b) its semiclassical approximation as described by trajectory surface hopping. Adapted and revised from Ref. 73]

The need to generate a large number of trajectories in surface hopping simulations poses a significant limitation due to the high computational cost. To address this challenge, semiempirical quantum chemical methods have proven to be a valuable solution. Semiempirical methods approximate the electronic structure using parametrized Hamiltonians, allowing substantial reductions in computational demand while maintaining an explicit quantum mechanical description of the key excited states. ⁷⁴ When combined with surface hopping nonadiabatic dynamics, these methods offer a powerful and practical strategy for investigating excited-state processes in proteins, especially in cases where ab initio approaches are computationally unfeasible. ^{64 , 75} In this context, semiempirical techniques enable the on-the-fly calculation of potential energy surfaces, gradients, and nonadiabatic couplings for systems of considerable size. Furthermore, their integration within a QM/MM framework provides an efficient and effective approach for accurately modeling chromophores embedded in complex protein environments. Although semiempirical methods enable extensive excited-state dynamics simulations, they are limited by their parametrization, restricted transferability, and reduced accuracy in describing electronically excited states. However, when carefully benchmarked against high-level calculations or experimental data, the combination of surface hopping and semiempirical quantum chemistry remains one of the most versatile and effective strategies for elucidating detailed mechanistic insights into photoactivation processes in biological systems. A possible alternative is represented by TDDFT which maintains a computational feasibility (even if more expensive than semiempirical methods) but is not limited by the need of parameterization. However, TDDFT is inherently a single-reference method, and as such, it struggles with systems/processes exhibiting a strong multi-reference character, such as conical intersections or diradicals. Moreover, standard hybrid exchange-correlation functionals fail to accurately describe long-range charge-transfer excitations. Range-separated hybrid functionals improve the description but do not fully eliminate the problem in all cases. Finally, TDDFT cannot describe double excitations and this can severely limit the applicability for states with significant double-excitation character, often found in conjugated systems.

3.3 Electron transfer

ET processes play a central role in the photoactivation mechanisms of light-responsive proteins. On the one hand, in photosystems, the sequence begins with excitation energy transfer to the reaction center, where photoactivation occurs via the excitation of the special pair of chlorophyll molecules. This excited state rapidly initiates a cascade of electron transfer steps through a series of cofactors, leading to long-range charge separation which is the key event in the conversion of light energy into chemical energy. On the other hand, photoinduced electron transfer is an alternative mechanism used by photoreceptors to photochemical reactions. In these cases, light absorption triggers an electronic excitation that leads to charge separation within the chromophore or between the chromophore and nearby residues, initiating structural or redox changes that propagate to the signaling domain.

To model the ET processes, quantum chemical calculations are typically carried out on truncated subsystems comprising the donor–acceptor (D–A) pair. In such approaches, environmental (protein and solvent) effects are generally incorporated at classical level by employing a QM/MM framework. Electrostatic or polarizable embedding schemes are employed to capture the influence of the local environment on the electronic structure and interactions of the D–A pair. ^{7 , 76 , 77 , 78 , 79 , 80 , 81 , 82 , 83}

Surface hopping described in the previous section can be effectively applied to study electron transfer by simulating the coupled dynamics of nuclear and electronic degrees of freedom. In this context, electron transfer is modeled as a transition between donor and acceptor states, with hopping events representing the actual charge transfer. The method enables the analysis of population dynamics, transfer rates, and the influence of nuclear motion and environmental factors, when combined with QM/MM.

In many cases, however, we do not need to simulate the real ET dynamics but we can apply a simplified kinetic model. In this case, the ET rate is typically computed using Marcus model ⁸⁴ according to:

where V is electronic coupling between Donor and Acceptor, λ is the reorganization energy and the driving force ΔG is the difference in free energy between the fully relaxed initial and final states.

Under the assumption of a harmonic approximation, this process can be represented by two parabolas with the same curvature (see Fig. 5(a)). Each parabola characterizes the dependence of the free energy on nuclear displacements along an appropriate reaction coordinate R, while constraining the electronic state to that corresponding to the minimum of the respective parabola. Consequently, each parabola represents a diabatic state of the system: one corresponding to the initial state, with the electron localized at the Donor, and the other corresponding to the final state, with the electron localized at the Acceptor. Within the diabatic representation, the electronic coupling V is the off-diagonal element of the electronic Hamiltonian.

Fig. 5:

Harmonic representation of a two-state electron transfer model, R is the collective variable representing the reaction coordinate. (a) Diabatic representation: initial and final diabatic states are described by free energy curves G _i (R) and G _i (R), respectively, which intersects at the transition state (TS). (b) Schematic representation of adiabatic free energy surfaces (solid lines) for the two-state model compared to the respective diabatic picture (dashed lines). Adapted and revised from Ref. 85].

Since diabatic states are not directly available from standard quantum chemical methods (which give adiabatic states), practical calculations rely on approximate schemes to extract or reconstruct diabatic couplings. A very popular approach for calculating the coupling is the Generalized Mulliken–Hush (GMH) which is based on donor/acceptor system described in terms of two adiabatic states |1⟩ and |2⟩ (see Fig. 5(b)). Within this framework, V is defined as

where ΔE = E ₂ − E ₁ is the energy difference between the two adiabatic states, μ ₁₁ and μ ₂₂ are the dipole moment in states 1 and 2 (along the direction of the donor–acceptor dipole), μ 12 = ⟨ 1 | μ ˆ | 2 ⟩ is the transition dipole moment between states 1 and 2. The GMH method can be applied with any electronic structure approach that provides reliable excited-state energy splittings and access to transition dipole moments. In practical applications the coupling must be computed over multiple geometries sampled from molecular dynamics to capture thermal fluctuations, as both geometry and environment significantly modulate V.

The other fundamental parameter of the Marcus rate, is the reorganization energy λ which quantifies the energy required to reorganize the nuclear configuration of both the donor–acceptor complex and its surrounding environment (protein, solvent). To account for both these two components, the total reorganization energy can be rewritten as:

where λ _in is the inner-sphere reorganization energy (nuclear relaxation of the donor–acceptor system) and λ _out the Outer-sphere reorganization energy (reorganization of the environment, e.g., solvent and protein matrix).

Within the harmonic approximation depicted in Fig. 5(a), the inner-Sphere reorganization Energy λ _in is defined as the difference between G _f (R _i ) e G _i (R _i ). In a more general context, the inner-sphere reorganization free energy is calculated through the so-called four-point scheme. ⁷⁶ Within this framework, the ET donor and acceptor are treated as independent entities; that is, structural reorganization of the donor does not affect the configuration of the acceptor, and vice versa. Consequently, the inner-sphere reorganization energy can be obtained as the sum of the individual distortion energies associated with the donor and the acceptor. In practice, this requires calculating the vertical energy gaps at both the donor and acceptor equilibrium geometries.

The outer-Sphere Reorganization Energy λ _out accounts for protein and/or solvent response. Using a simplified model where donor and acceptor are assumed to be embedded in spherical cavities within a continuum dielectric, λ _out becomes:

where Δq is the charge transferred, r _D , r _A are the radii of donor’s and acceptor’s cavities, R _DA the distance between them, and ɛ _s /ɛ _∞ the static/optical dielectric constant of the environment. To get a more accurate estimate, quantum chemical methods need to be used either in combination of continuum solvation models or MD simulations. If an ensemble of configurations (from classical or QM/MM MD) is available, one can compute the reorganization energy from the variance of the energy gap:

where ΔE(R) is the vertical energy gap at each configuration R and ⟨⋅⟩ denotes an average over the MD trajectory. This captures how fluctuations in the environment modulate the driving force for ET and thus contribute to the reorganization energy.

The Marcus model, although fundamental to understanding electron transfer, has key limitations: it assumes harmonic potentials and classical nuclear motion, making it less accurate for systems with anharmonicity or strong vibronic coupling. It is primarily valid in the nonadiabatic regime and it does not fully capture quantum effects like nuclear tunneling. Models that extend beyond Marcus theory aim to address its limitations by incorporating quantum effects and strong electronic coupling . ⁷⁸