Abstract
Metal–ligand bonding and noncovalent interactions (NCIs), such as hydrogen bonding or π–π interactions, play a crucial role in determining the structure, function, and selectivity of both biological and artificial metalloproteins. In this study, we employed a hybrid quantum mechanics/molecular mechanics (QM/MM) approach to investigate the ligation of water or cyanide in a mutated myoglobin system, in which the native heme scaffold was replaced with M-salophen or M-salen Schiff base complexes (M = Cr, Mn, Fe). Using our local vibrational mode analysis, particularly local vibrational mode force constants as intrinsic bond strength parameters, complemented with electron density and natural orbital analyses we explored the role of metal–ligand bonding and NCIs in different environments within the myoglobin pocket. Our analysis revealed that metal–ligand bonding, for both water and cyanide ligands, is strongest in the delta form of distal histidine and favors salophen prosthetic groups, as indicated by an overall increase in metal–ligand bond strength. Hydrogen bonding between the distal histidine and ligand also exhibited greater strength in the delta form; however, this effect was more pronounced with salen prosthetic groups. Additionally, the NCIs within the active pocket of the protein were found to be variable, highlighting the adaptability of local force constants. In summary, our data underscore the potential of computational methodologies in guiding the rational design of artificial metalloproteins for tailored applications, with local vibrational mode analysis serving as a powerful tool for bond strength assessment.
Introduction
Artificial metalloenzymes (ArMs), which differ from their native form and/or function through man-made assembly, have made an integral impact in all facets of chemistry. 1 The design and optimization of ArMs has become an increasingly valued field, particularly due to its promise of aiding new-to-nature reactions, 2 , 3 expanding biosynthetic pathways, 4 and its contribution to therapeutic drug treatment. 5 Achieving effective integration of a protein scaffold with an abiotic metal cofactor often requires a combination of experimental and computational techniques. 6 , 7 , 8 , 9 , 10 , 11 In this regard, heme proteins, which in their native form function as transporters, storage molecules, and electron transfer agents, have garnered significant interest for functional tuning through metal or prosthetic substitutions. 12 , 13
Myoglobin (Mb), a monomeric heme protein that transports molecular oxygen, is of particular interest to mutate to tune its function and activity. One such example is using Mb to enhance a cofactor’s catalytic activity for C–H bond hydroxylation or olefin cyclopropanation. 14 Another example is engineering myoglobin with an iron porphycene cofactor for the dehydration of aldoximes. 15 One proposal to effectively modify ArMs is to use noncovalent interactions (NCIs) to tune the selectivity and function of a protein scaffold. In parallel, Schiff bases, formed by the condensation of amines and aldehydes, have gained attention for their versatility in mimicking metal–ligand interactions. 16 Incorporating Schiff bases into myoglobin via NCIs offers a unique opportunity to investigate modified heme environments and their effects on protein functionality. 17
Previous experimental investigations have shown the importance of NCIs and the role of Schiff Base prosthetic groups within the Mb scaffold through the removal of the heme group and the insertion of Schiff bases. 18 , 19 , 20 Within the chiral cavity of apoMb, salophen or salen Schiff bases coordinated with Cr and Mn were introduced to investigate the H2O2-dependent sulfoxidation of thioanisole. 20 Similarly, prior research examined the Fe(III)-salophen Schiff base complex in the Mb protein, demonstrating enhanced cyanide association compared to apoMb. 18 These findings highlight the critical role of NCIs in stabilizing the system, as evidenced by increased stability following an A71G mutation as well as an increase in activity of sulfoxidation with H64D mutation. 19
NCIs are pivotal in the functionality and stability of artificial metalloenzymes. They play a critical role in dictating the spatial arrangement of cofactors, mediating interactions between protein scaffolds and metal centers, and fine-tuning the selectivity and reactivity of the enzyme. 21 In the context of Schiff base-modified Mb, NCIs, such as hydrogen bonding and π–π stacking, are essential for maintaining the integrity of the engineered active site and facilitating desired catalytic transformations. Therefore, this study aims to elucidate the trends of Schiff base Mb modifications (Schiff Base scaffold, metal, and role of distal histidine type and mutation) on the bond strengths of M–L (M = Cr, Mn, Fe; L = OH2, CN−) bonds, hydrogen bonds, and NCIs in Schiff Base Mb through a sophisticated computational QM/MM framework, utilizing local vibrational mode theory. Figure 1 displays the systems investigated in this work. In this, we hope to showcase the versatility of local modes as an efficient tool to aid in ArM design and optimization.
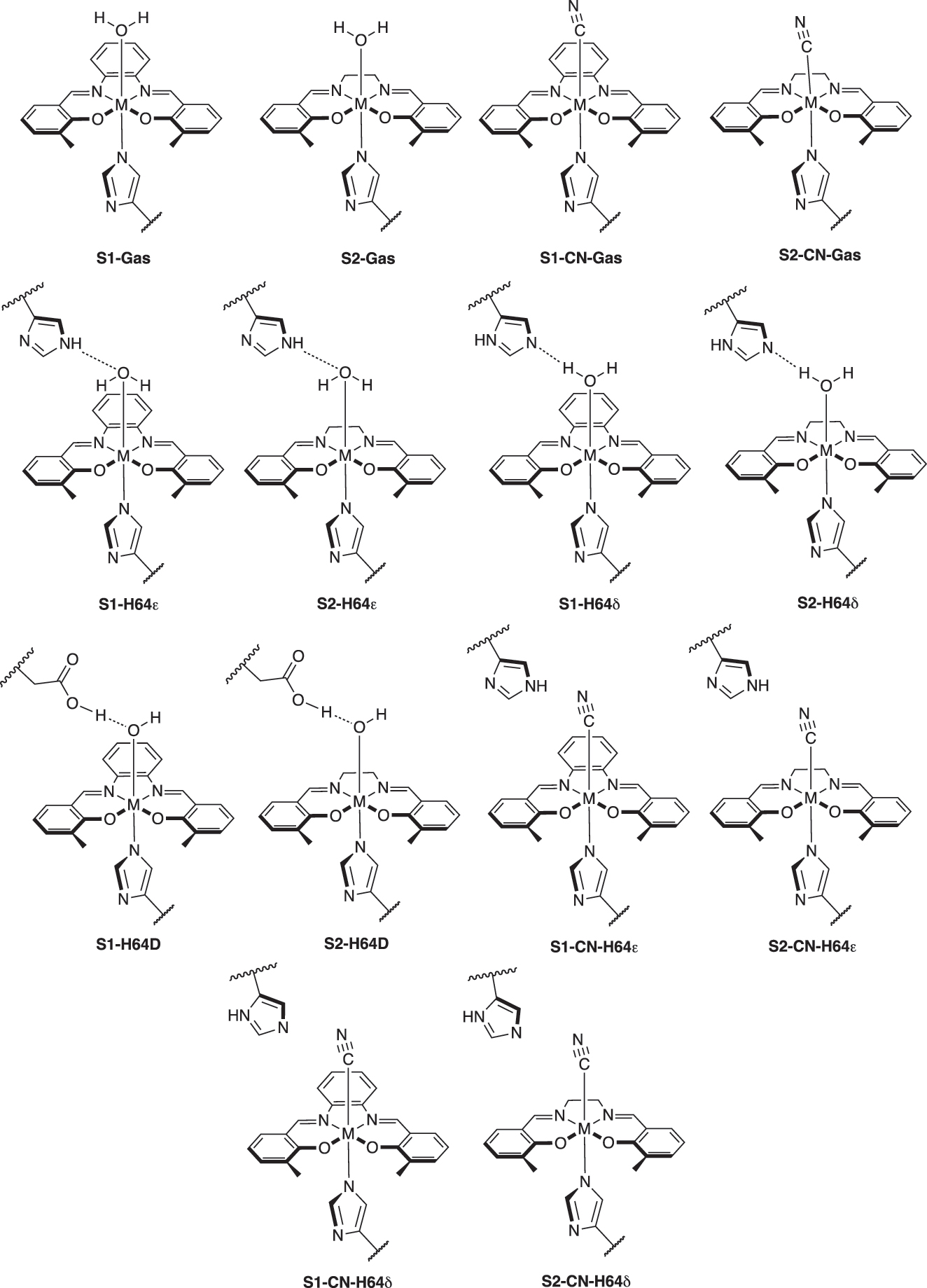
Sketches of active sites in myoglobin and gas phase models with ligands (OH2 and CN) investigated in this study (M = Cr, Mn, Fe). The label of CN indicates cyanide ligand (CN−). All metals were at the +3 oxidation state, with the water ligand producing an overall QM charge of +1 (Cr at the quartet state, Mn at the quintet state, and Fe at the sextet state for multiplicities), and the cyanide ligand producing an overall QM charge of 0.
Theoretical and computational methods
Local vibrational mode analysis
The local vibrational mode theory is briefly introduced here. Readers are encouraged to consult previous review articles for a detailed discussion of the mathematical formalism and applications. 22 , 23 Normal vibrational modes provide valuable electronic structure information. 24 , 25 However, as Wilson already pointed out in 1941, 26 these modes are generally delocalized in polyatomic molecules. Consequently, the common practice of using associated normal mode stretching force constants as bond strength descriptors is questionable. In contrast, local vibrational modes, derived from normal modes, offer local vibrational mode force constants that reflect the intrinsic strength of a chemical bond or weak chemical interaction, such as the metal–ligand interactions, H-bonds, and NCIs investigated in this work.
A local vibrational mode vector a n is defined as:
where K corresponds to the diagonal normal mode force constant matrix expressed in normal mode coordinates Q and d
n
corresponds to the nth normal mode vector in internal coordinates q. Both, quantities can be found in the output of a standard normal mode calculation, offered in most modern quantum chemistry packages,
27
i.e., the local mode analysis (LMA) can be applied with minimal additional computational cost. For each local mode a
n
, the associated local force constants
Additional local mode properties, such as local vibrational frequencies and intensities can be derived as well. 22 , 23
We have successfully applied local vibrational mode theory to assess the strength of covalent and non-covalent interaction across the periodic table 22 , 23 and to characterize π–π interactions, metal–π interactions, and π–H interactions across various chemical environments utilizing specific local mode force constants, designed for this purpose. Recent applications include uranium sandwich complexes, 28 metallocenes, 29 and enzymes. 30 , 31 , 32 , 33 , 34 , 35 Additional valuable features of local mode theory include the Characterization of Normal Modes (CNM) procedure. 36 , 37 CNM decomposes each normal mode into local mode contributions, enhancing the interpretation of vibrational spectra for diverse systems. These range from biological structures, such as DNA base pairs, 38 the exploration of the Jahn–Teller effect in metal–ligand bonding, 39 to the evaluation of potential vibrational Stark-effect probes. 36
In this study, we focused on local mode force constants (k a ) assessing metal–ligand bonding, hydrogen bonding within the distal pocket of the Schiff-base Mb, and NCIs within the active pocket of Mb. Utilizing the generalized Badger’s rule, 40 , 41 we transformed the local force constants into relative bond strength orders (BSO) via a power relationship BSO = A(k a ) B . Two reference molecules with known local force constants and BSO are used to obtain parameters for A and B, with the constraint that a zero value for the local force constant k a yields a zero BSO value. The reference molecules used in our study are presented in Table 1, where for metal–ligand bonds we designated scaled Mayer’s bond orders 42 , 43 , 44 instead of using the classical description of BSO = 1 for single bonds and BSO = 2 for double bonds.
Bond length d, local force constant k a , and bond strength order BSO of selected bonds in reference molecules used in our study.
| Bond | d (Å) | k a (mdyn/Å) | BSO | Molecule |
|---|---|---|---|---|
| M–L | 1.798 | 3.295 | 0.9766 | CuCH3 |
| M = L | 1.647 | 5.464 | 1.882 | NiCH2 |
| H…O/N | 1.144 | 1.202 | 0.5 | [F2H]− |
| 0.919 | 9.934 | 1.0 | FH |
We complemented LMA with Bader’s quantum theory of atoms in molecules (QTAIM) 45 , 46 , 47 to analyze the electron density ρ(r). Specifically, we utilized the Cremer-Kraka criterion 48 , 49 to characterize the covalent and electrostatic nature of bonds based on the local energy density H(r) = G(r) + V(r), where the kinetic density is G(r) and the potential energy is V(r). According to this criterion, the bond character between two atoms (A and B) at the bond critical point can be determined as follows: a negative H(r b ) indicates predominantly covalent character, while a positive H(r b ) signifies predominantly electrostatic character. In addition, we calculated the charge difference of the metal and oxygen utilizing natural population analysis (NPA) to further investigate the M–L bond interactions. 50
Computational methods
We first began by taking PDB structures (1V9Q for Mn(III) salophen, 19 1UFJ for Fe(III) salophen, 18 and 1J3F for Cr(III) salophen 19 ) to model salophen. PDBs with salophen were taken as the starting point and edited manually to model salen structures. Missing amino acids within the protein chain were added with Modeller in ChimeraX. 51 , 52 The sequences of missing amino acids can be found in the Supporting Information, Section 1. A similar procedure was conducted for cyanide ligands, using oxygen from water coordination as the starting point. For systems with mutation of H64D, the mutation was applied and the best score was selected with Dynameomics rotamer in ChimeraX. 52 , 53 All prosthetic groups with metals and water/cyanide coordination were modeled with Metal Center Parameter Builder (MCPB.py) to prepare the protein structure. 54 This approach ensures that molecular modeling of the metal in the protein is accounted for appropriately. Starting from pre-determined models that include the metal, Schiff base, and proximal/distal histidine (H93, H64) up to the β-carbons, QM optimization, and frequency calculations were done with ωB97X-D functional 55 and Pople’s 6-31G(d,p) basis set 56 , 57 as implemented with Gaussian16. 58 Bonded parameters were obtained from Seminario method. 59 For Cr, Mn, and Fe ions, as well as coordinating ligands, the Merz–Singh–Kollman atomic partial charges 60 were obtained with the aforementioned model chemistry and the restrained electrostatic potential (RESP) approach. 61 The coordinating ligands’ backbone (heavy and hydrogen) atoms were held to standard force field values. Metal center parameters were developed for use with the ff19SB AMBER forcefield. 62 After modeling the metal center, hydrogens were added with H++ server, 63 , 64 , 65 and the proteins were neutralized with Cl-atoms, then a water sphere of OPC waters was added 16 Å from the metal center utilizing tleap from AMBER. 66 Two protonation forms were modeled for the distal histidine: epsilon form (H64ϵ) and delta form (H64δ). After appropriate modeling of the protein’s metal center and corresponding waters in AMBER, H’s were minimized for 2000 steps using the steepest descent. TAOpackage was utilized to prepare minimized protein structures as inputs for QM/MM optimization. 67 The QM region incorporates the salophen/salen structure coordinated to the water and the proximal (H93) and distal (H64) histidines (average ∼70 atoms), while the remaining portion of the protein is considered the MM region (average ∼3204 atoms). All proteins were first optimized with mechanical embedding employing the ωB97X-D/6-31G(d,p)/AMBER level of theory, followed by electronic embedding with scaled charges (scalecharge = 333 300) to account for the polarization of the MM region in the QM wavefunction. 55 , 56 , 57 For both optimizations, the self-consistent field (SCF) was set to quadratic convergence, and optimized with quadmacro. 68 , 69 To account for potential spin state effects, we evaluated both high-spin and low-spin states for representative systems. These tests were conducted in the gas phase and with a few QM/MM systems, and the energetically preferred spin states for the water ligand were used for further analysis. For the CN− ligand, depending on the metal, it can either evoke a high-spin or low-spin state; therefore, for consistency, we have calculated all systems with CN− in the high-spin state. Detailed spin-state energetics and structural comparisons are provided in the Supporting Information (Section 2). Frequency calculations ensured no imaginary frequencies to confirm the protein structures were at a local minima. LMA was done with the LMODEA23 package to study metal–ligand bonding, hydrogen bonding, and NCIs. 70 QTAIM analysis was conducted with AIMALL, 71 and NBO analysis was done with NBO version 7.0. 72
Results and discussion
Metal–ligand bonding
This section explores the trends and nature of M–L bonding in Cr, Mn, and Fe systems, using local force constants, QTAIM energy densities, and natural population analysis (NPA) charge (as summarized in Table 2) to elucidate the relationship between structure and bonding characteristics. We first analyze trends in metal–ligand bonding for Cr, Mn, and Fe systems, focusing on the influence of ligand type (water, OH2, and cyanide, CN−, herein labeled CN), prosthetic group type (salphen, S1 and salen, S2) as well as distal histidine (H64ϵ, H64δ, and H64D). Figures 2(a)–(d), 3(a)–(d), and 4(a)–(d) display the different trends of the metal–ligand bond(s) concerning the bond strength (k a , mdyn/Å).
Table showing the distance, extitd between the M–L (M = Cr, Mn, Fe; L = H2O, CN) bond (in Å), local force constant, k a (mdyn/Å), bond strength order, BSO (M–L), energy density, H(r) (Hartree/Å3), and change in charge between the metal and ligand (Δe). The label of CN indicates cyanide ligand (CN−).
| Name | d | k a | BSO (M–L) | H(rH) | Δe |
|---|---|---|---|---|---|
| Cr-S1-Gas | 2.107 | 1.113 | 0.245 | 0.0425 | 2.782 |
| Cr-S2-Gas | 2.112 | 1.125 | 0.248 | 0.0427 | 2.781 |
| Cr-S1-CN-Gas | 2.038 | 1.881 | 0.483 | −0.1615 | 1.916 |
| Cr-S2-CN-Gas | 2.041 | 1.851 | 0.473 | −0.1566 | 1.909 |
| Cr-S1-H64ϵ | 2.185 | 0.631 | 0.117 | 0.0364 | 2.801 |
| Cr-S2-H64ϵ | 2.155 | 0.664 | 0.125 | 0.0410 | 2.799 |
| Cr-S1-H64δ | 2.047 | 1.261 | 0.288 | 0.0421 | 2.843 |
| Cr-S2-H64δ | 2.043 | 1.268 | 0.290 | 0.0447 | 2.831 |
| Cr-S1-H64D | 1.917 | 2.173 | 0.583 | −0.0353 | 2.919 |
| Cr-S2-H64D | 1.940 | 1.836 | 0.469 | −0.0145 | 2.927 |
| Cr-S1-CN-H64ϵ | 2.052 | 1.783 | 0.451 | −0.0141 | 1.905 |
| Cr-S2-CN-H64ϵ | 2.053 | 1.739 | 0.437 | −0.1371 | 1.895 |
| Cr-S1-CN-H64δ | 2.048 | 1.810 | 0.460 | −0.1507 | 1.884 |
| Cr-S2-CN-H64δ | 2.047 | 1.796 | 0.455 | −0.1509 | 1.886 |
| Mn-S1-Gas | 2.405 | 0.300 | 0.045 | −0.0346 | 2.912 |
| Mn-S2-Gas | 2.104 | 1.023 | 0.219 | −0.0435 | 2.606 |
| Mn-S1-CN-Gas | 1.979 | 2.087 | 0.553 | −0.2481 | 2.057 |
| Mn-S2-CN-Gas | 1.989 | 1.728 | 0.433 | −0.2364 | 2.047 |
| Mn-S1-H64ϵ | 2.623 | 0.127 | 0.015 | −0.0206 | 2.907 |
| Mn-S2-H64ϵ | 2.525 | 0.219 | 0.030 | −0.0292 | 2.903 |
| Mn-S1-H64δ | 2.235 | 0.600 | 0.110 | −0.0307 | 2.985 |
| Mn-S2-H64δ | 2.290 | 0.407 | 0.066 | −0.0328 | 2.959 |
| Mn-S1-H64D | 2.037 | 1.177 | 0.263 | −0.0271 | 3.111 |
| Mn-S2-H64D | 2.181 | 0.666 | 0.126 | −0.0257 | 2.716 |
| Mn-S1-CN-H64ϵ | 2.003 | 1.277 | 0.293 | −0.2180 | 1.992 |
| Mn-S2-CN-H64ϵ | 1.991 | 1.963 | 0.511 | −0.2250 | 2.003 |
| Mn-S1-CN-H64δ | 1.983 | 1.997 | 0.522 | −0.2325 | 2.022 |
| Mn-S2-CN-H64δ | 2.227 | 0.793 | 0.158 | −0.1051 | 2.095 |
| Fe-S1-Gas | 2.277 | 0.373 | 0.059 | −0.0435 | 3.041 |
| Fe-S2-Gas | 2.243 | 0.502 | 0.087 | −0.0459 | 3.042 |
| Fe-S1-CN-Gas | 2.086 | 1.529 | 0.370 | −0.2031 | 2.295 |
| Fe-S2-CN-Gas | 2.088 | 1.496 | 0.359 | −0.1993 | 2.278 |
| Fe-S1-H64ϵ | 2.683 | 0.030 | 0.002 | −0.0087 | 3.042 |
| Fe-S2-H64ϵ | 2.677 | 0.012 | 0.001 | −0.0089 | 3.042 |
| Fe-S1-H64δ | 2.158 | 0.675 | 0.128 | −0.0454 | 3.110 |
| Fe-S2-H64δ | 2.144 | 0.755 | 0.148 | −0.0428 | 3.100 |
| Fe-S1-H64D | 1.919 | 1.848 | 0.472 | −0.0845 | 3.235 |
| Fe-S2-H64D | 1.944 | 1.621 | 0.399 | −0.0719 | 3.237 |
| Fe-S1-CN-H64ϵ | 2.109 | 1.379 | 0.327 | −0.1814 | 2.270 |
| Fe-S2-CN-H64ϵ | 2.111 | 1.390 | 0.323 | −0.1814 | 2.250 |
| Fe-S1-CN-H64δ | 2.105 | 1.385 | 0.365 | −0.2046 | 2.266 |
| Fe-S2-CN-H64δ | 2.085 | 1.516 | 0.325 | −0.1889 | 2.253 |
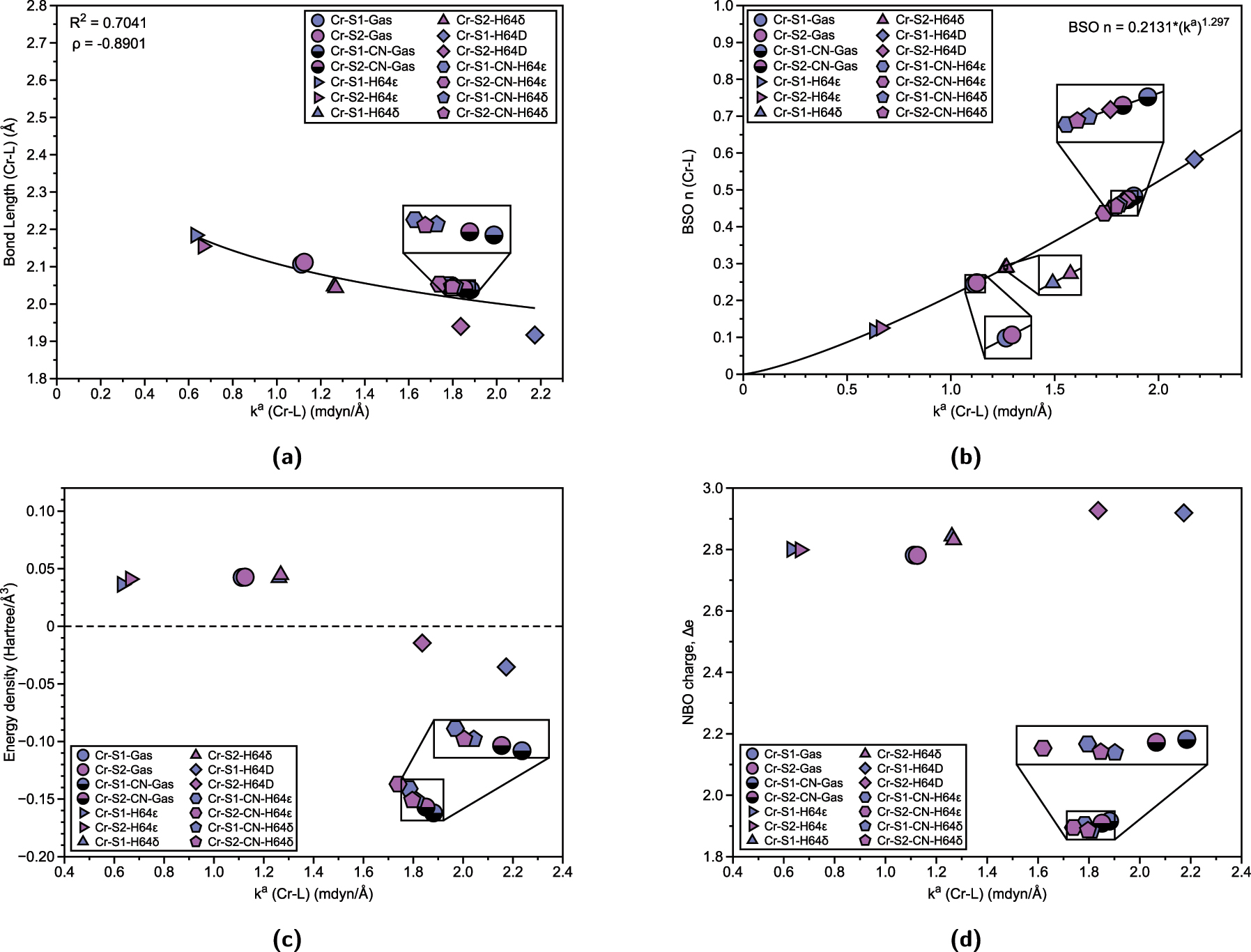
Properties of Cr–L bonds (L = OH2, CN) in Cr(III) Mb Schiff bases and corresponding gas phase models. (a) Relation between Cr–L bond length (Å) and local force constant k a (Cr–L). R 2 values are calculated based on power regression fit. Spearman correlation coefficient ρ is also displayed. (b) BSO n (Cr–L) calculated from local force constant via generalized Badger rule. (c) Relation between energy density H(r) and local force constant k a (Cr–L). (d) Relation between atomic charge difference Δe and local force constant k a (Cr–L).
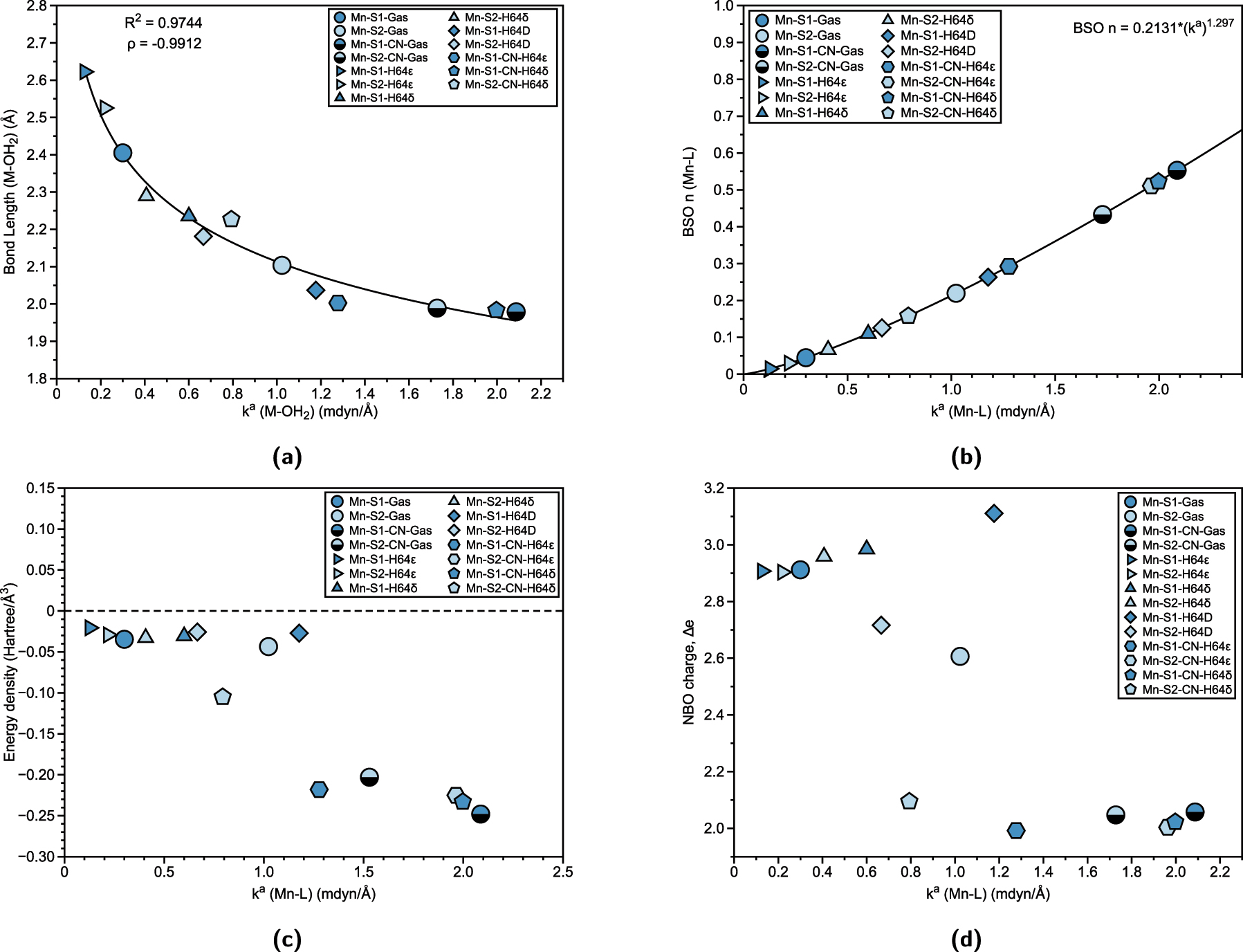
Properties of Mn–L bonds in Mn(III) Mb Schiff bases and corresponding gas phase models. (a) Relation between Mn–L bond length (Å) and local force constant k a (Mn–L). R 2 values are calculated based on power regression fit. Spearman correlation coefficient ρ is also displayed. (b) BSO n (Mn–L) calculated from local force constant via generalized Badger rule. (c) Relation between energy density H(r) and local force constant k a (Mn–L). (d) Relation between atomic charge difference Δe and local force constant k a (Mn–L).
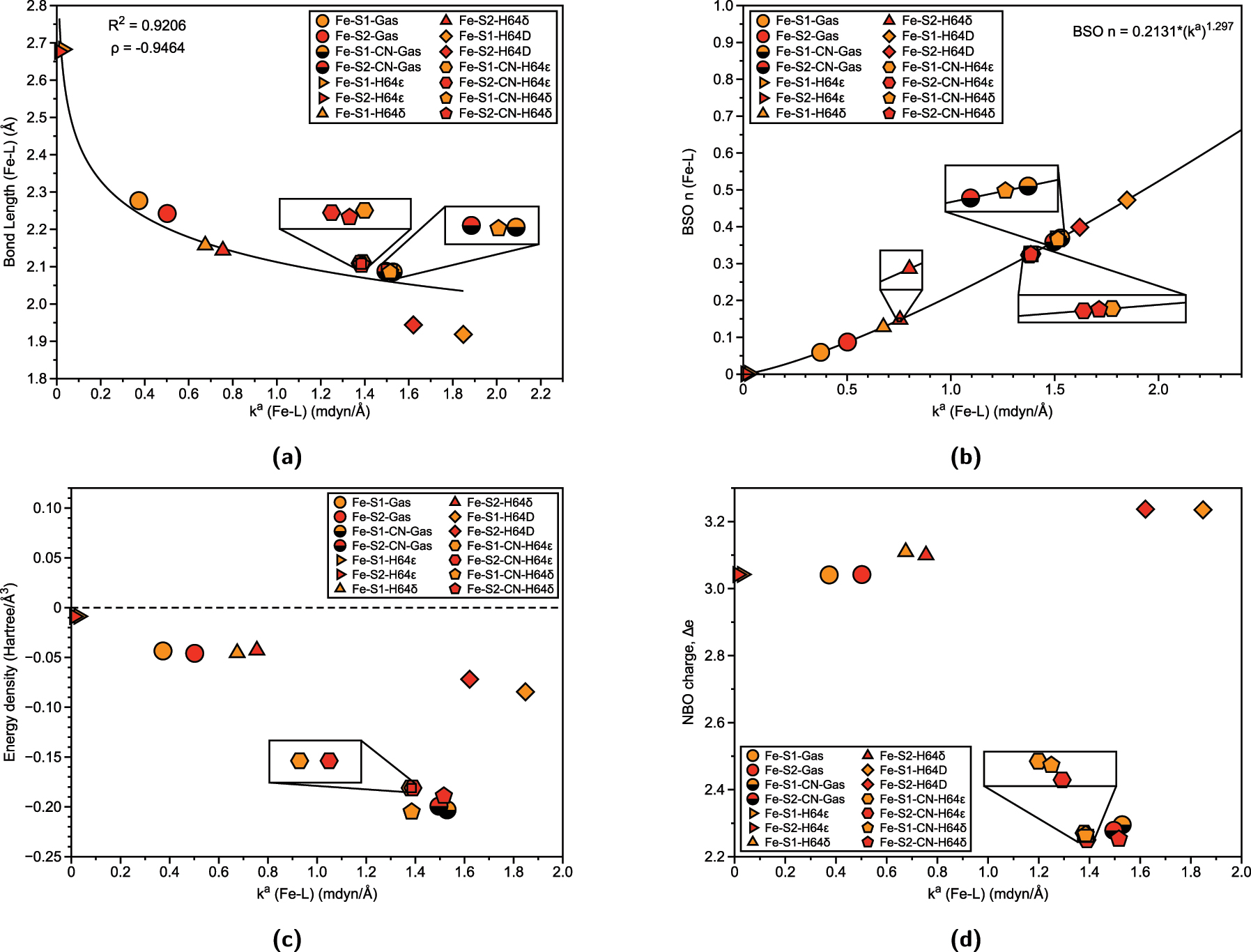
Properties of Fe–L bonds in Fe(III)Mb Schiff bases and corresponding gas phase models. (a) Relation between Fe–L bond length (Å) and local force constant. R 2 values are calculated based on power regression fit. Spearman correlation coefficient ρ is also displayed. (b) BSO n (Fe–L) calculated from local force constant via generalized Badger rule. (c) Relation between energy density H(r) and local force constant k a (Fe–L). (d) Relation between atomic charge difference Δe and local force constant k a (Fe–L).
For the chromium systems, Fig. 2(a) illustrates the correlation between bond length and strength, while Fig. 2(b) displays the local force constant as a function of BSO. Despite the correlation of bond length via power regression (R 2 = 0.7041) and local force constant in Fig. 2(a) appearing to have a weak correlation, we have also shown the Spearman correlation coefficient, ρ, to be consistent with the generalized Badger rule, which states that a shorter bond equates to a stronger bond strength, 41 where the negative sign of ρ reflects the expected inverse nature of the relationship. These analyses reveal that the strongest bonds are observed in systems where the distal histidine is mutated to aspartate (H64D), with the salophen (S1) (Cr-S1-H64D, 2.173 mdyn/Å) exhibiting slightly stronger bond compared to the salen (S2) (Cr-S2-H64D, 1.836 mdyn/Å), despite being similar bond lengths (1.917 Å and 1.940 Å, respectfully). Another noteworthy trend is the effect of the type of histidine on Cr–OH2 bonding. In both S1 and S2, the epsilon form of histidine (Cr-S1-H64 ϵ and Cr-S2-H64 ϵ) weakens the Cr–OH2 bond (0.631 mdyn/Å and 0.664 mdyn/Å) relative to the gas-phase structure (Cr-S1-Gas, 1.113 mdyn/Å and Cr-S2-Gas, 1.125 mdyn/Å), while the delta form (Cr-S1-H64 δ, 1.261 mdyn/Å and Cr-S2-H64 δ, 1.268 mdyn/Å) strengthens it. A similar pattern is observed for Cr–CN bonds: gas-phase structures exhibit the strongest bonds (Cr-S1-CN-Gas, 1.881 mdyn/Å and Cr-S2-CN-Gas, 1.851 mdyn/Å), with the S1 slightly stronger than S2 (average of S1 with CN ligand is 1.829 mdyn/Å compared to S2 average 1.795 mdyn/Å). For both Cr–OH2 and Cr–CN bonds, the H64δ form results in stronger bonds than the H64ϵ form, highlighting the influence of prosthetic group and histidine type on Cr–L bonding. Furthermore, Fig. 2(b) confirms that all Cr–OH2 and Cr–CN bonds have bond strength orders of less than one, indicating that these interactions are characterized as less than a formal single bond.
We now examine the nature of these bonds by analyzing energy density and natural population charges. Figure 2(c) compares the energy density (H(r), Hartree/Å3) with the local force constant for the Cr–L bonds. According to the Cremer–Kraka criterion, a negative energy density indicates covalent bonding, while a positive or near-zero energy density suggests electrostatic (noncovalent) interactions. 73 , 74 This analysis reveals that Cr–OH2 gas-phase structures, as well as the H64ϵ and H64δ forms of both S1 and S2, are characterized as electrostatic Cr–OH2 bonds. This is reflected in the weaker local force constants, which show a slight correlation between bond strength and energy density. However, the correlation coefficient values are relatively low, indicating a weak correlation. The outliers to this trend are the Cr–OH2 bonds in the H64D mutation, where proton transfer from water to aspartate induces a shift toward covalent bonding. This change is reflected in stronger local force constants and negative energy densities, signaling a more stabilized bond. For Cr–CN bonds, similar trends are observed, where gas-phase structures exhibit stronger bonds with greater covalency, while the H64ϵ form in both S1 and S2 results in weaker Cr–CN bonds and less covalent character. Cyanide ligands are known to be stronger ligands in the spectrochemical series, primarily due to their π-backbonding capabilities, which enhance their covalent interactions with metal centers. This stronger interaction is consistent with the observed trend that cyanide ligands form more covalent bonds with chromium compared to water ligands. However, as with the Cr–OH2 systems, the correlation between bond strength and energy density for the Cr–CN bonds remains weak, as reflected in the low correlation coefficients. Further insight is provided by the charge difference between chromium and the ligands, as shown in Fig. 2(d). The Cr–OH2 bond exhibits a charge difference ranging from 2.781 to 2.927, indicating a certain degree of charge transfer between chromium and the water ligand that is modulated by the electronic structure, based on the prosthetic group and histidine type. In contrast, the charge difference for the Cr–CN bond is significantly smaller (below 2.0), reflecting a more balanced charge distribution, which is characteristic of stronger metal–ligand interactions, underscoring the nature of cyanide as a stronger, more covalently bound ligand compared to water. It is important to note that NBO charge differences do not provide a strong predictor of bond strength, suggesting that they should be considered as one factor among others.
Figure 3(a) and (b) show the relationship between bond length and bond strength for Mn–L interactions, as well as the BSO plot with local force constants, respectively. There is a higher correlation (R 2 = 0.9744) of bond length and local force constant, (coupled with a strong negative ρ coefficient), with the general trends being similar to those in the chromium system. Specifically, the H64ϵ form results in a weaker and longer Mn–OH2 bond (Mn-S1-H64 ϵ, 0.127 mdyn/Å, 2.623 Å and Mn-S2-H64 ϵ, 0.219 mdyn/Å, 2.525 Å) compared to the gas-phase structures (Mn-S1-Gas, 0.300 mdyn/Å, 2.405 Å and Mn-S2-Gas, 1.023 mdyn/Å, 2.104 Å), while the H64δ form strengthens the Mn–OH2 bond for the S1 (Mn-S1-H64 δ, 0.660 mdyn/Å). However, the S2 in the H64δ form (Mn-S2-H64 δ, 0.407 mdyn/Å) exhibits a weaker Mn–OH2 bond than its gas-phase counterpart. This may be due to the lengthening of the Mn–OH2 bond as it goes from gas phase 2.104 Å to 2.290 Å in the S2 of H64δ. In contrast to the chromium system, where the strongest metal–ligand interactions are observed for the H64D mutation with Cr–OH2 bonds, the strongest Mn–L bonds are found with cyanide ligands. For manganese, the strongest bond occurs in the gas phase with the S1 (Mn-S1-CN-Gas), followed by the H64δ form of S1 (Mn-S1-CN-H64 δ) and the H64ϵ form of S2 (Mn-S2-CN-H64 ϵ). Figure 3(b) follows the trends observed in chromium, with the BSO of Mn–L bonds consistently showing values characteristic of interactions that are less than a single bond.
Unlike the chromium systems, Fig. 3(c) shows that there is less correlation between the water and cyanide ligands in terms of the local force constant. All of the Mn–L bonds exhibit covalent character, with stronger bonds demonstrating greater covalency than weaker bonds. In Fig. 3(d), the NBO charge difference (Δe) reveals a correlation between charge distribution and the local force constant, although there are two notable outliers for the Mn–OH2 bond (Mn-S2-H64D and Mn-S2-Gas). As observed previously, the water ligands show a greater charge difference between manganese and the oxygen of the water, while for cyanide ligands, the charge difference decreases significantly. The charge difference for cyanide ligands typically ranges from 1.992 to 2.095, suggesting a more balanced charge distribution compared to water ligands.
Lastly, for iron, Fig. 4(a) displays the relationship between bond length and bond strength for Fe–L interactions, while Fig. 4(b) shows the BSO plot with the local force constant for Fe–L bonds. Here, the correlation remains for bond length and local force constant (R 2 = 0.9175), with the observed trends being similar to those seen for chromium and manganese. Specifically, the distal histidine (H64ϵ) form results in the weakest and longest bonds for both salophen (S1) and salen (S2) (represented by right triangles, Fe-S1-H64 ϵ, 0.030 mdyn/Å, 2.683 Å and Fe-S2-H64 ϵ, 0.012 mdyn/Å, 2.677 Å). We have previously investigated aquamet-Mb, a water-ligand heme Mb protein, where it was determined that H64δ form was a stronger Fe–OH2 bond compared to H64ϵ form. 30 , 37 This shows that the mutation of distal histidine to aspartate (H64D) as well as the inclusion of cyanide ligands, leads to stronger Fe–L bonds in both protonation states of the distal histidine. The strongest Fe–L bond is observed in the H64D mutation with OH2 ligand, with the salophen (Fe-S1-H64D, 1.848 mdyn/Å) showing slightly stronger Fe–OH2 bond strength than the salen (Fe-S2-H64D, 1.621 mdyn/Å). Figure 4(b) further supports these trends, with Fe–L bonds consistently characterized by bonds less than a single bond, as seen in chromium and manganese systems.
As shown in Fig. 4(c), the Fe–OH2 bonds in the H64ϵ forms for both S1 and S2 (Fe-S1-H64 ϵ and Fe-S2-H64 ϵ) exhibit almost exclusively electrostatic character, with values indicating minimal covalent interaction (−0.0087 Hartree/Å3 and -0.0089 Hartree/Å3, respectively). In contrast, the remaining structures demonstrate greater covalent character. This trend is consistent with Fe–OH2 ligands showing less covalency compared to Fe–CN bonds. We also see a trend of reduced covalency that parallels the trend in Lewis acidity (Fe3+ > Mn3+ > Cr3+), where higher Lewis acidity enhances the metal’s ability to form stronger covalent bonds. As the metal’s Lewis acidity decreases, the bonding becomes more electrostatic, as with Cr–OH2 bonds, and can be reflected in weaker interactions with water ligands. This observation aligns with the behavior of the distal histidine residue: in the H64ϵ tautomer, the imidazole group acts as a Lewis acid, withdrawing electron density from the water ligand and thereby reducing its Lewis basicity, and generally leads to weaker, more electrostatic metal–ligand interactions. Conversely, the H64δ tautomer acts as a Lewis base, enhancing the water ligand’s donor ability and favoring stronger, more covalent bonding with the metal center. When analyzing the NBO charge difference (Δe) in Fig. 4(d), we observe that the charge difference for Fe–OH2 bonds is greater than that for the corresponding Cr and Mn systems, suggesting a stronger electrostatic component in the Fe–OH2 interactions. The Fe–CN ligands, however, show less variation in both force constant and charge difference, indicating more consistent bonding characteristics across different prosthetic groups and protonation states.
Noncovalent interactions
Due to the stability of these Schiff Base prosthetic groups in apomyoglobin protein via experimental characterization, we sought to understand the interplay of NCIs that transpire at the atomistic level. We explored two avenues of NCIs that occur: hydrogen bonding at the distal site (H64 or H64D), and π–π or π–H interactions that take place at the second coordination sphere and active site of myoglobin.
Hydrogen bonding
We first investigated the role of hydrogen bonding (H-bond) between the distal histidine (in both forms of protonation state) or its mutation to aspartate (H64D), and the ligands (both water and cyanide). Table 3 exhibits systems with H-bond’s distance (d, Å), local force constant (k a , mdyn/Å), BSO (H…N/O), and energy density (H(r), Hartree/Å3). The correlation between bond length and local force constant is consistent with the Badger rule, where a stronger bond indicates a shorter bond (Fig. 5(a), (c) and (e)). Several types of H-bonds are observed depending on the distal site of myoglobin. When the histidine is in the H64ϵ form, it acts as the H-bond donor, while either the oxygen from water or the nitrogen from cyanide serves as the H-bond acceptor. In the H64δ form, water acts as the H-bond donor, with nitrogen from cyanide accepting the hydrogen. However, no H-bond donor is present for cyanide ligands. In this case, the histidine undergoes a distortion that results in a very weak interaction between a proton from carbon in histidine and the nitrogen in cyanide (see Figs. S1–S5 in Supporting Information for a depiction of interactions). Finally, for the H64D mutation, proton transfer occurs from one of the hydrogens of water to the oxygen of aspartate, creating an H-bond with aspartate as the donor and water as the acceptor. The H-bond distances range from 1.4 to 2.9 Å, with an average distance of 1.96 Å.
Table showing the distance, d between the H…O/N bond (in Å), local force constant, k a (mdyn/Å), bond strength order, BSO (H…O/N), and energy density H(r) (Hartree/Å3).
| Name | d | k a | BSO (H…O/N) | H(r) |
|---|---|---|---|---|
| Cr-S1-H64ϵ | 2.026 | 0.188 | 0.272 | −0.006 |
| Cr-S2-H64ϵ | 1.994 | 0.177 | 0.267 | −0.005 |
| Cr-S1-H64δ | 1.645 | 0.317 | 0.323 | −0.063 |
| Cr-S2-H64δ | 1.651 | 0.328 | 0.327 | −0.055 |
| Cr-S1-H64D | 1.553 | 0.304 | 0.318 | −0.064 |
| Cr-S2-H64D | 1.477 | 0.228 | 0.290 | −0.151 |
| Cr-S1-CN-H64ϵ | 2.278 | 0.092 | 0.215 | 0.010 |
| Cr-S2-CN-H64ϵ | 2.275 | 0.074 | 0.200 | 0.009 |
| Cr-S1-CN-H64δ | 2.544 | 0.055 | 0.182 | 0.005 |
| Cr-S2-CN-H64δ | 2.587 | 0.057 | 0.184 | 0.006 |
| Mn-S1-H64ϵ | 1.948 | 0.215 | 0.284 | −0.006 |
| Mn-S2-H64ϵ | 2.035 | 0.157 | 0.256 | −0.006 |
| Mn-S1-H64δ | 1.651 | 0.394 | 0.347 | −0.054 |
| Mn-S2-H64δ | 1.769 | 0.307 | 0.320 | −0.013 |
| Mn-S1-H64D | 1.448 | 0.223 | 0.288 | −0.203 |
| Mn-S2-H64D | 1.455 | 0.377 | 0.342 | −0.167 |
| Mn-S1-CN-H64ϵ | 2.031 | 0.173 | 0.265 | 0.005 |
| Mn-S2-CN-H64ϵ | 2.045 | 0.123 | 0.237 | 0.005 |
| Mn-S1-CN-H64δ | 2.584 | 0.052 | 0.178 | 0.006 |
| Mn-S2-CN-H64δ | 2.485 | 0.100 | 0.221 | 0.008 |
| Fe-S1-H64ϵ | 1.902 | 0.229 | 0.290 | −0.004 |
| Fe-S2-H64ϵ | 1.904 | 0.180 | 0.268 | −0.030 |
| Fe-S1-H64δ | 1.713 | 0.306 | 0.319 | −0.004 |
| Fe-S2-H64δ | 1.708 | 0.307 | 0.320 | −0.030 |
| Fe-S1-H64D | 1.617 | 0.251 | 0.299 | −0.031 |
| Fe-S2-H64D | 1.521 | 0.238 | 0.294 | −0.096 |
| Fe-S1-CN-H64ϵ | 2.206 | 0.085 | 0.210 | 0.008 |
| Fe-S2-CN-H64ϵ | 2.083 | 0.129 | 0.240 | 0.005 |
| Fe-S1-CN-H64δ | 2.953 | 0.023 | 0.137 | 0.008 |
| Fe-S2-CN-H64δ | 2.440 | 0.073 | 0.199 | 0.005 |

Properties of hydrgoen bonding in M(III) Schiff bases. (a) Cr hydrogen bonding correlation between bond length and local force constant. R 2 values are calculated based on power regression fit. Spearman correlation coefficient ρ is also displayed. (b) Cr hydrogen bonding BSO (c) Mn hydrogen bonding correlation between bond length and local force constant. (d) Mn hydrogen bonding BSO. (e) Fe hydrogen bonding correlation between bond length and local force constant. (f) Fe hydrogen bonding BSO ωB97X-D/6-31G(d,p)/AMBER level of theory.
Figure 5(b) shows the bond strength order (BSO) (H…N/O) of the chromium systems in relation to their local force constant. The strongest H-bond interactions in the chromium systems occur with Cr–OH2 ligands. Specifically, Cr-S2-H64 δ (0.328 mdyn/Å and 1.651 Å) and Cr-S1-H64 δ (0.317 mdyn/Å and 1.645 Å) exhibit the strongest H-bond interactions. Comparatively, the H64ϵ form of histidine creates less favorable H-bonding geometries, leading to longer bonds and weaker interactions, as seen in Cr-S1-H64 ϵ (0.188 mdyn/Å and 2.206 Å) and Cr-S2-H64 ϵ (0.177 mdyn/Å and 2.026 Å). The mutation of the distal histidine to aspartate (H64D) creates a moderate H-bond interaction. Additionally, the presence of cyanide (Cr–CN) ligands weakens the H-bond interactions, with the weakest observed in Cr-S1-CN-H64 δ (0.055 mdyn/Å and 2.544 Å) and Cr-S2-CN-H64 δ (0.057 mdyn/Å and 2.587 Å).
For manganese, the trends differ slightly, as shown in Fig. 5(d). The strongest H-bonding interactions occur in Mn-S1-H64 δ and Mn-S2-H64D, demonstrating the adaptability of how both the metal–ligand bond and secondary interactions, such as H-bonding, influence the overall interaction, as captured by the local force constants. Mn-S2-H64 δ and Mn-S1-H64D exhibit moderate strength, followed by Mn-S1-H64 ϵ and Mn-S1-CN-H64 ϵ. These results suggest that, for water ligands, there is a slight preference for H64D and H64δ systems, though the trend is dependent on the prosthetic group type: preference for S1 when histidine is present and preference for S2 when H64D is present. The weakest H-bond occurs with the cyanide ligands, in Mn-S1-CN-H64 δ (0.052 mdyn/Å and 2.584 Å).
Following the manganese systems, the iron systems shown in Fig. 5(f) exhibit the strongest H-bond interactions in Fe-S2-H64 δ (0.307 mdyn/Å and 1.708 Å) and Fe-S1-H64 δ (0.306 mdyn/Å and 1.713 Å), followed by Fe-S1-H64D. Moderate H-bond strength is observed in Fe-S2-H64D and Fe-S1-H64 ϵ. The weakest H-bond occurs in Fe-S1-CN-H64 δ (0.023 mdyn/Å and 2.953 Å). Overall, the trends show that CN ligands exhibit weaker H-bonds overall, with H64δ being the weakest. Unlike the water ligand environment, where hydrogen from the water acts as the H-bond donor when switching from H64ϵ to H64δ, the CN ligand does not have an H-bond donor, and as discussed previously, the distal histidine distorts to have hydrogen from a nearby carbon form a weak nonclassical hydrogen bond (seen in Fig. S4). This can also be realized through energy density H(r) in Table 3, where all CN H-bonds are positive, indicating electrostatic character, unlike the rest of the H-bonds having negative covalency character.
H-bonding visualized by Characterization of Normal Modes
Since our investigation focused on the elucidation of differences in H-bonding at the distal histidine of the mutated Mb, we utilized in addition to the comparison of H-bond strengths CNM as an important tool to uncover sensitive differences in the H-bond normal mode composition. It is important to note that the CNM procedure requires a complete non-redundant and chemically meaningful set of N vib local mode parameters, with N vib = (3N − 6) for nonlinear molecule and (3N − 5) for a linear molecule being composed of N atoms. For QM/MM systems where the total number of QM and MM atoms can easily reach several thousand, this can be daunting task. To address this challenge, our group has developed two tools to streamline the CNM procedure for large systems. First, the Generalized Subsystem Vibrational Analysis (GSVA) projects the full N vib vibrational space of a large system, e.g., a QM/MM system into a reduced, user-defined subspace, such as the QM region of the QM/MM system. 75 Next, LModeAGEN (integrated in LModeA) which is based on graph theory, automatically generates a complete set of non-redundant, chemically meaningful local mode parameters. 76 , 77
As an example, CNM was implemented for Cr-S1-H64 ϵ and Cr-S1-H64 δ, both containing 3264 atoms, resulting in a total vibrational mode count (N vib ) of 9786. By restricting the analysis to the 72 QM atoms, N vib is reduced to 204 vibrational modes. Figure 6(a) and (b) illustrate a variety of normal vibrational modes, highlighting significant contributions from either the Cr–OH2 or Cr–N(H93) interactions, typically observed at lower frequencies, as well as stretching modes associated with the H-bonding distal histidine region. Figure 6(a), which depicts the CNM for Cr-S1-H64 ϵ, shows a strongly localized normal mode at 3663 cm−1 for the distal histidine N–H stretch, with 96 % local mode character. At the lower frequency of 61 cm−1, significant delocalization is observed, with only 16 % local mode character attributed to the H-bond (O…H). The O–H asymmetric stretches for water, occurring at 3758 cm−1 and 3870 cm−1, display varying degrees of delocalization, with local mode contributions of approximately 62 % and 36 %, respectively. In contrast, Fig. 6(b), which represents the CNM for Cr-S1-H64 δ, highlights the distinct nature of H-bonding associated with different protonation states of histidine. One O–H bond participating in an H-bond interaction with histidine results in a completely localized O–H stretch at 3921 cm−1, with 99 % local mode character. Additionally, at 2702 cm−1, the O–H bond involved in H-bonding to the distal histidine exhibits 92 % local mode character, with 7 % of the local mode contribution arising from the H-bond interaction (N…H). Utilizing CNM as a powerful tool, these findings highlight the pivotal role of protonation states and H-bonding interactions in shaping the vibrational properties and mode localization within the protein system.

Decomposition of selected normal vibrational modes into stretching, bending, and torsional local modes involving H-bond between water and distal histidine in myoglobin (a) in Cr-S1-H64 ϵ and (b) in Cr-S1-H64 δ.
Noncovalent local force constants
NCIs and their role in modifying metalloproteins have been extensively discussed in previous reviews and articles. 21 , 78 , 79 , 80 In the active pocket, or secondary coordination sphere, a variety of weak interactions occur with the heme prosthetic group in typical myoglobin proteins. 79 , 81 We have previously investigated π–π interactions for mutated tryptophan Mb’s utilizing a unique local force constant that takes the geometric center point of a ring and projects the stretching component utilizing Cremer-Pople’s curvilinear coordinates. 30 Additionally, studies validating the characterization of NCIs within a QM/MM framework demonstrated that the AMBER force field captures dispersion interactions with lower mean average error than other commonly used force fields. 82 However, these findings were based on cumulative energetic properties. We propose that our local mode approach offers a more direct and computationally efficient means of capturing these weak interactions, without sacrificing accuracy. This method could enable the efficient study of secondary interactions within metalloprotein systems, providing new insights into their role in structural and functional modulation.
To capture the range of weak interactions that could occur, we have narrowed the possibility of interactions to be within 4 Å of the active size, utilizing VMD software 83 to quantify the amino acids of interest. We then only considered two types of interactions: π–π and π–H interactions that are interacting with the Schiff base prosthetic group. By doing this, we can capture the direct NCIs local force constant that might affect the prosthetic group’s geometry. Overall three amino acids will be discussed: F43, V68, and H97. Their relative placement concerning the active pocket is shown in Fig. 7. It is important to note that certain interactions vary depending on the orientation of the Schiff base prosthetic group’s ring system. To address this, Fig. 8 provides a schematic with labels (A–F) representing the types of NCIs studied in myoglobin (Mb). Overall, six types of NCIs were identified across the 30 proteins analyzed. A brief description of each type is as follows: H97-A is either a π–π interaction for S1 or a π–H interaction for S2, since it lacks the additional ring. V68-B and V68-F are both π–H interactions, while F43-A/E are both π–π interactions, with F43-A occurring for S1 and F43-E occurring for S2. F43-C and F43-D are both π–π interactions regardless of whether it is an S1 or S2.
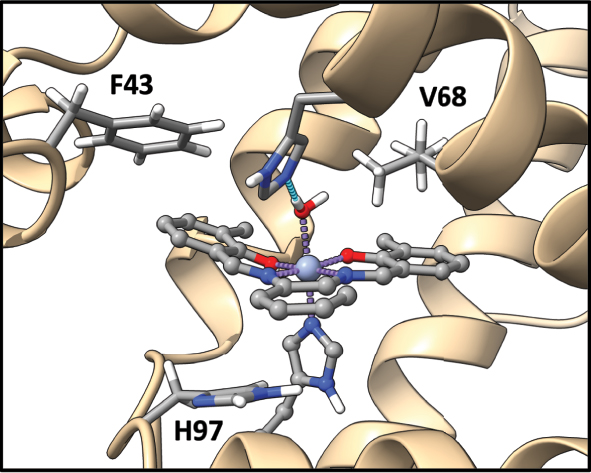
Noncovalent interactions of interest that occur within Schiff base myoglobin.
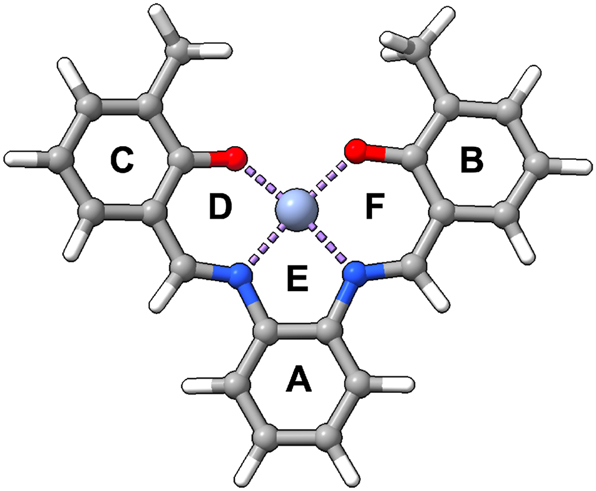
Labeling of rings within Schiff base salophen.
A preliminary analysis showed no obvious correlation between bond length and bond strength, showcasing that in this scenario the Badger rule does not apply (Fig. S6 in Supporting Information). It is also noteworthy to mention that due to the nature of the projection procedure (where we calculate utilizing Cremer’s mean ring plane 84 in the z direction 30 ) to calculate the unique local force constant, it creates a shorter local bond length than if one were to use normal parameters in LMODEA. A complete table of all NCI parameters calculated is shown in Table S6 of the Supporting Information, with the main focus presented here utilizing the Sz stretching (indicated by index 23 in LMODEA). The greatest interactions usually occur with H97-A, with weaker interactions for S2 (since it is a π–H interaction rather than a π–π interaction). However, there is a lot of variability, showcasing that every protein environment is different, which is captured by local force constants. While local mode force constants derived from harmonic analysis provide insight into the intrinsic vibrational stiffness of noncovalent interactions, it is important to emphasize the limitations of harmonic potentials in accurately capturing weak dispersion interactions and cooperative effects. These complexities likely contribute to the lack of correlation between local force constants and bond distances observed here. We therefore outline the potential for future work to investigate these aspects in greater detail, possibly through comparisons with more advanced models or pairwise dispersion energy calculations.
To better understand the influence of the collective 6 NCI interactions that occur, we have collected and plotted the average NCI local force constants in Fig. 9. From here we can make observations on the collective trends that affect the interaction of NCI from the type of prosthetic group, ligand, distal histidine protonation form, as well as the metal. Looking first at chromium, the highest average NCI local force constant is Cr-S2-H64 ϵ while the lowest average is Cr-S2-H64 δ. The general trend is that the S2 and H64ϵ create stronger NCIs, while for the H64D mutation, the S2 decreases in strength compared to S1. For CN ligands, minimal changes occur within the NCIs, indicating that the effect of the ligand does not induce a change in the secondary coordination sphere as much as the change of the distal histidine for chromium systems. For manganese systems the highest average is Mn-S1-H64D, with the lowest coming from Mn-S2-CN-H64 ϵ. No general trend is observed for the prosthetic group in H64ϵ or H64δ form, however there is a significant decrease in average local force constant going from S1 to S2 for H64D mutations. For CN ligands the trend is flipped between H64ϵ and H64δ, where S2 has greater local force constant than S1 with H64δ, and S1 has slightly greater local force constant than S2 with H64ϵ. Lastly, for iron the highest average local force constant is Fe-S2-H64D, with the lowest being Fe-S1-CN-H64 ϵ. There is not much of a difference going from H64ϵ to H64δ for S1, although there is an increase of local force constant going from the same direction for S2. It appears that for H64D mutation S2 has a higher average force constant than S1. For CN ligands S2 has a higher average with H64ϵ, whereas S1 has a higher average with H64δ.
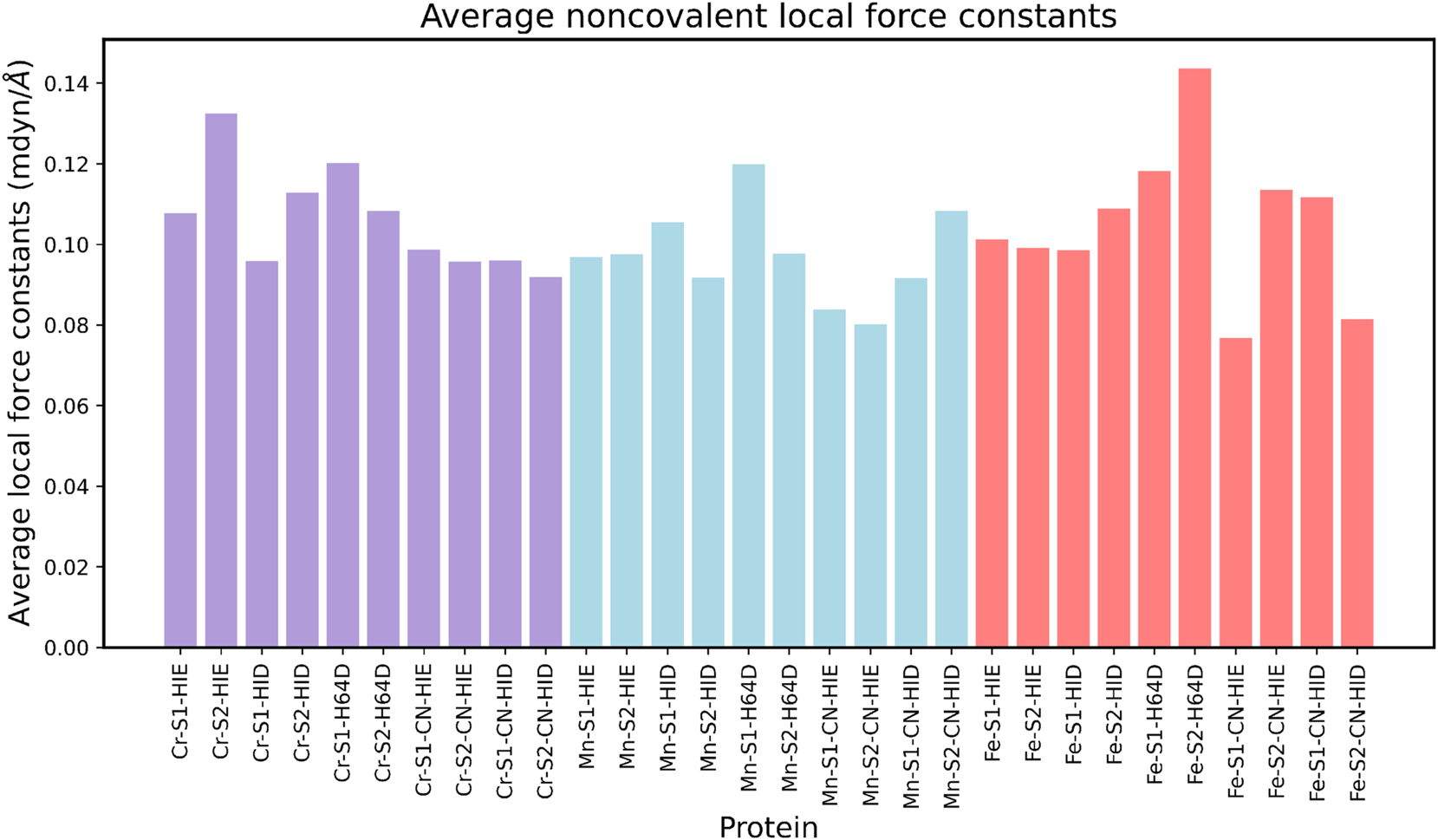
Average local force constants for noncovalent interactions. In this plot, HIE indicates H64ϵ, while HID indicates H64δ.
Conclusions
This study applied a robust computational investigation utilizing a QM/MM framework and LMA coupled with QTAIM and NBO to 42 systems (12 gas phase, 30 proteins), to quantify the M–L bond strength, H-bonds, and NCIs within Schiff Base Mb with either Cr, Mn, or Fe. Our objective was threefold: to investigate the effect of salophen, S1 and salen, S2 prosthetic groups, the protonation state of distal histidine, and ligands (water and cyanide) to M–L bond strengths, H-bonding, and NCIs. As such, our efforts has led us to the following conclusions:
The weakest M–OH2 interactions for Schiff base Mb occur with Fe–OH2, whereas the strongest occur with Cr–OH2 and Mn–OH2. This trend aligns with the Lewis acidity of the metal centers (Cr3+ > Mn3+ > Fe3+). In these instances, the preference for stronger M–OH2 bonds is with salophen S1.
For M–CN interactions, Mn–CN has both the weakest (Mn-S 2-CN -H64 δ ) and strongest (Mn-S 1-CN -H64 δ ) interactions where the preference for stronger M–CN bonds is with salophen S1.
The protonation state of distal histidine highly affects the strength of all interactions investigated, with preference for H64δ for stronger M–L bonds and stronger H-bonds. For NCIs, the preference for distal histidine protonation state can change depending on the type of ligand, metal, and prosthetic group used.
The role of H-bonding with the distal histidine is emphasized, with weaker H-bonds from cyanide ligands, and stronger H-bonds from salen S2 for Cr and Fe.
By analyzing six NCIs, we distinguished individual local force constant components and calculated the average across all 30 proteins, demonstrating that environmental tuning is effectively captured within the local force constant.
Overall, our investigation offers insight into utilizing local force constants to explore and quantify a variety of classical and nonclassical interactions, both strong and weak, to gain a holistic understanding of interaction that occurs not only within proteins but in other systems with a variety of what has been termed nonclassical interactions (in this case CH–π interactions). 80 Current advancements in quantum mechanics calculations allow for dynamic simulations with adaptive QM/MM interfaces, providing a more nuanced understanding of chemical interactions in complex biological systems. 85 Moreover, the integration of machine learning with QM methods is paving the way for automated, high-precision analyses of non-covalent interactions, 86 significantly enhancing our ability to predict and manipulate molecular behaviors. Additionally, the advent of quantum computing in quantum chemistry promises exponential speed-ups in calculating molecular properties, potentially revolutionizing how we model and understand these intricate systems at an atomic level. 87 In the future, we aim to refine the description of local force constants for NCIs and develop a more automated system to derive a nonredundant set incorporating fragments of NCIs such as π-stacking for the CNM procedure, ensuring accurate capture of normal modes with the noncovalent local mode component.
Funding source: National Science Foundation, NSF
Award Identifier / Grant number: CHE2102461
Award Identifier / Grant number: DGE-2034834
Acknowledgments
Computational resources provided by SMU’s O’Donnell Institute of Data Science and High Performance Computing.
-
Research ethics: Not applicable.
-
Informed consent: Not applicable.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Use of Large Language Models, AI and Machine Learning Tools: None declared.
-
Conflict of interest: All other authors state no conflict of interest.
-
Research funding: This work was supported by the National Science Foundation, Grant CHE2102461, and the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-2034834.
-
Data availability: All data are available via the manuscript and/or the supporting Information.
References
1. Vornholt, T.; Leiss-Maier, F.; Jeong, W. J.; Zeymer, C.; Song, W. J.; Roelfes, G.; Ward, T. R. Artificial Metalloenzymes. Nat. Rev. Methods Primers 2024, 4, 78. https://doi.org/10.1038/s43586-024-00356-w.Search in Google Scholar
2. Brouwer, B.; Della-Felice, F.; Illies, J. H.; Iglesias-Moncayo, E.; Roelfes, G.; Drienovská, I. Noncanonical Amino Acids: Bringing New-to-Nature Functionalities to Biocatalysis. Chem. Rev. 2024, 124, 10877–10923. https://doi.org/10.1021/acs.chemrev.4c00136.Search in Google Scholar PubMed PubMed Central
3. Vornholt, T.; Christoffel, F.; Pellizzoni, M. M.; Panke, S.; Ward, T. R.; Jeschek, M. Systematic Engineering of Artificial Metalloenzymes for New-to-Nature Reactions. Sci. Adv. 2021, 7, eabe4208. https://doi.org/10.1126/sciadv.abe4208.Search in Google Scholar PubMed PubMed Central
4. Bloomer, B. J.; Clark, D. S.; Hartwig, J. F. Progress, Challenges, and Opportunities with Artificial Metalloenzymes in Biosynthesis. Biochem 2023, 62, 221–228. https://doi.org/10.1021/acs.biochem.1c00829.Search in Google Scholar PubMed
5. Gao, L.; Zhang, Y.; Zhao, L.; Niu, W.; Tang, Y.; Gao, F.; Cai, P.; Yuan, Q.; Wang, X.; Jiang, H.; Gao, X. An Artificial Metalloenzyme for Catalytic Cancer-Specific DNA Cleavage and Operando Imaging. Sci. Adv. 2020, 6, eabb1421. https://doi.org/10.1126/sciadv.abb1421.Search in Google Scholar PubMed PubMed Central
6. Davis, H. J.; Ward, T. R. Artificial Metalloenzymes: Challenges and Opportunities. ACS Cent. Sci. 2019, 5, 1120–1136. https://doi.org/10.1021/acscentsci.9b00397.Search in Google Scholar PubMed PubMed Central
7. Alonso-Cotchico, L.; Rodriguez-Guerra, J.; Lledos, A.; Marechal, J. D. Molecular Modeling for Artificial Metalloenzyme Design and Optimization. Acc. Chem. Res. 2020, 53, 986–905. https://doi.org/10.1021/acs.accounts.0c00031.Search in Google Scholar PubMed
8. Jeong, W. J.; Yu, J.; Song, W. J. Proteins as Diverse, Efficient, and Evolvable Scaffolds for Artificial Metalloenzymes. Chem. Commun. 2020, 56, 9586. https://doi.org/10.1039/D0CC03137B.Search in Google Scholar
9. Maity, B.; Taher, M.; Mazumdar, S.; Ueno, T. Artificial Metalloenzymes Based on Protein Assembly. Coord. Chem. Rev. 2022, 469, 214593. https://doi.org/10.1016/j.ccr.2022.214593.Search in Google Scholar
10. Matsuo, T.; Hirota, S. Artificial Enzymes with Protein Scaffolds: Structural Design and Modification. Bioorg. Med. Chem. 2014, 22, 5638–5656. https://doi.org/10.1016/j.bmc.2014.06.021.Search in Google Scholar PubMed
11. Shafaat, H. S.; Manesis, A. C.; Yerbulekova, A. How to Build a Metalloenzyme: Lessons from a Protein-Based Model of Acetyl Coenzyme A Synthase. Acc. Chem. Res. 2023, 56, 984–993. https://doi.org/10.1021/acs.accounts.2c00824.Search in Google Scholar PubMed
12. Bhardwaj, M.; Kamble, P.; Mundhe, P.; Jindal, M.; Thakur, P.; Bajaj, P. Multifaceted Personality and Roles of Heme Enzymes in Industrial Biotechnology. 3 Biotech 2023, 13, 389. https://doi.org/10.1007/s13205-023-03804-8.Search in Google Scholar PubMed PubMed Central
13. Lemon, C. M. Diversifying the Functions of Heme Proteins with Non-Porphyrin Cofactors. J. Inorg. Biochem. 2023, 246, 112282. https://doi.org/10.1016/j.jinorgbio.2023.112282.Search in Google Scholar PubMed
14. Oohora, K.; Hayashi, T. Myoglobins Engineered with Artificial Cofactors Serve as Artificial Metalloenzymes and Models of Natural Enzymes. Dalton Trans. 2021, 50, 1940–1949. https://doi.org/10.1039/D0DT03597A.Search in Google Scholar
15. Kato, S.; Abe, M.; Gröger, H.; Hayashi, T. Reconstitution of Myoglobin with Iron Porphycene Generates an Artificial Aldoxime Dehydratase with Expanded Catalytic Activities. ACS Catal. 2024, 14, 13081–13087. https://doi.org/10.1021/acscatal.4c03220.Search in Google Scholar
16. Singh, P.; Yadav, P.; Sodhi, K. K.; Tomer, A.; Mehta, S. B. Advancement in the Synthesis of Metal Complexes with Special Emphasis on Schiff Base Ligands and Their Important Biological Aspects. Results Chem. 2024, 101222. https://doi.org/10.1016/j.rechem.2023.101222.Search in Google Scholar
17. Shahraki, S. Schiff Base Compounds as Artificial Metalloenzymes. Colloids Surf., B 2022, 218, 112727. https://doi.org/10.1016/j.colsurfb.2022.112727.Search in Google Scholar PubMed
18. Ueno, T.; Ohashi, M.; Kono, M.; Kondo, K.; Suzuki, A.; Yamane, T.; Watanabe, Y. Crystal Structures of Artificial Metalloproteins: Tight Binding of FeIII(Schiff-Base) by Mutation of Ala71 to Gly in Apo-Myoglobin. Inorg. Chem. 2004, 43, 2852–2858. https://doi.org/10.1021/ic0498539.Search in Google Scholar PubMed
19. Ueno, T.; Koshiyama, T.; Ohashi, M.; Kondo, K.; Kono, M.; Suzuki, A.; Yamane, T.; Watanabe, Y. Coordinated Design of Cofactor and Active Site Structures in Development of New Protein Catalysts. J. Am. Chem. Soc. 2005, 127, 6556–6562. https://doi.org/10.1021/ja045995q.Search in Google Scholar PubMed
20. Ohashi, M.; Koshiyama, T.; Ueno, T.; Yanase, M.; Fujii, H.; Watanabe, Y. Preparation of Artificial Metalloenzymes by Insertion of Chromium(III) Schiff Base Complexes into Apomyoglobin Mutants. Angew. Chem., Int. Ed. 2003, 42, 1005–1008. https://doi.org/10.1002/anie.200390256.Search in Google Scholar PubMed
21. Hirota, S.; Lin, Y.-W. Design of Artifcial Metalloproteins/Metalloenzymes by Tuning Noncovalent Interactions. J. Biol. Inorg. Chem. 2018, 23, 7–25. https://doi.org/10.1007/s00775-017-1506-8.Search in Google Scholar PubMed
22. Kraka, E.; Zou, W.; Tao, Y. Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory. WIREs: Comput. Mol. Sci. 2020, 10, 1480. https://doi.org/10.1002/wcms.1480.Search in Google Scholar
23. Kraka, E.; Quintano, M.; La Force, H. W.; Antonio, J. J.; Freindorf, M. The Local Vibrational Mode Theory and Its Place in the Vibrational Spectroscopy Arena. J. Phys. Chem. A 2022, 126, 8781–8798. https://doi.org/10.1021/acs.jpca.2c05962.Search in Google Scholar PubMed
24. Kelley, J. D.; Leventhal, J. J. Normal Modes and Coordinates. In Problems in Classical and Quantum Mechanics: Extracting the Underlying Concepts; Springer International Publishing, 2017; pp 95–117.10.1007/978-3-319-46664-4_4Search in Google Scholar
25. Wilson, E. B.; Decius, J. C.; Cross, P. C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill: New York, 1955.10.1149/1.2430134Search in Google Scholar
26. Wilson, E. B. Some Mathematical Methods for the Study of Molecular Vibrations. J. Chem. Phys. 1941, 9, 76–84. https://doi.org/10.1063/1.1750829.Search in Google Scholar
27. Barone, V.; Alessandrini, S.; Biczysko, M.; Cheeseman, J. R.; Clary, D. C.; McCoy, A. B.; DiRisio, R. J.; Neese, F.; Melosso, M.; Puzzarini, C. Computational Molecular Spectroscopy. Nat. Rev. Methods Primers 2021, 1, 38. https://doi.org/10.1038/s43586-021-00034-1.Search in Google Scholar
28. Peluzo, B. M. T. C.; Makoś, M. Z.; Moura, R. T.Jr.; Freindorf, M.; Kraka, E. Linear Versus Bent Uranium(II) Metallocenes – A Local Vibrational Mode Study. Inorg. Chem. 2023, 62, 12510–12524. https://doi.org/10.1021/acs.inorgchem.3c01761.Search in Google Scholar PubMed
29. Antonio, J. J.; Kraka, E. Metal–Ring Interactions in Group 2 ansa-metallocenes: Assessed with the Local Vibrational Mode Theory. Phys. Chem. Chem. Phys. 2024, 26, 15143–15155. https://doi.org/10.1039/d4cp00225c.Search in Google Scholar PubMed
30. Antonio, J. J.; Kraka, E. Non-Covalent π–interactions in Mutated aquomet-Myoglobin Proteins: A QM/MM and Local Vibrational Mode Study. Biochemistry 2023, 62, 2325–2337. https://doi.org/10.1021/acs.biochem.3c00192.Search in Google Scholar PubMed
31. Freindorf, M.; Antonio, J.; Kraka, E. Hydrogen Sulfide Ligation in Hemoglobin I of Lucina pectinata – a QM/MM and Local Mode Study. J. Phys. Chem. A 2023, 127, 8316–8329. https://doi.org/10.1021/acs.jpca.3c04399.Search in Google Scholar PubMed
32. Freindorf, M.; Antonio, J.; Kraka, E. Iron–Histidine Bonding in Bishistidyl Hemoproteins – a Local Vibrational Mode Study. J. Comput. Chem. 2024, 45, 574–588. https://doi.org/10.1002/jcc.27267.Search in Google Scholar PubMed
33. Freindorf, M.; Kraka, E. A Closer Look at the FeS Heme Bonds in Azatobacter Vinelandii Bacterioferritin: QM/MM and Local Mode Analysis. J. Comput. Chem. 2025, 46, e70012; https://doi.org/10.1002/jcc.70012.Search in Google Scholar PubMed PubMed Central
34. Freindorf, M.K. F.; Fleming, K.; Kraka, E. Iron-Histidine Coordination in Cytochrome b5: A Local Vibrational Mode Study. ChemPhysChem 2025, 26, e202401098; https://doi.org/10.1002/cphc.202401098.Search in Google Scholar PubMed
35. Freindorf, M.; Kraka, E. Metal-ligand and Hydrogen Bonding in the Active Site of Fe(III)-, Mn(III)- and Co(III)-myoglobins. Dalton Trans. 2025, 54, 4096–4111; https://doi.org/10.1039/D4DT03246B.Search in Google Scholar PubMed
36. Verma, N.; Tao, Y.; Zou, W.; Chen, X.; Chen, X.; Freindorf, M.; Kraka, E. A Critical Evaluation of Vibrational Stark Effect (VSE) Probes with the Local Vibrational Mode Theory. Sensors 2020, 20, 2358. https://doi.org/10.3390/s20082358.Search in Google Scholar PubMed PubMed Central
37. Machado, F. C.; Quintano, M.; Santos, C. V.Jr.; Neto, A. N. C.; Kraka, E.; Longo, R. L.; Moura, R. T.Jr. Theoretical Insights into the Vibrational Spectra and Chemical Bonding of Ln(III) Complexes with a Tripodal N4O3 Ligand Along the Lanthanide Series. Phys. Chem. Chem. Phys. 2025, 27, 17984–1803. https://doi.org/10.1039/d4cp03677h.Search in Google Scholar PubMed
38. Quintano, M.; Delgado, A. A. A.; MouraJr.R. T.; Freindorf, M.; Kraka, E. Local Mode Analysis of Characteristic Vibrational Coupling in Nucleobases and Watson–Crick Base Pairs of DNA. Electron. Struct. 2022, 4, 044005-1–044005-17. https://doi.org/10.1088/2516-1075/acaa7a.Search in Google Scholar
39. Quintano, M.; Moura, R. T.Jr.; Kraka, E. Exploring Jahn-Teller Distortions: A Local Vibrational Mode Perspective. J. Mol. Model. 2024, 30, 102-1–102-12. https://doi.org/10.1007/s00894-024-05882-8.Search in Google Scholar PubMed PubMed Central
40. Cremer, D.; Kraka, E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010, 14, 1524–1560. https://doi.org/10.2174/138527210793563233.Search in Google Scholar
41. Kraka, E.; Larsson, J. A.; Cremer, D. Generalization of the Badger Rule Based on the Use of Adibatic Vibrational Modes. In Computational Spectroscopy; Grunenberg, J., Ed.; Wiley: New York, 2010; pp 105–149.10.1002/9783527633272.ch4Search in Google Scholar
42. Mayer, I. Charge, Bond Brder an Valence in the Ab Initio Theory. Chem. Phys. Lett. 1983, 97, 270–274. https://doi.org/10.1016/0009-2614(83)80005-0.Search in Google Scholar
43. Mayer, I. Bond Orders and Valences from ab Initio Wave Functions. Int. J. Quantum Chem. 1986, 29, 477–483. https://doi.org/10.1002/qua.560290320.Search in Google Scholar
44. Mayer, I. Bond Order and Valence Indices: A Personal Account. J. Comput. Chem. 2007, 28, 204–221. https://doi.org/10.1002/jcc.20494.Search in Google Scholar PubMed
45. Bader, R. F. W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. https://doi.org/10.1021/ar00109a003.Search in Google Scholar
46. Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, 1995.Search in Google Scholar
47. Popelier, P. Atoms in Molecules: An Introduction; Prentice-Hall: Harlow, England, 2000.Search in Google Scholar
48. Cremer, D.; Kraka, E. Chemical Bonds Without Bonding Electron Density? Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem., Int. Ed. 1984, 23, 627–628. https://doi.org/10.1002/anie.198406271.Search in Google Scholar
49. Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281.Search in Google Scholar
50. Reed, A. E.; Weinstock, R. B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. https://doi.org/10.1063/1.449486.Search in Google Scholar
51. Eswar, N.; Webb, B.; Marti‐Renom, M. A.; Madhusudhan, M.; Eramian, D.; Shen, M.-y.; Pieper, U.; Sali, A. Comparative Protein Structure Modeling Using Modeller. Curr. Protoc. Bioinf. 2006, 15, 5.6.1–5.6.30. https://doi.org/10.1002/0471250953.bi0506s15.Search in Google Scholar PubMed PubMed Central
52. Meng, E. C.; Goddard, T. D.; Pettersen, E. F.; Couch, G. S.; Pearson, Z. J.; Morris, J. H.; Ferrin, T. E. UCSF ChimeraX: Tools for Structure Building and Analysis. Protein Sci. 2023, 32, e4792. https://doi.org/10.1002/pro.4792.Search in Google Scholar PubMed PubMed Central
53. Scouras, A. D.; Daggett, V. The Dynameomics Rotamer Library: Amino Acid Side Chain Conformations and Dynamics from Comprehensive Molecular Dynamics Simulations in Water. Protein Sci. 2011, 20, 341–352. https://doi.org/10.1002/pro.565.Search in Google Scholar PubMed PubMed Central
54. Li, P.; Merz, K. M. J. MCPB.py: A Python Based Metal Center Parameter Builder. J. Chem. Inf. Model. 2016, 56, 599–604. https://doi.org/10.1021/acs.jcim.5b00674.Search in Google Scholar
55. Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped atom-atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. https://doi.org/10.1039/B810189B.Search in Google Scholar
56. Ditchfield, R.; Hehre, W.; Pople, J. Self-Consistent Molecular-Orbital Methods. IX. an Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. https://doi.org/10.1063/1.1674902.Search in Google Scholar
57. Hariharan, P.; Pople, J. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Thermochim. Acta 1973, 28, 213–222. https://doi.org/10.1007/BF00533485.Search in Google Scholar
58. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A. V.; Bloino, J.; Janesko, B. G.; Gomperts, R.; Mennucci, B.; Hratchian, H. P.; Ortiz, J. V.; Izmaylov, A. F.; Sonnenberg, J. L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V. G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery, J. A.Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M. J.; Heyd, J. J.; Brothers, E. N.; Kudin, K. N.; Staroverov, V. N.; Keith, T. A.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A. P.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Millam, J. M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Farkas, O.; Foresman, J. B.; Fox, D. J. Gaussian16 Revision C.01; Gaussian Inc: Wallingford CT, 2016.Search in Google Scholar
59. Seminario, J. M. Calculation of Intramolecular Force Fields from Second-Derivative Tensors. Int. J. Quantum Chem. 1996, 60, 1271–1277. https://doi.org/10.1002/(SICI)1097-461X(1996)60:7%3C1271::AID-QUA8%3E3.0.CO;2-W.10.1002/(SICI)1097-461X(1996)60:7<1271::AID-QUA8>3.0.CO;2-WSearch in Google Scholar
60. Singh, U. C.; Kollman, P. A. An Approach to Computing Electrostatic Charges for Molecules. J. Comput. Chem. 1984, 5, 129–145. https://doi.org/10.1002/jcc.540050204.Search in Google Scholar
61. Bayly, C. I.; Cieplak, P.; Cornell, W.; Kollman, P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. https://doi.org/10.1021/j100142a004.Search in Google Scholar
62. Tian, C.; Kasavajhala, K.; Belfon, K. A. A.; Raguette, L.; Huang, H.; Migues, A. N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; Simmerling, C. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained Against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. https://doi.org/10.1021/acs.jctc.9b00591.Search in Google Scholar
63. Anandakrishnan, R.; Aguilar, B.; Onufriev, A. V. H++ 3.0: Automating pK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations. Nucleic Acids Res. 2012, 40, 537–541. https://doi.org/10.1093/nar/gks375.Search in Google Scholar
64. Gordon, J. C.; Myers, J. B.; Folta, T.; Shoja, V.; Heath, L. S.; Onufriev, A. H++: A Server for Estimating P Ka S and Adding Missing Hydrogens to Macromolecules. Nucleic Acids Res. 2005, 33, 368–371. https://doi.org/10.1093/nar/gki464.Search in Google Scholar
65. Myers, J.; Grothaus, G.; Narayanan, S.; Onufriev, A. A Simple Clustering Algorithm Can be Accurate Enough for Use in Calculations of pKs in Macromolecules. Proteins: Struct., Funct., Bioinf. 2006, 63, 928–938. https://doi.org/10.1002/prot.20922.Search in Google Scholar PubMed
66. Case, D.; Aktulga, H.; Belfon, K.; Ben-Shalom, I.; Berryman, J.; Brozell, S.; Cerutti, D.; III, T. C.; Cisneros, G.; Cruzeiro, V.; Darden, T.; Forouzesh, N.; Ghazimirsaeed, M.; Giambaşu, G.; Giese, T.; Gilson, M.; Gohlke, H.; Goetz, A.; Harris, J.; Huang, S. I. Z.; Izmailov, S.; Kasavajhala, K.; Kaymak, M.; Kovalenko, A.; Kurtzman, T.; Lee, T.; Li, P.; Li, Z.; Lin, C.; Liu, J.; Luchko, T.; Luo, R.; Machado, M.; Manathunga, M.; Merz, K.; Miao, Y.; Mikhailovskii, O.; Monard, G.; Nguyen, H.; O’Hearn, K.; Onufriev, A.; Pan, F.; Pantano, S.; Rahnamoun, A.; Roe, D.; Roitberg, A.; Sagui, C.; Schott-Verdugo, S.; Shajan, A.; Shen, J.; Simmerling, C.; Skrynnikov, N.; Smith, J.; Swails, J.; Walker, R.; Wang, J.; Wang, J.; Wu, X.; Wu, Y.; Xiong, Y.; Xue, Y.; York, D.; Zhao, C.; Zhu, Q.; Kollman, P. AMBER 2024; University of California: San Francisco, USA, 2024.Search in Google Scholar
67. Tao, P.; Schlegel, H. B. A Toolkit to Assist ONIOM Calculations. J. Comput. Chem. 2010, 31, 2363–2369. https://doi.org/10.1002/jcc.21524.Search in Google Scholar PubMed
68. Vreven, T.; Frisch, M. J.; Kudin, K. N.; Schlegel, H. B.; Morokuma, K. Geometry Optimization with QM/MM Methods II: Explicit Quadratic Coupling. Mol. Phys. 2006, 104, 701–714. https://doi.org/10.1080/00268970500417846.Search in Google Scholar
69. Bacskay, G. B. A Quadratically Convergent Hartree – Fock (QC-SCF) Method. Application to Closed Shell Systems. Chem. Phys. 1981, 61, 385–404. https://doi.org/10.1016/0301-0104(81)85156-7.Search in Google Scholar
70. Zou, W.; Moura, R.Jr.; Santos, C. V.Jr.; Quintano, M.; Bodo, F.; Freindorf, M.; Cremer, D.; Kraka, E. LModeA2025, Computational and Theoretical Chemistry Group (CATCO); Southern Methodist University: Dallas, TX, USA, 2025.Search in Google Scholar
71. Keith, T. A. AIMAll (Version 19.10.12); TK Gristmill Software: Overland Park KS, USA, 2019.Search in Google Scholar
72. Glendening, E. D.; Badenhoop, J. K.; Reed, A. E.; Carpenter, J. E.; Bohmann, J. A.; Morales, C. M.; Karafiloglou, P.; Landis, C. R.; Weinhold, F. NBO 7.0. Theoretical Chemistry Institute; University of Wisconsin: Madison, 2018.Search in Google Scholar
73. Kraka, E.; Cremer, D. Chemical Implication of Local Features of the Electron Density Distribution. In Theoretical Models of Chemical Bonding. The Concept of the Chemical Bond; Maksic, Z. B., Ed.; Springer Verlag: Heidelberg, Vol. 2, 1990; pp 453–542.10.1515/9783112611746-013Search in Google Scholar
74. Kraka, E.; Cremer, D. Dieter Cremer’s Contribution to the Field of Theoretical Chemistry. Int. J. Quantum Chem. 2019, 119, e25849. https://doi.org/10.1002/qua.25849.Search in Google Scholar
75. Tao, Y.; Zou, W.; Nanayakkara, S.; Freindorf, M.; Kraka, E. A Revised Formulation of the Generalized Subsystem Vibrational Analysis (GSVA). Theor. Chem. Acc. 2021, 140, 31-1–31-5. https://doi.org/10.1007/s00214-021-02727-y.Search in Google Scholar PubMed PubMed Central
76. Moura, R. T.Jr.; Quintano, M.; Antonio, J. J.; Freindorf, M.; Kraka, E. Automatic Generation of Local Vibrational Mode Parameters: from Small to Large Molecules and QM/MM Systems. J. Phys. Chem. A 2022, 126, 9313–9331. https://doi.org/10.1021/acs.jpca.2c07871.Search in Google Scholar PubMed
77. Quintano, M.; Moura, R. T.Jr.; Kraka, E. Frontier Article: Local Vibrational Mode Theory Meets Graph Theory: Complete and Non-Redundant Local Mode Sets. Chem. Phys. Lett. 2024, 849, 141416-1–1141416-13. https://doi.org/10.1016/j.cplett.2024.141416.Search in Google Scholar
78. Ding, K.; Yin, S.; Li, Z.; Jiang, S.; Yang, Y.; Zhou, W.; Zhang, Y.; Huang, B. Observing Noncovalent Interactions in Experimental Electron Density for Macromolecular Systems: A Novel Perspective for Protein – Ligand Interaction Research. J. Chem. Inf. Model. 2022, 62, 1734–1743. https://doi.org/10.1021/acs.jcim.1c01406.Search in Google Scholar PubMed
79. Van Stappen, C.; Deng, Y.; Liu, Y.; Heidari, H.; Wang, J.-X.; Zhou, Y.; Ledray, A. P.; Lu, Y. Designing Artificial Metalloenzymes by Tuning of the Environment Beyond the Primary Coordination Sphere. Chem. Rev. 2022, 122, 11974–12045. https://doi.org/10.1021/acs.chemrev.2c00106.Search in Google Scholar PubMed PubMed Central
80. Adhav, V. A.; Saikrishnan, K. The Realm of Unconventional Noncovalent Interactions in Proteins: Their Significance in Structure and Function. ACS Omega 2023, 8, 22268–22284. https://doi.org/10.1021/acsomega.3c00205.Search in Google Scholar PubMed PubMed Central
81. Jeong, W. J.; Lee, J.; Eom, H.; Song, W. J. A Specific Guide for Metalloenzyme Designers: Introduction and Evolution of Metal-Coordination Spheres Embedded in Protein Environments. Acc. Chem. Res. 2023, 56, 2416–2425. https://doi.org/10.1021/acs.accounts.3c00336.Search in Google Scholar PubMed
82. Kumbhar, S.; Fischer, F. D.; Waller, M. P. Assessment of Weak Intermolecular Interactions Across QM/MM Noncovalent Boundaries. J. Chem. Inf. Model. 2012, 52, 93–98. https://doi.org/10.1021/ci200406s.Search in Google Scholar PubMed
83. Humphrey, W.; Dalke, A.; Schulten, K. VMD – Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. https://doi.org/10.1016/0263-7855(96)00018-5.Search in Google Scholar PubMed
84. Cremer, D.; Pople, J. A. General Definition of Ring Puckering Coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358; https://doi.org/10.1021/ja00839a011.Search in Google Scholar
85. Böselt, L.; Thürlemann, M.; Riniker, S. Machine Learning in QM/MM Molecular Dynamics Simulations of Condensed-Phase Systems. J. Chem. Theory Comput. 2021, 17, 2641–2658. https://doi.org/10.1021/acs.jctc.0c01112.Search in Google Scholar PubMed
86. Bereau, T.; DiStasio, R. A.Jr.; Tkatchenko, A.; von Lilienfeld, O. A. Non-Covalent Interactions Across Organic and Biological Subsets of Chemical Space: Physics-Based Potentials Parametrized from Machine Learning. J. Chem. Phys. 2018, 148, 241706. https://doi.org/10.1063/1.5009502.Search in Google Scholar PubMed
87. Cao, Y.; Romero, J.; Olson, J. P.; Degroote, M.; Johnson, P. D.; Kieferová, M.; Kivlichan, I. D.; Menke, T.; Peropadre, B.; Sawaya, N. P. D.; Sim, S.; Veis, L.; Aspuru-Guzik, A. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. https://doi.org/10.1021/acs.chemrev.8b00803.Search in Google Scholar PubMed
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/pac-2025-0454).
© 2025 IUPAC & De Gruyter
Articles in the same Issue
- Frontmatter
- Review Articles
- Minimum energy path methods and reactivity for enzyme reaction mechanisms: a perspective
- The quantum revolution in enzymatic chemistry: combining quantum and classical mechanics to understand biochemical processes
- A quantum chemical perspective of photoactivated biological functions
- Does chemistry need more physics?
- Rotational dynamics of ATP synthase: mechanical constraints and energy dissipative channels
- Transforming dreams into reality: a fairy-tale wedding of chemistry with quantum mechanics
- The quantum chemistry revolution and the instrumental revolution as evidenced by the Nobel Prizes in chemistry
- Influence of symmetry on the second-order NLO properties: insights from the few state approximations
- The dichotomy between chemical concepts and numbers after almost 100 years of quantum chemistry: conceptual density functional theory as a case study
- How ‘de facto variational’ are fully iterative, approximate iterative, and quasiperturbative coupled cluster methods near equilibrium geometries?
- Electronic structure of methyl radical photodissociation
- Bridging experiment and theory: a computational exploration of UMG-SP3 dynamics
- Research Articles
- O–Li⋯O and C–Li⋯C lithium bonds in small closed shell and open shell systems as analogues of hydrogen bonds
- Metal–ligand bonding and noncovalent interactions of mutated myoglobin proteins: a quantum mechanical study
Articles in the same Issue
- Frontmatter
- Review Articles
- Minimum energy path methods and reactivity for enzyme reaction mechanisms: a perspective
- The quantum revolution in enzymatic chemistry: combining quantum and classical mechanics to understand biochemical processes
- A quantum chemical perspective of photoactivated biological functions
- Does chemistry need more physics?
- Rotational dynamics of ATP synthase: mechanical constraints and energy dissipative channels
- Transforming dreams into reality: a fairy-tale wedding of chemistry with quantum mechanics
- The quantum chemistry revolution and the instrumental revolution as evidenced by the Nobel Prizes in chemistry
- Influence of symmetry on the second-order NLO properties: insights from the few state approximations
- The dichotomy between chemical concepts and numbers after almost 100 years of quantum chemistry: conceptual density functional theory as a case study
- How ‘de facto variational’ are fully iterative, approximate iterative, and quasiperturbative coupled cluster methods near equilibrium geometries?
- Electronic structure of methyl radical photodissociation
- Bridging experiment and theory: a computational exploration of UMG-SP3 dynamics
- Research Articles
- O–Li⋯O and C–Li⋯C lithium bonds in small closed shell and open shell systems as analogues of hydrogen bonds
- Metal–ligand bonding and noncovalent interactions of mutated myoglobin proteins: a quantum mechanical study

