Startseite A note on soliton solutions of Klein-Gordon-Zakharov equation by variational approach
Artikel Open Access

A note on soliton solutions of Klein-Gordon-Zakharov equation by variational approach

  • Najeeb Alam Khan EMAIL logo , Fatima Riaz und Asmat Ara
Veröffentlicht/Copyright: 24. August 2016
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nonlinear Engineering
Aus der Zeitschrift Nonlinear Engineering Band 5 Heft 3

Abstract

In this paper, an investigation has been made to validate the variational approach to obtain soliton solutions of the Klein-Gordon-Zakharov (KGZ) equations. It is evident that to resolve the non-linear partial differential equations are quite complex and difficult. The presented approach is capable of achieving the condition for continuation of the solitary solution of KGZ equation as well as the initial solutions selected in soliton form including various unknown parameters can be resolute in the solution course of action. The procedure of attaining the solution reveals that the scheme is simple and straightforward.

Keywords: Variational principle; Solitary solution; Klein-Gordon-Zakharov equation (KGZ)

1 Introduction

Nonlinear partial differential equations (PDEs) and fractional differential equations (FDEs) are of huge concern for engineers, physicists and mathematicians} as the majority of physical systems are intrinsically nonlinear in nature. The solitary solutions of non linear PDEs and FDEs can illustrate many phenomena in physics and may also provide further understanding of the physical aspects of problems. In recent years, various methods have been developed to obtain the exact analytic, approximate analytic and solitary solution of the nonlinear PDEs and FDEs such as the Runge-Kutta method[1], tanh—sech method[2], extended tanh method[3], ansatz method[4,5], Hirota's method[6], Adomian decomposition method[7], He's variational approach[8—10], Homotopy analysis method[11,12], variational iteration method[13], Homotopy analysis transform method[14,15], residual power series method[16], etc.

In this paper, we consider the following Klein-Gordon-Zakharov equations with nonlinearity:

(1)Utt−Uxx+U+NU+U2U=0,
(2)Ntt−Nxx=U2xx.

The KGZ system is design to model the interaction of the Langmuir wave and the ion acoustic wave in plasma[17,18]. So far, many methods have been proposed to solve Zakharov system (ZS). For example, Glassey[19] presented an energy preserving finite-difference scheme for the ZS, Bekir and Aksoy[20] implemented the exp-function method to solve Zakharov—Kuznetsov and (2+1)-dimensional Broer—Kaup equations, In ref.[21,22], Chang et al. presented a conservative difference scheme for the generalized Zakharov system, Javidi et al.[23] proposed the exact and numerical solitary wave solutions of generalized Zakharov equation by the variational iteration method.

Also many other techniques are used to solve KGZ system, for instance, Zhang et al.[24] discussed Klein—Gordon—Zakharov system with different-degree nonlinearities in two and three space dimensions, proves instability of standing wave and derive a threshold for global existence and blowup, Shi et al.[25] proposed extended wave solutions for a nonlinear KGZ system by using the sine—cosine method and the extended tanh method, Wang et al.[26] implemented the conservative difference methods for the KGZ equations, Ismail and Biswas[27] found the 1-Soliton solution of the KGZ equation with power law nonlinearity.

In our study, we apply He's variational approach[14, 15] to find soliton solutions of Klein-Gordon-Zakharov equation and to achieve the new and more general explicit and exact special solutions of the form as presented in[16].

2 He's variational principle

We suppose the solitary wave solution of the KGZ equations in the following frame:

(3)Ux,t=vξeimx−nt,ξ=x−Ut.

Where, the real function v and constant wave speed U are to be further determined and m, n are constants.

Substituting Eq. (3) into Eq. (1) gives

(4)v″U2−1+v′2inU−2im−n2v+m2v+v+Nv+v3=0.

Equating imaginary part of Eq. (4) equal to zero

(5)v′2inU−2im=0.

On integrating Eq. (5) we get,

(6)v=k.

Where, k is constant of integration and mn=U.

Assuming,

(7)Nx,t=ψξ,ξ=x−Ut.

We have

(8)Nt=∂!ψ∂ξ∂ξ∂t=−Uψ′,Ntt=U2ψ″,Nx=∂ψ∂ξ∂ξ∂x=ψ′,Nxx=ψ″.

Substituting Eq. (8) into Eq. (2) gives,

(9)ψ″=v2″U2−1.

Integrating Eq. (9) twice, by taking the integration constant zero, we obtain,

(10)ψ=1U2−1v2.

Putting the value of N in real part of Eq. (4), we get

(11)v″U2−1−n2v+m2v+v+1U2−1v2v+v3=0.

Simplifying Eq. (11) arrived to the following results.

(12)v″+m2−n2+1U2−1v+U2U2−12v3=0.

Assigning,

(13)α=U2U2−12,

Eq. (12) becomes

(14)v″+m2−n2+1U2−1v+αv3=0.

Multiplying Eq. (14) by 2v' and simplifying it, we acquire:

(15)v′2+m2−n2+1U2−1v2+α2v4=0.

A variational formulation should be established using the semi-inverse method[14,15, 28, 29] as described by He[30]:

(16)J=∫0∞v′2+m2−n2+1U2−1v2+α2v4∂ξ.

The solitary wave solution is assumed to be in the following form[16]:

(17)v=ASechξ.

Where A is a constant to be further determined. Substituting Eq. (17) into Eq. (16) results in

(18)J=A22+3m2−3n2+U2−A2α+U2A2α3−1+U2.

For making J stationary with respect to A

(19)∂J∂A=0,
(20)∂J∂A=2A3α3+23A2+3m2−3n2+U2−1+U2+A2α=0.

After solving the above Eq. (20), we acquire the following value of A:

(21)A=1α2+3m2−3n2+U22−2U2,

Therefore Eq. (13) becomes

(22)v=1α2+3m2−3n2+U22−2U2Sechξ,

So, the solitary wave solution can be obtained as

(23)Ux,t=1α2+3m2−3n2+U22−2U2Sechmx−nteimx−nt,
(24)Nx,t=ψξ=1U2−1v2,
(25)Nx,t=1U2−1ASechξ2=1U2−12+3m2−3n2+U2(2−2U2)αSech2ξ.

The another soliton solution in the form as introduced by Ye and Mo[16]

(26)v=DSech2ξ.

Where D is an unknown constant to be further determined. Substituting Eq. (26) into Eq. (16), the following form is acquired.

(27)J=2D2(1+5m2−5n2+4U2)15(−1+U2)+8D4α35.

For making J stationary with respect to D

(28)∂J∂D=0,
(29)∂J∂D=4D(1+5m2−5n2+4U2)15(−1+U2)+32D3α35=0,
(30)D=12α7611−U2+5m21−U2−5n21−U2+4U21−U2.

Therefore Eq. (26) becomes

(31)v=12α7611−U2+5m21−U2−5n21−U2+4U21−U2Sech2ξ.

So the solitary wave solution can be obtained as

(32)Ux,t=DSech2ξeimx−nt,
(33)lUx,t=12α7611−U2+5m21−U2−5n21−U2+4U21−U2Sech2ξeimx−nt.
(34)Nx,t=ψξ=1U2−1v2,
(35)Nx,t=1U2−1DSech2ξ2=1U2−17(−1−5m2+5n2−4U2)24(−1+U2)αSech4ξ.

Generalized solution

Now we consider the generalized soliton solution of the form:

(36)v=HSechkξ.

Where H is an unknown constant to be further resolute. Substituting Eq. (36) into Eq. (16), we get the following form

(37)J=∫0∞D2(1+m2−n2)Sechξ2k−1+U2+12D4αSechξ4kD2k2Sechξ2+2kSinhξ2dξ.
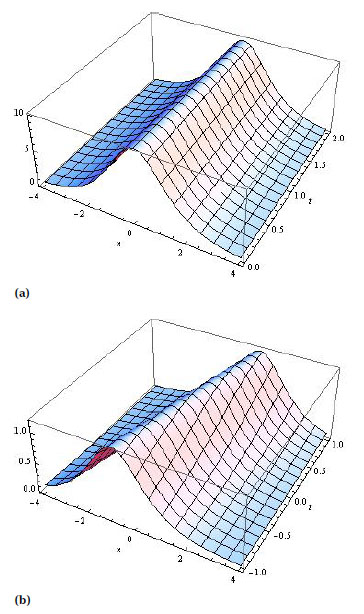
Fig. 1 Solitary waves of 1st soliton KGZ equation when, (a) U = 0.1 (b) U = 0.9
Fig. 1

Solitary waves of 1st soliton KGZ equation when, (a) U = 0.1 (b) U = 0.9

The generalized value of J which we can solve for any value of k by always assuming Re[k]≤ 0, if we solve Eq. (37) for k=1, we get the following form:

(38)J=H2(2+3m2−3n2+U2−H2α+H2U2α)3(−1+U2).

Which is exactly similar to Eq. (18), further solving gives us the same result for the unknown constant H$ as for A. Hence, now we can solve the Eq. (37) for any power of k by using any software like Mathematica, Matlab etc. Some more assumptions which we have to made to acquire the real soliton solutions of higher power is m > n and 0<U<1.

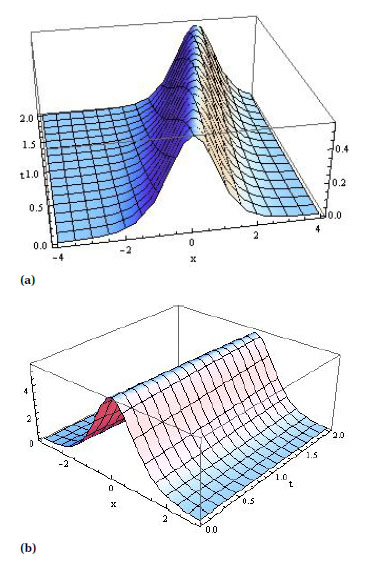
Fig. 2 Solitary waves of 2nd soliton KGZ equation when, (a) U = 0.1 (b) U = 0.9
Fig. 2

Solitary waves of 2nd soliton KGZ equation when, (a) U = 0.1 (b) U = 0.9

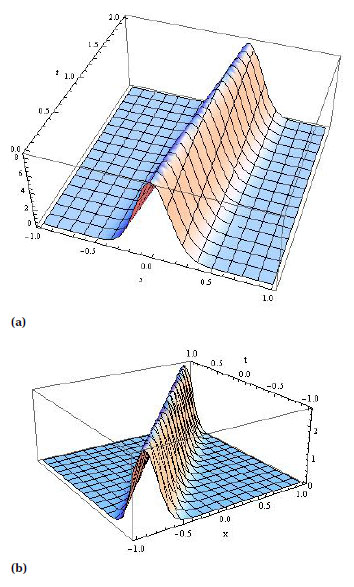
Fig. 3 Solitary waves of generalized soliton KGZ equation when, m = 5, n = 1 and k = 50 (a) U = 0.1 (b) U = 0.9
Fig. 3

Solitary waves of generalized soliton KGZ equation when, m = 5, n = 1 and k = 50 (a) U = 0.1 (b) U = 0.9

Conclusion

The special exact solutions for non-linear Klein-Gordon-Zakharov equations are of vital interest due to its significant applications. The He's variational principle is employed to acquire the solitary solutions for it. It consider the solution in soliton form and variational formula has been made by semi inverse method and solving for the unknown constants provided the required results. The solution obtained proves that He's method is a very beneficial and successful technique to get the solitary solutions for the system of K-G-Z equations.

References

[1] U. M. Ascher, S. J. Ruuth, R. J. Spiteri, 1997, Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations. App. Num. Math., 25(2–3), 151–167.10.1016/S0168-9274(97)00056-1Suche in Google Scholar

[2] A.M. Wazwaz, 2004, The tanh method for travelling wave solutions of nonlinear equations, Appl. Math. Comput., 154(3), 713–723.10.1016/S0096-3003(03)00745-8Suche in Google Scholar

[3] A.M. Wazwaz, 2007, The extended tanh method for abundant solitary wave solutions of nonlinear wave equations, Appl. Math. Comput. 187, 1131–1142.10.1016/j.amc.2006.09.013Suche in Google Scholar

[4] J. Hu, H. Zhang, 2001, A new method for finding exact traveling wave solutions to nonlinear partial differential equations, Phy. Lett. A, 286(2–3), 175–179.10.1016/S0375-9601(01)00291-2Suche in Google Scholar

[5] Ö. Güner, A. Bekir, F. Karaca, 2016, Optical soliton solutions of nonlinear evolution equations using ansatz method, Optik - International Journal for Light and Electron Optics, 127(1), 131–134.10.1016/j.ijleo.2015.09.222Suche in Google Scholar

[6] A.M. Wazwaz, 2008, The Hirota's direct method for multiplesoliton solutions for three model equations of shallow water waves, App. Math. and Comput., 201(1–2), 489–503.10.1016/j.amc.2007.12.037Suche in Google Scholar

[7] A.M.A. El-Sayed, M. Gaber, 2006, The Adomian decomposition method for solving partial differential equations of fractal order in finite domains, Phy. Lett. A, 359(3), 175–182.10.1016/j.physleta.2006.06.024Suche in Google Scholar

[8] J.H. He, 2004, Variational principles for some nonlinear partial differential equations with ariable coeflcients, Chaos Solitons Fractals, 19(4), 847–851.10.1016/S0960-0779(03)00265-0Suche in Google Scholar

[9] J.H. He, Erratum to: 2008, variational principle for twodimensional incompressible inviscid flow, Phys. Lett. A, 372, 5858–5859.10.1016/j.physleta.2008.07.043Suche in Google Scholar

[10] Y.H. Ye, L.F. Mo, 2009, He's variational method for the Benjamin–Bona–Mahony equation and the Kawahara equation, Comput. Math. Appl., 58(11–12), 2420–2422.10.1016/j.camwa.2009.03.026Suche in Google Scholar

[11] K. Vishal, S. Das, 2012, Solution of the nonlinear fractional diffusion equation with absorbent term and external force using optimal homotopy analysis method, Z. Naturforsch, 67a, 203–209.10.5560/zna.2012-0008Suche in Google Scholar

[12] V. Mishra, K. Vishal, S. Das, S.H. Ong, 2014, On the solution of the nonlinear fractional diffusion-wave equation with absorption: A homotopy approach. Zeitschrift für Naturforschung A, 69(3–4), 135-44.10.5560/zna.2013-0084Suche in Google Scholar

[13] S. Das, 2009, A note on fractional diffusion equations, Chaos, Solitons & Fractals, 42, 2074–2079.10.1016/j.chaos.2009.03.163Suche in Google Scholar

[14] S. Kumar, 2014, A new analytical modelling for telegraph equation via Laplace transform, Appl. Math. Model., 38(11), 3154–3163.10.1016/j.apm.2013.11.035Suche in Google Scholar

[15] S. Kumar, M.M. Rashidi, 2014, New Analytical Method for Gas Dynamics Equation Arising in Shock Fronts, Comp. Phy. Commun., 185(7), 1947–1954.10.1016/j.cpc.2014.03.025Suche in Google Scholar

[16] J.J. Yao, A. Kumar, S. Kumar, 2015, A fractional model to describe the Brownian motion of particles and its analytical solution, Adv. Mech. Eng., 7(10), Art. ID: 1687814015618874.10.1177/1687814015618874Suche in Google Scholar

[17] R. O. Dendy, Plasma Dynamics, Oxford University Press, Oxford, UK, 1990.Suche in Google Scholar

[18] V.E. Zakharov, 1972, Collapse of Langmuir waves, Sov. Phys. JETP., 35(5), 908–14.Suche in Google Scholar

[19] R. T. Glassey, 1992, Convergence of an energy-preserving scheme for the zakharov equations in one space dimension. Math. Comput., 58, 83–102.10.1090/S0025-5718-1992-1106968-6Suche in Google Scholar

[20] A. Bekir, E. Aksoy, 2010, Exact solutions of nonlinear evolution equations with variable coeflcients using exp-function method, App. Math. and Comput., 217(1), 430–436.10.1016/j.amc.2010.05.046Suche in Google Scholar

[21] Q. Chang, H. Jiang, 1994, A conservative difference scheme for the Zakharov equations, J. Comput. Phys. 113, 309–319.10.1006/jcph.1994.1138Suche in Google Scholar

[22] Q. Chang, B. Guo, H. Jiang, 1995, Finite difference method for generalized Zakharov equations, Math. Comput., 64, 537–553.10.1090/S0025-5718-1995-1284664-5Suche in Google Scholar

[23] M. Javidi, A. Golbabai, 2008, Exact and numerical solitary wave solutions of generalized Zakharov equation by the variational iteration method, Chaos, Solitons & Fractals, 36(2), 309–313.10.1016/j.chaos.2006.06.088Suche in Google Scholar

[24] Z. Gan, B. Guo, J. Zhang, 2009, Instability of standing wave, global existence and blowup for the Klein–Gordon–Zakharov system with different-degree nonlinearities, J. Diff. Eq., 246(10), 4097–4128.10.1016/j.jde.2009.03.003Suche in Google Scholar

[25] Q. Shi, Q. Xiao, X. Liu, 2012 Extended wave solutions for a nonlinear Klein–Gordon–Zakharov system, App. Math. and Comput., 218(17), 9922–9929.10.1016/j.amc.2012.03.079Suche in Google Scholar

[26] T. Wang, J. Chen, L. Zhang, 2007, Conservative difference methods for the Klein–Gordon–Zakharov equations, J. Comput. App. Math., 205(1), 430–452.10.1016/j.cam.2006.05.008Suche in Google Scholar

[27] M.S. Ismail, A. Biswas, 2010, 1-Soliton solution of the Klein– Gordon–Zakharov equation with power law nonlinearity, App. Math. and Comput., 217(8), 4186–4196.10.1016/j.amc.2010.10.035Suche in Google Scholar

[28] J.H. He, 2008, An elementary introduction of recently developed asymptotic methods and nanomechanics in textile engineering, Internat. J. Modern Phys. B, 22(9), 3487–4578.10.1142/S0217979208048668Suche in Google Scholar

[29] J.H. He, E.W.M. Lee, 2009, A constrained variational principle for heat conduction, Phys. Lett. A, 373, 2614–2615.10.1016/j.physleta.2009.05.039Suche in Google Scholar

[30] J.H. He, 2006, Some asymptotic methods for strongly nonlinear equations, Internat. J. Modern Phys. B, 20 (10), 1141–1199.10.1142/S0217979206033796Suche in Google Scholar

Received: 2016-1-8
Accepted: 2016-5-21
Published Online: 2016-8-24
Published in Print: 2016-9-1

© 2016 Walter de Gruyter GmbH, Berlin/Boston

This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Artikel in diesem Heft

  1. Frontmatter
  2. Original Articles
  3. Dynamic Analysis of Coupled Vehicle-Bridge System with Uniformly Variable Speed
  4. Research Article
  5. A note on soliton solutions of Klein-Gordon-Zakharov equation by variational approach
  6. Research Article
  7. Analytical and numerical validation for solving the fractional Klein-Gordon equation using the fractional complex transform and variational iteration methods
  8. Research Article
  9. Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet
  10. Research Article
  11. Homotopy analysis transform algorithm to solve time-fractional foam drainage equation
  12. Research Article
  13. Effects of Soret, Hall and Ion-slip on mixed convection in an electrically conducting Casson fluid in a vertical channel
  14. Research Article
  15. Chaos suppression of Fractional order Willamowski–Rössler Chemical system and its synchronization using Sliding Mode Control
  16. Research Article
  17. Comparative study of synchronization methods of fractional order chaotic systems
  18. Research Article
  19. Spectral Quasi-linearisation Method for Nonlinear Thermal Convection Flow of a Micropolar Fluid under Convective Boundary Condition
  20. Research Article
  21. Pattern recognition of ocean pH
https://doi.org/10.1515/nleng-2016-0001
Schlagwörter für diesen Artikel
Variational principle; Solitary solution; Klein-Gordon-Zakharov equation (KGZ)
Creative Commons
BY-NC-ND 3.0

Artikel in diesem Heft

  1. Frontmatter
  2. Original Articles
  3. Dynamic Analysis of Coupled Vehicle-Bridge System with Uniformly Variable Speed
  4. Research Article
  5. A note on soliton solutions of Klein-Gordon-Zakharov equation by variational approach
  6. Research Article
  7. Analytical and numerical validation for solving the fractional Klein-Gordon equation using the fractional complex transform and variational iteration methods
  8. Research Article
  9. Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet
  10. Research Article
  11. Homotopy analysis transform algorithm to solve time-fractional foam drainage equation
  12. Research Article
  13. Effects of Soret, Hall and Ion-slip on mixed convection in an electrically conducting Casson fluid in a vertical channel
  14. Research Article
  15. Chaos suppression of Fractional order Willamowski–Rössler Chemical system and its synchronization using Sliding Mode Control
  16. Research Article
  17. Comparative study of synchronization methods of fractional order chaotic systems
  18. Research Article
  19. Spectral Quasi-linearisation Method for Nonlinear Thermal Convection Flow of a Micropolar Fluid under Convective Boundary Condition
  20. Research Article
  21. Pattern recognition of ocean pH
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 30.10.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nleng-2016-0001/html
Button zum nach oben scrollen