Abstract
The transformation of coordinates between different geodetic datums has been a common practice within the geospatial profession. Relating different geodetic datums mostly involves the use of conformal transformation techniques, which could produce results that are not very often satisfactory for certain geodetic, surveying, and mapping purposes. This has been attributed to the inability of the conformal models to resolve the lack (non-exhaustivity) and the heterogeneity of double points existing within the Algerian local geodetic networks. Indeed, the Algerian geodetic network is divided into two main zones completely different in accuracy and points exhaustivity. The North is better and well defined in precision; on the other hand, the South is poorly defined because of the lack of heterogeneity of the points. Mathematical algebraic methods give closed-form solutions to geodetic transformation problems, requiring a high-level computer programming background. In everyday usage, the closed-form solutions are much simpler and have a higher precision than earlier procedures. Thus, it can be predicted that these new solutions will find their place in practice. The present work deals with an important theoretical problem of geodesy: we are looking for a mathematical dependency between two spatial systems using common pairs of points whose coordinates are given in both systems. In geodesy and photogrammetry, the most often used procedure to move from one coordinate system to another is the 3D, seven-parameter similarity transformation (Bursa–Wolf, Molodensky–Badekas, and Helmert).
1 Introduction
3D conformal transformations, also known as similarity transformations (since conformal transformations preserve shape and angles between vectors in space remain unchanged), are commonly used in surveying, photogrammetry, and geodesy. These transformations are necessary for the purposes of cartography, geodesy, and other topographical and cadastral work when the coordinates are generally expressed in the system in effect in a country. The present work consists of developing a strategy of observation, processing double geodetic networks with a view to the comparison between the different transformation models (Bursa–Wolf, Molodensky–Badekas, 2D-multiple regression, etc.), and the realization of a geographical coordinates planimetric conversion grid between the WGS84 system and other national systems like the Algerian North Sahara Datum (Kheloufi et al., 2009).
3D transformations are usually applied to convert coordinates related to one geodetic datum to another; this operation is commonly known as a datum transformation. In such applications, the rotations between the two 3D coordinate axes are small (usually less than 1 s of arc), and certain approximations are used to simplify rotation matrices; these simplified matrices are a common feature of the Bursa–Wolf and the Molodensky–Badekas transformations.
The transformation of GPS data into the geodetic local system, which is the basis of the mapping system in force in every country and in which the results of geodetic work must be expressed, requires knowledge of the passage parameters with the use of a suitable model. The choice of transformation model requires the availability of a dataset known in each of the two systems.
The transformation is presented either in similarity form nor under geographic formalism known as the Molodensky model (Figure 1) or a bi-dimensional 2D affine regression.
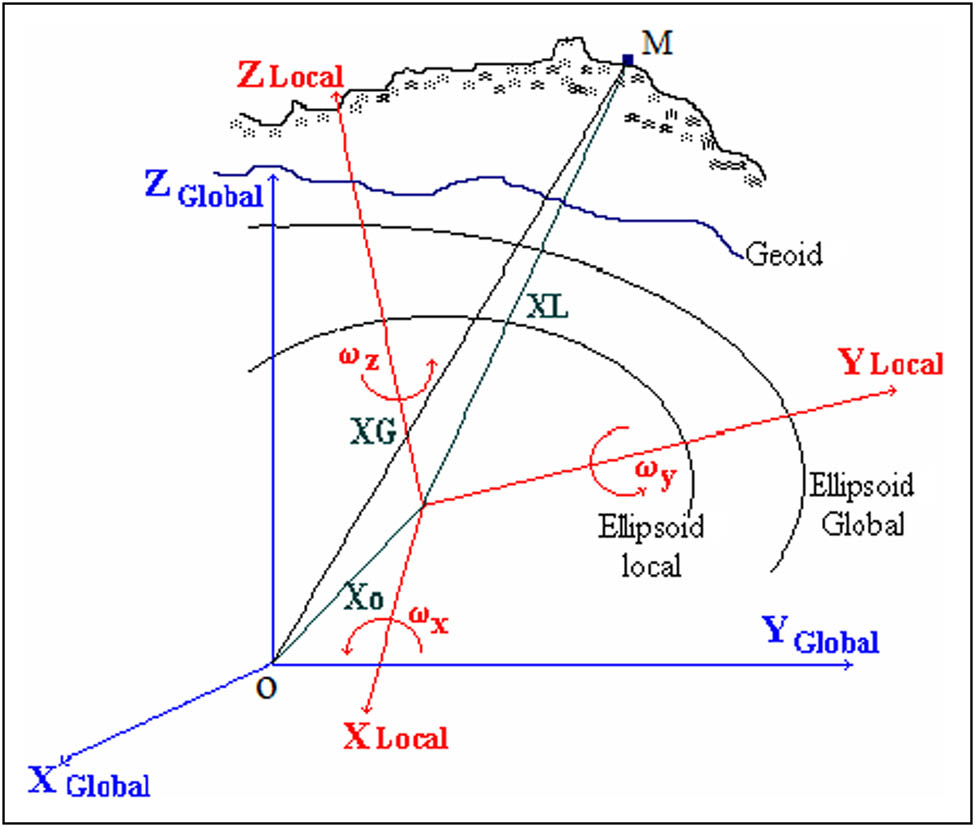
Translations and rotations between two systems.
1.1 General shape of geodetic transformation
Let I, J, K be the orthogonal base of system O, X, Y, Z and i, j, k be that of system O, x, y, z.
We have
The vector
Hence,
2 Earlier development of transformation formalisms
The names of the two transformations are an acknowledgment to the authors Bursa (1962), Wolf (1963), Molodensky et al. (1960), and Badekas (1969) of technical papers and reports on transformation methods related to the orientation of reference ellipsoids and 3D geodetic networks. 3D conformal transformations for single points are often given in the vectorial form (Collilieux et al., 2016).
The two most commonly used 3D models (Molodensky and Bursa) have the following global simplified formalism:
Molodensky–Badekas:
Bursa–Wolf:
where
The mathematical relationship can be written in such a way as to be able to consider the transformation parameters as unknown and thus be able to estimate them. Such a form is that we can estimate the transformation parameters knowing the coordinates in both systems by the following equation (Boateng, 2016):
These two equations could not be obtained without supposing some assumptions for a geodetic mathematical hypothesis in order to lead to these canonical linear formalisms (equation (7)).
In the Molodensky formalism Molodensky (1960), the computation of transformation parameters goes in general through the barycenter coordinates written in both systems (Kheloufi, 2012):
As a result, in matricial form, the Molodensky formalism for a set of n-points is as follows:
where
3 Some problems in Molodensky–Badekas and Bursa–Wolf transformations
In reality, the Molodensky transformation is described as shown in Figure 2, where the centroid G is displaced from O2 by translations t
X
, t
Y
, and t
Z
measured in the directions of the X, Y, and Z axes of system 2 and
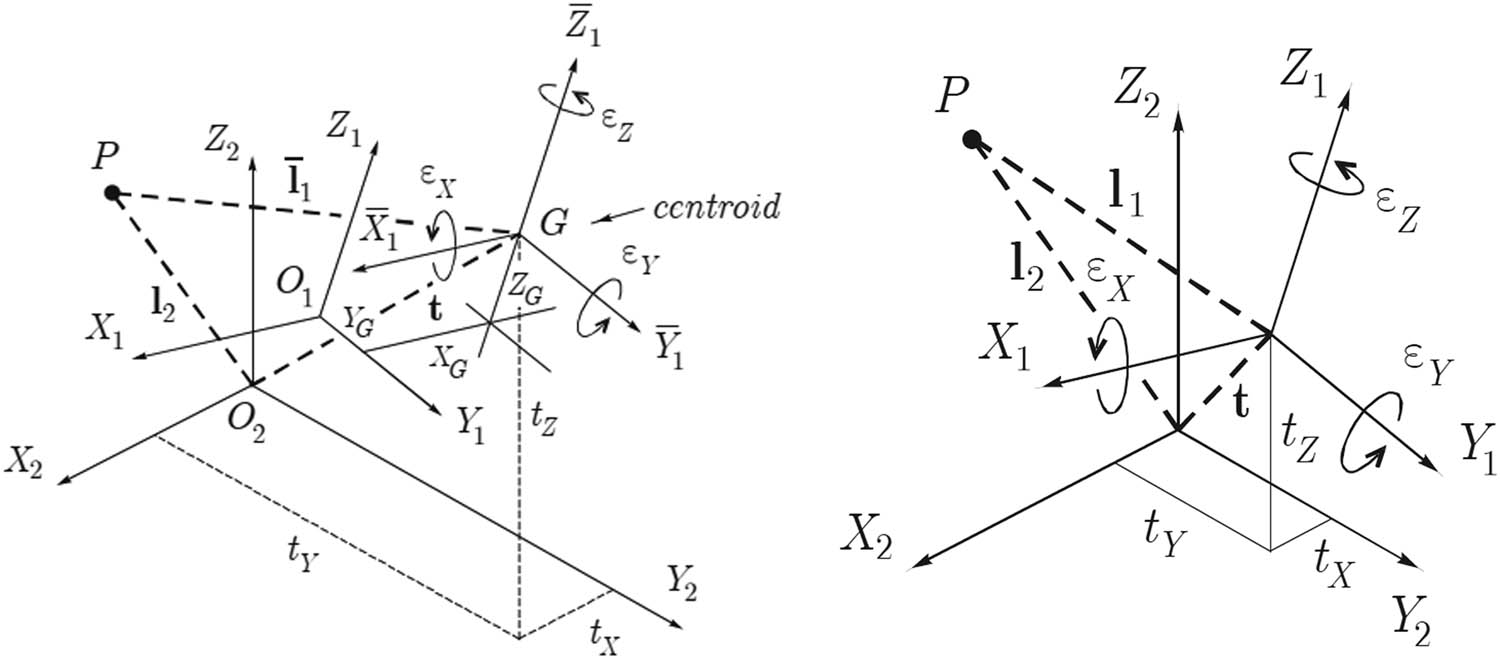
Illustration of Molodensky–Badekas barycenter and Bursa–Wolf transformation.
The Figure 2 illustrates graphically the complexity and differences in the implementation of the two 3D transformations relevant to the type of data (point coordinates) and the expected accuracy as a function of the purpose of the transformation.
3.1 Adopted assumptions
Because the mathematical formalism differs in substance and the geodetic network is not of the same type and size (order 0–4), some assumptions are mandatory for an accurate estimation of transformation parameters using either 3D or 2D models Helmert (1907), as shown below.
3.1.1 First assumption
By identifying the scalar products in a real nonlinear rotation matrix, we obtain
where E x , E y , and E z are rotations around the three axes OX, OY, and OZ, respectively.
In this study, the third coordinate, the orthometric height, would be assimilated as an ellipsoidal height, provided by satellite observation in the global navigation satellites systems (GNSS) survey (Marcin, 2011). This assimilation blemished the results considerably, but the assumptions made in this article have compensated for the lack of data and corrected them (Ziggah et al., 2017).
In addition, the double point coordinates have been attached to the last version of the terrestrial reference frame built on the base of GNSS permanent stations. These stations are dispatched all over the world, and their coordinates are determined by considering crustal deformations and geodynamics and processed by time series (Kheloufi, 2012).
Case in geodesy
Due to the construction of any two geodetic reference systems are close to each other and the orders of magnitude of the rotation angles are relatively small.
The parameters involved in a transformation are summarized as follows:
The translations T x , T y , and T z are less than a few hundred meters.
The rotations E x , E y , and E z are of the order of a few seconds of arc.
For small rotation angles, the rotation matrix may be simplified by the approximations:
cos ε x ≈ 1
sin ε x ≈ ε x (rad)
sin ε z , sin ε y ≈ 0
From equations (4) and (5), we obtain the simple linear form of the rotation matrix as in equation (9).
The scale factor is close to unity; we can write that K = 1 + δk and that δk < 0.000001.
The matrix became skew-symmetric and led us to conclude that this rotation matrix R (E x , E z , E y ) can be “linearized” as follows:
This late equation led to the previous writing of the linear transformation formalism for both 3D models (Molodensky and Bursa) in their rotation terms. In reality, the linearization lightens and facilitates the resolution by ordinary least squares (OLS) but causes a loss of precision due to concatenation to certain orders of the trigonometric functions Taylor development. One condition to recover the accuracy loss is to develop a new formalism, modify the existing one, or use high-quality data in processing (Navikova, 2020).
In this article, we are dealing with contesting, in one hand the 3D models with 2D ones like multiple regression equations (MRE’s) or geodetic lines and in other hand, we confront the different resolution methods such as nonlinear Levenberg–Marquardt (LM) and general linear least square (LLS).
3.1.2 Second assumption
In equation (6), the three coordinates of the barycenter should take into consideration the ponderation of every point in the system instead of taking by default the unity values; the equation above should be rewritten as follows (equation (10)):
where P i is the weight affected at every point in both systems. The ponderation is based on the influence of every point on the system by its quadratic error precision. Thus, the transformation deal with the centered reduced coordinates of both systems in consideration and minimize the effect of orientation by rotation around the barycenters. An alternative transformation from Cartesian to geodetic coordinates is considered in this study to face different types of coordinate files to be transformed (Cartesian and geodetic curved). For this purpose, a design derivative matrix A 3nx3 is implemented in the code source, as illustrated in equation (1) of the Appendix (Soler et al., 2012).
3.1.3 Third assumption
In case the linear models do not respond to the error-minimizing purpose of the transformation parameters, I have chosen the nonlinear least squares method for performing the equation system resolution adapted to our specific problem in order to avoid the accuracy loss due to truncation.
The LM is considered the most appropriate algorithm to resolve this problem efficiently because it takes into account the nonlinear aspect of formalism and is powerful to perform the resolution of nonlinear regression problems with a least squares stabilization parameter μk to improve the behavior of the algorithms around the minima.
Like all nonlinear optimization methods, LM is iterative. Initiated at the starting point X 0, the method produces a series of vectors X 1, X 2, … that converge toward a local minima X + for a regression function F described as follows:
where J is the Jacobian of the function based on the first derivative of F (
By resolving the equation above with δ X as a solution of nonlinear least squares, we have to bypass the embarrassing linearization passage and thus preserve the accuracy of the model.
4 Observations quality analysis in the least squares adjustment
4.1 Variance factor estimation
The variance factor (a posteriori standard deviation) is given by the following formula:
where n – p is the redundancy factor (number of degrees of liberty of the problem),
Unity variance value estimation allows to provide information relevant to the observations weight matrix and residues vector (lacks in measures, errors of the model, etc.) (Collilieux et al., 2016).
4.2 Residues and normalized residues estimation
After geodetic network adjustment, the assessed solution
The normalized residues u i are computed from the following formula:
In next step, the statstical analysis are shown as below:
4.2.1 Chi-squared test
The chi-squared test has the purpose of assessing a global judgment about the conformity hypothesis of residue distribution with normal distribution.
Let
with
The probability density of this function is
and
The test on zero assumption H
0
where
If
irrealistic observations ponderation;
errors occurrence;
residual systematism existence.
4.2.2 Student test
Student test is based on the determination of limits values b 1 and b 2 of tolerance interval as follows:
with t as the critical value of Student distribution, given by usual statistical tables. This value depends on redundance n − 1 and probability threshold α (Akyilmaz, 2007).
4.2.3 Tau (τ) test
Tau test consists of verifying the conformity of normalized residues ui to the normal law centred reducted, with riscα, ui is it belonging to the interval N (0,1).
The distribution of Tau (τ) can be derived from the distribution of student using the following formula:
with Ndl (= n − 1) as the number of degree of liberty of residues and t as the critical value of “Student” distribution.
If a component u
i
of the vector of normalized residuals satisfies the inequality:
5 Statistical study and results validation
For the validation purpose of this study, a set of 12 benchmarks (points whose coordinates are known in both systems) from the zero-order North Algerian network (Figure 3) are used. Indeed, the results obtained by implementing the 3D Molodensky–Badekas and Bursa–Wolf models show how much the two methods are almost similar but differ slightly in the triangular superior elements of variance–covariance matrix (VCV) (Table 2).
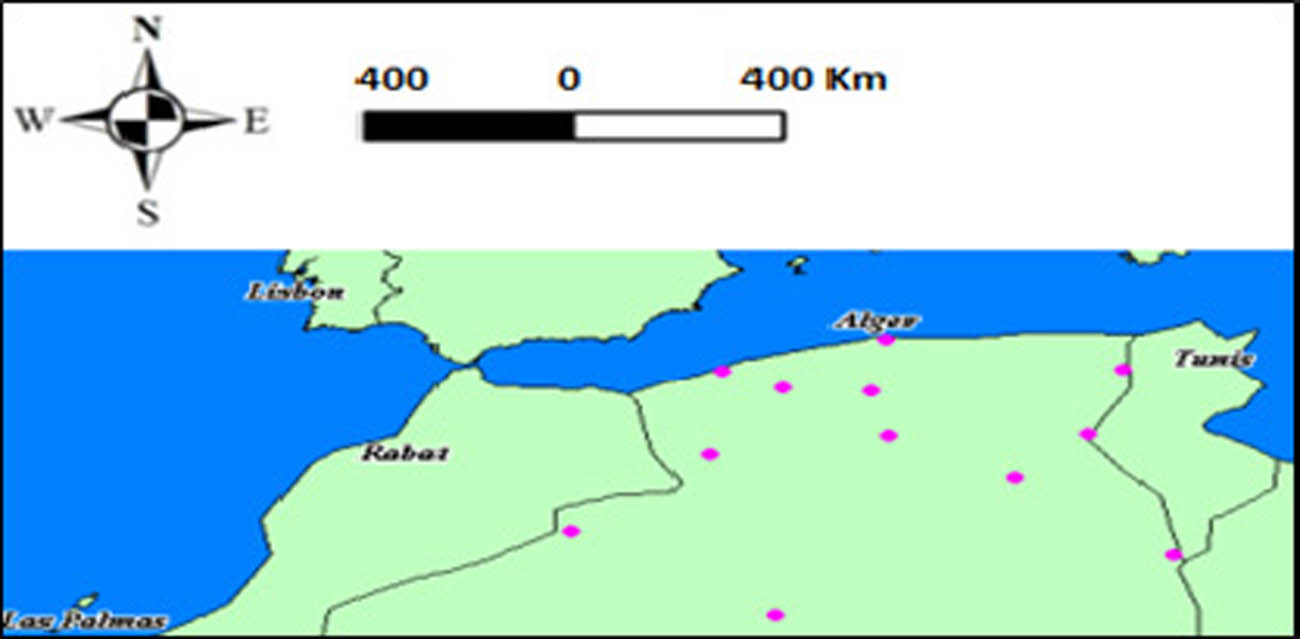
Distribution of zero-order North Algerian network of used benchmarks set for algorithm validation.
Computed transformation parameters and their accuracies compared with Algerian parameters (Institut National de Cartography et de Teledetection, INCT): a case of both formalisms (MB, BW)
| Parameters | Bursa–Wolf | Molodensky–Badekas | INCT official II |
|---|---|---|---|
| T X (m) | 76.0382 ± 0.0256 | 51.815 ± 0.01670 | 209.36300 |
| T Y (m) | −46.4270 ± 0.0247 | −62.000 ± 0.0121 | 087.81700 |
| T Z (m) | −114.334 ± 0.0312 | −106.000 ± 0.03070 | −404.61900 |
| δk (ppm) | 1.4344 ± 0.0261 | 1.6340 ± 0.00216 | 1.4547220 |
| ℇ X (s) | −0.12494 ± 0.0660 | −1.40041 ± 0.04820 | −0.0046122 |
| ℇ Y (s) | −0.4534 ± 0.1067 | 2.50843 ± 0.1300 | −3.4784221 |
| ℇ Z (s) | 0.0998 ± 0.0668 | −0.04657 ± 0.0500 | −0.5804847 |
Correlation matrices of transformation parameters obtained by two formalisms (MB and BW) with assumptions
| Correlation matrix (Bursa–Wolf) | ||||||
|---|---|---|---|---|---|---|
| 1 | −0.402 | −0.242 | −0.591 | −0.267 | −0.790 | 0.602 |
| −0.406 | 1 | 0.570 | −0.236 | 0.785 | 0.290 | −0.842 |
| −0.242 | 0.578 | 1 | −0.566 | −0.259 | 0.728 | −0.098 |
| −0.491 | −0.236 | −0.566 | 1 | −0.154 | −0.817 | 0.576 |
| −0.267 | 0.785 | −0.259 | −0.154 | 1 | 0.164 | −0.408 |
| −0.790 | 0.290 | 0.728 | −0.817 | 0.164 | 1 | −0.324 |
| 0.602 | −0.842 | −0.098 | 0.576 | −0.408 | −0.324 | 1 |
| Correlation matrix (Molodensky–Badekas) | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.137 | 0.497 | −0.099 | −0.777 | 0.294 | 0.199 |
| 0.137 | 1 | 0.2.76 | −0.744 | 0.464 | 0.0918 | −0.108 |
| 0.497 | 0.276 | 1 | −0.079 | 0.186 | 0.380 | −0.430 |
| −0.993 | −0.734 | −0.079 | 1 | 0.193 | −0.710 | 0.278 |
| −0.771 | 0.464 | 0.186 | 0.193 | 1 | 0.174 | −0.415 |
| 0.294 | 0.095 | 0.382 | −0.746 | 0.174 | 1 | −0.266 |
| 0.199 | −0.108 | −0.433 | 0.278 | −0.415 | −0.266 | 1 |
Bold values are the more significant.
The two global methods lead practically to the closed results on residues except that the Molodensky–Badekas formalism gives non-correlated parameters which means that minimal variance is well reached in the case of Molodensky–Badekas than Bursa–Wolf. Indeed the reduction of benchmark coordinates according to the centroid (barycenter) ones mitigates the effect of rotation between the two systems and thus decreases the errors over the geodetic points positions (Hashemi et al., 2013) and even their root mean square (RMS) (Table 1). The VCV matrix in Tables 2 and 3 clearly indicates the difference in precision between Molodensky and Buras–Wolf as displayed in bold, higher variance values indicate less precise results. The normal character denotes less correlation over the transformation parameter errors, thus more precision in the case of Molodensky–Badekas. In order to increase the reliability of transformation parameters, another 2D formalism should be adopted and compared to the 3D ones to carry out the effect of the third dimension on the accuracy of these parameters (Zavoti and Kalmár, 2016).
Accuracies obtained by GLS resolution for two global models without assumptions compared to MRE’s
| Model | Component | Minimum (m) | Maximum (m) | Mean (m) | RMS (m) |
|---|---|---|---|---|---|
| Bursa–Wolf | X | −1.685 | 2.686 | 1.293 | 1.838 |
| Y | −1.221 | 1.164 | 0.697 | 0.834 | |
| Z | −2.144 | 1.307 | 0.461 | 1.018 | |
| Molodensky Badekas model | X | −1.957 | 0.407 | −0.941 | 1.014 |
| Y | 1.242 | 0.541 | 0.602 | 0.413 | |
| Z | 2.120 | 2.019 | −1.398 | 2.058 | |
| Multiple regression equations | Λ | −0.063 | 0.319 | 0.110 | 0.164 |
| Φ | −0.407 | 0.634 | −0.164 | 0.366 |
Among these most commonly used formalisms, we can note multiple regression MREs, affine transformation, and others. For this purpose, we have converted geographic coordinates in both systems to Cartesian ones (Ligas and Banasik, 2011).
Institute of Cartography and Remote Sensing (INCT) undertook the computation of transformation parameters over the same GNSS observation points (12 points in North of Algeria) and found the values reported in Table 1.
The global RMS of these computations, which is approximatively equal to 0.9288 m for translations and 0.143 s for rotations for all components, is considered acceptable for cartographic work. In comparison to the standard deviation of INCT transformation parameters reported in the last column of Table 1, the accuracy reached in our case seems to be satisfactory (the maximum value was 0.03 m for Bursa–Wolf in Z-translation). In the histogram of Figure 5, RMS values of the determined parameters are far less than the values of the adopted parameters (INCT) because, wherever the method is used, it does not exceed 0.25 m. The geographic transformation as “VEIS” formalism is converted to a Cartesian one by the conversion of geographic coordinates (Featherstone, 2008), (George, 1999).
In Table 2, it is well demonstrated that the number of correlation coefficient values greater than half is 19 for the Bursa Wolf (BW) model and six for the Molodensky Badekas (MB) model. It denotes that Molodensky–Badekas formalism Aström (2001), by introducing the barycenter, decreases the correlations between the double points and thus attenuates the propagation of errors on the transformation parameters. If a point is suspect or badly defined, the reduction of its coordinates to those of the barycenter is supposed to decorrelate the errors and thus reduce their propagation.
5.1 Comparison between linear (general least square, GLS) and nonlinear adjustment (LM)
The comparison is not only limited to the use of transformation formalism but also concerns the adjustment technique used in relation to the type of problem to be resolved. Indeed, we are sometimes faced with particular cases of nonlinear systems that need special fitting techniques like “Levenberg–Marquardt,” “Steepest Decent,” “Newton algorithm” and many others (Ruffhead, 2020, 2021).
In this work, I have opted for LM to analyze and compare its purpose with that of the linear method “GLS” as it occurs. As mentioned in the third assumption above, this method does not take into consideration the linearization problem and thus avoids truncation of the equation using the Taylor development until certain order and no information about the system would be lost, thus preserving the accuracy of the results shown in Tables 3 and 4. Considering the Bursa–Wolf transformation as an example, the equation can be written as follows:
where
Accuracies obtained by GLS resolution for two global models with assumptions compared to MRE’s
| Model | Component | Minimum (m) | Maximum (m) | Mean (m) | RMS (m) |
|---|---|---|---|---|---|
| Bursa–Wolf | X | −1.426 | 2.686 | 1.293 | 0.238 |
| Y | −0.301 | 1.164 | 0.697 | 0.434 | |
| Z | −1.491 | 1.307 | 0.461 | 1.018 | |
| Molodensky–Badekas model | X | −1.417 | 0.407 | −0.841 | 0.801 |
| Y | 0.238 | 0.541 | 0.404 | 0.354 | |
| Z | −2.033 | 2.019 | −1.308 | 1.158 | |
| Multiple regression equations | Λ | −0.063 | 0.319 | 0.110 | 0.164 |
| Φ | −0.407 | 0.634 | −0.164 | 0.366 |
ds is a very small quantity, and
The above equation is considered simultaneously for a nonlinear process using the LM algorithm and a linear one illustrated by GLS. In the following, we present the comparison of results between the two fitting methods for both transformations.
The Table 4 present the results of statistical analysis for the global models and the multiple regression MRE’s algorithm. Table 3 concerns the generalized least squares, and Table 4 shows the nonlinear fitting of the global (3D) models. Globally, the RMS turn around the meters in the worst case (>2.058 for Molodensky–Badekas) and less than 20 cm for the MRE’s model. This denotes the possibility of improving the precision of position in the optimum case; geodetic positioning sometimes needs sub-centimeter (geodynamics and technical auscultation) as accuracy to be satisfied. In Table 5, was reported the same models processed by LM algorithm with resolving the equation (12), δ X is thus a solution of the nonlinear system applied for all models. For this purpose, all models and both linear and nonlinear algorithms have been implemented in the « Delphi10 » application (Figure 4). A GLS solution has been introduced to determine a unique set of geodetic coordinates, with accompanying accuracy prediction coordinates from different observing scenarios (Soler et al., 2012).
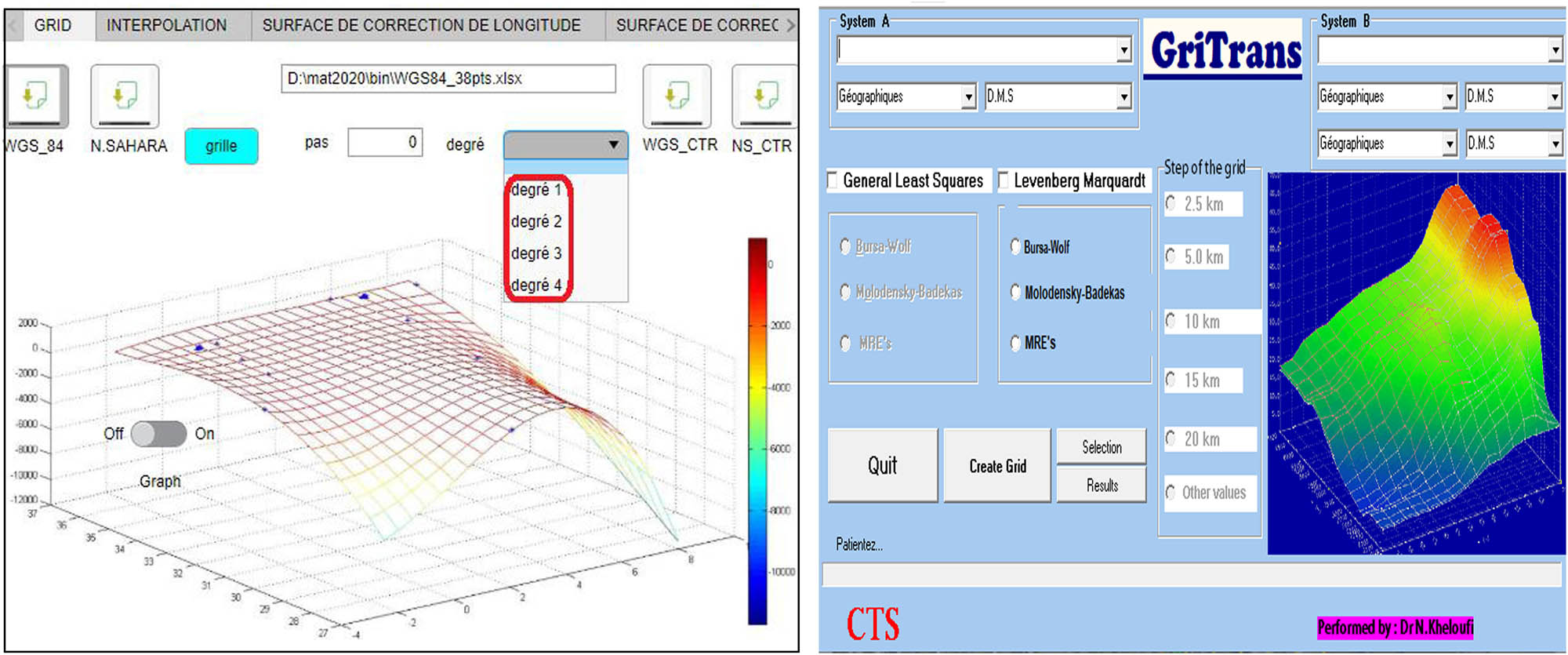
Screenshot of the application interface including both techniques.
According to the Table 5, the LM algorithm improves the accuracy of the global models if we take into consideration different assumptions (Acar, 2006). In this case, there is no need to appeal the multiple regression method because, for certain applications (geodetic works), we need to transform 3D cartesian components (X, Y, Z).
Nevertheless, the MRE remains interesting for limited area transformation in the case of cadastral surveys. In Figure 4, the choice of the degree of MRE is decisive for better accuracy; in our example, the choice of degree two in the interface (red framed degrees choices in Figure 4) is more suitable to obtain less error in transformation calculus (Figure 5), whereas degree three is not numerically stable because of the minus sign in the regression factors.
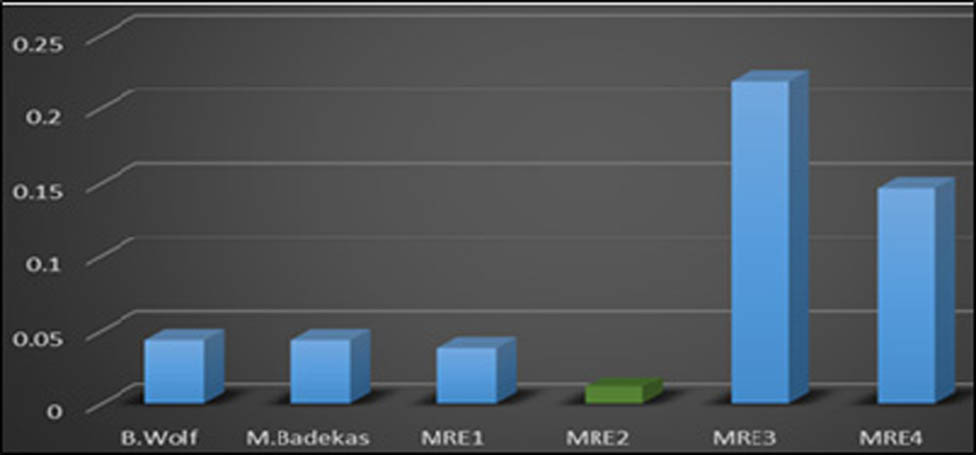
Variation of parameters RMS in meters for the used techniques (global models adjusted with GLS) and MREs.
We could improve the quality of transformation parameters issued by GLS by Zoning fitting and considering a zonage for a wide area, i.e., processing the method by set of benchmarks belonging to several restricted areas. In this case, we have partially resolved the problem because the obtained parameters are regional and not global, which is useful for a restricted area (Hok Sum, 2003).
In Tables 3–5, we present the results of data processing by both 3D and 2D models (Bursa–Wolf, Molodensky–Badekas, and MRE) with and without the assumptions explained above for carrying out the contribution of each model and also the contribution of assumptions taken into account in the improvement of precision in the processing of geodesic networks.
Results and analysis of the nonlinear (LM) process over the two global models
| Model | Component | Minimum (m) | Maximum (m) | Mean (m) | RMS (m) |
|---|---|---|---|---|---|
| Bursa–Wolf | X | 0.126 | 0.686 | 1.293 | 0.213 |
| Y | −0.101 | 0.164 | 0.697 | 0.762 | |
| Z | 0.572 | 1.102 | 0.461 | 1.015 | |
| Molodensky–Badekas model | X | −1.223 | 0.311 | −0.841 | 0.906 |
| Y | 0.103 | 0.264 | 0.404 | 0.325 | |
| Z | −1.695 | 1.019 | −1.308 | 1.065 |
For the global models, it is clear from tales that the three considered assumptions have brought improvements in accuracy (Table 4) better than the improvements brought about by the implementation of nonlinear least squares analysis “LM”. Indeed, the precisions revolve around 35 cm with Molodensky–Badekas and 40 cm with Bursa–Wolf once the assumption is considered (Table 4) compared to the results of Table 3, where these hypotheses have been omitted (Yang, 2014).
The results of Tables 3 and 4 show that 2D model MRE minimizes errors, and even its statistical analysis is very good considering the tests undertaken on it.
5.2 Results of statistical analysis over MREs
For the degree of freedom (DOF) = 4, a statistical test was performed over the multiple regression method relevant to the equation 24 of paragraph 3.2. The results obtained from the Student and chi-square tests (Zeggai, 2006) are shown in Tables 6 and 7.
Student and chi-square test over the longitude
| Sigma a priori (σ 0) | Sigma a posteriori (
|
Chi-square test | Student test |
|---|---|---|---|
| 0.025 s | 0.014 | Positive | Zero suspect observation |
The variable
Student and chi-square test over the latitude
| Sigma a priori (σ 0) | Sigma a posteriori (
|
Chi-square test | Student test |
|---|---|---|---|
| 0.025 s | 0.017 | Positive | Zero suspect observation |
The variable
5.3 Over the latitude
The origin of the ITRF2020 long-term frame is defined in such a way that there are zero translation parameters at epoch 2015.0 and zero translation rates between the ITRF2020 and the international laser ranging service solar lunar ranging long-term frame over the time span 1993.0-2021.0 UNGGIM (2017), (Table 8).
Transformation parameters at epoch 2015.0 and their rates from ITRF2020 to ITRF2014 (ITRF2014 minus ITRF2020)
| T 1 (mm) | T 2 (mm) | T 3 (mm) | D (10−9) | R 1 (mas) | R 2 (mas) | R 3 (mas) | |
|---|---|---|---|---|---|---|---|
| −1.4 | −0.9 | 1.4 | −0.42 | 0.000 | 0.000 | 0.000 | |
| ± | 0.2 | 0.2 | 0.2 | 0.03 | 0.007 | 0.006 | 0.007 |
| Rates | 0.0 | −0.1 | 0.2 | 0.00 | 0.000 | 0.000 | 0.000 |
| ± | 0.2 | 0.2 | 0.2 | 0.03 | 0.007 | 0.006 | 0.007 |
Altamimi (2022) considered that ITRF 2020 is very close to WGS84 in such a way as to consider them almost confused. That lead to consider a part of WGS84 data as of good quality even the classical North Sahara coordinates are badly determined as cited in the Introduction.
6 Discussion
After considering these assumptions, we can say that we are in conformity with the directives and resolutions of the “UN-GGIM”1 concerning the use of the international geodetic frames and attachment of our local systems to the latest versions of ITRF to minimize position errors during compensations because the difference between the ITRF2018 and the WGS84 is some centimeters. The global 3D models processed with OLS seem to be the most used and famous for this purpose. Nevertheless, in different fields of engineering and earth science, certain cases need more accuracy; the ordinary linear least squares prove to be limited.
Thus, we have to use new numerical methods of resolution that can provide great efficiency in polynomial modelization. Therefore, instead of being limited to linear models, we have to apply the nonlinear least squares resolution to resolve the transformation problem between geodetic systems.
This need appears especially in the case of the Nord Sahara datum (Algeria), on which the linear models are not very appropriate because of the lack of information about the geoid’s undulation (the third component is not accurately determined). In this article, our main aim is to carry out the importance of using the nonlinear least squares method (LM) applied over two 3D (global transformation) models and a 2D one (MRE) on a huge area benchmarks network (North Algeria).
Coordinate transformation parameters and their RMS have been computed by both the OLS and LM algorithms compared with multiple regression (Kheloufi et al., 2009) to compare, on the one hand, the linear adjustment within its two variants (local and global) with the MRE’s and, on the other hand, the linear adjustment and the nonlinear one. In this context, a set of 12 benchmarks localized in North Algeria have been integrated to compute the transformation parameters (3D and 2D). Tables 3, 4, and 5 show the difference in accuracies between different models (BW, MB, and MRE’s) processed by the same method (GLS) and also the difference between the methods themselves, i.e., GLS vs. LM. For example, the Molodensky formalism (Deakin, 2006) generally gave better precision when processed by GLS for the X and Y components (1.014 m against 1.838 m) except for the Y component, where Bursa–Wolf is near the meter when Molodensky–Badekas is about 2 m. Multiple regression, which is a 2D formalism, ensures sub-meter accuracy and is adapted for wide-area transformation processing like in North Algeria. In our case, for a near 500 km baseline length, the method turned out to be very efficient because it did not exceed a meter. For the global models, we could reach these performances with precision only because we have taken into consideration the assumptions cited above (assumptions 1, 2, and 3).
Previous studies that have been performed without including a hypothesis have given error-blemished results with less accuracy (Table 5). For both global models, we could not reach the submeter for several components, where even the X and Y components outperformed the geodetic expected errors.
The purpose of this work was to develop a solution to the crucial problem of transformations between geodetic reference frames, particularly between the system in force in Algeria, the North Sahara – Clarke 1880, and the system in which the coordinates resulting from the GPS campaigns are expressed, i.e., the WGS84. Through this multicriteria analysis, we could prove that the coordinate transformation problem could be solved to carry out reliable transformations within acceptable precisions for different applications (geodetic, geodynamic, and land survey). The calculation of these parameters required an investigation into the existence of double-point files of impeccable quality and homogeneous and dense exhaustiveness. This led us to use some files from previous undertaken by different institutions (centre des techniques spatiales, INCT, entreprise nationale de geophysique) and in different projects: PUBLIC WORKS DIVISION-DTP-Oran network, Reseau geodesique de Sonatrach-Sonatrach project, North Algeria densification campaign, etc., where the set of points are determined with a priori centimeter precision standard deviations.[1]
As the determination of the transformation parameters is also based on the numerical models and mathematical formalisms, our work focused on the treatment of double points in our disposition by different methods:
3D model of Molodensky–Badekas and Bursa–Wolf,
2D model of multiple regression equations,
Nonlinear LM algorithm confronted with LLS.
The results presented in this study highlight the strengths and weaknesses of each model on the basis of the parameter standard deviation and even the position RMS, as well as the residuals after transformations, as illustrated in tables and figures. Indeed, according to the obtained results, the comparison between the 3D models gives an advantage for the Molodensky–Badekas formalism compared to the Bursa–Wolf formalism and the advantage for the nonlinear adjustment at the expense of the linear one. The analysis made on the estimated parameters also shows a difference in precision between the 3D models and the multiple regression method, which gave low RMS (as shown in Figure 5, 2 cm for MREs and 4.5 cm for Bursa–Wolf).
As a perspective, we recommend the use of planimetric grid method with interpolation methods (plus proche voisin, bilinear, and kriging) for more accuracy improvement.
-
Conflict of interest: Authors state no conflict of interest.
Appendix A1 Mathematical formulation of coordinates conversion
The basic mathematical relationship between Cartesian and orthogonal curvilinear geodetic coordinates is attributed to Helmert and can be written in matrix form as follows:
where
In all the above equations, a and f are the semi-major axis and flattening of the selected ellipsoid, respectively.
A2 Least squares methodology for coordinates conversion
For the least squares resolution purpose, a derivative design matrix A called Jacobian is used.
The numerical value of matrix A is determined using any initial approximation of the parameters
References
Acar, M. 2006. “Deformation analysis with total least squares.” Natural Hazards and Earth System Sciences 6, 663–669.10.5194/nhess-6-663-2006Search in Google Scholar
Akyilmaz, O. 2007. “Total least squares solution of coordinate transformation.” Survey Review 39(303), 68–80.10.1179/003962607X165005Search in Google Scholar
Altamimi, Z. 2022 ITRF2020 [Data set]. IERS ITRS Center Hosted by IGN and IPGP. 10.18715/IPGP.2023.LDVIOBNL.Search in Google Scholar
Aström, H. 2001. Valeurs de précision lors de transformation. Office du cadastre de Berne, transformations.doc2.Search in Google Scholar
Badekas J. 1969, ‘Investigations related to the establishment of a world geodetic system’, Report No. 124, Department of Geodetic Science, Ohio State.Search in Google Scholar
Boateng, K. 2016. “Accuracy assessment of Cartesian (X, Y, Z) to geodetic coordinates (φ, λ, h) transformation procedures in precise 3D coordinate transformation – A case study of Ghana geodetic reference network.” Journal of Geosciences and Geomatics 4(1), 1–7.Search in Google Scholar
Bursa, M. 1962. “The theory for the determination of the non-parallelism of the minor axis of the reference ellipsoid and the inertial polar axis of the Earth, and the planes of the initial astronomic and geodetic meridians from the observation of artificial Earth satellites.” Studia Geophysica et Geodetica 6, 209–214.Search in Google Scholar
Collier, P. 2020. Practical Notes on Coordinate Transformation. March 2020 Swift Navigation, Inc.Search in Google Scholar
Collilieux, X., Z. Altamimi, P. Rebischung, and L. Métivier. 2016. “ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions.” Journal of Geophysical Research: Solid Earth.Search in Google Scholar
Deakin, R. E. 2006. “A note on the Bursa-Wolf and Molodensky-Badekas transformations.” School of Mathematical & Geospatial Sciences RMIT University.Search in Google Scholar
Featherstone, W. E. 2008. “Closed-form transformation between geodetic and ellipsoidal coordinates.” Western Australian Centre for Geodesy & The Institute for Geoscience Research, Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia.Search in Google Scholar
George, P. 1999. “Transforming Cartesian coordinates X,Y,Z to geographical coordinates φ, λ, h.” Department of Land Information Royal Melbourne Institute of Technology GPO Box 2476V, MELBOURNE, VIC, 3001, Australian Surveyor 44(1), 55–63.10.1080/00050326.1999.10441904Search in Google Scholar
Hashemi, A, M. Kalantari, and M. Kasser. 2013. “Direct solution of the 7 parameters transformation problem.” Applied Mathematics & Information Sciences 7(4), 1375–1382.10.12785/amis/070415Search in Google Scholar
Helmert, F. R. 1907. Die Ausgleichungsrechnung de der Methode der Square: mit Anwendungen auf die Geodäsie und die Theorie der Messinstrumente, Teubner Verlag, Leipzig 1907.Search in Google Scholar
Hok Sum, F A. 2003. “Comparative analysis of the performance of iterative and non-iterative solutions to the Cartesian to geodetic coordinate transformation.” Journal of Geospatial Engineering 5(2), 61–74.Search in Google Scholar
Kheloufi, N, S. Kahlouche, and R. Lamara. 2009. “Nonlinear Least Squares (Levenberg–Marquardt algorithms) for geodetic adjustment and coordinates transformation.” Geophysical Research Abstracts, Vol. 11, EGU-2009-333, 2009 EGU General Assembly 2009.Search in Google Scholar
Kheloufi, N. 2012. “Coordinates transformation by ‘Zoning Method’ for parameters computing between WGS84 and North Sahara.” Proceeding of the European Geosciences Union (EGU) Vienna 2012.Search in Google Scholar
Ligas, M. and P. Banasik. 2011. “Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations.” Geodesy and Cartography, Polish Academy of Sciences 60(2), 145–159.10.2478/v10277-012-0013-xSearch in Google Scholar
Molodenskiy, M. S. 1960. Metody izucheniya vnesnego gravitatsiononogo polya i figuri Zemli. Trudy CNIIGAIK Moscow, Vyp.131.Search in Google Scholar
Novikova, E. 2020. “The change of coordinate system versus the area of parcels.” Geodesy and Cartography 46(1), 26–33. 10.3846/gac.2020.6979.Search in Google Scholar
Plag, H. P. 2020. “Comprehensive overview of geodesy’s contribution to science and society.” Global Geodetic Observing System Meeting the Requirements of a Global Society on a Changing Planet.Search in Google Scholar
Ruffhead, A. 2020. Introduction to geodetic datum transformations and their reversibility. March 2020 In book: UEL ACE Surveying Working Paper No 01/2020.Search in Google Scholar
Ruffhead, A. 2021. “Derivation of rigorously-conformal 7-parameter 3D geodetic datum transformations.” Survey Review 53(376). 10.1080/00396265.2019.1665614.Search in Google Scholar
Soler, T, J. Y. Han, and N. D. Weston. 2012. “Alternative transformation from Cartesian to geodetic coordinates by least squares for GPS georeferencing applications.” Mathematics & Computer Science, Geosciences. 10.1016/j.cageo.20110.026.Search in Google Scholar
United Nations – Global Geospatial Information Management (UN-GGIM). 2017. Report to 7th Session about the UN-GGIM – Arab States Activities.Search in Google Scholar
Wolf, H. 1963. “Geometric connection and re-orientation of three-dimensional triangulation nets.” Bulletin Grodesique 68, 165–169. 10.1007/BF02526150.Search in Google Scholar
Yang, C. S. 2014. “Development of the process of coordinate transformation of local datum cadastral map to the world geodetic system-using adjusted coordinates.” Journal of the Korean Society of Surveying Geodesy Photogrammetry and Cartography 32(spc4_2), 401–412. 10.7848/ksgpc.2014.32.4-2.401.Search in Google Scholar
Zavoti, J. and J. Kalmár. 2016. “A comparison of different solutions of the Bursa–Wolf model and of the 3D, 7-parameter datum transformation.” Acta Geodaetica et Geophysica 51, 245–256.10.1007/s40328-015-0124-6Search in Google Scholar
Zeggai, A. 2006. Application de l’approchepar les équations de la régressionmultiple pour le passage d’undatum à l’autre (cas de l’Algérie), Revue XYZ • N° 106 – 1er trimestre 2006.Search in Google Scholar
Ziggah, Y., H. Youjian, P. B. Laari, and Z. Hui. 2017. “Novel approach to improve geocentric translation model performance using artificial neural network technology.” BCG-Boletim de Ciências Geodésicas – On-Line version. 10.1590/S1982-1702017000100014.Search in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Two adjustments of the second levelling of Finland by using nonconventional weights
- A gap-filling algorithm selection strategy for GRACE and GRACE Follow-On time series based on hydrological signal characteristics of the individual river basins
- On the connection of the Ecuadorian Vertical Datum to the IHRS
- Accurate computation of geoid-quasigeoid separation in mountainous region – A case study in Colorado with full extension to the experimental geoid region
- A detailed quasigeoid model of the Hong Kong territories computed by applying a finite-element method of solving the oblique derivative boundary-value problem
- Metrica – An application for collecting and navigating to geodetic control network points. Part II: Practical verification
- Global Geopotential Models assessment in Ecuador based on geoid heights and geopotential values
- Review Articles
- Local orthometric height based on a combination of GPS-derived ellipsoidal height and geoid model: A review paper
- Some mathematical assumptions for accurate transformation parameters between WGS84 and Nord Sahara geodetic systems
- Book Review
- Physical Geodesy by Martin Vermeer published by Aalto University Press 2020
- Special Issue: 2021 SIRGAS Symposium (Guest Editors: Dr. Maria Virginia Mackern) - Part II
- DinSAR coseismic deformation measurements of the Mw 8.3 Illapel earthquake (Chile)
- Special Issue: Nordic Geodetic Commission – NKG 2022 - Part I
- NKG2020 transformation: An updated transformation between dynamic and static reference frames in the Nordic and Baltic countries
- The three Swedish kings of geodesy – Speech at the NKG General Assembly dinner in 2022
- A first step towards a national realisation of the international height reference system in Sweden with a comparison to RH 2000
- Examining the performance of along-track multi-mission satellite altimetry – A case study for Sentinel-6
- Geodetic advances in Estonia 2018–2022
Articles in the same Issue
- Research Articles
- Two adjustments of the second levelling of Finland by using nonconventional weights
- A gap-filling algorithm selection strategy for GRACE and GRACE Follow-On time series based on hydrological signal characteristics of the individual river basins
- On the connection of the Ecuadorian Vertical Datum to the IHRS
- Accurate computation of geoid-quasigeoid separation in mountainous region – A case study in Colorado with full extension to the experimental geoid region
- A detailed quasigeoid model of the Hong Kong territories computed by applying a finite-element method of solving the oblique derivative boundary-value problem
- Metrica – An application for collecting and navigating to geodetic control network points. Part II: Practical verification
- Global Geopotential Models assessment in Ecuador based on geoid heights and geopotential values
- Review Articles
- Local orthometric height based on a combination of GPS-derived ellipsoidal height and geoid model: A review paper
- Some mathematical assumptions for accurate transformation parameters between WGS84 and Nord Sahara geodetic systems
- Book Review
- Physical Geodesy by Martin Vermeer published by Aalto University Press 2020
- Special Issue: 2021 SIRGAS Symposium (Guest Editors: Dr. Maria Virginia Mackern) - Part II
- DinSAR coseismic deformation measurements of the Mw 8.3 Illapel earthquake (Chile)
- Special Issue: Nordic Geodetic Commission – NKG 2022 - Part I
- NKG2020 transformation: An updated transformation between dynamic and static reference frames in the Nordic and Baltic countries
- The three Swedish kings of geodesy – Speech at the NKG General Assembly dinner in 2022
- A first step towards a national realisation of the international height reference system in Sweden with a comparison to RH 2000
- Examining the performance of along-track multi-mission satellite altimetry – A case study for Sentinel-6
- Geodetic advances in Estonia 2018–2022


