A detailed quasigeoid model of the Hong Kong territories computed by applying a finite-element method of solving the oblique derivative boundary-value problem
-
Robert Čunderlík
, Marek Macák
Abstract
New gravity and precise levelling measurements have been performed throughout the Hong Kong territories to modernize a vertical geodetic datum that is currently realized by heights of levelling benchmarks defined in the Hong Kong Principal Datum (HKPD). Modernization of the HKPD involved delivering various products, including new detailed geoid and quasigeoid models and newly determined orthometric and normal heights of levelling benchmarks. In this study, we present the result of gravimetric quasigeoid modelling. The method used to compute a detailed gravimetric quasigeoid model is based on the finite-element method to solve the geodetic boundary-value problem with oblique derivative boundary conditions considered directly at computational nodes on the discretized Earth’s topography. The result of a gravimetric quasigeoid modelling shows a good agreement with a geometric quasigeoid model at the Global Navigation Satellite System (GNSS)-levelling benchmarks. The standard deviation of differences between the gravimetric and geometric quasigeoid heights of ±3.3 cm is compatible with the expected accuracy of gravity, levelling, and GNSS measurements.
1 Introduction
In the Hong Kong territories, the geodetic datum currently used for height control is the Hong Kong Principal Datum (HKPD). The heights of HKPD levelling benchmarks were determined by adjusting levelling measurements but without involving gravity observations along levelling lines. To eliminate systematic errors due to disregarding the gravity information, Nsiah Ababio and Tenzer (2022a) used terrestrial and marine gravity measurements to interpolate gravity values along levelling lines and then computed the normal and orthometric corrections to levelled height differences to determine the normal and orthometric heights of HKPD levelling benchmarks. The result was presented as the Vertical Control Network 2022 (VCN2022). Since the current coverage of levelling network throughout the Hong Kong territories is not suitable for many surveying applications, Nsiah Ababio and Tenzer (2022b) compiled the detailed gravimetric geoid model HKGEOID-2022, with the primary purpose of converting the geodetic (ellipsoidal) heights measured by the Global Navigation Satellite System (GNSS) to the orthometric heights defined in the updated HKPD. Nevertheless, both products (i.e. the VCN2022 and the HKGEOID-2022) do not meet the requirements for many proposed or approved engineering projects to be realized between Hong Kong and mainland China, because the normal heights and the quasigeoid model are used for a practical realization of vertical geodetic control in mainland China, whereas the orthometric heights and geoid models are used in Hong Kong. To achieve consistency between both vertical data, a new detailed quasigeoid model was prepared, and normal heights of levelling benchmarks were determined at the Hong Kong territories. As stated previously, the normal heights of HKPD levelling benchmarks were already determined by Nsiah Ababio and Tenzerr (2022a). In this study, we present a new detailed quasigeoid model compiled according to the method developed by Minarechová et al. (2021). Their method is based on applying the finite-element method (FEM) to solve the oblique derivative boundary condition (BC).
Traditionally, gravity anomalies have been used to determine geoid/quasigeoid models by means of solving the geodetic boundary-value problems (BVPs). The gravity anomaly is defined as the actual gravity (typically measured on or above the topographic surface) and the normal gravity computed as a function of the geodetic latitude and the physical (normal or orthometric) height (above the sea level). Nowadays, GNSS techniques provide information about the vertical position of gravity points with respect to the reference ellipsoid in terms of the geodetic (ellipsoidal) rather than physical heights. The gravity disturbance is then obtained as the difference between the observed and normal gravity (both referred to the same point at or above the topographic surface). The availability of this gravity data resulted in development of various methods that have been applied to determine geoid/quasigeoid models from gravity disturbances.
Gravity disturbances define the oblique derivative BCs of the fixed gravimetric boundary-value problem (FGBVP) that represents an exterior oblique derivative geodetic BVP for the Laplace equation (Koch and Pope 1972, Bjerhammar and Svensson 1983, Holota 1997). A detailed overview of various procedures for solving the oblique derivative BVP can be found, for instance, in Minarechová et al. (2021). Here, we only mention numerically efficient approaches, most notably the FEM, the finite-volume method (FVM), and the boundary element method (BEM). Principal reasons for using these methods in gravimetric geoid/quasigeoid modelling, instead of applying classical procedures based on solving Stokes and Poisson’s integrals, rely on the possibilities of applying a direct refinement of the discretization by using a very detailed gravity data grid and considering a real topographic relief.
Meissl (1981) and Shaofeng and Dingbo (1991) applied the FEM to solve gravimetric problems. Klees (1995) and Lehmann and Klees (1999) developed the indirect BEM approach that was later improved by Klees et al. (2001). Čunderlík et al. (2008) and Čunderlík and Mikula (2010) introduced the direct BEM approach. Later, Čunderlík et al. (2012) discussed the applicability of the BEM to solve the oblique derivative problem. Fašková et al. (2007, 2010), Šprlák et al. (2011), and Mráz et al. (2016) applied the FEM. Nevertheless, the oblique derivative BC was not considered in these studies. Fašková (2008) applied for the first time the FVM in gravity field modelling by solving the geodetic BVP with the Neumann BC. Macák et al. (2012) applied the FVM to the oblique derivative BVP, and Macák et al. (2014, 2015) applied it to solve FGBVPs on uniform grids. Medľa et al. (2018) presented the FVM for solving the oblique derivative BVP on 3-D unstructured meshes above the real topography. Droniou et al. (2019) further improved this method by treating the oblique derivative BC so that its tangential component is considered an advection along a topographic relief regularized by a carefully designed surface diffusion term. Minarechová et al. (2021) applied the FEM to solve the oblique derivative BC. In this method, the oblique derivative is incorporated directly into computational nodes by using two tangential vectors for each node in order to improve numerical accuracy.
In this study, we applied the method developed by Minarechová et al. (2021) to compile a detailed gravimetric quasigeoid model in the Hong Kong territories. Since there are some inconsistencies in definitions and realizations of vertical and gravimetric data (such as different datum origins and application of different tidal systems and reference parameters), the gravimetric quasigeoid model is usually (optimally) fitted or combined with the geometric quasigeoid heights determined at the GNSS-levelling benchmarks from their geodetic and normal heights. In the method applied here, this fitting is implicitly carried out by compiling a quasigeoid model. The method applied for gravimetric quasigeoid modelling is briefly reviewed in Section 2. Input data acquisition is discussed in Section 3. Results are presented and analysed in Section 4. The study is summarized and concluded in Section 5.
2 Theory
A formulation of the oblique derivative of the BVP is explained in this section. We then briefly discuss its solution by means of applying the FEM according to the numerical procedure developed by Minarechová et al. (2021).
2.1 Oblique derivative BVP
In the most generalized form, the FGBVP is formulated as follows (Koch and Pope 1972, Bjerhammar and Svensson 1983, Holota 1997):
where S denotes the Lipschitz domain (in our case the Earth), T(x) is the disturbing potential (i.e. difference between values of the actual and normal gravity potential) at a point x = (x, y, z), δg(x) is the gravity disturbance, and the vector s(x) = −∇U(x)/|∇U(x)| is the unit vector normal to the equipotential surface of the normal potential U(x) at a point x. The expressions in equations (1)–(3) describe the exterior BVP for the Laplace equation, where the computation domain is situated outside the Earth and is infinite. Since the FEM requires a discretization of the whole computation domain by finite elements, the bounded domain Ω is constructed above the Earth (cf. Fašková et al. 2010) that is bounded by the lower surface Γ ⊂ ∂Ω representing a part of the Earth’s surface and an upper surface created at an appropriate altitude (depending on a vertical gravity data extension). In the case of local gravity field modelling, the domain Ω is also bounded by a geographical extension of the study area. The Dirichlet-type BC for the disturbing potential is then defined for the upper and geographical side boundaries. In the bounded domain Ω, we consider the following BVP (Minarechová et al. 2021):
where Γ ⊂ ∂Ω represents the part of the Earth’s topography, and ∂Ω − Γ represents the upper and geographical boundaries. As seen in equation (6), instead of
2.2 FEM solution to the oblique derivative BVP
To solve the BVP defined by equations (4) and (5), we applied the FEM approach based on the numerical procedure developed by Minarechová et al. (2021). It involved the following steps: The bounded 3D computational domain Ω was discretized by finite elements Ωe using the hexahedral elements with eight nodes (see Brenner and Scott 2002; or Reddy 2006). On an arbitrary element Ωe, a weak formulation of equation (4) was derived using the fundamental principles of FEM (Reddy 2006). To incorporate the oblique derivative BC in equation (5), for the row of elements that lie on the bottom boundary (i.e. the discretized Earth’s surface), the weak formulation was modified by splitting the oblique vector s into its normal and tangential components (Minarechová et al. 2021). On each hexahedral element Ωe, the unknown solution T was approximated by a linear combination of basis functions yielding an element stiffness matrix. Afterwards, a global stiffness matrix was assembled from all element matrices by using two principles: (i) continuity of primary variables at the inter-element nodes and (ii) “equilibrium” of secondary variables at the interface between two neighbouring elements. Finally, the Dirichlet BCs in equation (6) for nodes that lie on the ∂Ω − Γ were taken into consideration by establishing a global linear system of equations. For all details of this FEM approach, we refer readers to the study by Minarechová et al. (2021).
3 Data acquisition
We used terrestrial and marine gravity data, GGMs, levelling data, GNSS geodetic heights, and topographic and bathymetric models to compile a new gravimetric quasigeoid model and combine it with GNSS-levelling data. This section provides a brief summary of datasets and models and their use for a discretization of the Earth’s surface and a preparation of input BCs, namely, the Dirichlet BC generated from GGMs and the gravity disturbances as the oblique derivative BCs considered on the discretized Earth’s topography.
3.1 Terrestrial and shipborne gravity data
From the regional gravity survey conducted by Electronic and Geophysical Services Ltd in 1991, 640 gravity observations were done in the Hong Kong territories (Electronic and Geophysical Services Ltd 1991). These observations comprise 133 shipborne measurements, and 507 terrestrial measurements on land spaced at approximately 2 and 2–4 km apart, respectively. Terrestrial sites were accessed using either vehicles or helicopters, and measurements were performed by the Lacoste and Romberg “G” relative gravimeter. The seaborne gravity measurements were performed using the marine model H/U seabed gravimeter. The distribution of gravity data is shown in Figure 1. The gravity database has an accuracy of ±0.03 mGal deduced from its connection to the International Gravity Standardization Net 1971 (Evans 1990).
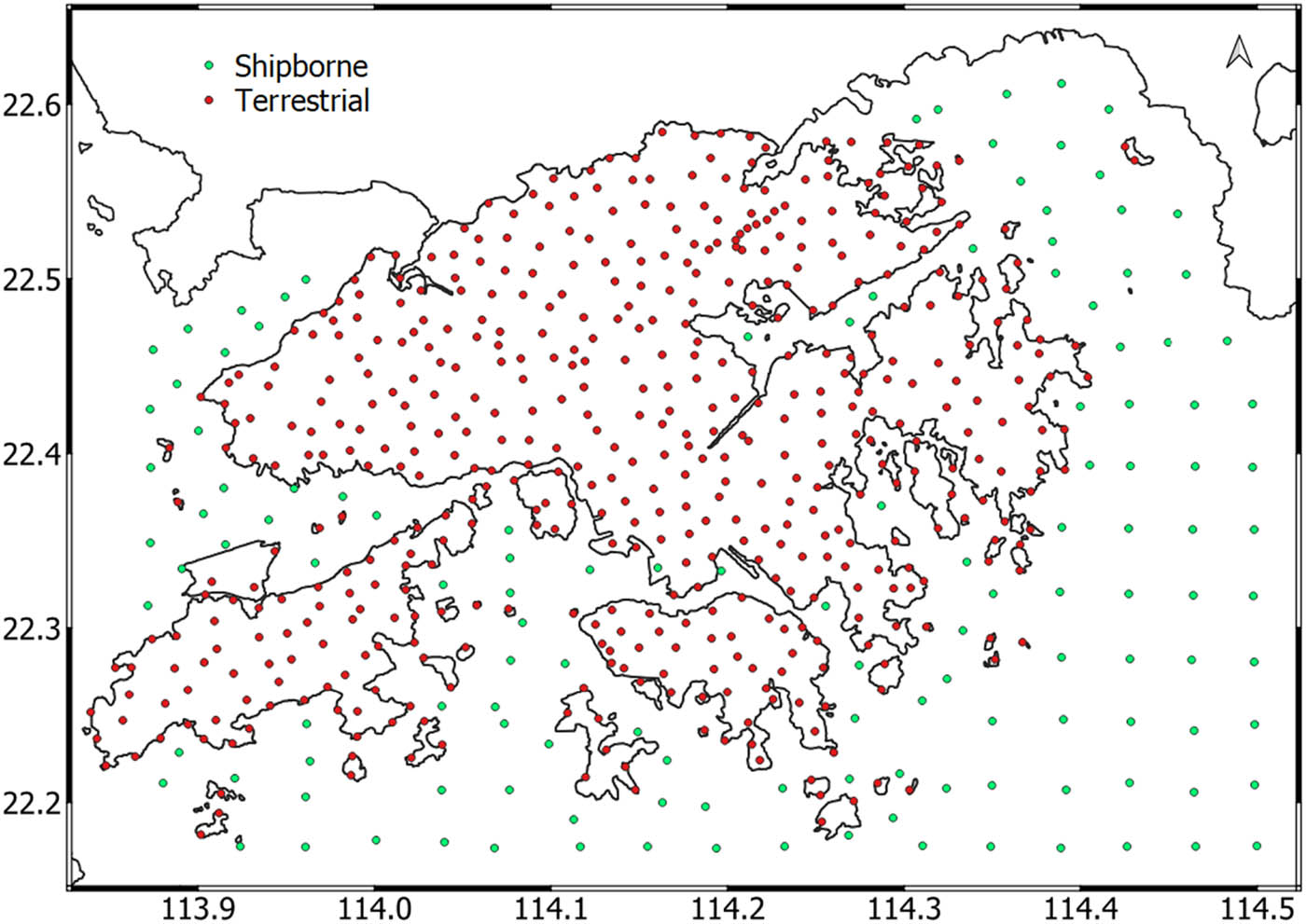
Distribution of the terrestrial and shipborne gravity data.
3.2 Discretization of the computational domain
The Hong Kong territories, covering a total area of about 1,100 km², are characterized by large topographic elevation changes with the maximum height reaching 957 m (Tai Mo Shan). Our 3D computational domain for the FEM numerical scheme was considered on such complicated topography. To get a reliable FEM numerical solution in this territory, we had to consider an extended area, as shown in Figure 2. Its size is approximately two times bigger than the size of the inner-zone area with the input terrestrial and shipborne gravity data. In this way, we minimized the impact of the Dirichlet BC prescribed on the side boundaries of the FEM solution inside the inner zone, as discussed by Fašková et al. (2010). Finally, the chosen computation area was bounded by meridians of 113.5°E and 114.8°E longitudes and parallels of 21.8°N and 22.9°N latitudes and discretized with the high-resolution 0.0005 deg × 0.0005 deg topographical grid.
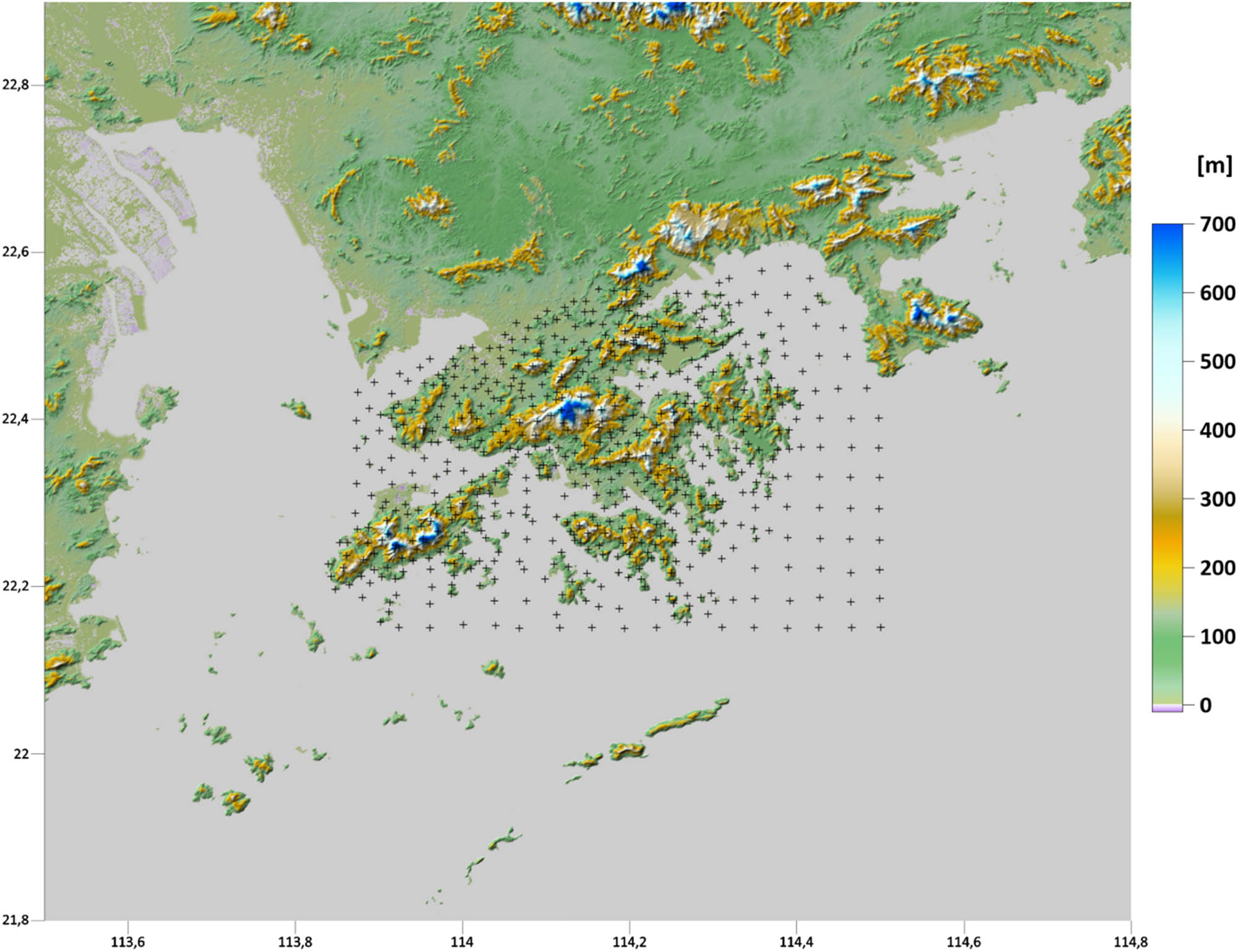
The discretized Earth’s topography in the Hong Kong territories and surrounding areas as the bottom boundary of the computational domain (the resolution 0.0005 deg × 0.0005 deg).
Within the Hong Kong territories, we used the HK_DTM_5m digital terrain model compiled by the Lands Department (www.landsd.gov.hk/en/spatial-data/open-data/kf_dtm.html). We also used the HKGEOID-2022 geoid model Nsiah Ababio and Tenzer (2022b) to obtain the geodetic (ellipsoidal) heights of computational nodes. In surrounding areas, we used the multi-error-removed improved-terrain (MERIT) digital elevation model (DEM) (Yamazaki et al. 2017) combined with the EGM2008 geoid model (Pavlis et al. 2012). The ellipsoidal heights of computational nodes offshore were interpolated from the DTU21 mean sea surface (Andersen et al. 2021). In this way, we constructed the bottom boundary of the 3D computational domain (Figure 2).
The upper boundary was chosen at the constant altitude of 200 km above the reference ellipsoid and was discretized with the same horizontal resolution of 0.0005 deg × 0.0005 deg. In the radial direction, the 3D computational domain was discretized non-uniformly depending on altitude. The radial size of finite elements on the Earth’s surface was set to 5 m while increasing linearly with altitude and exceeding 1 km for elements on the upper boundary. The whole 3D computational domain then consisted of 2,600 × 2,200 × 800 (longitude × latitude × height) = 4,576,000,000 finite elements (5,720,000 computational nodes on the discretized Earth’s topography).
3.3 Dirichlet BCs generated from GGMs
The Dirichlet BCs on the upper and side boundaries were generated from the GRACE/GOCE-based GGMs. In particular, we used the GO_CONS_GCF_2_DIR_R6 satellite-only GGM up to a degree/order of 300 (Bruinsma et al. 2014) to generate the disturbing potential on the upper boundary at an altitude of 200 km (Figure 3). The FEM solution was fixed to the gravity field information detected by the satellite missions CHAMP, GRACE, and GOCE. On the side boundaries, the disturbing potential was generated from the combined EIGEN-6C4 model up to a degree/order of 2160 (Förste et al. 2014).
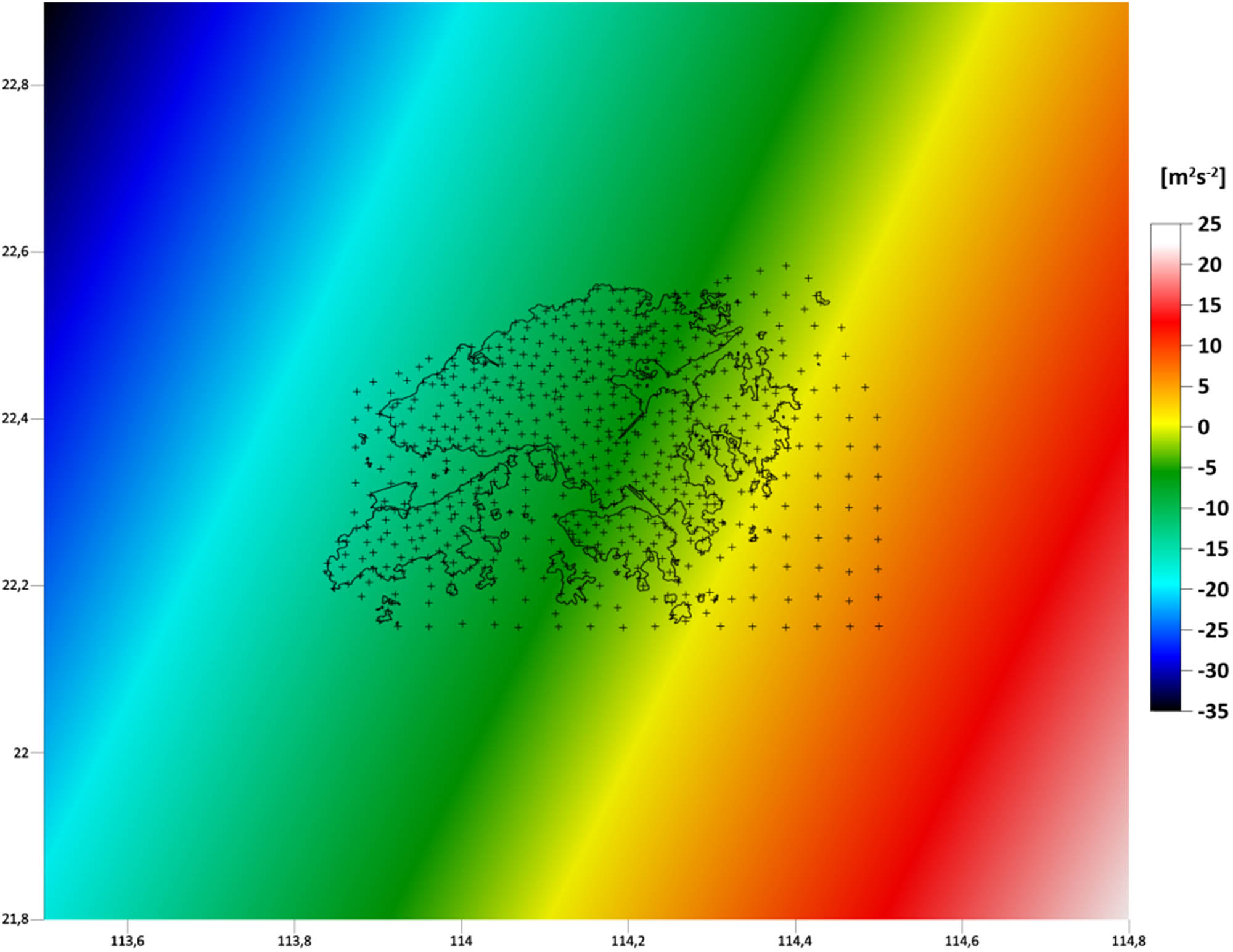
Disturbing potential at an altitude of 200 km above the reference ellipsoid as the Dirichlet BC on the upper boundary generated from the GO_CONS_GCF_2_DIR_R6 model up to a degree/order of 300.
3.4 Gravity disturbances on the discretized Earth’s surface
On the bottom boundary, the input gravity disturbances were generated directly at computational nodes that discretize the Earth’s surface. Due to different sources of gravity data, we divided the bottom boundary into three zones, as shown in Figure 4. The Hong Kong territories covered by available terrestrial and shipborne gravity measurements represent the inner zone (“Zone_IN”). Here, we used the method of a reverse reconstruction of the gravity acceleration from the complete Bouguer anomaly (CBA) map. Outside this area, we generated input data from a combined GGM refined by the residual terrain model (RTM) methodology (“Zone_OUT_lands”). Over open sea (“Zone_OUT_sea”), we interpolated gravity disturbances from the DTU21_GRAV dataset, providing the altimetry-derived gravity data.
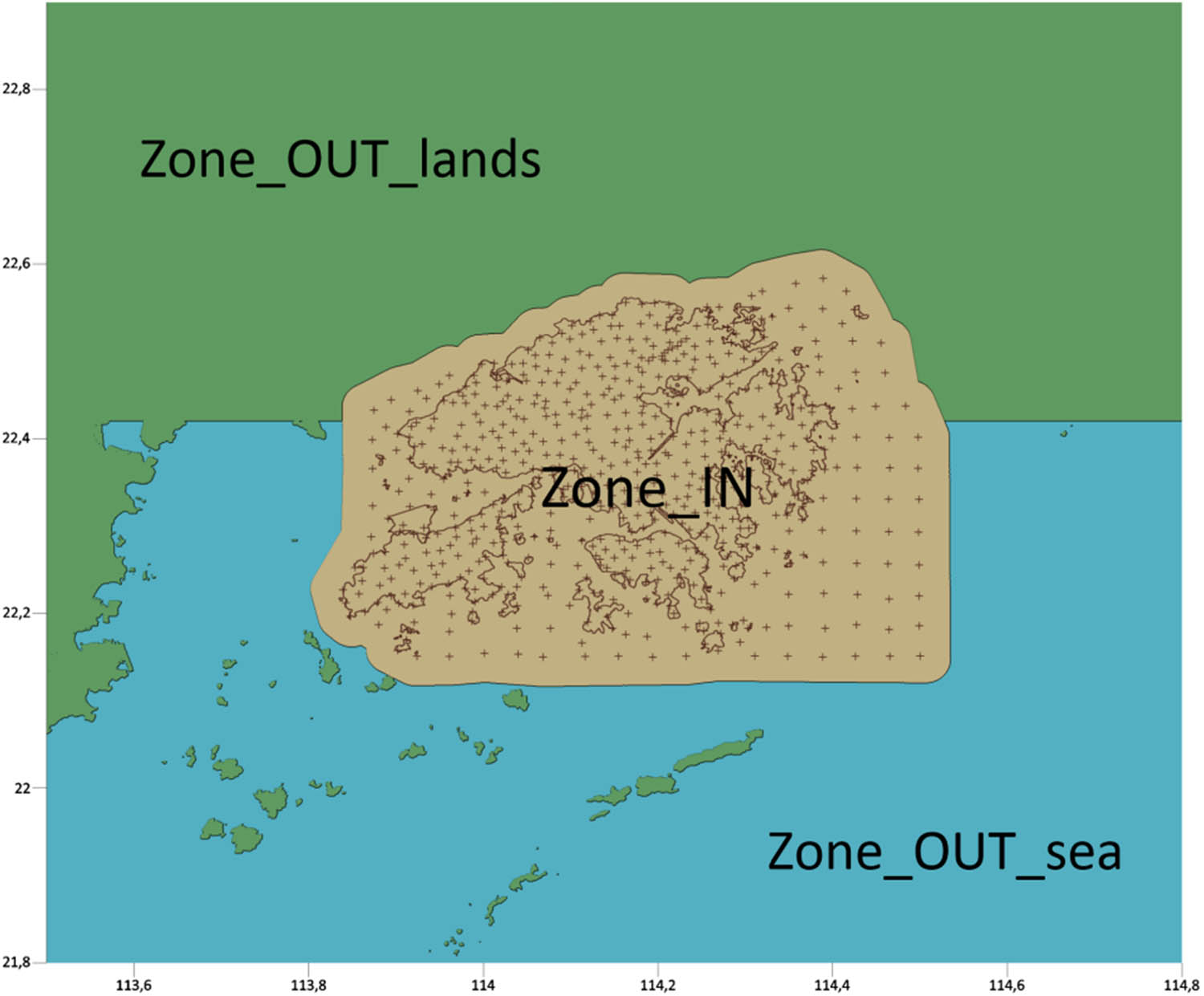
The bottom boundary divided into three zones with respect to gravity data sources.
3.4.1 Reconstruction of gravity from the CBA map
In the inner zone “Zone_IN” (Figure 4), we used the method of a reverse reconstruction of the gravity from the CBA map. The computation of the gravity value at an arbitrary point through a reverse reconstruction from the CBA map is considered to be the most accurate method (cf. Majkráková et al. 2016, or Zahorec et al. 2021). The reason is simple, an interpolation from the CBA map is more appropriate than, for example, from the free-air anomaly map. The first numerical step involved the computation of the CBA from the gravity measurements described in Section 3.1. We used a standard approach based on precise evaluation of the terrain/bathymetric corrections to a spherical distance of 166.7 km. For this purpose, we used TopoSK software (Zahorec et al. 2017) and the following DEMs: For the inner most zone (up to 250 m), we used HK_DTM_5m as the most detailed and available DEM of the Hong Kong territories. For the middle zone (250–5.2 km), we used HK_DTM_5m added by the Advanced Land Observing Satellite World 3D model version 2.1 (AW3D30) (Tadono et al. 2014; Takaku et al. 2018) and resampled to a resolution of 25 m. For the closer outer zone (5.2–28.8 km) and more distant outer zone (28.8–166.7 km), we used the MERIT DEM with resolutions of 3 and 30 arcsec, respectively. Bathymetric corrections were calculated using the SRTM15plus v.2.3 model (Tozer et al. 2019).
We used the CBA map for a correction density of 2,670 kg/m3 (Figure 5) to interpolate the CBA values on a regular grid of 50 m × 50 m. By the identical reverse calculation, including the evaluation of terrain/bathymetric corrections, we obtained values of the reconstructed gravity values at the FEM computational grid. From these values, we generated gravity disturbances at all grid points of the “Zone_IN” whose ellipsoidal heights had been reconstructed before (Section 3.2).
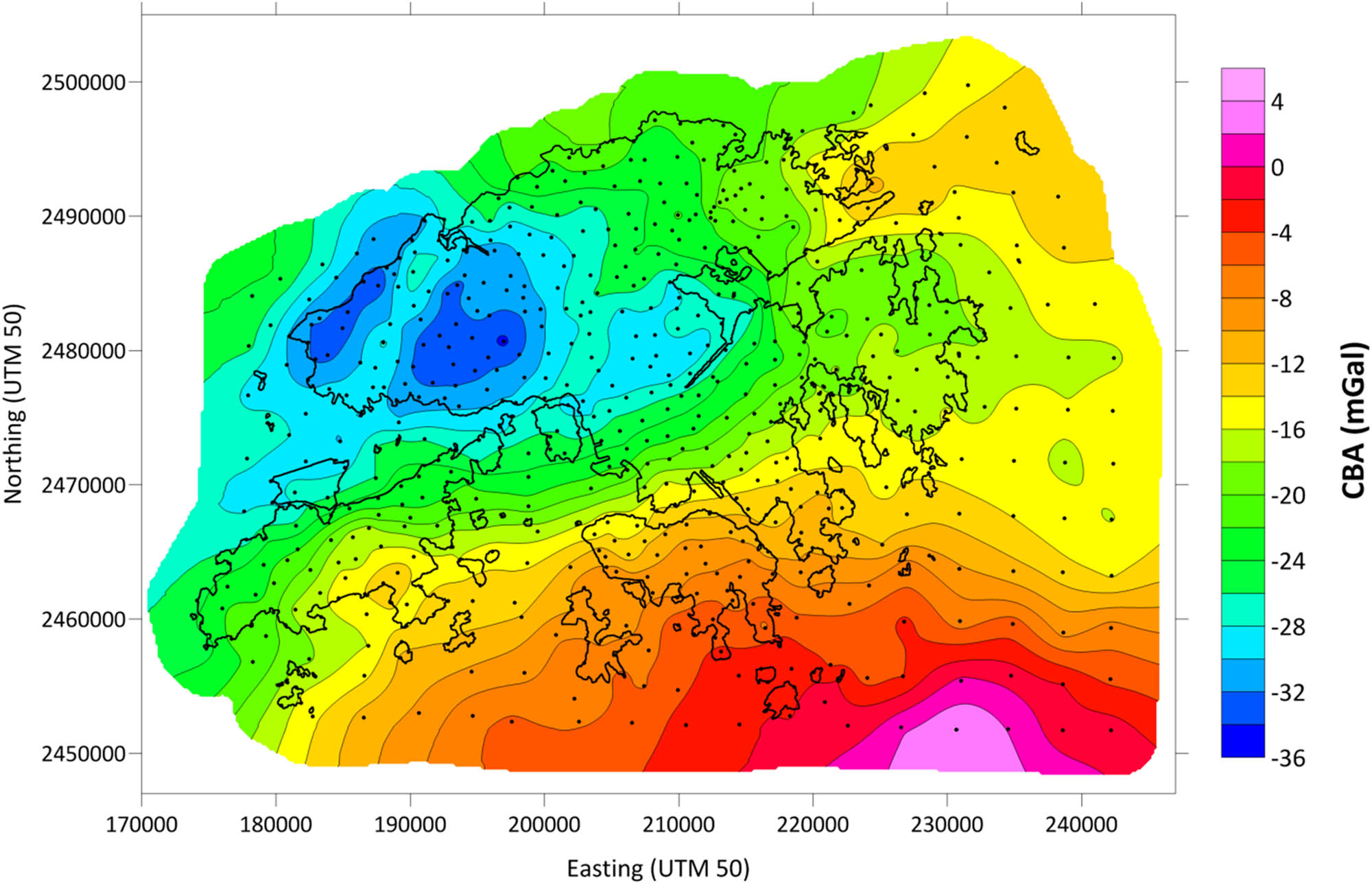
CBA map constructed from available gravity measurements (black dots).
3.4.2 GGM + RTM method
The input gravity disturbances at grid points of “Zone + OUT + lands” (Figure 4) were generated using the GGM + RTM methodology. We used the combined EIGEN-6C4 model up to a degree/order of 2,160. The RTM technique accounts for differences between the gravitational effect of the real terrain masses represented by high-resolution DEMs (the same used for CBA in Section 3.4.1) and smoothed mean elevation surface represented, for instance, by the DTM2006 model (Pavlis et al. 2007). The impact of RTM on the gravity generated from GGM is significant, as can be seen from the comparison with the gravity observed from terrestrial measurements in Figure 6.
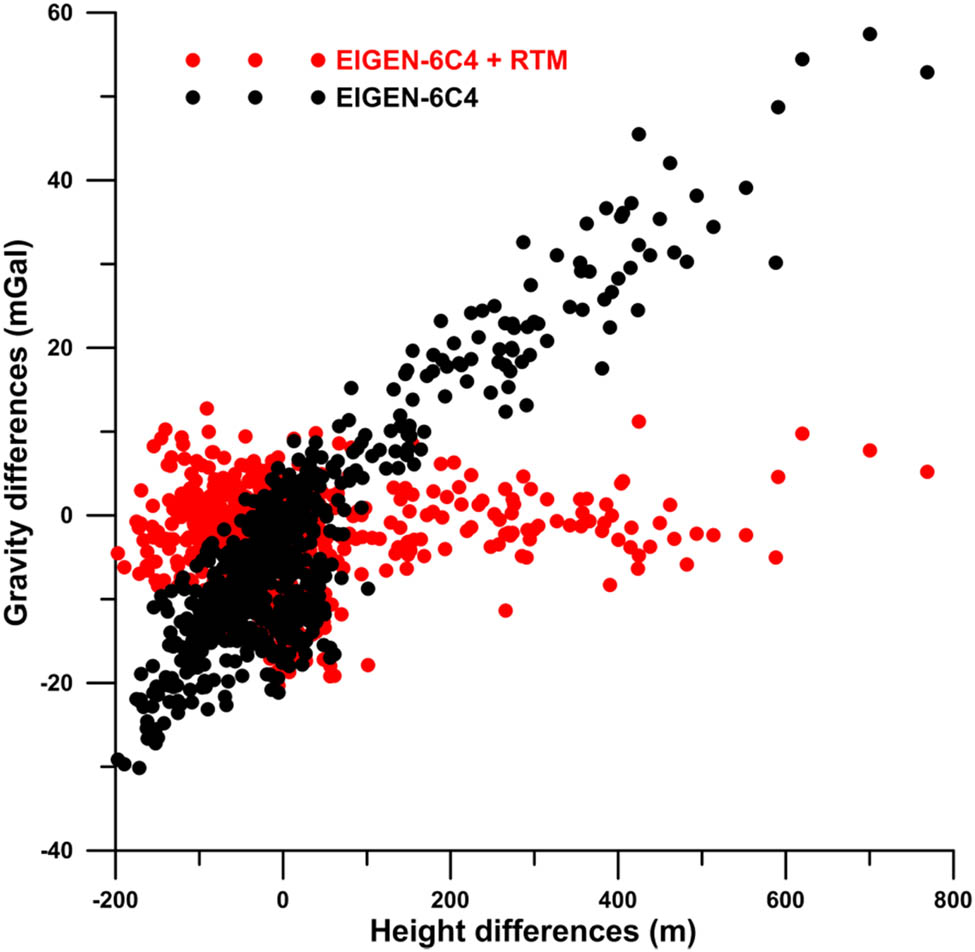
Differences of the gravity from terrestrial/shipborne measurements and the gravity generated from GGM without RTM (black) and with RTM (red). Gravity differences are shown as a function of height differences between the detailed DEM and DTM2006.
3.4.3 Altimetry-derived gravity data
At grid points over the open sea in “Zone_OUT_sea” (Figure 4), the gravity disturbances were transformed from the altimetry-derived gravity anomalies interpolated from the DTU21_GRAV data set. For this transformation, we used the EGM2008 model (Pavlis et al. 2012). Due to the worse accuracy of the altimetry-derived gravity data in shallow waters and coastal areas, we did not use them in Lingding Bay (the Pearl River estuary in the northwest of Hong Kong) and Mirs Bay (in the northeast of Hong Kong).
Combining the gravity disturbances generated in all three zones, we finally obtained the input dataset on the bottom boundary as the oblique derivative BC for our FEM numerical solution of FGBVP. The spatial pattern of the gravity disturbances is depicted in Figure 7. We could recognize some minor discontinuities in data along borders between the selected three zones. Nevertheless, the magnitudes of these discontinuities are not that significant because we do not have at disposal any original gravimetric measurements outside the Hong Kong territories. Note that gravity data over mainland China are not publicly available.
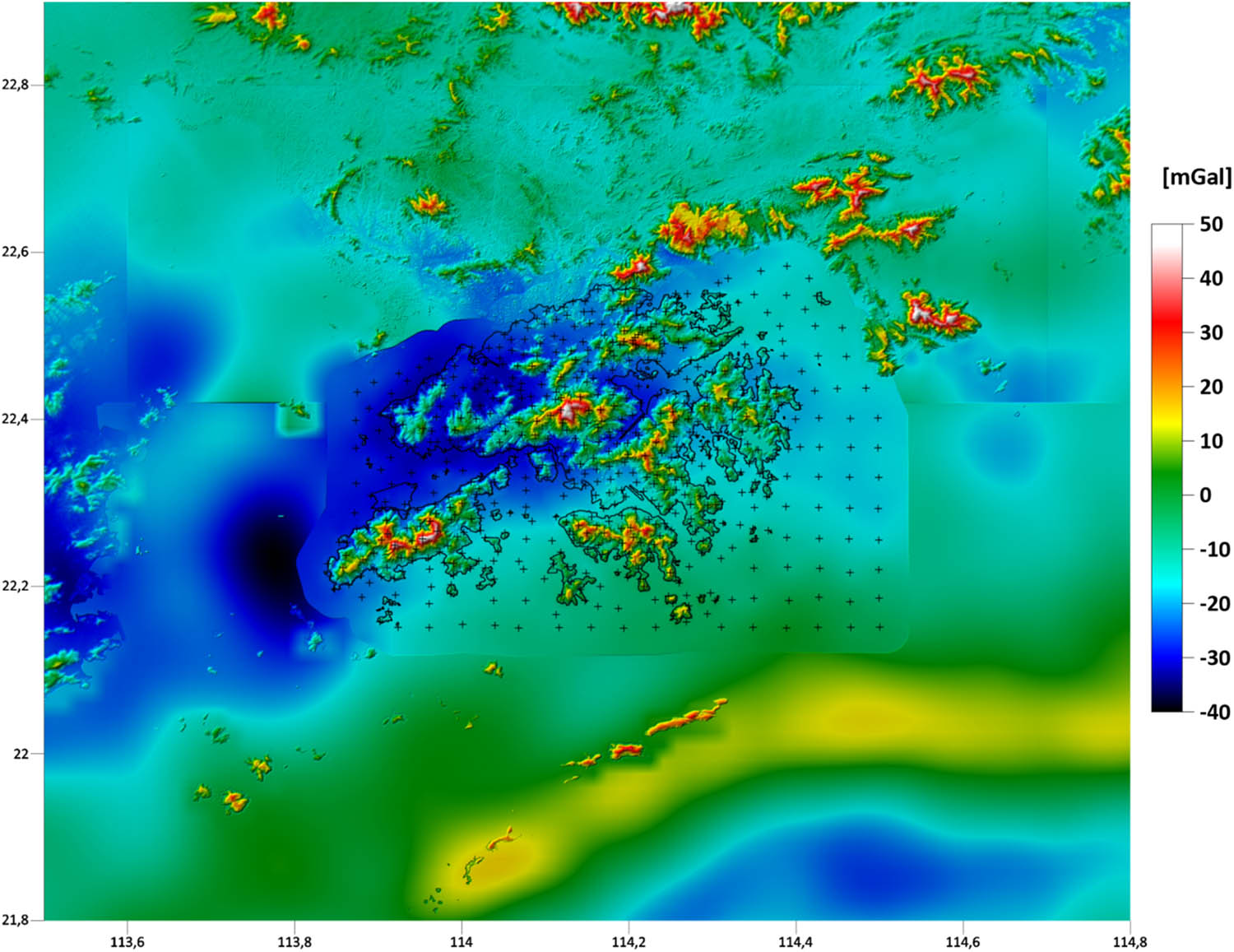
Gravity disturbances at the Earth’s surface as the oblique derivative BC on the bottom boundary.
3.5 GNSS-levelling data
From the current vertical control network database in Hong Kong, there are only 16 benchmarks with high-quality GNSS measurements of geodetic (ellipsoidal) heights referred to the WGS84 reference ellipsoid at the ITRF96 epoch. From these 16 points, there are 10 first-order bedrock benchmarks and 6 second-order benchmarks. The normal heights of these benchmarks were obtained after applying the normal correction to levelled height differences and a subsequent readjustment of the whole levelling network that provided the VCN2022 solution. The new network adjustment and analysis revealed that the accuracy of VCN2022 normal heights is about ±1–2 cm, and a similar accuracy characterizes the GNSS vertical measurements Nsiah Ababio and Tenzer (2022b). The distribution of the GNSS-levelling benchmarks and their respective quasigeoidal heights are shown in Figure 8.
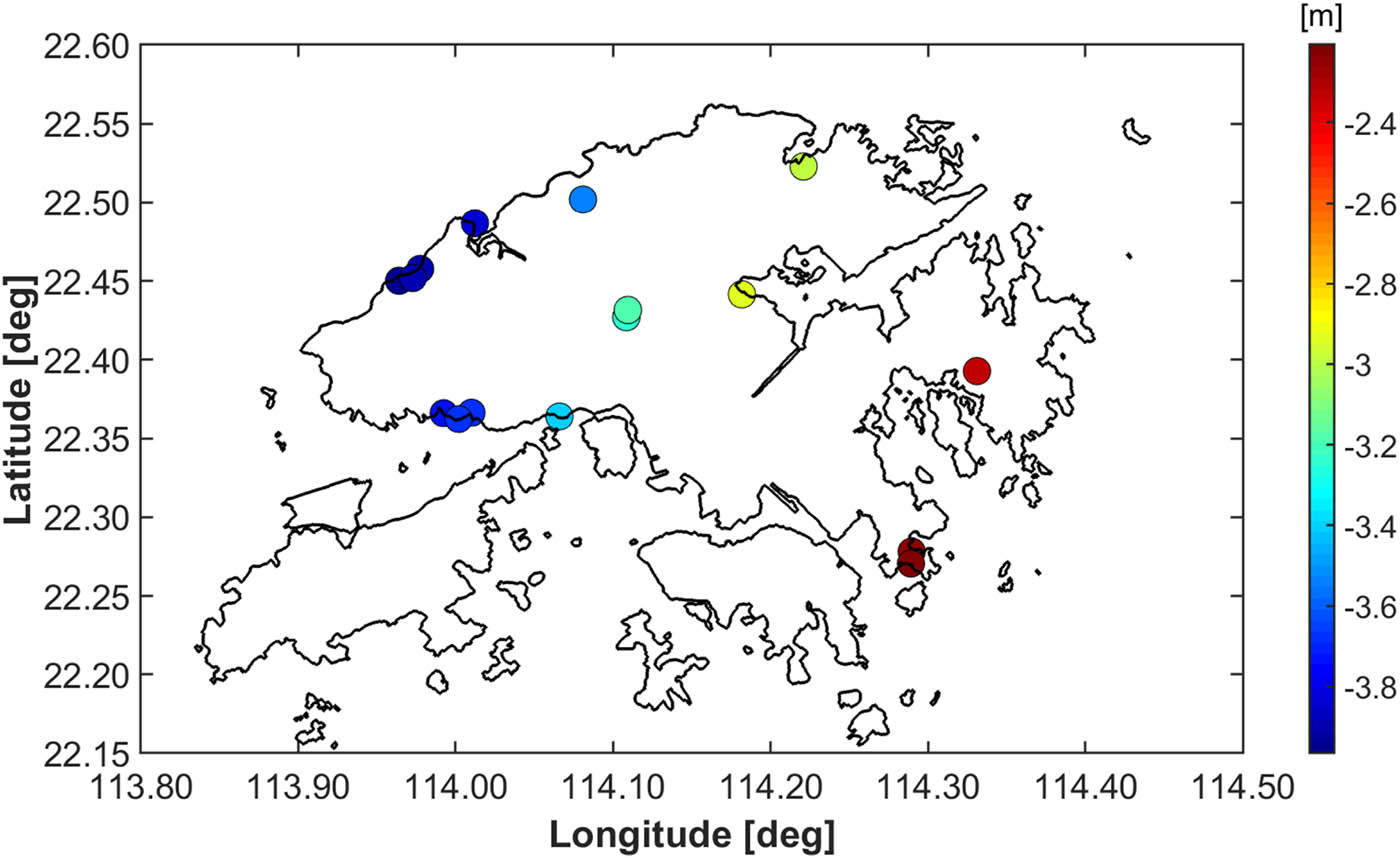
Distribution of GNSS-levelling benchmarks in the Hong Kong territories.
4 Results
A numerical solution of FGBVP based on using the FEM approach on a large 3D unstructured mesh with 4,576,000,000 finite elements (Section 3.2) required about 1.3 TB of internal memory. The large-scale parallel computations were performed on 176 cores of the cluster with the distributed memory and the NUMA (Non-Uniform Memory Access) architecture by using a hybrid parallelization (44 MPI processes, each with 4 Open MP threads). The BiCGSTAB linear solver converged after 5,970 iterations for a tolerance of 10−5. Hence, the parallel computations took about 35 h of CPU time.
A benefit of such large-scale computations is that they resulted in the disturbing potential obtained at every point of the entire 3D computational mesh, i.e. at all 4,576,000,000 finite elements. Hence, it is possible to derive different quantities of the local gravity field (e.g. the first, second, and higher derivatives in different directions) at every point. To get a local quasigeoid model, values of the disturbing potential T obtained on the bottom boundary (i.e. at the Earth’s surface; Figure 2) were converted to the quasigeoidal heights ξ by using the following formula:
where h is the geodetic (ellipsoidal) height, H N denotes the normal height, U is the normal gravity potential evaluated at the ith grid point at the Earth’s surface, γ is the mean normal gravity between the reference ellipsoid and the telluroid, and W 0 is the global geopotential value adopted for a realization of the International Height Reference System (IHRS) (Sánchez et al. 2016). Parameters of the normal gravity filed were computed from the WGS-84 reference ellipsoid. In this way, the quasigeoidal heights have been expressed with respect to the WGS-84 reference ellipsoid and to the W 0 value adopted for IHRS.
The local quasigeoid model over the Hong Kong territories (and surrounding areas) computed on a 0.0005 deg × 0.0005 deg grid is shown in Figure 9. To validate its precision, we compared the gravimetric quasigeoid heights with the corresponding geometric quasigeoid heights at GNSS-levelling benchmarks (Section 3.5). It is worth noting that the geometric quasigeoid heights were obtained from differences between the geodetic (ellipsoidal) heights (measured by the GNSS techniques) and the VCN2022 normal heights. In addition, we used 507 input terrestrial gravimetric measurements (Section 3.1) to validate the result of a gravimetric modelling. For this purpose, we converted the measured gravity anomaly data into the corresponding quasigeoid heights. The comparison of results is shown in Figure 10, with the statistics of differences summarized in Table 1.
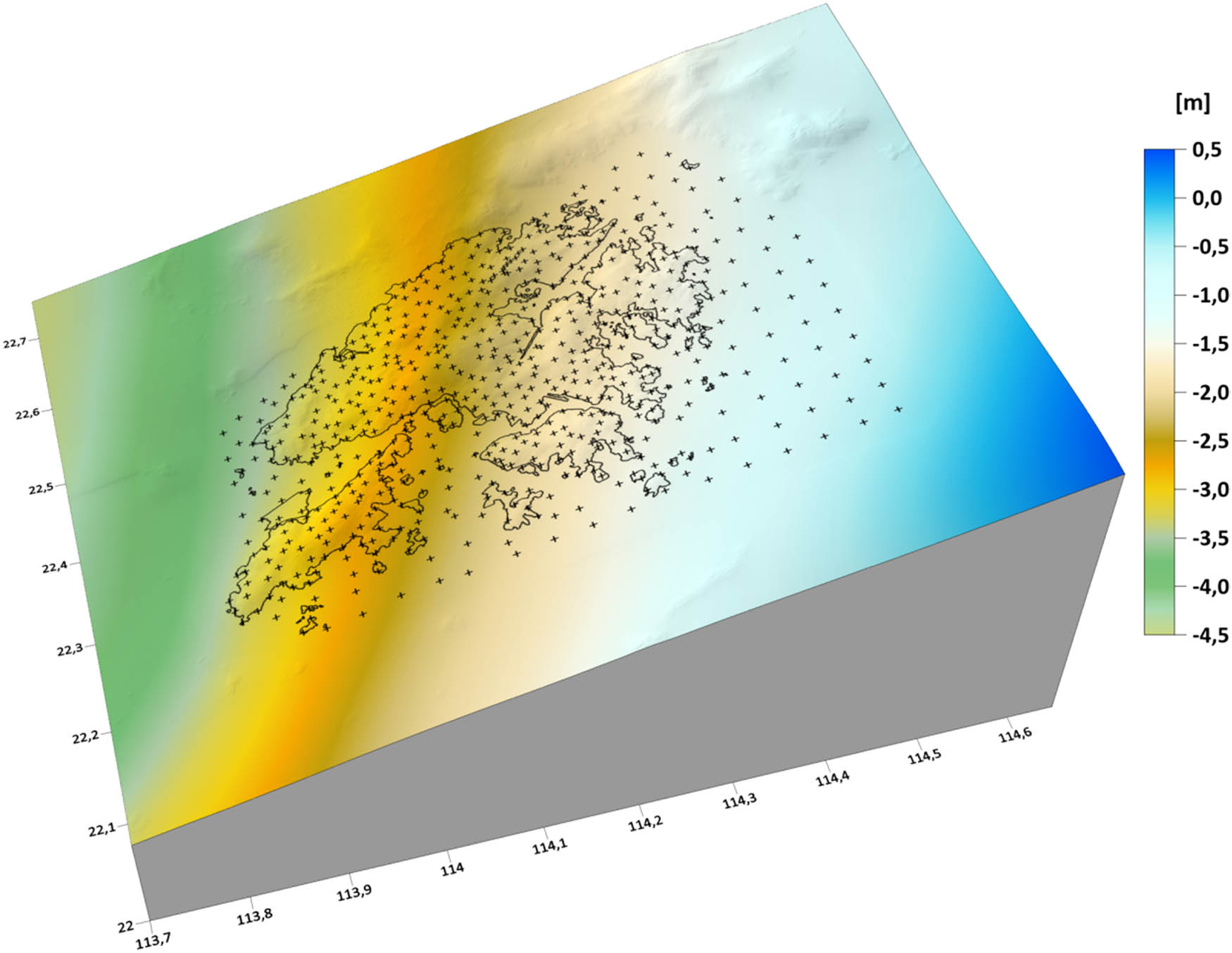
Local quasigeoid model in the Hong Kong territories presented as the FEM numerical solution of FGBVP (with a resolution of 0.0005 deg × 0.0005 deg).
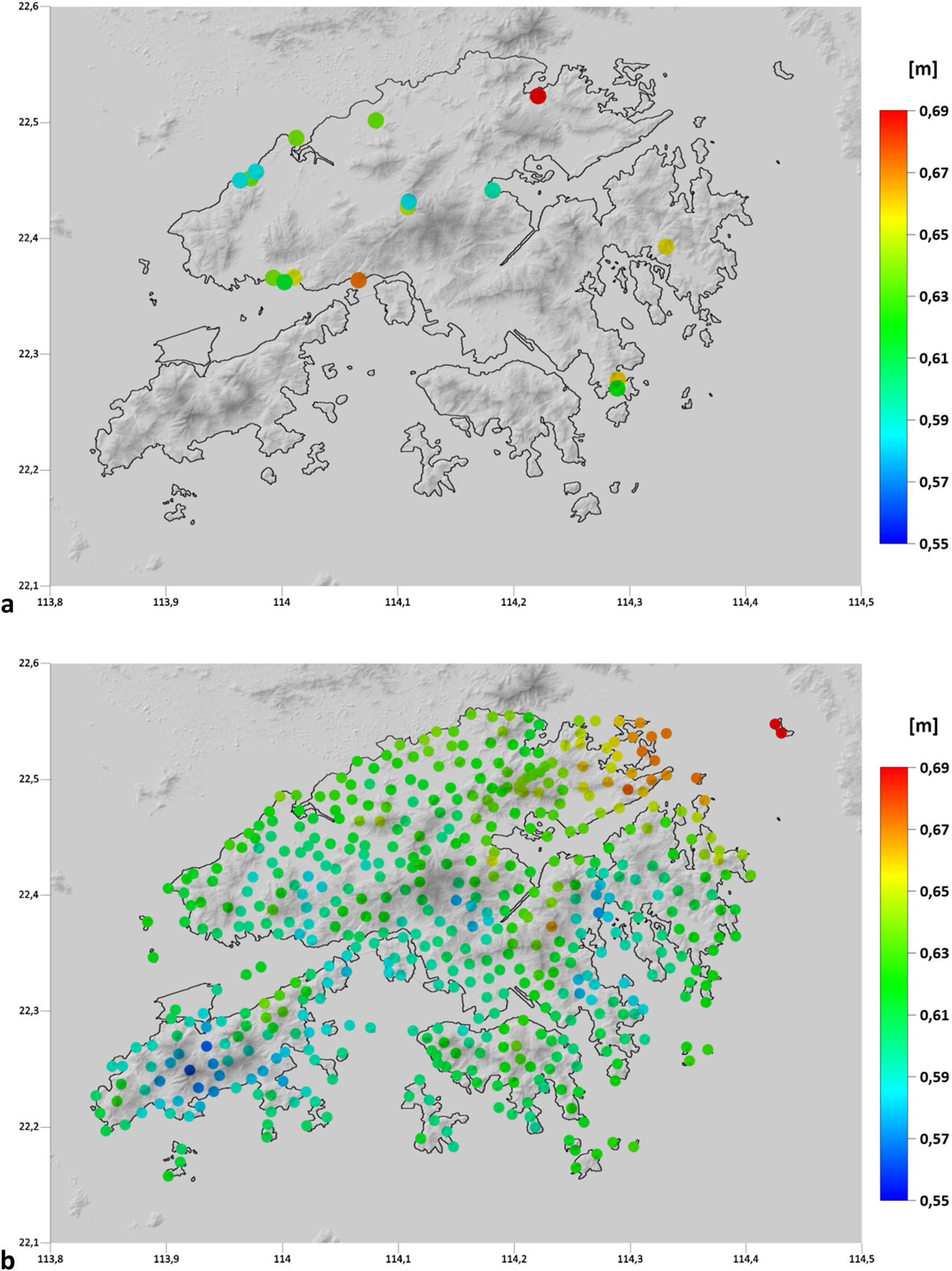
Validation of results: (a) Differences between the gravimetric and geometric quasigeoid heights at 16 GNSS-levelling benchmarks. (b) Differences between the quasigeoid heights obtained by solving FGBVP and computed from the measured gravity anomaly data at 507 gravity sites.
Validation of results: Statistics of differences between the gravimetric and geometric quasigeoid heights at GNSS-levelling benchmarks; statistics of differences between the quasigeoid heights obtained by solving FGBVP and computed from the measured gravity anomaly data
| Characteristic | GNSS-levelling benchmarks | Input gravimetric measurements |
|---|---|---|
| No. of points | 16 | 507 |
| Minimum | 58.4 cm | 56.2 cm |
| Maximum | 69.1 cm | 69.0 cm |
| Range | 10.7 cm | 12.8 cm |
| Mean | 63.2 cm | 61.3 cm |
| Median | 63.7 cm | 61.1 cm |
| SD | 3.3 cm | 2.2 cm |
As seen from the comparison, there is a reasonable agreement between the quasigeoid models with both the geometric quasigeoid heights at GNSS-levelling points and with the quasigeoid heights computed from measured gravity data. The mean values of both differences (63.2 and 61.3 cm; Table 1) differ by less than 2 cm. This finding indicates good consistency between gravity, GNSS, and levelling data in Hong Kong. Moreover, this finding also assures that despite high-quality GNSS-levelling measurements are only at 16 benchmarks that are very irregularly distributed and clustered only at some locations, the validation of results should be quite realistic.
5 Summary and concluding remarks
We have compiled the first detailed quasigeoid model in the Hong Kong territories by applying the FEM to solve the geodetic BVP with oblique derivative BCs considered directly at computational nodes on the discretized Earth’s topography. Since the problem is defined for the oblique derivative BCs, we first converted the terrestrial and seaborne gravity measurements into the gravity disturbances at the Earth’s surface by utilizing information about the geodetic heights obtained from the digital elevation and geoid models (inland) and the mean sea surface topography (offshore). The absence of gravity data in mainland China was resolved by using the gravity information from a high-resolution GGM.
The result of gravimetric modelling revealed that the quasigeoid surface within the Hong Kong territories is mostly below the WGS84 reference ellipsoid, with a prevailing smooth pattern of decreasing quasigeoid heights in the northwest direction. Small irregularities in this prevailing pattern, mostly only a few millimeters, are mainly attributed to a rough topography in Hong Kong.
The validation of the gravimetric quasigeoid model revealed a relatively good agreement with the geometric quasigeoid heights at GNSS-levelling benchmarks, with the standard deviation of differences between the gravimetric and geometric quasigeoid heights of ±3.3 cm. Obviously, this accuracy specification was obtained from a minimal number of GNSS-levelling benchmarks distributed very irregularly over the territories, with most of them scattered only at a few locations. Moreover, these benchmarks are located at low elevations. Nevertheless, this value quite closely reflects the accuracy estimates of the geometric quasigeoid heights at GNSS-levelling benchmarks of about ±1–2 cm as well as expected uncertainties at the level of about ±2–3 cm that are attributed to the accuracy of gravity measurements (and a lack of gravity data in mainland China). This argument is supported by the fact that the standard deviation of differences between the quasigeoid heights obtained from gravimetric modelling and computed from the measured gravity data was found to be ±2.2 cm. In addition to these findings, a relatively good consistency was confirmed between the reference systems defining gravity and GNSS-levelling measurements.
-
Funding information: The work presented in this article was supported by the Hong Kong GRF RGC project 15217222: Modernization of the levelling network in the Hong Kong territories. The contribution of coauthors RC and MM was supported by Grants VEGA 1/0486/20 and APVV-19-0460, and the contribution of coauthors PZ and JP by Grants VEGA 2/0100/20 and APVV-19-0150.
-
Conflict of interest: Authors state no conflict of interest.
References
Andersen, O. B., A. Abulaitijiang, S. Zhang, and S. K. Rose. 2021. A new high resolution Mean Sea Surface (DTU21MSS) for improved sea level monitoring, EGU General Assembly 2021, online, 19-30 Apr 2021, EGU21-16084.10.5194/egusphere-egu21-16084Search in Google Scholar
Bjerhammar, A. and L. Svensson. 1983. “On the geodetic boundary value problem for a fixed boundary surface. A satellite approach.” Bulletin Géodésique 57(1–4), 382–93.10.1007/BF02520941Search in Google Scholar
Brenner, S. C. and L. R. Scott. 2002. The mathematical theory of finite element methods. New York: Springer.10.1007/978-1-4757-3658-8Search in Google Scholar
Bruinsma, S., C. Förste, O. Abrikosov, J. Lemoine, J. Marty, S. Mulet, et al. 2014. “ESA’s satellite-only gravity field model via the direct approach based on all GOCE data.” Geophysical Research Letters 41(21), 7508–14.10.1002/2014GL062045Search in Google Scholar
Čunderlík, R. and K. Mikula. 2010. “Direct BEM for high-resolution gravity field modelling.” Studia Geophysica et Geodaetica 54(2), 219–38.10.1007/s11200-010-0011-0Search in Google Scholar
Čunderlík, R., K. Mikula, and M. Mojžeš. 2008. “Numerical solution of the linearized fixed gravimetric boundary-value problem.” Journal of Geodesy 82, 15–29.10.1007/s00190-007-0154-0Search in Google Scholar
Čunderlík R., K. Mikula, and R. Špir. 2012. “An oblique derivative in the direct BEM formulation of the fixed gravimetric BVP.” IAG Symposium 137, 227–31.10.1007/978-3-642-22078-4_34Search in Google Scholar
Droniou, J., M. Medl’a, and K. Mikula. 2019. “Design and analysis of finite volume methods for elliptic equations with oblique derivatives; application to Earth gravity field modeling.” Journal of Computational Physics 398, 108876.10.1016/j.jcp.2019.108876Search in Google Scholar
Electronic and Geophysical Services ltd. 1991. Regional gravity survey of Hong Kong. Final Report, Job Number HK50190, Hong Kong.Search in Google Scholar
Evans, R. B. 1990. Hong Kong gravity observation in July 1990 with BGS Lacoste and Romberg meter No.97 and international connections to IGSN 71, Report, British and Geology Survey, Hong Kong, China.Search in Google Scholar
Fašková, Z. 2008. “Numerical methods for solving geodetic boundary value problems.” PhD thesis, SvF STU, Bratislava, Slovakia.Search in Google Scholar
Fašková, Z., R. Čunderlík, J. Janák, K. Mikula, and M. Šprlák. 2007. “Gravimetric quasigeoid in Slovakia by the finite element method.” Kybernetika 43(6), 789–96.Search in Google Scholar
Fašková, Z., R. Čunderlík, and K. Mikula. 2010. “Finite element method for solving geodetic boundary value problems.” Journal of Geodesy 84(2), 135–44.10.1007/s00190-009-0349-7Search in Google Scholar
Förste, C. H., S. L. Bruinsma, O. Abrikosov, J.-M. Lemoine, J. C. Marty, F. Flechtner, et al. 2014. EIGEN6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse, GFZ Data Services.Search in Google Scholar
Holota, P. 1997. “Coerciveness of the linear gravimetric boundary-value problem and a geometrical interpretation.” Journal of Geodesy 71, 640–51.10.1007/s001900050131Search in Google Scholar
Klees, R. 1995. “Boundary value problems and approximation of integral equations by finite elements.” Manuscripta Geodaetica 20, 345–61.Search in Google Scholar
Klees, R., M. van Gelderen, C. Lage, and C. Schwab. 2001. “Fast numerical solution of the linearized Molodensky problem.” Journal of Geodesy 75, 349–62.10.1007/s001900100183Search in Google Scholar
Koch, K. R. and A. J. Pope. 1972. “Uniqueness and existence for the geodetic boundary value problem using the known surface of the earth.” Bulletin Géodésique 46, 467–76.10.1007/BF02522053Search in Google Scholar
Lehmann, R. and R. Klees. 1999. “Numerical solution of geodetic boundary value problems using a global reference field.” Journal of Geodesy 73, 543–54.10.1007/s001900050265Search in Google Scholar
Macák, M., Z. Minarechová, and K. Mikula. 2014. “A novel scheme for solving the oblique derivative boundary-value problem.” Studia Geophysica et Geodaetica 58(4), 556–70.10.1007/s11200-013-0340-xSearch in Google Scholar
Macák, M., R. Čunderlík, K. Mikula, and Z. Minarechová. 2015. “An upwind-based scheme for solving the oblique derivative boundary-value problem related to the physical geodesy.” Journal of Geodetic Science 5(1), 15.10.1515/jogs-2015-0018Search in Google Scholar
Macák, M., K. Mikula, and Z. Minarechová. 2012. “Solving the oblique derivative boundary-value problem by the finite volume method.” In: ALGORITMY 2012, 19th conference on scientific computing, Podbanske, Slovakia, September 9–14, 2012, Proceedings of contributed papers and posters, Publishing House of STU, pp. 75–84.Search in Google Scholar
Majkráková, M., J. Papčo, P. Zahorec, B. Droščák, J. Mikuška, and I. Marušiak. 2016. “An analysis of methods for gravity determination and their utilization for the calculation of geopotential numbers in the Slovak national leveling network.” Contributions to Geophysics and Geodesy 46(3), 179–202.10.1515/congeo-2016-0012Search in Google Scholar
Medľa, M., K. Mikula, R. Čunderlík, and M. Macák. 2018. “Numerical solution to the oblique derivative boundary value problem on non-uniform grids above the Earth topography.” Journal of Geodesy 92, 1–19.10.1007/s00190-017-1040-zSearch in Google Scholar
Meissl, P. 1981. The use of finite elements in physical geodesy. Report 313, Geodetic Science and Surveying, The Ohio State University.Search in Google Scholar
Minarechová, Z., M. Macák, R. Čunderlík, and K. Mikula. 2021. “On the finite element method for solving the oblique derivative boundary value problems and its application in local gravity field modelling.” Journal of Geodesy 95, 70.10.1007/s00190-021-01522-8Search in Google Scholar
Mráz, D., M. Bořík, and J. Novotný. 2016. “On the convergence of the h-p finite element method for solving boundary value problems in physical geodesy.” In: International symposium on Earth and environmental sciences for future generations, International Association of Geodesy Symposia, edited by Freymueller J. T. and Sánchez L., Vol. 147, Springer, Cham.10.1007/1345_2016_237Search in Google Scholar
Nsiah Ababio, A., and R. Tenzer. 2022a. “The use of gravity data to determine orthometric heights at the Hong Kong territories.” Journal of Applied Geodesy 16(4), 401–16.10.1515/jag-2022-0012Search in Google Scholar
Nsiah Ababio, A., and R. Tenzer. 2022b. Compilation of the new detailed geoid model HKGEOID-2022 for the Hong Kong territories. Marine Geodesy 45(6), 688–709.10.1080/01490419.2022.2124560Search in Google Scholar
Pavlis, N. K., J. K. Factor, and S. A. Holmes. 2007. “Terrain-related gravimetric quantities computed for the next EGM.” Proceedings of the 1st International Symposium of IGFS, Istanbul, pp. 318–23.Search in Google Scholar
Pavlis, N. K., S. A. Holmes, S. C. Kenyon, and J. K. Factor. 2012. “The development and evaluation of the Earth Gravitational Model 2008 (EGM2008).” Journal of Geophysical Research 117, B04406.10.1029/2011JB008916Search in Google Scholar
Reddy, J. N. 2006. An introduction to the finite element method. 3rd edn, McGraw-Hill Education, New York.Search in Google Scholar
Sánchez, L., R. Čunderlík, N. Dayoub, K. Mikula, Z. Minarechová , Z. Šíma, et al. 2016. “A conventional value for the geoid reference potential W0.” Journal of Geodesy 90(9), 815–35.10.1007/s00190-016-0913-xSearch in Google Scholar
Shaofeng, B. and C. Dingbo. 1991, “The finite element method for the geodetic boundary value problem.” Manuscripta Geodaetica 16, 353–9.Search in Google Scholar
Šprlák, M., Z. Fašková, and K. Mikula. 2011. “On the application of the coupled finite-infinite element method to the geodetic boundary value problem.” Studia Geophysica et Geodaetica 55, 479–87.10.1007/s11200-011-0028-zSearch in Google Scholar
Zahorec, P., I. Marušiak, J. Mikuška, R. Pašteka, and J. Papčo. 2017. “Numerical calculation of terrain correction within the bouguer anomaly evaluation (Program Toposk), (Chapter 5).” In: Understanding the Bouguer anomaly: a gravimetry puzzle, edited by Pašteka R., Mikuška J. and Meurers B., Elsevier, pp. 79–92. ISBN 978-0-12-812913-5.10.1016/B978-0-12-812913-5.00004-XSearch in Google Scholar
Zahorec, P., J. Papčo, R. Pašteka, M. Bielik, S. Bonvalot, C. Braitenberg, et al. 2021. “The first pan-Alpine surface-gravity database, a modern compilation that crosses frontiers.” Earth System Science Data 13(5), 2165–2209.10.5194/essd-13-2165-2021Search in Google Scholar
Tadono, T., H. Ishida, F. Oda, S. Naito, K. Minakawa, and H. Iwamoto. 2014. “Precise global DEM generation by ALOS PRISM, ISPRS-annals of the photogrammetry.” Remote Sensing and Spatial Information Sciences 4, 71–6.10.5194/isprsannals-II-4-71-2014Search in Google Scholar
Takaku, J., T. Tadono, K. Tsutsui, and M. Ichikawa. 2018. “Quality Improvements of “AW3D” Global DSM Derived from ALOS PRISM.” In: Proc. the 38th annual symposium of the IEEE Geoscience and Remote Sensing Society (IGARSS2018), Valencia, Spain, 22–27 July 2018, pp. 1612–5.10.1109/IGARSS.2018.8518360Search in Google Scholar
Tozer, B., D. T. Sandwell, W. H. F. Smith, C. Olson, J. R. Beale, and P. Wessel. 2019. “Global bathymetry and topography at 15 arc seconds: SRTM15+.” Earth Space Science 6(10), 1847–64.10.1029/2019EA000658Search in Google Scholar
Yamazaki, D., D. Ikeshima, R. Tawatari, T. Yamaguchi, F. O’Loughlin, J. C. Neal, et al. 2017. “A high accuracy map of global terrain elevations.” Geophysical Research Letters 44, 5844–53.10.1002/2017GL072874Search in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Two adjustments of the second levelling of Finland by using nonconventional weights
- A gap-filling algorithm selection strategy for GRACE and GRACE Follow-On time series based on hydrological signal characteristics of the individual river basins
- On the connection of the Ecuadorian Vertical Datum to the IHRS
- Accurate computation of geoid-quasigeoid separation in mountainous region – A case study in Colorado with full extension to the experimental geoid region
- A detailed quasigeoid model of the Hong Kong territories computed by applying a finite-element method of solving the oblique derivative boundary-value problem
- Metrica – An application for collecting and navigating to geodetic control network points. Part II: Practical verification
- Global Geopotential Models assessment in Ecuador based on geoid heights and geopotential values
- Review Articles
- Local orthometric height based on a combination of GPS-derived ellipsoidal height and geoid model: A review paper
- Some mathematical assumptions for accurate transformation parameters between WGS84 and Nord Sahara geodetic systems
- Book Review
- Physical Geodesy by Martin Vermeer published by Aalto University Press 2020
- Special Issue: 2021 SIRGAS Symposium (Guest Editors: Dr. Maria Virginia Mackern) - Part II
- DinSAR coseismic deformation measurements of the Mw 8.3 Illapel earthquake (Chile)
- Special Issue: Nordic Geodetic Commission – NKG 2022 - Part I
- NKG2020 transformation: An updated transformation between dynamic and static reference frames in the Nordic and Baltic countries
- The three Swedish kings of geodesy – Speech at the NKG General Assembly dinner in 2022
- A first step towards a national realisation of the international height reference system in Sweden with a comparison to RH 2000
- Examining the performance of along-track multi-mission satellite altimetry – A case study for Sentinel-6
- Geodetic advances in Estonia 2018–2022
Articles in the same Issue
- Research Articles
- Two adjustments of the second levelling of Finland by using nonconventional weights
- A gap-filling algorithm selection strategy for GRACE and GRACE Follow-On time series based on hydrological signal characteristics of the individual river basins
- On the connection of the Ecuadorian Vertical Datum to the IHRS
- Accurate computation of geoid-quasigeoid separation in mountainous region – A case study in Colorado with full extension to the experimental geoid region
- A detailed quasigeoid model of the Hong Kong territories computed by applying a finite-element method of solving the oblique derivative boundary-value problem
- Metrica – An application for collecting and navigating to geodetic control network points. Part II: Practical verification
- Global Geopotential Models assessment in Ecuador based on geoid heights and geopotential values
- Review Articles
- Local orthometric height based on a combination of GPS-derived ellipsoidal height and geoid model: A review paper
- Some mathematical assumptions for accurate transformation parameters between WGS84 and Nord Sahara geodetic systems
- Book Review
- Physical Geodesy by Martin Vermeer published by Aalto University Press 2020
- Special Issue: 2021 SIRGAS Symposium (Guest Editors: Dr. Maria Virginia Mackern) - Part II
- DinSAR coseismic deformation measurements of the Mw 8.3 Illapel earthquake (Chile)
- Special Issue: Nordic Geodetic Commission – NKG 2022 - Part I
- NKG2020 transformation: An updated transformation between dynamic and static reference frames in the Nordic and Baltic countries
- The three Swedish kings of geodesy – Speech at the NKG General Assembly dinner in 2022
- A first step towards a national realisation of the international height reference system in Sweden with a comparison to RH 2000
- Examining the performance of along-track multi-mission satellite altimetry – A case study for Sentinel-6
- Geodetic advances in Estonia 2018–2022

