Effect of knots and holes on the modulus of elasticity prediction and mapping of sugi (Cryptomeria japonica) veneer using near-infrared hyperspectral imaging (NIR-HSI)
Abstract
Naturally occurring knots reduce the mechanical strength of wood. Veneers from sugi (Cryptomeria japonica) served as research material to study the effect of knots and holes. Veneer samples were first subjected to a three-point bending test to obtain measured modulus of elasticity (MOE) values. Then, near-infrared (NIR) hyperspectral imaging (HSI) was used to construct a prediction model and map the predicted MOE values. This is the first attempt for MOE prediction from the entire veneer surface based on NIR-HSI technology, while the mathematical part relies on chemometrics and cross-validation partial least squares regression (CV-PLSR). Maps of MOE prediction values could distinguish between latewood (LW) and earlywood (EW), as well as between a sound knot and a dead knot.
Introduction
The modulus of elasticity (MOE) is one of the key data for wood product qualification. For example, in the case of wood flooring, MOE is also related to surface hardness and determines resistance to denting when a concentrated load is applied (Shmulsky and Jones 2010). MOE can be predicted by near-infrared (NIR) spectroscopy, which offers a unique combination of speed and simple sample preparation and high reproducibility (Schwanninger et al. 2011). The literature body is large with this regard (Gindl et al. 2001; Thumm and Meder 2001; Meder et al. 2003; Fujimoto et al. 2007, 2008, 2010, 2013; Kobori et al. 2015; Sofianto et al. 2017a,b). NIR spectroscopy for MOE prediction has the potential to increase productivity and efficiency.
Veneer as the basis material for laminated veneer lumber and plywood products must have adequate stiffness and quality grading before utilization. Veneer from sugi (Cryptomeria japonica (Thunb. ex L.f.) D.Don) is utilized for building, ceiling board, furniture and packing material. Afforestation of sugi is an important issue in Japan (Hayashi and Miyatake 2015), and its wood production volume was 11.23 M m3 in 2015 (Forestry Agency Ministry of Agriculture, Forestry, and Fisheries of Japan 2016).
NIR spectroscopy could also be utilized in sugi veneer for quality control (Meder et al. 2002). Tsuchikawa et al. (2005) applied NIR spectroscopy based on a point spectra measurement to predict the MOE of a wood sample, in the course of which a single measurement was performed with a diameter of around 4 cm on the sample surface. An industrial pilot project observed samples running with a speed of 120 m min−1 by NIR spectroscopy (Kobori et al. 2015; Sofianto et al. 2017a,b). This online technique allows the measurement with a greater area than in the case of a point measurement.
Previous research on MOE prediction via online NIR spectroscopy of sugi lumber (Sofianto et al. 2017a) concluded that there are more knots in sugi lumber compared to hinoki (Chamaecyparis obtusa (Siebold & Zucc.) Endl.) lumber (Kobori et al. 2015), which detract the prediction results. The negative influence of a knot is due to the interruption of continuity and orientation change of wood fibers (Forest Products Laboratory 1990). A loosened knot on the wood surface may leave a hole behind.
The central hypothesis of the present research is that NIR spectroscopy combined with MOE prediction mapping via hyperspectral imaging (NIR-HSI) is able to determine knot and hole ratios. There are NIR-HSI studies concerning the prediction of density (Mora et al. 2011; Ma et al. 2017), moisture content (MC) (Mora et al. 2011; Kobori et al. 2013), microfibril angle (MFA) (Ma et al. 2017), compression wood (Meder and Meglen 2012), chemical composition (Thumm et al. 2016), degree of acetylation (Inagaki et al. 2015) and the degree of wood weathering (Sandak et al. 2017). Improved NIR-HSI system devices for mapping nowadays are suitable for wider sample area analysis and this will certainly contribute to its more frequent application.
NIR-HSI records spatially resolved spectra of a whole veneer surface area leading to different spectra from wood, knots and holes. Fujimoto and Tsuchikawa (2010) reported that the knots show higher absorbances than defect-free normal wood. This is due to the fact that knots are a transverse section of branches that are mainly composed of cross-sections of tracheid cells. In the present research, knots are determined as round in shape and with a darker color and rougher texture than that of normal wood, i.e. the determination of knots is different from that of previous studies concerning knot ratios (Grant et al. 1984; Lam et al. 2004, 2005).
The concept of the present work for construction of the best MOE prediction model is the following: 1st recording NIR spectra of wood including knot and hole spectra (WiKH spectra) and wood without knot and hole spectra (WwKH spectra) across the entire veneer surface and 2nd spectral evaluation via cross-validation partial least squares regression (CV-PLSR). Then the MOE prediction values of the entire veneer sample were mapped to observe the effect of knots and holes on the MOE prediction values. The hypothesis is that NIR-HSI spectra from small section veneer samples predict well the effects of knots and holes if calibrated by MOE values determined by three-point bending tests.
Materials and methods
Materials
Rotary-cut (lathe) veneers with a tangential surface and a nearly round knot shape from sugi measuring 960×300×3.1 mm3 (L×T×R) were investigated. All veneer samples were provided by Iida Kogyo Co., Ltd. (Komaki, Aichi Prefecture, Japan), which were purchased from a plywood factory in Nakatsugawa, Gifu Prefecture, Japan. MOE values of 50 veneer samples were measured under air-dry conditions (12% MC). First, conventional MOE data were determined by static bending measurement before the veneer samples were cut into smaller samples (total of 750 samples) to fit the sample holder on the NIR-HSI device. The veneer was cut into 150×100×3.1 mm3 (L×T×R) pieces, as shown in Figure 1.

Flow chart of the CV-PLSR and mapping process.
Static bending MOE measurements (“MOE values”)
MOE values were determined on 50 veneer samples by the three-point bending test method. Span distance: 700 mm; 1st load 4.31 N (0.44 kg), 2nd load 7.55 N (0.77 kg), 3rd load 10.59 N (1.08 kg). The statistical information on the line of best fit through a supplied set of the three loadings and the flexure/deflection [S (kgf mm−1)] was obtained by the least squares method. The MOE value was calculated:
where g: gravitation (9.8 m s−2), L: the span of the bending test (700 mm), d and w are the thickness and width of the veneer (mm), respectively.
NIR-HSI measurements
The hyperspectral data or hypercube data (three-way data matrix) were acquired from the tangential surface of the small section veneer samples by means of a pushbroom line imaging system (Compovision; Sumitomo Electric Industries, Ltd., Tokyo, Japan), which was already described by Inagaki et al. (2015) and Ma et al. (2017). The device provides 320×533 spatial pixels (x and y position) and 256 spectral points [wavelength (z)] in the range 913–2518 nm with a 6.2-nm wavelength interval. In this study, the distance between the sample and the camera was manually adjusted to achieve a 12-cm horizontal field of view with a spatial resolution of 375×375 μm per pixel. This spatial resolution of 375 μm per pixel was obtained from dividing 12-cm screen lateral axis by 320 pixels (width), while 533 pixels on vertical axis (height) was adjusted to cover the length of the veneer wood sample. Two halogen lamps served as light source that were positioned above the sample holder to provide tube-shaped light. To obtain spectral images, each sample was positioned on the slider and scanned line-by-line for one-time measurement to be situated like in the wood industry. The movement speed of the conveyer was 75 mm s−1 and the exposure time 200 frame s−1. As a reference, a white standard (I0) was imaged under the same conditions, and a dark current (d) was obtained by turning off the light source and completely covering the lens with its cap. All collected spectral images were then converted to relative absorbance (A) values:
where A: relative absorbance, I: light intensity data of the sample, I0: white standard and d: dark current. The absorbance value was calculated by MATLAB R2017b (MathWorks, Natick, MA, USA).
Determining the ratio of wood, knots and holes
Figure 1 describes the essential experimental steps. A transformed RGB image from HSI was able to classify the part of each wood, knot and hole as the region of interest; then this model image served for an imitation RGB image as a binary image of each part (wood, knot and hole) by means of Adobe Photoshop CS5 (Adobe Systems Incorporated, San Jose, CA, USA). The ratios of these details are given in % as obtained by image analysis.
The hypercube data from every small section veneer samples could be transformed into RGB images. Calculation in MATLAB by reshaping three-dimensional (3D) to two-dimensional (2D) converted hypercube data (three-way data matrix) produced by NIR-HSI into red, green and blue (RGB) images (true color image) from the 750 small section veneer samples. The RGB images were then converted from reflection value of the hypercube data at 1185 nm for red (R), 1336 nm for green (G) and 1557 nm for blue (B). Then, Adobe Photoshop CS5 was used to make 750 RGB imitation images of the samples in black and white only referring to RGB images from hypercube data. RGB imitation images were masked manually by eye observation on the decided zone of wood, knot and hole for every sample. These RGB imitation images were then used in the next calculation in MATLAB to produce binary images by giving the value of 1 to those black (“intended part”) as for each (1) wood (including knot and hole location), (2) knot location only and (3) hole location only, and value of 0 to those white (“unintended part”) for the other area from the intended part on one image processing of small section veneer sample (see Figure 1). This simple thresholding was proposed to obtain the position of each (1), (2) and (3). The combination calculations between wood (including knot and hole location) with both knot and hole locations only would result in various ratio and spectra data.
The ratio data consist of (1) knot ratio (2) hole ratio, (3) wood including knot and hole ratio and (4) wood without knot and hole ratio. The spectra data consist of (1) knot spectra, (2) hole spectra, (3) wood without knot spectra, (4) wood without hole spectra, (5) wood without knot and hole (WwKH) spectra and (6) wood including knot and hole (WiKH) spectra. As explained in the Introduction, the holes spectra were removed from the data. Then, the main parameters for the spectra analyses included into MOE prediction calculations were only the WiKH and WwKH spectra. The rationale behind this scheme: the surrounding area of a hole is weak (low MOE) and surrounding area of a knot is also weak (low MOE). Because the ratio of hole area/whole veneer is higher than that of the hole, the correlation of the areal ratio of knot/MOE was higher. The ratio and spectral data from 15 of the 750 of small section veneer samples were constructed to obtain the ratio and mean spectra of each part (wood, knot and hole) for each of the 50 whole veneer samples. This means that one whole veneer sample consists of 15 small section veneers. Each small section veneer has data of ratio and mean spectra. These 15 small section veneers were constructed to one whole veneer with the total ratio and mean spectra data. Fifty whole veneer samples were considered in this research, meaning that 50 mean spectra were calculated and applied for the construction of the best prediction model. As mentioned above, the software MATLAB 2017b and Adobe Photoshop CS5 (for the RGB imitation images) were used.
The air-dry density data were calculated by dividing the air-dry weight (g) to the volume obtained from the dimensions of the veneer (cm3). Later, the density values were used alongside the wood, knot and hole ratios to calculate the correlation coefficient (r) based on a linear regression of the measured MOE values from the three-point bending measurement.
Statistical analysis
An effective wavelength range was selected from 970 to 2293 nm, and many pre-processing spectra treatments were applied such as standard normal variate (SNV) and multiple scatter correction (MSC) for scatter correction and second derivative (2nd deriv.) with 13 smoothing-point Savitzky-Golay polynomial derivative filters for spectral derivatives. Leave-one-out CV-PLSR, as a multivariate data analysis or chemometrics, was applied to obtain the best MOE prediction model constructed. Test-set validation was not applied in this research because of the small data set (n=50). The best MOE prediction model was considered as that with the lowest value of the root-mean-square error for cross-validation (RMSECV), followed by the highest value of the coefficient of determination for cross-validation (R2CV) and the highest value of the ratio of performance to deviation (RPD). Those RMSECV, R2CV and RPD values were obtained on the optimum number of latent variables (LV) from the leave-one-out CV-PLSR analysis applied.
Mapping of MOE prediction values
The mapping process steps based on WiKH spectra are briefly described in Figure 1. These spectra cover the entire veneer surface (wood, knots and holes). Here, the holes are symbolized by the value zero (0). The best MOE prediction model of CV-PLSR analyses resulted from WiKH spectra with the best pre-processing treatment (2nd deriv. with a 13 smoothing-point). Hypercube data (three-way data matrix) from the small section veneer samples were reshaped into a two-way data matrix and treated with 2nd deriv. with a 13 smoothing-point. Hypercube data that resulted from NIR-HSI measurement were in 3D, while mapping result were in 2D. Hypercube data (533×320×211), i.e. the three-way data matrix, was transformed into two-way data matrix (170560×211). The latter was pre-processed with the best pre-processing treatment before being multiplied with the regression coefficient on each wavelength (211×1). The MOE prediction result is the matrix-vector product (170560×1). Then, it was reshaped again to the spatial dimension of 533×320 as the mapping image of MOE prediction on veneer.
Mapping of the MOE prediction values for 750 images from small section veneer samples were constructed for the 50 whole veneer samples. The images of the mapped MOE prediction values were compared for three types of MOE values (low, medium and high) to observe the effect of knots and holes and the distribution of mapped MOE prediction values on the veneer surface around knots and holes. The measured data were averaged to obtain mean spectra with only one color of a more specific area on the veneer and constructed into 50 whole veneers. These describe clearly the distribution of the predicted MOE values in the whole veneer sample from the lowest to the highest MOE value. The NIR-HSI system does not measure the mechanical properties directly but they can be calibrated with measured MOE data. The veneers investigated here have only 3.1 mm thickness. Hence, almost all parts in the veneer samples can be captured as NIR passes through up to 2–3 mm in wood thickness.
Results and discussion
The total MOE data obtained from the three-point bending measurements for 50 sugi veneer samples provide minimum, maximum, mean and standard deviation (StD) values. The corresponding MOE data are, respectively, 4.26, 12.53, 7.66 and 1.68 GPa. The mean MOE value is almost the same as that of the sugi veneer (7.07 GPa) published by Fujimoto et al. (2013), but is less than that of sugi lumber samples (8.30 GPa) from previous research of a MOE prediction model based on NIR spectroscopy (Sofianto et al. 2017a).
The air-dry density of the veneer samples ranged from 0.31 to 0.45 g cm−3 with a mean value of 0.38 g cm−3 (Table 1). The calculation of the mean spectra is based on the area of each part of wood, knot and hole. The maximum knot ratio was very small (2.04%) and some samples were totally free of knots and holes and the knots and holes ratios were also small. These ratios were characterized by the r values of linear regression at a 95% confident level to explain the relationship between all independent variables with MOE values as the dependent variable. The presence of knots (i.e. the knot ratio) gave a significant negative r value (–0.54), i.e. only low amounts of knots are present. The hole ratio correlated with r=0.11 only insignificantly with MOE values, while the wood ratio and density showed a significant correlation.
Density and ratio of 50 veneer samples.
| Parameter | Min. | Max. | Mean | StD | r | Significance |
|---|---|---|---|---|---|---|
| Knot ratio (%) | 0 | 2.04 | 0.61 | 0.62 | −0.54 | s |
| Hole ratio (%) | 0 | 0.51 | 0.12 | 0.12 | 0.11 | ns |
| Wood ratio (%) | 97.94 | 100 | 99.27 | 0.62 | 0.51 | s |
| Density (g cm−3) | 0.31 | 0.45 | 0.38 | 0.02 | 0.30 | s |
StD, Standard deviation; r, correlation coefficient to MOE; s, significant; ns, not significant.
Figure 2 shows the WiKH and WwKH spectra, which are very similar. The absorbance value for the wood spectra is in the range of 0.11–1.18, while the knot spectra show values between 0.18 and 2.10. The NIR band assignment was done according to Schwanninger et al. (2011), see Tables 2 and 3 . The band maxima shifting was within 5 nm. As is visible, the wood components cellulose, hemicellulose and lignin can be assigned to NIR bands.

Knot spectra showing higher absorbance value than the wood spectra (WiKH and WwKH), while the different spectra for WiKH and WwKH spectra very small as of the different only from the small existence of the knot.
(a) Knot, (b) WiKH, (c) WwKH spectra obtained from 50 veneer samples using the NIR-HSI device and (d) their mean spectra.
Band assignments from knot spectra of sugi veneer by NIR-HSI.
| Band locationa wavelength (nm) | Band locationb wavelength (nm) | Component | Bond vibration |
|---|---|---|---|
| 1198–1204 | 1188–1195 | Lignin/(cellulose) | 2nd overtone C–H str. |
| 1370 | 1370 | Hemicellulose | 1st overtone C–H str.+C–H def. |
| 1476 | 1476 | Cellulose | 1st overtone O–H str. |
| 1595 | 1597 | Cellulose | 1st overtone O–H str. |
| 1709 | 1710 | Hemicellulose | 1st overtone C–H str. |
| 1728 | 1726 | Lignin | 1st overtone C–H str. |
| 1935 | 1916–1942 | Water | O–H asym. str.+O–H def. of H2O |
aThe present research; bbased on Schwanninger et al. (2011); str., stretching vibration; def., deformation vibration; asym, asymmetric.
Band assignments from wood spectra (WiKH and WwKH spectra) of sugi veneer by NIR-HSI.
| Band locationa wavelength (nm) | Band locationb wavelength (nm) | Component | Bond vibration |
|---|---|---|---|
| 1217 | 1212–1225 | Cellulose | 2nd overtone C–H str. |
| 1482 | 1477–1484 | Cellulose | 1st overtone O–H str. |
| 1595 | 1597 | Cellulose | 1st overtone O–H str. |
| 1677–1683 | 1677 | Lignin | 1st overtone Car–H str. |
| 1681 | Hemicellulose | 1st overtone C–H str. | |
| 1728–1734 | 1731 | Cellulose | 1st overtone C–H str. |
| 1791–1797 | 1791 | Lignin | 1st overtone C–H str. |
| 1793 | Cellulose | 1st overtone C–H str. | |
| 1935 | 1916–1942 | Water | O–H asym. str.+O–H def. of H2O |
aThe present research; bbased on Schwanninger et al. (2011); str., stretching vibration; def., deformation vibration; ar, aromatic; asym., asymmetric.
CV-PLSR analyses conducted for both WiKH and WwKH spectra showed almost similar results to those of the MOE prediction model, as summarized in Table 4. The PLSR data were optimized based on the best LV results. The 2nd deriv. spectra with a 13 smoothing-point gave the best MOE prediction model for both WiKH and WwKH spectra compared to other pre-processed spectra treatments. The data evaluation gave nearly identical RMSECV (0.88 GPa for WiKH and 0.87 GPa for WwKH) and R2CV values (0.69 for WiKH and 0.70 for WwKH). The RPD values, obtained by dividing the StD values of all the reference MOE data by the RMSECV value, were 1.92 (WiKH) and 1.93 (WwKH) with LV of 5. These RPD values in the range of 1.00–2.50 indicate that this prediction model, based on RPD values, would be suitable only for initial screening for veneer grading in the wood industry (Williams and Sobering 1993; Schimleck et al. 2003). The RMSECV values obtained are promising as they were under 1.00 GPa, similar to those reported by Sofianto et al. (2017a). Figure 3 shows the calibration and cross-validation results from the predicted MOE data vs. the measured MOE values based on NIR-HSI 2nd deriv. spectra for both the WiKH and WwKH approach. The WiKH spectra were selected for further analysis via 2nd derivatization focusing on the cellulose bands 1210, 1362 and 1589 nm, and the lignin bands in the range of 1684–1690 nm and 1791 nm. The band assignments obtained from 2nd deriv. spectra are summarized in Table 5.
Comparison of MOE prediction models between pre-processing spectra treatments using CV-PLSR.
| Pre-processing treatment | n | Number of LV | RMSEC (GPa) | RMSECV (GPa) | R2C | R2CV | RPD |
|---|---|---|---|---|---|---|---|
| (a) WiKH spectra | |||||||
| OSD | 50 | 4 | 0.86 | 0.96 | 0.71 | 0.64 | 1.75 |
| SNV | 50 | 5 | 0.86 | 0.99 | 0.71 | 0.61 | 1.70 |
| MSC | 50 | 5 | 0.86 | 0.99 | 0.71 | 0.61 | 1.70 |
| 2nd deriv. 13 sp | 50 | 5 | 0.73 | 0.88 | 0.79 | 0.69 | 1.92 |
| SNV+2nd deriv. 13 sp | 50 | 5 | 0.76 | 0.90 | 0.77 | 0.67 | 1.86 |
| 2nd deriv. 13 sp+SNV | 50 | 5 | 0.76 | 0.91 | 0.77 | 0.67 | 1.85 |
| (b) WwKH spectra | |||||||
| OSD | 50 | 4 | 0.85 | 0.94 | 0.72 | 0.66 | 1.79 |
| SNV | 50 | 5 | 0.83 | 0.96 | 0.72 | 0.63 | 1.76 |
| MSC | 50 | 5 | 0.83 | 0.96 | 0.72 | 0.63 | 1.76 |
| 2nd deriv. 13 sp | 50 | 5 | 0.73 | 0.87 | 0.79 | 0.70 | 1.93 |
| SNV+2nd deriv. 13 sp | 50 | 5 | 0.76 | 0.90 | 0.77 | 0.68 | 1.87 |
| 2nd deriv. 13 sp+SNV | 50 | 5 | 0.76 | 0.90 | 0.77 | 0.67 | 1.87 |
OSD, Original spectra data; MSC, multiplicative scatter correction; SNV, standard normal variate; 2nd deriv., second derivative; sp, smoothing-point; LV, latent variable; R2C, coefficient of determination for calibration; R2CV, coefficient of determination for cross-validation; RMSEC, root-mean-square error of calibration; RMSECV, root-mean-square error of cross-validation; RPD, ratio of performance to deviation (StDmeasured values/RMSECV).

Scatter plot of the measured and predicted MOE values using (a) WiKH and (b) WwKH spectra of 2nd deriv. with 13 smoothing-point (Savitzky-Golay).
Band assignments of 2nd deriv. WiKH spectra with a 13 smoothing-point (Savitzky-Golay algorithm) on sugi veneer at by NIR-HSI.
| Band locationa wavelength (nm) | Band locationb wavelength (nm) | Component | Bond vibration |
|---|---|---|---|
| 1210 | 1212–1225 | Cellulose | 2nd overtone C–H str. |
| 1362 | 1366 | Cellulose | 1st overtone C–H str.+C–H def. |
| 1589 | 1586–1596 | Cellulose | 1st overtone O–H str. |
| 1684–1690 | 1685 | Lignin | 1st overtone Car–H str. |
| 1791 | 1791 | Lignin | 1st overtone C–H str. |
aThe present research; bbased on Schwanninger et al. (2011); str., stretching vibration; def., deformation vibration; ar, aromatic.
The mapped MOE prediction data were constructed for three whole veneer samples (Figure 4) for low, medium and high MOE values. The higher MOE reference values are well reflected by the higher MOE mapping results. Expectedly, the mapping results are different for latewood (LW) and earlywood (EW). Sugi veneer with an irregular grain from the rotary lathe is a tangential surface veneer with a non-continuous surface variation of both LW and EW, which are clearly assignable to high and low MOE areas, respectively.
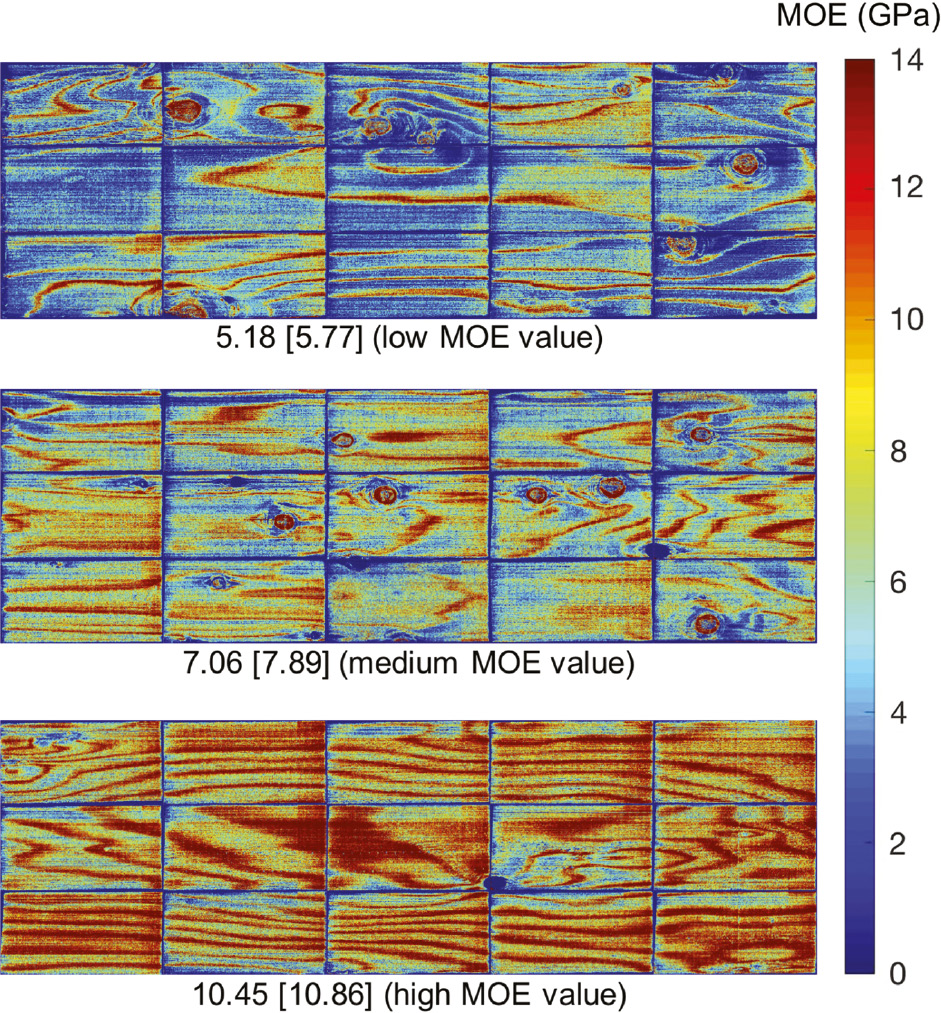
Mapping of the low, medium and high MOE prediction values of whole veneer samples with their mean NIR predicted values (average pixel value) and measured MOE values from a three-point bending test in the bracket.
Knots significantly decreased the MOE values (r=−0.54) by weakening the surrounding area, and the mapping results clearly show the low MOE areas around knots. The statement from the Wood Engineering Handbook Second Edition (Forest Products Laboratory 1990) has corroborated that the zone of distorted grain (cross-grain) around a knot has a less “parallel to piece” stiffness than straight-grained wood; thus, localized areas of low stiffness are often associated with knots. Holes had predicted MOE values of 0.0 GPa and showed no significant correlation (r=0.11). Areas surrounding holes could have both lower predicted MOE values and high predicted MOE values. It should be noted that knots have a weaker effect on the surrounding area than holes (Figure 5).

Mapping of the MOE prediction values around the knot and hole for prediction values and the RGB image.
The mapped MOE data also differentiated between a sound knot (intergrown knot) and a dead knot (encased knot), which was also identified previously (Hu et al. 2004, 2011; Fujimoto and Tsuchikawa 2010). Figure 6 shows that a sound knot has less predicted MOE values compared to a dead knot. The Forest Products Laboratory (1990) states that dead knots and knot-holes tend to be accompanied by less cross-grain than sound knots; therefore, they are generally less serious with regard to most mechanical properties. A dead knot will become a hole during the veneer processing. Regarding the chemical component inside, Sekine et al. (2013) found lower terpenoid (C5H8)n in a dead knot than a sound knot in Abies balsamea (L.) Mill.

Mapping of the MOE prediction values, RGB color images from hypercube data and conventional RGB color camera of a sound knot, a dead knot and a hole.
Figure 7 shows the mapping of the mean MOE prediction values based on NIR spectroscopy, while the measured values of the three-point bending test are presented in brackets. The predicted and measured values are almost the same (7.64 and 7.66 GPa, respectively) with StD of 1.51 and 1.68 GPa. The r value between the two data sets is 0.90, i.e. the mapping results are acceptable and stable. The second mapping of the mean MOE prediction values in the small section veneer samples for 50 whole veneer samples is also robust and reliable.

Mapping of the mean MOE prediction values of small section veneer samples (n=15) in whole veneer samples (n=50) with their mean NIR predicted values (average pixel value) and measured MOE values from a three-point bending test in the bracket.
Conclusions
The modeling and mapping of MOE prediction values for sugi veneer were successfully constructed based on NIR-HSI with CV-PLSR. The best MOE prediction model was from WiKH spectra of a 2nd deriv. that gave sufficient RMSECV (0.88 GPa) and R2CV (0.69) values. Knots had a significant negative correlation with MOE values due to the weakened surrounding area, which was clearly shown by lower predicted MOE values. Mapping could successfully discern LW from EW as well as sound knots from dead knots based on the observation of the predicted MOE values.
Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: This research was partly supported by the Research and Development Projects for Application in Promoting New Policy of Agriculture, Forestry, and Fisheries, Japan [No. 22003]. The authors gratefully thank Iida Kogyo, Co. Ltd., Komaki, Aichi, Japan, for providing the veneer samples and MOE veneer measurement by three-point bending test for the research.
Employment or leadership: None declared.
Honorarium: None declared.
References
Forest Products Laboratory – Wood Engineering Handbook, Second Edition. Prentice Hall, New Jersey, USA, 1990.Search in Google Scholar
Forestry Agency Ministry of Agriculture Forestry and Fisheries of Japan. (2016) Annual Report on Forest and Forestry in Japan Fiscal Year 2015 (Summary).Search in Google Scholar
Fujimoto, T., Tsuchikawa, S. (2010) Identification of sound and dead knots by near infrared spectroscopy. J. Near Infrared Spectrosc. 18:473–479.10.1255/jnirs.887Search in Google Scholar
Fujimoto, T., Yamamoto, H., Tsuchikawa, S. (2007) Estimation of wood stiffness and strength properties of hybrid larch by near-infrared spectroscopy. Appl. Spectrosc. 61:882–888.10.1366/000370207781540150Search in Google Scholar PubMed
Fujimoto, T., Kurata, Y., Matsumoto, K., Tsuchikawa, S. (2008) Application of near infrared spectroscopy for estimating wood mechanical properties of small clear and full-length lumber specimens. J. Near Infrared Spectrosc. 16:529–537.10.1255/jnirs.818Search in Google Scholar
Fujimoto, T., Kurata, Y., Matsumoto, K., Tsuchikawa, S. (2010) Feasibility of near-infrared spectroscopy for on-line grading of sawn lumber. Appl. Spectrosc. 64:92–99.10.1366/000370210790572016Search in Google Scholar PubMed
Fujimoto, T., Kawakami, K., Aimi, H., Shimizu, J., Hasegawa, K., Kobori, H., Tsuchikawa, S. (2013) Prediction of dry veneer stiffness using near infrared spectra from transverse section of green log. J. Wood Sci. 59:383–388.10.1007/s10086-013-1352-4Search in Google Scholar
Gindl, W., Teischinger, A., Schwanninger, M., Hinterstoisser, B. (2001) The relationship between near infrared spectra of radial wood surfaces and wood mechanical properties. J. Near Infrared Spectrosc. 9:255–261.10.1255/jnirs.311Search in Google Scholar
Grant, D.J., Anton, A., Lind, P. (1984) Bending strength, stiffness, and stress-grade of structural Pinus radiata: effects of knot and timber density. New Zealand J. Forestry Sci. 14:331–348.Search in Google Scholar
Hayashi, T., Miyatake, A. (2015) Recent research and development on sugi (Japanese cedar) structural glued laminated timber. J. Wood Sci. 61:337–342.10.1007/s10086-015-1475-xSearch in Google Scholar
Hu, C., Tanaka, C., Ohtani, T. (2004) Locating and identifying sound knots and dead knots on sugi by the rule-based color vision system. J. Wood Sci. 50:115–122.10.1007/s10086-003-0549-3Search in Google Scholar
Hu, C., Min, X., Yun, H., Wang, T. (2011) Automatic detection of sound knots and loose knots on sugi using gray level co-occurrence matrix parameters. Ann. For. Sci. 68:1077–1083.10.1007/s13595-011-0123-xSearch in Google Scholar
Inagaki, T., Mitsui, K., Tsuchikawa, S. (2015) Visualisation of degree of acetylation in beechwood by near infrared hyperspectral imaging. J. Near Infrared Spectrosc. 23:353–360.10.1255/jnirs.1181Search in Google Scholar
Kobori, H., Gorretta, N., Rabatel, G., Bellon-Maurel, V., Chaix, G., Roger, J.M., Tsuchikawa, S. (2013) Applicability of Vis-NIR hyperspectral imaging for monitoring wood moisture content (MC). Holzforschung 67:307–314.10.1515/hf-2012-0054Search in Google Scholar
Kobori, H., Inagaki, T., Fujimoto, T., Okura, T., Tsuchikawa, S. (2015) Fast online NIR technique to predict MOE and moisture content of sawn lumber. Holzforschung 69:329–335.10.1515/hf-2014-0021Search in Google Scholar
Lam, F., Barrett, J.D., Nakajima, S. (2004) Influence of knot area ratio based grading rules on the engineering properties of Hem-fir used in Japanese post and beam housing. Wood Sci. Technol. 38:83–92.10.1007/s00226-003-0214-4Search in Google Scholar
Lam, F., Barrett, J.D., Nakajima, S. (2005) Influence of knot area ratio on the bending strength of Canadian Douglas fir timber used in Japanese post and beam housing. J. Wood Sci. 51:18–25.10.1007/s10086-003-0619-6Search in Google Scholar
Ma, T., Inagaki, T., Tsuchikawa, S. (2017) Calibration of SilviScan data of Cryptomeria japonica wood concerning density and microfibril angels with NIR hyperspectral imaging with high spatial resolution. Holzforschung 71:341–347.10.1515/hf-2016-0153Search in Google Scholar
Meder, R., Meglen, R.R. (2012) Near infrared spectroscopic and hyperspectral imaging of compression wood in Pinus radiata D. don. J. Near Infrared Spectrosc. 20:583–589.10.1255/jnirs.1001Search in Google Scholar
Meder, R., Thumm, A., Bier, H. (2002) Veneer stiffness predicted by NIR spectroscopy calibrated using mini-LVL test panels. Holz als Roh- und Werkstoff. 60:159–164.10.1007/s00107-002-0296-ySearch in Google Scholar
Meder, R., Thumm, A., Marston, D. (2003) Sawmill trial of at-line prediction of recovered lumber stiffness by NIR spectroscopy of Pinus radiata cants. J. Near Infrared Spectrosc. 11:137–143.10.1255/jnirs.361Search in Google Scholar
Mora, C.R., Schimleck, L.R., Yoon, S.C., Thai, C.N. (2011) Determination of basic density and moisture content of loblolly pine wood disks using a near infrared hyperspectral imaging system. J. Near Infrared Spectrosc. 19:401–409.10.1255/jnirs.948Search in Google Scholar
Sandak, A., Burud, I., Flo, A., Thiis, T., Gobakken, L.R., Sandak, J. (2017) Hyperspectral imaging of weathered wood samples in transmission mode. Int. Wood. Prod. J. 8:9–13.10.1080/20426445.2016.1237079Search in Google Scholar
Schimleck, L.R., Doran, J.C., Rimbawanto, A. (2003) Near-infrared spectroscopy for cost effective screening of foliar oil characteristics in a Melaleuca cajuputi breeding population. J. Agric. Food Chem. 51:2433–2437.10.1021/jf020981uSearch in Google Scholar PubMed
Schwanninger, M., Rodrigues, J.C., Fackler, K. (2011) A review of band assignments in near infrared spectra of wood and wood components. J. Near Infrared Spectrosc. 19: 287–308.10.1255/jnirs.955Search in Google Scholar
Sekine, N., Shibutani, S., Yatagai, M. (2013) Chemical composition of the terpenoids in wood and knots of Abies species. Eur. J. Wood Wood Prod. 71:679–682.10.1007/s00107-013-0715-2Search in Google Scholar
Shmulsky, R., Jones, P.D. Forest Products and Wood Science, an Introduction, Sixth Edition. Wiley-Blackwell, Iowa, USA, 2011.10.1002/9780470960035Search in Google Scholar
Sofianto, I.A., Inagaki, T., Kato, K., Itoh, M., Tsuchikawa, S. (2017a) Modulus of elasticity prediction model on sugi (Cryptomeria japonica) lumber using online near-infrared (NIR) spectroscopic system. Int. Wood. Prod. J. 8:193–200.10.1080/20426445.2017.1378398Search in Google Scholar
Sofianto, I.A., Inagaki, T., Itoh, M., Tsuchikawa, S. (2017b) Mini Review. Stiffness and moisture content prediction model of wooden veneer using fast online near-infrared (NIR) spectroscopic system. Forest Res. Eng. Int. J. 1:40–43.10.15406/freij.2017.01.00006Search in Google Scholar
Thumm, A., Meder, R. (2001) Stiffness prediction of radiata pine clearwood test pieces using near infrared spectroscopy. J. Near Infrared Spectrosc. 9:117–122.10.1255/jnirs.298Search in Google Scholar
Thumm, A., Riddell, M., Nanayakkara, B., Harrington, J., Meder, R. (2016) Mapping within-stem variation of chemical composition by near infrared hyperspectral imaging. J. Near Infrared Spectrosc. 24:605–616.10.1255/jnirs.1206Search in Google Scholar
Tsuchikawa, S., Hirashima, Y., Sasaki, Y., Ando, K. (2005) Near-infrared spectroscopy study of the physical and mechanical properties of wood with meso- and micro-scale anatomical observation. Appl. Spectrosc. 59:86–93.10.1366/0003702052940413Search in Google Scholar PubMed
Williams, P.C., Sobering, D.C. (1993) Comparison of commercial near-infrared transmittance and reflectance instruments for analysis of whole grains and seeds. J. Near Infrared Spectrosc. 1:25–32.10.1255/jnirs.3Search in Google Scholar
©2019 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Editorials
- Editorial changes at Holzforschung
- Goodbye to Holzforschung
- Thanks to Oskar Faix
- Original Articles
- Orthotropic mechano-sorptive creep behavior of Chinese fir during the moisture adsorption process determined in tensile mode via dynamic mechanical analysis (DMA)
- Differences in the viscoelastic properties between earlywood and latewood in the growth rings of Chinese fir as analyzed by dynamic mechanical analysis (DMA) in the temperature range between −120°C and 120°C
- Failure conditions of solid wood on off-axis compression testing
- Effect of knots and holes on the modulus of elasticity prediction and mapping of sugi (Cryptomeria japonica) veneer using near-infrared hyperspectral imaging (NIR-HSI)
- Quantification of slip planes in the stem wood of Eucalyptus grandis
- DNA barcoding authentication for the wood of eight endangered Dalbergia timber species using machine learning approaches
- Chemical analysis and antioxidant activities of bark extracts from four endemic species of Hyrcanian forests in Iran
- Isolation of natural flavoring compounds from cooperage woods by pressurized hot water extraction (PHWE)
- Volatile organic compounds (VOCs) from lauan (Shorea ssp.) plyboard prepared with kraft lignin, soy flour, gluten meal and tannin: emissions during hot pressing and from panels as a function of time
- Plasma treatment of plastic film or decorative veneer and its effects on the peel strength and curling deformation of plastic film-reinforced pliable decorative sliced veneer (PR-RP-DSV)
Articles in the same Issue
- Frontmatter
- Editorials
- Editorial changes at Holzforschung
- Goodbye to Holzforschung
- Thanks to Oskar Faix
- Original Articles
- Orthotropic mechano-sorptive creep behavior of Chinese fir during the moisture adsorption process determined in tensile mode via dynamic mechanical analysis (DMA)
- Differences in the viscoelastic properties between earlywood and latewood in the growth rings of Chinese fir as analyzed by dynamic mechanical analysis (DMA) in the temperature range between −120°C and 120°C
- Failure conditions of solid wood on off-axis compression testing
- Effect of knots and holes on the modulus of elasticity prediction and mapping of sugi (Cryptomeria japonica) veneer using near-infrared hyperspectral imaging (NIR-HSI)
- Quantification of slip planes in the stem wood of Eucalyptus grandis
- DNA barcoding authentication for the wood of eight endangered Dalbergia timber species using machine learning approaches
- Chemical analysis and antioxidant activities of bark extracts from four endemic species of Hyrcanian forests in Iran
- Isolation of natural flavoring compounds from cooperage woods by pressurized hot water extraction (PHWE)
- Volatile organic compounds (VOCs) from lauan (Shorea ssp.) plyboard prepared with kraft lignin, soy flour, gluten meal and tannin: emissions during hot pressing and from panels as a function of time
- Plasma treatment of plastic film or decorative veneer and its effects on the peel strength and curling deformation of plastic film-reinforced pliable decorative sliced veneer (PR-RP-DSV)

