Abstract
A new perfect control algorithm dedicated to fractional-order right-invertible systems, i.e. plants with a greater number of input than output variables, is presented in this paper. It is shown that such a control strategy can be particularly applied with regard to practical tasks. Henceforth, the Grünwald-Letnikov difference operator Δα of an assumed order α can be truncated without loss of generality. For that reason, the so-called pole-free perfect control formula can be used to minimize the essential drawback of the Grünwald-Letnikov approach engaged, so as to define the intriguing issue regarding the robust perfect control for non-integer-order right-invertible LTI discrete-time state-space systems. Simulation examples show that the presented method can compete with a classical stable-pole one, for which the actual systems described by a fractional-order model often correspond with an inconvenient asymptotic perfect control solution given by the unlimited original operator Δα. In the end, the possibility of employing of author’s nonunique right inverses dedicated to nonsquare MIMO system matrices is demonstrated, thus giving rise to the introduction of a new powerful tool for robustification of non-integer-order closed-loop perfect control plants as well.
- Acronyms
- LTI
linear time-invariant
- MIMO
multi-input/multi-output
- MVC
minimum variance control
- SISO
single-input/single-output
8 Appendix
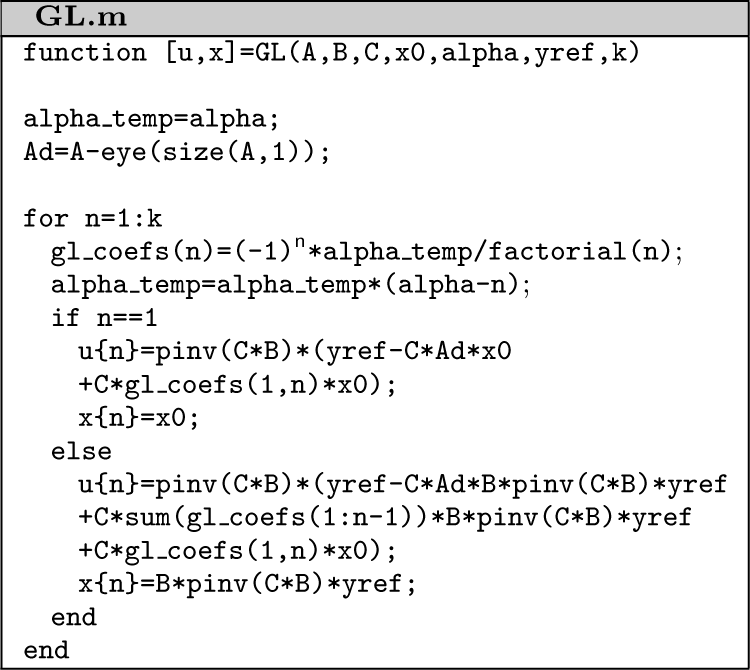
Program allowing to present the signal runs of truncated fractional-order perfect control is presented below.

Acknowledgements
Invaluable comments from the anonymous reviewers are gratefully acknowledged.
References
[1] A. Ben-Israel and T.N.E. Greville, Generalized Inverses, Theory and Applications. 2 Ed., Springer-Verlag, New York (2003).Suche in Google Scholar
[2] R. Cioć, Physical and geometrical interpretation of Grünwald-Letnikov differintegrals: measurement of path and acceleration. Fract. Calc. Appl. Anal. 19, No 1 (2016), 161–172; 10.1515/fca-2016-0009; https://www.degruyter.com/view/j/fca.2016.19.issue-1/issue-files/fca.2016.19.issue-1.xml.Suche in Google Scholar
[3] S. Dadhich and W. Birk, Analysis and control of an extended quadruple tank process. In: Proc. 13th IEEE European Control Conference (ECC’2014), Strasbourg, France (2014), 838–843; 10.1109/ECC.2014.6862290.Suche in Google Scholar
[4] M.J. Grimble, Controller performance benchmarking and tuning using generalised minimum variance control. Automatica38, No 12 (2002), 2111–2119; 10.1016/S0005-1098(02)00141-3.Suche in Google Scholar
[5] W.P. Hunek, New interesting facts about minimum-energy perfect control for LTI nonsquare state-space systems. In: Proc. 22nd IEEE International Conference on Methods and Models in Automation and Robotics (MMAR’2017), Miedzyzdroje, Poland (2017), 274–278; 10.1109/MMAR.2017.8046838.Suche in Google Scholar
[6] W.P. Hunek and M. Krok, Pole-free perfect control for nonsquare LTI discrete-time systems with two state variables. In: Proc. 13th IEEE International Conference on Control & Automation (ICCA’2017), Ohrid, Macedonia (2017), 329–334; 10.1109/ICCA.2017.8003082.Suche in Google Scholar
[7] W.P. Hunek and L. Wach, Towards a new stability criterion for fractional-order perfect control of LTI MIMO discrete-time systems in state-space. In: Proc. 3rd IEEE Conference on Cybernetics (CY- BCONF’2017), Exeter, England (2017), 134–139; 10.1109/CYB-Conf.2017.7985817.Suche in Google Scholar
[8] W.P. Hunek, New SVD-based matrix H-inverse vs. minimum-energy perfect control design for state-space LTI MIMO systems. In: Proc. 20th IEEE International Conference on System Theory, Control and Computing (ICSTCC’16), Sinaia, Romania (2016), 14–19; 10.1109/ICSTCC.2016.7790633.Suche in Google Scholar
[9] W.P. Hunek, An application of new polynomial matrix σ-inverse in minimum-energy design of robust minimum variance control for nonsquare LTI MIMO systems. In: Proc. 8th IFAC Symposium on Robust Control Design (ROCOND’2015), Bratislava, Slovakia (2015), 48, No 14, 150–154; 10.1016/j.ifacol.2015.09.449.Suche in Google Scholar
[10] W.P. Hunek, K.J. Latawiec, R. Stanisławski, M. Łukaniszyn, and P. Dzierwa, A new form of a σ-inverse for nonsquare polynomial matrices. In: Proc. 18th IEEE International Conference on Methods and Models in Automation and Robotics (MMAR’2013), Miedzyzdroje, Poland (2013), 282–286; 10.1109/MMAR.2013.6669920.Suche in Google Scholar
[11] W.P. Hunek and K.J. Latawiec, A study on new right/left inverses of nonsquare polynomial matrices. International J. of Applied Mathematics and Computer Science21, No 2 (2011), 331–348; 10.2478/v10006-011-0025-y.Suche in Google Scholar
[12] T. Kaczorek, Minimum energy control of fractional positive continuous-time linear systems using Caputo-Fabrizio definition. Bull. of the Polish Academy of Sciences – Technical Sciences65, No 1 (2017), 45–51; 10.1515/bpasts-2017-0006.Suche in Google Scholar
[13] T. Kaczorek, Minimum energy control of fractional descriptor positive discrete-time linear systems. International J. of Applied Mathematics and Computer Science24, No 4 (2014), 735–743; 10.2478/amcs-2014-0054.Suche in Google Scholar
[14] N.P. Karampetakis and P. Tzekis, On the computation of the generalized inverse of a polynomial matrix. IMA J. of Mathematical Control and Information18, No 1 (2001), 83–97; 10.1093/imamci/18.1.83.Suche in Google Scholar
[15] M.R. Katebi and A.W. Ordys, Minimum variance control. In: The Control Handbook, Electrical Engineering Handbook (Ed. by W.S. Levine), Ch. 62, 1089–1096, CRC Press and IEEE Press, Boca Raton, Florida, USA (1996).Suche in Google Scholar
[16] V. Kiryakova, Generalized Fractional Calculus and Applications. Longman Sci. & Technical, Harlow; Copubl. John Wiley & Sons, Inc., New York (1994).Suche in Google Scholar
[17] J. Klamka, Controllability and minimum energy control problem of fractional discrete-time systems. In: New Trends in Nanotechnology and Fractional Calculus Applications (Ed. by D. Baleanu, Z.B. Guvenc, and J.A.T. Machado), Ch. 45, 503–509, Springer, Dordrecht (2010); 10.1007/978-90-481-3293-5-45.Suche in Google Scholar
[18] A. Lamara, G. Colin, P. Lanusse, A. Charlet, D. Nelson-Gruel, and Y. Chamaillard, Pollutant reduction of a turbocharged diesel engine using a decentralized MIMO crone controller. Fract. Calc. Appl. Anal. 18, No 2 (2015), 307–332; 10.1515/fca-2015-0021; https://www.degruyter.com/view/j/fca.2015.18.issue-2/issue-files/fca.2015.18.issue-2.xml.Suche in Google Scholar
[19] M.D. Petković, P.S. Stanimirović, and M.B. Tasić, Effective partitioning method for computing weighted Moore-Penrose inverse. Computers & Mathematics with Appl. 55, No 8 (2008), 1720–1734; 10.1016/j.camwa.2007.07.014.Suche in Google Scholar
[20] P.S. Stanimirović, A finite algorithm for generalized inverses of polynomial and rational matrices. Appl. Mathematics and Computation144, No 2 (2003), 199–214; 10.1016/S0096-3003(02)00401-0.Suche in Google Scholar
[21] P.S. Stanimirović and M.D. Petković, Computing generalized inverse of polynomial matrices by interpolation. Appl. Mathematics and Computation172, No 1 (2006), 508–523; 10.1016/j.amc.2005.02.031.Suche in Google Scholar
[22] S. Vologiannidis and N.P. Karampetakis, Inverses of multivariable polynomial matrices by discrete Fourier transforms. MultidimensionalSystems and Signal Processing15, No 4 (2004), 341–361; 10.1023/B:MULT.0000037345.60574.d4.Suche in Google Scholar
[23] Ł. Wach and W.P. Hunek, Perfect control for fractional-order multivariable discrete-time systems. In: Theoretical Developments and Applications of Non-Integer Order Systems, Lect. Notes in Electr. Engin. 357, (Ed. by S. Domek and P. Dworak), Ch. 19, 233–237, Springer (2016); 10.1007/978-3-319-23039-9_19.Suche in Google Scholar
[24] T. Zhang, H.G. Li, Z.Y. Zhong, and G.P. Cai, Hysteresis model and adaptive vibration suppression for a smart beam with time delay. J. of Sound and Vibration358 (2015), 35–47; 10.1016/j.jsv.2015.08.017.Suche in Google Scholar
[25] T. Zhang, B.T. Yang, H.G. Li, and G. Meng, Dynamic modeling and adaptive vibration control study for giant magnetostrictive actuators. Sensors and Actuators A: Physical190 (2013), 96–105; 10.1016/j.sna.2012.11.001.Suche in Google Scholar
© 2019 Diogenes Co., Sofia
Artikel in diesem Heft
- Frontmatter
- Editorial Note
- FCAA related news, events and books (FCAA–Volume 22–2–2019)
- Discussion Paper
- The flaw in the conformable calculus: It is conformable because it is not fractional
- The failure of certain fractional calculus operators in two physical models
- Research Paper
- Inverse problems for a class of degenerate evolution equations with Riemann – Liouville derivative
- On Riesz derivative
- A note on fractional powers of strongly positive operators and their applications
- Semi-fractional diffusion equations
- Extremum principle for the Hadamard derivatives and its application to nonlinear fractional partial differential equations
- Well-posedness of fractional degenerate differential equations in Banach spaces
- Structure factors for generalized grey Browinian motion
- Linear stationary fractional differential equations
- Perfect control for right-invertible Grünwald-Letnikov plants – an innovative approach to practical implementation
- On fractional differential inclusions with Nonlocal boundary conditions
- On solutions of linear fractional differential equations and systems thereof
- Existence of mild solution of a class of nonlocal fractional order differential equation with not instantaneous impulses
- A CAD-based algorithm for solving stable parameter region of fractional-order systems with structured perturbations
- On representation and interpretation of Fractional calculus and fractional order systems
Artikel in diesem Heft
- Frontmatter
- Editorial Note
- FCAA related news, events and books (FCAA–Volume 22–2–2019)
- Discussion Paper
- The flaw in the conformable calculus: It is conformable because it is not fractional
- The failure of certain fractional calculus operators in two physical models
- Research Paper
- Inverse problems for a class of degenerate evolution equations with Riemann – Liouville derivative
- On Riesz derivative
- A note on fractional powers of strongly positive operators and their applications
- Semi-fractional diffusion equations
- Extremum principle for the Hadamard derivatives and its application to nonlinear fractional partial differential equations
- Well-posedness of fractional degenerate differential equations in Banach spaces
- Structure factors for generalized grey Browinian motion
- Linear stationary fractional differential equations
- Perfect control for right-invertible Grünwald-Letnikov plants – an innovative approach to practical implementation
- On fractional differential inclusions with Nonlocal boundary conditions
- On solutions of linear fractional differential equations and systems thereof
- Existence of mild solution of a class of nonlocal fractional order differential equation with not instantaneous impulses
- A CAD-based algorithm for solving stable parameter region of fractional-order systems with structured perturbations
- On representation and interpretation of Fractional calculus and fractional order systems

