Home Physical Sciences Shape unrestricted topological corner state based on Kekulé modulation and enhanced nonlinear harmonic generation
Article Open Access

Shape unrestricted topological corner state based on Kekulé modulation and enhanced nonlinear harmonic generation

  • Kai Guo EMAIL logo , Huiyuan Wang , Jiawei Xiong , Jintao Wu , Bingyi Liu and Zhongyi Guo ORCID logo EMAIL logo
Published/Copyright: June 3, 2024
Download Article (PDF)
Nanophotonics
From the journal Nanophotonics Volume 13 Issue 18

Abstract

Topological corner states have been extensively utilized as a nanocavity to increase nonlinear harmonic generation due to their high Q-factor and robustness. However, the previous topological corner states based nanocavities and nonlinear harmonic generation have to comply with particular spatial symmetries of underlying lattices, hindering their practical application. In this work, we design a photonic nanocavity based on shape unrestricted topological corner state by applying Kekulé modulation to a honeycomb photonic crystal. The boundaries of such shape unrestricted topological corner state are liberated from running along specific lattice directions, thus topological corner states with arbitrary shapes and high Q-factor are excited. We demonstrate enhancement of second (SHG) and third harmonic generation (THG) from the topological corner states, which are also not influenced by the geometry shape of corner. The liberation from the shape restriction of corner state and nonlinear harmonic generation are robust to lattice defects. We believe that the shape unrestricted topological corner state may also find a way to improve other nonlinear optical progress, providing great flexibility for the development of photonic integrated devices.

Keywords: topological photonics; nonlinear optics; topological corner states

1 Introduction

Topological states have been extensively investigated in not only condensed matter physics [1], [2], [3] but also in classical physics [4], [5], [6], such as acoustics [7], [8], [9], [10], [11], [12], [13], [14] and optics [15], [16], [17], [18], [19], [20], [21], [22], [23], because of their excellent topological protection characteristics. Very recently, higher-order topological insulators (HOTIs) have attracted a huge amount of research attentions since they break the conventional bulk-edge correspondence and support topological states of two or more dimensions lower than them [23], [24], [25], [26], [27]. Among them, two-dimensional photonic HOTI have been deeply studied [23], [24], [28], in which the zero-dimensional corner state could exist with several excellent properties such as topological robustness and high quality factor, indicating its promise as an excellent nanocavity [29], [30], [31], [32], [33]. It is these properties, as well as their subwavelength structural units, that make topological states useful in many fields, such as lasers [30], near-field imaging [34], [35], [36] and on-chip optical information processing [37].

As the two general issues in optics, topology and nonlinearity are combined in photonics, becoming a hot topic [34], [36], [[38], [39], [40], [41], [42], [43]]. It has been demonstrated that the efficiencies of the optical nonlinearity could be greatly enhanced with the help of the edge and corner states in topological photonic structures in comparison to the bulk state and the dielectric slab without any photonic structures [41], [42], [44], [45], [46], [47]. Besides, the edge and corner states provide us an opportunity to artificially engineer the frequency conversion process with topological robustness [41], [44], [45]. These results may bridge nonlinear optics with topological physics for the integrated nanophotonic circuit with excellent robustness. Specifically, the corner states contributing enhancement of optical nonlinearity is crucial for on-chip optical information technology which requires highly efficient photon–photon interaction. Among them, second (SHG) [42], [44], [45] and third harmonic generation (THG) [36], [43] enhancement from corner states have been extensively investigated since their high efficiencies are relatively high in comparison to high orders and the phase-matching requirements are easily satisfied.

However, in most of the reported photonic HOTIs, which are characterized with either quantized quadrupole momentum [48] or quantized dipole momentum [23], the two edges of a topological corner state should walk along fixed lattice directions due to the specific spatial symmetries of the underlying unit-cells [49]. For example, there are only a limited choices for angles of corners, such as 90° and 60° for square [24], [29], [32] and Kagome [26] lattices, respectively. From the perspectives of both fundamental physics and practical applications, it greatly hinders the development of HOTIs. In fact, the previous scheme usually relies on two discrete phase values (0 and π) of the Dirac gap (mass terms of the Hamiltonian) [19]. Recently, a topological cavity utilizes a complete 2π vortex phase of Dirac-mass to confine photons in-plane, i.e. a topological zero modes induced by Dirac vortices [50], [51]. It has been proposed that by introducing phase vortex at the corners of an acoustic HOTI through Kekulé modulation can help corner states break away from the limitation of lattice shape, i.e. topological corner states with arbitrary shapes can be excited theoretically [52], [53], [54]. This reduction of restrictive condition of the corner shape may promote the development of optical nonlinearity in topological photonics to a higher level.

In this work, we use Kekulé modulation to obtain the photonic HOTIs and demonstrate the enhancement of nonlinear harmonic generation from the Dirac-vortices based corner states with arbitrary shapes. The Kekulé modulation introduces a complete 2π vortex phase to various shaped corners, ensuring the definitely existence of topological corner states which no longer comply with specific spatial symmetries of underlying lattices. Numerical simulations demonstrated that the corner states based on Kekulé modulation exhibit high-density local field with high quality factor. To show the advantage of the designed photonic HOTI, we utilize these arbitrary shaped corner states to enhance SHG and THG. Finally, the robustness of topological corner states and the stability of the enhanced nonlinear harmonic generations are validated by introducing several defects. Such nonlinear harmonic generations from shape unrestricted corner states may greatly improve the flexibility of topology devices.

2 Results and discussion

2.1 Design of the system

Figure 1(a) schematically illustrates the overall diagram of the designed two-dimensional photonic crystal, which is made of dielectric slab with equilateral-triangular air-holes arranged in a triangular lattice. The gray and white regions indicate the dielectric slab and air-holes, respectively. The slab is assumed to be infinite in z-direction. Initially, all triangular air-hole structures are same. When we calculate the bands of the primitive unit cell, the C 3v symmetry guarantees Dirac cones emerging at corners K ± of the first Brillouin zone (FBZ) [55], [56]. When we consider an enlarged unit cell (marked by the orange line and shown in the zoom-in inset), the inequivalent Dirac cones at valleys K ± will be folded back and a double Dirac cone emerges at Γ point [49], [57]. As shown in Figure 1(b), the parts inside the red dotted line belong to the adjacent cells. The side lengths of the triangular-holes I, II and III are d a , d b1 and d b2, respectively. The lattice constant is a 0 = 1 μm.

Figure 1: Schematic of initial photonic crystal. (a) A dielectric slab with equilateral-triangular air-holes arranged in a triangular lattice. We assume the slab is infinite in z-direction. Lattice constant: a 0 = 1 μm. (b) A single lattice structure. d a , d b1 and d b2 denotes side length of the triangular-holes I, II and III, respectively. (c) Nontrivial and trivial patterns of a supercell.
Figure 1:

Schematic of initial photonic crystal. (a) A dielectric slab with equilateral-triangular air-holes arranged in a triangular lattice. We assume the slab is infinite in z-direction. Lattice constant: a 0 = 1 μm. (b) A single lattice structure. d a , d b1 and d b2 denotes side length of the triangular-holes I, II and III, respectively. (c) Nontrivial and trivial patterns of a supercell.

Herein, a Kekulé texture is imposed on the designed photonic crystal to alternate the coupling strength between adjacent sublattice and implement intervalley coupling, which is analogy to the alternating arrangement of single and double bonds in the benzene structural formula [58]. We set the side length of the triangle centered at r = (x, y) as

(1) d ( r ) = d 0 + δ d ⁡ cos ( K ⋅ r + φ )

d 0 is the initial side length, K = K + − K − is the Kekulé vector, δd and φ represents the strength and phase of the modulation. After imposing the Kekulé modulation, the side lengths of the triangular-holes become d a = d 0 + δdcos(φ), d b1 = d 0 + δdcos(φ + 2π/3) and d b2 = d 0 + δdcos(φ + 4π/3). Regarding the frequency range of interest, d 0 and δd as a 0/1.16 and a 0/1.9, respectively. The enlarged lattices corresponding to φ = 0 and φ = π could be classified as topological nontrivial and trivial cases, respectively, as schematically shown in Figure 1(c).

To study the optical responses, a two-dimensional HOTI made of AlGaAs slab is considered. The refractive index of AlGaAs and air is set as n = 3.0288 and n = 1, respectively. The second- and third-order nonlinear susceptibility tensors of AlGaAs contain non-zero components in the non-diagonal positions, i.e. the nonlinear responses are dependent on the crystalline structure of AlGaAs [59], [60], [61]. We focus on the transverse magnetic (TM) mode with out-of-plane electric field E z and in-plane magnetic field H x,y . For simplicity, the AlGaAs is assumed with specific crystalline structures for SHG and THG. The second-order nonlinear frequency conversion is conducted in AlGaAs with [111] crystalline structure, which is described by P z SHG = ε 0 χ ( 2 ) E z 2 with χ (2) = 1.0 × 10−10 m/V [60], [62]. The third-order nonlinear frequency conversion is conducted in AlGaAs with [001] crystalline structure, which is described by P z THG = ε 0 χ ( 3 ) E z 3 with χ (3) = 2.6 × 10−18 m2/V2 (the typical value of χ (3) varies from 1.6 × 10−17 m2/V2 to 6.2 × 10−19 m2/V2) [61], [62]. ɛ 0 is the permittivity of vacuum. All numerical full-wave simulations are performed in the COMSOL multiphysics software. It is worthy to note that the second- and third-order nonlinear processes are not calculated simultaneously.

2.2 Topological properties of the system

Figure 2(a)–(c) plot the band structures of the photonic crystal with δd = a 0/1.9, φ = 0 and δd = a 0/1.9, φ = π, respectively, exhibiting the same dispersion feature. The band structures are numerically calculated by employing the eigenvalue module of the COMSOL multiphysics software. The blue and red lines represent double degeneracy bands. The eigenfields of E z at Γ point (Figure 2(d) and (e)) show the band inversion between the dipole-like (p) and quadrupole-like (d) modes. The positions of p and d modes in the energy band judges that the modulation phase φ = 0 corresponds to trivial case, and φ = π makes the photonic crystal topological nontrivial, hosting pseudospin-Hall edge states. Figure 2(b) plots the band structure of the photonic crystal with δd = 0, and a four-fold degeneracy appears at the Γ point, which is guaranteed by the band-folding effect and C 6 rotation symmetry. Figure 2(f) shows the first Brillouin zones of the initial and enlarged photonic crystals. The Kekulé lattice has a smaller Brillouin zone (gray hexagon) and rotated over π/6 with respect to the original Brillouin zone (dashed line).

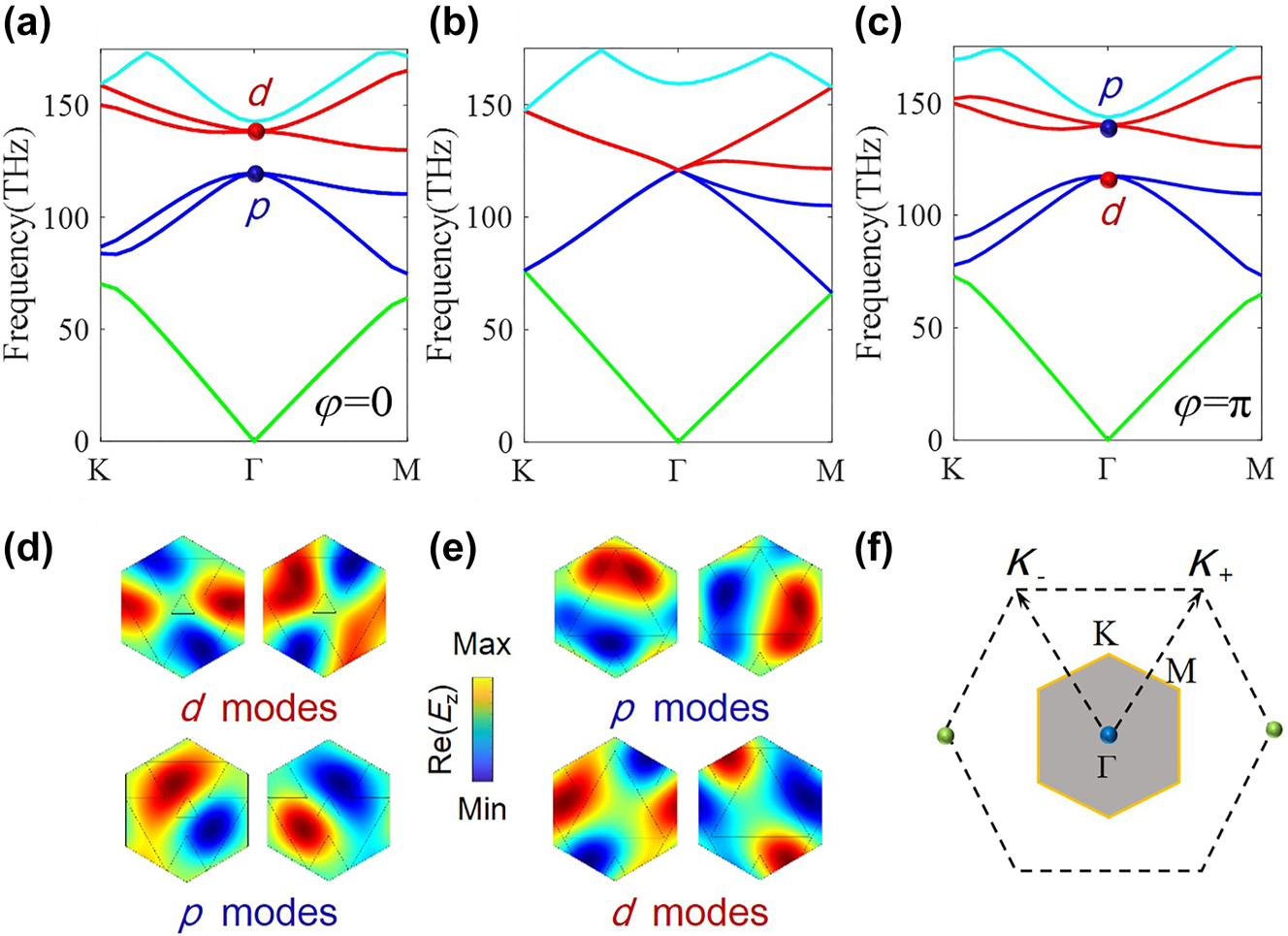
Figure 2: Band dispersion and mode patterns of the photonic crystal with homogeneous Kekulé modulations. (a) Band structure for δd = a 0/1.9 and φ = 0, corresponding to trivial case. (b) Band structure for δd = 0, i.e. the initial case. (c) Band structure for δd = a 0/1.9 and φ = π, corresponding to nontrivial case. In these three cases, d 0 = a 0/1.16. Eigenfield distributions of E z at Γ points of both (d) trivial and (e) nontrivial cases. (f) The first irreducible Brillouin zones of the initial triangular lattice and the enlarged unit cell (gray hexagon). Two K valleys (at the green Dirac points) are folded onto Γ point, through coupling by the Kekulé vector K = K + − K −.
Figure 2:

Band dispersion and mode patterns of the photonic crystal with homogeneous Kekulé modulations. (a) Band structure for δd = a 0/1.9 and φ = 0, corresponding to trivial case. (b) Band structure for δd = 0, i.e. the initial case. (c) Band structure for δd = a 0/1.9 and φ = π, corresponding to nontrivial case. In these three cases, d 0 = a 0/1.16. Eigenfield distributions of E z at Γ points of both (d) trivial and (e) nontrivial cases. (f) The first irreducible Brillouin zones of the initial triangular lattice and the enlarged unit cell (gray hexagon). Two K valleys (at the green Dirac points) are folded onto Γ point, through coupling by the Kekulé vector K = K + − K −.

A honeycomb-lattice photonic crystal with textured tight-binding hopping amplitude can be described by the Hamiltonian in the real space [50]

(2) H = ∑ r ∑ l = 1 3 ( t + δ t r , l ) a r † b r + s l + H.c.

where δt r,l = 0 indicates the initial photonic crystal, and a r and b r + s l denote the annihilation operator on sublattice A of the unit cell at r and its neighboring sublattice B with a displacement s l , respectively. In the designed honeycomb-lattice, s 1 = ( 0 , − 3 a 0 / 3 ) , s 2 = ( a 0 / 2 , − 3 a 0 / 6 ) , and s 3 = ( − a 0 / 2 , − 3 a 0 / 6 ) . The homogeneous Kekulé modulation on the side length of the triangular-holes may introduce a bond texture in the tight-binding model, and the hopping amplitude can be approximately written as t r , l = t 0 − 2 δ t 0 ⁡ cos K ⋅ r + s l + φ [52]. This hopping indicates intervalley couplings, i.e. the modes at k and k + K in the momentum space are coupled and folded onto the center of the superlattice Brillouin zone, as shown in Figure 2(f). After replacing the hopping in Eq. (2) with the modulated hopping, we adopt Fourier transform to the tight-binding Hamiltonian and obtain

(3) H ( k ) = ε k a k † b k + δ t 0 t 0 e i φ ε k + K a k + K † b k + δ t 0 t 0 e − i φ ε k − K a k − K † b k + H.c.

where ε k = t 0 ∑ l = 1 3 ⁡ exp ( i k ⋅ s l ) .

We calculate the energy dispersion of Eq. (3) for several typical values of δt 0 and φ. When δt 0 = 0, a four-fold degeneracy exists at the Γ point due to the band-folding effect, as shown in Figure 3(b). When δt 0 ≠ 0, the band-folding effect is broken and the C 6 symmetry will be reduced to C 3 symmetry, resulting in a complete bandgap around Γ point. It is demonstrated by Figure 3(a)–(c) which plot the energy dispersion for the cases with δt 0 = 0.5, φ = 0 and δt 0 = 0.5, φ = π, respectively. The results in Figure 3 are in good agreements with those in Figure 2(a)–(c). The spin Chern number can be calculated as C s = ∫ BZ Ω k d S , where Ω k is the Berry curvature and BZ represents the whole Brillouin zone. For the case with δt 0 = 0.5, φ = 0 and δt 0 = 0.5, φ = π, the spin Chern number is C s ± = ± 1 and C s ± = ± 0 , respectively. ‘±’ represents the top and bottom edge of the bandgap around the Γ point. The values of the spin Chern number indicate their opposite topological phases, agreeing well with the results in Figure 2.

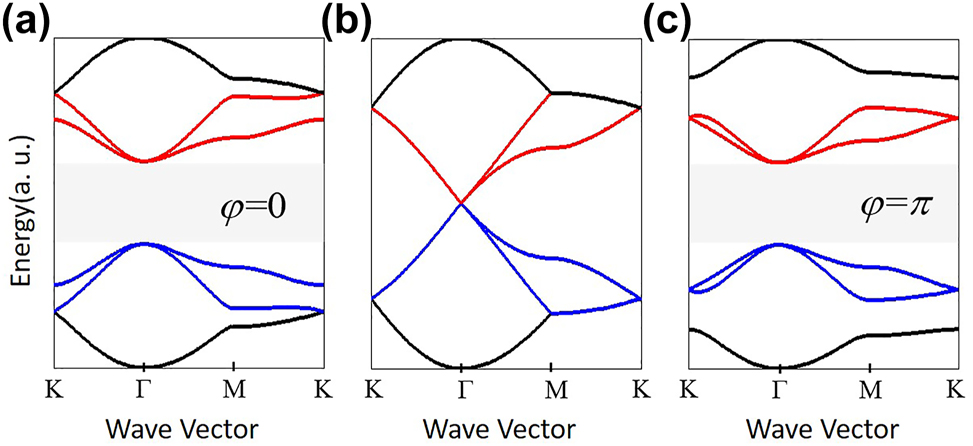
Figure 3: Energy dispersion calculated from the tight-binding Hamiltonian. (a) δt 0 = 0.5 and φ = 0, (b) δt 0 = 0, (c) δt 0 = 0.5 and φ = π.
Figure 3:

Energy dispersion calculated from the tight-binding Hamiltonian. (a) δt 0 = 0.5 and φ = 0, (b) δt 0 = 0, (c) δt 0 = 0.5 and φ = π.

For the low energy spectrum around the Γ point, the six-band Hamiltonian can be reduced to a four-band effective Hamiltonian [50], [53],

(4) H ( k ) = ν D τ 0 ⊗ k x σ 1 + k y σ 2 + m 1 τ 1 − m 2 τ 2 ⊗ σ 3

where k x and k y are the momentums, σ and τ are both Pauli matrices. m 1 and m 2 are on behalf of intervalley couplings introduced by the Kekulé texture. The two mass terms form a complex Dirac mass m = m 1 + im 2, winding in plane as m(r) ∝ eiφ(r) δd. Therefore, the Kekulé modulation opens a full band gap proportional to the value of δd, and it also brings in a phase vortex φ r for the Dirac mass, i.e. Dirac vortex, with negligible impact on the band gap size. It is worthy to note that this topological systems does not reply on two discrete phase values (0 and π) of the Dirac gap, where the topological corner states are characterized by either quantized quadrupole momentum [48] or quantized dipole momentum [23]. In contrast, the Kekulé modulation introduces complete 2π vortex phase through Dirac mass, and the winding number of the Dirac mass is the topological invariant of the vortex. This characteristic ensure emergence of topological corner state, which is independent on the geometry shapes.

2.3 Shape unrestricted corner states and nonlinear harmonic generation

To investigate, it is started by constructing a square domain of the above Kekulé modulated triangular lattice without regarding to its spatial symmetry, which is essential for many previous topological corner state in HOTIs [24], [26], [29], [32], [49]. As shown in Figure 4(a), the constructed HOTI could be divided into two different regions according to their modulation phases. The yellow square domain is fulfilled with Kekulé lattice, whose modulation phase φ r is smoothly aperiodic and satisfies two-dimensional Laplace’s equation Δ φ r = 0 with the boundary condition of φ r = 0 or φ r = 2 π at the edges of the square domain. The surrounding blue lattice is with modulation phase of φ r = 0 , serving as cladding. The inset schematically shows the constructed structure at the upper-left corner. Due to the continuity on the boundaries of the square domain, Δ φ r is uniquely determined by Eq. (1) when the structure is constructed. Around the four corners of the inner domain, the smooth profile introduce phase vortices, thereby guarantee existence of topological corner state.

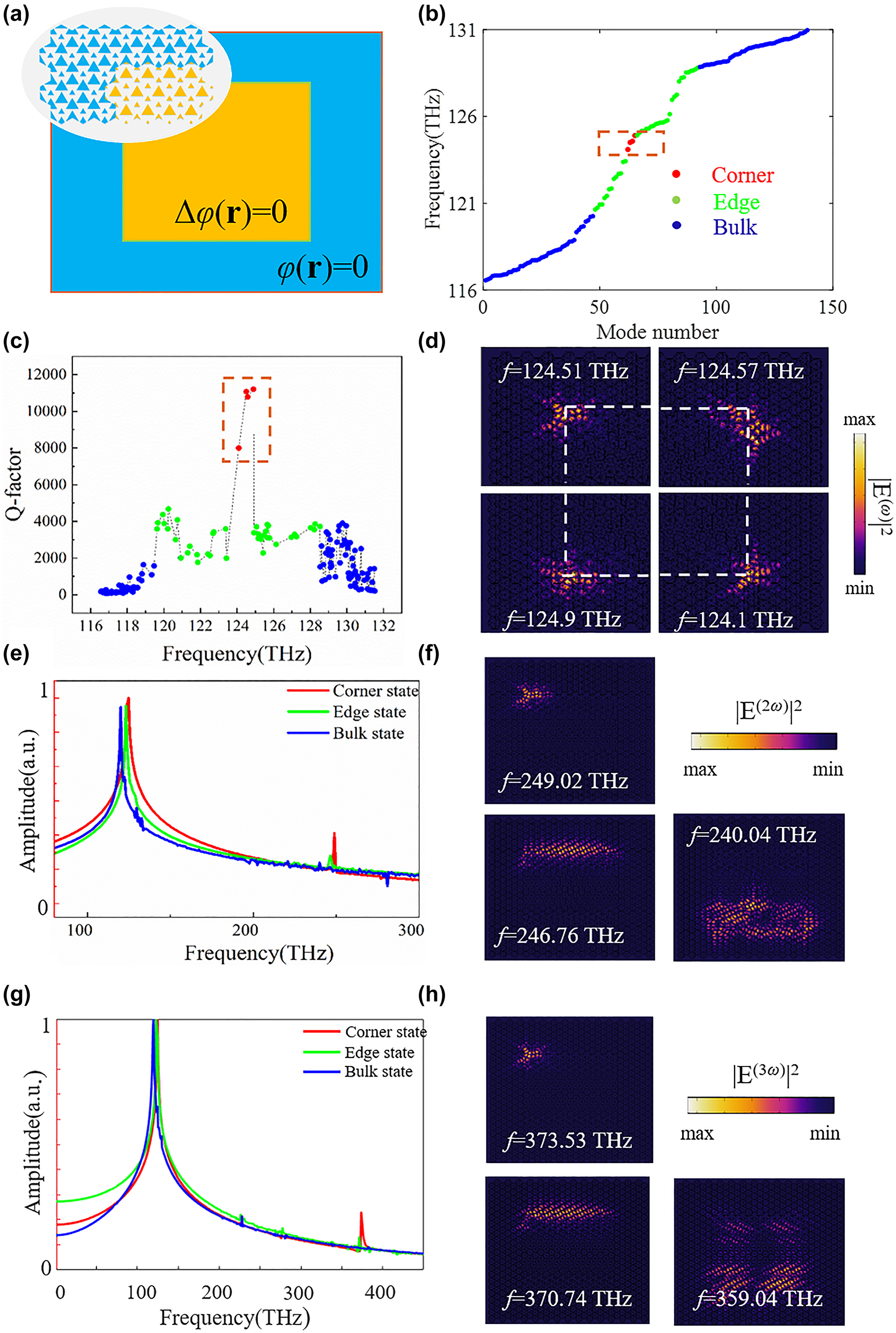
Figure 4: Corner states in a square HOTIs based on the Kekulé modulation and the enhanced nonlinear harmonic generatio. (a) Schematics of the constructed square HOTIs based on the Kekulé modulation. (b) Eigenmodes of the constructed HOTIs. (c) Q factor of the eigenmodes. (d) Electric field distributions of the topological corner states. (e) SHG frequency spectra obtained from the bulk, edge and corner state. (f) Electric field distributions of SHG corresponding to bulk, edge, and corner state. (g) THG frequency spectra obtained from the bulk, edge and corner state. (h) Electric field distributions of THG corresponding to bulk, edge, and corner state. The corner state in (g)–(h) indicates the upper-left corner.
Figure 4:

Corner states in a square HOTIs based on the Kekulé modulation and the enhanced nonlinear harmonic generatio. (a) Schematics of the constructed square HOTIs based on the Kekulé modulation. (b) Eigenmodes of the constructed HOTIs. (c) Q factor of the eigenmodes. (d) Electric field distributions of the topological corner states. (e) SHG frequency spectra obtained from the bulk, edge and corner state. (f) Electric field distributions of SHG corresponding to bulk, edge, and corner state. (g) THG frequency spectra obtained from the bulk, edge and corner state. (h) Electric field distributions of THG corresponding to bulk, edge, and corner state. The corner state in (g)–(h) indicates the upper-left corner.

The eigenmode simulation of the constructed square HOTI is studied and the results are plotted in Figure 4(b). The red, green and blue circles represent topological corner, edge and bulk states, respectively, and four topological corner modes exist in the eigen-spectrum of the designed structure. We also examine the Q factors of these eigenmode, as shown in Figure 4(c). The values of Q factor of the corner states could reach as high as 1.1 × 104, which are one order of magnitude higher than those of the bulk and edge states, verifying localization of the topological corner states. Note that, the slight differences in eigen-frequency and Q factor between the four corner states could be mainly attributed to the inconsistence between the rotational symmetries of the square structure and the triangular lattice. The electric field distributions corresponding to the four corner states are also shown in Figure 4(d), exhibiting confinement around the corners.

Inspired by the previous literature [29], these corner states could be regarded as topological cavity with less restrictions for lattice type and corner shape. This feature is beneficial for the enhancement of optical nonlinear processes, such as lasing and frequency conversion. As proofs-of-concept, the SHG and THG from the bulk, edge, and corner states are numerically investigated. The optical responses of the designed structure are calculated with a time-varying point excitation, which is written as E ω = E 0 ⁡ sin ω t . E 0 = 3 × 109 V/m is the peak intensity of the excitation and ω = 2πf, where f is the frequency of the excitation. We set f = 120.02, 123.38, and 124.51 THz, corresponding to bulk, edge, and corner states, respectively.

Figure 4(e) plots the SHG frequency spectra which are obtained from the time spectrum by a band-passing filter and Fourier transformation. The blue, green and red solid curves are extracted from the constructed structure when the bulk, edge and corner states are excited, respectively. The positions of the excitation and detection are optimized to achieve maximum value in each case. It could be easily observed that SHG is significantly enhanced from the corner state. While, the obtained frequency spectra from both bulk and edge states presents no obvious SHG signal. Figure 4(f) plots the electric field distributions of SHG corresponding to bulk, edge, and corner states (the upper-left corner). The SHG from the corner state is strongly confined to a small volume near the upper-left corner due to the localization of the corner state, in contrast, the SHG field corresponding to the bulk and edge states scatters to the volume and propagates along the interfaces, respectively. These results prove that the enhancement of SHG from the corner state relies on the existence of phase vortex, which is liberated from the spatial symmetry of the underlying lattice.

Similarly, the enhancement of THG from the corner state in comparison to the bulk and edge states is investigated and shown in Figure 4(g) and (h). Due to the strongly localized corner state, the THG field is also concentrated within a small volume near the upper-left corner, presenting behaviors which are totally different with the THG from the bulk and edge states. In simple words, the phase vortex introduced by Kekulé modulation ensures the existence of corner state and the enhancement of nonlinear harmonic generation.

Moreover, we build triangular, quadrangular, quinquangular HOTIs based on the above Kekulé modulated lattice (see the Supplementary Material). The existence of corner states in these arbitray shaped HOTIs and the enhanced nonlinear harmonic generation from them additionally demonstrate the advantage of the proposed method.

Besides these enclosed domains, the corners where the phase vortex exists in semi-enclosed domains can likewise support topological corner states, even the corners are formed with curved boundaries. Figure 5 presents the simulation results of five corner states formed in semi-enclosed domains. The region satisfying the two-dimensional Laplace’s equation Δ φ r = 0 is constructed with aperiodic Kekulé lattice, and the surrounding region is constructed with the lattice whose modulation phase is φ r = 0 . The boundaries between these two regions form a corner with phase vortex. The electric field distributions of the corner states are shown in the first panel of Figure 5, exhibiting strong field confinement around the corners. The eigenmode results shown in the second panel of Figure 5 demonstrate the existence of corner states. Note that the frequency of the corner states maintains around 124 ∼ 125 THz even though their shapes are significantly different, proving the topological robustness of the corner state from one aspect. Therefore, enhanced SHG and THG could be obtained from these various shaped corner states, which are completely unrestricted by the symmetry of the underlying lattice. The SHG and THG frequency spectra detected from these corner states are plotted in the third and fourth panels of Figure 5, respectively, presenting significant enhancement of SHG and THG from the corner states.

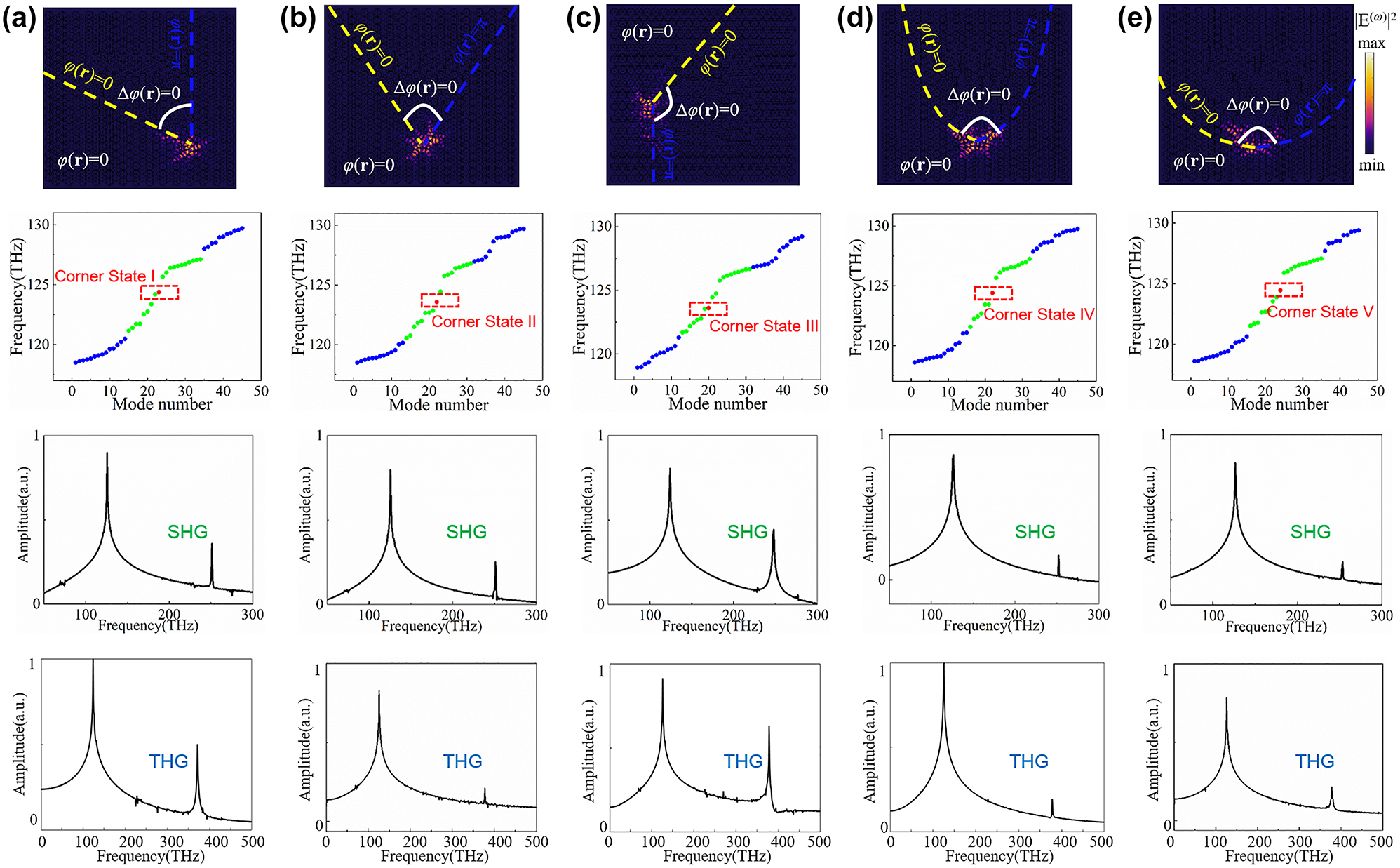
Figure 5: Topological corner states based on Dirac vortex in semi-enclosed domains and enhancement of nonlinear harmonic generation. Results of the corner states labeled as (a) I, (b) II, (c) III, (d) IV, (e) V. First panel: electric field distributions at the corner states. The yellow and blue dashed line marks the boundaries of the Kekulé modulated structure with φ(r) = 0 and φ(r) = 2π, respectively. The corners with a Dirac vortex of 2π-phase winding are outlined by the white solid lines. Second panel: eigenmode results of the semi-enclosed domains. Third panel: SHG frequency spectra obtained from the corner states. Fourth panel: THG frequency spectra obtained from the corner states.
Figure 5:

Topological corner states based on Dirac vortex in semi-enclosed domains and enhancement of nonlinear harmonic generation. Results of the corner states labeled as (a) I, (b) II, (c) III, (d) IV, (e) V. First panel: electric field distributions at the corner states. The yellow and blue dashed line marks the boundaries of the Kekulé modulated structure with φ(r) = 0 and φ(r) = 2π, respectively. The corners with a Dirac vortex of 2π-phase winding are outlined by the white solid lines. Second panel: eigenmode results of the semi-enclosed domains. Third panel: SHG frequency spectra obtained from the corner states. Fourth panel: THG frequency spectra obtained from the corner states.

To further demonstrate the advantage, we calculate the quality factors of the corner states and the efficiencies of both SHG and THG from the corner states in Figure 5. Herein, the SHG and THG efficiencies are defined as η SHG = P SH / P FF 2 and η THG = P TH / P FF 3 , respectively. P SH, P TH, and P FF represent the power of second, third harmonic and fundamental frequency wave, respectively. The calculated results are summarized in Table 1. All these corner states have high quality factors ranging from 5.5 × 103 to 1.2 × 104, indicating their great ability to harness fundamental field and generate nonlinear fields. In addition, the efficiencies of SHG from the corner states I, II, III, IV, and V are calculated to be 7.0 × 10−3 W−1, 6.6 × 10−3 W−1, 9.7 × 10−3 W−1, 7.8 × 10−3 W−1, and 8.4 × 10−3 W−1, respectively. Meanwhile, the efficiencies of THG from the corner states I, II, III, IV, and V are calculated to be 2.0 × 10−4 W−2, 1.6 × 10−4 W−2, 3.7 × 10−4 W−2, 2.2 × 10−4 W−2, and 3.4 × 10−4 W−2, respectively. The efficiencies of the obtained nonlinear harmonic generation are comparable to those observed in both topological resonances [42], [45] and a single bound state in the continuum resonance [63].

Table 1:

Quality factors of the various corner states in Figure 5, and the efficiencies of the corresponding SHG and THG.

Corner state Q-factor SHG THG
I 6.9 7.0 2.0
II 5.5 6.6 1.6
III 12 9.7 3.7
IV 8.4 7.8 2.2
V 9.8 8.4 3.4
Units ×103 ×10−3 W−1 ×10−4 W−2

The topological robustness of the proposed corner states based on the Dirac vortex and the nonlinear harmonic generation from them are investigated by introducing several structural defects. Figure 6(a)–(c) plot the electric field distributions at the corner states when the dielectric materials with the red boxes are removed. Compared to the results without defect in Figure 5(a), the electric field distribution maintains its profile well, presenting strong confinement of electric field at the corners. Figure 6(d) and (e) plot the SHG and THG frequency spectrum, respectively, obtained from the corner states when these structural defects exist. It is clearly shown that the enhanced SHG and THG from these three corner states are spectrally overlapped. It is because the topological states are protected by the global character of the system, making the local defects almost have no influence on the electric field distribution. In a word, the SHG and THG processes from these three corner states have similar performance. Therefore, these results demonstrate the advantage of the topological robustness of the designed corner states against the structural defects, and the stability of the SHG and THG from the corner states.

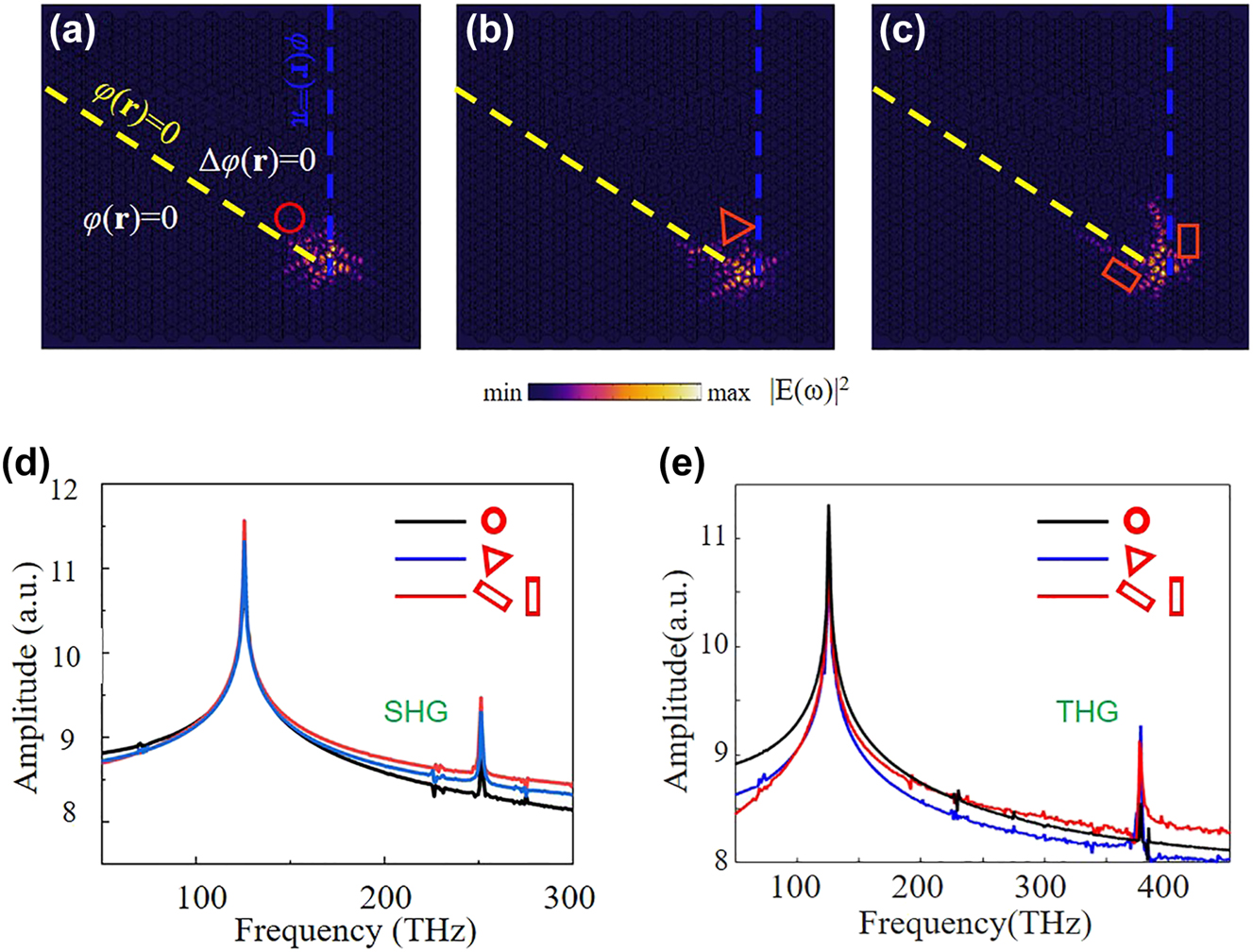
Figure 6: Topological robustness of the designed corner state and SHG, THG from the corner state. Electric field distributions at the corner states when dielectric materials within the (a) circle, (b) triangle, and (c) rectangles are removed. (d) SHG and (e) THG frequency spectrum obtained from the corner states when structure defects exist. The yellow and blue dashed line marks the boundaries of the Kekulé modulated structure with φ(r) = 0 and φ(r) = 2π, respectively.
Figure 6:

Topological robustness of the designed corner state and SHG, THG from the corner state. Electric field distributions at the corner states when dielectric materials within the (a) circle, (b) triangle, and (c) rectangles are removed. (d) SHG and (e) THG frequency spectrum obtained from the corner states when structure defects exist. The yellow and blue dashed line marks the boundaries of the Kekulé modulated structure with φ(r) = 0 and φ(r) = 2π, respectively.

As a closing remark, we would like to talk about the experimental feasibility of this study. The preparation of the designed structure in experiment could be possible with the advanced fabrication technology, such as patterning photoresist, reactive ion etching, and so on [64]. To excite the corner state, a tunable continuous-wave laser source can be collimated and focused around the corner. The frequency spectra could be collected by a microscope objective, and the fundamental and nonlinear harmonic generation signals could be separated by a filter.

3 Conclusions

In this work, we use Kekulé modulation to introduce phase vortices of 2π at the corner of topological insulators to construct HOTIs and topological corner state that does not rely on the symmetry of underlying lattice. The nonlinear effect is enhanced by the topological corner state, which is embodied in enhancement the efficiencies of nonlinear harmonic generation of the incident fundamental wave. By investigating various shaped corner states based on the Dirac vortex, including the quality factor and the efficiencies of both SHG and THG from them, it can be concluded that the nonlinear harmonic generation is significantly enhanced from these corner states with unrestricted shapes. Finally, the robustness of the corner states and the nonlinear harmonic generation are tested by introducing structural defects around the corners. Our results may lay the foundation for its future application in integrated optical devices.

Corresponding authors: Kai Guo, School of Computer and Information, Hefei University of Technology, Hefei 230009, China; and Key Lab of Modern Optical Technologies of Education Ministry of China, Soochow University, Suzhou 215006, China, E-mail: ; and Zhongyi Guo, School of Computer and Information, Hefei University of Technology, Hefei 230009, China, E-mail: 

Funding source: National Natural Science Foundation of China

Award Identifier / Grant number: 11804073

Award Identifier / Grant number: 61775050

Funding source: Key Lab of Modern Optical Technologies of Education Ministry of China, Soochow University

Award Identifier / Grant number: KJS2345

  1. Research funding: National Natural Science Foundation of China (Grants 11804073 and 61775050). This study was also funded by the Key Lab of Modern Optical Technologies of Education Ministry of China, Soochow University (Grant KJS2345).

  2. Author contributions: K.G. conceived the idea, checked the results and wrote the manuscript. H.W., J.X. and J.W. conducted the theoretical design and performed the numerical simulations. B.L. commented on the manuscript. Z.G. supervised the project. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: Authors state no conflicts of interest.

  4. Data availability: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] D. Xiao, M. C. Chang, and Q. Niu, “Berry phase effects on electronic properties,” Rev. Mod. Phys., vol. 82, no. 3, p. 1959, 2010. https://doi.org/10.1103/RevModPhys.82.1959.Search in Google Scholar

[2] M. Z. Hasan and C. L. Kane, “Colloquium: topological insulators,” Rev. Mod. Phys., vol. 82, no. 4, p. 3045, 2010. https://doi.org/10.1103/RevModPhys.82.3045.Search in Google Scholar

[3] X. L. Qi and S. C. Zhang, “Topological insulators and superconductors,” Rev. Mod. Phys., vol. 83, no. 4, p. 1057, 2011. https://doi.org/10.1103/RevModPhys.83.1057.Search in Google Scholar

[4] F. D. M. Haldane and S. Raghu, “Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry,” Phys. Rev. Lett., vol. 100, no. 1, p. 013904, 2008. https://doi.org/10.1103/PhysRevLett.100.013904.Search in Google Scholar PubMed

[5] Z. Wang, Y. Chong, J. D. Joannopoulos, and M. Soljačić, “Observation of undirectional backscattering-immune topological electromagnetic states,” Nature, vol. 461, no. 7265, pp. 772–775, 2009. https://doi.org/10.1038/nature08293.Search in Google Scholar PubMed

[6] V. V. Albert, L. I. Glazman, and L. Jiang, “Topological properties of linear circuit lattices,” Phys. Rev. Lett., vol. 114, no. 17, p. 173902, 2015. https://doi.org/10.1103/PhysRevLett.114.173902.Search in Google Scholar PubMed

[7] P. Wang, L. Lu, and K. Bertoldi, “Topological phononic crystals with one-way elastic edge waves,” Phys. Rev. Lett., vol. 115, no. 10, p. 104302, 2015. https://doi.org/10.1103/PhysRevLett.115.104302.Search in Google Scholar PubMed

[8] B. Z. Xia, et al.., “Topological phononic insulator with robust pseudospin-dependent transport,” Phys. Rev. B, vol. 96, no. 9, p. 094106, 2017. https://doi.org/10.1103/PhysRevB.96.094106.Search in Google Scholar

[9] Z. G. Chen and Y. Wu, “Tunable topological phononic crystals,” Phys. Rev. Appl., vol. 5, no. 5, p. 054021, 2016. https://doi.org/10.1103/PhysRevApplied.5.054021.Search in Google Scholar

[10] S. Y. Yu, et al.., “Elastic pseudospin transport for integratable topological phononic circuits,” Nat. Commun., vol. 9, no. 1, p. 3072, 2018. https://doi.org/10.1038/s41467-018-05461-5.Search in Google Scholar PubMed PubMed Central

[11] Z. Tian, et al.., “Dispersion tuning and route reconfiguration of acoustic waves in valley topological phononic crystals,” Nat. Commun., vol. 11, no. 1, p. 762, 2020. https://doi.org/10.1038/s41467-020-14553-0.Search in Google Scholar PubMed PubMed Central

[12] S. H. Mousavi, A. B. Khanikaev, and Z. Wang, “Topologically protected elastic waves in phononic metamaterials,” Nat. Commun., vol. 6, no. 1, p. 8682, 2015. https://doi.org/10.1038/ncomms9682.Search in Google Scholar PubMed PubMed Central

[13] G. C. Ma, M. Xiao, and C. T. Chan, “Topological phases in acoustic and mechanical systems,” Nat. Rev. Phys., vol. 1, no. 4, pp. 281–294, 2019. https://doi.org/10.1038/s42254-019-0030-x.Search in Google Scholar

[14] R. Fleury, A. B. Khanikaev, and A. Alù, “Floquet topological insulators for sound,” Nat. Commun., vol. 7, no. 1, p. 11744, 2016. https://doi.org/10.1038/ncomms11744.Search in Google Scholar PubMed PubMed Central

[15] L. Lu, J. D. Joannopoulos, and M. Soljačić, “Topological photonics,” Nat. Phys., vol. 8, no. 11, pp. 821–829, 2014. https://doi.org/10.1038/nphoton.2014.248.Search in Google Scholar

[16] T. Ozawa, et al.., “Topological photonics,” Rev. Mod. Phys., vol. 91, no. 1, p. 015006, 2019. https://doi.org/10.1103/RevModPhys.91.015006.Search in Google Scholar

[17] A. B. Khanikaev and G. Shvets, “Two-dimensional topological photonics,” Nat. Photonics, vol. 11, no. 12, pp. 763–773, 2017. https://doi.org/10.1038/s41566-017-0048-5.Search in Google Scholar

[18] H. F. Wang, S. K. Gupta, B. Y. Xie, and M. H. Lu, “Topological photonic crystals: a review,” Front. Optoelectron., vol. 13, no. 1, pp. 50–72, 2020. https://doi.org/10.1007/s12200-019-0949-7.Search in Google Scholar PubMed PubMed Central

[19] L. H. Wu and X. Hu, “Scheme for achieving a topological photonic crystal by using dielectric material,” Phys. Rev. Lett., vol. 114, no. 22, p. 223901, 2015. https://doi.org/10.1103/PhysRevLett.114.223901.Search in Google Scholar PubMed

[20] Y. D. Li, et al.., “Effective Hamiltonian for photonic topological insulator with non-Hermitian domain walls,” Phys. Rev. Lett., vol. 129, no. 5, p. 053903, 2022. https://doi.org/10.1103/PhysRevLett.129.053903.Search in Google Scholar PubMed

[21] Y. H. Yang, et al.., “Realization of a three-dimensional photonic topological insulator,” Nature, vol. 565, no. 7741, pp. 622–626, 2019. https://doi.org/10.1038/s41586-018-0829-0.Search in Google Scholar PubMed

[22] M. J. Chen, et al.., “Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide,” Nat. Commun., vol. 5, no. 1, p. 5782, 2014. https://doi.org/10.1038/ncomms6782.Search in Google Scholar PubMed

[23] B. Y. Xie, et al.., “Second-order photonic topological insulator with corner states,” Phys. Rev. B, vol. 98, no. 20, p. 205147, 2018. https://doi.org/10.1103/PhysRevB.98.205147.Search in Google Scholar

[24] X. D. Chen, W. M. Deng, F. L. Shi, F. L. Zhao, M. Chen, and J. W. Dong, “Direct observation of corner states in second-order topological photonic crystal slabs,” Phys. Rev. Lett., vol. 122, no. 23, p. 233902, 2019. https://doi.org/10.1103/PhysRevLett.122.233902.Search in Google Scholar PubMed

[25] A. Dutt, M. Minkov, I. A. D. Williamson, and S. H. Fan, “Higher-order topological insulators in synthetic dimensions,” Light Sci. Appl., vol. 9, no. 1, p. 131, 2020. https://doi.org/10.1038/s41377-020-0334-8.Search in Google Scholar PubMed PubMed Central

[26] M. Y. Li, et al.., “Higher-order topological states in photonic Kagome crystals with long-range interactions,” Nat. Photonics, vol. 14, no. 2, pp. 89–94, 2020. https://doi.org/10.1038/s41566-019-0561-9.Search in Google Scholar

[27] X. W. Luo and C. W. Zhang, “Higher-order topological corner states induced by gain and loss,” Phys. Rev. Lett., vol. 123, no. 7, p. 073601, 2019. https://doi.org/10.1103/PhysRevLett.123.073601.Search in Google Scholar PubMed

[28] B. Y. Xie, et al.., “Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals,” Phys. Rev. Lett., vol. 122, no. 23, p. 233903, 2019. https://doi.org/10.1103/PhysRevLett.122.233903.Search in Google Scholar PubMed

[29] Y. Ota, et al.., “Photonic crystal nanocavity based on a topological corner state,” Optica, vol. 6, no. 6, pp. 786–789, 2019. https://doi.org/10.1364/OPTICA.6.000786.Search in Google Scholar

[30] L. C. Yang, G. R. Li, X. M. Gao, and L. Lu, “Topological-cavity surface-emitting laser,” Nat. Photonics, vol. 16, no. 4, pp. 279–283, 2022. https://doi.org/10.1038/s41566-022-00972-6.Search in Google Scholar

[31] X. Wang, et al.., “Non-Hermitian high-quality-factor topological photonic crystal cavity,” Phys. Rev. A, vol. 105, no. 2, p. 023531, 2022. https://doi.org/10.1103/PhysRevA.105.023531.Search in Google Scholar

[32] A. Shi, et al.., “Coupled cavity-waveguide based on topological corner state and edge state,” Opt. Lett., vol. 46, no. 5, pp. 1089–1092, 2021. https://doi.org/10.1364/OL.418570.Search in Google Scholar PubMed

[33] X. Xin, et al.., “Cavity quantum electrodynamics with second-order topological corner state,” Laser Photon. Rev., vol. 14, no. 8, p. 1900425, 2020. https://doi.org/10.1002/lpor.201900425.Search in Google Scholar

[34] S. S. Kruk, W. L. Gao, D. Y. Choi, T. Zentgraf, S. Zhang, and Y. Kivshar, “Nonlinear imaging of nanoscale topological corner states,” Nano Lett., vol. 21, no. 11, pp. 4592–4597, 2021. https://doi.org/10.1021/acs.nanolett.1c00449.Search in Google Scholar PubMed

[35] A. Vakulenko, et al.., “Near-field characterization of higher-order topological photonic states at optical frequencies,” Adv. Mater., vol. 33, no. 18, p. 2004376, 2021. https://doi.org/10.1002/adma.202004376.Search in Google Scholar PubMed

[36] D. Smirnova, S. Kruk, D. Leykam, E. Melik-Gaykazyan, D. T. Choi, and Y. Kivshar, “Third-harmonic generation in photonic topological metasurfaces,” Phys. Rev. Lett., vol. 123, no. 10, p. 103901, 2019. https://doi.org/10.1103/PhysRevLett.123.103901.Search in Google Scholar PubMed

[37] X. T. He, et al.., “In-plane excitation of a topological nanophotonic corner state at telecom wavelengths in a cross-coupled cavity,” Photon. Res., vol. 9, no. 8, pp. 1423–1431, 2021. https://doi.org/10.1364/PRJ.419569.Search in Google Scholar

[38] S. Sergey, et al.., “Nonlinear light generation in topological nanostructures,” Nat. Nanotechnol., vol. 14, no. 2, pp. 126–130, 2019. https://doi.org/10.1038/s41565-018-0324-7.Search in Google Scholar PubMed

[39] K. K. Om and K. H. Kim, “Second-harmonic generation based on the dual-band second-order topological corner states,” Phys. Status Solidi Rapid Res. Lett., vol. 16, no. 1, p. 2100427, 2022. https://doi.org/10.1002/pssr.202100427.Search in Google Scholar

[40] K. K. Om and K. H. Kim, “Dual-band higher-order topological states and four-wave mixing in plasmonic valley-Hall metasurfaces,” Phys. Lett. A, vol. 488, no. 12, p. 129135, 2023. https://doi.org/10.1016/j.physleta.2023.129135.Search in Google Scholar

[41] J. Ma, K. Guo, F. J. Chen, K. Y. Zhou, S. T. Liu, and Z. Y. Guo, “Manipulating second harmonic generation in higher-order topological photonic crystals,” Ann. Phys., vol. 533, no. 11, p. 2100191, 2021. https://doi.org/10.1002/andp.202100191.Search in Google Scholar

[42] K. Guo, J. T. Wu, F. J. Chen, K. Y. Zhou, S. T. Liu, and Z. Y. Guo, “Second harmonic generation enhancement and directional emission from topological corner state based on the quantum spin Hall effect,” Opt. Express, vol. 29, no. 17, pp. 26841–26850, 2021. https://doi.org/10.1364/OE.432660.Search in Google Scholar PubMed

[43] D. Smirnova, D. Leykam, Y. D. Chong, and Y. Kivshar, “Nonlinear topological photonics,” Appl. Phys. Rev., vol. 7, no. 2, p. 021306, 2020. https://doi.org/10.1063/1.5142397.Search in Google Scholar

[44] Z. H. Lan, J. W. You, Q. Ren, W. E. I. Sha, and N. C. Panoiu, “Second-harmonic generation via double topological valley-Hall kink modes in all-dielectric photonic crystals,” Phys. Rev. A, vol. 103, no. 4, p. L041502, 2021. https://doi.org/10.1103/PhysRevA.103.L041502.Search in Google Scholar

[45] Y. F. Chen, Z. H. Lan, J. S. Li, and J. Zhu, “Topologically protected second harmonic generation via doubly resonant high-order photonic modes,” Phys. Rev. B, vol. 104, no. 15, p. 155421, 2021. https://doi.org/10.1103/PhysRevB.104.155421.Search in Google Scholar

[46] Q. C. Yuan, L. P. Gu, L. Fang, X. T. Gan, Z. G. Chen, and J. L. Zhao, “Giant enhancement of nonlinear harmonic generation in a silicon topological photonic crystal nanocavity chain,” Laser Photon. Rev., vol. 16, no. 5, p. 2100269, 2022. https://doi.org/10.1002/lpor.202100269.Search in Google Scholar

[47] H. P. Zhou, et al.., “Controllable second harmonic generation based on topological spin-dependent edge states,” J. Appl. Phys., vol. 131, no. 11, p. 113101, 2022. https://doi.org/10.1063/5.0083773.Search in Google Scholar

[48] L. He, Z. Addison, J. M. Eugene, and B. Zhen, “Quadrupole topological photonic crystals,” Nat. Commun., vol. 11, no. 1, p. 3119, 2020. https://doi.org/10.1038/s41467-020-16916-z.Search in Google Scholar PubMed PubMed Central

[49] Y. H. Liu, Y. Z. Wang, N. C. Hu, J. Y. Lin, C. H. Lee, and X. Zhang, “Topological corner modes in a brick lattice with nonsymmorphic symmetry,” Phys. Rev. B, vol. 102, no. 3, p. 035142, 2020. https://doi.org/10.1103/PhysRevB.102.035142.Search in Google Scholar

[50] C. Y. Hou, C. Chamon, and C. Mudry, “Electron fractionalization in two-dimensional graphenelike structures,” Phys. Rev. Lett., vol. 98, no. 18, p. 186809, 2007. https://doi.org/10.1103/PhysRevLett.98.186809.Search in Google Scholar PubMed

[51] X. M. Gao, et al.., “Dirac-vortex topological cavities,” Nat. Nanotechnol., vol. 15, no. 12, pp. 1012–1018, 2020. https://doi.org/10.1038/s41565-020-0773-7.Search in Google Scholar PubMed

[52] P. L. Gao, D. Torrent, F. Cervera, P. San-Jose, J. Sánchez-Dehesa, and J. Christensen, “Majorana-like zero modes in Kekulé,” Phys. Rev. Lett., vol. 123, no. 19, p. 196601, 2019. https://doi.org/10.1103/PhysRevLett.123.196601.Search in Google Scholar PubMed

[53] X. X. Wu, Y. Meng, Y. R. Hao, R. Y. Zhang, J. S. Li, and X. Zhang, “Topological corner modes induced by Dirac vortices in arbitrary geometry,” Phys. Rev. Lett., vol. 126, no. 22, p. 226802, 2021. https://doi.org/10.1103/PhysRevLett.126.226802.Search in Google Scholar PubMed

[54] G. C. Wei, Z. Z. Liu, L. C. Wang, J. Y. Song, and J. J. Xiao, “Coexisting valley and pseudo-spin topological edge states in photonic topological insulators made of distorted Kekulé lattices,” Photon. Res., vol. 10, no. 4, pp. 999–1010, 2022. https://doi.org/10.1364/PRJ.453803.Search in Google Scholar

[55] J. Y. Lu, C. Y. Qiu, M. Z. Ke, and Z. Y. Liu, “Valley vortex states in sonic crystals,” Phys. Rev. Lett., vol. 116, no. 9, p. 093901, 2016. https://doi.org/10.1103/PhysRevLett.116.093901.Search in Google Scholar PubMed

[56] X. Wu, et al.., “Direct observation of valley-polarized topological edge states in designer surface plasmon crystals,” Nat. Commun., vol. 8, no. 1, p. 1304, 2017. https://doi.org/10.1038/s41467-017-01515-2.Search in Google Scholar PubMed PubMed Central

[57] X. J. Zhang, et al.., “Symmetry-protected hierarchy of anomalous multipole topological band gaps in nonsymmorphic metacrystals,” Nat. Commun., vol. 11, no. 1, p. 65, 2020. https://doi.org/10.1038/s41467-019-13861-4.Search in Google Scholar PubMed PubMed Central

[58] C. Chamon, “Solitons in carbon nanotubes,” Phys. Rev. B, vol. 62, no. 4, p. 2806, 2000. https://doi.org/10.1103/PhysRevB.62.2806.Search in Google Scholar

[59] S. Sergey, et al.., “Nonlinear optical magnetism revealed by second-harmonic generation in nanoantennas,” Nano Lett., vol. 17, no. 6, pp. 3914–3918, 2017. https://doi.org/10.1021/acs.nanolett.7b01488.Search in Google Scholar PubMed

[60] J. D. Sautter, et al.., “Tailoring second-harmonic emission from (111)-GaAs nanoantennas,” Nano Lett., vol. 19, no. 6, pp. 3905–3911, 2019. https://doi.org/10.1021/acs.nanolett.9b01112.Search in Google Scholar PubMed

[61] L. Rodríguez-Suné, J. Trull, M. Scalora, R. Vilaseca, and C. Cojocaru, “Harmonic generation in the opaque region of GaAs: the role of the surface and magnetic nonlinearities,” Opt. Express, vol. 27, no. 18, pp. 26120–26130, 2019. https://doi.org/10.1364/OE.27.026120.Search in Google Scholar PubMed

[62] E. Mobini, D. H. G. Espinosa, K. Vyas, and K. Dolgaleva, “AlGaAs nonlinear integrated photonics,” Micromachine, vol. 13, no. 7, p. 991, 2022. https://doi.org/10.3390/mi13070991.Search in Google Scholar PubMed PubMed Central

[63] L. Carletti, K. Koshelev, C. D. Angelis, and Y. Kivshar, “Giant nonlinear response at the nanoscale driven by bound states in the continuum,” Phys. Rev. Lett., vol. 121, no. 3, p. 033903, 2018. https://doi.org/10.1103/PhysRevLett.121.033903.Search in Google Scholar PubMed

[64] Y. H. Yang, et al.., “Terahertz topological photonics for on-chip communication,” Nat. Photonics, vol. 14, no. 7, pp. 446–451, 2020. https://doi.org/10.1038/s41566-020-0618-9.Search in Google Scholar

Supplementary Material

This article contains supplementary material (https://doi.org/10.1515/nanoph-2024-0116).

Received: 2024-03-07
Accepted: 2024-05-15
Published Online: 2024-06-03

© 2024 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Editorial
  3. New frontiers in nonlinear nanophotonics
  4. Reviews
  5. Tailoring of the polarization-resolved second harmonic generation in two-dimensional semiconductors
  6. A review of gallium phosphide nanophotonics towards omnipotent nonlinear devices
  7. Nonlinear photonics on integrated platforms
  8. Nonlinear optical physics at terahertz frequency
  9. Research Articles
  10. Second harmonic generation and broad-band photoluminescence in mesoporous Si/SiO2 nanoparticles
  11. Second harmonic generation in monolithic gallium phosphide metasurfaces
  12. Intrinsic nonlinear geometric phase in SHG from zincblende crystal symmetry media
  13. CMOS-compatible, AlScN-based integrated electro-optic phase shifter
  14. Symmetry-breaking-induced off-resonance second-harmonic generation enhancement in asymmetric plasmonic nanoparticle dimers
  15. Nonreciprocal scattering and unidirectional cloaking in nonlinear nanoantennas
  16. Metallic photoluminescence of plasmonic nanoparticles in both weak and strong excitation regimes
  17. Inverse design of nonlinear metasurfaces for sum frequency generation
  18. Tunable third harmonic generation based on high-Q polarization-controlled hybrid phase-change metasurface
  19. Phase-matched third-harmonic generation in silicon nitride waveguides
  20. Nonlinear mid-infrared meta-membranes
  21. Phase-matched five-wave mixing in zinc oxide microwire
  22. Tunable high-order harmonic generation in GeSbTe nano-films
  23. Si metasurface supporting multiple quasi-BICs for degenerate four-wave mixing
  24. Cryogenic nonlinear microscopy of high-Q metasurfaces coupled with transition metal dichalcogenide monolayers
  25. Giant second-harmonic generation in monolayer MoS2 boosted by dual bound states in the continuum
  26. Quasi-BICs enhanced second harmonic generation from WSe2 monolayer
  27. Intense second-harmonic generation in two-dimensional PtSe2
  28. Efficient generation of octave-separating orbital angular momentum beams via forked grating array in lithium niobite crystal
  29. High-efficiency nonlinear frequency conversion enabled by optimizing the ferroelectric domain structure in x-cut LNOI ridge waveguide
  30. Shape unrestricted topological corner state based on Kekulé modulation and enhanced nonlinear harmonic generation
  31. Vortex solitons in topological disclination lattices
  32. Dirac exciton–polariton condensates in photonic crystal gratings
  33. Enhancing cooperativity of molecular J-aggregates by resonantly coupled dielectric metasurfaces
  34. Symmetry-protected bound states in the continuum on an integrated photonic platform
  35. Ultrashort pulse biphoton source in lithium niobate nanophotonics at 2 μm
  36. Entangled photon-pair generation in nonlinear thin-films
  37. Directionally tunable co- and counterpropagating photon pairs from a nonlinear metasurface
  38. All-optical modulator with photonic topological insulator made of metallic quantum wells
  39. Photo-thermo-optical modulation of Raman scattering from Mie-resonant silicon nanostructures
  40. Plasmonic electro-optic modulators on lead zirconate titanate platform
  41. Miniature spectrometer based on graded bandgap perovskite filter
  42. Far-field mapping and efficient beaming of second harmonic by a plasmonic metagrating
https://doi.org/10.1515/nanoph-2024-0116
Keywords for this article
topological photonics; nonlinear optics; topological corner states
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Editorial
  3. New frontiers in nonlinear nanophotonics
  4. Reviews
  5. Tailoring of the polarization-resolved second harmonic generation in two-dimensional semiconductors
  6. A review of gallium phosphide nanophotonics towards omnipotent nonlinear devices
  7. Nonlinear photonics on integrated platforms
  8. Nonlinear optical physics at terahertz frequency
  9. Research Articles
  10. Second harmonic generation and broad-band photoluminescence in mesoporous Si/SiO2 nanoparticles
  11. Second harmonic generation in monolithic gallium phosphide metasurfaces
  12. Intrinsic nonlinear geometric phase in SHG from zincblende crystal symmetry media
  13. CMOS-compatible, AlScN-based integrated electro-optic phase shifter
  14. Symmetry-breaking-induced off-resonance second-harmonic generation enhancement in asymmetric plasmonic nanoparticle dimers
  15. Nonreciprocal scattering and unidirectional cloaking in nonlinear nanoantennas
  16. Metallic photoluminescence of plasmonic nanoparticles in both weak and strong excitation regimes
  17. Inverse design of nonlinear metasurfaces for sum frequency generation
  18. Tunable third harmonic generation based on high-Q polarization-controlled hybrid phase-change metasurface
  19. Phase-matched third-harmonic generation in silicon nitride waveguides
  20. Nonlinear mid-infrared meta-membranes
  21. Phase-matched five-wave mixing in zinc oxide microwire
  22. Tunable high-order harmonic generation in GeSbTe nano-films
  23. Si metasurface supporting multiple quasi-BICs for degenerate four-wave mixing
  24. Cryogenic nonlinear microscopy of high-Q metasurfaces coupled with transition metal dichalcogenide monolayers
  25. Giant second-harmonic generation in monolayer MoS2 boosted by dual bound states in the continuum
  26. Quasi-BICs enhanced second harmonic generation from WSe2 monolayer
  27. Intense second-harmonic generation in two-dimensional PtSe2
  28. Efficient generation of octave-separating orbital angular momentum beams via forked grating array in lithium niobite crystal
  29. High-efficiency nonlinear frequency conversion enabled by optimizing the ferroelectric domain structure in x-cut LNOI ridge waveguide
  30. Shape unrestricted topological corner state based on Kekulé modulation and enhanced nonlinear harmonic generation
  31. Vortex solitons in topological disclination lattices
  32. Dirac exciton–polariton condensates in photonic crystal gratings
  33. Enhancing cooperativity of molecular J-aggregates by resonantly coupled dielectric metasurfaces
  34. Symmetry-protected bound states in the continuum on an integrated photonic platform
  35. Ultrashort pulse biphoton source in lithium niobate nanophotonics at 2 μm
  36. Entangled photon-pair generation in nonlinear thin-films
  37. Directionally tunable co- and counterpropagating photon pairs from a nonlinear metasurface
  38. All-optical modulator with photonic topological insulator made of metallic quantum wells
  39. Photo-thermo-optical modulation of Raman scattering from Mie-resonant silicon nanostructures
  40. Plasmonic electro-optic modulators on lead zirconate titanate platform
  41. Miniature spectrometer based on graded bandgap perovskite filter
  42. Far-field mapping and efficient beaming of second harmonic by a plasmonic metagrating
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 14.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2024-0116/html
Scroll to top button