Cryogenic nonlinear microscopy of high-Q metasurfaces coupled with transition metal dichalcogenide monolayers

2.1 Linear spectroscopy

As a resonant system, we study a dielectric metasurface that consists of a densely packed 2D array of TiO₂ nanodisks on a transparent SiO₂ substrate. The square lattice has the periods P of 470 nm. The cylinder diameter d is 450 nm and the height h is 120 nm. The size of the metasurface is 50 μm. The details on the sample fabrication can be found in the Supporting Materials (S1). The transmittance spectra of the sample for normal incidence are shown in Figure 2(a). The red curve is the experimental results and the black one is the numerical modeling. The inset shows a scanning electron microscopy (SEM) image of the metasurface. The spectral sensitivity of the linear experimental setup is limited by 900 nm and the scheme of the setup is presented in the Supporting Materials (S2.1). The details of numerical modeling can be found in the Supporting Materials as well (S3.1). The spectra have two resonant features. The nature of these resonances is the overlapped electrical dipole (ED, red curve) with magnetic quadrupole (MQ, blue curve) for the resonance at the wavelength of 745 nm and overlapped magnetic dipole (MD, green curve) with electric quadrupole (EQ, magenta curve) for the one at the wavelength of 695 nm according to the multipole decomposition shown in the Figure 2(b). The inset shows the geometry of the sample and the experiment. These resonances here and thereafter will be called geometric underlying in that they are not connected with the material resonances and properties of the media but are dictated by the nanostructuring only. The details of the decomposition can be found in the Supporting Materials (S3.2). The quality factor of the left resonance is about 185 and for the right one is approximately 80 extracted from the numerical data. The fitting formula for the resonances is the Fano formula [43]:

Figure 2:

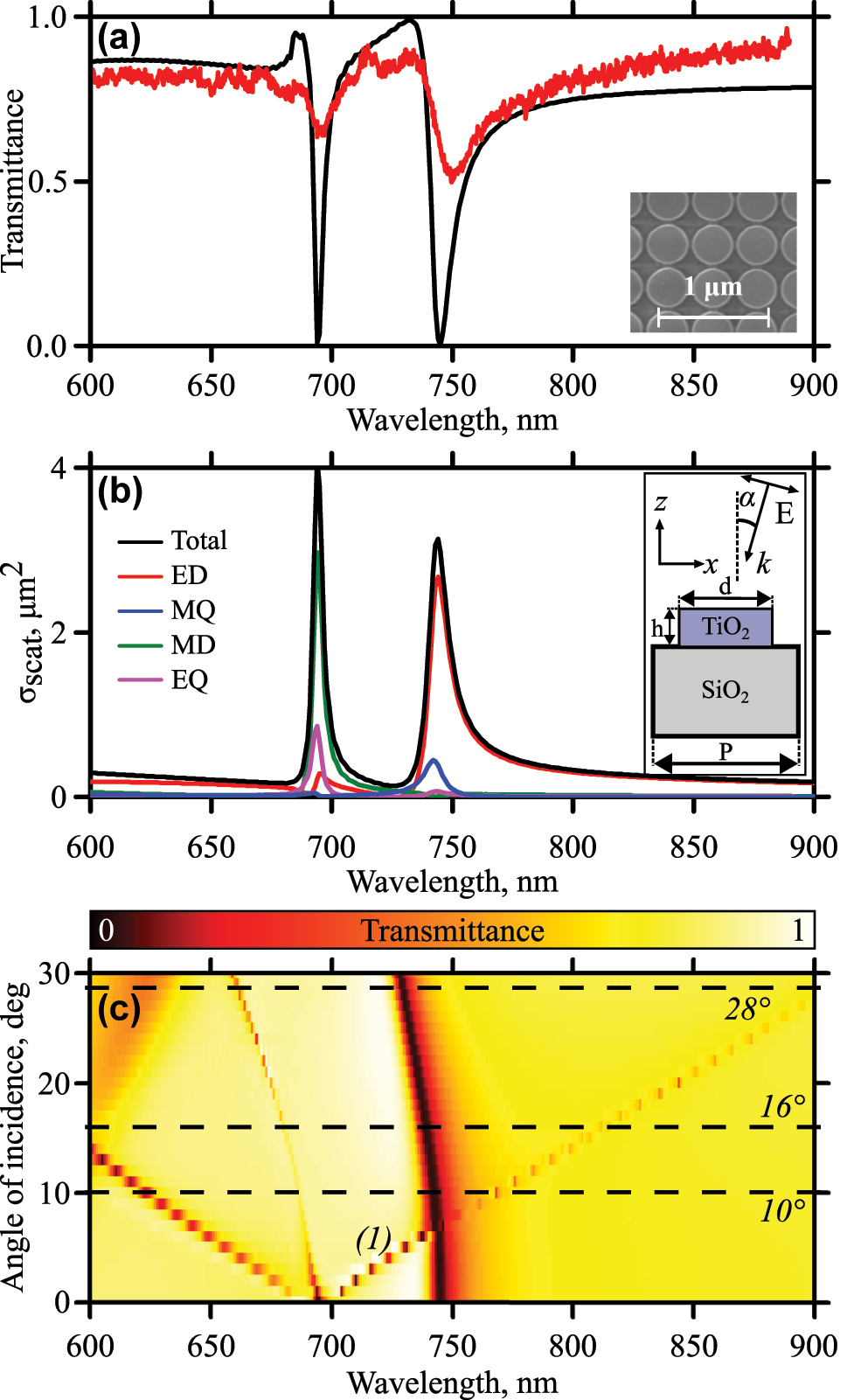
Linear optical characterization. (a) Transmittance spectra of the metasurface for normal incidence. The black curve is numerical calculations, red – experiment. The inset shows an SEM image of the sample. (b) Multipole decomposition. The inset shows the geometry of the sample and the experiment. (c) Angle-of-incidence-resolved numerical transmittance spectra of the sample. The dashed lines are angles chosen for nonlinear experiments.

Here, ω ₀ is the central frequency of the resonance, γ is the damping factor, and a ₁, a ₂, and b are real constants. The spectral positions of both resonances agree well for experimental and numerical data. The difference in depth of the dips is explained by deviations of the disk diameters in the array during the fabrication process averaging this parameter from the exact calculated one (evaluation gives ±10 nm) and finite convergence angle of incoming radiation in the optical experiment averaging the spectral width of the resonance (evaluation gives ±3°). The latter one limits the resolution of the spectra measurements. The numerical calculation also shows that the cooling process does not affect the transmittance spectrum significantly (see the Supporting Materials S3.3).

A comparison of field distribution for two polarizations (S and P) in the case of oblique incident radiation is carried out. The results are presented in the Supporting Materials (S3.4). In this situation, we are interested not only in large values of local fields in the structure but also in overlapping of these fields with nonlinear material. All radiation can be concentrated in the resonator and as a result make a small contribution to the generation of harmonics in the film. Thus, the localization of the field in the monolayer area is of prior importance when choosing the polarization of the incident wave. The strong field localization at the top of the cylinder is observed for P-polarized incoming light. In the case of S-polarized light, the field concentrates between the neighboring disks instead of their top. In addition, local field distributions for P-polarized light, obtained for SHG fields at λ/2, when excited at the fundamental wavelength λ, also exhibit local field concentration in the area of the flake (S3.7). All the above explains the necessity to use P-polarized light.

Figure 2(c) shows transmittance spectra for various angles of incidence of P-polarized incoming light. Variation of the angle of incidence from the normal case leads to shifts of the resonances. We are interested in the one that is marked on the graph as ‘(1).’ It moves toward longer wavelengths. Analyzing the behavior of diffraction maxima on the metasurface, we conclude that the described resonances are hybrid modes of the Mie resonance and the Rayleigh anomaly. The details of the analysis can be found in the Supporting Materials (S3.5). The shift of the resonance toward longer wavelengths allows the metasurface resonance to be spectrally overlapped with the resonances of the TMDC monolayer by tilting the sample. The MoSe₂ exciton resonances are observed in vicinity of 800 nm [23]. However, the position of photoluminescence peak strongly depends on the temperature [40] and strain [44]. It is also sensitive to electrostatic potential. When transferring the film on top of different materials, strain value may be the same, but local electrostatic potential may behave differently. That is why, the constituent materials of the structure also play an important role in the position of the exciton resonance. TiO₂ is not exactly a standard material for exfoliation. The results obtained for the monolayer exfoliated on TiO₂ metasurface may differ from previously reported data for Si or SiO₂ substrates. As for the results obtained in this article, three cases will be considered in the nonlinear experiments: 10° when resonances are not overlapped; 16° – overlapping the metasurface resonance with bright exciton of TMDC; 28° – overlapping of the metasurface resonance with the localized exciton of the MoSe₂. These angles are marked in Figure 2(c) by the dash lines.

2.2 Nonlinear spectroscopy

The monolayer of MoSe₂ is used as a nonlinear material, which has a high value of nonlinear susceptibility and an excitonic state around the wavelength of 800 nm. The flake is deterministically transferred onto the TiO₂ metasurface using an aligned transfer technique (described in the Supporting Materials (S1)). Briefly, monocrystalline flakes are mechanically exfoliated onto PDMS film, and subsequently, monolayer flakes are identified using an optical microscope. The flakes are then picked up by a polymer stamp and positioned onto the nanostructure using dual 4-axis stages integrated with an optical microscope. This technique ensures micrometer-level accuracy in the pick-and-place process.

Figure 3 shows both experimental and numerical results on second harmonic generation (SHG) spectroscopy. The nonlinear spectra are calculated only for the room temperature case by the finite element method in COMSOL Multiphysics software. The details of nonlinear calculations can be found in the Supporting Materials (S3.4). The measurements are performed at both room temperature (red dots) and 10 K (blue dots). All nonlinear spectra are normalized to the maximum SHG value observed for the case of overlapped geometric and excitonic resonances at 10 K. This value later will be denoted as I 2 ω max . Such overlap occurs at the angle of incidence equal to 16° and at the wavelength of 815 nm (see Figure 3(c)). The details on the experimental setup can be found in the Supporting Materials (S2.2). Briefly, the source is a Ti:Sapp femtosecond oscillator with a repetition rate of 80 MHz, pulse duration of 150 fs tuned in the wavelength range of 680–1,080 nm. The mean power at the sample remains fixed at 100 mW for any fundamental wavelength. This limits the scanning range to wavelengths from 750 to 1,000 nm. The spot size at the sample plane is 200 μm, which means the fluence is about 4 μJ/cm² and the peak intensity is about 0.03 GW/cm². The detector is an EMCCD (electron-multiplying charge-coupled device) camera. The panels 3(a–d) represent measurement results, while the panels 3(e–h) depict numerical modeling. The black curves in Figure 3 are the transmittance spectra. The confirmation of quadratic dependence of SHG signal on the pump power is presented in the Supporting Materials (S2.3).

Figure 3:

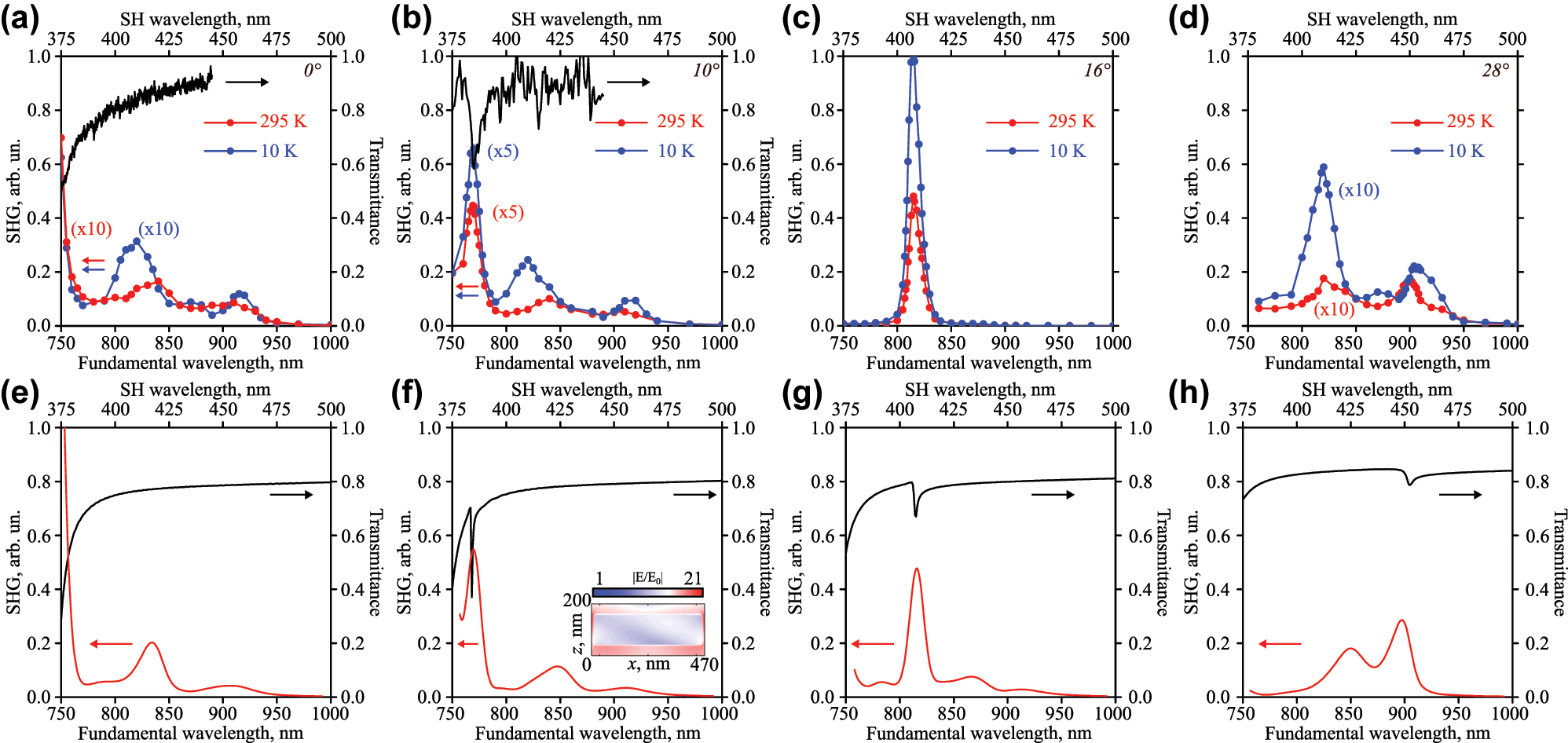
Optical second harmonic spectra for room temperature (red curves) and 10 K (blue curves), and transmittance spectra (black curves) for numerous angles of incidence: (a, e) 0°, (b, f) 10°, (c, g) 16°, (d, h) 28°. (a–d) Experiment, (e–h) numerical results. The inset on panel (f) shows normalized electric field distribution at the wavelength of the resonance of 770 nm in the plane of incidence XOZ in log scale.

The geometric resonances are almost absent for normal incidence in the studied spectral region as discussed above in the linear spectroscopy section (see Figures 2 and 3(a, e)). One of the resonances is centered around 745 nm and its edge appears in Figure 3(a). The nonlinear spectrum at room temperature (see Figure 3(a), red dots) demonstrates enhancement in the vicinity of these wavelengths. Three other emerged resonant features are now associated with the band structure of the nonlinear 2D material. The nature of the left one (λ = 840 nm (1.47 eV)) is the bright exciton in MoSe₂ [23]. The value of the SHG signal is only 1.6 % of I 2 ω max . During the cooling process, its position shifts to the lower wavelengths (higher energies) up to 820 nm (1.51 eV) at 10 K. This effect is accompanied by resonance shrinkage and quality factor growth leading to a 2-fold enhancement of the second harmonic signal up to 3 % of the I 2 ω max . This thermal behavior is typical and well-known from the literature [40]. Another interesting discovery resolved by second harmonic spectroscopy is the appearance of the trionic state of MoSe₂ tightly connected to the cooling process and bright exciton shrinkage [45]. The corresponding peak is observed at the wavelength of 880 nm (1.41 eV), see Figure 3(a) blue dots. It is not very pronounced and has an amplitude of only 1 % of I 2 ω max . The small binding energy of trions does not allow them to exist at room temperatures, so the peak is absent for room-temperature measurements. The final peak at the wavelength of 920 nm is associated with the localized exciton in MoSe₂. It lies below the bright exciton and the trion (i.e., at higher wavelengths). The redshift of the bound exciton peak relative to the trion has already been demonstrated in SHG experiments [23]. The localized exciton peak is also visible at both low (λ = 920 nm) and room (λ = 905 nm) temperatures. This fact is consistent with the theory predicting two-dimensional TMDCs to be able to host a variety of bound exciton complexes, which are stable at room temperature [46], [47]. Its amplitude is much lower than that of the bright exciton [48]. It reaches about 1 % of the I 2 ω max for both thermal cases. As for the origin of this state, traps can be related to defect potentials, which are often attributed to bound excitons in semiconductors [49], or can be related to the moiré potential caused by the presence of several monolayers in certain parts of the sample [50], [51]. In addition, the formation of localized states is observed even in monolayers [52]. This can be explained by the fact that the monolayer is not smooth enough, by its bending, by the presence of impurities, and the influence of the interface near the edge of the metasurface, where flakes bend toward the substrate. Previous studies of localized states in MoSe₂ have revealed comb-like lines in photoluminescence spectra at energies below the trion state (with a redshift in wavelength) in certain areas of the flake. However, the exact prediction of the energy level diagram is still under discussion [53]. Similar effects are observed in WSe₂ [54]. The exact nature of this resonance requires precise theoretical research, which is beyond the scope of this article as it focuses on nonlinear measurements. Moreover, following the previously obtained results, the position of the peak associated with the localized exciton slightly changes with the temperature, which is also consistent with literature [40].

The calculated nonlinear spectrum (see Figure 3(e)) at the room temperature case reproduces all main peculiarities: the enhancement of the signal for the geometric resonance near 750 nm, the signal for excitonic (λ = 840 nm) and localized (λ = 905 nm) resonances (compare red curves in the panels (a) and (e) in the Figure 3). The spectral positions are identical with the experiment, and the absolute values differ due to numerous factors that cannot be fully taken into account.

The minimum angle of incidence required to observe the geometric resonance for the studied wavelength range is 10° (see Figure 3(b, f)). The experimental (Figure 3(b)) and numerical (Figure 3(f)) transmittance spectra show the resonance near the wavelength of 770 nm. This high-Q feature arises from nearly equal contributions of the MD and EQ, with minor contributions from the ED and MQ multipoles according to the decomposition analysis (see the Supporting Materials (S3.2)). The SHG spectra demonstrate resonant amplification at both room and cryogenic temperatures. The spectral position does not change during cooling, which is expected, since this is dielectric-metasurface-induced resonance and there is no temperature dependence of TiO₂ as mentioned above (Section 2.1 and Supporting Materials (S3.3)). The signal of the second harmonic at room temperature is 9 % of I 2 ω max while at low temperature it increases up to 13 %, which is 1.5 times higher than that for the room temperature value. The SHG amplitudes for the room measurements remain unchanged and equal to 2 % for the bright exciton and 1 % for the localized exciton. The SHG values for low-temperature measurements are 5 % for the exciton and 2 % for the localized exciton. The numerical nonlinear spectrum (see Figure 3(f)) again reproduces all spectral features and their positions are in good agreement (compare red curves in the panels (b) and (f) in the Figure 3). The inset in the Figure 3(f) shows the local electric field distribution. The colormap represents the magnitude of the electric field sliced in the plane of incidence through the center of the disk for the unit cell of the metasurface at the wavelength of 770 nm. The hot spots are localized on the top edge of the disk and provide high field confinement inside the nonlinear 2D material, explaining the necessity to illuminate the sample with P-polarized light. These local fields yield significantly higher values of the nonlinear signal for the geometric resonance than the material resonances of MoSe₂ give.

If the angle of incidence is set to 16°, the geometric resonance is spectrally overlapped with the material one of MoSe₂ near the wavelength of 815 nm (see Figure 3(c, g)). The nonlinear signal increases by two orders of magnitude compared to the previously discussed results. The low-temperature signal of SHG is 2 times greater than that at room temperature. The nonlinear signal reaches the highest value of I 2 ω max because of effective local field distribution, pumping the bright exciton of the TMDC film. The numerical transmittance spectra show a narrow and shallow dip (see Figure 3(g)). The experimental setup does not allow to resolve such peculiarities because of limited capabilities due to the reasons mentioned in the Section 2.1.

The next angle of incidence of 28° is chosen to overlap the geometric resonance with the localized excitonic state of MoSe₂ near the wavelength of 900 nm (see Figure 3(d, h)). Nonlinear measurements (Figure 3(d)) show signal increase for the wavelengths of the bright (λ = 840 nm) and the localized (λ = 905 nm) excitons at room temperature. They reach 1.7 % I 2 ω max for both cases, while these values differ (1.7 %@840 nm vs. 1 %@905 nm of I 2 ω max ) for normal incidence when geometric and material resonances are not overlapped. It means that local electric field localization enhances nonlinear polarization. The numerical results (Figure 3(h), red curve) reproduce similar behavior. The black curve in Figure 3(h) demonstrates the transmittance spectrum with the weak resonance near the wavelength of 905 nm, which again cannot be resolved experimentally by the setup. The second harmonic signal increases by 3.5 times for the wavelength of the bright exciton (Figure 3(d), blue curve) and by 1.3 times at the wavelength of the localized exciton compared to the room-temperature case if the temperature decreases to 10 K. These values are 6 % of I 2 ω max for the left spectral peculiarity and 2 % of I 2 ω max for the right one. The enhancement for the localized exciton (λ = 920 nm) is less pronounced due to the temperature-dependent shift of the material resonance and misalignment with the position of the geometric resonance in the low-temperature case.