Entangled photon-pair generation in nonlinear thin-films

1 Introduction

The optical process of spontaneous parametric down-conversion (SPDC) in χ ⁽²⁾-materials [1], in which a pump (p) photon of wavelength λ _p can split into a pair of entangled signal (s) and idler (i) photons of lower energy, is an instrumental tool in optical quantum technologies. Predominant applications are quantum communication [2], quantum cryptography [3], [4], quantum imaging [5], [6] and sensing [7], and testing fundamental quantum effects [8]. The broad applicability of SPDC is due to its efficiency and versatility in generating pairs of entangled photons with high control over various optical degrees of freedom.

Nonlinear systems involving SPDC constitute to date the dominant approach to generate entangled photon-pair states and promise tangible real-world applications in the near future [9]. Entangled photon pairs have been generated in single nonlinear bulk crystals [10], crossed bulk crystals [11], or bulk crystals in a Sagnac loop [12]. More recently, several experiments of photon-pair generation in much smaller nonlinear systems such as single GaAs nanowires [13], dielectric nanoantennas [14], and metasurfaces with subwavelength thicknesses [15], [16], [17], [18] have been demonstrated. In particular, there has been a recent growing interest in pair generation in sub-wavelength-thin nonlinear crystals like lithium niobate and “zinc-blende” structures like gallium arsenide (GaAs) or gallium phosphide (GaP) [19], [20], [21], as well as in van der Waals [22] or transition metal dichalcogenide (TMD) crystals [23], [24]. Such nonlinear thin sources are interesting because they are not restricted by the longitudinal phase-matching condition; hence they are capable of generating photon pairs in a very wide spectral and angular range. This also motivates their use in quantum imaging applications, for pushing the resolution of such schemes to the limit [25], [26].

However, to the best of our knowledge, there has not yet been a comprehensive theoretical analysis of photon-pair generation in a thin and unstructured nonlinear slab, where the dynamics of entanglement generation is investigated and the conditions for generating a maximally entangled photon-pair state are identified. Such an analysis, which would be facilitated by a general theoretical framework, is an essential missing link for further development of extremely thin and broadband sources of entangled photon pairs. This theoretical framework should incorporate the Fabry–Pérot-type interferences due to multiple reflections of signal, idler and also pump photons within the nonlinear slab. Moreover, such a theory should be able to treat absorptive nonlinear layers, particularly in light of the more prevalent use of TMD systems which provide an enormous enhancement of the nonlinear coefficients near their excitonic lines that at the same time can also cause enhanced material absorption in the system [27]. Importantly, the formalism should also be able to describe the directional, spectral, and polarization properties of the generated photon pairs, including emission angles up to 90°.

In this work, we develop such a theoretical framework for describing SPDC in nonlinear thin-films, and use it to study the far-field properties of the generated pairs. Our formalism is based on the Green’s function (GF) quantization method [28]. In this method, SPDC is described using a quantization scheme of the electric field operator that utilizes the classical GF of the system and local bosonic excitations in the medium-assisted field [29], [30]. The GF, as a classical quantity, contains all the linear properties of the system. In our work, we construct this classical GF using a developed theory for the GF of multilayered optical systems [31]. Due to the generality of the GF method, we develop a comprehensive, fully vectorial framework capable of treating any thickness of the slab, ultra-thin or thick. It can further be used to incorporate lossy layers, near- and far-field radiation in the non-paraxial regime, as well as the generation of guided photonic modes inside the source. In the current work, we focus on far-field properties of the photons that are generated outside the slab. Furthermore, our model allows keeping track of any polarization and directionality effects in the pair-generation process, which we will exploit in this paper to reconstruct the polarization states of entangled photon pairs.

In this work we are treating SPDC in the low-gain regime of photon-pair generation. However, recently, the application of the GF quantization method has also been extended to treat the high-gain regime of the interaction [32], where the same classical GF can be used for description of high-gain effects. This further emphasizes the versatility of the GF approach in description of parametric down-conversion under different conditions. We also note that there are other methods for description of SPDC [1], [33], [34], [35], [36], [37], some of which were also developed for description of low-gain SPDC in multilayer systems [35], [36], [37]. Nonetheless, the GF method provides a general yet unified formulation for treatment of such systems, which we employ to perform a detailed investigation of SPDC and identify entanglement properties in thin-films. Specially, the GF method can naturally include the effect of internal losses, and also it provides a way towards description of high-gain effects [32], which allows for study of thin-film systems in more advanced scenarios beyond this work.

In this investigation, we will utilize numerical calculations to explore the far-field characteristics of photon-pair generation via SPDC within a GaAs thin film. This is part of a larger category of nonlinear materials characterized by a zinc-blende structure, a type of nonlinear material with a cubic lattice and point group 4 ̄ 3 m. This crystal structure is shared by various other prominent nonlinear materials, including III–V semiconductors such as gallium phosphide (GaP) and indium phosphide (InP), as well as II–VI semiconductors like zinc telluride (ZnTe), zinc selenide (ZnSe), and zinc sulfide (ZnS). Due to the cross-polarized nature of their nonlinear tensor, these materials are naturally predisposed for generating polarization-entangled Bell states [21], [38]. This holds significant promise for advancing various quantum information processing applications, ranging from quantum cryptography to quantum teleportation. By investigating the unique properties of photon-pair generation in GaAs and related nonlinear materials, we aim to contribute to the broader understanding and potential utilization of entangled photon pairs in cutting-edge quantum technologies.

The manuscript is organized as follows. In Section 2 we introduce a general framework to calculate the far-field joint detection probability of photon pairs generated in a nonlinear slab in a layered geometry using the GF formalism, and compute the far-field joint probability distribution. In Section 3, we explicitly write the general expression of the GF’s of a dielectric slab that contains multiple reflections of the signal and idler fields. In Section 4, the classical pump beam is treated. In Section 5, we numerically compute the far-field radiation for a nonlinear source made of GaAs deposited on a silicon dioxide (SiO₂) substrate, and study its far-field properties. In Section 6, we use a quantum tomography method to extract the polarization state of the generated photon pairs and show that one can generate maximally polarization-entangled photon pairs in such a simple system. Lastly, we summarize and conclude in Section 7.

2 Far-field joint spatial probability in Fourier domain

Consider a general nonlinear thin-film photon-pair source, as depicted in Figure 1. It comprises three layers with relative permittivities ϵ ₁, ϵ ₂, and ϵ ₃, where the nonlinear material (of thickness a) constitutes medium 2. Typically, medium 3 is a linear substrate and medium 1 is a linear cladding covering the nonlinear material (often air). Here, the system is illuminated by a pump beam from medium 3 propagating along the positive z-direction, and the down-converted photon pairs can be detected in media 1 or 3. It is important to note that the generated photon-pair amplitudes undergo multiple reflections inside the nonlinear slab. Although this paper does not delve into the dynamics of photon pairs that could be generated in the guided slab modes of medium 2, our formalism can handle such scenarios too. This is left to future works. In this work, we focus on studying the dynamics of photons generated into the free propagating modes of medium 1.

Figure 1:

Multilayered geometry where medium 2 is a nonlinear medium, in which SPDC happens due to a pump field impinging from medium 3. The joint signal and idler field can radiate to outside the slab to medium 1 and medium 3, after experiencing multiple reflections inside medium 2.

Using the GF method, we analyze SPDC in a nonlinear structure excited by a single-frequency pump beam E p ( r , t ) = E p ( r ) e x p − i ω p t + c.c. . The far-field coincidence detection rate for a pair of signal and idler photons of different frequencies as a function of the spatial coordinates follows [28], [38]:

The detection rate, R ≡ d 4 N d t d Ω s d Ω i d ω s , is the number of photon pairs given per units of solid angles dΩ _i (for the idler photon) and dΩ _s (for the signal photon), and per unit of signal-photon angular frequency ω _s . The idler angular frequency is fixed by conservation of energy to ω _i = ω _p − ω _s . The detection rate is also a function of the idler and signal photons’ detection polarization, which are along the unitary e _s and e _i directions. The α, β, γ, σ _s and σ _i indices run over the x, y, and z cartesian coordinates. G _ij (r, r′, ω) are the tensor-components of the electric GF, χ α β γ ( 2 ) ( r ) are the components of the second-order nonlinear tensor and the integral runs over the volume of nonlinearity V characterized by the position vector r. r _i and r _s are the positions for the detection of the idler and signal photons in the far-field, respectively, with n _i and n _s being the refractive indices of the detection medium at the idler and signal frequencies.

In our system, one can take advantage of the homogeneity in the x and y direction to work in the spatial frequencies domain. This approach offers an intuitive understanding of the far-field detection in terms of the angular modes of the signal and idler photons, simplifying numerical calculations. To do this, the GF, which is a solution of [ ∇ × ∇ × − ω 2 c 2 ϵ ( r , ω ) ] G ↔ ( r , r ′ , ω ) = I ↔ δ ( r − r ′ ) , with ϵ(r, ω) being the relative permittivity of the system, can be represented as an inverse Fourier transform of the form [39],

where q = k x x ̂ + k y y ̂ and r ⊥ = x x ̂ + y y ̂ are the two-dimensional real wave-vector and spatial vector in the x–y plane, respectively. We define ∫ − ∞ ∞ d q ≡ ∫ − ∞ ∞ d k x ∫ − ∞ ∞ d k y . Similarly, for a classical pump field treated in the undepleted pump approximation we have,

Then, by introducing Eqs. (2) and (3) into (1), we can separate the spatial integral into dr → dzdr _⊥. After rearranging terms, we can solve for dr _⊥ the integral

which results into the joint detection rate

with

Here, Eq. (6) is understood as a joint angular probability (JAP) amplitude. Equation (5) represents the detection rate for signal and idler photon-pairs generated through SPDC in a transversally homogeneous nonlinear source, accounting for spatial coordinates, frequencies, and detection polarization. Notably, R in the form of (5) resembles a Fourier transform integral, enabling Fourier analysis for interpreting the probability in the more intuitive angular domain.

However, since our focus is mainly on the far-field properties of the generated photon pairs, we will apply a far-field approximation to the probability rate similar to the classical Fraunhofer approximation for field diffraction [40]. We aim to detect both photon pairs in the far field in medium 1 with refractive index n ₁. Here, k 1 = ω c n 1 is the wave number of plane waves in medium 1, and k z , 1 = k 1 2 − k x 2 − k y 2 denotes the z-component of its wave vector k 1 = q + k z , 1 z ̂ . Note that k _x and k _y are the transversal components of the wave-vector for a photon generated in medium 2, which are also conserved in medium 1 due to the system’s transversal invariant nature.

The far-field approximation requires joint detection of photons at sufficiently long distances from the source, i.e. r _s ≫ r and r _i ≫ r. Additionally, we assume a finite-sized pump beam, implying that detection occurs at a much greater distance compared to the extent of the pump illumination across the nonlinear slab (see Appendix A for details).

Under this approximation the joint detection rate in Eq. (5) is simplified to (see Appendix A)

Here, q s = k x , s x ̂ + k y , s y ̂ , where k _x,s = k _1s  sinθ _s  cosφ _s and k _y,s = k _1s  sinθ _s  sinφ _s , refer to the transverse k-vector of the signal photon detected in the far-field at propagation angles {θ _s , φ _s }, and similarly for the idler photon. Thus, Eq. (7) describes the joint detection rate in the far-field as a function of the detection angles {θ _s , θ _i , φ _s , φ _i } in spherical coordinates. Note that k _z,1s and k _z,1i in Eq. (7) correspond to the detection medium 1. If the detection medium changes, these factors should be adjusted accordingly (see Appendix A). Also note that, R ̃ in Eq. (7) is z-independent, where R ̃ ( q s , q i , z s , z i , ω s , ω p − ω s ) = R ̃ ( q s , q i , ω s , ω p − ω s ) e i k z , 1 s z s e i k z , 1 i z i (see Appendix A).

In the far-field, the joint detection rate is proportional to the squared absolute value of R ̃ multiplied by the signal and idler z-components of the wave vector, k _z,1s and k _z,1i . In the paraxial regime (q ≪ k ₁ with q = q ), k _z,1s and k _z,1i tend to k _1s and k _1i , resulting in the far-field joint detection rate being directly proportional to the squared absolute value of R ̃ . This calculation extends the concept of classical Fraunhofer approximation [40] to two-photon joint-detection. As our model is capable of handling emission angles up to 90°, it highlights the importance of the factors k _z,1s and k _z,1i in the nonparaxial regime. The importance of the longitudinal wave-vectors in nonparaxial description of quantum-light propagation was also shown in studying the fundamental resolution limit of quantum imaging schemes [25]. Equations (5)–(7) constitute the main results of this section, to be numerically solved in Section 5.

3 Green’s function of a dielectric slab

The optical properties of the system at the signal and idler wavelengths are fully contained in their respective Green’s functions (GFs). To implement Eq. (7), we employ a GF suitable for the multilayered scheme depicted in Figure (1). In this scenario, the GFs for signal and idler, G ↔ ( r , r s ) and G ↔ ( r , r i ) connect a point r within the χ ⁽²⁾-nonlinearity region (medium 2, see Eq. (1)) to the detection positions r _s and r _i in medium 1.

If a plane wave of the form E(r) = Ee^ik⋅r , with k ⋅ k = k = ω c n satisfies Maxwell’s equation in a homogeneous medium of refractive index n, two possible wave vectors k for a given q are obtained, representing upward and downward propagation. These wave vectors take the form k + = q + k z z ̂ (upward) and k − = q − k z z ̂ (downward). When n is real and q > nω/c, k _z becomes imaginary, resulting in an evanescent wave. Additionally, at a given q, a solution can be either s-polarized (transverse electric) or p-polarized (transverse magnetic), defined by unit polarization vectors s ̂ and p ̂ as

These vectors are normalized according to s ̂ ⋅ s ̂ = 1 and p ̂ ± ⋅ p ̂ ± = 1 . Note that s ̂ is real, rests on the x–y plane, and is medium independent, while p ̂ can be complex and is medium dependent. Also, s ̂ does not depend on the direction of k, while p ̂ changes for upward- or downward-generated fields.

Using the s- and p-polarized fields, the GF in Fourier domain for such a system, where the field is generated in medium 2 and propagates outside the slab to medium 1, can be constructed as [31], [39]

where T ₂₁(q, z′, ω) is the generalized transmission coefficient of the s- and p-polarized fields generated from the source plane at z′ ∈ {−a, 0} and transmitted to medium 1 (see Appendix B for analytical expression). The unit vector s ̂ is parallel to the interface and p ̂ is perpendicular to the wave vector k and s ̂ . The subscript numbers in k _z indicate the corresponding medium.

The GF in Eq. (10) describes from right to left (apart from the phase factor e i k z , 1 z ) the contributions of a downward p-polarized wave generated in medium 2 that transform into an upward p-polarized wave in medium 1, an upward p-polarized wave in medium 2 that transform into an upward p-polarized wave in medium 1 and both the contribution of the upward/downward s-polarized waves generated in medium 2 that transfers to medium 1. All of them after multiple reflections and transmission, whose information is contained in the coefficients T ₂₁.

4 Pump field with multiple reflections

The pump field undergoes diffraction and multiple reflections within the slab. Illustrated in Figure 1, the pump originating from medium 3 propagates to z = −a, enters the slab, and reflects multiple times. Consequently, the amplitude of the pump field within medium 2 varies with z and is influenced by the slab’s thickness a.

In many theoretical calculations, it is common to assume a pump beam polarization parallel to the interface (e.g. x-polarized) for SPDC modeling. However, true transverse electromagnetic waves are idealizations and physical beams of light also contain a longitudinal polarization component. This longitudinal component may influence the photon-pair generation process if the material properties permit such excitation. For our calculations, we consider a pump field polarized in the x-direction right before the interface (z = −a) with a longitudinal component in the z-direction, given by

where k _z,3p represents the z-component of the pump wave vector in medium 3, and E _p,z is calculated from E _p,x using the transversality constraint k _p ⋅ E _p = 0 (see Appendix C.2).

Taking E p ( q , z = − a ) = U p ( q , z = − a ) e ̂ ( q ) one finds e ̂ ( q ) = k z , 3 p / k 3 p 2 − k y 2 x ̂ − k x / k 3 p 2 − k y 2 z ̂ , which allows us to express the pump field in the form

where we take e ̂ = x ̂ for k _x = k _z = 0. U _p (q, z = −a) is the angular spectrum of the pump field at the interface. We assume it follows a Gaussian distribution,

where w is the width of the Gaussian angular spectrum. The condition q 2 ≤ k 3 p 2 ensures that Eq. (3) comprises only propagating waves in medium 3. Moreover, the spectrum width influences the contribution of the z-component of the pump beam: larger w results in greater E _p,z . This is especially relevant in tightly focused pump beam scenarios (refer to Appendix C.1 for details).

At the interface, the pump beam can also be described using s- and p-polarized fields. After transmission into the slab, the z-dependent pump beam can be calculated as (see Appendix C.2 for details)

where Q ^(s)(q, z) is the transmission coefficient from medium 3 to medium 2, while E p ( s ) ( q , z = − a ) and E p ( p ) ( q , z = − a ) are s- and p-components of the pump before the slab. Unit vectors s ̂ , p ̂ 2 + , and p ̂ 2 − are defined in Eqs. (8) and (9) for medium 2.

5 Far-field joint-radiation properties

5.1 Degenerate photon-pair detection

Now that we have the model, let us consider a zinc-blende GaAs crystal (medium 2) with thickness a and orientation 100 . The crystal axes are aligned with the laboratory coordinates {x, y, z}. The GaAs is on a SiO₂ substrate (medium 3, assumed semi-infinite), with air as medium 1 for detection. The pump from medium 3 is described by Eq. (12) with λ _p = 500 nm and Gaussian angular spectrum (Eq. (13)) with w = 6.6 × 10⁵ m⁻¹ (corresponding to a beam waist of W = 3 μm). At degenerate wavelengths (λ _s = λ _i = 1 μm), we have ϵ _2s = ϵ _2i = 12.06 in GaAs, while the pump relative permittivity at λ _p = 500 nm in GaAs is ϵ _2p = 17.63 + 3.83i [41]. In SiO₂ substrate, ϵ _3p = 2.14 and ϵ _2s = ϵ _2i = 2.10 [42], while in the detection medium, ϵ _1p = ϵ _1s = ϵ _1i = 1. The non-vanishing elements of the second-order susceptibility tensor of GaAs are χ yzx ( 2 ) = χ zyx ( 2 ) = χ xzy ( 2 ) = χ zxy ( 2 ) = χ xyz ( 2 ) = χ yxz ( 2 ) = χ 0 ( 2 ) .

We start by computing the coincidence detection rate R ( far ) in Eq. (7) for unpolarized joint-detection. This involves summing over the three polarization directions of each signal and idler detector ( e = x ̂ , y ̂ , z ̂ ), resulting in nine combinations. Due to the relatively narrow angular range of our pump beam, opposite transverse wave vectors (q _s ∼ −q _i ) significantly contribute to the generation, as consequence of the transverse phase-matching condition (q _p = q _s + q _i ). For degenerate photon-pairs, this motivates investigating R ( far ) in terms of propagation angles {θ _s , φ _s } for the signal photon, where the idler is detected symmetrically at {θ _i = θ _s , φ _i = π + φ _s }. This configuration is shown in Figure 2(a) and is called φ-symmetric throughout the manuscript. The φ-symmetric setup has already been proven crucial for entangled state generation in nanoresonators [38] and will also show to be essential for thin films in this work.

Figure 2:

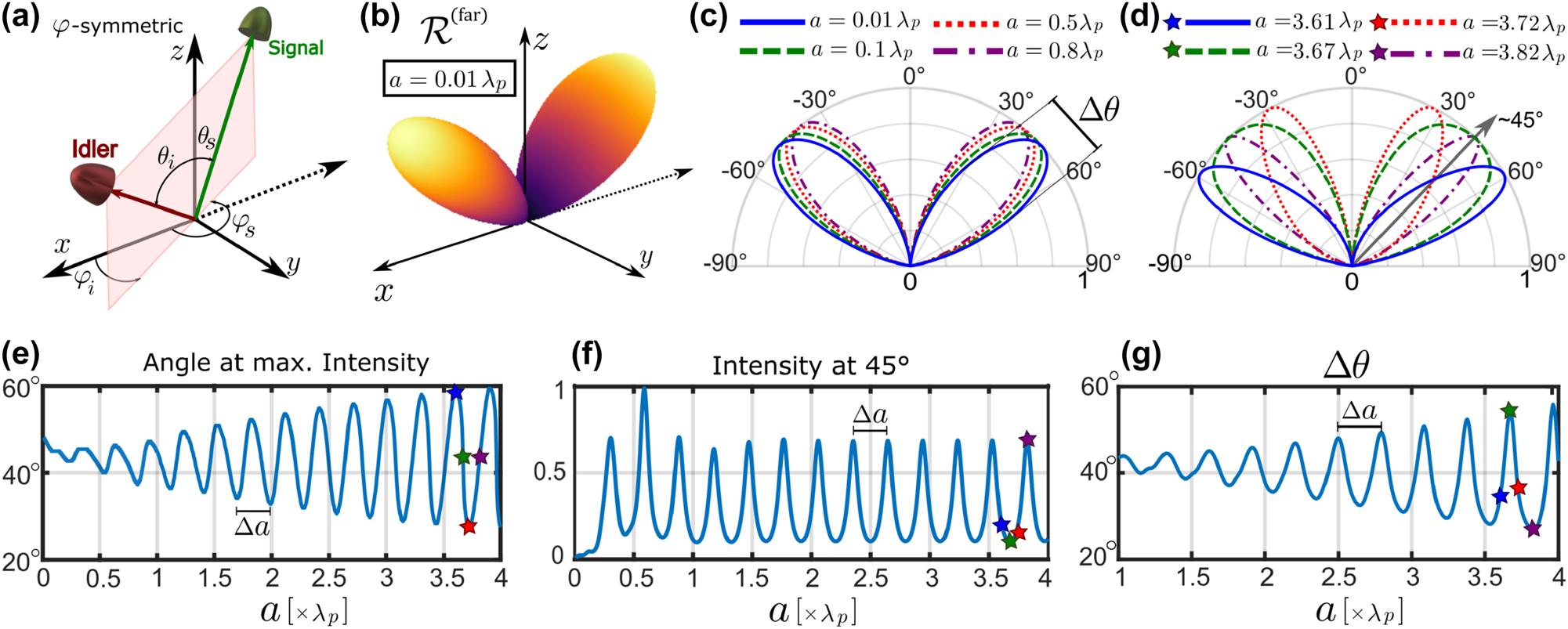
Far-field joint detection probability rate in the (a) φ-symmetric configuration, which is considered for all the results shown in this figure. (b) Probability rate for an ultra-thin film of GaAs of thickness a = 0.01λ _p in the φ-symmetric configuration. (c, d) Slice cut through far-field radiation pattern in the xz plane for different thicknesses (below and above a = λ _p ) of the slab with normalized intensities. (e) Angle of maximum joint emission as a function of the thickness of the slab. The four values plotted in (d) are marked by the stars, corresponding to the peak (blue star at ∼ 58.5 °), two in the middle (green and purple stars at ∼ 45 °) and the valley (red star at ∼ 27.5 °). (f) Intensity of joint detection at θ _s = 45° which exhibit FP oscillations. (g) Angle uncertainty Δθ of joint emission as a function of the thickness of the slab. The values in (d) are also in (f) and (g). The period of oscillation Δa ∼ 0.29λ _p .

The coincidence rate in the φ-symmetric configuration is shown in Figure 2(b) for an ultra-thin source of thickness a = 0.01λ _p , emphasizing again that both photons are detected in medium 1. Here, the χ yzx ( 2 ) and χ zyx ( 2 ) dominate the pair generation process due to weak y- and z-polarized and dominant x-polarized components of the pump field inside the slab. Note that y-components of the pump field are created inside the slab due to refraction, despite being zero outside (see Eq. (14)). Hence, all components of the GaAs nonlinear tensor participate in the generation process. Yet, the dominance of χ yzx ( 2 ) and χ zyx ( 2 ) components implies that signal and idler fields within the slab are mainly generated by y- and z-polarized point-like nonlinear sources, resulting in no radiation in the y–z plane, as observed in Figure 2(b). Additionally, emission at large angles is significantly reduced, despite the GaAs nonlinear tensor favoring stronger emission near θ _s = 90° for such an ultra-thin crystal. This reduction is mainly due to the strong decrease in transmittance from inside to outside of the slab at larger emission angles, ultimately reaching zero for outside emission angles of θ _s = 90° due to total internal reflection experienced by photons inside the slab.

In Figure 2(c), we display cuts along the xz-plane for various subwavelength thicknesses of the slab, a = 0.01λ _p , a = 0.1λ _p , a = 0.5λ _p , and a = 0.8λ _p . Figure 2(d) illustrates xz-plane cuts for larger slab thicknesses, a = 3.61λ _p , a = 3.67λ _p , a = 3.72λ _p , and a = 3.82λ _p , which are special points for understanding the Fabry–Pérot dynamics, marked in Figure 2(e)–(g). All graphs are normalized to one for better observation of angular dependencies. Figure 2(c) reveals minimal angle variations in joint emission radiation for different subwavelength thicknesses, primarily influenced by the nonlinear tensor structure and angle-dependent transmission at interfaces. In contrast, Figure 2(d) demonstrates more significant angular changes for larger slab thicknesses. This is mainly due to the Fabry–Pérot effect, which enhances or reduces radiation in some angles due to constructive or destructive interferences, respectively. Notably, the angular pattern is highly sensitive to slab thicknesses in this regime. To better understand the dynamics caused by Fabry–Pérot effect, we show in Figure 2(e) the angle of maximum intensity, (f) the intensity at θ _s = 45°, and (g) and the angular width of the emission pattern Δθ, respectively, all as a function of the slab thickness. In Figure 2(e), the maximum emission angle exhibits a growing oscillatory pattern with increasing the thickness. The oscillatory behavior occurs around a mean angle of ∼ 45 °. At the detection angle of θ _s = 45°, we plot in Figure 2(f), the detection intensity (normalized to maximum) as a function of the slab thickness. We clearly observe an etalon-like effect caused by the FP interferences, where peaks of intensity repeat periodically with increasing slab thicknesses, with a period of Δa ∼ 0.29λ _p . This period of oscillation is the same on all three plots of Figure 2(e)–(g). The angular uncertainty of emitted photons exhibits a similar thickness-dependent variation. We define the angle uncertainty Δθ as the difference between the angles at 50 % of the maximum intensity (full width at half maximum). In Figure 2(g), we again observe increasing oscillations for thicknesses above a = λ _p , while it remains relatively constant for subwavelength thicknesses, as also seen in Figure 2(c).

It can be verified, that the peaks and valleys in Figure 2(f), correspond to constructive and destructive interference conditions, satisfying the relations Δ = mλ _s and Δ = ( m + 1 2 ) λ s , respectively, where m is a positive integer. Δ = 2an _2s  cos(θ _2s ) is the optical path difference (OPD) between successive plane waves that are transmitted to medium 1 (being air) after a round trip in the slab [43]. θ _2s is the angle in medium 2 such that it yields θ _1s = 45° in medium 1 after refraction. The period of the resonance peaks is found by Δ a = λ s 2 n 2 s ⁡ cos ( θ 2 s ) , which results in Δa ≈ 0.29λ _p , which matches the numerical results. These points of constructive and destructive interferences for θ _1s = 45° also coincide with peaks and valleys of Δθ, see in Figure 2(g). We point out that the angles of constructive interference oscillate around the θ _1s = 45°, as the thickness is increased, which results in an oscillation of the angles of maximum intensity around θ _1s = 45° in Figure 2(e). This can also can be seen in Figure 2(d), where at thicknesses of a = 3.61λ _p or a = 3.72λ _p , the directionality plots are maximized at angles ∼ 58.5 ° or ∼ 27.5 °, respectively.

A crucial observation is that due to the inherent losses in GaAs at λ _p = 500 nm, there are constrictions on longitudinal phase-matching effect. Calculating the pump’s decay length inside the GaAs slab, denoted as α p = 1 / k 2 p ′ ′ , where k 2 p = k 2 p ′ + i k 2 p ′ ′ , yields α _p = 0.35λ _p . When compared with the coherence length of our system under normal incidence, L _c = π/Δk _‖, where Δ k ‖ = k 2 p ′ − k 2 s ⁡ cos θ 2 s − k 2 i ⁡ cos θ 2 i , we obtain L _c = 0.6λ _p for joint detection in medium 1 at θ _1s = θ _1i = 45°. Notably, the decay length is smaller than the coherence length (α _p < L _c ), which is important, as it limits the range of impact of longitudinal phase matching with increasing slab thicknesses. Consequently, the FP effect at the signal and idler wavelengths has a dominant effect in creating the oscillatory behavior observed in Figure 2(e)–(g), and not the longitudinal phase matching. Hence, the longitudinal phase matching, only affects the height of the first few peaks in Figure 2(f), while subsequent peak intensities stabilize.

5.2 Non-degenerate photon-pair detection

Now we consider a frequency non-degenerate scenario for photon-pair detection. Unlike the degenerate case, the φ-symmetric configuration is not expected to dominate in the non-degenerate case. For a normally incident plane-wave pump, with q _p = 0, the emitted pairs satisfy the transversal phase-matching condition of q _s = −q _i . This right away sets φ _i = φ _s + π for signal and idler photons in a pair. Then, taking θ as the emission angle with respect to the forward z-direction we get k x 2 + k y 2 = k 2 ⁡ sin 2 ⁡ θ for both signal and idler. Using the degeneracy factor r defined as r ≡ λ _s /λ _i , we get | sin θ s | = r n i / n s | sin θ i | as the relation between the angles of emission for signal and idler photons in a pair. In medium one, we have n _i = n _s = 1.

In Figure 3(a), we calculate the joint detection probability with a fixed signal detector at θ _s = 45°, φ _s = 180° for nondegeneracy factors r = 0.8, 1, 1.2, and 1.5 in the ultra-thin case (a = 0.01λ _p ). Here, smaller idler wavelengths (r > 1) tend to emit the idler closer to the optical axis, while larger idler wavelengths (r < 1) push the idler away from the optical axis. Maximum emission angles calculated using the relation between angles are θ _i (r = 0.8) = 62.11°, θ _i (r = 1) = 45°, θ _i (r = 1.2) = 36.1° and θ _i (r = 1.5) = 28.12°, matching Figure 3(a). For r = 1 the maximum coincidence rate lie along θ _s = θ _i , justifying the previously used φ-symmetric configuration. Additionally, in Figure 3(a), we observe that as the degeneracy factor r decreases, the uncertainty in idler angles increases, meaning weaker correlations in emitted photons.

Figure 3:

Coincidence detection rate in the non-degenerate case for (a) different degeneracy factors r for a fixed signal detector position at θ _s = 45°, φ _s = 180° and varying idler detector positions. The maximum angle of detection in the plot are θ _i (r = 0.8) ∼ 61.2°, θ _i (r = 1) ∼ 45°, θ _i (r = 1.2) ∼ 36.3° and θ _i (r = 1.5) ∼ 28.2°. (b) Joint detection probability as a function of θ _s and θ _i in the xz-plane (with fixed φ _s = 0 and φ _i = 180°) for r = 1.5. The thickness is a = 0.01λ _p in both graphs.

Due to transverse phase matching, most pairs are generated under the condition φ _s = φ _i + 180°, which suggests visualizing the joint-detection rate as a function of the angles {θ _s , θ _i }, in a particular plane defined by φ. In Figure 3(b) we plot R along the xz-plane, where φ _i = 0 and φ _s = 180°, as a function of θ _s and θ _i for r = 1.5 and a = 0.01λ _p . Here we can see that a better correlation in the non-degenerate case can be achieved by detecting at small angles, however this comes at expenses of the efficiency of the process. Additionally, emission at ∼ 45 °, dominant in the degenerate case, is no longer prevalent in the non-degenerate scenario, which is now shifted by transverse phase-matching. In the depicted scenario in Figure 3(b), these angles are θ _s = 55.35° and θ _i = 33.3°.

5.3 Absolute pair generation rates

A critical question revolves around the overall efficiency of the pair-generation process. The total number of pairs that can be collected by a lens of numerical aperture NA, is obtained by integrating the differential pair-rate R ≡ d 4 ⁡ N d t d Ω s d Ω i d ω s over the entire signal and idler solid angles that fall within the angle θ = arcsin(NA) where dΩ = sinθdθdφ, then summing over all possible detected polarization combinations, and finally integrating over the frequency range of the detected signal photons. To do this, we consider a 0.59λ _p ≈ 295 nm for the GaAs slab thickness, which corresponds to the maximum intensity peak in Figure 2(f). We assume a pump power of 1 mW spread over the Gaussian beam of width W = 3 μm with spectrum defined in Eq. (13), where the relation W = 2/w is satisfied in the paraxial regime. The incident pump power P _pump is related to the amplitude of the Gaussian spectrum through A = μ 0 π c P pump W 2 , in the paraxial pump limit. For ⟨100⟩ GaAs we take χ ₀ ⁽²⁾ ≈ 300 pm/V as an approximate value for its nonlinearity coefficient based on different frequency-dependent measurements [44].

After the solid-angle integrations, we obtain the quantity d² N _pair/(dtdω _s ), where we calculate this for the fixed signal frequency corresponding to the degenerate case, at which λ _s = λ _i = 1 μm. This quantity is dimensionless and represents the number of photon pairs per second that one can collect per units of signal photon frequency. For NA values of 0.6, 0.8 and 0.9 we obtain d² N _pair/(dtdω _s ) ≈ 5.2 × 10⁻¹³, 1.7 × 10⁻¹², and 2.6 × 10⁻¹², respectively. Assuming that the generation efficiency is more or less constant for about 10 nm of bandwidth for the signal photons (i.e. from 1 to 1.01 μm wavelength), which is a good approximation based on the result in Figure 4(b), we can multiply the derived d² N _pair/(dtdω _s ) by a corresponding Δω ≈ 1.87 × 10¹³. Then, we find the total rate of photon pairs with a bandwidth of 10 nm for the signal photons, collected with NA values of 0.6, 0.8, and 0.9, to be about 10, 32, and 49 Hz. These numbers are comparable to SPDC measurements in sub-micron-thick thin films [20], [23], once the measured rates are scaled appropriately for experimental collection efficiencies and detection bandwidths. Finally, we note that changing the width of the pump beam from 3 μm to 6 μm (carrying the same 1 mW of power), does not change the collected photon-pair rate appreciably, where with an NA = 0.9 for the collection lens and 10 nm bandwidth for the signal photon, we find a photon-pair rate of 51 Hz.

Figure 4:

Quantum polarization tomography. (a) Real and imaginary parts of the elements of the density matrix, ρ ̂ , for the polarization state of a degenerate (r = 1) photon pair, generated from an ultra-thin GaAs slab of thickness a = 0.01λ _p . The detectors are in a φ-symmetric configuration with θ _s = 45° and φ _s = 0. (b) Schmidt number and joint-coincidence rate as a function of the signal wavelength (bottom axis) and idler wavelength (top axis) for the ultra-thin GaAs slab in the same φ-symmetric configuration, for two thicknesses a = 0.01λ _p and a = 0.1λ _p .

6 Quantum polarization tomography

So far we have examined the mechanism of photon-pair generation by a thin-film nonlinear source, concentrating on the far-field directionality properties as functions of the slab thickness and photon-pair wavelengths. For this purpose, our investigation has focused only on polarization-independent joint-detection. However, we are also interested in the polarization state of the photon pairs, which we will study in this section. Although our model based on the GF quantization approach does not directly predict the quantum state of the photon pairs, but rather predicts detection rates, it still allows us to make these detection rates dependent on the specific wavelength, position, and polarization of the detected photon pairs. Utilizing this, one can determine the density matrices of the biphoton polarization states following a tomographic method [38], [45]. There, the density matrix ρ ̂ , expressed in the { HH , H V , V H , V V } basis, is retrieved from projective measurements computed for a set of 16 tomographic states { ψ ν } ν ∈ [ 1 ; 16 ] [38], [45]. The details of the tomographic approach can be found in the Appendix D.

Using this method, we examine the density matrix for several scenarios, starting with an ultra-thin slab (a = 0.01λ _p ) in a φ-symmetric configuration detection (θ _s = 45°, φ _s = 0) for r = 1. The pump is the same as in Section 5. In Figure 4(a), we display the real and imaginary parts of the density matrix ρ ̂ representing the polarization state. Remarkably, under these conditions, the density matrix corresponds to a maximally polarization-entangled state of the form ψ = H s V i − V s H i = H V − V H . For every photon-pair state, we assess the level of polarization entanglement by determining the Schmidt number, K. A value of K = 1 indicates a completely untangled polarization state, while a value of K = 2 means a fully entangled state (see Appendix D). We investigate entanglement for two thicknesses (a = 0.01λ _p and a = 0.1λ _p ), including non-degeneracy, in Figure 4(b) at the same φ-symmetric configuration. We plot both the Schmidt number (K) and the detection rate (normalized to one) as a function of the wavelength of the signal (bottom axis) and its corresponding idler photon (top axis). We observe that high-quality entanglement is preserved along an extremely broad range of wavelengths in both thicknesses, despite the joint-detection probability dropping at values r ≠ 1 due to moving away from the transversal phase-matching condition (as in Figure 3(b)). This demonstrates GaAs’s ability to produce polarization-entangled Bell states of the form ψ = H V − V H across a wide range of wavelengths, maintaining near-perfect entanglement at φ-symmetric detection with minor degradation at non-degenerate wavelengths.

It is interesting to explore the preservation of broad entanglement obtained in the φ-symmetric setup across various emission angles, especially in non-degenerate scenarios where the φ-symmetric configuration is not dominant. Figure 5 displays the Schmidt number (K) variation with {θ _i , φ _i }, with fixed signal detection at θ _s = 45° and φ _s = 0, for both degenerate (Figure 5(a) and (c)) and non-degenerate cases with r = 1.5 (Figure 5(b) and (d)), with a = 0.01λ _p and a = 1λ _p . Interestingly, while the angles of maximum entanglement (marked with red “*”) and maximum joint-probability (marked with green “x”) coincide for r = 1, they move in opposite directions for r = 1.5. Specifically, the angle of maximum detection rate approaches the optical axis rapidly, following transverse phase matching, whereas the angle of maximum entanglement shifts slightly away from the φ-symmetric angle. Notably, although entanglement slightly degrades in the non-degenerate φ-symmetric case (the values of K ∼ 1.98 and 1.99 in Figure 5(b) and (d)), there actually exists a close by angle at which the entanglement is maximum again at K ∼ 2. Moreover, the angles of maximum detection rate and entanglement are significantly apart for the non-degenerate case, indicating a trade-off between efficiency and entanglement with non-degenerate photon pairs, at least under the stated pumping conditions. Additionally, maximally polarization-entangled states exhibit strong robustness to changes in thickness and wavelengths, which parallels findings in Ref. [38], where similar responses were observed in Bell state generation in GaAs nonlinear nanoresonators.

Figure 5:

Schmidt number as a function of the idler angles {θ _i , φ _i } with fixed θ _s = 45° and φ _s = 0 for (a) a = 0.01λ _p and r = 1, (b) a = 1λ _p and r = 1.5, (c) a = 1λ _p and r = 1, (d) a = 1λ _p and r = 1.5. The angle of maximum entanglement and the angle of maximum detection rate are marked by a red “*” and a green “x”, respectively.

7 Summary and conclusion

In summary, we have developed a theoretical framework based on the classical Green’s function of the system, to comprehensively describe spontaneous parametric down-conversion (SPDC) in nonlinear thin films. This vectorial formalism is capable of treating subwavelength slab thicknesses, accounts for Fabry–Pérot effects, and can address absorption in the slab. Additionally, we have introduced a simplified formulation for numerical investigation of far-field properties of photon pairs detected within one of the media surrounding the slab. Using a zinc-blende 100 GaAs crystal as a specific example, deposited on a SiO₂ substrate with air as the detecting medium, we have computed probability rates for both degenerate and non-degenerate emissions. Through analytical calculations and numerical simulations, we examined and explained the impact of Fabry–Pérot interferences, characterized by oscillations in emitted angles and probability distributions.

Furthermore, we explored the potential of this system to produce polarization-entangled states. Employing a tomographic approach, we demonstrated that a GaAs slab can generate maximally polarization-entangled states of the form ψ = H V − V H , within a φ-symmetric configuration by analyzing its density matrix ρ ̂ . Our findings revealed that the entanglement achieved remains highly resilient against variations in wavelengths and thickness, even in non-degenerate scenarios. However, in the case of non-degenerate photons, achieving maximal entanglement entails a trade-off with the efficiency of the process, where the latter is affected by the transversal phase-matching condition. This suggests a nuanced interplay between entanglement quality and detection rates in such systems, which could potentially be manipulated by using spatially structured pump fields to reach maximum entanglement together with high detection rates.