Abstract
Double-walled carbon nanotubes have shown competitive properties in broadband optical pulse generation owning to the intrinsic electronic properties. Synchronization of ultrafast optical pulses in multiple wavelengths is a key technique for numerous applications, such as nonlinear frequency conversion, ultrafast pump-probe, coherent Raman scattering spectroscopy, coherent optical synthesis, etc. In this work, we demonstrate the mode-locking and synchronization of 1.55 µm pulses with 1 µm and 1.9 µm pulses via a single saturable absorber based on double-walled carbon nanotubes. The large optical nonlinearity and broadband optical absorption in the double-walled carbon nanotubes enable independent and synchronized mode-locking in >900 nm bandwidth. In addition, we present a creative concept to realize multi-wavelength synchronization from a single laser system. Our results demonstrate a straightforward and feasible approach towards pulse synchronization over ultra-broad bandwidth with flexible wavelength selection in the near-infrared region.
1 Introduction
The rapid development of ultrafast pulse generation technologies has spurred great advancements in science and applications. As an extension of single wavelength sources, dual-wavelength synchronized ultrashort optical pulses with a large wavelength difference and superior stability are important tools for numerous applications in nonlinear frequency conversion, ultrafast pump-probe, coherent Raman scattering spectroscopy, coherent optical synthesis, and many other timing and wavelength dominated nonlinear optics [1–4]. The synchronization of dual-wavelength ultrafast pulses has been intensively investigated since the invention of Ti:sapphire lasers thanks to their ultrabroad homogeneous gain spectrum and easy self-mode-locking by Kerr lens medium. Ingenious configuration design allows the oscillation of dual-wavelength pulses in a single or double-cavity with a shared Ti:sapphire rod, where mode-locked synchronization was achieved by tuning the dispersion or moving the reflection mirror position [5–7]. Despite a second gain module is not required in these methods, the two laser beams need to overlap in the gain medium for self-synchronization, which induces instability when gain competition arises in the case the overlap mode volume is large [8]. Modified approaches were proposed later via introducing active feedback to the oscillators or simply by using two separate gain media (e.g., Ti:sapphire and Nd:YVO4 or Ti:sapphire and Cr:forsterite) in the synchronized lasers [9, 10], while both add more complexity to the solid-state laser system.
In contrast, fiber lasers that adopt rare earth elements as optical gain and amplification media enable the coverage of a large wavelength range at the infrared region and provide other inherent advantages, such as compactness, free optical alignment, and large optical nonlinearity [11, 12]. In principle, it is not difficult to synchronize dual-wavelength pulses in fiber if stable mode-locking is obtained in two resonators. The key criterion is to simultaneously lock the modes over a broadband wavelength range with an appropriate modulator. During the past decades, semiconductor saturable absorber mirrors (SESAMs) have been well developed for passive mode-locking [13], which is advantageous to the availability of controllable parameters for different types of lasers (e.g., solid-state lasers, semiconductor lasers, fiber lasers) [14–16], but is usually limited in operation bandwidth for a single device. For instance, dual-wavelength pulse synchronization in ytterbium and erbium fiber lasers has been demonstrated either by optical injection method (i.e., master–slave synchronization) or in a shared fiber cavity configuration (i.e., coupled synchronization) [17, 18], where different SESAM devices designed for 1 µm and 1.55 µm wavelengths are employed to mode-lock them separately.
Recently, the rapid progress in nanomaterials research has promoted new solutions to facilitate the mode-locking in fiber lasers. Representative works are the demonstrations of using single-walled carbon nanotubes and graphene as self-modulation devices (i.e., saturable absorbers) [19–22]. Compared with single-walled carbon nanotubes, where the characteristic absorption peaks corresponding to their operation wavelengths need to be tailored by mainly careful control of the nanotube diameter distribution during the material synthesis, the relatively flat spectrum absorption of double-walled carbon nanotubes (DWCNTs) contributed by the inner and outer tubes’ excitonic transition energies can be a better alternative in multiple-wavelength laser operations [23, 24].
In this work, we present a directly coupled fiber laser configuration mode-locked with a shared DWCNT saturable absorber for three wavelengths, which are emitted by the ytterbium, erbium, and thulium ions doped in different gain fibers. In one setup, an erbium cavity is employed to couple with a ytterbium cavity for the synchronization of pulses at 1 and 1.55 µm wavelengths. In another setup, an erbium cavity is used to couple with a thulium cavity to synchronise pulses at 1.55 µm and 1.9 µm wavelengths. The same DWCNT saturable absorber is utilized in these two setups to mode-lock the three wavelengths with a maximum spectral space of up to ∼900 nm. In both synchronisation cases, the DWCNT saturable absorber film is positioned at the common section of the laser resonators, in which pulse attraction induced by the cross-phase modulation provides a self-motivated mechanism for the synchronization of two pulses at different wavelengths. The use of a variable optical delay line in the erbium cavity permits high precision round trip frequency (repetition rate) tuning of the 1.55 µm laser. Experimental results find that the self-synchronization forms and the dual-wavelength pulses oscillate in the same repetition rate when one laser optical cavity length is tuned approach to the other. Our DWCNT sample performs outstanding resistance to potential thermal and optical damages, as demonstrated by the superior stability of the synchronized operation during a few hours of continual surveillance.
2 Material synthesis and characterization
The pristine DWCNTs were synthesized by floating catalyst chemical vapor deposition method in a vertically placed tube furnace. The furnace was heated to 1100 °C to satisfy the chemical reaction temperature, in which CH4 and gas-phase precursors, including ferrocene, sulfur and carrier gases (N2 and H2), were utilized to synthesize DWCNTs in the reactor [25]. The covalently bonded DWCNTs were synthesized by a gas-phase reaction in the hot zone of reactor. The aerosol-like nanotubes were easily collected by a large-area membrane filter at room temperature, and the film thickness could be precisely controlled by the collection time. Figure 1(a) shows the broadband optical absorption spectrum of the DWCNT film measured by an ultraviolet–visible–near infrared spectrometer (Agilent Cary 5000). The large absorption span enables it a potential application for ultrafast pulse generation with working wavelengths ranging from ∼1 μm to 2 μm. The Raman spectrum of the DWCNTs excited by a 514 nm laser (Horiba Jobin-Yvon Labram HR 800) is shown in Figure 1(b). Obvious peaks in the Raman shift at 190 cm−1 are observed from the radial breathing mode (RBM), which corresponds to the formation of the inner tube in the DWCNT film. The dominant peak located at ∼1594 cm−1 is a graphite-like (G) band, and the peak located at ∼1351 cm−1 is the D band, referring to the disordered properties originating from the vacancies or any defects. The intensity ratio of G/D is widely used to evaluate the quality of nanotubes. Here the ratio is as high as 15, indicating the good quality of DWCNTs. To investigate the nanostructure and morphology of the DWCNTs, scanning electron microscopy (SEM, Zeiss Sigma VP) and Cs-corrected transmission electron microscopy (TEM, JEM2200FS, JEOL Ltd) are used to observe the microstructures of the DWCNTs. The SEM image in Figure 1(c) shows a uniform network structure formed by the disordered stacking of DWCNTs. In addition, CNTs with a diameter of about ∼5 nm were observed in Figure 1(d), which shows the obvious double-walled structure in our sample.
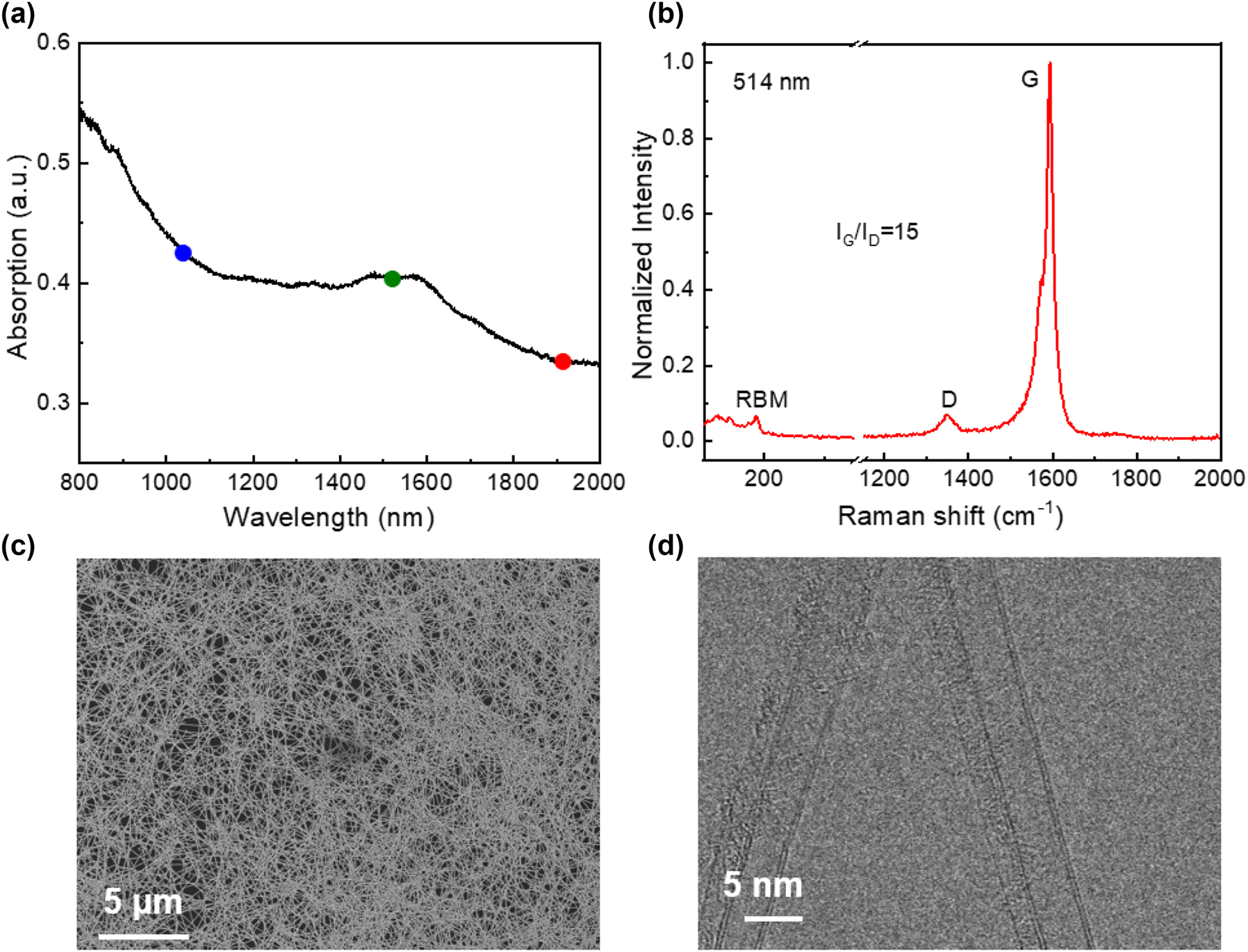
Material characterization of the DWCNT film. (a) Broadband optical absorption spectrum of the DWCNT film (The blue, green, and red disks indicate the 1 µm, 1.55 µm, and 1.9 µm wavelengths); (b) Raman spectroscopy of the synthesized DWCNT film excited by a 514 nm laser; (c) SEM; and (d) TEM images of the synthesized DWCNT film.
3 Experimental setup
The experimental setup of the dual-wavelength fiber laser is schematically shown in Figure 2. We construct a composite fiber cavity with ytterbium-doped fiber and erbium-doped fiber for the synchronisation of pulses at ∼1 µm and 1.55 µm wavelengths, which are managed in two fiber loops bridged by a common branch. The broadband DWCNT film coated on the fiber end is placed in the common fiber to work as a joint saturable absorber in the composite cavity. The two individual wavelength lasers are combined and divided by two 1060/1550 nm wavelength division multiplexers (WDMs). Couplers (with 90:10 ratio, 10 % output), polarization-independent isolators and polarization controllers (PCs) working at 1 µm and 1.55 µm wavelengths are incorporated into each resonator to extract the intracavity light, start the mode-locking and ensure unidirectional operation, respectively. A segment of 1.2 m erbium-doped fiber (Fibercore I-25) is used for the telecom band emission at ∼1.55 µm, which is pumped by a 976 nm laser diode via a 980/1550 nm WDM. The ytterbium-doped fiber is pumped by another 976 nm laser diode via a 980/1060 nm WDM. High-gain ytterbium-doped fiber (Yb800-4/125, 0.22 m) with 800 dB/m absorption at 975 nm is employed for the mission at ∼1 µm. A section of ∼2.6 m polarization-maintaining fiber (Thorlab PM980) is added to the 1 µm laser to form a fiber-based Lyot filter for intra-cavity spectral filtering, which facilitates the start of mode-locking in the all-normal-dispersion resonator [26]. A variable optical delay line (OZ OPTICS ODL-650) is employed in the 1.55 µm laser resonator to adjust the optical length. The total length of each oscillator is approximately 10 m. The output performance of the dual-wavelength laser is assessed by a power meter (Thorlabs PM100D), an optical spectrum analyzer (Anritsu MS9740A), an autocorrelator (APE PulseCheck 150), a digital oscilloscope (Siglent SDS5104X), and a radio frequency spectrum analyzer (Anritsu MS2692A) assisted by an ultrafast photodiode detector (EOT ET-5000F).
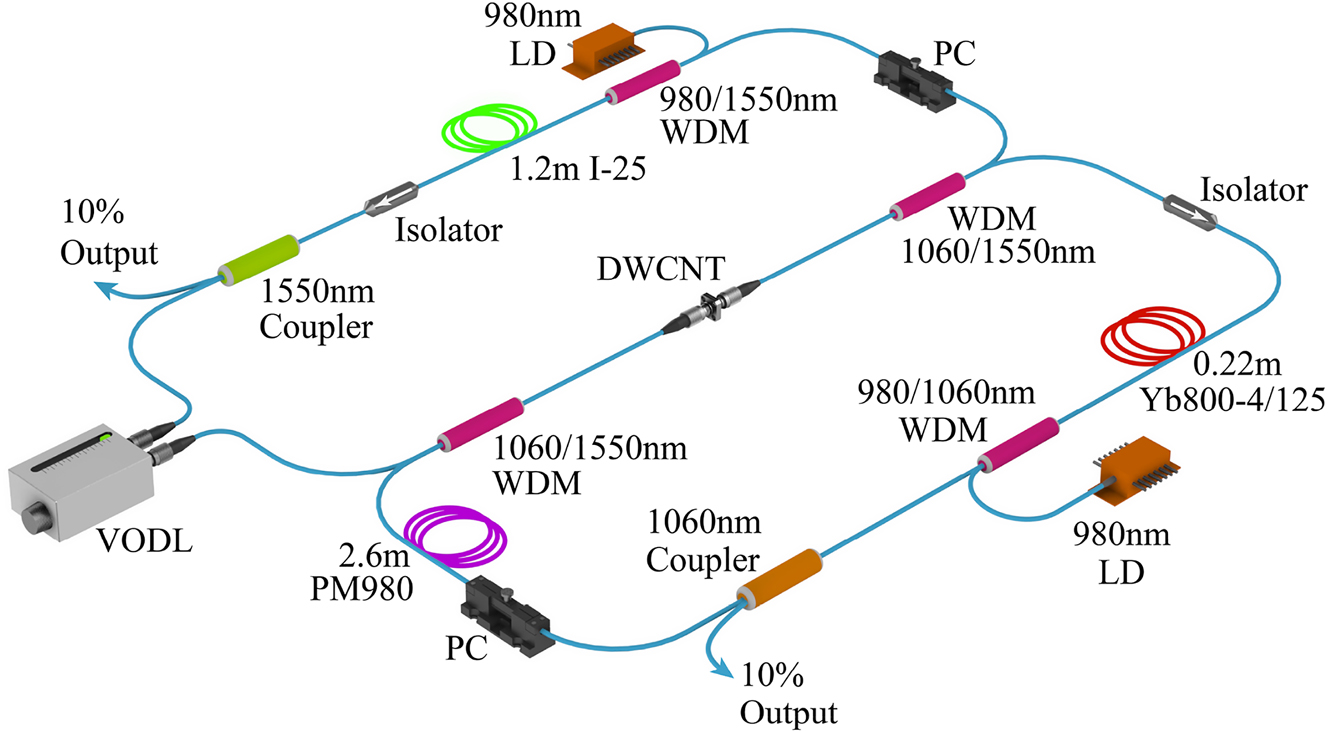
Experimental setup of the dual-wavelength fiber laser. LD, laser diode; WDM, wavelength division multiplexer; PC, polarization controller; VODL, variable optical delay line; DWCNT, double-walled carbon nanotube. The fiber rings in green, red, and purple represent the erbium-doped fiber, ytterbium-doped fiber, and polarization-maintaining fiber.
4 Synchronization of 1.55 µm laser with 1 µm laser
Independent fundamental mode-locking is observed in the ytterbium laser and erbium laser when their pump powers are in the range of 61.8–67.9 mW and 22.5–28.5 mW, respectively. Further increasing the pump power will turn the fundamental frequency pulse to multiple pulses rather than material damage, which benefits our nanotube robustness against optical intensity. The initial mismatch of the ytterbium cavity and the erbium cavity is a few centimeters, which can be compensated by tuning a variable optical delay line placed in the erbium cavity. Synchronized mode-locking is obtained when the two cavities’ lengths are approximately equal via reducing the optical delay in the erbium cavity. Mode-locked laser spectra were measured from the 10 % output couplers in both cavities, as shown in Figure 3(a) and (b). The synchronized pulses are mode-locked at the central wavelength of ∼1032.58 nm, with ∼0.36 nm bandwidth in the ytterbium laser, and ∼1558.48 nm, with ∼5.90 nm bandwidth in the erbium laser, respectively. Figure 3(c) and (d) show the autocorrelation traces of the synchronized pulses, giving ∼8.75 ps pulse width in the ytterbium laser and ∼495 fs pulse width in the erbium laser. The output powers measured at 1 µm and 1.55 µm laser are ∼210.1 µW and 203.7 µW, respectively.
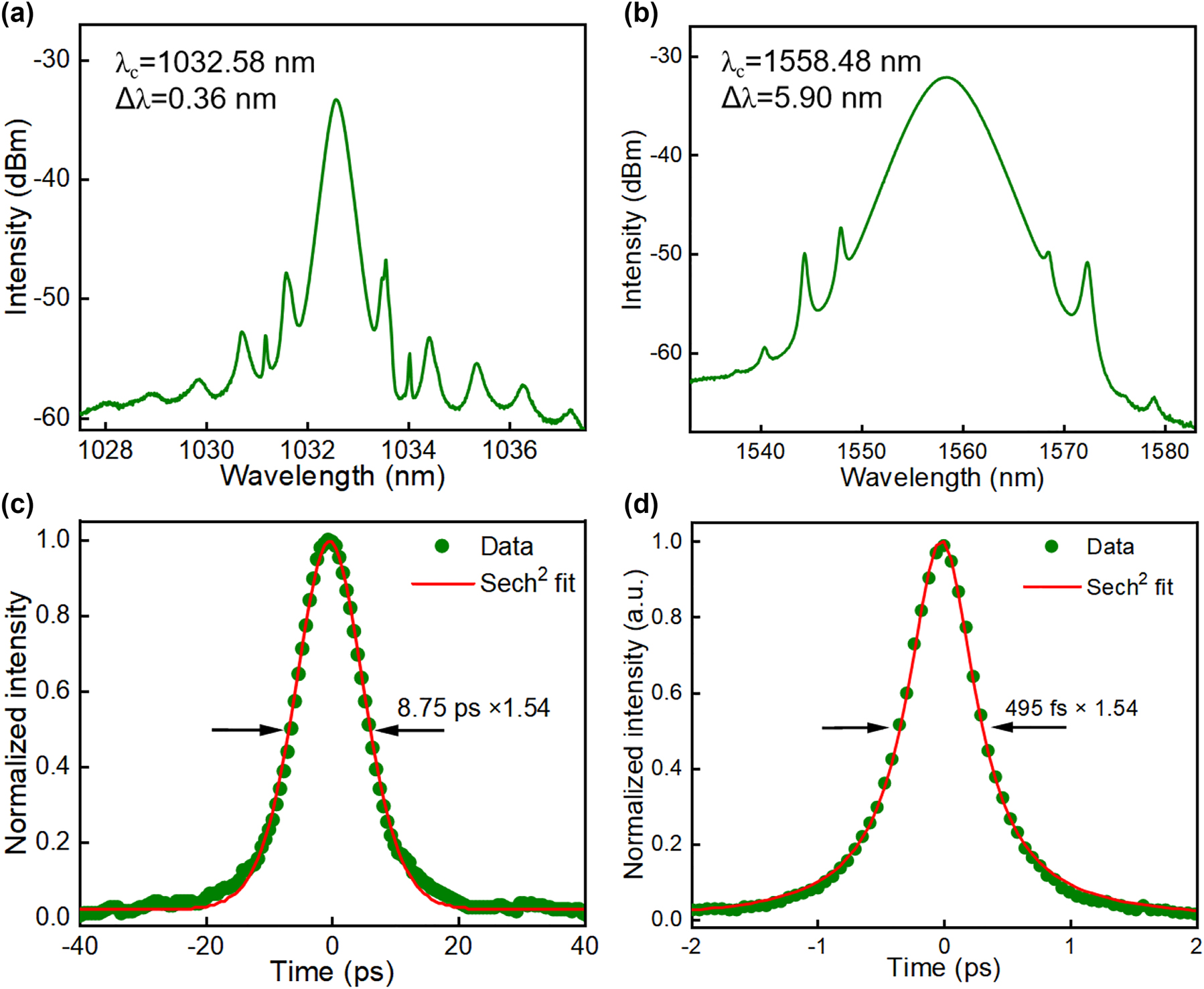
Synchronized lasers at 1 and 1.55 µm. (a) 1 µm ytterbium laser output soliton spectrum; (b) 1.55 µm erbium laser output soliton spectrum; (c) 1 µm ytterbium laser pulse autocorrelation trace; (d) 1.55 µm erbium laser pulse autocorrelation trace.
Synchronization of the two lasers can be characterized either in the time domain or frequency domain. Figure 4(a) and (b) are the mode-locked pulse trains and radio frequency spectrum measured when the synchronization is attained by tuning the delay in the erbium cavity. The synchronized frequency is ∼20.56883 MHz, corresponding to ∼48.617 ns pulse period. From the independent mode-locking, the fundamental repetition rate of the ytterbium laser is measured as ∼20.56880 MHz. After synchronisation, the ytterbium laser frequency slightly shifts to ∼20.56883 MHz, attributed to the refractive index change mainly caused by cross-phase modulation. Our further investigations focus on the frequency tuning characteristic when different erbium cavity offsets are applied. Here we define Δf as the frequency offset to the fundamental repetition rate of the ytterbium laser, which is determined by a fixed cavity length. In the case that the erbium cavity length is shorter than the ytterbium cavity length, mode-locked synchronization forms when the two cavity lengths are getting closer by increasing the delay, as shown in Figure 4(c), where the ytterbium laser frequency offset is up to ∼60 Hz at an erbium cavity offset of ∼41.3 µm. Further decreasing the erbium laser repetition rate (i.e., increasing the erbium cavity length) from the synchronization initiation point, the synchronization repetition rate keeps going down to ∼20.56871 MHz, showing a tuning range of ∼150 Hz. On the contrary, the laser repetition rates are measured again when the erbium cavity length is decreased. Synchronization and non-synchronization are observed, but the synchronization frequency range is significantly enlarged to ∼300 Hz, as seen in Figure 4(d). This can be attributed to faster propagation of the erbium laser pulse in negative dispersion fiber, which causes more stable synchronization while the erbium cavity is shorter than the ytterbium cavity. Meantime, the tunability of the erbium laser cavity offset also leads to the peak wavelength shift in both lasers, which is due to the cross-phase modulation in anomalous dispersion [27, 28]. Here we define Δλ as the peak wavelength shift to the original peak wavelength of the lasers before synchronization. Figure 4(e) plots the ytterbium and erbium laser peak wavelength shift as a function of the erbium cavity offset in the same tuning range as Figure 4(c). It can be clearly seen that the peak wavelengths present a hop when synchronization starts at ∼41.3 µm offset, and then shift to blue and red in the erbium and ytterbium lasers as the increase of offset. Noteworthy that the peak wavelengths return to their original values when the synchronization is detached at ∼99.12 μm offset, confirming that the shift is a result of cross-phase modulation. Peak wavelength shifts are measured as ∼0.051 nm in the erbium laser and ∼0.054 nm in the ytterbium laser, as shown in Figure 4(e). Interestingly, our followed reversal delay tuning experiment presents a similar wavelength tunability behavior, but with the erbium laser red-shifted and ytterbium laser blue-shifted instead. Experimental results are plotted in Figure 4(f), which shows ∼0.088 nm and 0.137 nm tuning of the erbium laser and the ytterbium laser, respectively. According to the relation of frequency and wavelength, the wavelength is blue-shifted (red-shifted) when the frequency is increased (decreased). Higher frequency wave of the pulse propagates faster in our negative dispersion cavity. Before tuning the delay, the erbium cavity is longer than the ytterbium cavity, the 1.55 µm pulse falls behind the 1 µm pulse when they propagate along the common arm. As the erbium cavity length approaches the ytterbium cavity by reducing the delay, the dual-wavelength pulses start to overlap in the time domain and pull each other, which causes an increase of the pulse repetition rate and blue-shift of the peak wavelength in the erbium laser, but reversal changes in the ytterbium laser. This pulling effect will result in the maximum overlap of the two pulses if the two cavity lengths are approximately equal.
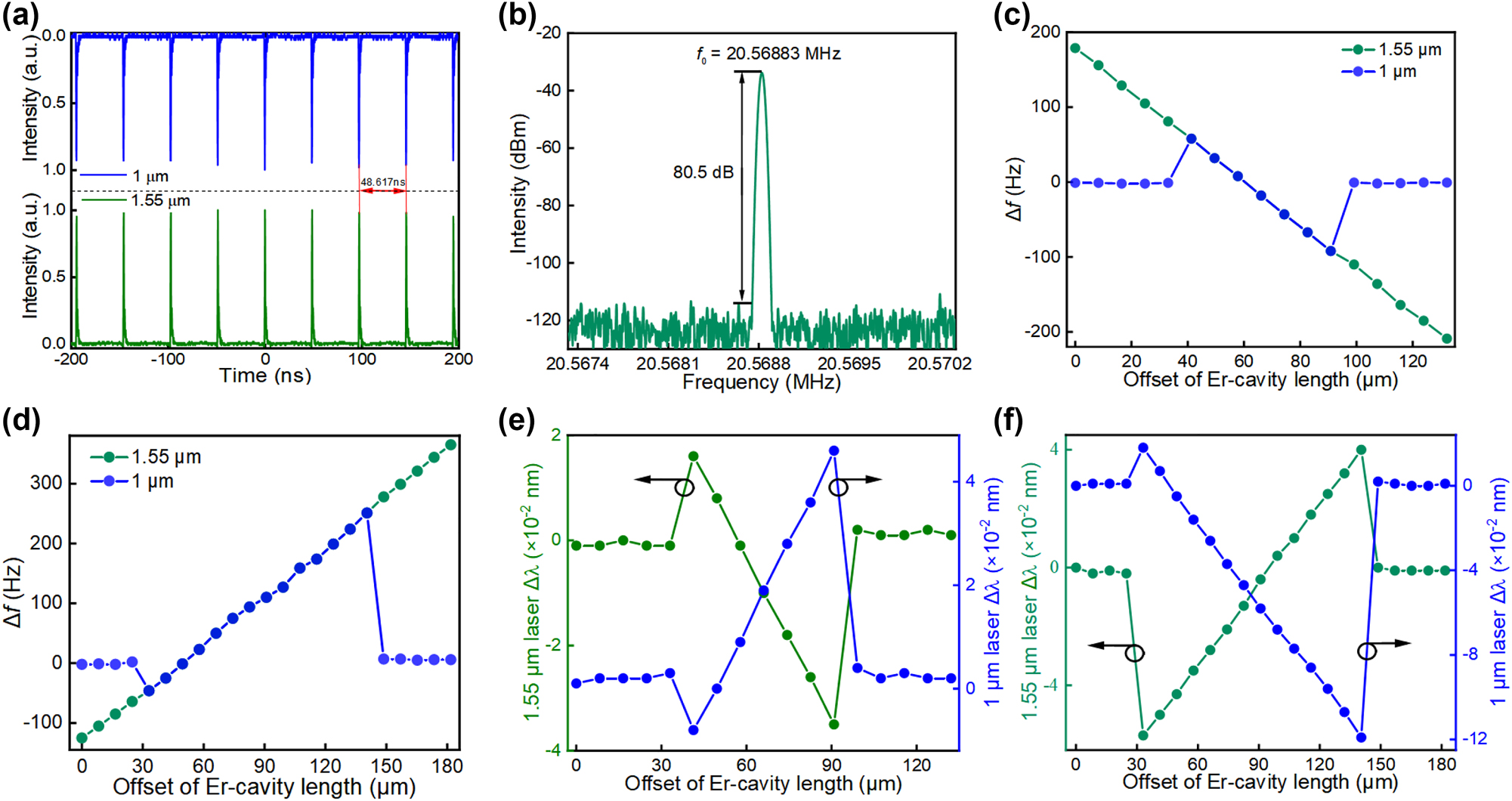
Synchronized laser repetition rates and peak wavelengths tunability as a function of the erbium cavity offset. (a) Synchronized laser pulse trains measured from ytterbium and erbium resonators; (b) radio frequency spectrum of the synchronized lasers; frequency offset of synchronized pulses as a function of cavity length difference when the erbium cavity length is increased (c) and decreased (d); peak wavelength shift versus cavity length difference when the erbium cavity length is increased (e) and decreased (f).
5 Synchronization of the 1.55 µm laser with a 1.9 µm laser
In principle, the flat optical absorption spectrum of our DWCNT saturable absorber supports its availability for mode-locking of a wide range of wavelengths up to mid-infrared. As an important wave band for eye-safe applications and a potential alternative band in optical communication, thulium fiber lasers working around 2 µm have attracted increasing attention. The synchronization of dual-wavelength pulses enabled by our DWCNT sample can be extended to this wavelength region if proper fiber components are used. As a demonstration, we constructed a dual-wavelength laser with an erbium fiber cavity and a thulium fiber cavity in the same layout as the 1 µm and 1.55 µm laser setup (Figure 2). The same DWCNT saturable absorber synchronizing the 1 µm and 1.55 µm pulses is used again to mode-lock longer wavelengths. A 0.6 m erbium doped fiber (Liekki Er80-8/125) and a 2 m thulium doped fiber (OFS TMDF200) are utilized as gain media. The thulium doped fiber is pumped by a 1550 nm laser pre-amplified by an erbium-doped fiber amplifier through a 1550/1950 nm WDM. Another variable optical delay line is connected in the 1.55 µm cavity to adjust its optical length. The total length of each fiber cavity is approximately 11 m. An additional optical spectrum analyzer (APE waveScan) for the 1.9 µm laser is combined with the measurement equipment in the above experiment to analyze the laser performance.
Stable mode-locking of the erbium laser and thulium laser is obtained independently when the pump powers reach 65.1 mW and 115.3 mW, respectively. Again, dual-wavelength pulse synchronization can be obtained when the erbium cavity length is tuned to approximately equal to the length of the thulium cavity. The mode-locked laser spectra remain the same in their independent operation, which centers at 1559.56 nm with 5 nm 3 dB bandwidth and 1924.3 nm with 3.8 nm 3 dB bandwidth in the erbium laser and thulium laser, respectively, as shown in Figure 5(a) and (b). Pulse autocorrelation traces measured in Figure 5(c) and (d) unveil pulse durations of 532 fs and 2.66 ps in the erbium laser and thulium laser.
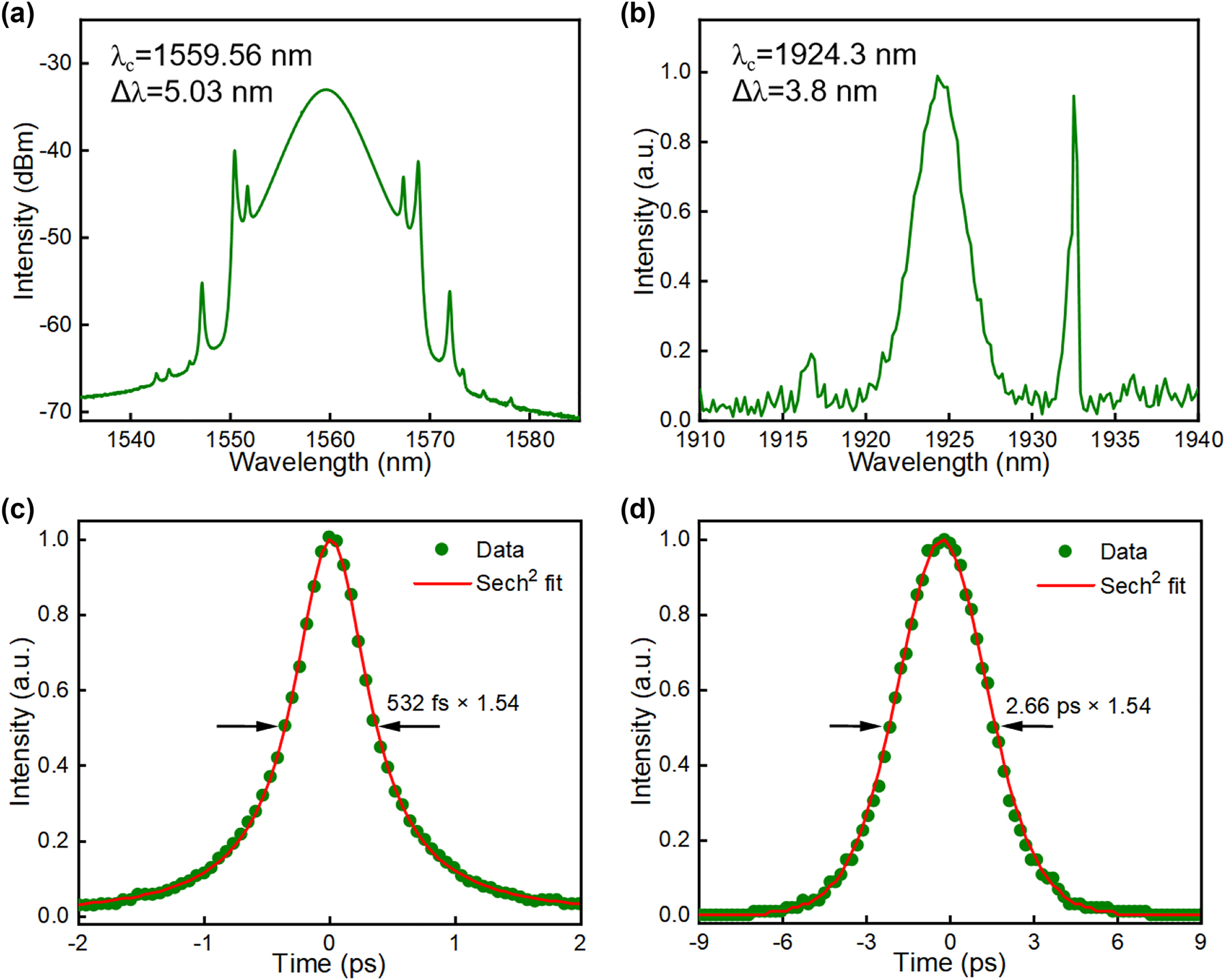
Synchronized lasers at 1.55 and 2 µm. (a) 1.55 µm erbium laser output soliton spectrum; (b) 2 µm thulium laser output soliton spectrum; (c) 1.55 µm erbium laser pulse autocorrelation trace; (d) 2 µm thulium laser pulse autocorrelation trace.
Figure 6(a) and (b) are the synchronized pulse trains and radio frequency spectrum of the Erbium laser and thulium laser when their pump powers are ∼69.6 mW and 121 mW, respectively. The adjacent pulse spacing of the synchronized signal is ∼53.17 ns, corresponding to a repetition rate of ∼18.80749 MHz. The signal-to-noise contrast of >67 dB in Figure 6(b) verifies high stability in the synchronization mechanism. Again, we measure the dual-wavelength laser frequencies (repetition rates) as a function of the cavity offset by tuning the erbium cavity length in two opposite directions. The cavity mismatch tolerances reach ∼661 µm and 248 µm when the erbium cavity length increases and decreases, respectively, as shown in Figure 6(c) and (d). The tuning of synchronization frequency also accompanies the shifts of the peak wavelengths, which shows the same characteristic as the observation from the ytterbium and erbium lasers. However, the synchronization range of the erbium laser and thulium laser is much larger, which corresponds to the maximum frequency range of ∼1.1 kHz and causes the peak wavelength shift up to ∼0.38 nm and 10.2 nm for the 1559.56 nm and 1924.3 nm pulses, respectively (Figure 6(e)). The larger wavelength tuning may be attributed to the stronger nonlinear refractive index modulation as the pulse energy is much larger than that of the erbium and ytterbium lasers. In addition, we also study the influence of common fiber arm length on the synchronization performances, the experimental result is plotted in Figure 7. Via adjustment of the common fiber length from ∼2 m to 12 m, it can be seen that the maximum cavity mismatch tolerance is expanded up to ∼2360 μm at the optimal common fiber length of ∼6 m. This is a balanced consequence between the cross-phase modulation and group velocity dispersion.
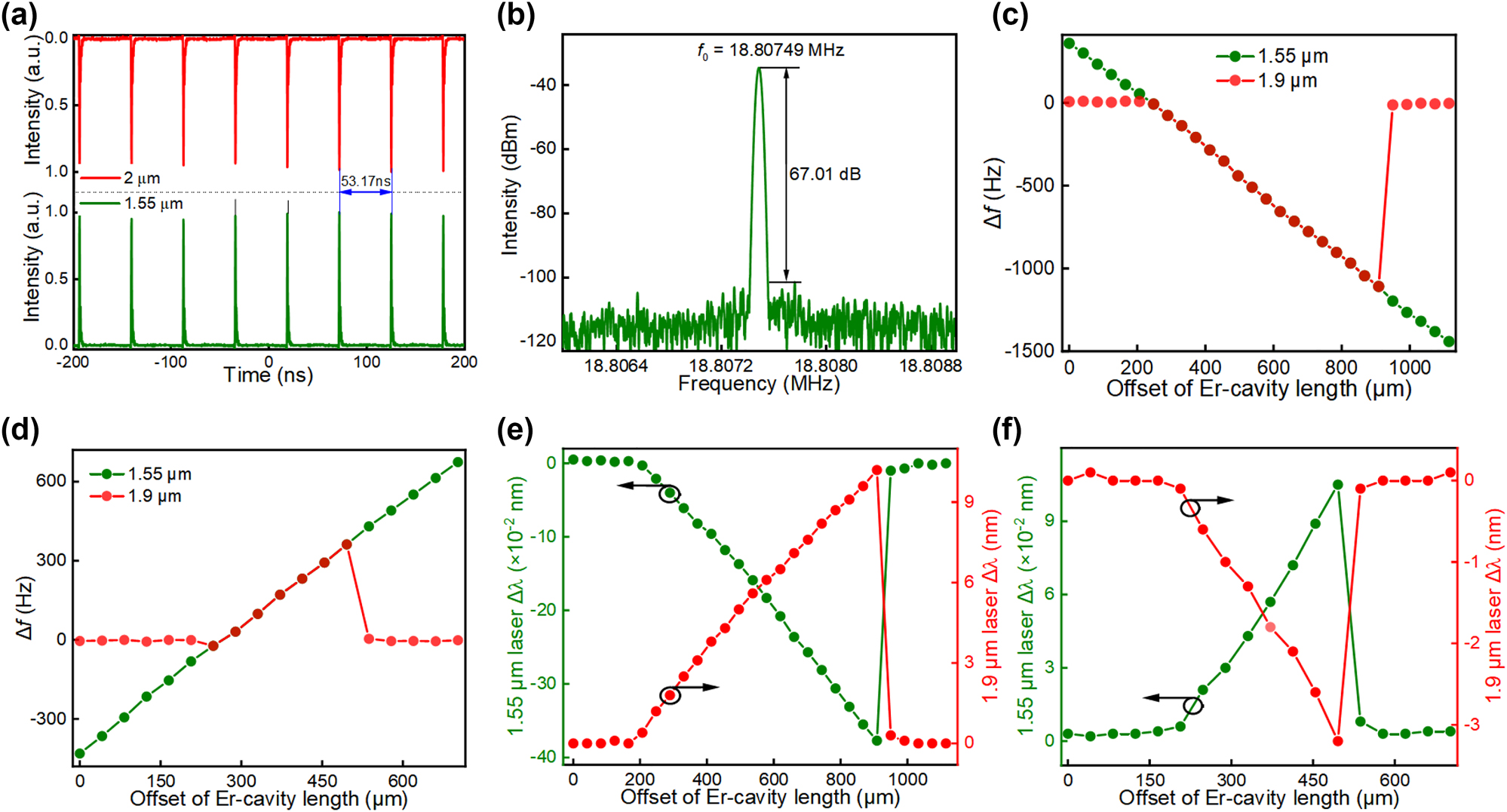
Synchronized laser repetition rates and peak wavelength tunability as a function of the Erbium cavity offset. (a) Synchronized laser pulse trains measured from the erbium and thulium resonators; (b) radio frequency spectrum of the synchronized lasers; frequency offset of synchronized pulses as a function of cavity length difference when the erbium cavity length is increased (c) and decreased (d); peak wavelength shift versus cavity difference when the erbium cavity length is increased (e) and decreased (f).
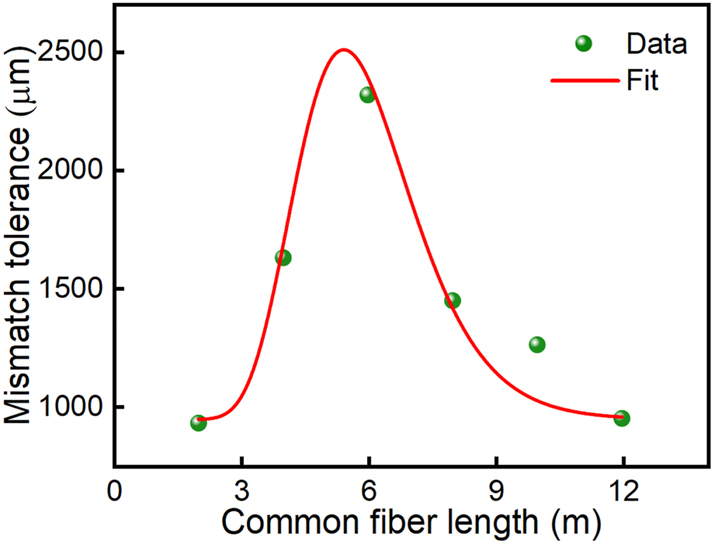
Mismatch tolerance as a function of the common fiber length.
To date, ultrafast pulse synchronization has been investigated in solid-state lasers, fiber lasers and their combined platforms. In solid-state lasers, Ti:sapphire has dominated the gain sources because of its broadband homogeneous gain spectrum and simplicity for self-mode-locking. Other gain media (such as Cr:forsterite and Nd:YVO4) are also options to extend the laser wavelength to a longer wavelength region. Particularly, fiber gain media with rare-earth doping further extend the synchronization laser from 1 µm to 2 µm, which is also the motivation for using DWCNT saturable absorber in this work. In terms of the synchronization technique, passive, active, and their hybrid method have been adopted as per the mode-locking mechanism. To give an overview of the performances of the previously studied dual-wavelength synchronization lasers, we summarize and list the key parameters of these lasers in Table 1 below. In comparison, our work demonstrates the synchronization of multiple wavelengths in ∼900 nm coverage with a single DWCNT saturable absorber, in which the largest cavity mismatch tolerance up to ∼2360 µm is achieved in the synchronization between 1559.56 nm and 1924.3 nm pulses.
Synchronization of mode-locked lasers with different strategies.
| Gain medium | Wavelength | Pulse width | Synchronization method | Repetition rate | Maximum mismatch | Refs |
|---|---|---|---|---|---|---|
| Ti:sapphire rod | 790 nm, 760 nm | 80 fs, 100 fs | Cross mode-locking | 80.4 MHz | 3 µm | [29] |
| Ti:sapphire rod | 830 nm, 760 nm | 30 fs, 64 fs | Self-mode-locking | 76 MHz | 1 µm | [30] |
| Ti:sapphire rod | 755 nm, 750 nm | 25 fs, 80 fs | Master-slave mode-locking | 75.918 MHz | 1.2 µm | [31] |
| Ti:sapphire rod | 800 nm, 855 nm | 50 fs, 109 fs | SESAM mode-locking with active feedback | 119 MHz | / | [32] |
| Ti:sapphire rod | 774 nm, 840 nm | 55 fs, 65 fs | Dye mode-locking | 85 MHz | / | [5] |
| Ti:sapphire rod | 760 nm, 780 nm | 105 fs, 80 fs | Cross mode-locking | 79.5 MHz | 3 µm | [6] |
| Ti:sapphire rod | 853 nm, 767 nm | 95 fs, 110 fs | Self-mode-lock | 82 MHz | / | [7] |
| Ti:sapphire crystal, Cr:forsterite crystal | 820 nm, 1250 nm | 18 fs, 40 fs | SESAM and Kerr-lens mode-locking | 78.8487 MHz | 0.6 µm | [8] |
| Ti:sapphire crystal, Nd:YVO4 crystal | 850 nm, 1064 nm | 180 fs, 8 ps | Master-slave mode-locking | 82.6 MHz | 20 µm | [9] |
| Ti:sapphire crystal, Cr:forsterite crystal | 833 nm, 1225 nm | 30 fs | InGaAs mode-locking with active feedback | 82 MHz | / | [10] |
| Ti:sapphire crystal, Cr:forsterite crystal | 820 nm, 1230 nm | 17 fs, 46 fs | Active (feedback)-passive hybrid mode-locking | 101 MHz | / | [33] |
| Cr:forsterite crystal, Erbium fiber | 1550 nm, 1250 nm | / | Master-slave mode-locking | 40.75 MHz, 81. 5 MHz | 9 µm, 12 µm | [34] |
| Ytterbium fiber, Erbium fiber | 1060 nm, 1550 nm | 2 ps, 1 ps | Master-slave mode-locking | 40 MHz | 140 µm | [17] |
| Ytterbium fiber, Erbium fiber | 1040 nm, 1550 nm | 13 ps, 200 fs | Master-slave mode-locking | 29 MHz | 20 µm | [18] |
| Erbium fiber | 1540 nm, 1578 nm; 1557 nm | 82 fs, 500 fs | Master-slave mode-locking | 47.66 MHz | 54 μm | [35] |
| Ytterbium fiber, Erbium fiber | 1067.1 nm, 1535.48 nm | 6.1 ps, 2.1 ps | Single-walled carbon nanotube mode-locking | 6.54 MHz, 13.08 MHz | 1400 µm | [36] |
| Ytterbium fiber, Erbium fiber | ∼1030 nm, ∼1562 nm | ∼110 fs, ∼70 fs | Master-slave mode-locking with active feedback | 43.28 MHz | 160 µm | [37] |
| Erbium fiber, Thulium fiber | 1558.5 nm, 1938 nm | 915 fs, 1.57 ps | Graphene mode-locking | 20.5025 MHz | 780 µm | [38] |
| Erbium fiber, Thulium fiber | 1563.5 nm, 1931.9 nm | 700 fs, 1.77 ps | Graphene mode-locking | 12.905 MHz | / | [39] |
| Ytterbium fiber | 1043 nm, 1057 nm | 7.9 ps, 5.9 ps | Nonlinear polarization rotation mode-locking | 38.1100 MHz | 160 µm | [40] |
| Ytterbium fiber, Erbium fiber | 1032.58 nm, 1558.48 nm | 8.75 ps, 495 fs | DWCNT mode-locking | 20.5688 MHz | ∼500 µm | This work |
| Erbium fiber, Thulium fiber | 1559.56 nm, 1924.3 nm | 532 fs, 2.66 ps | DWCNT mode-locking | 18.8075 MHz | ∼2360 µm | This work |
6 Design of synchronization of all three lasers at 1, 1.55, and 1.9 µm
Our work presented above demonstrates the synchronization of triple wavelengths in ∼900 nm coverage with two individual laser systems. To obtain triple-wavelength ultrafast laser synchronization from a single laser system would be more significant since it may have more potential applications, like high-energy femtosecond pulse emission and multi-photon pump-probe investigations. Here we propose a conceptual diagram of the triple-wavelength synchronized fiber laser system in Figure 8, which is an upgrade based on Figure 2. The ytterbium and erbium cavities keep the same configurations depicted in Figure 2, and the thulium cavity uses the same configuration described in Section 5. The total length of the thulium cavity is modified the same as the ytterbium cavity. Two triple-wavelength WDMs replace the original dual-wavelength WDMs at the two ends of the common arm to couple three ring resonators. Cross-phase modulation induced pulse attraction leads to the synchronization of all three lasers at 1, 1.55, and 1.9 µm. Further, multi-wavelength (more than triple wavelengths) synchronization could also be achieved with a broader coverage if multi-wavelength WDMs are applied at the two ends of the common arm. Since passive synchronization can only be achieved with optical path differences of the cavities on the order of microns, more optical variable delay lines work at different wavelengths and could be applied in the cavities to tune the optical lengths precisely and promote multi-wavelength synchronization.
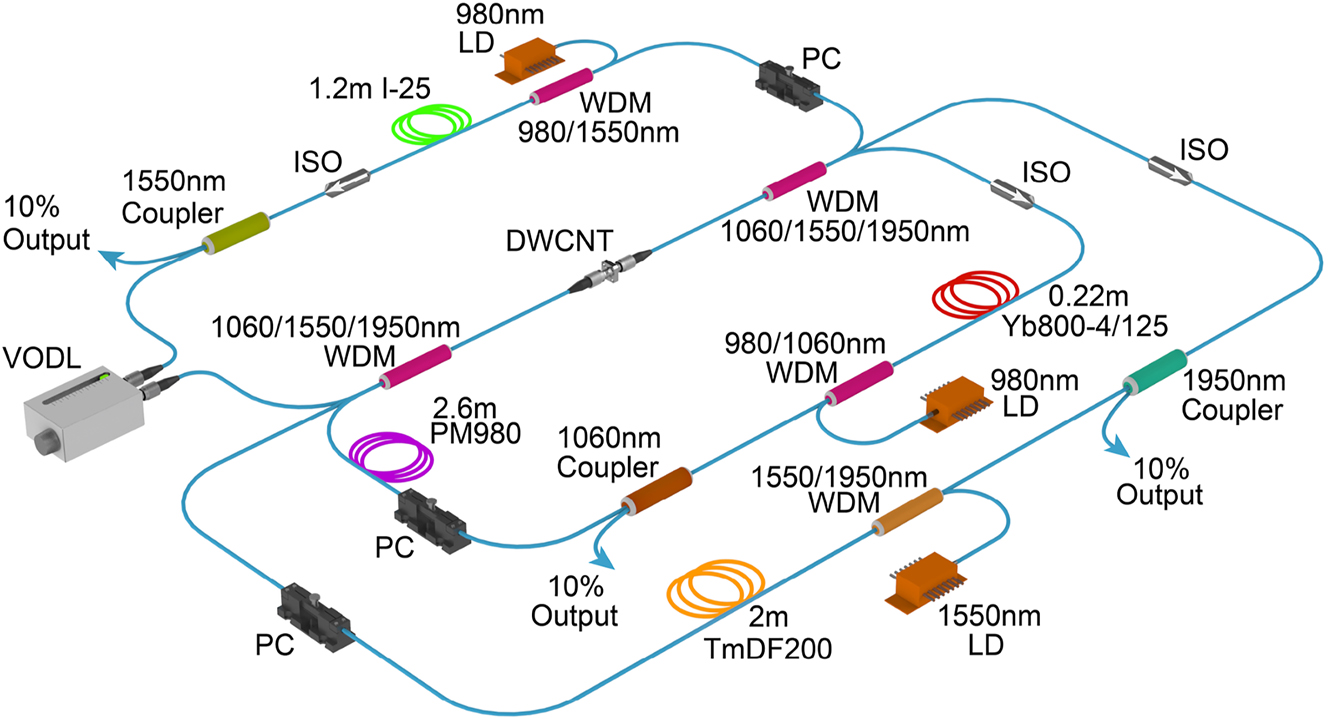
Conceptual diagram of the triple-wavelength synchronized fiber laser system.
Although the triple-wavelength synchronized fiber laser system proposed here is still a conceptual methodology, which is limited by existing fabrication technology of multi-wavelength WDM, the development of optical components will certainly enable the system to be implemented in the near future for applications.
7 Conclusions
In conclusion, we demonstrate the synchronization of a 1.55 µm laser with a 1 µm laser and a 1.9 µm laser, respectively, by using the same DWCNT film as a saturable absorber. The two synchronization lasers adopt the same cavity layout with two ring fiber resonators coupled in a shared section, where the broadband DWCNT saturable absorber is placed to start the mode-locking of different wavelengths. Our results indicate that the tuning range of repetition rate and wavelength are strongly relevant to the common arm length, which can be attributed to the interaction between cross-phase modulation and cavity dispersion. Via the optimization of common arm fiber length, we obtain the largest synchronization cavity mismatch tolerance up to ∼2360 µm in the erbium and thulium fiber laser. Also, we present a creative concept to realize multi-wavelength synchronization from a single laser system. Our work finds a simple and compact solution for the construction of dual-wavelength synchronized fiber lasers operating at typical technical wavelengths from near-infrared to the mid-infrared range, which will facilitate a number of application demands where pulse synchronization is indispensable.
Funding source: Academy of Finland Flagship Programme, Photonics Research and Innovation
Award Identifier / Grant number: PREIN, 320167
-
Author contributions: J. Z., D. L. and Z. S. conceived the idea and developed the analyticalframework. P. L., Q. Z., Z. X. and E. I. K. fabricated and characterized the DWCNTs. J. Z.,X. C., B. Z. and W. G. carried out experimental works. Z. S. supervised the study. All authorsparticipated in discussions of the results. J. Z. and D. L. wrote the manuscript with feedbackfrom all authors. All authors have accepted responsibility for the entire content of thismanuscript and approved its submission.
-
Research funding: This research was supported by the Academy of Finland Flagship Programme, Photonics Research and Innovation (PREIN, 320167); The State Scholarship Fund of China.
-
Conflict of interest statement: The authors declare no conflicts of interest.
-
Data availability: Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
[1] C. R. Phillips, J. Jiang, C. Mohr, et al.., “Widely tunable midinfrared difference frequency generation in orientation-patterned GaAs pumped with a femtosecond Tm-fiber system,” Opt. Lett., vol. 37, pp. 2928–2930, 2012, https://doi.org/10.1364/ol.37.002928.Search in Google Scholar
[2] M. C. Fischer, J. W. Wilson, F. E. Robles, and W. S. Warren, “Invited Review Article: Pump-probe microscopy,” Rev. Sci. Instrum., vol. 87, p. 031101, 2016.10.1063/1.4943211Search in Google Scholar PubMed PubMed Central
[3] M. Baumgartl, M. Chemnitz, C. Jauregui, et al.., “All-fiber laser source for CARS microscopy based on fiber optical parametric frequency conversion,” Opt. Express, vol. 20, pp. 4484–4493, 2012, https://doi.org/10.1364/oe.20.004484.Search in Google Scholar
[4] C. Manzoni, O. D. Mücke, G. Cirmi, et al.., “Coherent pulse synthesis: towards sub-cycle optical waveforms: coherent pulse synthesis: towards sub-cycle optical waveforms,” Laser Photonics Rev., vol. 9, pp. 129–171, 2015, https://doi.org/10.1002/lpor.201400181.Search in Google Scholar
[5] M. R. X. De Barros and P. C. Becker, “Two-color synchronously mode-locked femtosecond Ti:sapphire laser,” Opt. Lett., vol. 18, pp. 631–633, 1993, https://doi.org/10.1364/ol.18.000631.Search in Google Scholar PubMed
[6] D. R. Dykaar and S. B. Darack, “Sticky pulses: two-color cross-mode-locked femtosecond operation of a single Ti:sapphire laser,” Opt. Lett., vol. 18, pp. 634–636, 1993, https://doi.org/10.1364/ol.18.000634.Search in Google Scholar PubMed
[7] J. M. Evans, D. E. Spence, D. Burns, and W. Sibbett, “Dual-wavelength self-mode-locked Ti:sapphire laser,” Opt. Lett., vol. 18, pp. 1074–1076, 1993, https://doi.org/10.1364/ol.18.001074.Search in Google Scholar PubMed
[8] Z. Wei, Y. Kobayashi, Z. Zhang, and K. Torizuka, “Generation of two-color femtosecond pulses by self-synchronizing Ti:sapphire and Cr:forsterite lasers,” Opt. Lett., vol. 26, pp. 1806–1808, 2001, https://doi.org/10.1364/ol.26.001806.Search in Google Scholar PubMed
[9] W. Seitz, T. R. Schibli, U. Morgner, et al.., “Passive synchronization of two independent laser oscillators with a Fabry–Perot modulator,” Opt. Lett., vol. 27, pp. 454–456, 2002, https://doi.org/10.1364/ol.27.000454.Search in Google Scholar PubMed
[10] T. R. Schibli, J. Kim, O. Kuzucu, et al.., “Attosecond active synchronization of passively mode-locked lasers by balanced cross correlation,” Opt. Lett., vol. 28, pp. 947–949, 2003, https://doi.org/10.1364/ol.28.000947.Search in Google Scholar PubMed
[11] A. Martinez and Z. Sun, “Nanotube and graphene saturable absorbers for fibre lasers,” Nat. Photonics, vol. 7, pp. 842–845, 2013, https://doi.org/10.1038/nphoton.2013.304.Search in Google Scholar
[12] R. Mary, D. Choudhury, and A. K. Kar, “Applications of fiber lasers for the development of compact photonic devices,” IEEE J. Sel. Top. Quant. Electron., vol. 20, pp. 72–84, 2014, https://doi.org/10.1109/jstqe.2014.2301136.Search in Google Scholar
[13] U. Keller, “Recent developments in compact ultrafast lasers,” Nature, vol. 424, pp. 831–838, 2003, https://doi.org/10.1038/nature01938.Search in Google Scholar PubMed
[14] M. Gaponenko, P. W. Metz, A. Härkönen, et al.., “SESAM mode-locked red praseodymium laser,” Opt. Lett., vol. 39, pp. 6939–6941, 2014, https://doi.org/10.1364/ol.39.006939.Search in Google Scholar PubMed
[15] A. H. Quarterman, K. G. Wilcox, V. Apostolopoulos, et al.., “A passively mode-locked external-cavity semiconductor laser emitting 60-fs pulses,” Nat. Photonics, vol. 3, pp. 729–731, 2009, https://doi.org/10.1038/nphoton.2009.216.Search in Google Scholar
[16] L. A. Gomes, L. Orsila, T. Jouhti, and O. G. Okhotnikov, “Picosecond SESAM-based ytterbium mode-locked fiber lasers,” IEEE J. Sel. Top. Quant. Electron., vol. 10, pp. 129–136, 2004, https://doi.org/10.1109/jstqe.2003.822918.Search in Google Scholar
[17] M. Rusu, R. Herda, and O. G. Okhotnikov, “Passively synchronized two-color mode-locked fiber system based on master-slave lasers geometry,” Opt. Express, vol. 12, pp. 4719–4724, 2004, https://doi.org/10.1364/opex.12.004719.Search in Google Scholar PubMed
[18] M. Rusu, R. Herda, and O. G. Okhotnikov, “Passively synchronized erbium (1550-nm) and ytterbium (1040-nm) mode-locked fiber lasers sharing a cavity,” Opt. Lett., vol. 29, pp. 2246–2248, 2004, https://doi.org/10.1364/ol.29.002246.Search in Google Scholar PubMed
[19] S. Y. Set, H. Yaguchi, Y. Tanaka, et al.., OFC 2003 Optical Fiber Communications Conference, Atlanta USA, 2003.Search in Google Scholar
[20] T. Hasan, Z. Sun, F. Wang, et al.., “Nanotube–polymer composites for ultrafast Photonics,” Adv. Mater., vol. 21, pp. 3874–3899, 2009, https://doi.org/10.1002/adma.200901122.Search in Google Scholar
[21] Z. Sun, T. Hasan, F. Torrisi, et al.., “Graphene mode-locked ultrafast laser,” ACS Nano, vol. 4, pp. 803–810, 2010, https://doi.org/10.1021/nn901703e.Search in Google Scholar PubMed
[22] Q. Bao, H. Zhang, Y. Wang, et al.., “Atomic-layer graphene as a saturable absorber for ultrafast pulsed lasers,” Adv. Funct. Mater., vol. 19, pp. 3077–3083, 2009, https://doi.org/10.1002/adfm.200901007.Search in Google Scholar
[23] T. Hasan, Z. Sun, P. Tan, et al.., “Double-wall carbon nanotubes for wide-band, ultrafast pulse generation,” ACS Nano, vol. 8, pp. 4836–4847, 2014, https://doi.org/10.1021/nn500767b.Search in Google Scholar PubMed PubMed Central
[24] M. Chernysheva, A. Bednyakova, M. Al Araimi, et al.., “Double-wall carbon nanotube hybrid mode-locker in tm-doped fibre laser: a novel mechanism for robust bound-state solitons generation,” Sci. Rep., vol. 7, pp. 1–11, 2017.10.1038/srep44314Search in Google Scholar PubMed PubMed Central
[25] Q. Zhang, J. S. Nam, J. Han, et al.., “Large‐diameter carbon nanotube transparent conductor overcoming performance–yield tradeoff,” Adv. Funct. Mater., vol. 32, p. 2103397, 2022, https://doi.org/10.1002/adfm.202103397.Search in Google Scholar
[26] Y. S. Fedotov, S. M. Kobtsev, R. N. Arif, A. G. Rozhin, C. Mou, and S. K. Turitsyn, “Spectrum-pulsewidth-and wavelength-switchable all-fiber mode-locked Yb laser with fiber based birefringent filter,” Opt. Express, vol. 20, pp. 17797–17805, 2012, https://doi.org/10.1364/oe.20.017797.Search in Google Scholar
[27] M. Betz, F. Sotier, F. Tauser, S. Trumm, A. Laubereau, and A. Leitenstorfer, “All-optical phase locking of two femtosecond Ti:sapphire lasers: a passive coupling mechanism beyond the slowly varying amplitude approximation,” Opt. Lett., vol. 29, pp. 629–631, 2004, https://doi.org/10.1364/ol.29.000629.Search in Google Scholar PubMed
[28] Z. Wei, Y. Kaboyashi, and K. Torizuka, “Passive synchronization between femtosecond Ti:sapphire and Cr:forsterite lasers,” Appl. Phys. B, vol. 74, pp. s171–s176, 2002, https://doi.org/10.1007/s00340-002-0881-0.Search in Google Scholar
[29] D. R. Dykaar, S. B. Darack, and W. H. Knox, “Cross-locking dynamics in a two-color mode-locked Ti:sapphire laser,” Opt. Lett., vol. 19, pp. 1058–1060, 1994, https://doi.org/10.1364/ol.19.001058.Search in Google Scholar PubMed
[30] A. Leitenstorfer, C. Fürst, and A. Laubereau, “Widely tunable two-color mode-locked Ti:sapphire laser with pulse jitter of less than 2 fs,” Opt. Lett., vol. 20, pp. 916–918, 1995, https://doi.org/10.1364/ol.20.000916.Search in Google Scholar PubMed
[31] C. Furst, A. Leitenstorfer, and A. Laubereau, “Mechanism for self-synchronization of femtosecond pulses in a two-color Ti:sapphire laser,” IEEE J. Sel. Top. Quant. Electron., vol. 2, pp. 473–479, 1996, https://doi.org/10.1109/2944.571746.Search in Google Scholar
[32] T. Miura, H. Nagaoka, K. Takasago, et al.., “Active synchronization of two mode-locked lasers with optical cross correlation,” Appl. Phys. B, vol. 75, pp. 19–23, 2002, https://doi.org/10.1007/s00340-002-0994-5.Search in Google Scholar
[33] Y. Kobayashi, D. Yoshitomi, M. Kakehata, H. Takada, and K. Torizuka, “Long-term optical phase locking between femtosecond Ti:sapphire and Cr:forsterite lasers,” Opt. Lett., vol. 30, pp. 2496–2498, 2005, https://doi.org/10.1364/ol.30.002496.Search in Google Scholar PubMed
[34] D. Yoshitomi, Y. Kobayashi, M. Kakehata, et al.., “Ultralow-jitter passive timing stabilization of a mode-locked Er-doped fiber laser by injection of an optical pulse train,” Opt. Lett., vol. 31, pp. 3243–3245, 2006, https://doi.org/10.1364/ol.31.003243.Search in Google Scholar PubMed
[35] T. Walbaum, M. Löser, P. Gross, and C. Fallnich, “Mechanisms in passive synchronization of erbium fiber lasers,” Appl. Phys. B, vol. 102, pp. 743–750, 2011, https://doi.org/10.1007/s00340-010-4350-x.Search in Google Scholar
[36] M. Zhang, E. J. R. Kelleher, A. S. Pozharov, E. D. Obraztsova, S. V. Popov, and J. R. Taylor, “Passive synchronization of all-fiber lasers through a common saturable absorber,” Opt. Lett., vol. 36, pp. 3984–3986, 2011, https://doi.org/10.1364/ol.36.003984.Search in Google Scholar
[37] B. W. Tsai, S. Y. Wu, C. Hu, W. W. Hsiang, and Y. Lai, “Subfemtosecond hybrid synchronization between ultrafast Yb and Er fiber laser systems by controlling the relative injection timing,” Opt. Lett., vol. 38, pp. 3456–3459, 2013, https://doi.org/10.1364/ol.38.003456.Search in Google Scholar PubMed
[38] J. Sotor, G. Sobon, J. Tarka, et al.., “Passive synchronization of erbium and thulium doped fiber mode-locked lasers enhanced by common graphene saturable absorber,” Opt. Express, vol. 22, pp. 5536–5543, 2014, https://doi.org/10.1364/oe.22.005536.Search in Google Scholar
[39] K. Y. Lau and M. Z. Zulkifli, “1.56 µm and 1.93 µm synchronized mode-locked fiber laser with graphene saturable absorber,” Infrared Phys. Technol., vol. 112, p. 103606, 2021, https://doi.org/10.1016/j.infrared.2020.103606.Search in Google Scholar
[40] J. H. Wang, J. R. Tian, Z. X. Zhang, Z. Q. Gao, Y. F. Wu, and Y. R. Song, Second Optics Frontier Conference (OFS 2022), Online China, 2022.Search in Google Scholar
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Research Articles
- Broadband synchronization of ultrafast pulse generation with double-walled carbon nanotubes
- Noncontractible loop states from a partially flat band in a photonic borophene lattice
- Experimental investigation of a near-field focusing performance of the IP-Dip polymer based 2D and 3D Fresnel zone plate geometries fabricated using 3D laser lithography coated with hyperbolic dispersion surface layered metamaterial
- 100-Gbps per-channel all-optical wavelength conversion without pre-amplifiers based on an integrated nanophotonic platform
- Multi-height metasurface for wavefront manipulation fabricated by direct laser writing lithography
- Enabling infinite Q factors in absorbing optical systems
- Erbium emitters in commercially fabricated nanophotonic silicon waveguides
- Four-dimensional experimental characterization of partially coherent light using incoherent modal decomposition
- Fine-tuning biexcitons-plasmon coherent states in a single nanocavity
- Möbius edge band and Weyl-like semimetal flat-band in topological photonic waveguide array by synthetic gauge flux
- Dual-band optical collimator based on deep-learning designed, fabrication-friendly metasurfaces
- Thickness insensitive nanocavities for 2D heterostructures using photonic molecules
- Beam-steering metasurfaces assisted coherent optical wireless multichannel communication system
- Asymmetric metasurface photodetectors for single-shot quantitative phase imaging
- Room-temperature unidirectional routing of valley excitons of monolayer WSe2 via plasmonic near-field interference in symmetric nano-slits
Articles in the same Issue
- Frontmatter
- Research Articles
- Broadband synchronization of ultrafast pulse generation with double-walled carbon nanotubes
- Noncontractible loop states from a partially flat band in a photonic borophene lattice
- Experimental investigation of a near-field focusing performance of the IP-Dip polymer based 2D and 3D Fresnel zone plate geometries fabricated using 3D laser lithography coated with hyperbolic dispersion surface layered metamaterial
- 100-Gbps per-channel all-optical wavelength conversion without pre-amplifiers based on an integrated nanophotonic platform
- Multi-height metasurface for wavefront manipulation fabricated by direct laser writing lithography
- Enabling infinite Q factors in absorbing optical systems
- Erbium emitters in commercially fabricated nanophotonic silicon waveguides
- Four-dimensional experimental characterization of partially coherent light using incoherent modal decomposition
- Fine-tuning biexcitons-plasmon coherent states in a single nanocavity
- Möbius edge band and Weyl-like semimetal flat-band in topological photonic waveguide array by synthetic gauge flux
- Dual-band optical collimator based on deep-learning designed, fabrication-friendly metasurfaces
- Thickness insensitive nanocavities for 2D heterostructures using photonic molecules
- Beam-steering metasurfaces assisted coherent optical wireless multichannel communication system
- Asymmetric metasurface photodetectors for single-shot quantitative phase imaging
- Room-temperature unidirectional routing of valley excitons of monolayer WSe2 via plasmonic near-field interference in symmetric nano-slits


