Voltage Lifts of Graphs from a Category Theory Viewpoint
-
Gejza Jenča
ABSTRACT
We prove that the notion of a voltage graph lift comes from an adjunction between the category of voltage graphs and the category of group labeled graphs.
1. Introduction
In this paper, a graph means a structure sometimes called a symmetric multidigraph – that means that it may have multiple darts with the same source and target, and the set of all darts of the graph is equipped with an involutive mapping λ that maps every dart to a dart with source and target swapped.
A voltage graph is a graph in which every dart is labeled with an element of a group in a way that respects the involutive symmetry λ, so that the label of a dart d is inverse to the label of λ(d). Similarly, a group labeled graph has all vertices labeled with elements of a group.
In [8], Gross introduced the construction of a derived graph of a voltage graph. Nowadays, derived voltage graphs are called (ordinary) voltage graph lifts – this is the terminology we will use in the present paper. Let us mention in passing that in [9], voltage graphs were generalized to a more general notion of permutation voltage graphs, in which the darts are labelled with permutations.
After their discovery, voltage graph lifts were extensively investigated in many papers. Voltage graph lifts were applied for example in the research concerning the degree-diameter problem [3,4], lifting graph automorphisms [15] and several other areas of graph theory.
In the present paper, we prove that there is an adjunction

between the category Volt of voltage graphs and a category Lab of group labeled graphs. We prove that for every object G of Volt, the underlying graph of the voltage graph LR(G) is isomorphic to the voltage graph lift of G.
2. Preliminaries
We assume basic knowledge of category theory; for notions not explained here see [14,16].
2.1. Adjunctions
There are several different but equivalent definitions of an adjoint pair of functors. For our purposes, the following is the most convenient one.
Definition 2.1
([14: (ii) of Theorem IV.1]). Let
of

commutes.
The family
An important fact concerning the notion of an adjoint pair of functors is that each of the functors F, G determines the other one and the counit, up to isomorphism.
We will need another (perhaps more familiar) characterization of an adjoint pair of functors. For objects O1, O2 of a category
See [14: section IV.1].
2.2. Pullbacks
Let f: X → A, q: B → A be a pair of morphisms in a category

Then a pullback is the limit of this diagram. In other words, it is an object (denoted by X ×A B) equipped with morphisms q*(f): X ×A B → B and f*(q): X ×A B → X such that the square (2.3) in the diagram

commutes and for every object V and a pair of morphisms vX : V → X and vB: V → B such the outer square of the diagram (2) commutes, there is a unique morphism u: V → X ×A B such that both triangles (2.1) and (2.2) commute. We say that q*(f) is a pullback of f along q and that f*(q) is a pullback of q along f.
Let us describe pullbacks in the usual category of sets and mappings, denoted by Set.
Example 2.2.
Consider a diagram of shape (1) in Set. A pullback X ×A B can be constructed as a subset of the direct product of sets X × B, given by
and the maps f*(q) and q*(f) are the projections:
Note that, whenever A is a singleton, f(x) = q(b) for all pairs (x, b) ∈ X × B, so in this case X ×AB = X × B.
2.3. Graphs
A graph is a quintuple G = (V, D, s, t, λ), where
D is the set of darts of G;
V is the set of vertices of G;
s, t: D → V are the source and target maps, respectively;
λ: D → D is a mapping such that λ ○ λ = idD;
s ○ λ = t.
The mapping λ is called the dart-reversing involution of G. Note that t ○ λ = s ○ λ ○λ = s ○idD = s.
All the data in a graph (V, D, s, t, λ) can be expressed graphically by a commutative diagram:

We write V(G) for the set of vertices of G and D(G) for the set of darts of G. Usually we will identify G with the pair (V(G), D(G)) and discard s, t, λ from the signature. We say that s, t, λ are the structure maps of G.
Note that λ comes from an action of
semiedges: λ(d) = d;
loops: non-semiedges with s(d) = t(d);
links: all the other edges, that means λ(d) ≠ d and s(d) ≠ t(d).
A morphism of graphs f: G → H is a pair of mappings (fV, fD), where fV : V(G) → V(H) and fD: D(G) → D(H) are such that for every dart d ∈ D(G), s(fD(d)) = fV(s(d)), t(fD(d)) = fV(t(d)) and λ(fD(d)) = fD(λ(d)). Clearly, graphs equipped with morphisms form a category, denoted by Graph.
2.4. Graphs are functors
As outlined above, every graph is a diagram in Set. This can be formulated as follows: a graph is a functor from a certain finite category gph to the category Set. This category gph has two objects {D, V}, and three non-identity morphisms {s, t, λ} that behave as in the diagram (3). The morphisms of graphs can then be represented as natural transformations of functors from gph to Set, so the category Graph can be identified with a category of functors [gph, Set].
2.5. Pullbacks of graphs
Since graphs are functors, it follows that limits/colimits in Graph can be computed pointwise: we can compute a limit/colimit separately for vertices and darts and then equip the resulting sets with structure maps to obtain a graph.
In particular, given a pair of morphisms f1, f2

in Graph, we can compute the pullback simply as
The projections

are computed in the obvious way:
2.6. Group labeled graphs
A group labeled graph is a triple (G, Γ, β), where G is a graph, Γ is a group and β: V(G) → Γ is a mapping, called a Γ-labeling on G.
A morphism of group labeled graphs (G, Γ, β) → (G′, Γ′, β′) is a pair (f, h), where f: G → G′ is a morphism of graphs and h: Γ → Γ′ is a morphism of groups such that, for all v ∈ V(G), h(β(v)) = β′(fV(v)). The composition of morphisms is defined in a straightforward way: (f1, h1) ○ (f2, h2) = (f1 ○ f2, h1 ○ h2). Clearly, the class of all group labeled graphs equipped with their morphisms forms a category, which we denote by Lab.
Let X be a set. Let
Let us write U: Grp → Set for the “forgetful” functor that maps a group to its underlying set and denote
Proposition 2.3.
The functor
Proof.
Obviously, for every set X and a graph G,
hence
Corollary 2.4.
For every pair Γ1, Γ2 of groups,
Proof.
Every right adjoint functor preserves limits. □
A Γ-labeling β on a graph G is the same thing as a morphism of graphs

Composition of morphisms in Lab corresponds to horizontal pasting of such commutative squares. This shows that the category Lab is isomorphic to the comma category
2.7. Voltage graphs
A voltage graph is a triple (G, Γ, α), where G is a graph and α: D(V) → Γ is a mapping such that α(λ(d)) = (α(d))−1, called a Γ-voltage on G.
A morphism of voltage graphs (G, Γ, α) → (G′, Γ′, α′) is a pair (f, h), where f: G → G′ is a morphism of graphs and h: Γ → Γ′ is a morphism of groups such that, for all d ∈ D(G), h(α(d)) = α′(fD(d)). The composition is defined similarly as in Lab. The class of all voltage graphs equipped with morphisms of voltage graphs forms a category, which we denote by Volt.
Similarly as for Lab, it is possible to represent Volt as a certain category of morphisms in Graph. Indeed, consider the digraph ℓ(Γ) with a single vertex v and D(ℓ(Γ)) = Γ. Both s and t are just constant maps with the constant v and λ: D(ℓ(Γ)) → D(ℓ(Γ)) is given by λ(a) = a−1; ℓ is then a functor from Grp to Graph. Note that the edge {a, λ(a)} of ℓ(Γ) is a semiedge for a = a−1, otherwise it is a loop.
Proposition 2.5.
ℓ is a right adjoint functor.
Proof.
The proof is very similar to the proof of Proposition 2.3 however one needs to replace the intermediate category Set with the category
Corollary 2.6.
For every pair Γ1, Γ2 of groups, ℓ(Γ1 × Γ2) ≃ ℓ(Γ1) × ℓ(Γ2).
Proof.
Every right adjoint functor preserves limits. □
A voltage α on a graph G is the same thing as a morphism of graphs α: G → ℓ(Γ). Under this identification, a morphism in Volt (f, h): (G, Γ, α) → (G′, Γ′, α′) is the same thing as a commutative square in Graph

and composition of morphisms corresponds to horizontal pasting of such squares. This shows that the category Volt is isomorphic to the comma category Graph ↓ ℓ.
2.8. Derived voltage graphs
Definition 2.7
([10]). Let (G, Γ, α) be a voltage graph. There is a voltage graph lift of (G, Γ, α), denoted by (Gα, Γ, α′)
V(Gα) = V(G) × Γ;
D(Gα) = D(G) × Γ;
s(d, x) = (s(d), x);
t(d, x) = (t(d), x.α(d));
λ(d, x) = (λ(d), x.α(d));
α′(d, x) = α(d).
Let us remark that in the original definition in [8], the voltage graph lift of a voltage graph is just a graph (not a voltage graph).
For every voltage graph (G, Γ, α), there is a morphism ϵ(G,Γ,α) of graphs from Gα to G given by the projection
Example 2.8.
Consider the

A
2.9. Fibrations and covers
An in-neighbourhood N(v) of a vertex v of a graph is the set of darts with target v. A morphism of graphs f: G′ → G is a fibration if for every vertex v ϵ V(G′), fD restricted to N(v) is a bijection from N(v) to N(f(v)). A fibration is a covering if and only if it is surjective on vertices. The following proposition is well known.
Proposition 2.9.
For every voltage graph (G, Γ, α), the canonical projection p: Gα → G given by pv(v, x) = v and pD (d, x) = d is a covering.
A covering f: G′ → G is regular if there is a group Γ that acts freely on G′ and an isomorphism i: G′/Γ → G such that i ○ ωΓ = f, where ωΓ: G′ → G′/Γ is the quotient map of the action.
For every voltage graph (G, Γ, α), Γ acts freely on Gα and the canonical projection p: Gα → G is a regular covering associated with this action. Moreover, it can be proved that every regular covering f: G′ → G is isomorphic to the canonical projection for some voltage on G (see [8] or [10], Theorems 2.2.1 and 2.2.2).
The more general notion of permutation voltage graphs can be used to represent all coverings of graphs [9].
3. The adjunction between Volt and Lab
Consider a group labeled graph (G, Γ, β). If we want to construct a voltage graph from (G, Γ, β), it is natural to equip darts of G with a voltage given by the “quotient” of labels along the edge. Formally, there is a voltage graph L(G, Γ, β) = (G, Γ, α) with the voltage α given by the rule α(d) = β(s(d))−1β(t(d)), see Figure 2. For an abelian group Γ, this construction of a voltage graph from a Γ-labeled graph is well known in the theory of flows on graphs [2: Chapter II]; in this context, the vertex labels are called potentials. It is clear that every L(G, Γ, β) satisfies the Kirchhoff laws. Moreover, it is easy to check that every voltage graph (G, Γ, α) that satisfies the Kirchhoff laws is in the range of the functor L.

A
For every group Γ, there is a morphism of graphs
If we identify
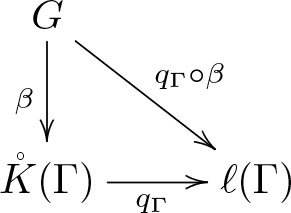
So in what follows, we sometimes write L(β) for qΓ ○ β.
Proposition 3.1
The family of morphisms {qΓ}Γϵobj(Grp) is a natural transformation from
Proof.
Let h: Γ → Γ′ be a morphism of groups. We need to prove that the naturality square at h

commutes. For vertex components of the morphisms, this is trivial because ℓ(Γ′) has only one vertex. For every
□
Let (f, h): (G, Γ, β) → (G′, Γ′, β′) be a morphism in Lab. Consider the diagram

Since (f, h) is a morphism in Lab, the square (4.1) commutes. By Proposition 3.1, the square (4.2) commutes. The left and right vertical composites qΓ ○ β and qΓ′ ○ β′ are L(β) and L(β′), respectively. So the whole diagram (4) commutes and we see that (f, h) is a morphism from L(β) to L(β′) in Volt. Thus, we may put L(f, h) = (f, h), and it is then clear that L is a functor.
Theorem 3.2.
L is a left adjoint functor.
Proof.
Let us describe a right adjoint functor R: Volt → Lab associated to the functor L. For every voltage graph (G, Γ, α), we put

To specify R on morphisms, we use the fact that pullback is a limit. In detail, let
be a morphism of voltage graphs. Consider the diagram in Graph

The cell (6.1) is a pullback square, the cell (6.5) is a naturality square for q at h, and the middle cell (6.3) is just the (f, h) morphism in Volt. Therefore, the boundary of the diagram consisting of (6.1), (6.5) and (6.3) commutes, meaning that
Since (6.4) is a pullback square over the span (α′, qΓ′), there is a unique morphism u such that both (6.2) and the outer square of (6) commute. Since the outer square of (6) commutes, (u, h) is a morphism from R(α) to R(α′) in Lab, and we may put R(f, h) – (u, h). We omit the proof of functoriality of R since it it just a straightforward exercise in the “universality of the pullback”.
However, it is also possible to observe that R is a functor by describing u explicitly:
To specify the counit, we first note that for a voltage graph (G, Γ, α), LR(G, Γ, α) is the voltage graph

Note that the commutativity of (7) follows from the commutativity of (5).
To prove that the family of all these ϵ(G, γ, α) is a counit of the adjunction L ⊣ R, we need to prove that for every group labelled graph (G′, Γ′, β) and every morphism of voltage graphs
there is a unique morphism of group labelled graphs (u, w): (G′, Γ′, β) → R(G, Γ) such that the diagram in Volt

commutes. If such (u, w) exists, then ϵ(G, Γ,α) ○ L(u, w) = (f, h) in Volt implies that idΓ ○ w – h in Grp, so w = h, and the uniqueness of w is thus clear. What remains to prove is the existence and uniqueness of u, under the assumption w = h.
The assumption that (f, h) in (8) is a morphism of voltage graphs means that the diagram

in Graph commutes. Consider the diagram

The outer border of (10) is the commutative square (9) – the (f, h) morphism we want to express as in (8). In particular, we already know that the outer border of (10) commutes. The square (10.4) commutes because it is the naturality square for q at h. From this, we obtain
and by the universality of the pullback
Note that the commutative square (10.1) is just a Lab-morphism (u, h): (G′, Γ′, β) → R(G, Γ, α). Applying the functor L on (u, h), that means, pasting of the squares (10.1) and (10.4) gives us a morphism L(u, h): L(G′, Γ′, β) → LR(G, Γ, α). The cell (10.3) is just ϵ(G, Γ, α). Composing in Volt ϵ(G, Γ, α) ○ L(u, h) gives us the Volt-morphism
and we already know that α*(qΓ) ○ u = f, so ϵ(G, Γ, α) ○ L(u, h) = (f, h). It remains to note that we have already proved the uniqueness of u. □
Let us examine the structure of R(G, Γ, α) for the case of a single-vertex graph G. By our main result Theorem 3.5 and [10: Theorem 2.2.3], we see that R(G, Γ, α) is a Cayley graph. However, it is perhaps interesting to describe the behaviour of our construction in this case.
Definition 3.3.
Let Γ be a group and let S be a subset of Γ that is closed under taking inverses. The Cayley graph of Γ induced by S [7]) is the graph
The structural maps of
Naturally, every
Corollary 3.4.
Let Γ be a group and let S be a subset of Γ that is closed with respect to taking inverses. Let (G, Γ, α) be a voltage graph with a single vertex v, such that D(G) = S and α(x) = x. As a group-labeled graph, R(G, Γ, α) is isomorphic to the Cayley graph of Γ induced by S.
Proof.
Let us compute R(G, Γ, α) as a pullback (5). Clearly, since V(ℓ(Γ)) is a singleton,
For darts, we can compute a pullback in Set
The pullback square in Set is

where j is the inclusion of S into Γ. We have
The structure maps of the pullback graph are
and its labeling is given by β(v, x) = x. Moreover, note that there are obvious isomorphisms of sets {v} × Γ ≃ Γ and
and it is easy to see that this pair of isomorphisms of sets give us an isomorphism
Theorem 3.5.
For every voltage graph (G, Γ, α), the graph LR(G, Γ, α) is isomorphic to the voltage graph lift of (G, Γ, α).
Proof.
We adopt the notations of Definition 2.7 here. The underlying graph of LR(G, Γ, α) is
As V(ℓ(Γ)) is a singleton,
so V(LR(G, Γ, α)) = V(Gα) and we may put jv(v, x) = (v, x).
For darts, we see that
The structure maps of
Let us note that
and
It remains to prove that the graph isomorphism j preserves voltages and is thus a morphism in Volt. The voltage of a dart (d, (x1, x2)) of LR(G, Γ, α) is equal to
Let us collect some consequences of Theorem 3.5.
Using Corollary 2.6, we may construct a product of a pair of voltage graphs (G1, Γ1, α1), (G2, Γ2, α2) in Volt as the voltage graph (G1 × G2, Γ1 × Γ2, α1 × α2), where (α1 × α2)(d1, d2) = (α1(d1), α2(d2)). Due to Corollary 2.4, the products in Lab can be described similarly.
Corollary 3.6.
Let (G1, Γ1, α1), (G2, Γ2, α2) be voltage graphs. Then
Proof.
Let us compute
Since R is a right adjoint functor, it preserves limits, therefore
A nice characterization of a fibration using pullback can be found in [1] (the authors attribute this observation to Frank Piessens) a morphism f: G → G′ is a fibration if and only if the square is

a pullback in Set. The proof of the following theorem is then an easy consequence of the so-called two-pullbacks lemma.
Theorem 3.7
([1: Theorem 45]). A pullback of a fibration in Graph along an arbitrary morphism is a fibration.
From this, we obtain a new proof of the fact that the canonical projection pα : Gα → G is a covering.
Proof of Proposition 2.9. By Theorem 3.5 Gα is isomorphic to the pullback
4. Conclusion
Let us outline a possible direction for future research, concerning the voltage graphs and the voltage graph lift construction.
4.1. Group actions instead of groups
For every group Γ, one can construct the category Act(Γ) of all actions of Γ on sets, equipped with equivariant maps. Moreover, for every morphism of groups h: Γ1 → Γ2 there is an obviously defined functor Act (h): Act (Γ2) → Act (Γ1) and this gives us a functor Act : Grpop → Cat.
Let us mention that the categories Act (Γ) are sometimes called permutational categories [12] and figure prominently in the theory of cellular embeddings of graphs [6,13].
From the functor Act, we may construct the category
In this context, the
The pullback of a voltage α: G → ℓ(Γ) along the q(X, Γ, ☉) morphism is then a generalization of the permutation voltage graph lift construction [9], sometimes called a voltage space [15]. It seems that this more general construction arises from an adjunction, as well.
4.2. Bifibrational viewpoint
The obvious projection functors Volt → Grp and Lab → Grp arise as a pullback (in the category of all categories) of the codomain fibration
along the functors
Funding statement: This research is supported by grants VEGA 2/0142/20 and 1/0006/19, Slovakia and by the Slovak Research and Development Agency under the contracts APVV-18-0052 and APVV-20-0069.
Acknowledgement
The author is indebted to both anonymous referees for their valuable comments that helped to improve the paper.
References
[1] BOLDI, P.—VIGNA, S.: Fibrations of graphs, Discrete Math. 243 (2002), 21–66.10.1016/S0012-365X(00)00455-6Search in Google Scholar
[2] BOLLOBÁS, B.: Modern Graph Theory, Springer Science & Business Media, 1998.10.1007/978-1-4612-0619-4Search in Google Scholar
[3] BRANKOVIĆ, L.—MILLER, M.—PLESNÍK, J.—RYAN, J.—ŠIRÁŇ, J.: Large graphs with small degree and diameter: A voltage assignment approach, Australas. J. Combin. 18 (1998), 65–76.Search in Google Scholar
[4] BRANKOVIĆ, L.—MILLER, M.—PLESNÍK, J.—RYAN, J.—ŠIRÁŇ, J.: A note on constructing large Cayley graphs of given degree and diameter by voltage assignments, Electron. J. Combin. 5 (1998), R9.10.37236/1347Search in Google Scholar
[5] BROWN, R.: Topology and Groupoids, www.groupoids.org, 2006.Search in Google Scholar
[6] BRYANT, R. P.—SINGERMAN, D.: Foundations of the theory of maps on surfaces with boundary, Q. J. Math. 36 (1985), 17–41.10.1093/qmath/36.1.17Search in Google Scholar
[7] CAYLEY, A.: Desiderata and suggestions: No. 2. The Theory of Groups: Graphical Representation, Amer. J. Math. 1 (1878), 174–176.10.2307/2369306Search in Google Scholar
[8] GROSS, J. L.: Voltage graphs, Discrete Math. 9 (1974), 239–246.10.1016/0012-365X(74)90006-5Search in Google Scholar
[9] GROSS, J. L.—TUCKER, T. W.: Generating all graph coverings by permutation voltage assignments, Discrete Math. 18 (1977), 273–283.10.1016/0012-365X(77)90131-5Search in Google Scholar
[10] GROSS, J. L.—TUCKER, T. W.: Topological Graph Theory, Courier Corporation, 2001.Search in Google Scholar
[11] JACOBS, B.: Categorical, Logic and Type Theory, Elsevier, 1999.Search in Google Scholar
[12] JONES, G. A.: Combinatorial categories and permutation groups, Ars Math. Contemp. 10(2) (2016), 237–254.10.26493/1855-3974.545.fd5Search in Google Scholar
[13] JONES, G. A.—SINGERMAN, D.: Theory of maps on orientable surfaces, Proc. Lond. Math. Soc. 3 (1978), 273–307.10.1112/plms/s3-37.2.273Search in Google Scholar
[14] LANE, S. M.: Categories for the Working Mathematician. Grad. Texts in Math. 5, Springer-Verlag, 1971.10.1007/978-1-4612-9839-7Search in Google Scholar
[15] MALNIČ, A.—NEDELA, R.—ŠKOVIERA, M.: Lifting graph automorphisms by voltage assignments, European J. Combin 21 (2000), 927–947.10.1006/eujc.2000.0390Search in Google Scholar
[16] RIEHL, E.: Category Theory in Context, Courier Dover Publications, 2016.Search in Google Scholar
© 2023 Mathematical Institute Slovak Academy of Sciences
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Voltage Lifts of Graphs from a Category Theory Viewpoint
- Extensions and Congruences of Partial Lattices
- On Recurrences in Generalized Arithmetic Triangle
- The Asymptotics of the Geometric Polynomials
- D(4)-Triples with Two Largest Elements in Common
- Hardy-Leindler Type Inequalities for Multiple Integrals on Time Scales
- A New Version of q-Hermite-Hadamard’s Midpoint and Trapezoid Type Inequalities for Convex Functions
- Existence and Finite-Time Stability Results for Impulsive Caputo-Type Fractional Stochastic Differential Equations with Time Delays
- On Oblique Domains of Janowski Functions
- Sharp Approximations for the Generalized Elliptic Integral of the First Kind
- Topological Properties of Jordan Intuitionistic Fuzzy Normed Spaces
- Evaluation of Norm of (p, q)-Bernstein Operators
- Weyl ρ-Almost Periodic Functions in General Metric
- Certain Fixed Point Results On 𝔄-Metric Space Using Banach Orbital Contraction and Asymptotic Regularity
- Yamabe Solitons and τ-Quasi Yamabe Gradient Solitons on Riemannian Manifolds Admitting Concurrent-Recurrent Vector Fields
- On the Bivariate Generalized Gamma-Lindley Distribution
- New Insights on the Multivariate Skew Exponential Power Distribution
- On Locally Finite Orthomodular Lattices
Articles in the same Issue
- Voltage Lifts of Graphs from a Category Theory Viewpoint
- Extensions and Congruences of Partial Lattices
- On Recurrences in Generalized Arithmetic Triangle
- The Asymptotics of the Geometric Polynomials
- D(4)-Triples with Two Largest Elements in Common
- Hardy-Leindler Type Inequalities for Multiple Integrals on Time Scales
- A New Version of q-Hermite-Hadamard’s Midpoint and Trapezoid Type Inequalities for Convex Functions
- Existence and Finite-Time Stability Results for Impulsive Caputo-Type Fractional Stochastic Differential Equations with Time Delays
- On Oblique Domains of Janowski Functions
- Sharp Approximations for the Generalized Elliptic Integral of the First Kind
- Topological Properties of Jordan Intuitionistic Fuzzy Normed Spaces
- Evaluation of Norm of (p, q)-Bernstein Operators
- Weyl ρ-Almost Periodic Functions in General Metric
- Certain Fixed Point Results On 𝔄-Metric Space Using Banach Orbital Contraction and Asymptotic Regularity
- Yamabe Solitons and τ-Quasi Yamabe Gradient Solitons on Riemannian Manifolds Admitting Concurrent-Recurrent Vector Fields
- On the Bivariate Generalized Gamma-Lindley Distribution
- New Insights on the Multivariate Skew Exponential Power Distribution
- On Locally Finite Orthomodular Lattices

