Scalable and effective multi-level entangled photon states: a promising tool to boost quantum technologies

1 Introduction

Photons (the quantum states of light) are essential building blocks for both exploring the fundamental nature of physics and for applied science, as they enable the development of new disparate technologies such as quantum communications [1], [2], [3], metrology [4], [5], [6], computing [7], [8], [9], [10], boson sampling [11, 12], and quantum sensing [13]. Photons hold indeed several advantageous and unique features that mediate their exploitation in quantum technologies. For instance, in stark contrast to other quantum systems such as trapped ions [14, 15] and ultra-cold atoms [16] that typically necessitate cryogenic temperatures, photons can be operated at room temperature, which entails an easy out-of-the-lab reproducibility and use of photonic platforms. Furthermore, photons can propagate over long distances (hundreds of kilometers [17], [18], [19], thus allowing quantum communications between locations that are situated thousands of km apart [20, 21]) both in free space and in telecom-compatible optical fibers. Such propagation has typically negligible impacts on photon state coherence. This means that decoherence (given by the loss of a definite phase relation between the quantum states of a system) can only affect those photons that are exposed to a different environment and thus to uncorrelated noise contributions (for instance, when they travel through distinct channels). This property makes optical quantum states particularly suitable for, e.g., satellite-based [20, 21] and fiber-based [19, 22, 23] quantum communications. Photonic platforms are also characterized by low (<10⁻⁵) error rates, which are several orders of magnitude below platforms that are instead based on quantum matter. This property makes photonics a very reliable platform to achieve fault-tolerant quantum computers in the near future [24]. Finally, photons possess a number of distinct degrees of freedom (DOFs) which are useful, for instance, for scalable information encoding. Specifically, DOFs such as the optical path [25], [26], [27], the orbital angular momentum (OAM) [28, 29], the generation time [30], [31], [32], [33], [34], and the frequency [35], [36], [37] (the latter two also known as time- and frequency-bins, respectively) enable access to high-dimensional discrete quantum states (i.e., multi-level or ‘qudits’). The use of d-level photonic systems offers significant advantages with respect to their two-level counterparts (qubits) in terms of practicability and applications. For instance, qudits can increase the sensitivity in quantum imaging schemes, the key-rate and robustness of quantum communication protocols, as well as they allow, as previously mentioned, for more efficient and error-tolerant quantum computation [2]. Finally, d-level photon states are more noise tolerant relative to qubits, with their robustness improving for an increasing number of levels [38, 39].

In this context, the time and the frequency DOFs offer a unique, robust framework to generate qudits on integrated photonic platforms (on chip) [35, 37], as well as to manipulate and process multiple temporal and spectral components in a single spatial mode (such as in a standard optical fiber) [33, 37, 40]. This allows the generation and control of complex (multi-partite and/or multi-level) quantum states while keeping the size and complexity of the photonic platforms relatively low. In quantum optics, single photons are typically generated by using emissions from, e.g., quantum dots [41] and vacancy defects (for example, in diamonds) [42], while photon pairs are generated by mainly using two nonlinear processes. One is spontaneous parametric down-conversion (SPDC), which is achieved in second-order nonlinear media such as χ ⁽²⁾ crystals (e.g., BBO [43, 44] or KTP [45]) and waveguides made of, e.g., periodically poled lithium niobate (PPLN) [46], [47], [48]. The other is spontaneous four-wave mixing (SFWM), which is achieved in third-order nonlinear media such as silicon-based integrated chips [49, 50] and microcavity resonators (made of, e.g., silicon nitride [51], [52], [53] and Hydex [31, 37, 54, 55]). Following the advantageous photon properties and the several platforms exploitable for their generation, quantum science is increasingly investing in quantum photonics toward out-of-the-lab affordable applications. In this context, a widespread use of quantum photonics requires photons to be generated in integrated, CMOS-compatible chips [56], [57], [58], as well as to be manipulated through optical devices that are compatible with off-the-shelf communication infrastructures, such as optical fibers.

Another key resource for fundamental quantum physics, as well as for the enhancement and development of the related technology applications, is entanglement [29, 59]. This phenomenon describes purely quantum correlations between microscopic systems that persist independently of the physical distance between them or the basis in which those quantum systems are measured. As such, the properties of two or multiple entangled states can only be defined by a wave function that is overall nonseparable [60]. Many entangled systems can be exploited for nonclassical technologies. For example, superconducting qubits [61], neutral atoms [62, 63], and ion traps [64, 65] are typically explored for the realization of quantum computers. In this review we focus on entangled photon states, specifically, discrete optical Bell [66] and cluster [67] states, as they are very promising resources for quantum technology applications [8, 24] (see Section 2 for a detailed description of the topic). For a widespread use of quantum photonics, a complete characterization of photon coherence and entanglement, to be achieved via experimentally practical techniques, is of crucial importance. Ideally, in order to be considered experimentally doable, these techniques would make use of single-qudit projections (as few and as simple as possible), as well as be robust toward experimental noise [38, 39]. Such a robustness includes, for example, high tolerance toward white noise, which is one of the most common profiles in practical scenarios and is seen mainly arising from losses, measurement inaccuracies, as well as from the settings used for quantum state analysis (filters, fibers, phase modulators, etc.). While two-partite entanglement can easily be characterized using feasible methods (e.g., quantum interference and Bell’s inequality violation [37, 38], quantum state tomography [68], [69], [70], and Schmidt decomposition [37, 71]), the characterization of complex entanglement remains challenging, especially in the case of multipartite quantum systems. Extending the approaches established for the characterization of bi-partite entanglement to multipartite states is not straightforward, as these are limited to very restricted cases. For example, the Schmidt mode decomposition for complex quantum states is currently restricted to three-partite systems [72], while the extension of the Bell inequality to multipartite systems (the so-called Mermin inequality) is limited to Greenberger–Horne–Zeilinger (GHZ) [73, 74] and four-partite cluster [75] states.

In this paper, we review our recent advancements in the on-chip generation and fiber-based manipulation of entangled photon pairs for the realization and characterization of d-level Bell [37] and cluster [33] states by exploiting the frequency and time domains. We further report on a recent theoretical approach we developed to identify and characterize complex entanglement via feasible measurement techniques [39]. In Section 2, we provide a generic overview of multi-level Bell and cluster states, by emphasizing the importance of cluster states for quantum photonics applications. In Section 3, we focus on our recent work that describes the generation of multi-level entangled photon pairs through integrated quantum frequency combs (QFCs), which are light sources with a broadband spectrum of equally spaced frequency modes [40, 55, 76], [77], [78], [79], [80], [81]. In Section 4, after outlining the problems related to complex entanglement characterization, we review our approach, based on multi-level stabilizer witnesses, for feasible entanglement identification and characterization of arbitrarily complex photon states. In Section 5, we explain the extent to which these results can contribute to enhancing a broad variety of photon-based quantum technologies.

2 Multi-level entangled photons: Bell and cluster states

Bell states are defined by a class of d ² two-partite entangled states [82, 83] (where d is the number of levels), and are the simplest and most exploited class of entangled states, especially for quantum communication protocols such as quantum state teleportation [17, 83], [84], [85], [86], super-dense coding [87], quantum repeaters [88, 89], and quantum key distribution (QKD) [19, 32, 90, 91]. These technologies can be indeed enhanced by using Bell states. This is the case for, e.g., QKD. While most of QKD protocols are based on single photon generation and transmission [21, 92], employing Bell states allows the use of an exchanged cryptographic key that is device-independent, meaning that no trusted quantum source is needed [93]. This consequently strengthens the security of QKD protocols.

Cluster states are a class of genuine multi-partite entangled states (that is, entanglement is shared across all the quantum parties composing the system), that were introduced first for qubits by Briegel and Raussendorf [67] and then for qudits by Zhou et al. [94]. From a physical point of view, a cluster state is defined as an ensemble of qudits that are located at sites a ∈ ℤ ^D of a D-dimensional lattice in the Euclidean space (with D = 1, 2, 3) and that are entangled via Hamiltonian interactions. In this case, D refers to the Euclidean space in which the cluster state lattice is defined, and it is not related to the dimensionality d of the photonic system, which is provided instead by the Hilbert space, the size of which is given by d ^N , where d represents the chosen DOF (time, frequency, etc.), and N represents the number of particles (or, equivalently, the number of parties). A cluster state can assume different lattice structures, such as box or horseshoe graphs. When qudits undergo interactions with their nearest neighbors in a one-dimensional lattice (i.e., a chain), the cluster state assumes a linear form. The lattice structure of a cluster state can always be converted into another structure by applying unitary operations on the individual qudits. As local unitary operations do not affect entanglement, the resulting state is still a cluster state that is locally equivalent to the previous one and exhibits the same genuine multi-partite entanglement [67]. Two crucial properties characterize cluster states and distinguish them from any other entangled system: maximal connectedness (that is, any cluster state pair can be projected into a Bell state by means of projection measurements on the remaining qudits) and the highest persistency of entanglement (that is, a maximal number of projection measurements is required to fully destroy cluster state entanglement) [67, 94]. These properties allow cluster states to be used as entanglement resources, e.g., to generate Bell or GHZ states by performing local operations on the individual qudits. While two- and three-partite cluster states are locally equivalent to Bell and GHZ states, respectively, in the case of N ≥ 4 parties, cluster states form a unique class of genuine multi-partite entanglement [67, 95].

The most important quantum technology application of cluster states is their use as physical resources for the so-called one-way (or measurement-based) quantum computers, which were proposed for the first time by Raussendorf and Briegel [95, 96]. One-way quantum computers significantly differ from traditional quantum computing schemes that, similarly to classical computing, are based on two-qubit logic gates, which consist of nonlinear interactions driven by single photon states [24, 97]. Since a single photon weakly interacts with matter, two-qubit gate quantum computers are very difficult to implement with scalable platforms. On the one hand, photonic programmable simulators with excellent capabilities have already been demonstrated with matter-based quantum technologies, for example, the 51-atom quantum simulator [62] and diamond-based quantum nanophotonics [98]. On the other hand, very few technologies are considered really promising for scalable quantum computers, in particular, those are based on superconductors [99], trapped ions [64, 65], and silicon photonic circuitry [8, 100, 101]. Due to their tight connection with cluster states, we focus our overview on “one-way photonic quantum computing platforms”. The working principle of a one-way quantum computer consists of encoding information into a given cluster state, processing it, and finally reading it out by means of projection measurements on the individual parties composing the cluster state. The measurement itself thus plays the ‘gating’ action, which is why one-way quantum computers do not necessitate two-qubit logic gates. In these one-way operations, cluster states can be processed only once, as their entanglement is destroyed by the projection measurements. The advantages of one-way quantum computers over their logic-based counterparts are manifold. First, despite the use of a complex physical resource (i.e., the cluster state), the necessary computing operations (i.e., the projections) are relatively simple, in contrast to the complex quantum logic circuits required for two-qubit gate computing schemes [102, 103]. The other advantage of one-way photonic quantum computation is the ability to create large (multipartite and/or high-dimensional) photonic cluster states that are sufficiently free of errors and large enough to allow for topological error corrections. This, in turn, enables fault-tolerant operations [24]. Technology based on cluster states seems the only approach enabling, in the near future, the implementation of a device capable of realizing a comparable number of physical qubits and fidelity in such a way to allow the use of error correction codes. The recent rapid progress of quantum computers [9, 24] has thus intensified the investigation and realization of large cluster states, both in the continuous variable (CV) and in the discrete variable (DV) formalism. For example, in the CV formalism, we recall the cluster state generation based on GHZ states and passive linear optics [104], as well as the very recent demonstration of massive, entangled 2D cluster states obtained by means of squeezed quantum states of light [105, 106]. However, for the purposes of this review, we focus on DVs, specifically on DV linear cluster states, whose lattice is a one-dimensional chain. We refer the reader to, e.g., Refs. [104], [105], [106], [107], [108], [109], [110], [111], [112], [113], [114] for further details on large cluster states realized by using CVs. In contrast with the CV formalism, the demonstration of DV cluster states and one-way photonic quantum computers has been limited so far to two-level systems [95, 115], [116], [117], while the realization of d-level cluster states and the implementation of high-dimensional one-way quantum operations were only achieved in 2019 via the use of the discrete time and frequency domains [33].

3 Scalable approaches for the generation and processing of multi-level entangled photon pairs

Several sources have been exploited for the on-chip generation of multi-level entangled photon pairs, such as arrays of multiple PPLN-based integrated waveguides [26], as well as silicon [27, 118] and silicon-silica [119] monolithic platforms. Approaches based on waveguide arrays mainly exploit path-encoded photon states [26, 120]. While these qudit sources are suitable for the implementation of quantum circuits in gate-based computing schemes [121], increasing the quantum state dimensionality comes at the cost of a growing number of waveguides. This significantly hampers the integrability of the photonic platforms, as well as enhances their complexity. The use of microring resonators for photon pair generation represents a promising approach to address both integrability and complexity issues. First, microrings can be integrated on a chip and are compatible with state-of-the-art CMOS fabrication techniques [35, 52, 54, 122]. Second, they enable the generation of integrated QFCs that, by allowing for entanglement generation over many spectral lines in a single spatial mode, have been demonstrated particularly promising for integrated and scalable quantum photonics [40, 55, 76], [77], [78], [79], [80], [81, 123]. Specifically, QFCs have been exploited for the generation of scalable multi-level photon states in the time and frequency domains, which can be manipulated simultaneously in a single spatial mode (e.g., in a fiber) and are robust over long-distance propagation [33, 37, 40, 77, 124]. Recently, we have demonstrated the robustness of two-level time-bin entanglement over a 40-km long fiber [31], as well as the robustness of d-level frequency-bin entanglement over a 24.2-km long fiber [37]. Furthermore, Ikuta and Takesue demonstrated a four-level time-bin entanglement distribution over a 100-km long fiber [124]. In this sense, advancement in transmission techniques can make time and frequency qudits also compatible with telecommunication speeds (i.e., ∼GHz rates), with immediate network applications.

Here, we focus on the realization of d-level photon pairs by means of integrated QFCs generated within a microring resonator made of silica or high-index glass (i.e., Hydex) [40, 55, 76], [77], [78], [79]. Specifically, such photon pairs are the basis for the preparation of multi-level frequency-entangled Bell states [37], as well as of four-partite three-level (qutrit) time- and frequency-entangled cluster states [33].

3.1 Multi-level frequency-entangled Bell states

In order to generate frequency-entangled qudit pairs, a single resonance of a silicon nitride microring resonator was excited through a spectrally-filtered mode-locked laser [79, 125] at a wavelength of 1550 nm. This excitation resulted in the SFWM-mediated generation of photon pairs (signal, s, and idler, i) spectrally symmetric to the pump and covering multiple resonances of the microcavity. In particular, each photon was generated into a quantum superposition of multiple frequency modes that, together with the energy conservation of the SFWM process, enabled the realization of d-level frequency-entangled two-photon states represented by a wave function of the form

(3.1.1) | Ψ s , i ⟩ = 1 d ∑ k = 1 d | k s ⟩ | k i ⟩ ,

where k and d denote the frequency qudit and the single-state dimensionality, respectively. A frequency dimensionality of d = 10 was reached per photon, leading to a 10 × 10-dimensional Hilbert space.

After filtering the pump, the two photons were sent into a manipulation and detection scheme (illustrated in Figure 1b and c, respectively). A concatenation of standard telecommunications components such as programmable spectral phase filters and electro-optic phase modulators (EOMs) was used for the manipulation/processing scheme, while two superconducting nanowire single-photon detectors (SNSPDs) were used for the detection scheme.

Figure 1:

Scheme for the generation (a), manipulation/processing (b), and detection (c) of multi-level frequency-entangled photon pairs. The inset in the left panel depicts the signal and idler photons being generated in a superposition of multiple frequency modes. The inset in the central panel reports the sidebands produced by the phase modulator for shifting and mixing the frequency modes. Adapted from [37].

The programmable filters were used to impose arbitrary phase and amplitude masks on the spectral modes, while the EOM was used for the deterministic and coherent shifting and mixing of the different qudits (accomplished through the generation of modulation sidebands from the EOM). We first made use of these components to determine the quantum state dimensionality through the measurement of the lower and upper bounds of the Schmidt mode number, estimated via the joint spectral intensity (i.e., via spectrally resolved coincidences) and the second-order coherence function, respectively. The lower and upper bounds resulted in K _low = 9.4 and K _up = 10.45 ± 0.53, confirming a number of relevant orthogonal frequency modes equal to 10. This led us to the conclusion that each photon was generated in a ten-level frequency qudit (i.e., a 10 × 10-dimensional Hilbert space). We then exploited the manipulation scheme to characterize the two-photon entanglement through quantum interference and quantum state tomography measurements, which were specifically obtained by the two-photon projections

(3.1.2) | Ψ proj ⟩ = 1 d ∑ k = 0 d − 1 e i k θ | k ‾ + k ⟩ s ∑ k = 0 d − 1 e i k θ | k ‾ + k ⟩ i .

Here, θ is the phase difference between the signal and the idler, and k ‾ denotes the frequency qudit selected for the projection. Limited by the electro-optic phase modulation efficiency, our quantum state analysis focused on the d = 2, 3, and 4 level cases. To validate the presence of two-photon entanglement, we extracted the visibility from the retrieved quantum interference. Raw (without background subtraction) visibilities of V _d=2 = 83.6%, V _d=3 = 86.6%, and V _d=4 = 86.4% were measured for d = 2, 3, and 4, respectively (see Figure 2a–c). All these values exceed their respective Bell inequality violation thresholds of 70.7, 77, and 81.7%, thus confirming the generation of two-photon entangled qudits.

Figure 2:

Two-photon quantum interference patterns (left panel) for the case of (a) d = 2, (b) d = 3, and (c) d = 4 levels. The raw visibilities reported in each pattern (83.6, 86.6, and 86.4%) demonstrate the Bell inequality violation for the respective thresholds (70.7, 77, and 81.7%). Two-photon quantum state tomography (right panel) for the case of (d) d = 2, (e) d = 3, and (f) d = 4 levels. Fidelities of 88.5, 80.9, 76.6% were obtained for d = 2, 3, and 4, respectively, demonstrating a good agreement between the expected and the measured frequency-entangled Bell states. Adapted from [37].

Finally, to validate the quality of the generated qudit entanglement, we extracted the fidelity from the density matrices reconstructed through quantum state tomography. Fidelities of F _d=2 = 88.5%, F _d=3 = 80.9%, and F _d=4 = 76.6% were obtained for d = 2, 3, and 4, respectively, confirming a good agreement between the measured and the ideal frequency qudit Bell states (see Figure 2d–f).

3.2 Four-partite three-level time- and frequency-entangled cluster states

To generate four-partite cluster states, we exploited the concept of hyper-entanglement [126], which allowed us to make use of just two photons. Hyper-entangled states are multi-partite quantum systems that are simultaneously entangled in two or more independent DOFs, such as polarization, optical path, linear or orbital angular momentum orbital angular momenta [116, 117, 127]. From an experimental viewpoint, two DOFs can be considered independent if they can be individually manipulated. In a hyper-entangled state, each DOF represents a party, while the particles can be seen as the ‘carriers’ for each party. Hyper-entanglement thus enables the realization of multi-partite photon states by means of a reduced number of particles, with significant experimental advantages. For example, the use of hyper-entanglement allows for a reduced size and complexity of the required photonic platforms, an enhanced detection rate (which scales as p ^N , with 0 < p < 1 being the detection probability), as well as an access to a Hilbert space of equal or larger size relative to that accessible through entanglement in a single DOF. In view of this, hyper-entanglement has been considered a promising resource for, e.g., quantum communication protocols, such as remote state preparation in quantum teleportation [128] and super-dense quantum coding [87]. While hyper-entanglement has been widely used to realize multi-partite cluster states, such sources have been limited to qubits, meaning that only four-partite cluster states could be achieved with two hyper-entangled photons in DV platforms [116, 129].

In our work, we exploited the concept of hyper-entanglement for the first time in higher dimensions by making use of two DOFs that are intrinsically the same, that is, time and frequency (time- and frequency-bin entanglement are indeed the discrete forms of energy-time entanglement [30]). In order to consider time and frequency as independent DOFs, it is necessary that the product between the temporal and the spectral mode separations (Δt and Δν, respectively) exceeds the Einstein–Podolsky–Rosen (EPR) limit that is defined for quantum correlations and that is equal to one [130] (namely, Δt · Δν > 1). As we will show, we exceeded the EPR limit, thus enabling the generation of hyper-entanglement with time and frequency modes, which we were able to access and manipulate individually and independently.

Here, as illustrated schematically in Figure 3 [33], we generated time-entanglement by exciting a microring resonator with three optical pulses delayed by Δt = 24 ns (with a pump repetition rate of 250 MHz, corresponding to 4 ns, Figure 3a), while we realized frequency-entanglement by selecting three emission resonances of the microcavity, each separated by Δν = 200 GHz (corresponding to the microring free spectral range, Figure 3b). Such an excitation (centered at 1550 nm) led to the SFWM-enabled generation of signal and idler photons having an emission bandwidth over three cavity resonances and being simultaneously entangled in time and frequency (Figure 3c). Specifically, we could realize a four-partite three-level hyper-entangled state, where the number of parties (four) was given by the time and frequency modes (individually ‘carried’ by each photon), while the number of levels was given by the number of modes (three) per party. As we can see, the product between the time- and the frequency-mode separation (Δt = 24 ns and Δν = 200 GHz, respectively) is much higher than the EPR limit (specifically, Δt · Δν = 4800).

Figure 3:

Scheme for the generation of time–frequency hyper-entanglement. (a) An optical pulse train composed of three pulses excites a nonlinear medium, where photon pairs (signal and idler) are generated through SFWM in a superposition of three time modes, given by the number of pulses. This results in a three-level time-bin entangled two-photon state. (b) A single pulse excites a nonlinear medium placed inside a cavity, where photon pairs are created in a superposition of three spectral modes, given by the number of selected cavity resonances per photon. This leads to a three-level frequency-bin entangled state. (c) Merging the concepts of (a) and (b), an optical pulse train excites a nonlinear cavity, thus generating a photon pair which is simultaneously entangled in time and frequency (i.e., a three-level hyper-entangled two-photon state). Adapted from [33].

However, such a hyper-entangled state is still bi-separable, which means that there is no entanglement between the time and the frequency modes of each photon. In other words, nondestructive projection measurements on the time-entangled state | Ψ 〉 time = ( | 1 s , 1 i 〉 + | 2 s , 2 i 〉 + | 3 s , 3 i 〉 ) do not affect the frequency-entangled state | Ψ 〉 freq = ( | a s , a i 〉 + | b s , b i 〉 + | c s , c i 〉 ) , and vice versa (where | 1 〉 , | 2 〉 , | 3 〉 and | a 〉 , | b 〉 , | c 〉 denote the time and the frequency qutrits, respectively). This feature characterizes instead a cluster state |Ψ_cluster> that is hyper-entangled in time and frequency. Specifically, the cluster state wave function targeted in this experiment is

(3.2.1) | Ψ Cluster 〉 = | 1 s , 1 i 〉 ( | a s , a i 〉 + | b s , b i 〉 + | c s , c i 〉 )                                                   + | 2 s , 2 i 〉 ( | a s , a i 〉 + e i 2 π / 3 | b s , b i 〉 + e − i 2 π / 3 | c s , c i 〉 )                                                   + | 3 s , 3 i 〉 ( | a s , a i 〉 + e − i 2 π / 3 | b s , b i 〉 + e i 2 π / 3 | c s , c i 〉 ) ,

which differs from the bi-separable state by the phase factors α = e ^i2π/3 and β = e^−i2π/3. Adding these phases to the bi-separable quantum state required the coherent access and manipulation of its individual time and frequency modes. We accomplished this task by developing and implementing a controlled-phase (C-phase) gate (see Figure 4) made of fiber-based optical components, specifically, two circulators, a fiber Bragg grating (FBG) array (with frequencies matched to the QFC), and an EOM.

Figure 4:

Cluster state generation through the controlled-phase gate. Left panel: a separable hyper-entangled state is used as the input to the C-phase gate. Central panel: controlled phase gate, consisting of the two circulators, the fiber Bragg mirrors for frequency-to-time mapping, and the phase modulator for adding the specific phase terms in such a way to transform the separable state into the target cluster state. Right panel: four-partite three-level cluster state obtained as C-phase gate output. The two density matrices have been constructed analytically. Adapted from [33].

As described in Figure 4, we sent the quantum state as C-phase gate input through the first circulator and reflected the spectral modes through the FBG array so as to perform frequency-to-time mapping (that is, each frequency mode was temporally dispersed into different time slots). We then added the phase factors α and β through the phase modulator and finally sent the quantum state back to the FBG through the second circulator, in order to reverse the frequency-to-time mapping and obtain the targeted cluster state | Ψ cluster 〉 as output.

We then used the realized cluster state to implement proof-of-principle high-dimensional one-way quantum operations, which were performed by means of two-partite qutrit projections either in time or in frequency. Time and frequency projections resulted in the generation of orthogonal bipartite frequency- and time-entangled states, respectively, the presence of which was validated through quantum interference measurements (for extracting both phases and amplitudes of the cluster state). The orthogonality of such bipartite states was confirmed by estimating the relative phase shift in their respective quantum interference pattern, while their entanglement was confirmed through Bell inequality violations. For time-bin quantum interference, we performed frequency-projections in the basis { | a s , a i 〉 , | b s , b i 〉 , | c s , c i 〉 } through optical filtering, and finally used a two-arm interferometer for simultaneous projections into the superposition of two-time bins (i.e.,  | 1 〉 + e i φ | 2 〉 and | 2 〉 + e i φ | 3 〉 per photon, with φ being a phase – see Figure 5), which resulted in different phase shifts. For frequency-bin quantum interference, we performed time-projections in the basis { | 1 s , 1 i 〉 , | 2 s , 2 i 〉 , | 3 s , 3 i 〉 } through temporal gating (i.e., in the detection), we then added spectral phases and finally mixed the three frequency modes through electro-optic modulation to perform projections of the form | a 〉 + e i φ | b 〉 + e i 2 φ | c 〉 per photon (see Figure 5). Such frequency and time projections resulted in nine different quantum interference patterns, which are showed in Figure 5.

Figure 5:

Quantum interference measurements performed for one-way quantum operations. (a–c) illustrate the results obtained from time-bin interference, while (d–f) depicts the results obtained from frequency-bin interference. Each pattern is reported together with the visibility measured from each projection. All the obtained visibilities exceed the thresholds necessary to violate their respective Bell inequalities (i.e., 70.7% for time-projections and 77.4% for frequency-projections). Adapted from [33].

A fit between the measured interference patterns and the expected bipartite wave functions allowed us to extract all the phase terms composing the two-partite quantum states, while their amplitudes were estimated through 3⁴ = 81 coincidence measurements between all the possible combinations of the temporal and spectral modes. The modulus squared of the scalar product between the measured wave functions was almost zero (on the order of 1 × 10⁻³ ± 2 × 10⁻²), from which we confirmed the orthogonality of the generated bipartite quantum states. From each quantum interference pattern, we finally extracted the respective raw visibility that, violating the Bell inequality, confirmed the realization of two-partite three-level entangled states via time and frequency projections. According to the working principle of measurement-based quantum computers described in Section 2, the successful accomplishment of these operations allowed us to confirm the proof-of-concept implementation of high-dimensional one-way quantum processing.

As a final task, we also validated the genuine four-partite qutrit entanglement of the generated cluster state. While quantum state tomography measurements would have provided full information about the cluster state density matrix, those would have necessitated at least 3⁸ = 6561 projections (see Section 4), the unfeasibility of which is determined not only by their huge number but also by the intricate measurement techniques they require. For example, they may entail multiple projections to be performed at the same time on a d-level system, which is experimentally impractical. For this reason, we needed to explore a more accessible and feasible technique to validate genuine cluster state entanglement. To this end, we made use of a four-partite three-level witness operator that we derived from a theoretical approach developed by our group to determine experimentally feasible universal entanglement witnesses (see Section 4). Specifically, we constructed the witness by using high-dimensional stabilizers composed of the generalized 3 × 3 Pauli matrices (see Section 4) and measured its expectation value, given by

(3.2.2) 〈 W cluster 〉 = 5 / 3 − 1 / 3 Re ( 〈 I 1 I 2 Z 3 Z 4 † 〉 + 〈 Z 1 † Z 2 I 3 I 4 〉 + 〈 I 1 Z 2 X 3 X 4 〉 + 〈 X 1 X 2 Z 3 I 4 〉 + 〈 Z 1 I 2 X 3 X 4 〉 + 〈 Z 1 † Z 2 † X 3 X 4 〉 + 〈 X 1 X 2 I 3 Z 4 〉 + 〈 X 1 X 2 Z 3 † Z 4 † 〉 ) .

Here, Z = | 0 〉 〈 0 | + e i 2 π / 3 | 1 〉 〈 1 | + e − i 2 π / 3 | 2 〉 〈 2 | and X = | 0 〉 〈 1 | + | 1 〉 〈 0 | + | 2 〉 〈 1 | are the 3 × 3-dimensional Pauli matrices corresponding to σ _z and σ _x , respectively, I = | 0 〉 〈 0 | + | 1 〉 〈 1 | + | 2 〉 〈 2 | is the identity, † denotes the transpose conjugate, R e indicates the real part, and each term within the bracket 〈 〉 represents the stabilizer (the matrices are here expressed in the most generic qudit basis { | i 〉 } with i = 0, 1, 2). The subscripts 1, 2, 3, 4 denote the qutrit with respect to each Pauli matrix is applied and measured. Specifically, 1 and 2 are respectively the temporal modes of the signal and the idler, while 3 and 4 are their corresponding frequency modes. To determine the expectation value of such a witness, two types of time and frequency projections were needed: one in the I and Z computational basis ( { | 1 〉 , | 2 〉 , | 3 〉 } and { | a 〉 , | b 〉 , | c 〉 } , and one in the X basis (superpositions of the time and frequency modes | t 1 〉 = 1 / 3 ( | 1 〉 + | 2 〉 + | 3 〉 ) , | t 2 〉 = 1 / 3 ( | 1 〉 + e i 2 π / 3 | 2 〉 + e − i 2 π / 3 | 3 〉 ) , | t 3 〉 = 1 / 3 ( | 1 〉 + e i 2 π / 3 | 2 〉 + e − i 2 π / 3 | 3 〉 ) and | f a 〉 = 1 / 3 ( | a 〉 + | b 〉 + | c 〉 ) , | f b 〉 = 1 / 3 ( | a 〉 + e i 2 π / 3 | b 〉 + e − i 2 π / 3 | c 〉 ) , | f c 〉 = 1 / 3 ( | a 〉 + e i 2 π / 3 | b 〉 + e − i 2 π / 3 | c 〉 ) , respectively).

Projections into the time and the frequency basis { | 1 〉 , | 2 〉 , | 3 〉 } and { | a 〉 , | b 〉 , | c 〉 } were performed through temporal gating (in the detection) and optical filtering, respectively, while projections into the basis { | f a 〉 , | f b 〉 , | f c 〉 } were carried out through electro-optic phase modulation. Projections into the basis { | t 1 〉 , | t 2 〉 , | t 3 〉 } were performed by first assessing the cluster state phases via simultaneous projections into the superposition of two-time modes each, which were accomplished with a two-arm interferometer. The states | t 1 〉 , | t 2 〉 , | t 3 〉 were then reconstructed through the measured quantum interference patterns (see Figure 5). 81 projections were necessary to determine the expectation value of each stabilizer, which led to a total of 81 × 8 = 648 measurements to evaluate the expectation value of the whole witness. From the described projections, we could experimentally extract 243 parameters having a real value between 0 and 1, and used them to determine the expectation value of each stabilizer, which resulted in eight complex numbers having an absolute value smaller than 1 (see Figure 6). We then calculated the expectation of the whole witness by taking the real part of these eight expectation values individually and then summing them up, as shown in Figure 6. We measured (within seven std) a negative expectation value of W = − 0.28 ± 0.04 that, according to the definition of witness operators (see Section 4), confirmed the generation of a genuine four-partite three-level entangled cluster state.

Figure 6:

Measurement of the entanglement witness. Real and imaginary (blue and red bars, respectively) parts of the measured expectation values for the individual terms comprising the witness operator. Since only the eight real parts contribute to the expectation value of the witness, this results in a real number that, being negative, confirms the genuine four-partite three-level entanglement of the generated cluster state. Adapted from [33].

Finally, we made use of the approach we developed in Ref. [39] and describe in Section 4, to test the robustness of the measured cluster state witness over incoherent (white) noise that, being typically caused by losses and measurement setting imprecisions, effects the quantum state purity. The measured cluster state witness can tolerate up to 37.5% of incoherent noise (see Section 4). By comparing this value with the noise threshold of a four-partite two-level cluster state (that is, 33%), we can see that, given the same number of parties, qutrits are more robust than qubits toward white noise, which is a further validation that noise sensitivity decreases with a growing number of levels [38, 39].

4 Experimentally feasible techniques for entanglement identification and characterization: witness operators

A surge in the complexity of the quantum state generally increases the number and difficulty of measurements needed for its characterization. One example of this is quantum state tomography, which necessitates at least d ^2N projections for a full reconstruction of the density matrix. With a growing number of photons/parties N and/or levels d, the quantity as well as the complexity of the measurements needed for quantum state tomography drastically increase, thus hampering its experimental feasibility. On the other hand, quantum photonic applications demand a practical and accessible characterization of quantum states and entanglement independently of their complexity. A promising route toward this purpose is provided by witness operators, which were introduced by Horodecki [60, 131, 132]. A witness W is a Hermitian operator that is used in experiments to validate whether a measured quantum state is close to the ideal target, how much it differs from the target, and whether it is entangled or not. A witness is typically designed in such a way that its expectation value (the quantity measured experimentally) is not negative for all separable states and negative for some entangled states. A witness further allows to distinguish between different classes of entangled states, as it is constructed to be tailored to a specific quantum state [133]. Therefore, according to the witness definition, measuring a non-negative expectation value only provides information that the generated quantum state is not close to the target, while it can still be entangled but belonging to a different class of (entangled) states. For instance, a witness that is constructed to detect the presence of a four-partite cluster state, if applied to a four-partite GHZ state, results in a non-negative expectation value, even though GHZ states are entangled [39]. A main advantage of using witness operators is that important information about the structure and phase components of the investigated quantum state can be retrieved from their measurement, a direct consequence of the fact that these operators are constructed to be tailored to classes of entangled states. As such, while witnesses, in contrast with quantum state tomography, do not provide full knowledge about the density matrix, they enable a deep understanding about how the structures as well as the phase components of a quantum state are affected by, e.g., experimental conditions, quantum state evolution, and interaction with environment and/or with other systems.

Due to its typically complex mathematical structure, measuring a witness operator is a difficult task from an experimental perspective [60]. The realization of complex quantum states, as well as their potential applications for, e.g., quantum photonics, have intensified the need of developing witnesses that are straightforward to be measured in practice. This task has been partially achieved by Tóth and Gühne, who have developed witness operators for the feasible identification of complex quantum states such as cluster and GHZ states by making use of stabilizers [133]. A stabilizer is a quantum operator that, when applied to a given quantum state | ψ 〉 , keeps it unchanged overall (besides a potential global phase factor). As such, a set of stabilizers is unique to a given quantum state (similarly to witnesses) and forms a so-called stabilizer group that allows for full state density matrix reconstruction [39]. The feature that makes stabilizers advantageous for quantum information science and applications is that they can be expressed in terms of Pauli matrices. This means that stabilizers can be measured through single-particle projections, which are considered experimentally easy operations, especially in contrast to joint measurements. This makes stabilizers optimal candidates for the construction of experimentally feasible witness operators, as has been done by Tóth and Gühne for two-level GHZ and cluster states [133]. However, while the stabilizer formalism has been developed also for d-level cluster states through the use of generalized (i.e., high-dimensional) Pauli matrices [94], prior to our work [39], no d-level entanglement witness had been constructed by using high-dimensional stabilizers. Generalized Pauli matrices may be very difficult indeed to be measured, as they typically necessitate single-qudit projections into a simultaneous superposition of multiple levels. Furthermore, the experimentally feasibility of these projections can significantly depend on the photon degree of freedom that is measured. For instance, d-level projections in time are more difficult to execute compared to d-level projections in frequency, as they may require the use of, e.g., multi-arm interferometers, which are particularly challenging to implement and stabilize [134]. The feasibility of d-level projections can be further affected by the efficiency of the measurement devices. This is the case for, e.g., electro-optic phase modulation, the efficiency of which decreases with a growing number of level projections [37].

As shown in this review, our group addressed this issue and developed a theoretical approach to construct high-dimensional stabilizer-based multi-partite d-level entanglement witnesses that allow for the identification of any arbitrarily complex quantum state and that are feasible for practical measurements [39]. We also tested the robustness of these operators against white noise and showed that, also in the case of multi-partite quantum systems, qudits are less sensitive than qubits. Specifically, the noise tolerance of qudits increase with a growing number of levels. As shown here, we finally developed a technique for customizing a witness to realistic experimental scenarios by considering two examples which are very common in quantum optics: one example is related to measurement restrictions caused by losses, the other to the measurement settings available, such that d-level projections are avoided [39].

The starting point of this approach consists in judiciously modifying and simplifying what we call a ‘theoretically optimal’ witness that is used to identify the presence of a generic pure quantum state | ψ 〉 as well as those states close to it and that is given by

Here, I is the identity operator, ρ = | ψ 〉 〈 ψ | is the quantum density matrix, and α is a coefficient designed such that all separable quantum systems result in a non-negative expectation value of the witness. While such a theoretically optimal witness has a very high noise tolerance (due to its large mathematical bounds), the measurement of its expectation value is not experimentally feasible, especially as the quantum state complexity increases (for example, it would necessitate the determination of the full density matrix ρ). In order to make the witness measure practical, we introduce two new operators, i.e.,  W meas and Θ = W meas − ρ , which comprise measurement settings that are respectively easy and challenging to implement in practice. The only constraint about the operator W meas , which can be completely arbitrary, is that it must be Hermitian (i.e., observable). After having introduced these two operators, the goal is to replace Θ with its largest eigenvalue, that is, with a scalar number that represents the worst possible measurement outcome and that results in the maximal expectation value of Θ. In other words, such a scalar number is defined so as 〈 Θ 〉 ≤ λ max ( Θ ) = 〈 λ max ( Θ ) ⋅ I 〉 . Such a replacement leads to a witness operator that is feasible to implement in practice, and which we define as ‘experimentally optimal’, given by

By examining Figure 7, which depicts the complexity of the witness measurement settings as a function of the noise tolerance of the witness, we can observe the differences between a theoretically and an experimentally optimal witness (the orange square and the green circle, respectively). Determining the expectation value of a witness typically requires several measurements, which introduce an experimental noise floor (the grey area) that grows as the complexity of the measurement settings increases. In this scenario, the high noise tolerance provided by a theoretically optimal witness comes at the cost of several intricate measurements, which makes it almost impossible to be measured in practice. On the other hand, while an experimentally optimal witness has lower noise tolerance, determining its expectation value requires measurements that are reduced in both number and complexity, with the significant advantage of decreasing the experimental noise floor. Since measuring a negative witness expectation value with a high statistical confidence (here, defined as σ – the shaded green or orange area in Figure 7) already provides a necessary and sufficient condition to confirm the generation of a targeted quantum state, an experimentally optimal witness should provide, in the best-case scenario, the maximal σ with which we measure its negative expectation value. In view of this, our approach aims to maximize the measurement confidence σ and, as such, to determine a witness providing the best possible compromise between its noise tolerance and experimental complexity. Such a goal can be accomplished by properly choosing the measurement settings that are required to measure W meas of Eq. (4.2).

Figure 7:

Complexity of the measurement settings versus the noise tolerance of the witness. A theoretically optimal witness (orange square) has the highest noise tolerance, at the cost of complex measurement settings, which increase the experimental noise floor (grey area). An experimentally optimal witness (green circle) has a lower noise tolerance, but requires less complex measurement settings, which makes the experimental noise floor decrease. The goal is to maximize the measurement confidence σ (shaded orange and green area) with which a negative witness expectation value is measured. Adapted from [39].

In our work [39], we focused on multi-partite d-level optical cluster states and constructed the operator W meas by making use of high-dimensional stabilizers, so as to derive a witness capable of identifying the presence of such states in an experimentally feasible manner that simultaneously boasts a high noise tolerance. The generic expression of this experimentally optimal witness is given by

where the parenthesis encloses W meas , while S k ( l ) denotes the stabilizer to the power of l that is applied to the kth qudit. The experimental feasibility of this witness is given by the fact that the determination of its expectation value only necessitates two measurement settings, which are defined by the sets {X ⁽¹⁾, Z ⁽²⁾, X ⁽³⁾, Z ⁽⁴⁾, …} and {Z ⁽¹⁾, X ⁽²⁾, Z ⁽³⁾, X ⁽⁴⁾, …}, respectively, containing the generalized Pauli matrices needed to measure the odd and the even stabilizers. The two measurement settings typically include the transpose conjugates of the Pauli matrices, due to their non Hermicity. While we derived the witness in Eq. (4.3) by only making use of the so-called main stabilizers (equal in number to the quantum state parties) [133], we can always define a complete set of d ^N stabilizers (achievable by permuting the N main stabilizers) that enable the reconstruction of the full quantum state density matrix and that can also be used to construct the witness.

We finally used the witness of Eq. (4.3) to investigate the robustness of multi-partite d-level cluster states against white noise, which effects the density matrix of a generic cluster state ρ N , d = | C N , d 〉 〈 C N , d | as [38, 39]

where 0 ≤ ε _noise ≤ 1 is the noise amount introduced to the quantum system. Considering that the noise threshold ε _th of the witness tolerance is defined as the maximum noise that will result in a negative expectation value of the witness, we derived such a threshold to be [39]

Three important aspects can be seen from this result. First, the noise tolerance of cluster states increases with a growing number of levels. Second, given a fixed number of parties N, ε _th also increases with a growing number of levels, ideally reaching the limit of ε _th = 0.5 as d → ∞ (see Figure 8 for the case of N = 4 parties and d up to 10 levels). Vice versa, for a fixed quantum state dimensionality d, ε _th decreases with a growing number of parties N, in a similar manner as it was showed for two-level cluster states [133]. This was the first demonstration that, also in the case of multi-partite quantum systems, qudits are more robust to noise than qudits, with a tolerance growing with an increasing number of levels [39]. Third, with the noise threshold of Eq. (4.5), we have demonstrated for the first time that different cluster states exhibiting the same Hilbert space size can have different noise tolerances. Specifically, the higher the quantum state dimensionality d, the higher the robustness. For instance, eight-partite two-level and four-partite four-level cluster states have the same Hilbert space size (i.e., 2⁸ = 4⁴ = 256), but significantly different noise tolerances, which are 26.67 and 40%, respectively. This is a direct consequence of the fact that qudits become stronger as the single state dimensionality increases, as demonstrated in our work [39].

Figure 8:

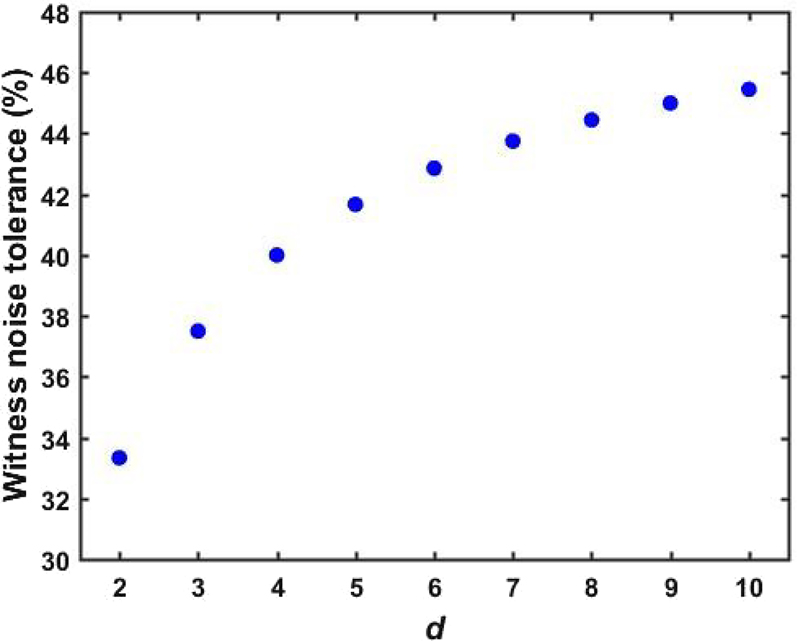
Noise tolerance of the witness as a function of the quantum state level d, given a fixed number of parties N = 4. We can observe that the witness robustness toward white noise increases with a growing number of levels. While we report here only up to d = 10, such a tolerance saturates at 50% for d → ∞.

Identifying the presence as well as the entanglement of two- and multi-partite d-level photon states with practical and accessible techniques is of fundamental importance for quantum photonic applications. However, there are some experimental scenarios in which it is impossible to identify a witness Eq. (4.3), for example, when there are some experimental restrictions that hamper the measurement of some stabilizers. The approach described in this review enables customizing witness operators in such a way as to select and use specific stabilizers and/or other operators according to the experimental restrictions and available measurement settings. Such a customization targets the use of these witness operators also in quantum photonics.

We consider as a first example the four-partite qutrit cluster state that has been shown in Section 3.2. Measuring the matrices Z, Z ^†, and I requires temporal gating and optical filtering/diffraction in the time- and in the frequency-domains, respectively. As long as the detectors used have sufficient temporal resolution and the frequency separation is accessible, these measurements are typically feasible and introduce low losses (around −1 to −2 dB). Measuring X and X ^† instead requires stable optical interferometers and electro-optic phase modulation in the time and spectral domains, respectively. Those measurements, besides adding significant experimental complexity, introduce higher losses (from −5 to −20 dB). In this scenario, among the 3⁸ = 81 stabilizers that uniquely describe the cluster state density matrix [33, 39], it is convenient to select those operators whose measure introduces minimal experimental complexity and losses. In particular, a specific measurement restriction would be to use either the interferometer (for time-bin superposition) or the frequency shifter (for phase modulation), but not both at the same time. Our approach allows for the selection of 20 out of the 81 stabilizers that can be measured according to this restriction and that can thus be used to construct an ‘experimentally-customized’ witness. This operator has the form

where the explicit expression of the stabilizers within the parenthesis is reported in the supplemental material of Ref. [39]. Such witness can tolerate up to 45% of white noise, a value that is 20% higher than the 37.5% of noise tolerated by the witness of Eq. (3.2.2). This is a direct consequence of the fact that the witness has been customized with respect to specific measurement conditions. This brings us to the important conclusion that, given the same quantum state, different experimental restrictions lead to different experimentally optimal witnesses having, in turn, different noise sensitivities.

Targeting quantum communications applications, we now consider the example of a time-bin qutrit photon Bell state of the form | Ψ 〉 time = 1 / 3 ( | 1 s , 1 i 〉 + | 2 s , 2 i 〉 + | 3 s , 3 i 〉 ) . We focus in particular on the experimental restriction in which it is impossible to perform d-level projections at a time, which implies the impossibility of measuring a stabilizer. Our approach allows constructing a witness through alternative, experimentally feasible operators to be used in lieu of (some) stabilizers. Measuring a stabilizer witness would necessitate simultaneous three-level projections onto time qutrits, which may be a very difficult task. For example, it would require the use of unbalanced three-arm interferometers that, on the top of being challenging to implement and stabilize, are not readily available. Rather, the only available measurement setting is a stable two-arm interferometer, which only allows for projections on a two-level basis. In practice, this means that it is only possible to perform measurements in the basis of Z and I (i.e., in the computation time-bin basis), but not in the basis of X (i.e., in a superposition), see Section 3.2. Such a restriction makes necessary the construction of a witness that can be measured by means of only two-level projections, a practical task that is enabled by using our approach. To this end, we introduce two-level projection operators and replace those stabilizers containing the X (X ^(†)) matrix with them. The action of these operators (comparable to partial trace operators [135]) is to project onto a superposition of only two modes at a time, while removing the third mode (that is, the action of a two-arm interferometer on a qutrit time-bin state). In the qudit basis { | i 〉 } , the two-dimensional projectors read X 1,2 = | 0 〉 〈 1 | + | 1 〉 〈 0 | , X 1,3 = | 0 〉 〈 2 | + | 2 〉 〈 1 | , and X 2,3 = | 1 〉 〈 2 | + | 2 〉 〈 1 | , which are identical to three out of the eight Gell–Mann matrices [136]. Here, the subscripts label the qudit onto which the projection is performed. The customized witness constructed by using these operators as well as those stabilizers that can be measured through a two-arm interferometer is given by

The customized witness can tolerate up to 37.5% of noise, which is lower than the noise tolerated by the witness directly constructed from Eq. (4.3) (i.e., 50%). However, such a lower noise threshold is compensated by simplified measurement settings (i.e., a two-arm rather than a three-arm interferometer), by lower measurement complexity (i.e., two-level rather than three-level projections), as well as by a decreased number of projections (i.e., 39 projections rather than the 81 required for the witness derived from Eq. (4.3)).

5 Conclusion and outlooks

The use of integrated, CMOS-compatible quantum optical platforms for the generation of complex entangled photon states, as well as the use of off-the-shelf fiber-based components for their processing, pave the way toward the development of ‘user-friendly’, accessible quantum photonic technologies. Important achievements toward this direction have been obtained in, e.g., quantum communications, [137], [138], [139]. While satellite quantum communications based on polarization-encoded photon states have made fast progress toward their practical exploitation (e.g., for QKD [140]), quantum communication protocols based on time- and frequency-encoded photon states are still the main subject of proof-of-concept demonstrations. The on-chip generation and fiber-based transmission of multi-level frequency-entangled photons demonstrated in Ref. [37] offer a promising solution toward extending these proof-of-principle demonstrations to practical quantum communication protocols to be implemented based on frequency-encoded photon transmission over fibers. To this end, the approach reported here has to be improved accordingly, for example, by boosting the efficiency of the modulation techniques, as well as by engineering modulators with higher bandwidths (so as to enhance the number of spectral components that can be processed by maintaining high efficiency) and implementing more on-chip integrated circuits (for instance, on-chip devices for photon state manipulation and processing). Finally, the km-long fiber propagation that was demonstrated in the lab can be extended in such a way to reproduce fiber-based photon transmission among two out-of-the lab locations situated km apart. This way, it would be possible to implement and improve fiber-based communication links in a similar manner as it has been widely demonstrated for satellite-based communication links [140], [141], [142].

The proof-of-principle one-way quantum operations that we have demonstrated in Ref. [33] suggest a promising route toward the implementation of quantum computing algorithms on photonic platforms that are compatible with both CMOS chips and with fiber-based networks [3, 143]. The use of a few photons also provides the advantages of increasing both detection rates and coherence time, dramatically reducing the scale and complexity of quantum optical platforms, as well as enhancing their robustness against white noise [38]. A further step toward a broad use of quantum photonics is the generation and processing of time and/or frequency modes at speeds that are compatible with current GHz telecommunication transmission rates. Achieving this goal would enhance the applications of the measurement-based quantum operations reported in this review.

Determining the presence as well as the entanglement of complex photon states via feasible measurement techniques is an important milestone for quantum photonic applications. However, progress toward this direction is still in its early stages. In this sense, the approach reviewed here to derive experimentally optimal witness operators and to customize them toward experimental conditions and available measurement settings represents an initial step toward this end. While our approach has been derived specifically for optical quantum states by considering specific DOFs such as time and frequency, it can be extended to other DOFs that are widely exploited in other photonic platforms, such as OAM [28, 29] and optical path [25], [26], [27]. Finally, the approach reported here can be further improved and, under judicious modification, can be extended to mixed states [144, 145], describing systems interacting with the surrounding environment. A quantum state that undergoes interaction with its environment can drastically change its phase and structure. In particular, it is affected by dissipation and decoherence, and it can also become entangled with the contiguous environment [146]. In this case, we can explore dynamic (i.e., evolving) entanglement. Understanding the evolution of the quantum system, its properties, as well as its entanglement, has several applications in many fields, including quantum computing and other engineering areas. Our approach, with proper modifications, could allow such investigations in a feasible manner.