Abstract:
Modeling hospitalization is complicated because the follow-up time can be censored due to death. In this paper, we propose a shared frailty joint model for survival time and hospitalization. A random effect semi-parametric proportional hazard model is assumed for the survival time and conditional on the follow-up time, hospital admissions or total length of stay is modeled by a generalized linear model with a nonparametric offset function of the follow-up time. We assume that the hospitalization and the survival time are correlated through a latent subject-specific random frailty. The proposed model can be implemented using existing software such as SAS Proc NLMIXED. We demonstrate the feasibility through simulations. We apply our methods to study hospital admissions and total length of stay in a cohort of patients on hemodialysis. We identify age, albumin, neutrophil to lymphocyte ratio (NLR) and vintage as significant risk factors for mortality, and age, gender, race, albumin, NLR, pre-dialysis systolic blood pressure (preSBP), interdialytic weight gain (IDWG) and equilibrated Kt/V (eKt/V) as significant risk factors for both hospital admissions and total length of stay. In addition, hospitalization admissions is positively associated with vintage.
1 Introduction
Hospitalization is a main contributor to the total cost of care and identification of the related risk factors is of interest in many health care studies. The main difficulty in modeling hospitalization data is due to the fact that the frequency of hospitalization and the total length of hospitalizations are functions of follow-up time that can be informatively censored due to death. Since both the hospitalization outcome and time-to-death are related to the underlying health, it is desirable to jointly model them as bivariate outcomes. Mixed types of multivariate outcomes are common in many fields of science and social science. Various statistical models and methods have been proposed to deal with different types of mixed outcomes [1]. For example, Fitzmaurice and Laird [2] proposed regression models for continuous and binary outcomes. They focused on marginal regression models with a set of covariates and treated the association between continuous and binary response as a nuisance characteristic of the data. Sammel, Ryan, and Legler [3] proposed latent variable models for mixed discrete and continuous outcomes. They modeled the associations among the outcomes by an unobserved latent variable which depends on a set of covariates. Catalano [4] proposed a latent variable model for continuous and ordinal outcomes, and extended it to allow for clustering of the bivariate outcomes. Dunson and Herring [5] proposed latent variable models for mixed discrete outcomes including count, binary and discrete event time. A Bayesian approach was introduced for inference where conditionally-conjugate priors were chosen to facilitate posterior computation. However, these methods can not handle censored data which is needed for joint modeling of survival time and hospitalization in health studies.
Our research is motivated by the need for improvement in care for end-stage renal disease (ESRD) patients. Hemodialysis (HD) is the most frequently used treatment modality for ESRD patients. In general, HD patients suffer from multiple comorbidities, such as diabetes and cardiovascular diseases, resulting in frequent hospitalizations and substantial mortality. In spite of improvements over the years, hospitalization and mortality rates of ESRD patients on HD remain much higher than those of the general population [6]. In this article we are interested in identifying risk factors for hospitalization and mortality. The data come from an observational study of patients on HD in Fresenius Medical Care. Covariates at baseline and outcomes including survival time, hospital admissions and total length of hospital stay at follow-up were collected. Approximately 20 % of patients died during the follow-up period and observational times for hospitalization outcomes of these patients are censored due to death. Since both survival time and hospitalization are associated with the underlying health condition, it is likely that these outcomes from the same subject are correlated. Therefore, it is necessary to develop a joint model for survival time and hospitalization. Details of the data are given in Section 5.
In this article we propose a semi-parametric latent variable model for joint modeling of a survival time and an outcome from exponential family. The survival time is modeled by a semi-parametric proportional hazard model with a subject-specific random effect. The hospitalization related endpoint, such as the number of admissions, length of stay or whether a subject has ever been hospitalized, can be modeled by a generalized linear mixed effects model. Since the hospitalization outcome may only be observed before death, an offset function will be included in the generalized linear model to take into account the follow-up time. To allow a flexible relationship between the hospitalization endpoint and the follow-up time, we introduce a nonparametric smooth offset function that includes parametric functions, such as logarithm, as special cases. When the offset function is parametric, these models reduce to the standard generalized mixed effects models and parameters of interest may be interpreted in terms of the constant conditional means such as incident rate, mean duration and average probability. The smooth offset function allows deviation from this rigid assumption. The forms of the baseline hazard function and the offset function are usually unknown. They will be modeled non-parametrically using spline functions with non-negative and, when appropriate, monotone constraints. A latent random variable will be used to model potential correlation between survival time and hospitalization outcome from the same subject [7].
We note that there is a large body of literature on the joint modeling of survival hazard function and hospitalization rate. See for example Lancaster and Intrator [8], Wang, Qin, and Chiang [9], Huang and Wolfe [10], Liu, Wolfe, and Huang [11], Huang, Qin, and Wang [12], and the references therein. These studies treated hospitalizations as recurrent events and focused on modeling the intensity function of the recurrent process. In this article, our main interest is on the expected number of hospitalizations and expected total length of stays which account for a major part of the total cost of care. We also note that there have been various proposals on the joint modeling of survival time and longitudinal data [13, 14]. We are interested in identifying risk factors at the baseline for the bivariate cross-sectional outcomes of hospitalization and time-to-death in the follow-up. Therefore methods for the joint modeling of longitudinal and survival data do not apply to our situation.
The rest of this article is organized as follows. Section 2 introduces the semi-parametric latent variable model. Section 3 provides details about our estimation procedure. Section 4 and Section 5 present simulation results and applications to patients on HD. The article ends with a discussion in Section 6.
2 The semi-parametric latent variable model
2.1 The overall model
For subject
where
2.2 A spline model for the baseline hazard
The form of the baseline hazard function
where
2.3 A spline or monotone spline model for the offset function
When
where
For Poisson data, it is natural to assume that the expectation of
where
3 Estimation
The full likelihood is
where
Our goal is then to obtain parameter estimates by maximizing the likelihood. Since there is no closed form solution, we apply the Newton-Raphson methods to compute parameter estimates numerically. For stability, we apply the Newton-Raphson ridge optimization where a pure Newton step is used when the Hessian is positive definite and when the Newton step successfully increases the value of the likelihood, otherwise a multiple of the identity matrix is added to the Hessian matrix [17]. To calculate the gradient and Hessian matrix, we need to evaluate integrals derived from the likelihood function. The Gaussian quadrature method is used to approximate these integrals. We estimate random effects
Numerically stable implementations of these methods can be obtained from a variety of publicly available softwares [18]. In our simulation and example, we employed SAS procedure Proc NLMIXED to perform the computation. Proc NLMIXED has an appealing feature which allows a user-specified log likelihood functions with respect to the random effects. See Littell et al. [17] for details on this procedure.
The number and location of knots are fixed in the above discussion. While increasing the number of knots has the capability to model a more flexible function, having too many knots will increase the complexity of the model and result in over-fitting. A data-driven procedure for the selection of number and location of knots is desirable. We allow
4 Simulations
We generate simulation samples from the following model
where
The baseline hazard
Simulation under each setting is repeated 500 times. For the estimation of parameters, we compute bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP). The 95 % confidence interval is constructed as the MLE plus-minus 1.96 times the standard errors obtained from the variance-covariance matrix. For the estimation of functions
for each replicate, where
Bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP) based on the joint model when
| β | |||||
|---|---|---|---|---|---|
| Bias | 0.007 | 0.045 | −0.064 | 0.337 | |
| MSE | 0.017 | 0.037 | 0.066 | 0.65 | |
| CP | 0.938 | 0.981 | 0.809 | 0.965 | |
| Bias | 0.002 | 0.014 | −0.008 | 0.149 | |
| MSE | 0.010 | 0.022 | 0.871 | 0.936 | |
| CP | 0.946 | 0.946 | 0.871 | 0.936 | |
| n = 1,000 | Bias | 0.002 | 0.008 | 0.003 | 0.063 |
| MSE | 0.005 | 0.01 | 0.031 | 0.062 | |
| CP | 0.94 | 0.948 | 0.916 | 0.94 |
Bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP) based on the joint model when
| σ2 | |||||
|---|---|---|---|---|---|
| Bias | 0.033 | 0.084 | 0.106 | 0.779 | |
| MSE | 0.025 | 0.064 | 0.109 | 2.833 | |
| CP | 0.966 | 0.968 | 0.774 | 0.957 | |
| n = 500 | Bias | 0.016 | 0.046 | 0.03 | 0.381 |
| MSE | 0.016 | 0.030 | 0.088 | 0.912 | |
| CP | 0.955 | 0.973 | 0.842 | 0.953 | |
| n = 1,000 | Bias | 0.004 | 0.017 | 0.005 | 0.127 |
| MSE | 0.007 | 0.011 | 0.053 | 0.156 | |
| CP | 0.947 | 0.966 | 0.890 | 0.951 |
Bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP) based on the joint model when
| Bias | −0.003 | 0. | 0.016 | 0.056 | |
| MSE | 0.011 | 0.025 | 0.06 | 0.075 | |
| CP | 0.968 | 0.963 | 0.925 | 0.951 | |
| n = 500 | Bias | −0.006 | 0.008 | 0.007 | 0.044 |
| MSE | 0.007 | 0.015 | 0.038 | 0.052 | |
| CP | 0.944 | 0.962 | 0.912 | 0.930 | |
| Bias | 0.002 | 0.003 | 0.011 | 0.017 | |
| MSE | 0.003 | 0.008 | 0.022 | 0.025 | |
| CP | 0.950 | 0.946 | 0.942 | 0.928 |
Bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP) based on the joint model when
| Bias | 0.033 | 0.064 | 0.025 | 0.346 | |
| MSE | 0.020 | 0.064 | −0.025 | 0.346 | |
| CP | 0.958 | 0.973 | 0.859 | 0.936 | |
| Bias | 0.014 | 0.036 | −0.014 | 0.227 | |
| MSE | 0.013 | 0.027 | 0.070 | 0.386 | |
| CP | 0.945 | 0.955 | 0.850 | 0.951 | |
| Bias | 0.009 | 0.015 | −0.009 | 0.117 | |
| MSE | 0.006 | 0.011 | 0.040 | 0.100 | |
| CP | 0.954 | 0.950 | 0.892 | 0.942 |
Integrated Mean Square Error (IMSE) of the baseline hazard
| 0.078 | 0.079 | ||
| w(t) = t/2 | 0.050 | 0.052 | |
| 0.027 | 0.027 | ||
| 0.109 | 0.151 | ||
| n = 500 | 0.063 | 0.097 | |
| 0.033 | 0.052 | ||
| 0.665 | 0.066 | ||
| 0.456 | 0.043 | ||
| 0.230 | 0.025 | ||
| 0.856 | 0.165 | ||
| 0.662 | 0.114 | ||
| 0.340 | 0.057 |
Table 1–Table 5 summarize performances of parameter and function estimates under four simulation settings. Overall the proposed estimation procedure perform well: bias and MSE are small, and the coverages of 95 % confidence intervals are close to the nominal value except for
As an illustration, Figure 1 shows the
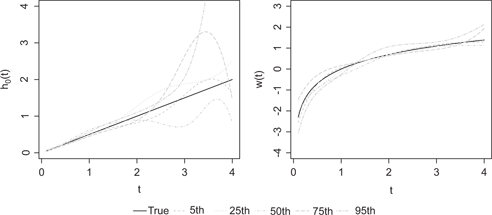
True function (solid lines) and estimates (dashed lines) of h0(t) = t/2 (left) and w(t) = log(t) (right) correspond to the 5th, 25th, 50th, 75th and 95th percentiles of the IMSE when h0(t) = t/2, w(t) = log(t) and n = 500.
We have also evaluated performance of our estimation procedure in a more complicated simulation setting. The data was generated from the following model
where
We summarize bias, MSE and coverage probability of 95 % CP for the estimations of parameters in Table 6. The
Bias, mean squared error (MSE) and coverage probability of 95 % confidence intervals (CP) based on the joint model when
| Bias | −0.020 | −0.027 | 0.037 | −0.068 | −0.113 | 0.146 | |
| MSE | 0.006 | 0.018 | 0.010 | 0.037 | 0.083 | 0.086 | |
| CP | 0.949 | 0.965 | 0.963 | 0.946 | 0.839 | 0.979 |
Summary statistics of covariates.
| (Min, Max) | Mean (Std) | |
|---|---|---|
| Age (year) | (1.00, 96.62) | 62.39 (14.84) |
| BMI (kg/ | (13.75, 49.51) | 27.65 (6.46) |
| Albumin (g/dL) | (1.60, 4.74) | 3.84 (0.37) |
| IDWG (%) | (0.41, 7.99) | 3.48 (1.05) |
| PreSBP (mmHg) | (81.88, 219.29) | 149.38 (18.86) |
| eKt/V | (0.68, 3.77) | 1.46 (0.26) |
| NLR | (0.51, 31.18) | 3.70 (2.32) |
| Vintage (year) | (0.08, 7.90) | 2.56 (1.92) |

True function (solid lines) and estimates (dashed lines) of
5 Application
We now apply the proposed method to model mortality and hospitalization outcomes for patients on HD. Baseline covariates are collected from 1999 HD patients from 1 January 2007 to 31 December 2007. Survival time, the number of hospital admissions and total length of stay of these patients during the period of 1 January 2008 and 31 December 2009 are collected. 1078 (53.93 %) patients are male. 984 (49.22 %) patients are black, 834 (41.72 %) patients are white, the rest are from other races. Time-varying covariates are calculated as the averages in baseline period for each patient. The summary statistics for these covariates are listed in Table 7.
In previous studies, albumin and systolic blood pressure before dialysis (preSBP) have been found as significant risk factors for mortality [20–22]. Erdem, Kaya, Karatas, Dilek, and Akpolat [23] observed that HD patients with high neutrophil to lymphocyte ratio (NLR) levels have increased risk of short term mortality. Our preliminary analysis indicates that time in years since initiation of dialysis (vintage), inter-dialytic weight gain (IDWG) and a measure of dialysis capability eKt/V also have significant effect on mortality. In addition, we will include gender, race and BMI.
In modeling the hospitalization, the number of hospital admissions is usually the primary outcome which will be studied in Section 5.1 using a Poisson model. We are sometimes also interested in whether a patient has ever been hospitalized as a binary outcome. Since the probability of ever been hospitalized can be derived from the Poisson model, we omit the details of modeling the binary outcome in this paper. Given the subject has been hospitalized, a further goal is to identify the risk factors that lead to longer total length of stay which will be studied in Section 5.2 using a Gamma model. For simplicity we will consider the same set of covariates for all models.
5.1 Joint analysis of mortality and hospital admission
359 (17.96 %) patients died during the follow-up period. The number of hospital admissions in the data ranges from 0 to 37 with mean 2.53. We consider the following joint model:
where
As in the previous section we set the interior knots for baseline hazard and offset function equally spaced within the time period. The number of knots ranges from 2 to 4. Among all the combinations, the AIC selects 2 knots for the baseline hazard and 2 knots for the offset function.
We summarize the estimation results in Table 8. Tests are constructed based on asymptotic properties of the MLEs after selection of the knots. All covariates except BMI are significantly associated with the expected number of hospital admissions, while age, albumin, NLR, eKt/V and vintage are significantly associated with the hazard function. Overall age, NLR and vintage are positively associated with both hazard and the number of hospital admissions, while albumin and eKt/V are negatively associated with the outcomes. Furthermore, pre-dialysis SBP and IDWG are positively associated with the number of hospital admissions, and female patients tend to have more hospital admissions.
The latent random variable is significant (
Joint modeling of mortality and hospitalization of ESRD data.
| Covariates | Estimate | SE | p-value | |
|---|---|---|---|---|
| Mortality | Age | 0.0355 | 0.0048 | |
| Albumin | −1.2736 | 0.1681 | ||
| PreSBP | −0.0004 | 0.0031 | 0.8990 | |
| NLR | 0.1061 | 0.0217 | ||
| BMI | −0.0198 | 0.0106 | 0.0619 | |
| Male | 0.0748 | 0.1210 | 0.5365 | |
| IDWG | 0.0684 | 0.0625 | 0.2737 | |
| eKt/V | −0.5936 | 0.2474 | 0.0165 | |
| Vintage | 0.1244 | 0.0307 | ||
| Race(White) | 0.1341 | 0.2151 | 0.5329 | |
| Race(Black) | −0.2446 | 0.2184 | 0.2629 | |
| Hospitalization | Age | 0.0089 | 0.0022 | |
| Albumin | −0.8126 | 0.0856 | ||
| PreSBP | 0.0072 | 0.0015 | ||
| NLR | 0.0776 | 0.0129 | ||
| BMI | −0.0026 | 0.0049 | 0.5974 | |
| Male | −0.1612 | 0.0600 | 0.0073 | |
| IDWG | 0.1018 | 0.0307 | 0.0009 | |
| eKt/V | −0.2360 | 0.1170 | 0.0437 | |
| Vintage | 0.0386 | 0.0157 | 0.0140 | |
| Race(White) | 0.2634 | 0.1094 | 0.0162 | |
| Race(Black) | 0.3130 | 0.1069 | 0.0035 | |
| 0.6008 | 0.2172 | 0.0057 | ||
| 1.2225 | 0.2039 |
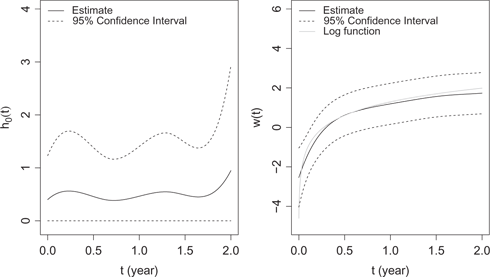
The estimated baseline function
5.2 Joint analysis of mortality and total length of stay
To further investigate the features of patients with hospitalizations, another interesting application is to model mortality and total length of hospital stay. We will focus on the patients who had positive length of stays (1396 patients). The total length of stay ranges from 1 to 368 with mean 26.13. We consider the following joint model:
where
Similar process for knots selection applies, which results in 2 knots for the baseline hazard and 2 knots for the offset function. The estimation results are summarized in Table 9. All covariates except BMI and vintage are significantly associated with the expectation of total length of stay, while age, albumin, NLR and vintage are significantly associated with the hazard function. We note that conclusions about risk factors are consistent with those in the previous subsection except for race: the total length of hospital stays of white patients is not significantly different from that of other races while white patients have significantly larger number of hospitalizations than other races. The latent random variable is borderline significant (
Joint modeling of mortality and hospitalization of ESRD data.
| Covariates | Estimate | SE | p-value | |
|---|---|---|---|---|
| Mortality | Age | 0.0302 | 0.0053 | |
| Albumin | −1.0237 | 0.1730 | ||
| PreSBP | −0.0040 | 0.0035 | 0.2472 | |
| NLR | 0.0751 | 0.0228 | 0.0010 | |
| BMI | −0.0204 | 0.0118 | 0.0843 | |
| Male | 0.0830 | 0.1340 | 0.5359 | |
| IDWG | 0.0939 | 0.0704 | 0.1826 | |
| eKt/V | −0.4920 | 0.0704 | 0.0812 | |
| Vintage | 0.0944 | 0.0332 | 0.0045 | |
| Race(White) | −0.0361 | 0.2303 | 0.8754 | |
| Race(Black) | −0.3373 | 0.2335 | 0.1489 | |
| Length of Stay | Age | 0.0070 | 0.0022 | 0.0017 |
| Albumin | −0.5335 | 0.0870 | ||
| PreSBP | 0.0047 | 0.0016 | 0.0036 | |
| NLR | 0.0484 | 0.0137 | 0.0004 | |
| BMI | −0.0045 | 0.0051 | 0.3788 | |
| Male | −0.1269 | 0.0626 | 0.0430 | |
| IDWG | 0.0740 | 0.0319 | 0.0205 | |
| eKt/V | −0.2495 | 0.1234 | 0.0433 | |
| Vintage | 0.0275 | 0.0165 | 0.0955 | |
| Race(White) | 0.1338 | 0.1123 | 0.2336 | |
| Race(Black) | 0.2933 | 0.1110 | 0.0084 | |
| 0.2108 | 0.1094 | 0.0542 | ||
| 1.8883 | 0.5550 | 0.0007 |
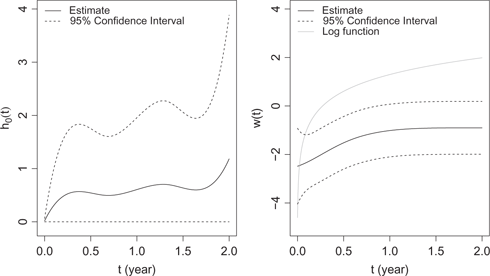
The estimated baseline function
6 Discussion
In this article, we propose a semi-parametric joint model for survival time and hospitalization. In particular, we consider the number of hospital admissions and total length of stay as hospitalization outcomes. A shared random effect is introduced to account for the within subject correlation between the two outcomes. The baseline hazard and offset functions are modeled non-parametrically through B-spline or monotone B-spline bases in order to gain flexibility. With fixed number of knots, the techniques to numerically obtain maximum likelihood estimation are presented. We have also discussed the AIC method for selecting the number of knots. Standard large sample properties of maximum likelihood estimation apply when knots are fixed. Simulation results indicate that the proposed estimation method performs well.
Throughout this article, we assume Normal distribution for the random effect. Our method can be easily generalized to other parametric distributions for the random effect. We used B-spline bases with non-negative coefficients to model the non-negative baseline hazard. An alternative approach is to model the logarithm of the baseline hazard using B-spline bases without constraints on coefficients. However the approach cannot be implemented using the SAS NLMIXED procedure since the likelihood involves an intractable integral. We have analyzed different aspects of the hospitalization separately. One future research is to build a joint model for survival time, hospital admission and length of stay. Our methodology may also be extended to the case of the zero-inflated Poisson model.
Funding statement: National Science Foundation, Grant DMS-1507620; National Institutes of Health, Grant R01GM104470.
Acknowledgements
We thank the associated editor and two referees for constructive comments that substantially improved an earlier draft.
References
1. De Leon A, Chough KC. Analysis of mixed data: methods & applications. Boca Raton, FL: Chapman and Hall/CRC, 2013.10.1201/b14571Suche in Google Scholar
2. Fitzmaurice G, Laird N. Regression models for a bivariate discrete and continuous outcome with clustering. J Am Stat Assoc 1995;90:845–852.10.1080/01621459.1995.10476583Suche in Google Scholar
3. Sammel M, Ryan L, Legler J. Latent variable models for mixed discrete and continuous outcomes. J R Stat Soc Ser B (Stat Method) 1997;59:667–678.10.1111/1467-9868.00090Suche in Google Scholar
4. Catalano P. Bivariate modelling of clustered continuous and ordered categorical outcomes. Stat Med 1997;16:883–900.10.1002/(SICI)1097-0258(19970430)16:8<883::AID-SIM542>3.0.CO;2-ESuche in Google Scholar
5. Dunson D, Herring A. Bayesian latent variable models for mixed discrete outcomes. Biostatistics 2005;6:11–25.10.1093/biostatistics/kxh025Suche in Google Scholar
6. Collins A, Foley R, Chavers B, Gilbertson D, Herzog C, Ishani A, US renal data system 2013 annual data report. American journal of kidney diseases 2014;63(1 Suppl):A7.10.1053/j.ajkd.2013.11.001Suche in Google Scholar
7. McCulloch C. Joint modelling of mixed outcome types using latent variables. Stat Methods Med Res 2008;17:53–73.10.1177/0962280207081240Suche in Google Scholar
8. Lancaster T, Intrator O. Panel data with survival: hospitalization of HIV-positive patients. J Am Stat Assoc 1998;93:46–53.10.1080/01621459.1998.10474086Suche in Google Scholar
9. Wang M-C, Qin J, Chiang C-T. Analyzing recurrent event data with informative censoring. J Am Stat Assoc 2001;96:1057–1065.10.1198/016214501753209031Suche in Google Scholar
10. Huang X, Wolfe RA. A frailty model for informative censoring. Biometrics 2002;58:510–520.10.1111/j.0006-341X.2002.00510.xSuche in Google Scholar
11. Liu L, Wolfe RA, Huang X. Shared frailty models for recurrent events and a terminal event. Biometrics 2004;60:747–756.10.1111/j.0006-341X.2004.00225.xSuche in Google Scholar
12. Huang C-Y, Qin J, Wang M-C. Semiparametric analysis for recurrent event data with time-dependent covariates and informative censoring. Biometrics 2010;66:39–49.10.1111/j.1541-0420.2009.01266.xSuche in Google Scholar
13. Rizopoulos D. JM: An R package for the joint modelling of longitudinal and time-to-event data. J Stat Softw 2010;35:1–33.10.18637/jss.v035.i09Suche in Google Scholar
14. Tsiatis A, Davidian M. Joint modeling of longitudinal and time-toevent data: an overview. Stat Sin 2004;14:809–834.Suche in Google Scholar
15. Usvyat L, Kooman J, van der Sande F, Wang Y, Maddux F, Levin N, et al. Dynamics of hospitalizations in hemodialysis patients: results from a large US provider. Nephrol Dial Transplant 2014;29:442–448.10.1093/ndt/gft219Suche in Google Scholar
16. Ramsay J. Monotone regression splines in action. Stat Sci 1988;4:425–441.10.1214/ss/1177012761Suche in Google Scholar
17. Littell R, Milliken G, Stroup W, Wolfinger R, Schabenberger O. SAS for mixed models, 2nd . Cary, NC: SAS Institute Inc., 2006.Suche in Google Scholar
18. Press W, Teukolsky S, Vetterling W, Flannery B. Numerical recipes 3rd edition: the art of scientific computing. New York, NY: Cambridge University Press, 2007.Suche in Google Scholar
19. Akaike H. Information theory and an extension of the maximum likelihood principle. Second Int Symp Inf Theory 1973;:267–281.Suche in Google Scholar
20. He J, Whelton P. Elevated systolic blood pressure and risk of cardiovascular and renal disease: overview of evidence from observational epidemiologic studies and randomized controlled trials. Am Heart J 1999;138:S211–S219.10.1016/S0002-8703(99)70312-1Suche in Google Scholar
21. Hsu C, McCulloch C, Iribarren C, Darbinian J, Go A. Body mass index and risk for end-stage renal disease. Ann Intern Med 2006;144:21–28.10.7326/0003-4819-144-1-200601030-00006Suche in Google Scholar PubMed
22. Phelan P, O’Kelly P, Walshe J, Conlon P. The importance of serum albumin and phosphorous as predictors of mortality in ESRD patients. Ren Fail 2008;30:423–429.10.1080/08860220801964236Suche in Google Scholar PubMed
23. Erdem E, Kaya C, Karatas A, Dilek M, Akpolat T. Neutrophil to lymphocyte ratio in predicting short-term mortality in hemodialysis patients. J Exp Clin Med 2013;30:129–132.10.5835/jecm.omu.30.02.008Suche in Google Scholar
© 2016 Walter de Gruyter GmbH, Berlin/Boston
Artikel in diesem Heft
- Research Articles
- A Comparison of Some Approximate Confidence Intervals for a Single Proportion for Clustered Binary Outcome Data
- Effect of Smoothing in Generalized Linear Mixed Models on the Estimation of Covariance Parameters for Longitudinal Data
- Adaptive Design for Staggered-Start Clinical Trial
- A Binomial Integer-Valued ARCH Model
- Testing Equality in Ordinal Data with Repeated Measurements: A Model-Free Approach
- Mendelian Randomization using Public Data from Genetic Consortia
- Tree Based Method for Aggregate Survival Data Modeling
- Multi-locus Test and Correction for Confounding Effects in Genome-Wide Association Studies
- Semiparametric Regression Estimation for Recurrent Event Data with Errors in Covariates under Informative Censoring
- Joint Model for Mortality and Hospitalization
- Effect Estimation in Point-Exposure Studies with Binary Outcomes and High-Dimensional Covariate Data – A Comparison of Targeted Maximum Likelihood Estimation and Inverse Probability of Treatment Weighting
- Sample Size for Assessing Agreement between Two Methods of Measurement by Bland−Altman Method
- Using Relative Statistics and Approximate Disease Prevalence to Compare Screening Tests
- Multiple Comparisons Using Composite Likelihood in Clustered Data
Artikel in diesem Heft
- Research Articles
- A Comparison of Some Approximate Confidence Intervals for a Single Proportion for Clustered Binary Outcome Data
- Effect of Smoothing in Generalized Linear Mixed Models on the Estimation of Covariance Parameters for Longitudinal Data
- Adaptive Design for Staggered-Start Clinical Trial
- A Binomial Integer-Valued ARCH Model
- Testing Equality in Ordinal Data with Repeated Measurements: A Model-Free Approach
- Mendelian Randomization using Public Data from Genetic Consortia
- Tree Based Method for Aggregate Survival Data Modeling
- Multi-locus Test and Correction for Confounding Effects in Genome-Wide Association Studies
- Semiparametric Regression Estimation for Recurrent Event Data with Errors in Covariates under Informative Censoring
- Joint Model for Mortality and Hospitalization
- Effect Estimation in Point-Exposure Studies with Binary Outcomes and High-Dimensional Covariate Data – A Comparison of Targeted Maximum Likelihood Estimation and Inverse Probability of Treatment Weighting
- Sample Size for Assessing Agreement between Two Methods of Measurement by Bland−Altman Method
- Using Relative Statistics and Approximate Disease Prevalence to Compare Screening Tests
- Multiple Comparisons Using Composite Likelihood in Clustered Data

