Abstract
Woven compression bandage (CB) is one of the elastic textiles that exert pressure on muscles. With a defined tensile strength, it is possible to create the required compression on the given body parts. This work aims to investigate the relationship between woven fabric deformation, porosity, and tensile stress properties of three main types of woven CBs. All bandage samples are applied on human leg using two- and three-layer bandaging techniques. Bandage porosity is calculated for all frames at different weave angles using NIS software. Woven bandage construction parameters which are given by the preparation of warp and weft yarns, twist, count, and density along with woven fabric weave, type of weaving, and finishing process are the main factors that influence the bandage properties. Several methods considering thread distributions have been developed to determine the woven fabric's porosity during the tensile stress. Experimental results confirm that bandage porosity is directly proportional to the bandage extension and weave angle that ranges from 44° to 90°. The novelty of candidate study is to introduce practical remarks to the patient for optimizing the required bandage pressure by suitable extension or applied tension or weave angle for two- and three-layer bandaging systems.
1 Introduction
Medical textiles and garments are designed to meet both the safety and the comfort of human beings [1, 2]. Fabric porosity can be defined as follows: the volume of voids among fibers [3, 4]. Medical compression bandages (MCBs) are the cornerstone in the treatment of chronic venous ulcers. MCBs aim to provide graduated compression to the lower limb from the ankle to the knee to improve venous return, accelerate venous flow, reduce venous reflux by realignment of valves, improve venous pump action, and reduce edema [5, 6]. To design effective compression bandages (CBs), researchers have attempted to describe the interface pressure applied by these bandages using mathematical models [6, 7, 8, 9]. Usually, nurses or patients are applying the CB on the part of body using uniaxial stress. CBs are produced with optimum stretch using highly twisted warp yarns such as 100% cotton or elastomeric filament (Lycra or Spandex) with cotton or viscose such as cotton/polyamide/polyurethane (CO-PA-PU) or using two or more polymeric yarns having different melting points such as viscose/polyamide (VIPA) by steaming then heat setting.
1.1 Modeling of fabric porosity
A lot of models for description of porosity in woven fabrics were presented, some of them described the porosity between yarns (the inter-yarn porosity) and the others described the porosity between fibers inside the yarn (the intra-yarn porosity). According to the theory of a two-dimensional (2D) model, the porosity (S) is defined as a complement to the woven fabric cover factor (CF; Figure 1).
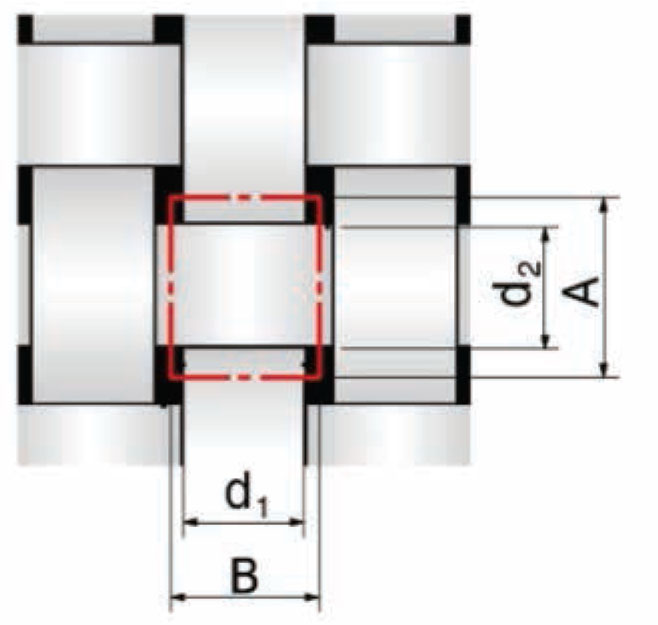
Structure of interlacing cell in woven fabric crossing point of plain weave, warp and weft diameter (d1, d2), warp and weft distance (B, A).
Woven fabric CF is given on the basis of illustrated structure of woven fabric in Figure 1 by equation (1):
Based on the known parameters of warp and weft densities (D1 and D2), we can write equation (2):
An area of pores is calculated as the perpendicular projection of woven fabric (horizontal porosity) [2]. Real values can be measured as illustrated in equation (3):
where do and du are the diameters of warp yarn and weft yarn, respectively, and Do and Du are the sets of warp yarn and weft yarn, respectively.
While dealing with 2D fabrics, porosity is defined as the ratio of the projected geometrical area of the opening across the material to the total area of the material [10, 11]. A classical 2D model of porosity seems insufficient for a tightly woven fabric. Neighboring yarns are very close, and the projected area of inter-yarn pores approaches to zero. As air flows through the woven fabric, it flows around the yarns, and it does not flow only in the perpendicular direction [12, 13]. Gee introduced the well-known “ends plus intersection theory,” which he modified, and called the “curvature theory” [14]. Until then, a “maximum theory” had been the subject of several researches. Some researchers [15, 16, 17, 18, 19] used a more theoretical approach, whereas others [20] used more experimental means. M. Kienbaum successfully joined theoretical and experimental investigations and presented his own theory which can be applied to all weaves and different yarn structures [2].
1.2 Effect of mechanical tensile stress on woven CBs
The venous as well as lymph system disorders or lower and upper extremities are often treated by utilizing compression garments which can provide compression therapy. By compression therapy, we limit the flow of diseased surface veins and increase the flow through deeper veins and reduce swelling. Patients who are compliant with compression therapy have a significantly improved ulcer healing rate and a decreased rate of recurrence. Even if the ulcers do recur, the interval to recurrence is more prolonged. Compression is thought to either correct or improve venous hypertension, mainly owing to an improvement of the venous pump and lymphatic drainage. Compression also improves blood flow velocity through deep and superficial veins [21]. For the creation of optimal compression on the lower and upper limbs by CB, it is necessary to observe the rules for application. The condition and shape of the bandage during application to any body part are in a straightened position similar to the uniaxial stress (Figure 2). Applied force on the bandage is given by final compression effect on the body. Deformation of structure and increasing of woven fabric porosity are given by these forces. This study aims to analyze the effect of applied load as a function of bandage extension and weave angle on woven CB structure and porosity for both two- and three-layer systems at ankle and mid-calf positions, as illustrated in Figures 2–6. CB applied with spiral 50% overlap technique will overlay the leg with two layers of bandage, whereas CB applied with 66% overlap will result in three layers of bandage [22].
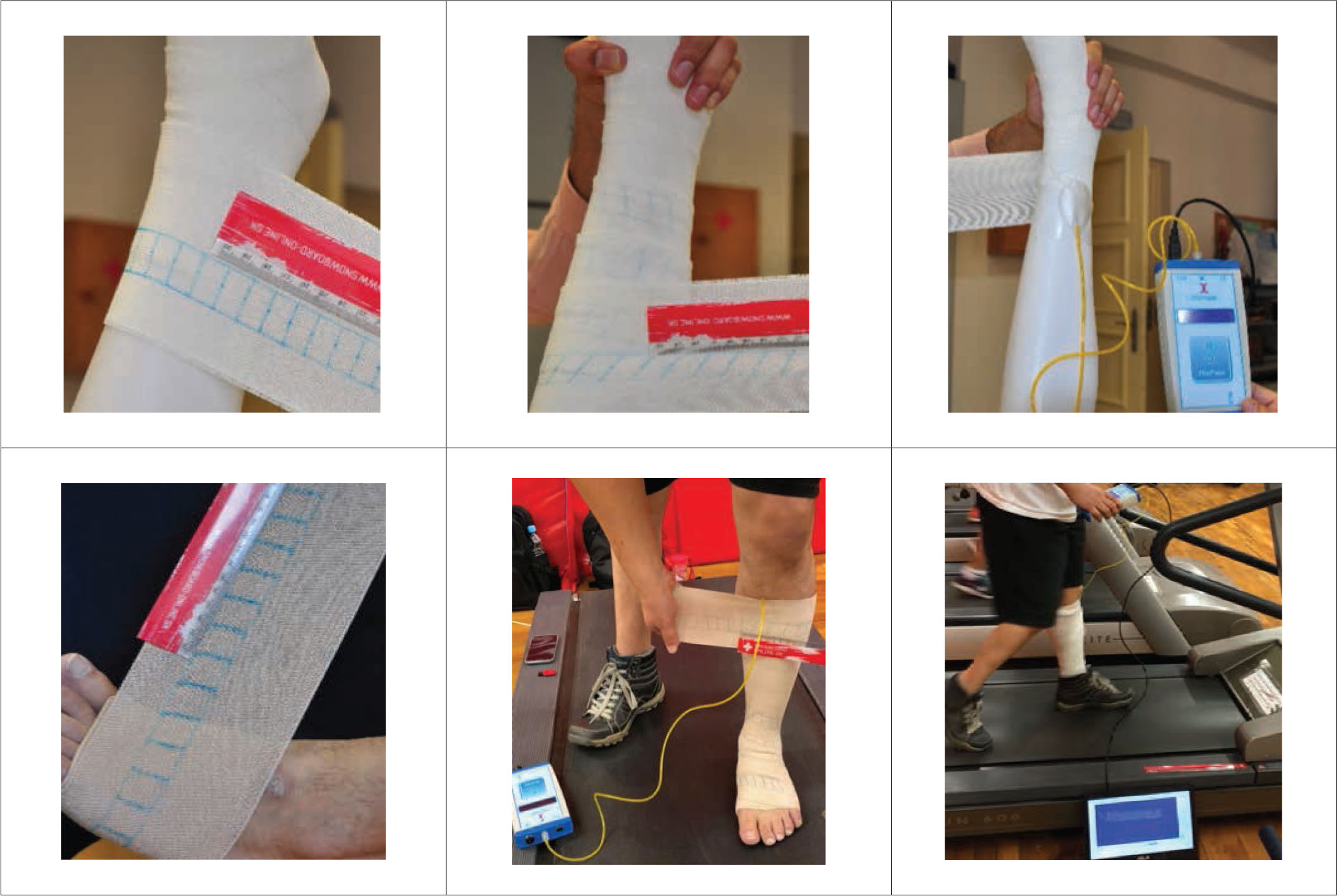
Application of CB on mannequin and real leg. CB, compression bandage
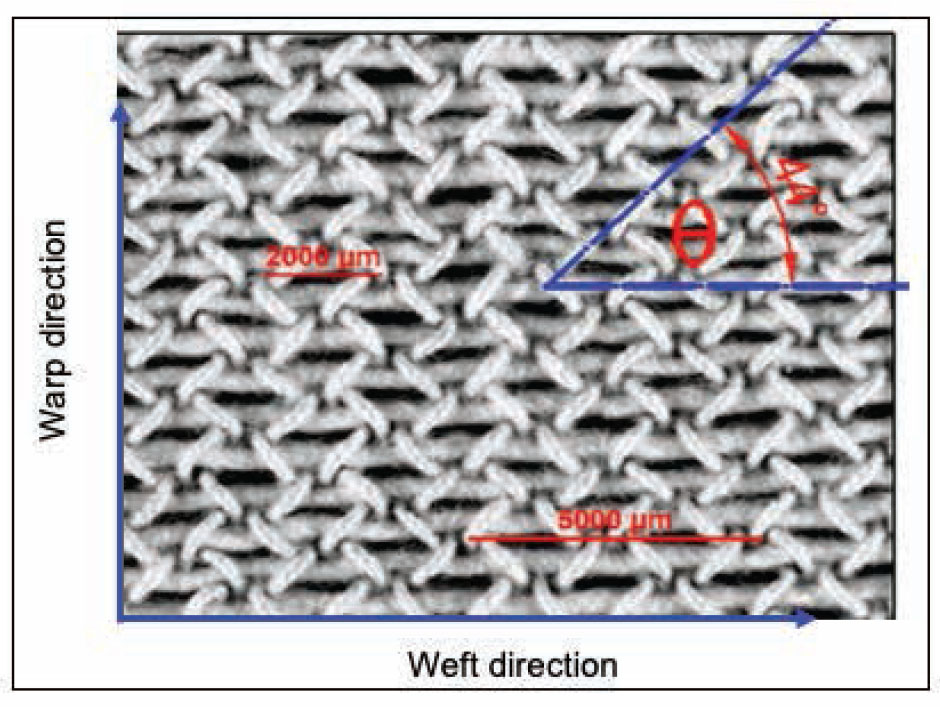
Measurement of weave angle (θ)
Relationship between extension, weave angle, and porosity for cotton bandage
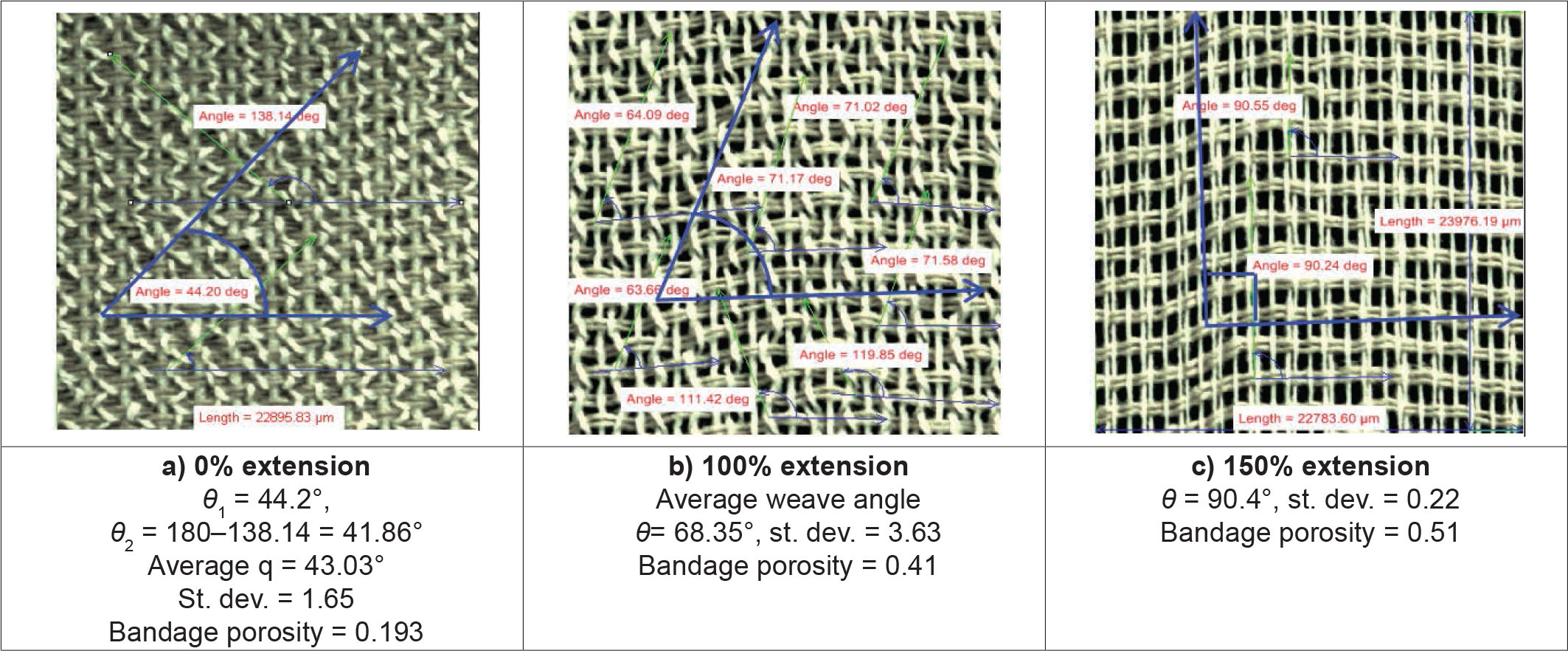
Relationship between extension, weave angle, and porosity for cotton/polyamide/polyurethane bandage

Relationship between extension, weave angle, and porosity for viscose/polyamide bandage
2 Experimental work
2.1 Materials
Three types of woven CBs were used for the analysis of bandage behavior during mechanical stress and compression pressure measuring. These bandages were produced according to the specifications given in Figure 7.

Characteristics of woven compression bandage; OE, open end
2.2 Testing procedure
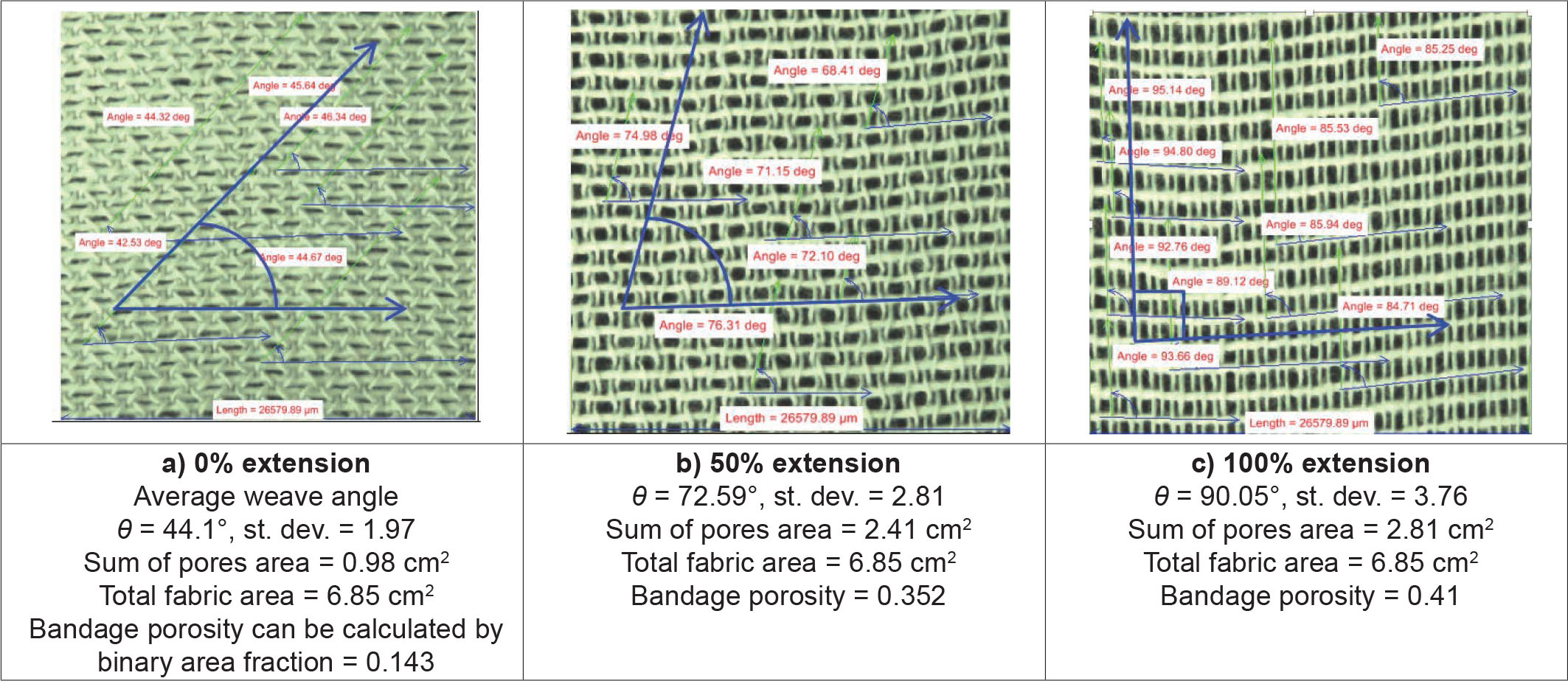
Uniaxial stress and tensile force are a priority for the application of CB and the creation of optimal compression effect. CB loading–unloading is evaluated according to the standard test method ISO 13934-1:1999(E) [23]. Testometric M350-5CT was used to measure the tension developed in the bandage during extension to its end of elasticity using constant traverse speed of 100 mm/min. The device gage length was set to 200 mm, and the load cell of 100 N was used. High-speed camera was used during mechanical stress for the analysis of structure deformation and changing of woven bandage porosity during different extensions, as illustrated in Figure 8. Based on this method, it is possible to predict the corresponding bandage porosity given by tension along CB. The influence of CB structure was tested for three basic types of woven CBs (Figures 4–6).

Setup of Testometric M350-5CT instrument and high-speed camera
The same three types of bandages were worn on both mannequin model and real leg to test and analyze the effect of woven CB extension and porosity on bandage pressure at ankle and mid-calf position in both static and walking conditions. Recalculations of tensile force based on a specified extension range during bandage application are illustrated. Practical bandage pressure is measured using PicoPress tester, which gives both digital readings and graphical charts. The ankle and calf positions were adjusted to leg circumference of 21.4 and 32.4 cm, respectively, for mannequin model, and 25.6 and 38.9 cm, respectively, for real leg as shown in Figure 2.
It is possible to predict the final compression effect as a function of bandage pressure. For the validation of pressure given by woven CBs, the measured results using PicoPress were compared with theoretical compression forces calculated by Laplace's law equations (4, 5) as follows [24, 25, 26]:
The level of pressure exerted on a medical device matches with the Laplace's equation stating that the pressure (P is expressed in Pascal) of a compression applied to the skin surface is directly proportional to the tension (T in Newton) of the compression material and number of layers and inversely proportional to the radius of curvature (R in meter) of limb surface to which it is applied and the bandage width (W in meter) [27].
Prediction of fabric properties is based on a combination of mathematical modeling and experimental research, including development and application of nonstandard methods for the definition and measuring of the fabric structure [28]. One of the main aims of this study is to analyze the relationship between applied tensions and weave angle, given by the changing of bandage porosity. During mechanical stress test, we can illustrate the fabric porosity as a function of weave angle (equation 6 and Figure 3).
where S is the fabric porosity and θ is the weave angle.
3 Results and discussions
3.1 Loading–unloading uniaxial test for woven CBs
When the three bandage types were subjected to uniaxial stress at full extension (i.e., closer to end point of elasticity), CO-PA-PU bandage achieved approximately 300 N at 200% extension, whereas VI-PA and cotton bandages had 280 and 750 N at 150% extension, respectively. These results confirm the highest elasticity and comfort properties of the CO-PA-PU bandage compared with 100% cotton bandage. Figure 9 illustrates that all bandage samples recovered its original length after relaxation. This elastic recovery is due to the optimum extensibility of bandages in elasticity zone; moreover, there is no dwell time while stretching the CB samples. But when these bandages are worn or wrapped on human body, there will be a bit residual deformation due to higher applied bandage tension and longer treatment time.
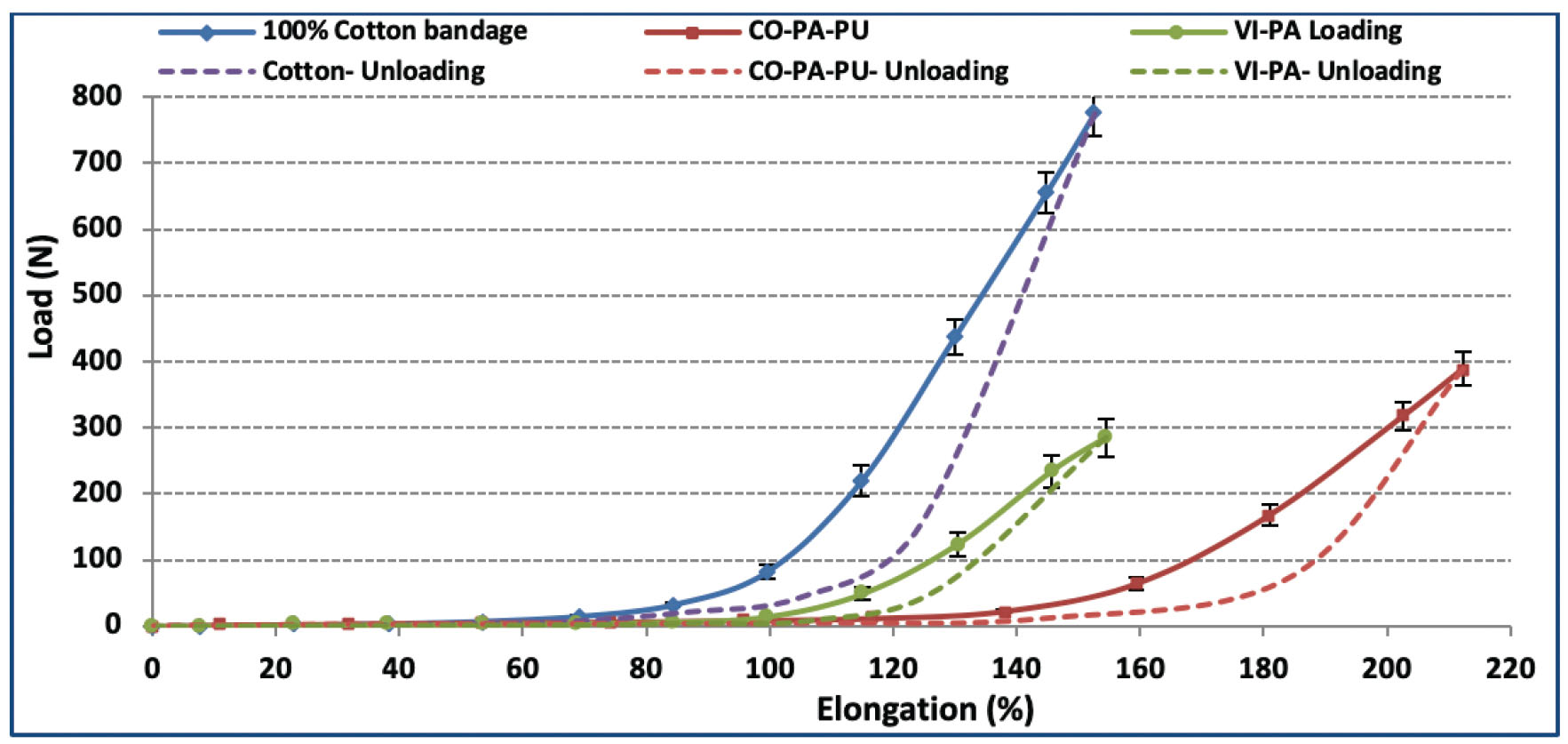
Loading–unloading curves for cotton, cotton/polyamide/polyurethane, and viscose/polyamide bandages
3.2 Optimum fabric tension for woven CBs
As the optimum required bandage tension is approximately 10 N, that value is achieving the required bandage pressure (4,000 Pa or 30 mmHg) according to Laplace's equation (4) for two-layer bandaging at radius 5 cm and bandage width 10 cm. Figure 10 confirms that CO-PA-PU and VI-PA bandages require 110% and 92% extension, respectively, while cotton bandage requires only 60% extension to achieve the required bandage tension 10 N (Table 1). The cotton bandage extension depends on the highly twisted plied yarns (1,200 turns/m) that enables to achieve the required bandage stretch, but these bandages have lower extension compared with CO-PA-PU that contains a 6% of elastomeric filament (polyurethane) which gives higher extensibility. Although the VI-PA bandage consists of two types of yarns having different thermal and melting points, in which case the stretch is given by steaming then heat setting at the required percent of shrinkage.
Optimum fabric tension for cotton, cotton/polyamide/polyurethane, and viscose/polyamide bandages
Effect of bandage extension on applied tension and pressure
| Calculated Laplace's pressure (mmHg) | ||||||
|---|---|---|---|---|---|---|
| Extension (%) | Applied tension (N) | Ankle position | Mid-calf position | |||
| Two layers | Three layers | Two layers | Three layers | |||
| Cotton bandage | 40 | 4 | 14.74 | 22.11 | 9.69 | 14.54 |
| 50 | 6 | 22.11 | 33.17 | 14.54 | 21.81 | |
| 60 | 10 | 36.86 | 55.28 | 24.23 | 36.35 | |
| 70 | 13 | 47.91 | 71.87 | 31.50 | 47.25 | |
| VI-PA bandage | 50 | 3.5 | 12.90 | 19.35 | 8.48 | 12.72 |
| 75 | 7 | 25.80 | 38.70 | 16.96 | 25.44 | |
| CO-PA-PU bandage | 50 | 4.5 | 16.58 | 24.88 | 10.90 | 16.36 |
| 100 | 9.5 | 35.01 | 52.52 | 23.02 | 34.53 | |
CO-PA-PU, cotton/polyamide/polyurethane; VI-PA, viscose/polyamide
3.3 Effect of bandage structure and weave angle on bandage porosity
The factors affecting bandage porosity such as warp and weft yarn count, density, twist, CF, and fabric structure are changing during bandage extension. The main variable during bandage application is the applied tension to achieve the required compression. Figures 4–6 confirm that bandage porosity is significantly increased by increasing weave angle and bandage extension. Statistical analysis of the obtained results using linear regression (ANOVA) concluded that the bandage extension and type have significant effect on weave angle (sig.P = 0 < 0.05; Table 2). Moreover, the combined effects of bandage type and extension are significantly influencing the bandage porosity (P = 0 < 0.05) as listed in Table 3.
Statistical analysis of the relationship between bandage extension and weave angle
| ANOVAa | ||||||
|---|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean square | F | Sig. | |
| 1 | Regression | 16,175.052 | 1 | 16,175.052 | 343.050 | 0.000b |
| Residual | 2,027.478 | 43 | 47.151 | |||
| Total | 18,202.530 | 44 | ||||
| 2 | Regression | 16,574.873 | 2 | 8,287.437 | 213.849 | 0.000c |
| Residual | 1,627.657 | 42 | 38.754 | |||
| Total | 18,202.530 | 44 | ||||
- a
Dependent variable: weave angle.
- b
Predictors: (constant), extension.
- c
Predictors: (constant), extension, bandage type
Statistical analysis of the relationship between bandage type, extension, and porosity
| ANOVAa | ||||||
|---|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean square | F | Sig. | |
| 1 | Regression | 0.702 | 1 | 0.702 | 89.393 | 0.000b |
| Residual | 0.338 | 43 | 0.008 | |||
| Total | 1.040 | 44 | ||||
| 2 | Regression | 0.987 | 2 | 0.493 | 391.993 | 0.000c |
| Residual | 0.053 | 42 | 0.001 | |||
| Total | 1.040 | 44 | ||||
- a
Dependent variable: porosity.
- b
Predictors: (constant), extension.
- c
Predictors: (constant), extension, bandage type
3.4 Comparison between calculated pressure and measured compression using PicoPress
Hundred percent cotton, VI-PA, and CO-PA-PU bandages were worn one by one on real leg to test the real compression pressure at ankle and mid-calf position in both static and walking conditions at different extension levels. Ankle and calf positions were adjusted at leg circumference of 25.6 and 38.9 cm, respectively. Deviation percent was calculated as the difference between measured compression using PicoPress and calculated pressure by Laplace's equation, as listed in Tables 4 and 5.
Calculated pressure by Laplace's equation vs. measured compression at ankle position using PicoPress (R = 4.07 cm)
| Bandage type | No. of layers (wraps) | Extension (%) | Measured compression using PicoPress (mmHg) | Calculated pressure values (mmHg) | |||
|---|---|---|---|---|---|---|---|
| Laplace's equation | Deviation percent | Al Khaburi's equation | Deviation percent | ||||
| 100% cotton | 2 | 40 | 13.98 | 14.74 | 5.16 | 14.43 | 3.12 |
| 50 | 20.98 | 22.11 | 5.11 | 21.65 | 3.09 | ||
| 60 | 31.8 | 36.86 | 13.73 | 36.08 | 11.86 | ||
| 70 | 41.75 | 47.91 | 12.86 | 46.90 | 10.98 | ||
| 3 | 40 | 20.21 | 22.11 | 8.59 | 21.33 | 5.25 | |
| 50 | 27.8 | 33.17 | 16.19 | 32.00 | 13.13 | ||
| 60 | 44.31 | 55.28 | 19.84 | 53.33 | 16.91 | ||
| 70 | 56.91 | 71.87 | 20.82 | 69.33 | 17.91 | ||
| VI-PA | 2 | 50 | 12.47 | 12.9 | 3.33 | 12.62 | 1.19 |
| 75 | 24.34 | 25.8 | 5.66 | 25.24 | 3.57 | ||
| 3 | 50 | 20.95 | 19.35 | −8.27 | 18.80 | −11.44 | |
| 75 | 37.24 | 38.7 | 3.77 | 37.60 | 0.96 | ||
| CO-PA-PU | 2 | 50 | 16.61 | 16.58 | −0.18 | 16.23 | −2.34 |
| 100 | 32.1 | 35.01 | 8.31 | 34.27 | 6.33 | ||
| 3 | 50 | 26.06 | 24.88 | −4.74 | 24.00 | −8.58 | |
| 100 | 43.43 | 52.52 | 17.31 | 50.66 | 14.27 | ||
CO-PA-PU, cotton/polyamide/polyurethane; VI-PA, viscose/polyamide
Relationship between measured compression and bandage extension, number of layers, and bandage type at ankle position
| Coefficientsa | ||||||
|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | ||||
| B | Standard error | Beta | t | Sig. | ||
| 1 | (Constant) | 9.038 | 2.170 | 4.165 | 0.000 | |
| Extension | 10.199 | 0.970 | 0.840 | 10.509 | 0.000 | |
| 2 | (Constant) | −6.497 | 2.266 | −2.867 | 0.006 | |
| Extension | 10.199 | 0.606 | 0.840 | 16.839 | 0.000 | |
| No. of layers | 10.357 | 1.211 | 0.427 | 8.550 | 0.000 | |
| 3 | (Constant) | −17.745 | 1.773 | −10.011 | 0.000 | |
| Extension | 11.886 | 0.394 | 0.979 | 30.157 | 0.000 | |
| No. of layers | 10.357 | 0.703 | 0.427 | 14.731 | 0.000 | |
| Bandage type | 4.499 | 0.475 | 0.307 | 9.465 | 0.000 | |
- a
Dependent variable: measured compression using PicoPress
The obtained results in Table 4 confirm that there is a significant deviation when applying Laplace's equation for two- and three-layer bandaging ranging from ±0.18% to ±20.82%. Although Jawad Al Khaburi developed equation (7) to include the increase in limb circumference due to multilayer bandaging, the equation has improved the deviation range from ±0.96% to ±17.91% as follows [28, 29]:
where
Results of Table 6 conclude that the deviation when applying Laplace's equation for mid-calf position is ranging from ±0.74% to ±11.87%, while the deviation range of Al Khaburi's equation is ranging from ±0.84% to ±10.10%.
Pressure and compression values at mid-calf position (R = 6.19 cm)
| Bandage type | No. of layers (wraps) | Extension (%) | Measured compression using PicoPress (mmHg) | Calculated pressure values (mmHg) | |||
|---|---|---|---|---|---|---|---|
| Laplace's equation | Deviation percent | Al Khaburi's equation | Deviation percent | ||||
| 100% cotton | 2 | 40 | 9.5 | 9.69 | 1.96 | 9.54 | 0.42 |
| 50 | 13.21 | 14.54 | 9.15 | 14.31 | 7.69 | ||
| 60 | 23.08 | 24.23 | 4.75 | 23.85 | 3.23 | ||
| 70 | 32.75 | 31.50 | −3.97 | 31.00 | −5.65 | ||
| 3 | 40 | 13.21 | 14.54 | 9.15 | 14.20 | 6.97 | |
| 50 | 20.42 | 21.81 | 6.37 | 21.30 | 4.13 | ||
| 60 | 32.77 | 36.35 | 9.85 | 35.49 | 7.66 | ||
| 70 | 42.21 | 47.25 | 10.67 | 46.14 | 8.52 | ||
| VI-PA | 2 | 50 | 8.21 | 8.48 | 3.18 | 8.36 | 1.79 |
| 75 | 15.67 | 16.96 | 7.61 | 16.72 | 6.28 | ||
| 3 | 50 | 12.24 | 12.72 | 3.77 | 12.47 | 1.84 | |
| 75 | 22.42 | 25.44 | 11.87 | 24.94 | 10.10 | ||
| CO-PA-PU | 2 | 50 | 9.83 | 10.90 | 9.82 | 10.73 | 8.39 |
| 100 | 22.85 | 23.02 | 0.74 | 22.66 | −0.84 | ||
| 3 | 50 | 17.4 | 16.36 | −6.36 | 15.97 | −8.95 | |
| 100 | 32.89 | 34.53 | 4.75 | 33.72 | 2.46 | ||
CO-PA-PU, cotton/polyamide/polyurethane; VI-PA, viscose/polyamide
3.5 Effect of bandage extension on its porosity
Figure 11 ensures the direct relationship between bandage extension and its porosity. Hundred percent cotton bandage achieved the porosity of 0.35, 0.41, and 0.47 at the extension of 50%, 100%, and 150%, respectively, whereas CO-PAPU reached 0.29, 0.41, and 0.5; moreover, VI-PA bandage achieved 0.45, 0.58, and 0.67, respectively (Table 8).
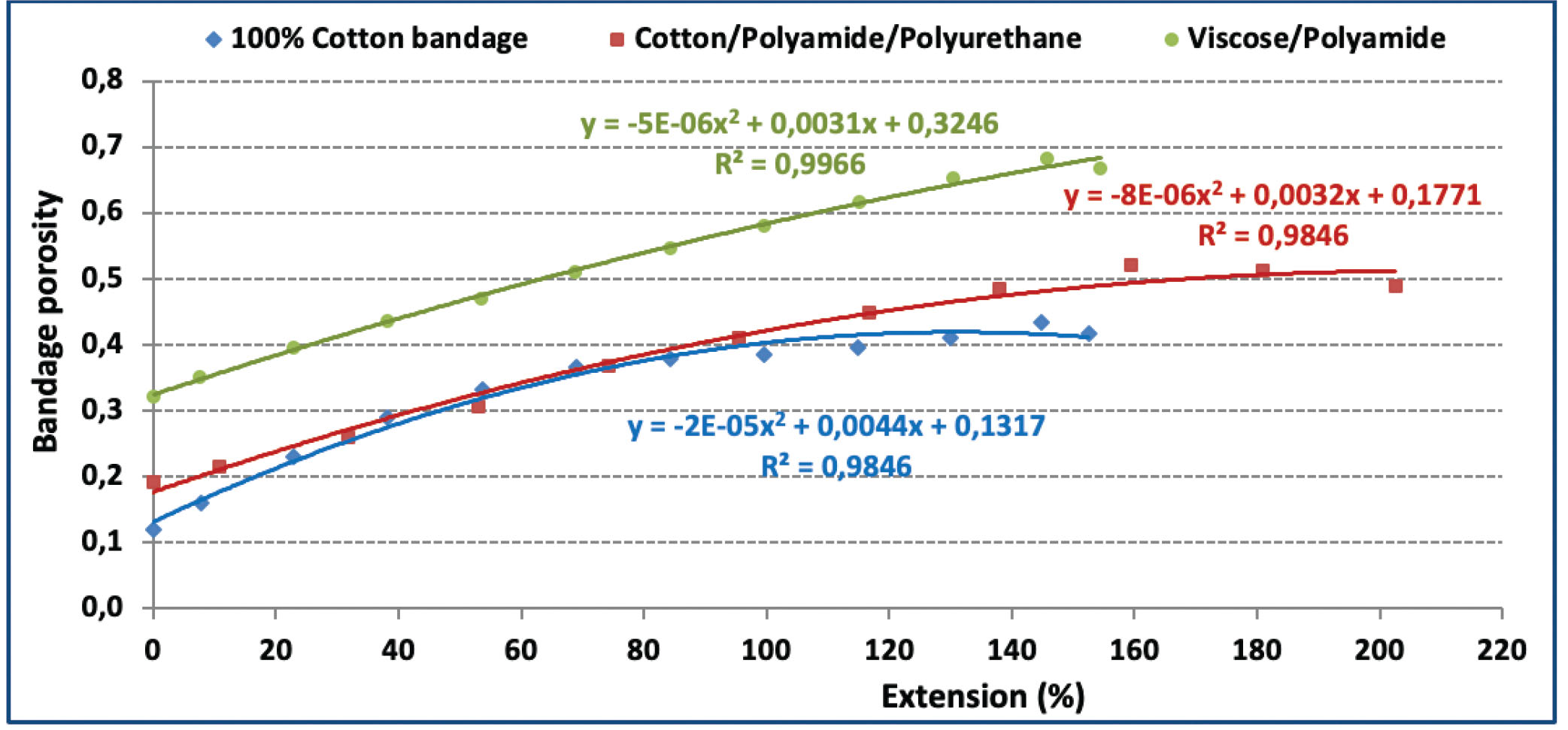
Effect of bandage extension on its overall porosity
Statistical analysis of measured compression at mid-calf position
| Coefficientsa | ||||||
|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | ||||
| B | Standard error | Beta | t | Sig. | ||
| 1 | (Constant) | 3.619 | 1.626 | 2.225 | 0.031 | |
| Extension | 8.461 | 0.727 | 0.864 | 11.632 | 0.000 | |
| 2 | (Constant) | −7.343 | 1.849 | −3.971 | 0.000 | |
| Extension | 8.461 | 0.494 | 0.864 | 17.123 | 0.000 | |
| No. of layers | 7.308 | 0.988 | 0.373 | 7.394 | 0.000 | |
| 3 | (Constant) | −15.558 | 1.714 | −9.077 | 0.000 | |
| Extension | 9.694 | 0.381 | 0.990 | 25.436 | 0.000 | |
| No. of layers | 7.308 | 0.680 | 0.373 | 10.750 | 0.000 | |
| Bandage type | 3.286 | 0.460 | 0.278 | 7.149 | 0.000 | |
- a
Dependent variable: measured compression using PicoPress.
Statistical analysis of the relationship between bandage extension and porosity
| Coefficientsa | ||||||
|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | ||
| B | Standard error | Beta | ||||
| 1 | (Constant) | 0.214 | 0.018 | 11.626 | 0.000 | |
| Extension | 0.030 | 0.002 | 0.764 | 12.190 | 0.000 | |
| 2 | (Constant) | 0.152 | 0.027 | 5.636 | 0.000 | |
| Extension | 0.030 | 0.002 | 0.764 | 12.652 | 0.000 | |
| Bandage type | 0.031 | 0.010 | 0.183 | 3.031 | 0.003 | |
- a
Dependent variable: fabric porosity
3.6 Effect of bandage porosity on corresponding applied tension
Figure 12 illustrates the relationship between binary area fraction – which represents the bandage porosity – and the applied tension. Hundred percent cotton bandage only needs 0.38 porosity (at 60% extension) to achieve the required bandage tension of 10 N, whereas CO-PA-PU and VI-PA bandages require porosity of 0.43 (at 110% extension) and 0.57 (at 92% extension) to reach that tension which is required for optimum compression. Statistical analysis confirmed that there is a significant relationship between bandage porosity and applied tension, as concluded in Table 9.
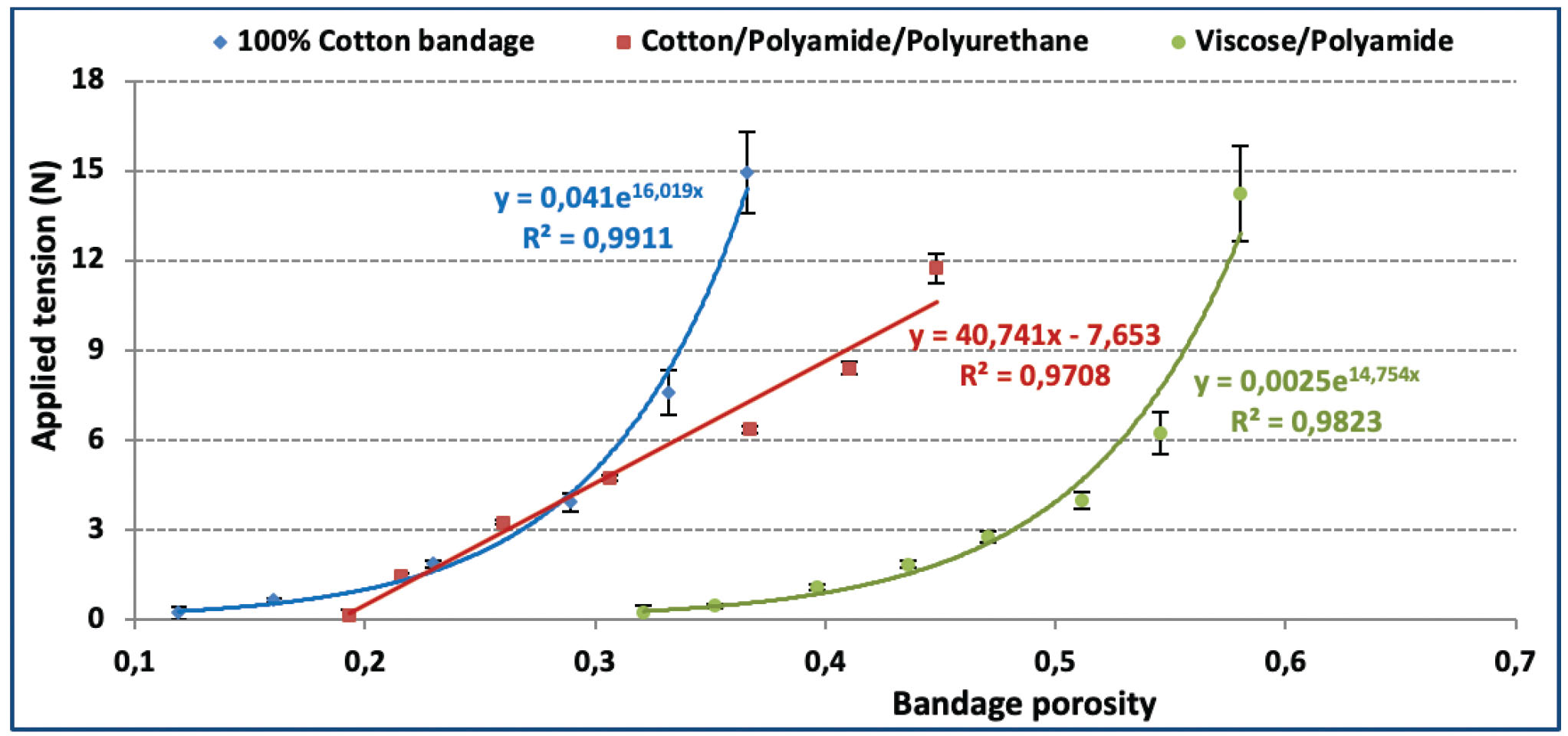
Effect of overall porosity on bandage tension
Statistical analysis of the relationship between bandage porosity and applied tension
| Coefficientsa | ||||||
|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | ||
| B | Standard error | Beta | ||||
| 1 | (Constant) | 47.909 | 12.901 | 3.713 | 0.000 | |
| Bandage type | −13.455 | 5.972 | −0.246 | −2.253 | 0.027 | |
| 2 | (Constant) | 16.351 | 17.269 | 0.947 | 0.347 | |
| Bandage type | −16.533 | 5.877 | −0.302 | −2.813 | 0.006 | |
| Porosity | 100.908 | 38.294 | 0.283 | 2.635 | 0.010 | |
- a
Dependent variable: bandage tension
4 Conclusion
This work analyzed the influence of tensile stress on the woven CB structure and porosity for both ankle and mid-calf positions in static (using mannequin) and dynamic conditions (on human leg while walking). Statistical analysis of the obtained results confirmed that bandage porosity is significantly increased with weave angle and bandage extension. There is a significant deviation when applying Laplace's equation for all the three bandages that reach its maximum level ±20.82% at ankle position compared with practical measured compression by PicoPress. Jawad Al Khaburi developed this equation to include the increase in limb circumference; this assumption decreased the deviation to be ±17.91%. The optimum applied tension is directly proportional to bandage extension and its porosity for all bandage types. Hundred percent cotton bandage only needs 60% extension to achieve the required bandage tension of 10 N, whereas CO-PA-PU and VI-PA bandages require 110% and 92% extension, respectively, to reach that tension which is required for the optimum compression. The obtained results could improve the awareness of patients and nurses to achieve the optimum bandage pressure by adjusting the gradual decreasing applied tension as a function of bandage extension, weave angle, and porosity for both two- and three-layer bandaging techniques.
Acknowledgments
This work is supported by Student Grant Scheme (SGS 21249) by Technical University of Liberec, Czech Republic. I would like to acknowledge the assistance and cooperation of my colleagues (Amany Khalil and Nareerut Jariyapunya), especially during the testing of my samples.
References
[1] Roaldsen, K. S., Elfving, B., Stanghelle, J. K., Mattsson, E. (2012). Effect of multilayer high-compression bandaging on ankle range of motion and oxygen cost of walking. Phlebology, 27(1), 5–12.10.1258/phleb.2011.010084Search in Google Scholar PubMed PubMed Central
[2] Elnashar, E. A. (2005). Volume porosity and permeability in double-layer woven fabrics. AUTEX Research Journal, 5(4), 207–217.10.1515/aut-2005-050404Search in Google Scholar
[3] Lawrence, M., Jiang, Y. (2017). Porosity, pore size distribution, micro-structure. In Bio-aggregates Based Building Materials (pp. 39–71). Springer (Dordrecht).10.1007/978-94-024-1031-0_2Search in Google Scholar
[4] Neckář B., Das, D. (2012). Theory of structure and mechanics of fibrous assemblies (1st ed.). Woodhead Publishing (India).10.1533/9780857093028.1Search in Google Scholar
[5] Nelson E. A., Hillman A., Thomas K. (2014). Intermittent pneumatic compression for treating venous leg ulcers. Cochrane Database of Systematic Reviews, (5). DOI: 10.1002/14651858.CD001899.pub4.Search in Google Scholar PubMed
[6] Agale, S. V. (2013). Chronic leg ulcers: epidemiology, aetiopathogenesis, and management. Ulcers. http://dx.doi.org/10.1155/2013/413604.10.1155/2013/413604Search in Google Scholar
[7] Fletcher, J., et al. (2013). Principles of compression in venous disease: a practitioner’s guide to treatment and prevention of venous leg ulcers. Wounds International. Available: www.woundsinternational.com.Search in Google Scholar
[8] Halfaoui, R., Chemani, B. (2016). New approach to predict pressure produced by elastic textile in the therapeutic treatment of venous leg. Journal of Fundamental and Applied Sciences, 8(2), 297–312.10.4314/jfas.v8i2.9Search in Google Scholar
[9] Al Khaburi, J., Dehghani-Sanij, A. A., Nelson, E. A., Hutchinson, J. (2012). Effect of bandage thickness on interface pressure applied by compression bandages. Medical Engineering and Physics, 34(3), 378–385.10.1016/j.medengphy.2011.07.028Search in Google Scholar PubMed
[10] Cay, A., Atrav, R., Duran, K. (2007). Effects of warp-weft density variation and fabric porosity of the cotton fabrics on their colour in reactive dyeing. Fibres and Textiles in Eastern Europe, 1(60), 91–94.Search in Google Scholar
[11] Rashid, A., Hani, A. (2013). Analysis of woven natural fiber fabrics prepared using self-designed handloom. International Journal of Automotive and Mechanical Engineering. DOI: 10.15282/ijame.8.2013.10.0098.Search in Google Scholar
[12] Gooijer. H. (1998). Flow resistance of textile materials.Search in Google Scholar
[13] Szosland, J., Babska, A., Gasiorowska, E. (1999). Air-penetrability of woven multi-layer composite textiles. Fibres and Textiles in Eastern Europe, 7(1), 34–37.Search in Google Scholar
[14] Gee, N. C. (1953). Cloth setting and setting theories. Textile Manu, 80, 381–384.Search in Google Scholar
[15] Peirce, F. T., Womersley, J. R. (1978). Cloth Geometry. Textile Institute (Manchester, England).Search in Google Scholar
[16] Love, L. (1954). Graphical relationships in cloth geometry for plain, twill, and sateen weaves. Textile Research Journal, 24(12), 1073–1083.10.1177/004051755402401208Search in Google Scholar
[17] Kemp A. (1958). An extension of pierce’s cloth geometry to the treatment of non-circular threads. Journal of the Textile Institute Transactions, 49, 44–49.10.1080/19447025808660119Search in Google Scholar
[18] Hamilton J.B. (1964). A general system of woven-fabric geometry. Journal of the Textile Institute Transactions, 55, 66–82.10.1080/19447026408660209Search in Google Scholar
[19] Weiner, L. (1971). Textile fabric design tables, Technomic (Stamford, USA).Search in Google Scholar
[20] Seyam, A., El-Shiekh, A. (1993). Mechanics of woven fabrics: Part III: critical review of weaveability limit studies. Textile Research Journal, 63(7), 371–378.10.1177/004051759306300701Search in Google Scholar
[21] Valencia, I. C., Falabella, A., Kirsner, R. S., Eaglstein, W. H. (2001). Chronic venous insufficiency and venous leg ulceration. Journal of the American Academy of Dermatology, 44(3), 401–424.10.1067/mjd.2001.111633Search in Google Scholar PubMed
[22] Aboalasaad, A. R. R., Sirková, B. K. (2018). Analysis and prediction of woven compression bandages properties. The Journal of The Textile Institute, 1–7. https://doi.org/10.1080/00405000.2018.1540284.10.1080/00405000.2018.1540284Search in Google Scholar
[23] ISO 13934-1:1999(E): Textiles -Tensile properties of fabrics-Part 1: Determination of maximum force and elongation at maximum force using the strip method.Search in Google Scholar
[24] Schuren, J., Mohr, K. (2008). The efficacy of Laplace’s equation in calculating bandage pressure in venous leg ulcers. Wounds UK, 4(2), 38–47.Search in Google Scholar
[25] Siddique, H. F., et al. (2018). Development of V-shaped compression socks on conventional socks knitting machine. Autex Research Journal. DOI: https://doi.org/10.1515/aut-2018-0014.10.1515/aut-2018-0014Search in Google Scholar
[26] Rimaud, D., Convert, R., Calmels, P. (2014). In vivo measurement of compression bandage interface pressures: the first study. Annals of Physical and Rehabilitation Medicine, 57(6–7), 394–408. Doi: 10.1016/j.rehab.2014.06.005.Search in Google Scholar PubMed
[27] Sirková, B. K., Mertová, I. (2013). Prediction of woven fabric properties using software ProTkaTex. Autex Research Journal, 13(1), 11–16.10.2478/v10304-012-0017-5Search in Google Scholar
[28] Khaburi, J. A., Dehghani-Sanij, A. A., Nelson, A., Hutchinson, J. (2011). The effect of multi-layer bandage on the interface pressure applied by compression bandages. World Academy of Science, Engineering and Technology, 5(6), 1169–1174.10.1109/ICMA.2011.5985672Search in Google Scholar
[29] Chassagne, F., Molimard, J., Convert, R., Giraux, P., Badel, P. (2018). Numerical model reduction for the prediction of interface pressure applied by compression bandages on the lower leg. IEEE Transactions on Biomedical Engineering, 65(2), 449–457.10.1109/TBME.2017.2774598Search in Google Scholar PubMed
© 2020 Abdelhamid R.R. Aboalasaad et al., published by Sciendo
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles in the same Issue
- Fuzzy Logic Method for Predicting the Effect of Main Fabric Parameters Influencing Drape Phenomenon
- The Study on Effects of Walking on the Thermal Properties of Clothing and Subjective Comfort
- A Study on Improving Dyeability of Polyester Fabric Using Lipase Enzyme
- The Impact and Importance of Fabric Image Preprocessing for the New Method of Individual Inter-Thread Pores Detection
- Influence of Tensile Stress on Woven Compression Bandage Structure and Porosity
- Application of Silica Aerogel in Composites Protecting Against Thermal Radiation
- Multicriteria Decision-Making in Complex Quality Evaluation of Ladies Dress Material
- A Study of the Consumption of Sewing Threads for Women's Underwear: Bras and Panties
- Study of the Properties and Cells Growth on Antibacterial Electrospun Polycaprolactone/Cefuroxime Scaffolds
- How High-Loft Textile Thermal Insulation Properties Depend on Compressibility
- Lyocell Fabric Dyed with Natural Dye Extracted from Marigold Flower Using Metallic Salts
- Evolution of Physicochemical Structure of Waste Cotton Fiber (Hydrochar) During Hydrothermal Carbonation
- Analysis of the Thermal Insulation of Textiles Using Thermography and CFD Simulation Based on Micro-CT Models
- Circular Fashion – Consumers’ Attitudes in Cross-National Study: Poland and Canada
Articles in the same Issue
- Fuzzy Logic Method for Predicting the Effect of Main Fabric Parameters Influencing Drape Phenomenon
- The Study on Effects of Walking on the Thermal Properties of Clothing and Subjective Comfort
- A Study on Improving Dyeability of Polyester Fabric Using Lipase Enzyme
- The Impact and Importance of Fabric Image Preprocessing for the New Method of Individual Inter-Thread Pores Detection
- Influence of Tensile Stress on Woven Compression Bandage Structure and Porosity
- Application of Silica Aerogel in Composites Protecting Against Thermal Radiation
- Multicriteria Decision-Making in Complex Quality Evaluation of Ladies Dress Material
- A Study of the Consumption of Sewing Threads for Women's Underwear: Bras and Panties
- Study of the Properties and Cells Growth on Antibacterial Electrospun Polycaprolactone/Cefuroxime Scaffolds
- How High-Loft Textile Thermal Insulation Properties Depend on Compressibility
- Lyocell Fabric Dyed with Natural Dye Extracted from Marigold Flower Using Metallic Salts
- Evolution of Physicochemical Structure of Waste Cotton Fiber (Hydrochar) During Hydrothermal Carbonation
- Analysis of the Thermal Insulation of Textiles Using Thermography and CFD Simulation Based on Micro-CT Models
- Circular Fashion – Consumers’ Attitudes in Cross-National Study: Poland and Canada

